MATLAB作业
matlab整理

作业一:P55:1.在一个MATLAB命令中,6+7i和6+7*i有何区别?i和I有何区别?解:在MATLAB中6+7i是一个复数常量,6+7*i则是一个表达式。
i是虚数单位,而I是单位向量。
4.要产生均值为3,方差为1的500个正态分布的随机序列,写出相应的表达式。
解:y=3+sqrt(1)*randn(500)5.求下列矩阵的对角线元素、上三角矩阵、逆矩阵、行列式的值、秩、迹。
(1) A =1 -12 35 1 -4 23 0 5 211 15 0 9(2) B =0.43 43 2-8.9 4 21解:(1)A=[1,-1,2,3;5,1,-4,2;3,0,5,2;11,15,0,9]主对角元素:D=diag(A)上三角矩阵:B=triu(A)下三角矩阵:C=tril(A)逆矩阵:X=inv(A)行列式的值:E=det(A)秩:F=rank(A)逆:G=trace(A)运行结果:A =1 -12 35 1 -4 23 0 5 211 15 0 9主对角元素:D =1159上三角矩阵:B =1 -12 30 1 -4 20 0 5 20 0 0 9下三角矩阵:C =1 0 0 05 1 0 03 0 5 011 15 0 9逆矩阵:X =-0.1758 0.1641 0.2016 -0.0227 -0.1055 -0.1016 -0.0391 0.0664 -0.0508 -0.0859 0.1516 0.0023 0.3906 -0.0313 -0.1813 0.0281 行列式的值:E =1280秩:F =4逆:G =16(2)B = [0.43,43,2;-8.9,4,21]主对角元素:D=diag(B)上三角矩阵:Y=triu(B)下三角矩阵:C=tril(B)逆矩阵:X=pinv(B)行列式的值:E=det(B)秩:F=rank(B)迹:G= trace(B)运行结果:B =0.4300 43.0000 2.0000-8.9000 4.0000 21.0000主对角元素:D =0.43004.0000上三角矩阵:Y =0.4300 43.0000 2.00000 4.0000 21.0000下三角矩阵:C =0.4300 0 0-8.9000 4.0000 0逆矩阵:X =0.0022 -0.01750.0234 -0.0017-0.0035 0.0405行列式的值:E = 1.2526e+003秩:F=3迹:G =5.43006. 当A=[34,NaN,Inf,-Inf,-pi,eps,0]时,求函数all(A)、any(A)、isnan(A)、isinf(A)、isfinite(A)的值。
MATLAB作业

MATLAB作业⼀、必答题:1. MATLAB系统由那些部分组成?答:MATLAB系统主要由开发环境、MATLAB语⾔、MATLAB数学函数库、图形功能和应⽤程序接⼝五个部分组成。
2. 如何启动M⽂件编辑/调试器?答:在操作界⾯上选择“建⽴新⽂件”或“打开⽂件”操作时,M⽂件编辑/调试器将被启动。
在命令窗⼝中键⼊“edit”命令也可以启动M⽂件编辑/调试器。
3. 存储在⼯作空间中的数组能编辑吗?如何操作?答:存储在⼯作空间的数组可以通过数组编辑器进⾏编辑:在⼯作空间浏览器中双击要编辑的数组名打开数组编辑器,再选中要修改的数据单元,输⼊修改内容即可。
4. 在MATLAB中有⼏种获得帮助的途径?答:在MATLAB中有多种获得帮助的途径:(1)帮助浏览器:选择view菜单中的Help菜单项或选择Help菜单中的MATLAB Help菜单项可以打开帮助浏览器;(2)help命令:在命令窗⼝键⼊“help” 命令可以列出帮助主题,键⼊“help 函数名”可以得到指定函数的在线帮助信息;(3)lookfor命令:在命令窗⼝键⼊“lookfor 关键词”可以搜索出⼀系列与给定关键词相关的命令和函数(4)模糊查询:输⼊命令的前⼏个字母,然后按Tab键,就可以列出所有以这⼏个字母开始的命令和函数。
5. 有⼏种建⽴矩阵的⽅法?各有什么优点?答:(1)以直接列出元素的形式输⼊;(2)通过语句和函数产⽣;(3).在m⽂件中创建矩阵;(4)从外部的数据⽂件中装⼊。
6. 命令⽂件与函数⽂件的主要区别是什么?答:命令⽂件: M⽂件中最简单的⼀种,不需输出输⼊参数,⽤M ⽂件可以控制⼯作空间的所有数据。
运⾏过程中产⽣的变量都是全局变量。
运⾏⼀个命令⽂件等价于从命令窗⼝中顺序运⾏⽂件⾥的命令,程序不需要预先定义,只要依次将命令编辑在命令⽂件中即可。
函数⽂件:如果M⽂件的第⼀个可执⾏⾏以function开始,便是函数⽂件,每⼀个函数⽂件定义⼀个函数。
MATLAB实验练习题(计算机)-南邮-MATLAB-数学实验大作业答案
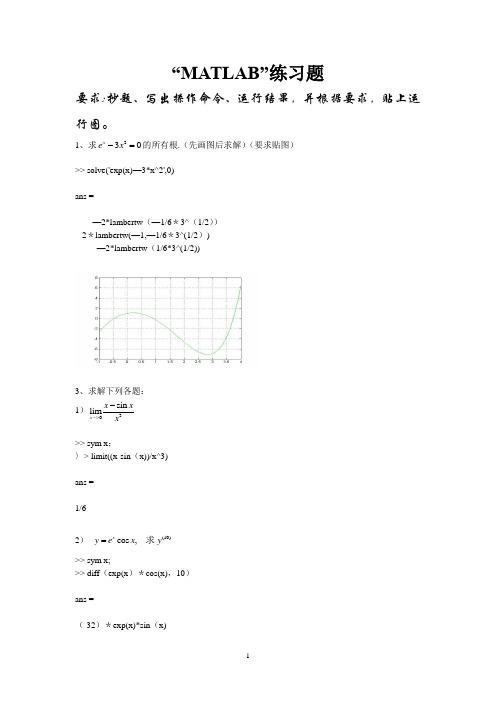
“MATLAB”练习题要求:抄题、写出操作命令、运行结果,并根据要求,贴上运行图。
1、求230x e x -=的所有根.(先画图后求解)(要求贴图)>> solve('exp(x)—3*x^2',0)ans =—2*lambertw (—1/6*3^(1/2))-2*lambertw(—1,—1/6*3^(1/2))—2*lambertw (1/6*3^(1/2))3、求解下列各题:1)30sin lim x x x x ->->> sym x ;〉> limit((x-sin (x))/x^3)ans =1/62) (10)cos ,x y e x y =求>> sym x;>> diff (exp(x )*cos(x),10)ans =(-32)*exp(x)*sin (x)3)21/20(17x e dx ⎰精确到位有效数字)〉〉 sym x;〉〉 vpa((int(exp(x^2),x,0,1/2)),17)ans =0.544987104183622224)42254x dx x+⎰〉> sym x ;>〉 int (x^4/(25+x^2),x)ans =125*atan (x/5) - 25*x + x^3/35)求由参数方程arctan x y t⎧⎪=⎨=⎪⎩dy dx 与二阶导数22d y dx 。
〉> sym t;>> x=log(sqrt (1+t^2));y=atan(t);〉> diff (y ,t )/diff (x ,t)ans =1/t6)设函数y =f (x )由方程xy +e y = e 所确定,求y ′(x ).>> syms x y ;f=x *y+exp(y )—exp (1);〉> -diff(f,x )/diff (f,y)ans =-y/(x + exp (y))7)0sin 2x e xdx +∞-⎰>〉 syms x ;>〉 y=exp(-x)*sin(2*x );〉> int(y ,0,inf )ans =2/58) 08x =展开(最高次幂为)〉> syms xf=sqrt(1+x);taylor(f,0,9)ans =— (429*x^8)/32768 + (33*x^7)/2048 — (21*x^6)/1024 +(7*x^5)/256 - (5*x^4)/128 + x^3/16 - x^2/8 + x/2 + 19) 1sin (3)(2)x y e y =求〉> syms x y ;>〉 y=exp(sin (1/x));>〉 dy=subs (diff(y,3),x ,2)dy =—0.582610)求变上限函数2x x ⎰对变量x 的导数.>> syms a t ;>〉 diff (int(sqrt(a+t),t,x ,x^2))Warning: Explicit integral could not be found 。
MATLB实验作业

实验一MATLAB运算基础1、用逻辑表达式求下列分段函数的值。
t=0:0.5:2.5y=t.^2.*((t>=0)&(t<1))+(t.^2-1).*(( t>=1)&(t<2))+(t.^2-2*t+1).*((t>=2 )&(t<3))2、求[100,999]之间能被21整除的数的个数。
p=rem([100:999],21)==0;sum(p)3、建立一个字符串向量,删除其中的大写字母。
ch='KdDdfKaWdsfCI',k=find(ch>=' A'&ch<='Z'),ch(k)=[]4、输入矩阵,并找出A中大于或等于5的元素。
A=[1 2 3;4 5 6;7 8 9],[m,n]=find(A>=5),for j=1:length(m)x(j)=A(m(j),n(j))xend5、求矩阵的行列式值、逆和特征根。
a11=input('a11='),a12=input('a12 ='),a21=input('a21='),a22=input('a22 ='),A=[a11,a12;a21,a22],DA=det(A),IA=inv(A),EA=eig(A) 6、不采用循环的形式求出和式的数值解。
sum(2.^[0:63])实验二1、1行100列的Fibonacc数组a,a(1)=a(2)=1,a(i)=a(i-1)+a(i-2),用for循环指令来寻求该数组中第一个大于10000的元素,并指出其位置i。
n=100;a=ones(1,n);for i=3:na(i)=a(i-1)+a(i-2);if a(i)>10000a(i),break;end;end,i2、编写M脚本文件,定义下列分段函数,并分别求出当()、()和()时的函数值。
MATLAB与控制系统仿真大作业

>> G1=tf(num,den);
>> G1=zpk(G1)
G1 =
5 (s+0.6) ----------------(s+3) (s+2) (s+1)
>> num=[2 1]; den=[1 2.9 1]; G2=tf(num,den); >> G2=zpk(G2)
G2 =
2 (s+0.5)
>> xlabel('x') ylabel('exp(-2.*x)')
三、simulink 建模(每题 10 分,共 20 分)
1、已知单位负反馈的开环传递函数为 G(s) =
2 s2 + 4s
,试利用
simulink
建立系在单位阶跃输入作用下的模型。
要求答案包括:(1)simulink 建模结构图;
(2)在同一个坐标中的阶跃信号和响应曲线图。
2、已知系统的开环传递函数为
G1(s)
=
2s2 + 5s + 6 s2 + 2s + 3
、G2 (s)
=
s2
s+6 + 7s +1
,H
(s)
=
5(s + 2) s +10
求:建立 Simulink 仿真模型,并求出其系统在单位阶跃响应;
要求答案包括:(1)simulink 建模结构图;
x=
-2.9709
0.5491
3.6000
0.0509
2. 已知下列矩阵
2 3 1
−1 3 5
A
=
MATLAB平时作业(图文版)

MATLAB 平时作业第一章 习题16. 以下两种说法对吗?(1)“MATLAB 的数值表达精度与其指令窗中的数据显示精度相同。
”答:此种说法错误。
MATLAB 提供了控制数据显示格式的控制指format ,该指令并不改变MATLAB 内存中变量的精度,只是改变其显示精度。
(2)“MATLAB 指令窗中显示的数值有效位数不超过7位。
”答:此种说法错误。
当变量小于1000时,使用format 或format short 后,或者默认情况下,变量的显示精度最多不超过7位,但显示精度不等于变量的精度。
7. 想要在MATLAB 中产生二维数组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321S ,下面哪些指令能实现目的? S=[1,2,3;4,5,6;7,8;9]S=[1 2 3;4 5 6;7 8 9]S=[1,2,3;4,5,6;7,8,9] %整个指令在中文状态下输入 答:操作如图:第1、2条指令可以实现,第3条指令不可实现。
第三章 习题31.在MATLAB 中,先运行指令A=magic(3), B=[1,2,1;3,4,3;5,6,7], C=reshape(1:6,3,2)生成阵列33⨯A ,23⨯B ,23⨯C ,然后根据运行结果回答以下问题:运行结果如图:(1)计算A*B, B*A ,这两个乘积相同吗? 计算结果如图:答:不同。
(2)计算A\B, B/A ,左除、右除结果相同吗?计算结果如图:答:不同。
(3)计算B( : ,[1,2]).*C和C.*B( : , [1,2]),这两个乘积相同吗?计算结果如图答:相同。
(4)计算A\A和A.\A,这两个计算结果相同吗?计算结果如图:答:相同。
(5)计算A\eye(3)和inv(A),这两个计算结果相同吗?计算结果如图:答:不同。
(提示:根据对计算结果的目测回答问题)2.在MATLAB中,先运行A=[1, 2; 3, 4],b=0.5,C=[4, 2; 1, 0.5], 然后根据计算结果回答以下问题:创建数据步骤略(1)计算A^b和A.^b, 这两个计算结果相同吗?答:不同。
Matlab习题及答案
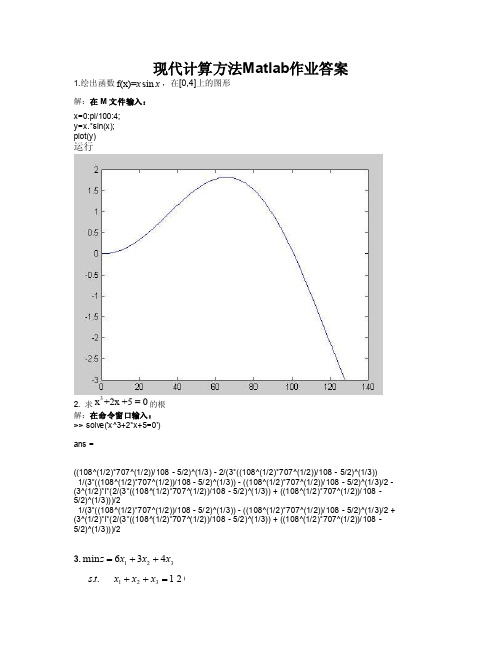
现代计算方法Matlab 作业答案1.绘出函数f(x)=sin x x ,在[0,4]上的图形解:在M 文件输入:x=0:pi/100:4;y=x.*sin(x);plot(y)运行2. 求3x +2x +5 = 0的根解:在命令窗口输入:>> solve('x^3+2*x+5=0')ans =((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3) - 2/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3))1/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)) - ((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)/2 -(3^(1/2)*i*(2/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)) + ((108^(1/2)*707^(1/2))/108 -5/2)^(1/3)))/21/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)) - ((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)/2 +(3^(1/2)*i*(2/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)) + ((108^(1/2)*707^(1/2))/108 -5/2)^(1/3)))/23.321436min x x x z ++=120..321=++x x x t s301≥x5002≤≤x203≥x解:运用单纯形法计算此题,首先把约束条件化成标准形式:,,,,,205030120654321635241321≥=-=+=-=++x x x x x x x x x x x x x x x(1)在M 文件输入SimpleMthd 函数:function [x,minf] = SimpleMthd(A,c,b,baseVector)sz = size(A);nVia = sz(2);n = sz(1);xx = 1:nVia;nobase = zeros(1,1);m = 1;for i=1:nViaif (isempty(find(baseVector == xx(i),1)))nobase(m) = i;m = m + 1;else;endendbCon = 1;M = 0;while bConnB = A(:,nobase);ncb = c(nobase);B = A(:,baseVector);cb = c(baseVector);xb = inv(B)*b;f = cb*xb;w = cb*inv(B);for i=1:length(nobase)sigma(i) = w*nB(:,i)-ncb(i);end[maxs,ind] = max(sigma);if maxs <= 0minf = cb*xb;vr = find(c~=0 ,1,'last');for l=1:vrele = find(baseVector == l,1);if (isempty(ele))x(l) = 0;elsex(l)=xb(ele);endendbCon = 0;elsey = inv(B)*A(:,nobase(ind));if y <= 0disp('不存在最优解!');x = NaN;minf = NaN;return;elseminb = inf;chagB = 0;for j=1:length(y)if y(j)>0bz = xb(j)/y(j);if bz<minbminb = bz;chagB = j;endendendtmp = baseVector(chagB);baseVector(chagB) = nobase(ind);nobase(ind) = tmp;endendM = M + 1;if (M == 1000000)disp('找不到最优解!');x = NaN;minf = NaN;return;endend(2)在命令窗口输入:clear allA=[1 1 1 0 0 0;1 0 0 -1 0 0;0 1 0 0 1 0;0 0 1 0 0 -1];c=[6 3 4 0 0 0];b=[120;30;50;20];[xm,mf]=SimpleMthd(A,c,b,[3 4 5 6])xm =0 50 70mf =4304.计算下面函数在区间(0,1)内的最小值。
matlab作业

matlab作业第一次作业[实验目的]1。
了解并熟悉Matlab,并在此基础上学习基本操作2.掌握Matlab 的基本操作和常用命令3。
了解Matlab常用的函数、运算符和表达式4.掌握Matlab的工作方法和M文件的相关知识5.在Matlab中学习矩阵和数组的运算1,[实验任务]1。
P11:例1_4写一个函数,求方程AX 2+Bx+C = 0的解2.P16: 1。
计算表达式e 12+23 3log25/tan 21.3。
写m命令文件找到?k +?1/k的值是k?1k?15010 4.编写函数文件并计算?k!并找出k=20时表达式的值k?1n3。
例2_2使用函数生成矩阵A =100020003,B = 00200000000104。
例2_3 (1)生成三阶魔方矩阵A;(2)生成一个四阶单位矩阵B 5。
示例2_10数组操作示例6。
例2_11计算sin(k?/2)(k=?2,?1,0)值7。
P27:2。
矩阵A=456,B=556,计算A*B,A.*B,并比较差值789123468323。
已知矩阵A=5,212,B=,计算A>B,A==B,A2)12,【实验步骤和结果】例1 _ 4函数y =洁(A,B,c)如果(绝对值(A)>洁(1,2,2) 9有复数根: >洁(A,B,c)(exp(1)12)+(23 3)* log2(5)/tan(21) ans =21.4426 e+0053。
函数s = J(m)s = 0;k = 1;而k v=[1 2 3] A=diag(v,0) B=diag(v,1)v =1 2 33A =1 0 02 0 03 B =100 000 200 000 300 000A =魔法(3)A =8 1 6 3 5 7 4 9 2> > B =眼睛(4)B =1 0 0 0 0 0 0 0 0 0 0 1例2-11。
a = 1:5 a =1 2 3 4 5> > b = 3:2:11 b =43 5 7 9 11> > a.ans =1 4 9 16 25> > a . * b94 5 6;7 8 9]A =1 2 3 4 5 6 7 8 9> > B =[4 6 8;5 5 6;3 2 2]B = 4 6 8 5 5 6 3 2> > A * Bans =23 22 26 59 61 74 95 100 122> > A . * Bans =4 12 245。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一:应用MATLAB 和工具箱完成以下的内容。
(1)绘制下列函数的二维曲线
32)7.7/()2.3()1(6+-++-=x x x
x x y 并求其3=x 时的值。
(2)求解线性方程组:
⎪⎪⎩⎪⎪⎨⎧=+++=-+-=+++=+-12
2247
32258232432143214321421x x x x x x x x x x x x x x x
(3)求解下列函数的偏导数'y
tan2+
=
y2
+
x
x
x
并绘制)
(y
x
,
f的二维图形
(y
,
x
f及)'
f =(tan((x + (x + (2*x)^(1/2))^(1/2))^(1/2))*((1/(2*x)^(1/2) + 1)/(2*(x +
(2*x)^(1/2))^(1/2)) + 1)*(tan((x + (x + (2*x)^(1/2))^(1/2))^(1/2))^2 + 1))/(x + (x + (2*x)^(1/2))^(1/2))^(1/2)
(4)绘制函数
116
942
22=++z y x 的三维图形,并通过改变观察点来获得该图形在各个坐标平面上的投影。
(5)使用M 函数文件,画出下列分段函数所表示的曲线。
⎪⎩
⎪⎨⎧≤<≤<+=x x x x x y 1100,1,13
同时,在图形中对各段曲线进行标记。
二:写出心得体会;
Matlab心得体会
本学期通过对 MATLAB 的系统环境,数据的各种运算,矩阵的分析和处理,程序设计,绘图,数值计算及符号运算的学习,初步掌握了 MATLAB 的实用方法。
通过理论课的讲解与实验课的操作,使我在短时间内学会使用MATLAB ,同时,通过上机实验,对理论知识的复习巩固实践,可以自己根据例题编写设计简单的程序来实现不同的功能,绘制出比较满意的二维三维图形,在实践中找到乐趣。
MATLAB 是一个实用性很强,操作相对容易,比较完善的工具软件,使用起来比较方便,通过操作可以很快看到结果,能够清晰的感觉到成功与失败,虽然课程中也会出现一些小问题,但是很喜欢这门课程。
在为学习这门课前就听说了他的强大,因为现在的很多模型都是需要这些分析软件的。
它不仅有强大的运算功能,还有强大的绘图功能,虽然学习了有一个学习,但是我对他的了解额仅仅是一点点,或许连入门都谈不上。
因为我学习时了解到一个现实。
就是 matlab 的学习依赖有比较好的数学功底,其中我看最经常运用到的就是矩阵。
我从网上了解到 matlab 是一门高等数学和计算机技术结合的东西,学习它必须具有相应的数学和计算机知识。
然而很可惜。
特别是我今年还是大四。
虽然这学期的学习的时间短暂,就算时间足够,老师也不能把所有的都讲解给我们,因为一个软件的功能需要我们自己不断的去摸索,老师也不可能知道所有。
老师只是个指路人,最终的学习还是要靠自己。
而且在摸索的过程中,我们能够发现和体会学习的快乐。
痛并快乐着是种常态了吧。
自我感觉学习 matlab 与其说是学习一门软件,更不如说是学习一门语言。
用一种数理的语言描述现象,揭示表象下的规律。
此外,我认为 matlab 中的作图功能很强大,不仅简单的函数现象可以明确画出,而且一些点状物,甚至立体图也可以画出。
大一上微积分的时候,老师曾经多次在课件中加入用matlab 画出的图来。
不论是一维二维三维等等,都能很好的画出来。
只要能编写出函数式,在短短的几秒之内,他就会呈现在你眼前。
另外就是图形的直观性,这是由阴影的制作的。
而且可以根据需要,坐标图上加标题,坐标轴标记,文本注释级栅格等,也可以指定图线形式,比如是虚线。
颜色也可以自己来定。
可以在同一张图上画,也可以单个显示。
在学习的过程中,因为以前学过 access 中的 select 语言,觉得就编写这方面是有共性的,但是 matlab 的编程语言似乎更多更复杂一点,这是由于涉及的数学模型,数学公式更多的原因。
可是今年的这门课真的是让我感到没学到什么,估计也是因为我抱着看一看的随意态度来的吧,也没有那种遇到不懂的就一定要弄懂它的决心和毅力。
说什么都是借口了,无法掩饰我没有学好它的事实。
事实上,我觉得今年这门课的重点并不是让我们掌握这种软件的具体用法,而是主要向我们展示如何用它去解决一些金融问题,数学问题。
这点让我很郁闷,因为我不懂得原理,听起来这门课倍感吃力啊。
可是嘛,年轻没有什么不可以,又有谁可以断言我接下来的生活中不能好好学习这个东西为自己的工作,学习,生活,研究兴趣带来方便呢。
从大学开学的见闻到现在学习 MATLAB ,感觉这是一个很好的软件,语言简便,实用性强。
作为一个做新手,想要学习好这门语言,可以说还是比较难的。
在我接触这门语言的这些天,除了会画几个简单的图形,其他的还是有待提高。
从另一个方面也对我们大学生提出了两个要求——充实的课外基础和
良好的英语基础。
在现代,几乎所有好的软件都是来自国外,假如不会外语,想学好是非常难的。
其实想要学习好一们语言,不能只靠老师,关键是自己。
每个人内心深处都是有抵触意识的,不可能把老师的所有都学到。
学习这门语言,不光是学习一种语言,更重要的事学习一种方法,一种学习软件的方法,还有学习的态度。
总结一下,学习任何一门语言:态度决定一切。
不论是英语还是计算机语言。
其实以前上高中的时候接触过这种编程语言,当时记得最头疼的就是循环语句,但是在 matlab 中这种东西用的就比较少了。
语言语句都是很简洁利落的,都是一枪瞄死靶心的那种,很直接,这也让我减轻不少心理负担。
其实学习这种事,与其说学习什么具体的东西,更不如说是学习一种态度,从种种波折中认识到自己的局限性,不足。
心情会沮丧,也会豁然开朗。
光想不练假把式,不论想的再多,不实际运用还是没有用的。
书山有路勤为径,学海无涯苦作舟。
华山再高,顶有过路。
几点对于学好 matlab 很重要:兴趣、悟性、勤奋、坚持。
兴趣,不知道哪位名人说过“兴趣是最好的老师。
”我觉得非常有道理,一个人一旦对某事物有了浓厚的兴趣,就会主动去求知、去探索、去实践,并在求知、探索、实践中产生愉快的情绪和体验。
这样才能主动学习,并且学好到精通。
悟性,通常人认为指顿悟,慧根,我觉得就是对一个问题不断的思索,将自己的体会和感受融合,获得属于自己的知识。
有很多事情、问题,都是可以想明白的。
只有不停的想,才能想明白,想透彻。
勤奋,一勤天下无难事。
从古到今,有多少名人不是有勤奋而得来成功的。
现在的年轻人,一代比一代聪明。
要不被别人淘汰,要超越别人,只有靠时间堆出来。
每天多学一些,多积累一些。
学习 matlab 也一样,想要学会,使用熟练,不花时间练习,写代码,亲自运行调试,是很难掌握好的。
坚持,认准了的事情,就坚持做到底,直到有所收获。
事实上,很多人实现不了自己的目标,很大程度上就是少了一种坚持、非要把事情干到底的精神,他们往往浅尝辄止,因此眼睁睁失去了可能到手的成功。
光有兴趣,只有三分钟的热情是很难成事的。
很多事情的成功取决于踏平坎坷地坚持的毅力。
看准了的事情,如果没有百折不挠的坚持,绝难取得成功。
看准的事情就不屈不挠地坚持干下去直至成功,才是智者的唯一选择。
每一个人都明白所有梦想的实现都需要努力,然而,很多人只所以没有实现心中的梦想,就在于多了空想、犹豫,少了努力坚持。
总而言之,学习MATLAB让我受益匪浅,感谢学校给了我学习的机会,感谢老师的悉心教导。
