最新定轴转动刚体的动能计算
定轴转动刚体的动能计算

我们已知,定轴转动刚体的转动惯量I、角 速度ω分别与直线运动中刚体的质量M、速度v 对应,但教材上并未给出计算刚体旋转动能的 公式。我们猜想刚体的动能是否为
1 2 E k = Iω 2 下面来证明此公式:
设所有刚体均匀,密度为1,则质量和体积 在数值上相等。 考虑半径为R的圆环绕轴线转动:
I = mR 2 = 2πR 3 . 1 1 2 3 2 2 E k = ∫ •Rd θ • (Rω ) = πR ω = Iω . 2 2 0
若圆盘剖面如图,质量向轴集中,则使其转速达 到ω所需的能量就较少。将这种情况应用于吸尘器, 平动摩擦阻力f仍不变。故将底盘质量向轴集中也能节 省动能。 另外,我们可见,调整绕轴线转 动圆盘的质量分布,可以影响能量与 转速的对应关系。将动能(可由电能 转轴 转化而来,而电能容易控制)作输入, 转速作输出,同时对转子的质量分布加以调整;或者 反过来,以转速作输入,能量作输出;这种方法应是 有广阔的应用前景。
v f= µN. ωr
2
C O C’
v
ω
摩擦力集中在上半个月牙形内。
由于滑动摩擦力µN与接触面积无 2v 关,若切去盘中心O半径为 r − ω 的小圆盘,如图易知摩擦力增加
2v 2 ∆f = µN. ωr1
P
2
v
C O C’
Q
ω
其中Δf是区域P、Q的摩擦力, P、Q的圆心分别是C和C’。
在吸尘器模型中,设吸尘器使用距离 为s,采用开孔的底盘,增加了摩擦力, 却减少了驱动底盘转动的能量。当
P
2 v
m小盘 2 2 1 2 µN • • s ≤ ω r1 ω r1 2 v
C O
C’
Q
ω
时,即 了能量的。
3-3 力矩的功 刚体绕定轴转动的动能定理

3.3 力矩的空间累积效应
一 力矩作功 v v dW = F dr = Fτ ds
v v
dθ v
v F τ
v F
= Fτ rdθ
dW = Mdθ
力矩的功 W =
v dr
o
r
x
∫θ
θ2
1
M dθ
2
3.3 力矩的空间累积效应
dW dθ 力矩的功率 二 力矩的功率 P = =M = Mω dt dt v v v v 比较 W = F dr P = F v ∫
13
3.3 力矩的空间累积效应
解 (1) 如图取面 ) 积元ds 积元 = drdl,该面元 , 所受的摩擦力为
v df
df =
mg
πR
2
o
r
dl dr
drdl
R
此力对点o的力矩为
rdf =
mg
πR
2
rd r d l
14
3.3 力矩的空间累积效应
于是,在宽为 的 于是,在宽为dr的 圆环上, 圆环上,唱片所受的摩 擦力矩为
3.3 力矩的空间累积效应
力的时间累积效应: 的时间累积效应: 冲量、动量、动量定理. 冲量、动量、动量定理. 力矩的时间累积效应 的时间累积效应: 力矩的时间累积效应: 角冲量、角动量、角动量定理. 角冲量、角动量、角动量定理. 力的空间累积效应: 力的空间累积效应: 效应 力的功、动能、动能定理. 力的功、动能、动能定理. 力矩的空间累积效应: 力矩的空间累积效应: 效应 力矩的功、转动动能、动能定理. 力矩的功、转动动能、动能定理.
m,l O
v FN
θ mg
10
3.3 力矩的空间累积效应
3.3刚体定轴转动中的功与能

解:以 ω 和 ω 分别表示冲孔前后的飞轮的角速度
1 2
ω = (1 − 0 .2 )ω = 0.8ω
2 1
2
2
2πn ω = = 8πrad ⋅ s 60
1 1
−1
1
1 1 1 由转动动能定理 A = Jω − Jω = Jω (0 .8 − 1) 2 2 2 1 又 J = mr A = −5 .45 × 10 J 2
课后习题 3-8
θ1
θ2
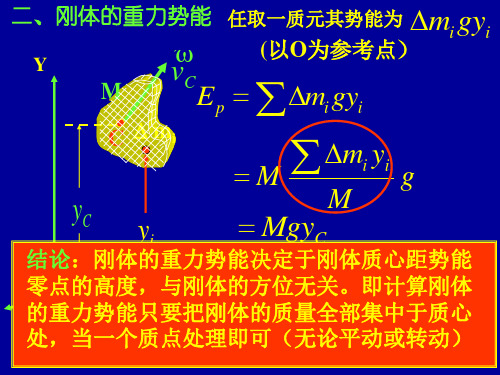
二、刚体的转动动能和重力势能
1.绕定轴转动刚体的动能 绕定轴转动刚体的动能 绕定轴转动刚体的
∆ ,∆ ,⋅⋅⋅,∆ ,⋅⋅⋅,∆ m m m m r r r r r, r ,⋅⋅⋅, r ⋅⋅⋅, r r r r r v ,v ,⋅⋅⋅,v ,⋅⋅⋅,v
1 2 i
1 2 i, N
N
Q = rω v 1 E= ∆ v m 2
2 2 2
1 1
2
3
质量M的圆盘滑轮可绕通过盘心的水平轴转 例3-7半径R质量 的圆盘滑轮可绕通过盘心的水平轴转 半径 质量 滑轮上绕有轻绳,绳的一端悬挂质量为m的物体 的物体。 动,滑轮上绕有轻绳,绳的一端悬挂质量为 的物体。 当物体从静止下降距离h时 物体速度是多少? 当物体从静止下降距离 时,物体速度是多少? 以滑轮、 解:以滑轮、物体和地球组成系统为研究对 由于只有保守力做功,故机械能守恒。 象。由于只有保守力做功,故机械能守恒。 设终态时重力势能为零 初态:动能为零,重力势能为mgh 初态:动能为零,重力势能为 末态: 末态:动能包括滑轮转动动能和物体平动动能 由机械能守恒
i i
i i i
2
1
2
i
N
刚体的定轴转动定律

刚体的定轴转动定律1. 介绍刚体是物理学中的一个重要概念,它指的是在运动过程中形状和大小保持不变的物体。
刚体的定轴转动定律是描述刚体绕固定轴线转动的规律和性质,对于我们理解刚体的运动和应用相关物理问题具有重要意义。
2. 刚体的转动惯量2.1 定义刚体绕轴线转动时,其转动惯量是衡量刚体抵抗转动运动的特性。
转动惯量的大小取决于刚体的质量分布以及轴线的位置和方向。
2.2 转动惯量的计算方法转动惯量可以通过积分计算得到,对于一个质量为m的刚体,其转动惯量可以用以下公式表示: [ I = r^2 dm ] 其中,r是质量元dm到转轴的距离。
对于一些常见的简单形状的刚体,转动惯量可以通过一些公式直接计算得到,例如:- 细杆绕直线轴线转动:[ I = mL^2 ] - 球体绕直径轴线转动:[ I = MR^2 ] - 圆环绕直径轴线转动:[ I = MR^2 ]3. 定轴转动的角动量3.1 定义角动量是描述物体转动的物理量,刚体的角动量可以通过转动惯量和角速度的乘积得到。
3.2 角动量的守恒对于一个孤立系统,如果没有外力矩作用,刚体的角动量将保持不变,这就是角动量守恒定律的内容。
3.3 角动量定理角动量定理描述了外力矩对刚体角动量的影响,它可以表示为以下公式: [ = ] 其中,()是作用在刚体上的外力矩,(L)是刚体的角动量。
4. 牛顿第二定律与角加速度4.1 牛顿第二定律牛顿第二定律描述了刚体转动的加速度与作用力的关系,其公式为: [ = I] 其中,()是作用在刚体上的合外力矩,(I)是刚体的转动惯量,()是刚体的角加速度。
4.2 角加速度的计算对于旋转轴与力矩不垂直的情况,我们可以通过以下公式计算刚体的角加速度:[ = ] 其中,()是力矩与旋转轴之间的夹角。
5. 定轴转动的动能5.1 定义刚体的转动动能是由于其转动而具有的能量,它可以通过转动惯量和角速度的平方的乘积得到。
5.2 动能定理动能定理描述了外力对刚体转动动能的影响,它可以表示为以下公式: [ W = K ] 其中,(W)是作用在刚体上的合外力所做的功,(K)是刚体的转动动能。
3.刚体的定轴转动

2 3 2
2
6.16 10
3
2
3.14 m / s
2
2
6.16 10 m / s
例3-2:一飞轮在时间t 内转过角度 at bt 3 ct 4式中a、b、c都 是常量。求它的角加速度。 解:飞轮上某点的角位置可用θ 表示为: at bt 3 ct 4 将此式对t 求导数,即得飞轮角速度的表达式为:
O
刚体定轴转动的描述
(1) 定轴转动的角量描述
角位置: (t )
角位移: (t ) (t 0 ) 角速度:
d dt d
dt d
2
角加速度:
dt
2
角速度和角加速度均为矢量,定轴转动中其方向沿转轴的
方向并满足右手螺旋定则。
说明:在刚体的定轴转动中加速度、角加速度和角位移通常用 代数量表示。通常规定:当刚体作逆时针转动时,这些角量均 取正值;反之,取负值。
观察圆盘O和圆盘上一点P的运动:
O点的运动:沿着直线向前移动 圆盘上其他点的运动:除向前移动外,还绕圆盘中心O且垂直于盘面的轴转动。
1.刚体的平动:在运动过程中,若刚体上任意一条直线在各个时 刻的位置始终彼此平行,则这种运动叫做平动。
特点:刚体内所有点具有相同的位移、速度和加速度。 --刚体上任一点的运动规律即代表刚体的平动规律。
2
2
则整个刚体的转动动能为:
Ek
1 2
m i vi
2
1 2
m i ri
2
2
1 2
J
2
二、 力矩的功和功率
1.力矩的功
定轴转动刚体的动能计算

其中
包含刚体质心系中刚体的动能,这里不再推了。
成立。
这便证明了刚体定轴转动的动能 ω:8π(4Hz)
r1:0.
2.由
可知,既然能量是线性的,定轴转动的刚体的转动惯量也是线性的。
故将底盘质量向轴集中也能节省动能。
将动能(可由电能
公式。 转化而来,而电能容易控制)作输入,
转速作输出,同时对转子的质量分布加以调整; 《力学》,杨维纮,中国科学技术大学04级理学院教材。
❖ 本幻灯片参考材料:
《力学》,杨维纮,中国科学技术大学04级理 学院教材。
其他便没有了。限于客观原因,作者并没有准备 充分资源。日后若条件允许,也许能做出更有价 值的成果。
版权所有,商用付酬。
❖ 本文拟得出定轴转动下刚体 的动能表达式,并讨论教材例6.4 中电熨斗模型的改良及其他一些 简单应用。
参考系下“所有”的动能。若转轴亦运动, 这便证明了刚体定轴转动的动能公式。
若转轴亦运动,求刚体的总动能只需再加上刚体关于轴速度的动能,即
求刚体的总动能只需再加上刚体关于轴速 4中我们知半径r、自转角速度ω、平动速度v<< ω 、滑动摩擦系数μ、对地面压力N的圆盘受阻力
由于滑动摩擦力μN与接触面积无关,若切去盘中心O半径为 的小圆盘,如图易知摩擦力增加
体的动能为
E kB E kA 1 2M A 2B r2(rA是 BA距 B)离 .
4.由分析2及正交轴定理可求出刚体 作定点转动的动能公式:
E k O E k x E k y E k z 1 2 I xx 2 I yy 2 I zz 2 .
5.由分析1~4可得刚体作任意运动 的一般的动能公式:
度的动能,即 2.由
可知,既然能量是线性的,定轴转动的刚体的转动惯量也是线性的。
刚体定轴转动的功和能

(解毕 )
· 10 ·
Chapter 4. 刚体的转动
§4. 5 刚体定轴转动的功和能
五、刚体的机械能守恒
当系统中只有保守力作功,系统的机械能守恒:
E0 E
其中 E
m ,l
l 2
1 mv 2 1 J 2 2 2
C
mgh 1 kx 2 2
滑轮(R, M),m从静止开始下落,求下落 h 时物体的速 度及加速度。 系统 = 弹簧 + 滑轮 + 物体 + 地球: 提示: 机械能守恒
k
M ,R
2mgh kh 2 答案: v m M / 2
m
2(mg kh) a 2m M
ቤተ መጻሕፍቲ ባይዱ
减速、加速?
h
· 13 ·
Chapter 4. 刚体的转动
三、刚体绕定轴转动的动能定理
W Md
0
M J J d dt
d ω 0 J dt d 0 J d
·4 ·
Chapter 4. 刚体的转动
§4. 5 刚体定轴转动的功和能
1 1 2 2 积分得: W J J 0 2 2
1 2 [定义] 刚体转动动能: E k J 2 1 1 2 2 W J J 0 E k E k 0 E k 2 2
mg
前例 已知:匀质细杆 (m,l ),光滑轴,从竖直位置静 止摆下,求细杆摆到θ 位置时的角速度。
· 11 ·
Chapter 4. 刚体的转动
§4. 5 刚体定轴转动的功和能
解:以杆、地球为一系统,则系统机械能守恒:
刚体的能量定轴转动的动能定理
三、转动动能
刚体绕定轴以角速度旋转 刚体的动能应为各质元动能之 和为此将刚体分割成很多很小的
r i vi mi
M
质元 m1, m2 mi mn
r 任取一质元 mi 距转轴 i ,则该质元动能:
mivi2 / 2 mi (ri)2 / 2 miri22 / 2
故刚体的转动动能:
n
Ek Ek
在一微小过程中 力矩作的功
dA Md (1)
在一微小过程中
XX 力1矩O1作的2功2 M M
dA Md (1)
在考虑一个有限过程,设
在力矩作用下,刚体的角
位置由 功
1
2
则力矩的
A dA 2 Md (2) 1
力矩的功反映力矩对空间的积累作用,力矩越 大,在空间转过的角度越大,作的功就越大。 这种力矩对空间的积累作用的规律是什么呢?
/2 mg L cosd
0
2
mgL / 2
N
YZ
XO
r
mg
依动能定理
A力矩
1 2
J2
1 2
J02
A力矩
mg
L 2
mg
L 2
1 2
J
2
0
mgL J
mgL 1 mL2
3g L
3
XX
1
1 O
2
2
2 1
Md
1 2
J
2 2
1 2
J12
M
M
例)设一细杆的质量为m,长为L,一端支以
枢轴而能自由旋转,设此杆自水平静止释放。
求: 当杆过铅直位置时的角速度:
N
YZ
XO
r
mg
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
EkE定轴 1 2M 刚体 •v轴 2.
___________________________ _______________________
2.由
dEk
1 2
不规则的物体绕任意定轴转动:
dI dmd 2 .
ImNaoge dE
k
1 2
dm
•
v
2 dm
,
v
dm
d.
No
dE
k
1 2 • dmd 2
2.
Image 即
dE
k
1 2
dI
•
2.
成立。
___________________________ _______________________
这便证明了刚体定轴转动的动能 公式。
I2
可知,既然能量是线性
的,定轴转动的刚体的转动惯量也是线性
的。
3.若刚体在轴A的转动惯N量oIA已知, 由分析2及平行轴定理,将轴Im移a到gBe点时刚
体的动能为
E kB E kA 1 2M A 2Br2(rA是 BA距 B)离 .
___________________________ _______________________
2
1I2.
2
成立。
___________________________ _______________________
长为l的直细棒绕中垂线转动:
I 1 ml2 1 l3. 12 12
No
l
Image
ImNaoge Ek
2 l
1 •dl•l2
2
1 l32
24
1 I2.
2
2
成立。
___________________________ _______________________
C O
Image r1
2
1
C’
Q
时,即 s m小盘 3r13 时整体来讲是节省 了能量的。 4vN
r1为小盘半径。
___________________________ _______________________
s m小盘 3r13
4vN
C
O
在实际生活中,各项数值如下:
C’
m小盘:2kg
考虑半径为R的圆环绕轴线转动:
Im2 R2R3.
Ek
21•Rd•R2
02
R32
1I2.
2
成立。
___________________________ _______________________
半径为R的圆盘绕轴线转动:
I1mR2 R4.
2
2
ImNaoge Ek
2R1•rdRd•r2
002
R42
P
2v
C’
Q
其中Δf是区域P、Q的摩擦力, P、Q的圆心分别是C和C’。
___________________________ _______________________
在吸尘器模型中,设吸尘器使用距离
为s,采用开孔的底盘,增加了摩擦力,
却减少了驱动底盘转动的能量。当
No
P
2v
2vN•1•sm小盘 2r2
版权所有,商用付酬。
___________________________ _______________________
❖ 本文拟得出定轴转动下刚体 的动能表达式,并讨论教材例6.4 中电熨斗模型的改良及其他一些 简单应用。
___________________________ _______________________
Image 其中 EkxEkyEkz包含刚体质心系中刚体的动能,这里
不再推了。
___________________________ _______________________
在教材例6.4中我们知半径r、自 转角速度ω、平动速度v<< ω 、滑动 摩擦系数μ、对地面压力N的圆盘受阻 力
f v N. r
No ω:8π(4Hz)
r:0.3m
r1:0.25m v:0.2m/s
Image μ:0.3
N:5kg*g=50N.
P
2v
Q
解得:s最大值是41.28m.这样的距离不用说 是家用吸尘器,除草都行了。因此,吸尘器底部
做成圆环更节能。
___________________________ _______________________
4.由分析2及正交轴定理可求出刚体 作定点转动的动能公式:
No E k O E k x E k y E k z 1 2 I xx 2 I yy 2 I zz 2 .
5.Im由a分ge析1~4可得刚体作任意运动
的一般的动能公式:
No E k E k x E k y E k z1 2 M v 轴 2x v 轴 2y v 轴 2z.
3
当转动周期、密度相同时,若 R 2r4 ,则I1=I2,E1=E2.亦即,半径r的圆环与 半径R的圆柱如此旋转时有相同动能,但
定轴转动刚体的动能计算及一些 简单应用®
___________________________ _______________________
❖ 本幻灯片参考材料:
《力学》,杨维纮,中国科学技术大学04级理 学院教材。
其他便没有了。限于客观原因,作者并没有准备 充分资源。日后若条件允许,也许能做出更有价 值的成果。
由本文前面特殊情况刚体动能公式,半径 为r,环壁厚为1(r<<1)的圆环与半径为R的圆 柱绕轴线转动的情况如下:
圆环I1: 2r3.E1 12I2.m1 2r1.
ImNaoge 圆柱 (盘):I2 R 24.E2 12I2.m2 R2.
___________________________ _______________________
我们已知,定轴转动刚体的转动惯量I、角
速度ω分别与直线运动中刚体的质量M、速度v
对应,但教材上并未给出计算刚体旋转动能的
公式。我们猜想刚体的动能是否为
Ek
1 2
Iω
2
下面来证明此公式:
___________________________ _______________________
设所有刚体均匀,密度为1,则质量和体积 在数值上相等。
C O
2v
No
C’
Image
摩擦力集中在上半个月牙形内。
___________________________ _______________________
由于滑动摩擦力μN与接触面积无 关,若切去盘中心O半径为 r 2v 的小圆盘No,如图易知摩擦力增加
2fIm a2vgeN.
r1
C O
