离散数学一、二章检测题及答案
《离散数学》练习题答案

《离散数学》练习题一答案一、单项选择题(每小题2分,共8分) 1—5 . D C B C C 6—10 . A B D C A11—15 C B C D A 16—20 C C B D C 21—25 C C B D C 26—30. D C B A D 31. C二、填空题(每空1分,共11分)1. nn 2. P 、Q 的真值同时为1 3.4. 奇5. 126. Q P ⌝∧7. 9 8.Q P ⌝→ 9.P ,Q 的真值都为010.D B C A ⊆⊆ , 11. 0 12. c b =13. 14 14. c 15. P Q ↔ 或 Q P ↔ 16. b 17. 假 18. 219. 17 20. 0 21. 有余(补)分配格 22. 假 23. 2 24. 17 25. 0 26. 有余(补)分配格 27. ()()Q P Q P ⌝∧∨∧⌝28.{}d d a b b a a c a d c b a b b a , , , , , , , , , , , , , , ,, ,29.⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=100000010000101000110100101010111101R M30. 7 31.1968339=三、解答题(共81分)3.(10分)设G 是平面图,有n 个顶点,m 条边,f 个面,k 个连通分支,证明:1+=+-k f m n 。
证明:对于图G 的每个连通分支都是连通平面图,因此由欧拉公式,有2111=+-f m n 2222=+-f m n… …2=+-k k k f m n其中i i i f m n , , 分别是第i 个连通分支中的顶点数、边数和面数,则1 , , 212121-+=+++=+++=+++k f f f f m m m m n n n n k k k将上述k 个等式相加,有k k f m n 21=-++-,即1+=+-k f m n4.(8分)化简下列布尔表达式。
离散数学第一学期习题及答案

第一章部分习题及参考答案1 设p、q的真值为0;r、s的真值为1,求下列各命题公式的真值。
(1)p∨(q∧r)(2)(p↔r)∧(﹁q∨s)(3)(⌝p∧⌝q∧r)↔(p∧q∧﹁r)(4)(⌝r∧s)→(p∧⌝q)2.判断下面一段论述是否为真:“π是无理数。
并且,如果3是无理数,则2也是无理数。
另外6能被2整除,6才能被4整除。
”3.用真值表判断下列公式的类型:(1)(p→q) →(⌝q→⌝p)(2)(p∧r) ↔(⌝p∧⌝q)(3)((p→q) ∧(q→r)) →(p→r)4.用等值演算法判断下列公式的类型,对不是重言式的可满足式,再用真值表法求出成真赋值.(1) ⌝(p∧q→q)(2)(p→(p∨q))∨(p→r)(3)(p∨q)→(p∧r)5.用等值演算法证明下面等值式:(1)(p→q)∧(p→r)⇔(p→(q∧r))(2)(p∧⌝q)∨(⌝p∧q)⇔(p∨q) ∧⌝(p∧q)6.求下列公式的主析取范式与主合取范式,并求成真赋值(1)(⌝p→q)→(⌝q∨p)(2)⌝(p→q)∧q∧r(3)(p∨(q∧r))→(p∨q∨r)7.在自然推理系统P中构造下面推理的证明:(1)前提:p→q,⌝(q∧r),r结论:⌝p(2)前提:q→p,q↔s,s↔t,t∧r结论:p∧q8.在自然推理系统P中用附加前提法证明下面推理:前提:p→(q→r),s→p,q结论:s→r9.在自然推理系统P中用归谬法证明下面各推理:前提:p→⌝q,⌝r∨q,r∧⌝s结论:⌝p参考答案:1.(1)p∨(q∧r)⇔0∨(0∧1) ⇔0(2)(p↔r)∧(﹁q∨s) ⇔(0↔1)∧(1∨1) ⇔0∧1⇔0(3)(⌝p∧⌝q∧r)↔(p∧q∧﹁r) ⇔(1∧1∧1)↔ (0∧0∧0)⇔0 (4)(⌝r∧s)→(p∧⌝q) ⇔(0∧1)→(1∧0) ⇔0→0⇔12.p: π是无理数 1q: 3是无理数0r: 2是无理数 1s: 6能被2整除 1t: 6能被4整除0命题符号化为:p∧(q→r)∧(t→s)的真值为1,所以这一段的论述为真。
离散数学练习题(含答案)

离散数学试题第一部分选择题一、单项选择题1.下列是两个命题变元p,q的小项是( C )A.p∧┐p∧q B.┐p∨qC.┐p∧q D.┐p∨p∨q2.令p:今天下雪了,q:路滑,则命题“虽然今天下雪了,但是路不滑”可符号化为( D )A.p→┐q B.p∨┐qC.p∧q D.p∧┐q3.下列语句中是命题的只有( A )A.1+1=10 B.x+y=10C.sinx+siny<0 D.x mod 3=24.下列等值式不正确的是( C )A.┐(∀x)A⇔(∃x)┐AB.(∀x)(B→A(x))⇔B→(∀x)A(x)C.(∃x)(A(x)∧B(x))⇔(∃x)A(x)∧(∃x)B(x)D.(∀x)(∀y)(A(x)→B(y))⇔(∀x)A(x)→(∀y)B(y)5.谓词公式(∃x)P(x,y)∧(∀x)(Q(x,z)→(∃x)(∀y)R(x,y,z)中量词∀x的辖域是( C )A.(∀x)Q(x,z)→(∃x)(∀y)R(x,y,z))B.Q(x,z)→(∀y)R(x,y,z)C.Q(x,z)→(∃x)(∀y)R(x,y,z)D.Q(x,z)6.设A={a,b,c,d},A上的等价关系R={<a,b>,<b,a>,<c,d>,<d,c>}∪I A,则对应于R的A的划分是( D )A.{{a},{b,c},{d}} B.{{a,b},{c},{d}}C.{{a},{b},{c},{d}} D.{{a,b},{c,d}}7.设A={Ø},B=P(P(A)),以下正确的式子是( A )A.{Ø,{Ø}}∈B B.{{Ø,Ø}}∈BC.{{Ø},{{Ø}}}∈B D.{Ø,{{Ø}}}∈B8.设X,Y,Z是集合,一是集合相对补运算,下列等式不正确的是( A )A.(X-Y)-Z=X-(Y∩Z)B.(X-Y)-Z=(X-Z)-YC.(X-Y)-Z=(X-Z)-(Y-Z)D.(X-Y)-Z=X-(Y∪Z)9.在自然数集N上,下列定义的运算中不可结合的只有( D )A.a*b=min(a,b)B.a*b=a+bC.a*b=GCD(a,b)(a,b的最大公约数)02324# 离散数学试题第1 页共4页02324# 离散数学试题 第 2 页 共4页D .a*b=a(mod b)10.设R 和S 是集合A 上的关系,R ∩S 必为反对称关系的是( A ) A .当R 是偏序关系,S 是等价关系; B .当R 和S 都是自反关系; C .当R 和S 都是等价关系; D .当R 和S 都是传递关系11.设R 是A 上的二元关系,且R ·R ⊆R,可以肯定R 应是( D ) A .对称关系; B .全序关系; C .自反关系; D .传递关系 12.设R 为实数集,函数f :R →R ,f(x)=2x ,则f 是( B ) A .满射函数 B .单射函数 C .双射函数 D .非单射非满射第二部分 非选择题二、填空题1.设论域是{a,b,c},则(∀x)S(x)等价于命题公式 S(a)∧S(b)∧S(c) ;(x ∃)S(x)等价于命题公式 S(a)∨S(b) ∨S(c) 。
离散数学练习题2 答案
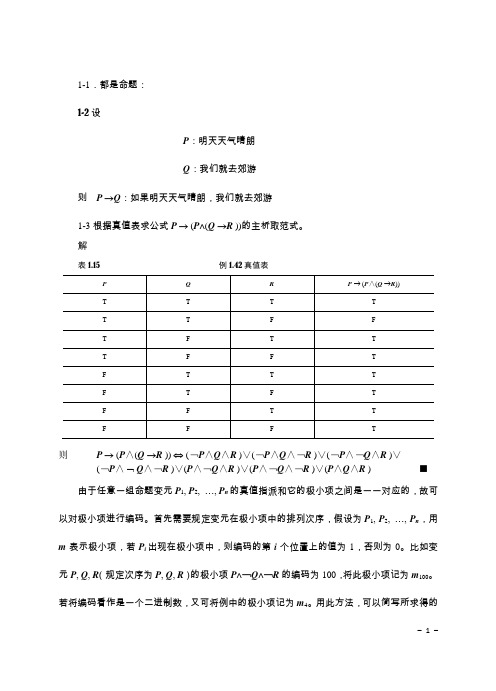
1-1.都是命题:1-2设P:明天天气晴朗Q:我们就去郊游则P →Q:如果明天天气晴朗,我们就去郊游1-3根据真值表求公式P → (P∧(Q →R ))的主析取范式。
解表1.15 例1.42真值表则P → (P∧(Q →R )) ⇔ (﹁P∧Q∧R )∨(﹁P∧Q∧﹁R )∨(﹁P∧﹁Q∧R )∨⌝(﹁P∧Q∧﹁R )∨(P∧﹁Q∧R )∨(P∧﹁Q∧﹁R )∨(P∧Q∧R ) ■由于任意一组命题变元P1, P2, …, P n的真值指派和它的极小项之间是一一对应的,故可以对极小项进行编码。
首先需要规定变元在极小项中的排列次序,假设为P1, P2, …, P n,用m表示极小项,若P i出现在极小项中,则编码的第i个位置上的值为1,否则为0。
比如变元P, Q, R(规定次序为P, Q, R)的极小项P∧﹁Q∧﹁R的编码为100,将此极小项记为m100。
若将编码看作是一个二进制数,又可将例中的极小项记为m4。
用此方法,可以简写所求得的给定公式的主析取范式。
P → (P∧(Q →R )) ⇔m0∨m1∨m2∨m3∨m4∨m5∨m7(规定P, Q, R的次序为P, Q, R)公式P → (P∧(Q →R ))的主析取范式。
解P → (P∧(Q →R ))⇔﹁P∨(P∧(﹁Q∨R ))⇔ (﹁P∨P)∧(﹁P∨﹁Q∨R)⇔ (﹁P∨﹁Q∨R )⇔ (﹁P∨﹁Q∨R )1-4试证明(﹁P →Q )∧(P →R )∧(﹁Q∨S ) ⇒S∨R。
证明(1)﹁P →Q P(2)﹁Q∨S P(3)Q →S T, (2), E16(4)﹁P →S T, (1), (3), I13(5)﹁S →P T, (4), E18(6)P →R P(7)﹁S →R T, (5),(6), I13(8)﹁﹁S∨R T, (7),E16(9)S∨R T, (8), E11-5如果迈克有电冰箱,则或者他卖了洗衣机,或者他向别人借了钱。
离散数学一、二章检测题及答案

四.证明题(共 38 分)
1. (10 分)符号化下列命题并推证其结论. 任何人如果他喜欢音乐,他就不喜欢体育.每个人或者喜欢体育,或者喜欢美术.有的 人不喜欢美术.因而有的人不喜欢音乐. (设 M(x):x 喜欢音乐,S(x):x 喜欢体育,A (x):x喜欢美术. ) 该命题符号化为: ( ( x) (M(x)→ S(x) )∧( x) (S(x)∨A(x) )∧( x) A(x) )→( ( x) M(x) ) 前提: ( x) (M(x)→ S(x) ) , ( x) (S(x)∨A(x) ) , ( x) A(x) 结论: ( x) M(x) 证: (1) ( x) A(x) P (2) A(a) ES(1) (3) ( x) (S(x)∨A(x) ) (4)S(a)∨A(a) (5)S(a) (6) ( x) (M(x)→ S(x) ) (7)M(a)→ S(a) (8)S(a)→ M(a) (9) M(a) (10) ( x) M(x) 2. (12 分) (1).用 CP 规则证明 P (Q R ), Q ( R S ), P Q S ; P US(3) T(2) (4)I P US(6) T(7)E T(5) (8)I EG(9)
(1 分)
由 8 得出了矛盾,根据归谬法说明原推理正确(1 分)
3.(6 分) 指出下面推理证明过程中的错误, 并给出正确的证明.
用谓词演算的推理规则证明:
x(Q ( x) R ( x)) x(Q ( x) Z ( x)) x( R ( x) Z ( x))
证: (1) x(Q ( x) R ( x)) (2) Q (a ) R (a ) (3) x(Q ( x) Z ( x)) (4) (5)
(完整版)离散数学习题答案

离散数学习题答案习题一及答案:(P14-15)14、将下列命题符号化:(5)李辛与李末是兄弟解:设p :李辛与李末是兄弟,则命题符号化的结果是p (6)王强与刘威都学过法语解:设p :王强学过法语;q :刘威学过法语;则命题符号化的结果是p q∧(9)只有天下大雨,他才乘班车上班解:设p :天下大雨;q :他乘班车上班;则命题符号化的结果是q p →(11)下雪路滑,他迟到了解:设p :下雪;q :路滑;r :他迟到了;则命题符号化的结果是()p q r∧→15、设p :2+3=5. q :大熊猫产在中国. r :太阳从西方升起.求下列复合命题的真值:(4)()(())p q r p q r ∧∧⌝↔⌝∨⌝→解:p=1,q=1,r=0,,()(110)1p q r ∧∧⌝⇔∧∧⌝⇔(())((11)0)(00)1p q r ⌝∨⌝→⇔⌝∨⌝→⇔→⇔()(())111p q r p q r ∴∧∧⌝↔⌝∨⌝→⇔↔⇔19、用真值表判断下列公式的类型:(2)()p p q→⌝→⌝解:列出公式的真值表,如下所示:p qp⌝q⌝()p p →⌝()p p q→⌝→⌝001111011010100101110001由真值表可以看出公式有3个成真赋值,故公式是非重言式的可满足式。
20、求下列公式的成真赋值:(4)()p q q⌝∨→解:因为该公式是一个蕴含式,所以首先分析它的成假赋值,成假赋值的条件是:()10p q q ⌝∨⇔⎧⎨⇔⎩⇒0p q ⇔⎧⎨⇔⎩所以公式的成真赋值有:01,10,11。
习题二及答案:(P38)5、求下列公式的主析取范式,并求成真赋值:(2)()()p q q r ⌝→∧∧解:原式()p q q r ⇔∨∧∧q r ⇔∧()p p q r ⇔⌝∨∧∧,此即公式的主析取范式,()()p q r p q r ⇔⌝∧∧∨∧∧37m m ⇔∨所以成真赋值为011,111。
*6、求下列公式的主合取范式,并求成假赋值:(2)()()p q p r ∧∨⌝∨解:原式,此即公式的主合取范式,()()p p r p q r ⇔∨⌝∨∧⌝∨∨()p q r ⇔⌝∨∨4M ⇔所以成假赋值为100。
离散数学第1-2章参考答案-命题逻辑谓词逻辑

Page 49 第17题解:(1)令①P:李明学习努力;②Q:李明成绩好;③R:李明不热衷于玩扑克;(2)已知条件符号化,即①P→Q:如果李明学习努力,那么他成绩好;②R→P:如果李明不热衷于玩扑克,那么他就努力学习;(3)所求结论符号化,即①¬Q→¬R:李明成绩不好,所以李明热衷于玩扑克;(4)证明:原命题符号化为P→Q,R→P ¬Q→¬R;①P→Q P规则;②R→P P规则;③R→Q T规则①②;④Q∨¬R T规则③;⑤¬Q→¬R T规则④;(5)得证。
Page 50 第32题(2)解: P∨(¬P→(Q∨(¬Q→R)));⇔ P∨(P∨(Q∨(Q∨R)));⇔P∨Q∨R;①主合取范式为:P∨Q∨R;因为 P∨Q∨R ⇔∏M0 ⇔∑m1,2,3,4,5,6,7;②主析取范式为:∨(¬P∧¬Q∧R)∨(¬P∧Q∧¬R)∨(¬P∧Q∧R)∨(P∧¬Q∧¬R)∨(P∧¬Q∧R)∨(P∧Q∧¬R)∨(P∧Q∧R);Page 50 第32题(4)解: (P∧¬Q∧R)∨(¬P∧Q∧¬S);⇔ ((P∧¬Q∧R)∧(S∨¬S))∨((¬P∧Q∧¬S)∧(R∨¬R));⇔(P∧¬Q∧R∧S)∨(P∧¬Q∧R∧¬S)∨(¬P∧Q∧R∧¬S)∨(¬P∧Q∧¬R∧¬S);①主析取范式为:(¬P∧Q∧¬R∧¬S)∨(¬P∧Q∧R∧¬S)∨(P∧¬Q∧R∧¬S)∨(P∧¬Q∧R∧S) ⇔∑m4,6,10,11⇔∏M0,1,2,3,5,7,8,9,12,13,14,15;②主合取范式为:(¬P∨¬Q∨¬R∨¬S)∧(¬P∨¬Q∨¬R∨S)∧(¬P∨¬Q∨R∨¬S) ∧(¬P∨¬Q∨R∨S)∧(¬P∨Q∨¬R∨S)∧(¬P∨Q∨R∨S)∧(P∨¬Q∨¬R∨¬S) ∧(P∨¬Q∨¬R∨S)∧(P∨Q∨¬R∨¬S)∧(P∨Q∨¬R∨S)∧(P∨Q∨R∨¬S)∧(P∨Q∨R∨S);Page 50 第32题(6)解: (P→Q)→(P∨R);⇔¬(¬P∨Q)∨(P∨R);⇔(P∧¬Q)∨(P∨R);⇔(P∨R)∧(P∨¬Q∨R);⇔ ((P∨R)∨(¬Q∧Q))∧(P∨¬Q∨R);⇔(P∨¬Q∨R)∧(P∨Q∨R)∧(P∨¬Q∨R);⇔(P∨¬Q∨R)∧(P∨Q∨R);①主合取范式为:(P∨¬Q∨R)∧(P∨Q∨R);⇔∏M0,2;⇔∑m1,3,4,5,6,7;①主合取范式为:(¬P∨¬Q∨R)∧(¬P∨Q∨R)∧(P∨¬Q∨¬R)∧(P∨¬Q∨R)∧(P∨Q∨¬R)∧(P∨Q∨R);Page 51 第37题(2)解: P→Q P→(P∧Q)①P P规则(附加前提);②P→Q P规则;③Q T规则①,②,I;④P∧Q T规则①,③,I;⑤P→(P∧Q) CP规则;Page 51 第37题(4)解: (P∨Q)→R ⇒ (P∧Q)→R①P∧Q P规则(附加前提);②P T规则①,I;③P∨Q T规则②,I;④(P∨Q)→R P规则;⑤R T规则③,④,I;⑥(P∧Q)→R CP规则;Page 51 第38题(3)解:﹁(P→Q)→﹁(R∨S),((Q→P)∨﹁R),R ⇒ P↔Q①﹁(P↔Q) P规则(假设前提);②﹁((P→Q)∧(Q→P)) T规则①,I;③R P规则;④((Q→P)∨﹁R) P规则;⑤R→(Q→P) T规则④,I;⑥(Q→P) T规则③⑤,I;⑦R∨S T规则③,I;⑧﹁(P→Q)→﹁(R∨S) P规则;⑨(R∨S)→(P→Q) T规则⑧,I;⑩(P→Q) T规则⑦⑨,I;⑪(P→Q)∧(Q→P) T规则⑥⑩,I;⑫得证间接证明法②⑪;Page 51 第39题(1)解:(1)符号化已知命题①P:明天是晴天;②Q:明天下雨;③R:我去看电影;④S:我不看书;条件符号化:P∨Q,P→R,R→S;结论符号化:①﹁S→Q(2)证明:P∨Q,P→R,R→S ⇒﹁S→Q①P→R P规则;②R→S P规则;③P→S T规则①②;④﹁S→﹁P T规则③,I;⑤P∨Q P规则;⑥﹁P→Q T规则⑤,I;⑦﹁S→Q T规则④⑥,I;Page 51 第39题(2)解:(1)符号化已知命题①P:明天不下雨;②Q:能够买到车票;③R:我去参观计算机展览会;条件符号化:P∧Q→R;结论符号化:①﹁R→﹁P(2)证明:P∨Q,P→R,R→S ⇒﹁S→Q①P∧Q→R P规则;②﹁R P规则(附加前提);③﹁(P∧Q) T规则①②;④﹁P∨﹁Q T规则③,I;⑤也就是说或者明天下雨或者买不到票,所以原命题说不能参加计算机展览的原因只是明天下雨是不完全的,故原命题无效。
离散数学考试题目及答案

离散数学考试题目及答案一、单项选择题(每题2分,共20分)1. 集合A={1,2,3},集合B={3,4,5},则A∩B的元素个数为:A. 0B. 1C. 2D. 3答案:B2. 函数f: X→Y是一个双射,当且仅当:A. f是单射且满射B. f是单射C. f是满射D. f是双射答案:A3. 命题p: "x是偶数",命题q: "x是3的倍数",下列逻辑运算中,表示"x是6的倍数"的是:A. p∧qB. p∨qC. ¬p∧¬qD. ¬p∨¬q答案:A4. 有向图G中,若存在从顶点u到顶点v的有向路径,则称顶点u可达顶点v。
若G中任意两个顶点都相互可达,则称G为:A. 强连通图B. 弱连通图C. 无向图D. 有向无环图答案:A5. 在二进制数系统中,下列哪个数的值最大?A. 1010B. 1100C. 1110D. 1101答案:C6. 布尔代数中,逻辑或运算符表示为:A. ∧B. ∨C. ¬D. →答案:B7. 有限自动机中,状态q0是初始状态,状态q1是接受状态。
若存在从q0到q1的ε-转移,则该自动机:A. 仅在输入为空时接受B. 仅在输入非空时接受C. 无论输入为何都接受D. 无法确定是否接受答案:C8. 命题逻辑中,若命题p和q都为真,则p∧q的真值是:A. 真B. 假C. 可能为真,也可能为假D. 无法确定答案:A9. 集合{1,2,3}的子集个数为:A. 4B. 6C. 7D. 8答案:D10. 若关系R在集合A上是自反的,则对于A中的任意元素a,有:A. (a,a)∈RB. (a,a)∉RC. (a,a)是R的自反对D. (a,a)不是R的自反对答案:A二、填空题(每题3分,共15分)1. 集合A={1,2,3}的幂集包含__个元素。
答案:82. 若函数f: X→Y是满射,则对于Y中的任意元素y,至少存在X中的一个元素x,使得f(x)=__。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
天津理工大学中环信息学院《离散数学》第一、二章检测题请将填空题答案填入下面相应位置1. ;2. ;3. ;4. ;5. ;6. ;7. ;8. ;9. ;10. ;11. ;12. ;13. ;14. ;15. 。
一、填空题(每空2分,共30分)1.设P 表示“我将去书店”, Q 表示“我有时间”,则命题“我将去书店,仅当我有时间”符号化为 。
P Q →2.设P 表示“天下雨”, Q 表示“我骑自行车上班”,则命题“除非下雨,否则我骑自行车上班”符号化为 。
P Q ⌝→34.设命题公式A则命题公式A 的主析取范式为 , 主合取范式为 。
()()()P Q R P Q R P Q R ⌝∧∧⌝∨∧⌝∧⌝∨∧⌝∧()()()()()P Q R P Q R P Q R P Q R P Q R ∨∨∧∨∨⌝∧∨⌝∨⌝∧⌝∨⌝∨∧⌝∨⌝∨⌝5.设个体域{,,}A a b c =,消去公式中的量词,则()()x P x ∀∧()()x Q x ∃⇔。
()()()(()()())P a P b P c Q a Q b Q c ∧∧∧∨∨6.命题公式P Q →的逆反式是 。
Q P ⌝→⌝7.设命题公式⌝(P Q ↔)的主析取范式为()()P Q Q P ∧⌝∨∧⌝ 。
8.谓词公式 )()()(x x P x ∃⇔∀⌝ , )()()(x x P x ∀⇔∃⌝ 。
(),()P x P x ⌝⌝9.设()G x 表示“x 是金子”, ()F x 表示“x 是闪光的”,则命题“金子是闪光的,但闪光的不一定是金子”符号化为 。
()(()())()(()())x G x F x x F x G x ∀→∧⌝∀→或()(()())()(()())x G x F x y F y G y ∀→∧∃∧⌝10.N 个命题变元可以构成互不等价的命题公式 个。
(22N )二、单项选择题(每小题2分,共20分)1.设)(x S 表示x 是演员。
)(x T 表示x 是老师,),(y x A 表示x 钦佩y 。
则命题“所有演员都钦佩某些老师”符号化为( 2 )。
(1).(()(,))x S x A x y ∀→; (2).))),()(()((y x A y T y x S x ∧∃→∀;(3).()()(()()(,))x y S x T y A x y ∀∃∧∧; (4).()()(()()(,))x y S x T y A x y ∀∃∧→. 2.下列蕴含式不成立的是( 1 ).(1).(()())()()x F x G x xF x xG x ∀∨⇒∀∨∀; (2).(())()x F x G xF x ∀∧⇒∀;(3). (()())()()x F x G x xF x xG x ∃∧⇒∃∧∃; (4).(())()x F x G xF x ∃∧⇒∃. 3.下列等价式不成立的是( 2 ).(1).(()())()()x F x G x xF x xG x ∀∧⇔∀∧∀;(2).(()())()()x F x G x xF x xG x ∃∧⇔∃∧∃(3).(())()x F x G xF x G ∀∧⇔∀∧(4).(())()x F x G xF x G ∃∧⇔∃∧4.谓词公式(()(,))()x P x yR x y Q x ∀∨∃→中量词(x ∀)辖域是( ).(4)(1).(()(,))x P x yR x y ∀∨∃; (2).()P x ;(3).()Q x ; (4).(()(,))P x yR x y ∨∃.5.下列哪个命题是真命题( 2 ).(1).如果2+3=5,则太阳从西方升起; (2).如果2+3=6,则太阳从西方升起;(3).严禁吸烟; (4).我正在说谎.6.谓词演算中,()P a 是)()(x P x ∀的有效结论,其理论依据是( 1 ).(1).全称指定规则(US ); (2).全称推广规则(UG );(3).存在指定规则(ES ); (4).存在推广规则(EG ).7.下列哪个命题是假命题( 1 ).(1).如果2是偶数,那么一个命题公式的析取范式唯一;(2).如果2是偶数,那么一个命题公式的析取范式不唯一;(3).如果2是奇数,那么一个命题公式的析取范式唯一;(4).如果2是奇数,那么一个命题公式的析取范式不唯一.8.下列公式中不是前束范式的是( 3 )。
(1).()()(()())x y Q x R y ∀∃∧; (2).()()()((,)(,,))x y z Q x z R x y z ∀∀∃→;(3).(,)()()(,,)Q x z x y R x y z →∃∀; (4).()()(,)x y Q x y ∀∃.9.下列等价公式正确的是( )。
(2)(1).P Q Q P →⇔→; (2).P Q P Q →⇔⌝∨;(3).P Q Q P →⇔⌝∨; (4).P Q Q P →⇔⌝∨⌝.10.以下推理错误的是( )。
(2)(1).,P P Q Q ⌝∨⇒; (2).P Q P ∨⇒;(3).,Q P Q P ⌝→⇒⌝; (4).,P P Q Q →⇒.三、简答题(每小题6分,共12分)1. 求谓词公式)),()()()(()),()()((z y Q z y P y y x Q x P x ∃∧∃→→∀的前束析取范式.)),()()()(()),()()((z y Q z y P y y x Q x P x ∃∧∃→→∀))],()(()),()()[()()(()),()()()(()),()(()),()()()(()),()(()),()()()(()),()()((z y Q u P y x Q x P z u x z y Q z u P u y x Q x P x z y Q z y P y y x Q x P x z y Q z y P y y x Q x P x ∧∨⌝∧∃∃∃⇔∃∧∃∨⌝∧∃⇔∃∧∃∨⌝∧∃⇔∃∧∃∨∨⌝∀⌝⇔2.求命题公式 (())P Q R P ∨→→的主析取范式和主合取范式。
()()()()(())(())1(())1()()()(()())(()())1()()()()()()1()()()()P Q R PP Q R P P Q R P P R Q R PP Q R P Q Q R R P P Q R P Q R P Q R P Q R P Q R P Q R P Q R P Q R P Q R P Q R P Q R ∨→→⇔⌝⌝∨∨∨⇔∨∧⌝∨⇔∧⌝∨∧⌝∨⇔∨∧⌝⇔∧∨⌝∧∨⌝∨∨⌝∧∧⌝⇔∧∧∨∧⌝∧∨∧∧⌝∨∧⌝∧⌝∨∧∧⌝∨⌝∧∧⌝⇔∧∧∨∧⌝∧∨∧∧⌝∨∧⌝∧⌝分分分分()()24567013()((1(()()()1P Q R m m m m m M M M P Q R P Q R P Q R ∨⌝∧∧⌝⇔∨∨∨∨⇔∧∧⇔∨∨∧∨∨⌝∧∨⌝∨⌝这是主析取范式))分这是主合取范式)分四.证明题(共38分)1.(10分)符号化下列命题并推证其结论.任何人如果他喜欢音乐,他就不喜欢体育.每个人或者喜欢体育,或者喜欢美术.有的人不喜欢美术.因而有的人不喜欢音乐.(设M(x):x 喜欢音乐,S(x):x 喜欢体育,A(x):x喜欢美术.)该命题符号化为:((∀x)(M (x )→⌝S (x ))∧(∀x)(S (x )∨A (x ))∧(∃x )⌝ A (x ))→((∃x )⌝ M (x ))前提:(∀x)(M (x )→⌝S (x )),(∀x)(S (x )∨A (x )),(∃x )⌝ A (x ) 结论:(∃x )⌝ M (x )证:(1)(∃x )⌝ A (x ) P(2)⌝ A (a ) ES (1)(3)(∀x)(S (x )∨A (x )) P(4)S (a )∨A (a ) US (3)(5)S (a ) T (2)(4)I(6)(∀x)(M (x )→⌝S (x )) P(7)M (a )→⌝S (a ) US (6)(8)S (a )→⌝ M (a ) T (7)E(9)⌝ M (a ) T (5)(8)I(10)(∃x )⌝ M (x ) EG (9)2.(12分)(1).用CP 规则证明S Q P S R Q R Q P →⇒→→∨⌝∨⌝),(),(;1. P P 6. )(S R → T(4,5) I (1分)2. ()P Q R ⌝∨⌝∨ P 7. R T(3,4) I (1分)3. Q R ⌝∨ T(1, 2) I (2分) 8. S T(6,7) I (1分)4. Q P(附加前提) 9. )(S Q → CP (1分)5. )(S R Q →→ P(2).用归谬法证明 ,(),A B C B C S A →⌝⌝∨∧⌝⇒⌝.证: 1 (A P 附加前提) (1分) 2 A B P →⌝3 1,2B T I ⌝ (1分)4 C B P ⌝∨5 3,4C T I ⌝ (1分)6 C S P ∧⌝7 6C T I (1分) 8 5,7C C T I ∧⌝ (1分) 由8得出了矛盾,根据归谬法说明原推理正确(1分)3.(6分) 指出下面推理证明过程中的错误, 并给出正确的证明.用谓词演算的推理规则证明:))()(())()(())()((x Z x R x x Z x Q x x R x Q x ∧∃⇒∧∃∧→∀证: (1) ))()((x R x Q x →∀P (6))(a Z T(4) I (2) )()(a R a Q → US(1) (7) )(a R T(2),(5) I (3) ))()((x Z x Q x ∧∃ P (8) )()(a Z a R ∧ T(6),(7) I(4) )()(a Z a Q ∧ ES(3) (9) ))()((x Z x R x ∧∃ EG(8)(5) )(a Q T(4) I该证明的错误在于: (1)、 (2) 与 (3)、 (4) 的顺序颠倒了,应该先指定存在后指定全称。
(2分)正确的证明是:(4分)(1) ))()((x Z x Q x ∧∃ P (6) )(a Z T(2) I(2) )()(a Z a Q ∧ ES (1) (7) )(a R T(4),(5) I(3) ))()((x R x Q x →∀ P (8) )()(a Z a R ∧ T(6),(7) I(4) )()(a R a Q → US (3) (9) ))()((x Z x R x ∧∃ EG(8)(5) )(a Q T(2) I4.(10分)公安人员审理某珠宝商店的钻石项链的失窃案,已知侦察结果如下:(1)营业员A 或B 盗窃了钻石项链(2)若B 作案,则作案时间不在营业时间(3)若A 提供的证词正确,则货柜未上锁(4)若A 提供的证词不正确,则作案发生在营业时间(5)货柜上了锁试问:作案者是谁要求写出推理过程。
