结构力学-力法习题
结构力学习题及答案(武汉大学)

结构力学习题第2章平面体系的几何组成分析2-1~2-6 试确定图示体系的计算自由度。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图2-7~2-15 试对图示体系进行几何组成分析。
若是具有多余约束的几何不变体系,则需指明多余约束的数目。
题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图题2-13图题2-14图题2-15图题2-16图题2-17图题2-18图题2-19图题2-20图题2-21图2-1 1=W 2-1 9-=W 2-3 3-=W 2-4 2-=W 2-5 1-=W 2-6 4-=W2-7、2-8、2-12、2-16、2-17无多余约束的几何不变体系 2-9、2-10、2-15具有一个多余约束的几何不变体系 2-11具有六个多余约束的几何不变体系2-13、2-14几何可变体系为2-18、2-19 瞬变体系2-20、2-21具有三个多余约束的几何不变体系第3章静定梁和静定平面刚架的内力分析3-1 试作图示静定梁的内力图。
(a)(b)(c) (d)习题3-1图3-2 试作图示多跨静定梁的内力图。
(a)(b)(c)习题3-2图3-3~3-9 试作图示静定刚架的内力图。
习题3-3图习题3-4图习题3-5图习题3-6图习题3-7图习题3-8图习题3-9图3-10 试判断图示静定结构的弯矩图是否正确。
(a)(b)(c) (d)部分习题答案3-1 (a )m kN M B ⋅=80(上侧受拉),kN F RQB 60=,kN F L QB 60-=(b )m kN M A ⋅=20(上侧受拉),m kN M B ⋅=40(上侧受拉),kN F RQA 5.32=,kN F L QA 20-=,kN F LQB 5.47-=,kN F R QB 20=(c) 4Fl M C =(下侧受拉),θcos 2F F L QC =3-2 (a) 0=E M ,m kN M F ⋅-=40(上侧受拉),m kN M B ⋅-=120(上侧受拉)(b )m kN M RH ⋅-=15(上侧受拉),m kN M E ⋅=25.11(下侧受拉)(c )m kN M G ⋅=29(下侧受拉),m kN M D ⋅-=5.8(上侧受拉),m kN M H ⋅=15(下侧受拉) 3-3 m kN M CB ⋅=10(左侧受拉),m kN M DF ⋅=8(上侧受拉),m kN M DE ⋅=20(右侧受拉) 3-4 m kN M BA ⋅=120(左侧受拉)3-5 m kN M F ⋅=40(左侧受拉),m kN M DC ⋅=160(上侧受拉),m kN M EB ⋅=80(右侧受拉)3-6 m kN M BA ⋅=60(右侧受拉),m kN M BD ⋅=45(上侧受拉),kN F QBD 46.28=3-7 m kN M C ⋅=70下(左侧受拉),m kN M DE ⋅=150(上侧受拉),m kN M EB ⋅=70(右侧受拉) 3-8 m kN M CB ⋅=36.0(上侧受拉),m kN M BA ⋅=36.0(右侧受拉) 3-9 m kN M AB ⋅=10(左侧受拉),m kN M BC ⋅=10(上侧受拉) 3-10 (a )错误 (b )错误 (c )错误 (d )正确第4章 静定平面桁架和组合结构的内力分析4-1 试判别习题4-1图所示桁架中的零杆。
结构力学力法习题答案

结构力学力法习题答案结构力学力法习题答案结构力学是一门研究物体在受力作用下的变形和破坏规律的学科。
在学习结构力学的过程中,习题是必不可少的一部分。
通过解答习题,我们可以更好地理解和应用力学原理,提高解决实际问题的能力。
下面,我将为大家提供一些结构力学力法习题的详细解答,希望对大家的学习有所帮助。
习题一:一根悬臂梁的长度为L,截面为矩形,宽度为b,高度为h,材料的弹性模量为E。
在悬臂梁的自重和外力作用下,求悬臂梁的最大弯矩和最大挠度。
解答:首先,我们需要根据悬臂梁的几何形状和受力情况,绘制出受力图。
在这个问题中,悬臂梁受到自重和外力的作用,自重作用在悬臂梁的重心处,外力作用在悬臂梁的端点处。
根据受力图,我们可以得到悬臂梁在端点处的反力和弯矩分布。
接下来,我们可以根据结构力学的基本原理,利用力平衡和力矩平衡的方程,求解出悬臂梁的最大弯矩和最大挠度。
在这个问题中,我们可以利用弯矩-曲率关系,得到最大弯矩的表达式。
然后,我们可以利用悬臂梁的边界条件,求解出最大挠度的表达式。
习题二:一根悬臂梁的长度为L,截面为圆形,直径为d,材料的弹性模量为E。
在悬臂梁的自重和外力作用下,求悬臂梁的最大弯矩和最大挠度。
解答:与习题一类似,我们需要绘制出悬臂梁的受力图,根据受力图求解出悬臂梁的最大弯矩和最大挠度。
在这个问题中,悬臂梁的截面为圆形,因此我们需要利用圆形截面的惯性矩和弯矩-曲率关系,求解出最大弯矩的表达式。
习题三:一根梁的长度为L,截面为矩形,宽度为b,高度为h,材料的弹性模量为E。
梁的两端固定,受到均布载荷q的作用,求梁的最大弯矩和最大挠度。
解答:在这个问题中,梁的两端固定,因此我们需要考虑边界条件对梁的受力和变形的影响。
首先,我们需要绘制出梁的受力图,根据受力图求解出梁的最大弯矩。
然后,我们可以利用梁的边界条件,求解出最大挠度的表达式。
通过以上三个习题的解答,我们可以看到,在结构力学的学习中,我们需要灵活运用力学原理,结合具体的问题,综合考虑几何形状、材料性质和边界条件等因素,才能得到准确的解答。
结构力学力法练习共65页文档

61、奢侈是舒适的,否则就不是奢侈 。——CocoCha nel 62、少而好学,如日出之阳;壮而好学 ,如日 中之光 ;志而 好学, 如炳烛 之光。 ——刘 向 63、三军可夺帅也,匹夫不可夺志也。 ——孔 丘 64、人生就是学校。在那里,与其说好 的教师 是幸福 ,不如 说好的 教师是 不幸。 ——海 贝尔 65、接受挑战,就可以享受胜利的喜悦 。——杰纳勒 尔·乔治·S·巴顿
谢谢!
结构力学课后答案-第6章--力法

习题6-1试确定图示结构的超静定次数。
(a)(b)(c)(d)(e)(f)(g)所有结点均为全铰结点2次超静定6次超静定4次超静定3次超静定II去掉复铰,可减去2(4-1)=6个约束,沿I-I截面断开,减去三个约束,故为9次超静定沿图示各截面断开,为21次超静定I II 刚片I与大地组成静定结构,刚片II只需通过一根链杆和一个铰与I连接即可,故为4次超静定(h)6-2试回答:结构的超静定次数与力法基本结构的选择是否有关?力法方程有何物理意义?6-3试用力法计算图示超静定梁,并绘出M 、F Q 图。
(a)解:上图=l1M pM 01111=∆+p X δ其中:EIl l l l l l l EI l l l l EI 8114232332623232333211311=⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯+⨯⨯⨯+⎪⎭⎫ ⎝⎛⨯⨯⨯⨯=δEIl F l lF l lF EI l pp p p817332322263231-=⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯=∆0817*******=-EI l F X EI l p p F X 211=p M X M M +=11l F p 61l F p 61F PA2l 3l 3B2EIEIC题目有错误,为可变体系。
+pF p lF 32X 1=1M 图p Q X Q Q +=11p F 21⊕p F 21(b)解:基本结构为:l1M 3l l2M l F p 21pM l F p 31⎪⎩⎪⎨⎧=∆++=∆++0022221211212111p p X X X X δδδδp M X M X M M ++=2211pQ X Q X Q Q ++=22116-4试用力法计算图示结构,并绘其内力图。
(a)l2l 2l2lABCD EI =常数F Pl 2E FQ 图F PX 1X 2F P解:基本结构为:1M pM 01111=∆+p X δpM X M M +=11(b)解:基本结构为:EI=常数qACEDB4a 2a4a4a20kN/m3m6m6mAEI 1.75EIB CD 20kN/mX 1166810810计算1M ,由对称性知,可考虑半结构。
李廉锟《结构力学》笔记和课后习题(含考研真题)详解-第7章 力 法【圣才出品】

第7章 力 法
7.1 复习笔记【知识框架】
【重点难点归纳】
一、概述(见表7-1-1) ★★
表7-1-1 概述
二、超静定次数的确定(见表7-1-2) ★★★★
表7-1-2 超静定次数的确定
三、力法的基本概念(见表7-1-3) ★★★
力法的基本概念,包括基本未知量、基本体系、基本结构以及基本方程见表7-1-3,此外,表中还归纳了超静定结构的力法分析步骤。
表7-1-3 力法的基本未知量、基本体系和基本方程
四、力法的典型方程(见表7-1-4) ★★★
表7-1-4 力法的典型方程
五、对称性的利用 ★★★★
1.对称结构及作用荷载的对称性(表7-1-5)
表7-1-5 对称结构及作用荷载的对称性
2.非对称荷载的处理(表7-1-6)
表7-1-6 非对称荷载的处理。
结构力学力法题
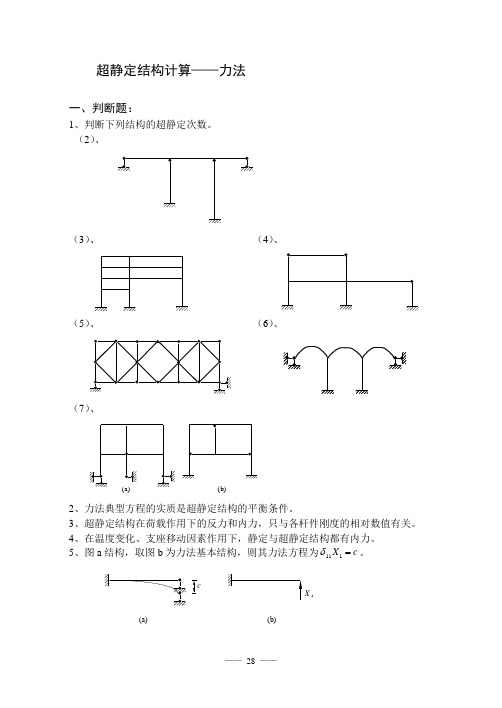
超静定结构计算——力法一、判断题:1、判断下列结构的超静定次数。
(2)、(3)、 (4)、(5)、 (6)、(7)、(a)(b)2、力法典型方程的实质是超静定结构的平衡条件。
3、超静定结构在荷载作用下的反力和内力,只与各杆件刚度的相对数值有关。
4、在温度变化、支座移动因素作用下,静定与超静定结构都有内力。
5、图a 结构,取图b 为力法基本结构,则其力法方程为δ111X c =。
(a)(b)X16、图a 结构,取图b 为力法基本结构,h 为截面高度,α为线膨胀系数,典型方程中∆12122ta t t l h =--()/()。
t 21t l Ah(a)(b)X1二、计算题:8、用力法作图示结构的M 图。
3mm9、用力法作图示排架的M 图。
已知 A = 0.2m 2,I = 0.05m 4,弹性模量为E 0。
q =2kN/m11、用力法计算并作图示结构的M 图。
ql /213、用力法计算图示结构并作出M 图。
EI =常数。
(采用右图基本结构。
)l 2/3l /3/3l /315、用力法计算图示结构并作M 图。
EI =常数。
2m2m 2m2m16、用力法计算图示结构并作M 图。
EI =常数。
l l qll19、已知EI = 常数,用力法计算并作图示对称结构的M 图。
ql lq20、用力法计算并作图示结构的M 图。
EI =常数。
a a21、用力法作图示结构的 M 图 。
EI = 常数。
q2ql24、用力法计算并作出图示结构的M 图。
E = 常数。
P26、用力法计算图示结构并作M 图。
EI =常数。
ll /2l /2l /2l /229、已知EA 、EI 均为常数,用力法计算并作图示结构M 图。
ll34、用力法求图示桁架杆BC 的轴力,各杆EA 相同。
aD37、用力法作图示结构杆AB 的M 图。
各链杆抗拉刚度E A 1相同。
梁式杆抗弯刚度为E I E Ia E A ,=21100,不计梁式杆轴向变形。
40、图示结构支座A 转动θ,EI =常数,用力法计算并作M 图。
李廉锟《结构力学》(第6版)笔记及课后习题(含考研真题)详解-力法(圣才出品)

表 7-1-8 超静定结构位移的计算
七、最后内力图的校核(见表 7-1-9) ★★★ 超静定结构计算较为繁琐,大量运用数字与符号,因而极容易出错,通过校核能够有效
10 / 99
圣才电子书 十万种考研考证电子书、题库视频学习平台
2.什么是力法的基本结构和基本体系?它们在计算中起什么作用?基本体系与原结构 有何异同?
答:(1)基本结构和基本体系的定义 ①力法的基本结构是指将原超静定结构中的多余联系去掉后所得到的静定结构; ②基本体系是指基本结构在原有荷载和多余未知力共同作用下的体系。 (2)基本结构和基本体系在计算中的作用 ①力法的基本方程中系数和自由项的求解以及最终结构内力和反力的计算均是在基本 结构上进行的; ②基本体系是在建立力法的基本方程时,方程右端数值确定的关键,也即位移协调条件。 (3)基本体系与原结构异同点 ①不同点:基本体系用未知力代替了原结构的约束; ②相同点:基本体系与原结构最后的变形相同,这也是建立力法典型方程的位移条件。
答:(1)荷载作用下,超静定结构的内力只与各杆的刚度相对值有关,而与其刚度绝 对值无关。
14 / 99
圣才电子书 十万种考研考证电子书、题库视频学习平台
(2)当计算支座移动的超静定结构时,把移动的支座视为多余约束,那么典型方程的 右端就不为零,此时需要根据多余约束处已知的位移条件建立典型方程。
6.超静定结构的内力在什么情况下只与各杆刚度的相对大小有关?什么情况下与各杆 刚度的绝对大小有关?
降低错误率,保证计算结果的正确性。各阶段校核内容见表 7-1-9。 表 7-1-9 最后内力图的校核
八、支座移动和温度改变时超静定结构的计算(见表 7-1-10) ★★
山东省专升本考试土木工程结构力学(力 法)模拟试卷2(题后含答

山东省专升本考试土木工程结构力学(力法)模拟试卷2(题后含答案及解析)全部题型 2. 结构力学结构力学判断题1.无荷载就无内力,这句话只适用于静定结构,不适用于超静定结构。
( )A.正确B.错误正确答案:A 涉及知识点:力法2.下图所示结构截断三根链杆,可以变成一个简支梁,故它有三次超静定。
( )A.正确B.错误正确答案:B解析:截断三根杆后,A点有两个自由度。
知识模块:力法3.下图所示两次超静定结构,可以选下图(b)为基本结构进行力法汁算。
( )A.正确B.错误正确答案:B解析:解除约束后左半部分成为几何瞬变体系。
知识模块:力法4.求超静定结构的位移时,可将虚拟单位荷载加在任意静定的基本体系上。
( )A.正确B.错误正确答案:A 涉及知识点:力法5.超静定结构支座移动时,如果刚度增大一倍,内力也增大一倍,而位移不变。
( )A.正确B.错误正确答案:A解析:支座移动产生的内力与刚度的绝对值成正比,所以刚度增大一倍,内力也增大一倍;由公式:可见支座移动引起的位移与刚度无关。
知识模块:力法6.在下图所示的两结构中,(a)中拉杆的轴力N与(b)中的水平反力XB的关系是:当拉杆的刚度EA=有限值时,N<XB;当拉杆的刚度EA=无穷大时,N=XB。
( )A.正确B.错误正确答案:A 涉及知识点:力法单项选择题7.在力法典型方程中,恒大于零的是( )A.主系数B.副系数C.自由项D.右端项正确答案:A 涉及知识点:力法8.在力法典型方程中,副系数( )A.恒大于零B.恒小于零C.恒等于零D.可正、可负、可为零正确答案:D 涉及知识点:力法A.多余未知力B.支座反力C.角位移D.独立的结点线位移正确答案:A 涉及知识点:力法10.打开联接三刚片的复铰,相当于去掉几个约束? ( )A.2B.3C.4D.5正确答案:C 涉及知识点:力法11.力法方程中的系数δki表示的是基本结构由( )A.Xi产生的Xk方向的位移B.Xi=1产生的Xk方向的位移C.Xi=1产生的Xi方向的位移D.Xk=1产生的Xi方向的位移正确答案:B 涉及知识点:力法12.图(a)结构如选图(b)为基本体系,其力法方程为( )A.δ11X1+△1P=0B.δ11X1+△1P=a/EAC.δ11X1+△1P=一X1a/EAD.δ11X1+△1P=X1a/EA正确答案:C 涉及知识点:力法13.力法方程的实质是( )A.平衡条件B.位移条件C.物理条件D.互等定理正确答案:B 涉及知识点:力法A.静定结构B.超静定结构C.可变体系D.不变体系正确答案:C解析:力法基本结构也可以是超静定结构。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
结构力学自测题(第五单元)
力法
姓名 学号
一、是 非 题(将 判 断 结 果 填 入 括 弧 :以 O 表 示 正 确 ,以 X 表 示 错 误 )
1、图 示 结 构 用 力 法 求 解 时,可 选 切 断 杆 件
2、4 后 的 体 系 作 为 基 本 结 构 。
(
)
1
2
3
4
5
a b a
b
2、图 示 结 构 中 ,梁 AB 的 截 面 EI 为 常 数,各 链 杆 的E A 1相 同, 当 EI 增 大 时 ,则 梁 截 面 D 弯 矩 代 数 值 M D 增
大 。
(
)
C
3、图 a 所 示 结 构,取 图 b 为 力 法 基 本 体 系 ,线 胀
系 数 为
α ,则∆1= t t l h -322
α
) 。
(
)
l
o +2t 1
X (a)
(b)
4、图 示 对 称 桁 架 ,各 杆 EA l , 相 同 ,N P AB = 。
(
)
5、图 a 所 示 梁 在 温 度 变 化 时 的 M 图 形 状 如 图 b 所 示 ,对 吗 ? ( )
(a)
(b)
0C 图 -50C +15M
二、选 择 题 ( 将 选 中 答 案 的 字 母 填 入 括 弧 内 )
1、图 a 所 示 结构 ,EI = 常数 ,取 图 b 为 力 法 基 本 体 系,则 下 述 结 果 中 错 误 的 是: A .δ230= ; B .δ
310= ; C .∆20P = ; D .δ120= 。
(
)
l
l
l
l
/2X (a)
P (b)
2、图 示 连 续 梁 用 力 法 求 解 时 ,最 简 便 的 基 本 结 构 是 :
A .拆 去
B 、
C 两 支 座 ;
B .将 A 支 座 改 为 固 定 铰 支 座 ,拆 去 B 支 座 ;
C .将 A 支 座 改 为 滑 动 支 座 ,拆 去 B 支 座 ;
D .将 A 支 座 改 为 固 定 铰 支 座 ,B 处 改 为 完 全 铰 。
(
)
3、图 示 结 构 H B 为 : A .P ; B .-P
; C .P 2 ; D .-
P 。
(
)
4、图 示 两 刚 架 的 EI 均 为 常 数 ,并 分 别 为 EI = 1 和 EI = 10,这 两 刚 架 的 内 力 关 系 为:
(
)
A .M 图 相 同;
B .M 图 不 同;
C .图 a 刚 架 各 截 面 弯 矩 大 于 图 b 刚 架 各 相 应 截 面
弯
矩;
D .图 a 刚 架 各 截 面 弯 矩 小 于 图 b 刚 架 各 相 应 截 面 弯 矩。
/2/2
/2(a)
l
l /2/2
/2
(b)
l l
5、在 力 法 方 程
δ
ij
j c i X ∑+=∆∆1 中 :
A B.
C. D
.;;;.∆∆∆i i i =><000前三种答案都有可能。
(
)
三、填 充 题 ( 将 答 案 写 在 空 格 内 )
1、图 示 结 构 超 静 定 次 数 为 。
2、力 法 方 程 等 号
左 侧 各 项 代 表 , 右 侧 代 表 。
3、图 示 结 构,EI =常 数 , 在 给 定 荷 载 作
用 下 ,
Q AB =_____________。
l l l
4、试 绘 出 图 示 结 构 用 力 法 计 算 时 ,未 知 量 最 少 的 基 本 结 构 。
l l
1
1
2
l
5、图 a 结 构 中 支 座 转 动 θ,力 法 基 本 结 构 如 图 b ,力 法 方 程 中 ∆1c = 。
l
A
(a)
X 2
(b)
θ
四、已 知 图 示 基 本 体 系 对 应 的 力 法 方 程 系 数 和 自 由 项 如 下:
δδ112232==l EI /(),δδ12210==,∆14548P ql EI =-/(),∆2448P ql EI =/(),作 最 后 M 图 。
l
l
五、已 知 EA 、EI 均 为 常 数 , 试 用 力 法 计 算 并 作 图 示 对 称 结 构 M 图 。
l
l
六、力 法 计 算 ,并 作 图 示 对 称 结 构 由 支 座 移 动 引 起 的 M 图 。
EI = 常 数 。
l /2
l
七、用 力 法 计 算 并 作 图 示 结 构 的
M 图 。
各 杆 截 面 相 同 ,EI = 常 数 ,矩
形 截 面 高 为 h ,材 料 线 膨 胀 系 数 为 α 。
l
C
C
-20-5
C
-5
八、已 知 各 杆 的 E A 相 同 , 用 力 法 计 算 并 求 图 示 桁 架 的 内 力 。
九、图 b 为 图 a 所 示 结 构 的M 图 , 求 荷 载 作 用 点 的 相 对 水 平 位 移 。
EI 为 常 数 。
l
/2/2
Pl /4
Pl /16Pl /16
Pl /16
Pl /16
M 图
(a) (b)
自测题(第五单元)力法
答案
一、1 X 2 O 3 X 4 X 5 O 二、1 D 2 D 3 C 4 A 5 D 三、
1、 6
2、
基 本 体 系 沿 基 本 未 知 力 方 向 的 位 移 (2分); 原 结 构 沿 基 本 未 知 力 方 向 的 位 移 (2分)。
3、23m l ( 5 分 )
l 1M p 图
3m 43
m 23
m M 图
δ113
4=l EI ,∆12
12P ml EI =-,X m l 13=,Q m l AB =23
4、
l l 1
2/2
(6分)
5、
-l θ (6分)
四、
524
2ql ql 224
18
12ql 2ql 图 ()
分 4M
X ql X ql 1252424
=
=- , (3分 ) 五、
利 用 对 称 性 知
N E F =0, 取 半 结 构 计 算 , (1 分 )
X 1 =
M P 图
)δ1173=l EI , (4 分 ) ()∆112P ml EI =-, (4 分 )
∴=
X m
128
(2 分 ) 14
14
1
1
M 图 (⨯
m 28
) (4 分 )
六、
δ11317242==-l EI c c /,/, ∆317/12l EIc X =。
图
M X 1
6EIC
7l
(10分 )
七、
基 本
结 构 :
(3分 )
()()EI l h l h l X EI
hl h l t δαα113112
43525915859==
+=-+/,,∆ (4分 ) 1
1
M 图 ⨯
+⎛⎝ ⎫
⎭
⎪15859αhl EI h l () (3分)
八、
一 次 超 静 定 ,
δ11138621931==-..EA
P EA
P ∆ (5 分 )
X P 105=. (5 分
)
0707.P 0707.P
-05.P
05.P
-05.P
-05.P
N 图
(5 分)
九、
虚 拟 状 态 ,
l 4 分 )
∆=51923
Pl EI
(靠 拢 ) (6 分 )。
