确定运货卡车和运输路线的最佳数量即每条线路上个站点的顺
运筹学运输问题相关知识点

运筹学运输问题相关知识点运筹学,旨在通过数学模型和优化方法来解决各种决策问题,其中运输问题是运筹学中的一个重要分支。
运输问题旨在帮助我们确定如何在不同地点之间运输物品以达到最佳效益。
首先,运输问题基于以下几个基本假设:一是物流成本在运输过程中是线性的,二是物品在不同地点之间的运输是无差异的,三是供应和需求之间是平衡的。
在解决运输问题时,需要考虑以下几个关键要素:1.运输网络:此步骤涉及识别和描述供应地点、运输路径和需求地点。
通常使用图形表示来可视化运输网络,以便更好地理解和分析问题。
2.供应量和需求量:确定每个供应地点可提供的物品数量和每个需求地点所需的物品数量。
供应量和需求量之间必须达到平衡。
3.运输成本:每个运输路径的费用是决策的重要因素。
这可以涉及运输距离、运输方式、燃料成本等因素。
通常通过构建费用矩阵来表示各个路径的费用。
4.运输方案:确定如何分配物品以满足需求,并选择最佳的运输路径。
这通常通过使用线性规划模型来实现,以最小化总运输成本为目标。
解决运输问题的常见方法包括:1.西北角规则:该方法从供应和需求具有最大值的角度着手,逐步分配物品,直到达到平衡。
这种方法简单易行,但不一定能够找到全局最优解。
2.最小成本法:该方法根据运输路径的成本递增顺序,逐一分配物品,直到平衡为止。
这种方法能够找到最优解,但可能需要更多的计算量。
3.转运法:该方法通过寻找“供应地点里程+需求地点里程最小”的路径来决策,直至达到平衡。
这种方法在有多个供应地点和多个需求地点时非常实用。
除了基本的运输问题之外,还有其他一些相关的运筹学问题,如多品种运输问题、多目标运输问题和带有时间窗口的运输问题等。
这些问题在实际应用中都有广泛的应用,并且可以通过相应的数学模型和优化方法来解决。
综上所述,运筹学中的运输问题是一个重要的决策问题。
它涉及到寻找最佳的物品配送方案,以最小化总运输成本。
通过合适的数学模型和算法,我们可以有效地解决这类问题,为实际的物流管理提供有力的支持。
初二数学运输问题

初二数学运输问题
摘要:
一、初二数学运输问题简介
1.运输问题的背景和实际意义
2.初二数学运输问题的基本内容
二、运输问题的基本模型和解决方法
1.基本模型:产销平衡模型
2.基本解决方法:线性规划
三、初二数学运输问题在生活中的应用
1.货物运输调度
2.交通路线规划
3.资源分配优化
四、初二数学运输问题的拓展思考
1.运输问题的变形和扩展
2.运输问题与其他数学领域的关联
正文:
初二数学运输问题涉及到货物运输、交通路线规划等实际问题,通过数学方法对其进行建模和求解,具有重要的实际意义。
运输问题属于线性规划的一个子领域,主要研究如何在满足一定约束条件的前提下,使得目标函数达到最优值。
运输问题的基本模型是产销平衡模型,即在多个产地和销地之间进行货物
运输,要求满足供需平衡和运输容量约束。
解决运输问题的基本方法是线性规划,将问题转化为求解线性方程组,通过计算得到最优解。
在生活中,初二数学运输问题有着广泛的应用。
例如,在货物运输调度中,通过运输问题的求解,可以有效地安排运输车辆的行驶路线和货物装载方案,提高运输效率。
在交通路线规划中,运输问题可以帮助我们找到最佳的道路使用方案,减少交通拥堵。
此外,运输问题还可以应用于资源分配优化等方面。
初二数学运输问题作为线性规划的一个实际应用,可以帮助学生更好地理解线性规划的基本思想和方法。
通过对运输问题的拓展思考,学生可以尝试解决一些变形和扩展的运输问题,进一步锻炼自己的数学思维能力。
车辆调度方法

34 图 扫描法设计行车路线
1000
4000
车辆调度方法
图上作业法
——物资调拨
图上作业法
图上作业法的原则可以归纳为: 流向划右方,对流不应当; 里圈、外圈分别算,要求不能过半圈长; 如若超过半圈长,应去运量最小段; 反复运算可得最优方案。
1.运输线路不成圈的图上作业法
对于运输线路不成圈的流向图,只要不出现对流现象,就
是最优调运方案。
2.运输线路成圈的图上作业法
第一步 作出初始方案
A (36) B (23)
C (13)
D
+20 -30
-50
+20
(18)
E
(45)
F
-20
G (29)
I (23) H
(25)
+100
-70
-30
+60
A
B 30
C 20
D
+20 -30
-50
+20
60
E
20
80 F
-20
I 10 -30
H
G
+60 50
9
4
K
0C
8)以B为初始结点,计算与之
相连的点的位势值;
11
6
11 B
9)从剩余位势中选出最小者,
10
D6
标注箭头和位势值;
5
《智慧运输运营》题库

一、单项选择题1.运输作业物流运输合理化:就是在保证物资流向合理的前提下,在货物的运量、运距、流向和()等整个运输过程中,确保运输质量,以适宜的运输工具、最少的运输环节、最佳的运输线路、最低的运输费用使物资运至目的地。
A、流通环节B、中间环节C、运费D、交通线正确答案: B2.在运输过程中,运输时间、运输工具周转率、运输货损以及运费等技术经济指标,都与( )存在正比例关系。
A、货物重量B、运输距离C、运输时间D、车辆速度正确答案: B3货物运输量计划是预计在计划期内完成的货物运输量和周转量,通常以(A、日B、周C、月D、年正确答案: D4.运输环节越多运费越高,货损率也()。
A、基本不变B、不变C、随之增加D、随之减少正确答案: C5.运输环节越(A、多)运费越高,货损率也随之增加。
B、少C、简单D、复杂正确答案: A6.运输环节越多,运费越高、(A、运输货损率B、运输成本C、运输时间D、风险程度)也随之增加。
)为计划期。
正确答案: A)的重要措施。
7.运输工具主要是由运输方式决定。
发挥运输工具的作用,也是(A、运输合理化B、降低运输货损率C、减少运输成本D、降低环境污染正确答案: A)决定。
发挥运输工具的作用,也是运输合理化的重要措施。
8.运输工具主要是由(A、运输路线B、运输成本C、运输时间D、运输方式正确答案: D9.运输是物流过程中花费时间较长的环节,运输时间过长会造成运输成本()。
A、减少B、增加C、不变D、微调正确答案: B)会造成运输成本增加。
10.运输是物流过程中花费时间较长的环节,运输时间(A、减少B、过长C、不变D、微调正确答案: B)的比例,运费降低可以提高整个物流系统的竞争力。
11.运费在全部物流费用中占有(A、最大B、最小C、50%D、60%正确答案: A)可以提高整个物流系统的竞争力。
12.运费在全部物流费用中占有最大的比例,运费(A、取消B、提高C、稳定D、降低正确答案: D)经济行为造成的。
案例 5 福勒批发公司(Folwer Distributing Company)

案例五福勒批发公司(Folwer Distributing Company)福勒批发公司是一家大型酿酒厂啤酒和葡萄酒的地区性特许经销商,罗伊·福勒是该公司的老板。
罗伊面临的主要问题是如何有效地将啤酒和葡萄酒产品运送到客户所在地。
罗伊拥有自己的送货卡车,但工会也会安排司机向零售商店兜售卡车上库存的啤酒和葡萄酒,司机希望增加财源来提高自己的收入。
罗伊很高兴看到司机们积极进行销售,但他也希望能够尽量减少所需车辆的数量和运输距离。
背景罗伊·福勒是朝鲜战争的退伍军人,退伍后曾买了两辆公共汽车为家乡的居民提供交通服务。
罗伊既当司机也当维修工,在这个行业努力奋斗。
为控制费用,罗伊只买了一个牌照,在两辆公共汽车上交换使用(当其中一辆汽车送去修理或由于其他原因无法行驶时)。
当这个城市建立起自己的交通系统时,罗伊被挤出了这个行业。
罗伊在运输行业经验促使他建立啤酒经销网,将当地仓库的啤酒卖给仓库周边地区各种各样的零售商店。
后来,那家酿酒厂发展成为大型啤酒生产厂,罗伊的经销网也发展壮大起来。
虽然罗伊已经成为该地区ᴰ大的经销商,但控制成本仍然是保持其竞争力的关键。
配送服务通常的路径规划就是将零售商店和其它客户点的送货任务分派给特定的司机和卡车。
司机们组织起来竞标这些线路。
他们将根据各自的资历赢得不同的线路,并充当这些路线上的推销员,为提高收入而进一步开发新客户。
司机们收取佣金,而且众所周知他们在销售旺季每周收入可达4000美元。
可以设想,司机们很注意保护各自线路的构成和设计,如果罗伊试图重新设计运输路线,必然会面临与工会的冲突。
另一类客户被称为预售客户,由第二类运输路线提供服务。
预售客户指那些送货之前已经发出订单的客户(不是等销售人员上门才订货)。
因此,企业有机会优化第二类运输路线的设计。
这些客户订购的货物被放在单独的卡车上,与那些佣金客户的订货分开,设计送货路线时也不会受那么多工会规定的限制,可以根据实际需要制订计划。
成人教育 《运输与配送管理》期末考试复习题及参考答案

运输与配送管理练习题A一、名词解释1规模原理2.全挂汽车列车3.摘取式分拣4.配装二、单项选择题1.运输业属于第三产业的()A.服务部门B.流通部门C.销售部门D.生产部门2.管道运输的最主要不足之处是()A.运输物品受限制B.运输费用比较高C.污染太重D.运输时间长3.下列货物不属于特种货物的是()A.爆炸品B.鲜鱼虾C.稀有金属D.化肥4.铁路送达速度一般高于公路运输,但在短途运输中,其送达速度却低于公路运输,其原因是()A.短途运输时,铁路的技术速度低B.铁路运输在途中停留时间和始发、终发端的作业时间较长C.公路加速度快5.海尔配送中心已做到中心城市6~8小时配送到位,区域销售24小时配送到位,全国主干线分拨配送平均3.5天到位,这种配送中心属于()配送中心模式A.基于供应的B.基于资源集成的C.基于销售的D.基于生产的6.下列哪项不属于配送中心的主要功能()A.储存功能B.分拣功能C.配送功能D.计划功能7.配送中心的业务活动是以()发出的订货信息作为驱动源A.生产订单B.客户订单C.采购订单D.内部订单8.最优经济订购批量只考虑()两个因素A.物资间隔和进货时间B.采购费用和进货时间C.保管费用和采购费用D. 保管费用和物资价格9.将一箱玫瑰(约合0.5吨)从广州运往北京,选用()运输方式比较合适A.铁路B.公路C.水路D.航空10.下列哪项不是批量拣选的优点()A.前置时间短 B.适合配送批量大的订单作业C.对量少、次数多的配送,批量拣取更有效 D.增加单位时间的拣货量三、简答题1. 长途汽车的运输费用有哪些?2.物流配送在物流系统中的作用3. 配送中心作业管理的内容有哪些?4. 在运用线性规划解决运输问题时,如果供应总量与需求总量不相等怎么办?四、论述题运输的规模原理、距离原理及速度原理的内涵?论述它们对运输方式的选择有哪些影响?运输与配送管理练习题A答案一.名词解释:1.规模原理是指随着一次装运量的增大,使每单位重量的运输成本下降。
管理运筹学04运输问题

例4-1的最小元素法
运价表 1 产
地
B1
A1
3
A2
1
A3
7
销量
3
销 B2
11
9 4 6
地
产
B3
B4
量
3
10
7
2
84
10
59
5
6 20
方案表 1
产
地
B1
A1
A2
3
A3
销量
3
销 B2
6
地
产
B3
B4
量
7
4
9
5
6 20
2020/6/24
例4-1的最小元素法
运价表 2
产
销
地
地
B1
A1
B2
B3
11
3
A2 (3)
9
2
A3
销量
3
4
10
6
5
产
B4
量
10
7
8
4
5
9
6 20
方案表 2
产
销
地
B1
B2
A1
A2 (3)
A3
销量
3
6
地
B3
B4
1
5
6
产 量 7
4 9 20
2020/6/24
例4-1的最小元素法
运价表 3
产
销
地
B1
A1
B2
B3
11
3
A2 (3)
(1)
A3
销量
3
4
10
6
助理物流师考试练习题(计算题)
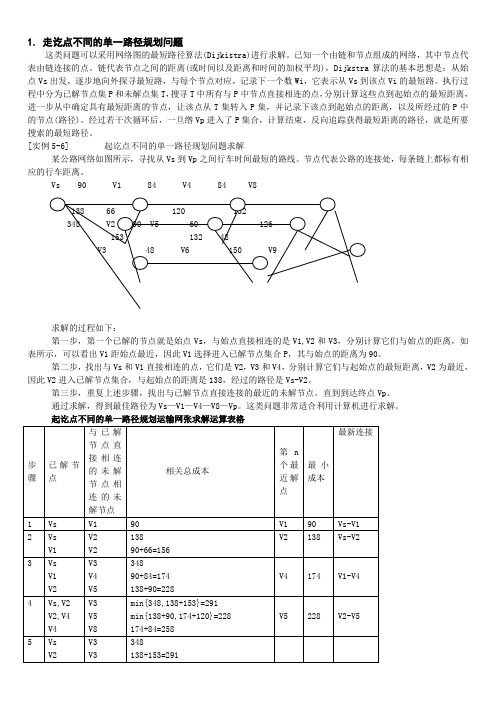
1.走讫点不同的单一路径规划问题这类问题可以采用网络图的最短路径算法(Dijkistra)进行求解。
已知一个由链和节点组成的网络,其中节点代表由链连接的点。
链代表节点之间的距离(或时间以及距离和时间的加权平均),Dijkstra算法的基本思想是:从始点Vs出发,逐步地向外探寻最短路,与每个节点对应,记录下一个数Wi,它表示从Vs到该点Vi的最短路。
执行过程中分为已解节点集P和未解点集T,搜寻T中所有与P中节点直接相连的点,分别计算这些点到起始点的最短距离,进一步从中确定具有最短距离的节点,让该点从T集转入P集,并记录下该点到起始点的距离,以及所经过的P中的节点(路径)。
经过若干次循环后,一旦绺Vp进入了P集合,计算结束,反向追踪获得最短距离的路径,就是所要搜索的最短路径。
[实例5-6] 起讫点不同的单一路径规划问题求解某公路网络如图所示,寻找从Vs到Vp之间行车时间最短的路线。
节点代表公路的连接处,每条链上都标有相应的行车距离。
Vs 90 V1 84 V4 84 V8求解的过程如下:第一步,第一个已解的节点就是始点Vs,与始点直接相连的是V1,V2和V3,分别计算它们与始点的距离,如表所示,可以看出V1距始点最近,因此V1选择进入已解节点集合P,其与始点的距离为90。
第二步,找出与Vs和V1直接相连的点,它们是V2,V3和V4,分别计算它们与起始点的最短距离,V2为最近,因此V2进入已解节点集合,与起始点的距离是138,经过的路径是Vs-V2。
第三步,重复上述步骤,找出与已解节点直接连接的最近的未解节点。
直到到达终点Vp。
通过求解,得到最佳路径为Vs—V1—V4—V8—Vp。
这类问题非常适合利用计算机进行求解。
2. A公司以每箱100美元向日本B公司出口某商品2000箱。
货物出口前,由A公司向中国人民保险公司投保水渍险、包装破裂及淡水雨淋险。
水渍险、包装破裂险及淡水雨淋险的保险费率分别为0.6%、0.1%和0.3%,按发票金额110%投保。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、确定运货卡车和运输路线的最佳数量即每条线路上个站点的顺序。
将最佳设计方案与现有路线相比,是否合理?通过ROUTER软件,我们得到最佳的配送路线如图所示:原始的配送路线:现在的最优配送路线:新设计的线路带来的好处:1)降低总的运输成本由于我们选择了软件ROUTER来处理节约法中的附加的约束条件,这样计算机给中的配送路线图也就是在此约束条件下的最优配送线路方案。
运用这种方案计算出来的运输成本就是最节约的。
图中的739.93美元就是在这种情况下,一天内公司所用支付的运输成本。
在最优线路下的运输成本也同时是最少的。
所以说新的方案会降低运输成本。
2)提高运输效率,节约运输时间新的运输方案是最节约的方案,在线路选择上,将更集中的配送点归为一条线路,这样不仅节约了运输成本,还提高了运输效率,节约了运输的时间。
由于公司规定,司机每天在路上时间超过8小时,就要支付双倍工资。
新的方案的实际,使得运输线路最短、最优,配送点最集中,运输的时间也会最少,这样将为公司节约更多的成本。
3)提高顾客满意度新的配送线路可以使公司在更快的时间内将货物送达之顾客,顾客肯定是满意配送速度快的公司,这样公司就可以在市场竞争中获胜。
同时新的线路可以减少公司的运输成本,这样公司也可以考虑在向收取顾客的价钱中采取一些优惠的政策,这样不仅可以保留住公司的固定的消费群体,还可以吸引更多的顾客。
但同时新的设计路线也会带来一个问题,就是由于新的线路要求增加一辆运货卡车,这样就会给公司带来购买新卡车和调用新司机的成本。
虽然新的路线在运输成本上节省了很多,并且为公司配置了新的运输线路,但是不知公司是否愿意为此支付诸如新卡车费、卡车修理费、司机工资、司机加班费等额外的费用。
2. 对罗伊·福勒来说,在限制性时间窗口内提供服务,而不是在早晨8:00至下午5:00之间提供服务的成本是多少?他该怎么做才能降低这种成本?1)分析: 这道题的意思是让我们分析限制性时间窗口对成本的增加造成了多大的影响。
2)步骤:第一步:改变有限制性时间窗口顾客的时间窗口,把TW Begin1与TW End1的时间全部设置为480与1020,即所有顾客都可以在8:00AM---5:00PM之间收货。
第二步:根据ROUTER软件,得出新的规划路线。
对比原来的路线,新的路线在数量上由原来的6条减少为现在的5条。
新路线的产生是因为公司现在进行配送计划已经不用考虑到不同顾客期望在不同的时间段中收到货物。
由于没有时间窗口的限制,配送计划的制定就只需要考虑卡车的载重量,工人的工作时间,顾客的期望送货时间,路线最少化,从而得到最经济的配送方案。
第三步:根据ROUTER软件,得出在没有时间窗口的情况下的总运输费用是676.79美元,而原来的成本是739.93美元。
3)思考:如何减少由于时间窗口的限制导致的增加的成本?解决途径:①.公司可以和有时间窗口限制的顾客进行谈判,搞好关系,争取得到他们在时间上的宽松许可。
②.公司可以对有时间窗口限制的顾客进行聚类分析,如果他们的需求量够大,公司又有能力的情况下,可以考虑移动现在仓库的位置,或者建立一个DC,便于对这类时间要求高,需求量又打的顾客进行服务。
③.如果有的顾客时间要求高,需求量又少,并且所处位置会增加公司配送路线的费用,公司可以考虑利用适当的外包服务。
3. 假设现有大型卡车价格为35000美元,可装货600箱,罗伊应该购买吗?预计如果使用该卡车,运行成本每英里增加0.05美元。
1)分析:先不考虑卡车的购买价格,而关注购买后的运输成本是多少。
2)步骤:第一步:根据题目所给条件,把软件中的Cap.in weight 即每辆车的载货量从500箱变为600箱,而美英里的运行成本(Vehicle cost per mi.)从0.9美元增加到0.95美元。
其他条件不变。
第二步:根据ROUTER软件,得出改变卡车后新的规划路线。
对比旧的路线,新的路线由数量上从6条减少为5条,原来的四条路线为D-12-D,D-5-1-4-3-D,D-7-13-10-D,D-8-20-11-9-14-D,现在合并为了三条路线,D-12-3-4-1-5-D,D-7-13-D,D-10-11-20-9-14-D。
这主要是因为卡车的载重量变大了,原来由于载重量的限制而导致要用6条线路的因素现在不存在了。
第三步:根据ROUTER软件,得出改变卡车后每天的运输成本,为735.32美元,而对比原来每天的运输成本739.93,大概平均每天的运输成本节约了4.61美元,从运输成本上来说罗伊是应该购买的。
但如果考虑新卡车的购买成本,发现问题并不是这么简单。
新卡车每辆的购买费用是35000美元,而现在使用的卡车只使用了三年(使用寿命是7年),如果按报废价格被卖,只能得到原来购买成本(20000美元)的10%即2000美元,一辆车每年运输的节约成本为250*4.61=1152.5美元,而35000 〉(2000+1152.5)美元。
所以考虑到新车的购买成本,罗伊不应该购买。
4.如果罗伊可利用外部运输服务为需要50箱货物,或低于50箱货物的客户送货,成本为每个客户35000美元。
罗伊应该使用这种运输服务吗?1)分析罗伊应该对外包运输服务后引起的自营运输成本的减少与外包成本的增加进行权衡,以确定是否将部分运输业务外包。
根据题意,在罗伊自营的运输业务中,删去需求量小于等于50箱的那些小客户,用新的客户数据表进行运输路线和的规划,如果新方案的运营成本加上外包成本比原有方案的运营成本小,则接受该方案,将部分业务外包出去。
2)步骤:仍然使用Logwear进行规划求解。
①.对原方案数据表中的数据进行删减,删掉需求量小于等于50箱的小客户4个,具体说是5、11、14、18,客户数目减少为17个。
②.运行程序得到新的运输方案③.调用报告生成新的运输成本报告表可以看到,删减小客户后的新方案,一天的自营运输费用为652.46美元。
外包出去的4个客户,每天带来35*4=140美元的外包费用。
则一天的运营总成本为652.46+140=792.46美元与原方案每天739.93的运营成本相比是增加了。
从节约成本的角度,罗伊应该维持原有的运输方案,不采用外包运输。
但事实常常不那么简单,公司应综合考虑外包带来的诸如服务水平提高等因素来最终作出是否外包的决策。
5.工会正在谈判要求每天工作7个半小时(不包括午餐时间),多余时间为加班时间。
这将会对路线设计和成本带来什么影响?1)分析:题目中改变的条件就一个,即司机的工作时间由原来的8小时缩短为现在的7个半小时。
工作时间的减少要求我们重新设计线路,必然会引起成本的改变。
2)步骤:第一步:改变ROUTER软件中的属性设置,把After how many hours will overtime begin 由原来的8.5改为8。
然后按ROUTER软件得出线路图。
其他条件不变。
第二步:根据ROUTER软件得出改变工作时间后的线路图。
但发现路线与原来的路线并没有差别,也就是说,改变了工作时间的影响程度还不至于影响到公司改变路线。
第三步:根据ROUTER软件得出改变工作时间后的成本,为741.90美元,比原来的739.93美元增加了2美元左右。
由于路线并没有改变,我们认为,是由于多余的半小时算成了加班时间,工资是按照平时标准的双倍给付,所以增加了运输成本。
6、罗伊考虑把仓库放在更中心的地点(X=20,Y=25)。
仓库建筑的租用成本与现在的一样,但预售需求的部分的一次性搬家成本为15000美元。
搬家在经济上会对预售需求有利吗?仓库的位置转移,必然会带来配送路线的变化。
我们利用ROUTER软件进行新的配送路线的规划。
首先,我们在ROUTER上将仓库的位置坐出改变,如下图所示:新的仓库位置改变后,我们继续运行软件,这样就可以得到了新的配送路线图,如下所示:从图中可以看到,仓库位置转换后,我们可以看到需要7辆车来进行配送,并且新路线的运输费用为716.91美元。
从近期来看,如果公司转移仓库位置仅仅是短时期内的举动,那么公司最好还是不要选择这种方案。
原因主要有以下三点:(1)运输成本降低幅度小。
原来仓库没有搬迁之前的运输总成本为739.93,而现在搬迁后的运输总成本为716.91。
从数据上来看,搬迁后一天仅仅减少了20美元左右,运输总成本降低的幅度不大。
(2)搬迁仓库位置需要支付15000美元的搬家费用,相比起一天节约的20多美元的运输成本,搬家费用是一笔很大的支出。
(3)仓库搬迁后,新的配送路线需要7辆运货车来配送,这样一来公司又会支付昂贵的卡车购买费,对公司的财务来说也是必很大的支出。
但如果仓库的搬迁是公司的一项长期性的决策,那么这样的举动是很有必要的。
原因主要有以下三点:(1)虽然为了仓库搬迁,公司要支付昂贵的搬家费用和购买卡车的费用。
但是一天的货物运输会比从前的节省20多美元。
这样长期下来,公司其实是在不断盈利当中的。
(2)公司将仓库搬至比较中心的位置,使在为公司做宣传,吸引更多的顾客。
因为仓库的位置越靠近中心,知道、了解仓库的顾客就越多,顾客总是会选择自己亲眼看到的仓库进行业务来往,所以公司抓住顾客的这种心理,将仓库搬至中心处无疑是为公司做招牌,吸引更多的客户。
(3)公司将仓库搬住中心处,也就是更加贴进居民区,这样一来,更加方便仓库员工和司机的上下班,调动了员工的工作积极性,提高了他们的工作效率。
7.每天的车辆调度,使用计算机软件,预计会有怎样的问题,将如何处理?我们虽然使用计算机软件规划出了最优的运输方案,但并不是一劳永逸。
方案在付诸实施时必然会遇到一些问题,因为计算机软件在计算时只是从数值上求得了最优结果。
最为明显的一例,方案中所列的运输线路并不一定都能走,如设计出5、1、4、3的运输路线,很可能由于5到1这一段是单行线而使方案不具备可操作性。
另外还应考虑交通拥堵、收费站等问题。
因此,用计算机求解出的最优方案也需要管理调度人员根据实际情况进行调整和实施。
我们认为“三阶段法”是用于实施方案的一个较好方法。
首先,分析人员预览实际问题,考察有无例外情况,如是否有需要特别送货的客户或必须要固定的线路,单独特殊处理;然后,求助于计算机,对简化后的问题进行规划求解;最后,分析人员对求解的结果进行分析,再根据实际情况对该结果加以修正直至找到可以接受的方案。
最优方案并不一定是“好方案”,只有具有可操作性的方案才是好方案!“三阶段法”示意。
