数学建模模型
数学建模—函数模型及其应用

(k为常数,k≠0);
(4)指数型函数模型:f(x)=abx+c(a,b,c为常数,a≠0,b>0,b≠1);
(5)对数型函数模型:f(x)=mlogax+n(m,n,a为常数,m≠0,a>0,a≠1);
(6)幂型函数模型:f(x)=axn+b(a,b,n为常数,a≠0);
1 (),∈1 ,
了该车相邻两次加油时的情况.
加油时间
2020年5月1日
2020年5月15日
加油量(升)
12
48
加油时的累计里程(千米)
35 000
35 600
注:“累计里程”指汽车从出厂开始累计行驶的路程.
在这段时间内,该车每100千米平均耗油量为(
A.6升 B.8升
C.10升 D.12升
)
答案 B
解析 因为第一次油箱加满,所以第二次的加油量即为该段时间内的耗油量,
3
log 4 8 + = 1,
+ = 1,
解析依题意得
即 2
解得 a=2,b=-2.则
log 4 64 + = 4,
3 + = 4.
y=2log4x-2,当 y=8 时,即 2log4x-2=8,解得 x=1 024.
关键能力 学案突破
考点1
利用函数图像刻画实际问题
【例1】 (2020北京东城一模,10)
故耗油量V=48升.而这段时间内行驶的里程数S=35 600-35 000=600千米.
所以这段时间内,该车每100千米平均耗油量为
48
×100=8升,故选B.
600
3.(2020北京平谷二模,9)溶液酸碱度是通过pH计算的,pH的计算公式为
数学建模方法模型

数学建模方法模型一、统计学方法1 多元回归1、方法概述:在研究变量之间的相互影响关系模型时候用到。
具体地说:其可以定量地描述某一现象和某些因素之间的函数关系,将各变量的已知值带入回归方程可以求出因变量的估计值,从而可以进行预测等相关研究。
2、分类分为两类:多元线性回归和非线性线性回归;其中非线性回归可以通过一定的变化转化为线性回归,比如:y=lnx可以转化为y=u u=lnx来解决;所以这里主要说明多元线性回归应该注意的问题。
3、注意事项在做回归的时候,一定要注意两件事:(1)回归方程的显著性检验(可以通过 sas 和 spss 来解决)(2)回归系数的显著性检验(可以通过 sas 和 spss 来解决)检验是很多学生在建模中不注意的地方,好的检验结果可以体现出你模型的优劣,是完整论文的体现,所以这点大家一定要注意。
4、使用步骤:(1)根据已知条件的数据,通过预处理得出图像的大致趋势或者数据之间的大致关系; (2)选取适当的回归方程;(3)拟合回归参数;(4)回归方程显著性检验及回归系数显著性检验(5)进行后继研究(如:预测等)2 聚类分析1、方法概述该方法说的通俗一点就是,将n个样本,通过适当的方法(选取方法很多,大家可以自行查找,可以在数据挖掘类的书籍中查找到,这里不再阐述)选取m 聚类中心,通过研究各样本和各个聚类中心的距离Xij,选择适当的聚类标准,通常利用最小距离法(一个样本归于一个类也就意味着,该样本距离该类对应的中心距离最近)来聚类,从而可以得到聚类结果,如果利用sas软件或者spss软件来做聚类分析,就可以得到相应的动态聚类图。
这种模型的的特点是直观,容易理解。
2、分类聚类有两种类型:(1)Q型聚类:即对样本聚类;(2)R型聚类:即对变量聚类;通常聚类中衡量标准的选取有两种:(1)相似系数法(2)距离法聚类方法:(1)最短距离法(2)最长距离法(3)中间距离法(4)重心法(5)类平均法(6)可变类平均法(8) 利差平均和法在具体做题中,适当选区方法;3、注意事项在样本量比较大时,要得到聚类结果就显得不是很容易,这时需要根据背景知识和相关的其他方法辅助处理。
数学建模中模型的名词解释

数学建模中模型的名词解释数学建模作为一门学科,是将实际问题转化为数学问题,并运用数学理论和方法来解决问题的过程。
在数学建模中,模型是其中最为重要的概念之一。
模型在解决实际问题时起着关键的作用,可以帮助我们更好地理解现象和规律,并进行预测和优化。
一、模型的定义模型是对实际问题的抽象和简化,通过数学形式来描述。
它可以是数学方程、图表或者其他数学表达形式。
模型的建立需要根据实际问题的特点和需求,选择合适的数学方法和变量,并对其进行适当的假设和简化。
二、数学模型的分类数学模型可以分为动态模型和静态模型两种类型。
1.动态模型动态模型是描述事物随时间变化的模型。
在动态模型中,时间是一个重要的变量,用来描述事物的演化过程。
动态模型可以采用微分方程、差分方程等数学方法进行描述,常见的动态模型包括物理系统的运动学模型、生态系统的种群动力学模型等。
2.静态模型静态模型是描述事物特定状态的模型。
在静态模型中,时间不再是一个重要的变量,模型的关注点集中于某一特定时刻或特定状态下的问题。
静态模型可以采用代数方程、优化模型等进行描述,常见的静态模型包括线性规划模型、统计回归模型等。
三、模型的构建步骤建立数学模型的过程可以分为问题的理解、建立数学模型、求解模型和模型的验证四个步骤。
1.问题的理解问题的理解是建立数学模型的第一步,需要深入了解问题的背景和需求,明确问题的目标和限制条件,分析问题的关键因素和变量。
2.建立数学模型建立数学模型是将实际问题转化为数学问题的过程,需要根据问题的特点和要求选择合适的数学方法和变量,并针对问题进行适当的假设和简化。
建立数学模型时,需要考虑模型的可解性、可行性和合理性。
3.求解模型求解模型是通过数学方法和计算工具,对建立的数学模型进行求解和分析,得到问题的解答或者优化结果。
求解模型时,需要选择合适的求解算法和计算方法,进行模型的计算和推导。
4.模型的验证模型的验证是对模型求解结果的合理性和可靠性进行分析和评价的过程。
数学建模 模型 大全
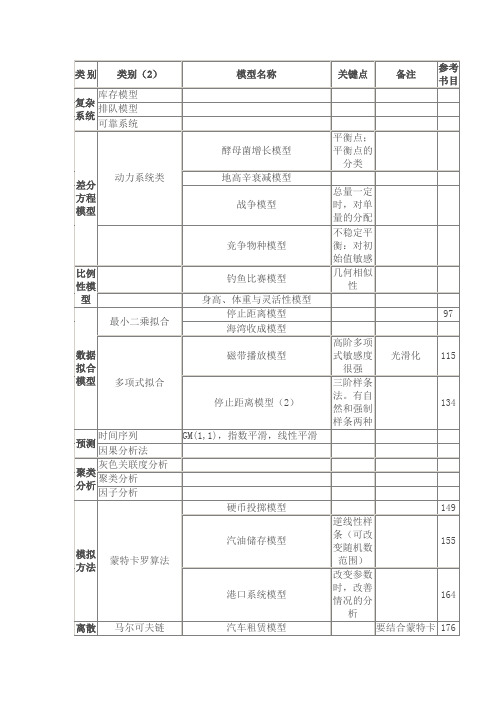
Scheafer微分方程模型
Lanchester战斗模型
350
SIR模型
军备竞赛的经济模型
355
混沌与分形模型
连续优化问题
Steiner树
库存模型
制造模型
最陡上升梯度方法
375
石油转运模型
Lagrange乘子法
注意里面涉及到的经济学概念和意义
381
航天飞机的水箱模型
渔业模型
注意各种“最优”的意义
155
港口系统模型
改变参数时,改善情况的分析
164
离散概率模型
马尔可夫链
汽车租赁模型
要结合蒙特卡罗算法
176
投票趋势模型
177
Markov决策
串联和并联系统模型
178
线性规划模型
无约束类
生产计划模型
192
取整数类
载货模型
194
动态规划类
1Hale Waihona Puke 7多目标规划类投资问题
有时须对目标进行取舍。可采取加权
系统层次分析
97
海湾收成模型
多项式拟合
磁带播放模型
高阶多项式敏感度很强
光滑化
115
停止距离模型(2)
三阶样条法。有自然和强制样条两种
134
预测
时间序列
GM(1,1),指数平滑,线性平滑
因果分析法
聚类分析
灰色关联度分析
聚类分析
因子分析
模拟方法
蒙特卡罗算法
硬币投掷模型
149
汽油储存模型
逆线性样条(可改变随机数范围)
图标模型
军备竞赛模型
民防、移动发射台、多弹头
数学建模图论模型

任意两点均有通路的图称为连通图。
连通而无圈的图称为树,常用T=<V,E>表示树。
若图G’是图 G 的生成子图,且G’又是一棵树, 则称G’是图G 的生成树。
例 Ramsey问题
图1
图2
并且常记: V = v1, v2, … , vn, |V | = n ; E = {e1, e2, … , em}ek=vivj , |E | = m
称点vi , vj为边vivj的端点 在有向图中, 称点vi , vj分别为边vivj的 始点和终点. 该图称为n,m图
8
对于一个图G = V, E , 人们常用图形来表示它, 称其 为图解 凡是有向边, 在图解上都用箭头标明其方向.
4、P'代替P,T'代替T,重复步骤2,3
定理2 设 T为V的子集,P=V-T,设 (1)对P中的任一点p,存在一条从a到p的最短路径,这条路径仅有P中的
点构成, (2)对于每一点t,它关于P的指标为l(t),令x为最小指标所在的点, 即:
l(x)mli(tn )} t{ ,T
(3)令P’=P Ux,T’=T-{x},l’(t)表示T'中结点t关于P'的指标,则
解:用四维01向量表示人,狼,羊,菜例在过河西河岸问的题状态(在
岸则分量取1;否则取0),共有24 =16 种状态; 在河东岸 态类似记作。
由题设,状态(0,1,1,0),(0,0,1,1),(0,1,1,1)是不允许的
其对应状态:(1,0,0,1), (1,1,0,0),(1,0,0,0)也是不允许
数学建模分类模型

数学建模分类模型
数学建模分类模型是利用数学技术,在计算机环境中构建出一系列的
分类模型,它可以对对象进行划分,根据划分的结果选择合适的计算模型,以便完成对象属性的计算和分类。
数学建模分类模型有很多,主要有线性
分类模型、非线性分类模型、支持向量机分类模型、决策树分类模型、朴
素贝叶斯分类模型、神经网络分类模型等。
线性分类模型是在定义的特征
空间中建模,主要利用一个或多个线性超平面将实例空间划分成多个子空间;非线性分类模型是在数据特征的特征空间中建立的模型,通过训练数
据生成某种更复杂的函数模型来划分数据;支持向量机分类模型是基于寻
找最大边界线分类模型,它能够正确分类线性不可分的数据;决策树分类
模型是基于递归地划分样本的一种建模方法;朴素贝叶斯分类模型是一种
生成模型,基于贝叶斯定理和特征条件独立性假设;神经网络分类模型是
一种基于多层神经元结构构建问题分类模型。
数学模型与数学建模

数学模型与数学建模数学模型是运用数学方法描述现实或抽象问题的一种工具或方法。
数学模型又可分为解析模型和仿真模型两种。
解析模型是指基于已知公式和数据进行分析求解,得到数学表达式或数值解的模型。
仿真模型是指利用计算机建立的模拟系统模型,根据模型建立的规则模拟输入变量所产生的输出结果。
数学建模是指通过数学知识把实际问题抽象为数学问题,并基于其建立数学模型。
数学建模技术可应用于各个领域,如自然科学、工程技术、社会科学、医学等。
下面就对数学模型和数学建模的一些概念和应用进行详细介绍。
一、数学模型的分类数学模型主要包括解析模型和仿真模型。
下面分别介绍:1、解析模型解析模型是指通过已知数据和公式,进行分析推导求解数学表达式或数值解的模型。
它是基于数学理论和分析方法的,其主要步骤为:建立问题的数学模型、求解模型、验证模型和应用模型。
解析模型主要包括以下几种类型:(1)几何模型几何模型是指通过几何图形描述实际问题的模型。
如,根据实际问题的条件,建立几何图形,求解图形的面积、周长、体积等数学问题,就是利用几何模型进行的建模。
几何模型常用于计算机图形学、工程地质学、建筑工程学等领域。
(2)微积分模型微积分模型是指通过微积分的方法求解实际问题的模型。
微积分是数学分析的基础,微积分模型广泛应用于科学工程领域。
如在热力学、流体力学、电磁学、生物学等领域,常用微积分模型来研究问题。
(3)代数模型代数模型是指通过代数方程和不等式描述实际问题的模型。
如根据实际问题建立代数模型求解方程组、解析几何等问题。
代数模型广泛应用于物理、经济、金融等领域。
(4)概率统计模型概率统计模型是指通过概率统计理论描述实际问题的模型。
如,许多保险公司的经营决策是基于概率统计模型的建立和分析的。
又如,酒店的房价决定也取决于概率统计模型。
2、仿真模型仿真模型是指利用计算机模拟系统建立的模型。
计算机可以模拟出一些人工难以模拟或难以观测的复杂系统,并通过模拟结果对系统进行推理分析或进行决策。
常见数学建模模型

常见数学建模模型一、线性规划模型线性规划是一种常用的数学建模方法,它通过建立线性函数和约束条件,寻找最优解。
线性规划可以应用于各种实际问题,如生产调度、资源分配、运输问题等。
通过确定决策变量、目标函数和约束条件,可以建立数学模型,并利用线性规划算法求解最优解。
二、整数规划模型整数规划是线性规划的一种扩展形式,它要求决策变量为整数。
整数规划模型常用于一些离散决策问题,如旅行商问题、装箱问题等。
通过引入整数变量和相应的约束条件,可以将问题转化为整数规划模型,并利用整数规划算法求解最优解。
三、非线性规划模型非线性规划是一类目标函数或约束条件中存在非线性项的优化问题。
非线性规划模型常见于工程设计、经济优化等领域。
通过建立非线性函数和约束条件,可以将问题转化为非线性规划模型,并利用非线性规划算法求解最优解。
四、动态规划模型动态规划是一种通过将问题分解为子问题并以递归方式求解的数学建模方法。
动态规划常用于求解具有最优子结构性质的问题,如背包问题、最短路径问题等。
通过定义状态变量、状态转移方程和边界条件,可以建立动态规划模型,并利用动态规划算法求解最优解。
五、排队论模型排队论是一种研究队列系统的数学理论,可以用于描述和优化各种排队系统,如交通流、生产线、客户服务等。
排队论模型通常包括到达过程、服务过程、队列长度等要素,并通过概率和统计方法分析系统性能,如平均等待时间、系统利用率等。
六、图论模型图论是一种研究图结构和图算法的数学理论,可以用于描述和优化各种实际问题,如网络优化、路径规划、社交网络等。
图论模型通过定义节点、边和权重,以及相应的约束条件,可以建立图论模型,并利用图算法求解最优解。
七、随机模型随机模型是一种考虑不确定性因素的数学建模方法,常用于风险评估、金融建模等领域。
随机模型通过引入随机变量和概率分布,描述不确定性因素,并利用概率和统计方法分析系统行为和性能。
八、模糊模型模糊模型是一种用于处理模糊信息的数学建模方法,常用于模糊推理、模糊控制等领域。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五邑大学 数学建模 课程考核论文2010-2011 学年度第 2 学期102030405060708090第一季度第三季度东部西部北部论文题目 抑制物价快速上涨问题得分学号姓名(打印) 姓名(手写)ap0808221 林加海 ap0808204陈荣昌指导老师—邹祥福——2011.6.20抑制物价快速上涨问题摘要本文通过一个多元线性回归模型较好地解决了影响物价因素的问题。
使我国经济快速发展的同时,使百姓得到真的实惠,又保证了经济的长远的发展。
物价问题比较复杂。
在本次实验中我们参阅大量资料把影响物价的的因素主要概括括需求性因素(消费,投资,进出口,政府支出等)、货币性因素(货币供给量)、结构性因素(房地产价格,农产品价格等)以及其他因素(如预期因素等)。
总结出原先物价计算方法的不足之处,需要建立一种新的计算和预测的方法。
首先,为了确定物价和影响因素之间的关系我们用了多元线性回归,从国家统计局找到相关数据经过挑选,建立了函数关系,为了使函数更具有说服力我们进一步用了残差分析,检验所得到的结果的合理性 。
本文利用matlab 软件实现了拟合出多元线性回归函数y=86.4798967193207+0.00441024146152813*x1+4.32730555279258e-007*x2+0.00377788223112076*x3+2.70211635024846e-006*x4+7.58738000216411e-005*x5,置信度95%,且20.932609896853743,_R F ==检验值8.30338450288840>,但是显著性概率.α=005相关的0.055839341752489056>0.p =。
再利用逐步回归的方法,拟合出Y=94.4958+0.00771506*x1+5.8917e-007*x2+0.00250019*x3+1.90595e-006*x4+6.62396e-005*x5.93269896853743R =200,修正的R 2值.R α=20897797,F_检验值=26.3535,与显著性概率相关的p 值=..<000106754005,残差均方RMSE =0.204517,以上指标值都很好,说明回归效果比较理想。
通过对物价形成及演化问题的讨论,提出以量化分析为基础的调节物价的方法,深入分析找出影响物价的主要因素,并就此分析现在物价的上涨情况,根据《关于稳定消费价格总水平保障群众基本生活的通知》,根据模型分析给出抑制物价的政策建议,并对未来的形势走向根据模型给出预测。
关键字:物价,逐步回归分析,上涨因素,预测,多元回归分析问题重述2010年国家统计局公布我国10月宏观经济数据,居民消费价格指数同比上涨4.4%,其中食品类价格上涨10.1%,蔬菜价格涨了31%,创两年来的新高。
普通百姓日常开支大幅增加,国家出台《关于稳定消费价格总水平保障群众基本生活的通知》,要求各地和有关部门及时采取16项措施,进一步做好价格调控监管工作,稳定市场价格,切实保障群众基本生活。
我们通过收集数据、建立模型、定量分析,分析原因和得出结果。
最后,我们根据模型建立及分析得到的结果,给有关部门写一份建议报告,给出具体的意见。
问题分析在计算综合指数时,一般有两种形式:拉氏指数和帕氏指数。
以基期销售量为权数,得到的指数为拉氏指数100p q p q∑∑以报告期的销售量为权数,得到的指数为帕氏指数1101p q p q∑∑.也可采用一般加权平均数或调和加权平均数的方式来计算。
权数选择很重要,如果用基期销售量作权数,一般采用加权算术平均数形式0000010000p kp p q q p p q p q =∑∑∑∑相当于拉氏数。
如果用报告期销售量作权数,一般采用调和加权平均数形式1111011111p p 1qqp p q p q kp =∑∑∑∑相当于帕氏指数。
我国现行物价指数基本上是通过调查个体价格。
计算个体价格指数,然后采用固定数量加权形式逐级汇总编制物价指数的,即kw w ∑∑。
其权数w 根据基期销售额并参照报告期的市场变化来确定。
这种指数形式本质上与帕氏指数的原理是一致的。
如在编制全社会的零售物价指数时,首先将全部零售商品区分为十四大类商品;在各大类商品中又分小类,在小类中再分细类·从各商品集团中选到代表规格品,调查并用加权平均法计算代表规格品的价格,再计算物价指数,然后依据代表规格品物价指数及所给定 权数,逐级汇总计算各类指数,最后汇总为全社会零售物价指数。
但是现行的物价指数存在以下主要问题:首先,零售物价指数反应不全。
生产资料的销售是零售市场的一部分,只有一起包括在内才能反映整个零售市场的价格变动情况。
其次。
生活费用价格指数反映越界。
生活费用是零售物价与服务项目的加权,但零售物价包括了生产资料,这造成了其不能准确反映居民生活费用价格水平。
再者,生产资料价格指数计算范围不全,不能准确、全面反映全社会生产资料价格水平。
由于存在多种形式的供应方式,各种形式的扶贫、脱贫、新技术推广配套供应,粮食定购等供应方式,目前的生产资料价格指数就不能准确、全面反映全社会生资价格水平。
因此,我们根据所学知识,建立一个新的物价指数模型,更加科学的预测物价指数的变动及发展规律。
根据相关理论,我们我们考虑如下因素:需求性因素(消费,投资,进出口,政府支出等)、货币性因素(货币供给量)、结构性因素(房地产价格,农产品价格等)以及其他因素(如预期因素等)。
模型假设及符号说明(1) 社会的发展平衡稳定,排除突发事件导致数据的突变。
(2) 假设因素之间的联系较小,不存在一个因素的变化导致其他因素的剧烈变化。
(3) 所给数据真实据可靠,反应实际情况(4) 对价格的齐次性: 若所有商品的价格均上升k 倍, 物价指数也上升k 倍; ( 5) 对货币单位的独立性: 物价指数与货币单位的选择无关, 即只要商品的实际价格不变, 仅仅货币单位改变, 物价指数不应改变;( 6) 物价指数介于单种商品价格比值的最小值和最大值之间; ( 7) 物价指数不因某种商品被淘汰而失去意义.考虑数据的可得性,最终选择以下变量作为分析研究对CPI 的影响 X1 房地产业价格X2 固定资产投资总额 X3 进出口总额 X4 货币供应量X5社会零售商品总额模型建立房地产业价格。
近几年,我国房地产价格一路攀升,已经影响到居民购房的基本能力,同时也引起相关行业价格的波动。
固定资产投资总额。
投资会引起银行信贷资金的扩张,增加货币投放量,引发通货膨胀。
进出口总额。
进出口是拉动经济增长的重要马车,尤其出口增加迅速时,外汇资金迅速增加,引导投资扩大,也会造成物价波动。
货币供应量。
货币供应量一直都是价格波动的重要原因。
社会零售商品总额。
该指标是体现社会总需求的基本数据,反映需求变化对物价的影响,当该指标迅速上升,使社会总需求超过总供给,引起价格变化。
由于我国每月公布的CPI 数据是按同比来计算的,故在数据选择的时候,对数据进行了一定的变换。
其中每期流量数据,经变换后表示的是每期CPI 所表现的价格变动时间内所产生的流量。
对于某些存量数据,选择的是当月的存量数据。
一般在生产实践和科学研究中,人们得到了参数(),,n x x x =⋅⋅⋅1和因变量y 的数据,需要求出关系式()y f x =,这时就可以用到回归分析的方法。
如果只考虑f 是线性函数的情形,当自变量只有一个时,即,(),,n x x x =⋅⋅⋅1中n =1时,称为一元线性回归,当自变量有多个时,即,(),,n x x x =⋅⋅⋅1中n ≥2时,称为多元线性回归。
进行线性回归时,有4个基本假定: ① 因变量与自变量之间存在线性关系; ② 残差是独立的;③ 残差满足方差奇性; ④ 残差满足正态分布。
在Matlab 软件包中有一个做一般多元回归分析的命令regeress ,调用格式如下:[b, bint, r, rint, stats] = regress(y ,X,alpha) 或者[b, bint, r, rint, stats] = regress(y ,X) 此时,默认alpha = 0.05. 这里,y 是一个1n ⨯的列向量,X 是一个()1n m ⨯+的矩阵,其中第一列是全1向量(这一点对于回归来说很重要,这一个全1列向量对应回归方程的常数项),一般情况下,需要人工造一个全1列向量。
回归方程具有如下形式:011m m y x x λλλε=++⋅⋅⋅++其中,ε是残差。
在返回项[b,bint,r,rint,stats]中, ①01m b λλλ=⋅⋅⋅是回归方程的系数;②int b 是一个2m ⨯矩阵,它的第i 行表示i λ的(1-alpha)置信区间; ③r 是1n ⨯的残差列向量;④int r 是2n ⨯矩阵,它的第i 行表示第i 个残差i r 的(1-alpha)置信区间; 注释:残差与残差区间杠杆图,最好在0点线附近比较均匀的分布,而不呈现一定的规律性,如果是这样,就说明回归分析做得比较理想。
⑤ 一般的,stast 返回4个值:2R 值、F_检验值、阈值f ,与显著性概率相关的p 值(如果这个p 值不存在,则,只输出前3项)。
注释: (1)一般说来,2R 值越大越好。
(2)人们一般用以下统计量对回归方程做显著性检验:F_检验、t_检验、以及相关系数检验法。
Matlab 软件包输出F_检验值和阈值f 。
一般说来,F_检验值越大越好,特别的,应该有F_检验值f >。
(3)与显著性概率相关的p值应该满足p alpha>,则说明回归<。
如果p alpha方程中有多余的自变量,可以将这些多余的自变量从回归方程中剔除(见下面逐步回归的内容)。
这几个技术指标说明拟合程度的好坏。
这几个指标都好,就说明回归方程是有意义的。
模型求解物价指数的多元回归模型的建立x1=[131 135 106 136 136 134 134 133 133 ]';x2=[13014.0268 29792.6847 46742.7492 67358.2972 98047.3795 119866.2477 140997.7447 165869.5752 1877566.105 ]';x3=[3240.7 3288.5 3399.8 3365.2 3464.2 3504.7 3492.6 3530.3 3523.6 ]';x4=[112334.2 11321.7 11510.4 12455.0617 12329.9 12252.8 12569.8 13536.5 14284.8 ]';x5=[40758.58 42865.79 39080.58 39657.54 38652.97 38904.85 39543.16 39922.76 41854.41 ]';y=[102.7 102.7 102.8 103.10 102.90 103.30 103.50 103.60 104.40 ]';e=ones(9,1);x=[e,x1,x2,x3,x4,x5];[b,bint,r,rint,stats]=regress(y,x)rcoplot(r,rint)b =86.47989671932070.004410241461528134.32730555279258e-0070.003777882231120762.70211635024846e-0067.58738000216411e-005bint =57.6517132316945 115.308080206947-0.0265424325364306 0.0353629154594868-3.33477737109042e-007 1.19893884766756e-006-0.00174313787047828 0.00929890233271979-8.66465282394733e-006 1.40688855244442e-005-0.000255471673027052 0.000407219273070334r =-0.00230129081566588-0.0947201675733851-0.007947891111300010.23520987922069-0.275521820521206-0.04805001848914970.1392305359018880.0590379858630854-0.00493721247502776rint =-0.00947859076926696 0.0048760091379352-0.194633870082707 0.00519353493593699-0.0249417458137498 0.00904596359114981-0.0339258210359711 0.504345579477352-0.627136483142244 0.0760928420998317-0.823808535953563 0.727708498975263-0.597472706733677 0.875933778537452-0.511054271191228 0.629130242917399-0.0119320358327282 0.0020576108826727stats =0.932609896853743 8.3033845028884 0.0558393417524896 0.0551600473900416因此y=86.4798967193207+0.00441024146152813*x1+4.32730555279258e-007*x2+0.00 377788223112076*x3+2.70211635024846e-006*x4+7.58738000216411e-005*x5其中:b 为回归系数估计值;bint为置信区间;stats包括判定系数R2,显著性检验F,概率p;r为残差;rint为置信区间。
