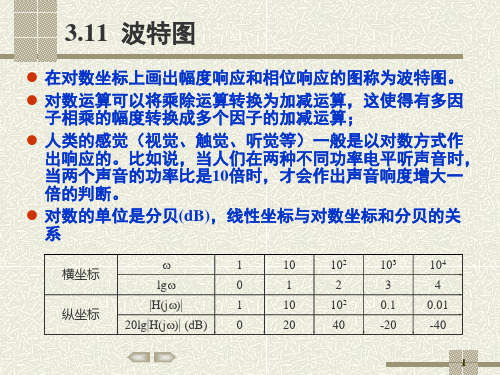
手把手教你看懂波特图
波特图jieshao
假设：)()()(ωϕωωj e j H j H =。
对其取对数：[][][])()()()(ln )(ln )(ln )(ωϕωωϕωωωωϕj G j j H e j H j H j +=+==其虚部正是系统的相频特性，而实部：[])(ln )(ωωj H G =称为对数增益，反映了系统幅频特性，单位奈培（Np, Neper ）。
一般情况下不用自然对数，而取常用对数，定义： [])(log 20)(ωωj H G =单位：分贝(Deci-Bel,dB)。
奈培与分贝的转换关系：1 Np = 8.686 dB在理论分析中，一般使用Np ；在实际应用中，一般使用dB用分贝表示增益，解决了信号动态范围与精度之间的矛盾。
如果在频率坐标中同样使用对数坐标，则同样可以解决频率的范围与精度之间的矛盾。
这样一来就形成了波特图。
✧ 波特图的横坐标可以用ωlog ，也可以用f log ; ✧ 在波特图的横坐标上，一般直接标注频率值；✧ 波特图的横坐标上只能表示0>ω或者0>f 频率下的系统特性。
图中的二、三象限并非表示频率小于零的部分，而是表示频率小于1（大于零）部分频率特性。
✓ 根据系统频率特性的共扼对称性,不难得到频率小于零部分的特性。
✧ 在波特图的纵坐标上，可以标注系统幅频特性值（如图中红字所示），也可以标注分贝值。
✧ 为了方便参数的判读，实际工程中的波特图中的刻度也不是按照等间隔设置的，而是按照对数间隔设置。
例如下图。
有专用的对数坐标图纸可以用于手工绘制波特图。
波特图的纵坐标上同样也只表示了系统幅频特性中大于零的部分。
图中的三、四象限并非表示系统的幅频特性小于零，而是表示系统的幅频特性小于1（大于零）。
三、 线性系统的波特图1、一般系统的波特图⎪⎪⎭⎫⎝⎛-==∑∑==∏∏--=n i i m i i j n i imi ie pj zj H j H 11110)(αβωωω∑∑∑∑====-+=---+===ni pi mi zi ni imi i G G H p j z j H j H G 110110)()(log 20log 20log 20log 20)(log 20)(ωωωωωω所以，不仅系统的相频特性是各个零点或极点的相频特性的叠加，而且系统的幅频特性是各个零点或极点的相频特性的叠加。
第13章13-67 波特图 电路分析基础 教学课件
1+
25 Q2
½ +
5 Q
0
=
1+
25 Q2
½ –
5 Q
0
，0， 2 =
三点画出三段渐近线，再根据(1)=
84.3°， (0)= 0°， (2)= – 84.3° ，三点数值画平滑 曲线
90 (°)
°
84.3°
45 ° 0 0.1
– 45° –
2 1.0 0 1 0
–84.3°
10.0
0
电路分析基础——第三部分：13-6~7 19/29
lnH(j) = lnB(j) – lnA(j)
= lnK + ln(1+j/Z1) + ln(1+j/Z2) + ••• + ln(1+j/Zm)
– ln(1+j/P1) – ln(1+j/P2) – ••• – ln(1+j/Pn)
= [lnK+ ln|1+j/Z1| + ln|1+j/Z2| + ••• + ln|1+j/Zm|
相位特性
分别相当于一条平行于横轴、交纵轴于 90° 的直线和一条 平行于横轴、交纵轴于 – 90° 的直线。
电路分析基础——第三部分：13-6~7 11/29
由多个一阶复合的高阶系统的波特图 （dB ~ lg 曲线）
复合高阶系统系统函数可以表示为
H(j) =
B(j) A(j)
=
K
(1+j/Z1)(1+j/Z2)•••(1+j/Zm) (1+j/P1)(1+j/P2)•••(1+j/Pn)
信号与系统3-8波特图课件
G2(dB) 20dB/ dec
20
1()
90
0 0.1
1
10
20
0
(a) 幅度的波特图
(b) 相位的波特图
4
一阶极点因子
一阶极点因子为
H1 (s)
s
a
a
1 1 s/
a
H1 ( j)
1
1
j
/a
G1 20 lg | 1 j / a |
11
二阶极点因子
幅度波特图
= a 称为转折频率,最大误差
G1( a ) 20 lg(b a / a)dB
二阶极点因子的相位
1
()
arc
tan( 1
b
/
2
a /
a
)
在低频段，当<< a 时
1() 0
在高频段，当>> a 时
1() 180
当= a 时
1 () 90
转折频率也称截止频率
G1(dB)
a
0
20
40
10 a
40dB/ dec
1()
0.1 a 0 90 180
a
10 a
90/ dec
12
二阶零点因子
二阶零点因子
H 2 (s)
s2
bs a
a
1
bs /
a
s2
/
a
画法与二阶极点的画法相同，仅仅有一个正负号 的变化。
G2 (dB)
40 20
0
a
40dB/ dec
10 a
波特图方法
University of Science and Technology of China§1.5 波特图方法xdxu@2010年3月26日提纲1. 对数坐标系2. 常数项K’3. 负实极点4. 实零点5. 复共轭极点6. 复共轭零点7. 实例分析1. 对数坐标系波特图定义：以对数为标尺、用折线绘制的幅频、相频特性曲线称为伯德图，或波特图波特图方法的优势采用对数坐标系便于表示较大的幅度动态范围和较宽的频率跨度将频率特性的绘制与系统函数的极零点分布直接联系起来，简化系统频率响应曲线的绘制波特图方法还可以近似估算系统的频率响应参数，快速了解通带特征1. 对数坐标系第二步：绘制出常数项、实极点，实零点，复共轭极点和复共轭零点等各单项的幅频和相频波特图第三步：将各个单项线性叠加在一起，即可完整获得系统的幅频和相频波特图3. 负实极点提示绘图时，必须标明转折点坐标和直线斜率方便起见，转折点坐标实际仍然以角频率值标注，而并非其对数值，即横坐标度量单位仍以rad/s计4. 实数零点（1） （2）0 iz≠0 iz=5. 复共轭极点误差分析以转折点处折线近似导致的误差最大 该点误差与阻尼系数有关7. 实例分析第二步根据该系统的各单项参数，绘制出各单项的幅频波特图和相频波特图，标明转折点及折线斜率7. 实例分析第三步线性叠加出完整的幅频波特图和相频波特图()φω7. 实例分析例：根据波特图求频率响应参数已知上例中系统幅频波特图如图所示，试确定系统的通带特性，求通带增益和截止频率。
7. 实例分析第一步分析幅频波特图，获得系统的通带特性，确定待估计的具体频率响应参数0ωlH高通系统：，。
波特图的见解
对应的频率特性是 G( j ) j 1 幅频特性
G ( j ) 2 2 1
相频特性
G( j ) arctg
当 0 时， G( j 0) 1 ， G( j0) 00 ； 1 时， G ( j 1 ) 2 ， G ( j 1 ) 45 0 ； 当 T 当 时， G( j) ，G( j) 900 ；
当ω 由零至无穷大变化时，惯性环节的频率特性 在 G( j ) 平面上是正实轴下方的半个圆周，
Im
.
0
0.5
G
0
1
Re
450
1/ T
图5-4 惯性环节的频率响应
1 1 T 证明： G( j ) j 2 2 jT 1 1 T 1 T 2 2
对应的频率特性是
G ( j ) 1 jT 1
1 1 T 2 2
幅频特性
G( j )
相频特性
G ( j ) arctgT
当 0 时， G( j 0) 1 ， G( j0) 00 ； 1 1 1 1 G ( j ) 45 0 ； 0.707 当 时， G ( j ) ， T T T 2 当 时， G( j) 0 ， G( j) 900 ；
Im
1 2 ( )
G
1
Re
0
图5-8
0
二阶微分环节频率特性图
（七） 不稳定惯性环节 不稳定惯性环节的传递函数为
G ( s) 1 1 Ts
对应的频率特性是 幅频特性 相频特性
1 G ( j ) 1 jT
G ( j )
波特图补充
()
90
1
10
1 102 10 T2 T2
()
-90 -180
10 T 2
19
例1
S 4 S 25 计算此网络的增益和相频特性，画波特图
2
H s
25 S
解：极点为
p 1 , 2 2 j 21
p1
1 T2
25 s
5
2T 2 0 .4
G()
(dB)
20
20dB/10倍频
1 -20
10
100
-20dB/10倍频
7
()
90º
1 -90º
10
100
8
(3) 一阶零点 （极点）
G 20 lg j Z 1
令
Z1 1 T1
tg
1
Z 1
G
当远离断点时，此折线较精确地表示实
际曲线，在断点处误差最大为3dB
12
() 90º
45º
+45º /10倍频
1
1 10 T1
10 1 102 10 103
T1 T1
104
13
(4) 共轭复零点(极点） 设二次因式如下，其中2是Z2的实部
H ( ) j Z 2 j Z
25 ( s 25 s
2
H (s)
s 4 s 25
2
s 25
1)
s 0 . 04 s 0 . 16 s 1
2
25
20
作图步骤： 幅值：1. 对复数共轭极点，画一条从
波特图
(二)波特图的画法
1.一般画法 画波特图时，分三个频段进行，先画幅频特性，顺序是中
频段、低频段和高频段。将三个频段的频率特性(或称频率
响应)合起来就是全频段的幅频特性，然后再根据幅频特性 画出相应的相频特性来。 (1)中频段 中频时电压放大倍数的表达式为 A usM
ri R S ri Pgm R c ，
③再画相频特性。 在10fL至0.1fH之间的中频区，Φ =－180°； 当f<0.1fL时，Φ = –90°； 当f>10fH前，Φ = –270°； 在0.1fL至10fL 之间以及0.1fH至10fH之间，相频特性分别 为两条斜率为 –45°/十倍频程的直线。以上五段直线构成 的折线就是放大电路的相频特性。
第三章
多级放大电路与频率响应
3.1多级放大电路
一、多级放大电路
(一)多级放大电路的组成
图3-1 多级放大电路的组成框图
一、多根据每级所处的位置和作用的不同，多级放大 电路大致可分为三部分：输入级、中间级和输出级。
输入级（前置级）：一般要求有较高的输入阻抗，使 它与信号源相接时，索取电流很小。所以常采用高输 入阻抗的放大电路，如射极输出器、场效应管放大电 路等。 中间级：一般承担着主要的电压放大的任务，故称之 为电压放大级，常采用共射电路。
2
A uSL
(3-6)
总相角为
180
0
arctan
fL f
(3-7)
现在，我们用折线近似的方法，画低频段的幅频特性 和相频特性。
图3-11 低频段对数频率响应 (a)低频对数幅频特性； (b)低频对数相频特性
先看式(3-8)中的第二项。f>>fL时，
波特五力分析模型详解
波特五力分析模型详解五种力量模型将大量不同的因素汇集在一个简便的模型中，以此分析一个行业的基本竞争态势。
五种力量模型确定了竞争的五种主要来源，即供应商和购买者的议价能力，潜在进入者的威胁，替代品的威胁，以及最后一点，来自目前在同一行业的公司间的竞争。
一种可行战略的提出首先应该包括确认并评价这五种力量，不同力量的特性和重要性因行业和公司的不同而变化，如下图所示：[编辑]1．供应商的议价能力供方主要通过其提高投入要素价格与降低单位价值质量的能力，来影响行业中现有企业的盈利能力与产品竞争力。
供方力量的强弱主要取决于他们所提供给买主的是什么投入要素，当供方所提供的投入要素其价值构成了买主产品总成本的较大比例、对买主产品生产过程非常重要、或者严重影响买主产品的质量时，供方对于买主的潜在讨价还价力量就大大增强。
一般来说，满足如下条件的供方集团会具有比较强大的讨价还价力量：- 供方行业为一些具有比较稳固市场地位而不受市场剧烈竞争困挠的企业所控制，其产品的买主很多，以致于每一单个买主都不可能成为供方的重要客户。
- 供方各企业的产品各具有一定特色，以致于买主难以转换或转换成本太高，或者很难找到可与供方企业产品相竞争的替代品。
- 供方能够方便地实行前向联合或一体化，而买主难以进行后向联合或一体化。
（注：简单按中国说法，店大欺客）[编辑]2．购买者的议价能力购买者主要通过其压价与要求提供较高的产品或服务质量的能力，来影响行业中现有企业的盈利能力。
一般来说，满足如下条件的购买者可能具有较强的讨价还价力量：- 购买者的总数较少，而每个购买者的购买量较大，占了卖方销售量的很大比例。
- 卖方行业由大量相对来说规模较小的企业所组成。
- 购买者所购买的基本上是一种标准化产品，同时向多个卖主购买产品在经济上也完全可行。
- 购买者有能力实现后向一体化，而卖主不可能前向一体化。
（注：简单按中国说法，客大欺主）[编辑]3．新进入者的威胁（threat of new entrants）新进入者在给行业带来新生产能力、新资源的同时，将希望在已被现有企业瓜分完毕的市场中赢得一席之地，这就有可能会与现有企业发生原材料与市场份额的竞争，最终导致行业中现有企业盈利水平降低，严重的话还有可能危及这些企业的生存。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
波特图基础
当你心血来潮想学习一下运算放大器时，有一张图是你跳不过去的坎。
波特图在运算放大器的稳定性分析中起着无法替代的作用。
他能够直接反映出你所设计的电路是否稳定，你的电路对你信号的影响。
然而，波特图有时并不是那么通俗易懂。
波特图是用来反映一个系统网络对于不同频率的信号的放大能力。
一般是由二张图组合而成，一张幅频图表示频率响应（电压增益随频率的变化而发生增大或衰减、相位随频率而发生变化关系）增益的分贝值对频率的变化，另一张相频图则是频率响应的相位对频率的变化。
幅频图：X 轴是以指数标度表示频率的变化，Y 轴是根据分贝的定义做的放大倍数。
相频图：X 轴也是以指数标度表示频率的变化，Y 轴以线性标度表示相位的变化。
分 贝：在电压增益中： ⎪⎪⎭
⎫ ⎝⎛⨯=IN OUT V V dB log 20 在功率增益中： ⎪⎪⎭
⎫ ⎝⎛⨯=IN OUT P P dB log 10
为什么是-3分贝：当信号增益比初始降低了3分贝时，带入你会发现信号的功率下降了一半。
所以通常将-3分贝对应的频率叫做-3分贝通频带。
大于该频率的信号一般被视为没有进行相应的放大。
下降速率：有十倍频程（decade ）跟二倍频程（octave ）两种基本单位，-20dB/decade 与-6dB/octave 是一样的，数学推导就不在这里叙述了。
零点与极点：单个极点响应在波特
图上具有按 -20dB/decade 或
-6db/octave 斜率下降的特点。
在极
点位置，增益为直流增益减去3dB 。
在相位曲线上，极点在频率上具有
-45°的相移。
相位在的两边以45°
/decade 的斜率变化为0°和 -90°。
单极点可用简单RC 低通网络来表
示。
单个零点响应在波特图上具有按
+20dB/decade 或+6db/octave 斜率上升（对应于下降）的特点。
在零点位置，增益为直流增益加 3dB 。
在相位曲线上，零点在其频率上具有+45°的相移。
相位在的两边以+45°/decade 斜率变化为 0°与+90°。
单零点可用简单RC 高通网络来表示。
在幅频图中确定频率：
用尺子量出L 与D 的长度，λ为D 左侧刻度的值。
频率D L p f 10)(⨯=λ。
举个栗子：由良好的读图能力得：
L=1cm ，D=2cm 。
D 的左侧刻度为10Hz 。
当
前频率()Hz p f 6.31101021≈⨯=。