温州大学数学分析(A)2007真题

合集下载

人大2007年数学分析真题

2007数学分析试题：（请将答案做再答题纸上，再试题上做题无效）（本试卷共六道大题，满分150分）一、（本题满分20分）设()f x 在∞（0，）内可导，并且存在p ＞0使得()lim p x f x x →+∞=1. (1) 对任何1＞|δ|＞0，求极限lim x →+∞[(1)]()p f x f x p x δδ+-； (2) 求二次极限0l i m δ→l i m x →+∞[(1)]()p f x f x p xδδ+-； (3) 若'()f x 单增，证明对任何h ＞0，x ∈(0,)+∞，只要x -h ∈(0,)+∞，就有()f x -()f x h -≤'()hf x ≤()f x h +-()f x ；(4) 证明：lim x →+∞'1()p f x px -=1.二、（本题满份25分）设直线y =ax (0＜a ＜1)与抛物线y =2x 在第一象限所围成的平面图形的面积为1s ，y =ax ，y =2x 与直线x =1所围成的平面图形的面积为2s .(1) 试确定a 的值使得1s +2s 达到最小,并求出最小值；(2) 求该最小值所对应的平面图形绕x 轴旋转一周所得旋转体的体积；(3) 用定积分表示该最小值所对应的平面图形绕x 轴旋转一周所得旋转体的侧面积(不必求出它的值).（1）设p ∈(0,1)，将()f x =cos px 在[,]ππ-展开为以2π为周期的傅立叶级数；（2）利用11x+的麦克老林展开式，证明：p ∈(0,1)时， 1101p x dx x -+⎰=0(1)nn p n ∞=-+∑；（3）证明：p ∈(0,1)时，1101p px x dx x --++⎰= sin p π．四、（本题满分20分）证明边长分别为,,,a b c d 的凸边形中，当,a b 边的夹角α满足cos α=22222()a b c d ab cd +--+，并且,c d 的夹角γ满足α+γ=π时，该四边形的面积最大，并且最大面积为 S =1()sin 2ab cd a +．五、（本题满分20分）设 [,]a b ⨯[,)c +∞={(,)x y |,a x b c y ≤≤≤<+∞}，(,)f x y 定义在[,]a b ⨯[,)c +∞上．(1) 叙述含参变量x 的无穷限广义积分()I x ＝(,)c f x y dy +∞⎰在[,]a b 上一致收敛的柯西原理；(2) 叙述函数级数1()n n x μ+∞=∑在[,]a b 上一致收敛的柯西原理； (3) 证明：()I x ＝(,)c f x y dy +∞⎰在[,]a b 上一致收敛的充要条件是对任何发散+∞的数列1{}n n A +∞=，(,1,2,...)n A c n >=，函数项级数11(,)n n A A n f x y dy -+∞=∑⎰在在[,]a b 上一致收敛，其中0A =c ．设V 是空间二维单连通的有界区域，其边界∑是简单光滑曲面，点00,0,0()P x y z ∈V .u =(,,)u x y z 在_V =V ⋃∑上具有连续偏导数,在V 内具有二阶连续偏导数,且满足22u x ∂∂+22u y ∂∂+22uz ∂∂=0.(1) 证明:0lim t +→214t πtudS ∑⎰⎰=00,0,0()u x y z ,其中t ∑是含在V 内的球面222000()()()x x y y z z -+-+-=2t ()0t >; (2) 设_n =(,,)n x y z 为t ∑上点(,,)p x y z 处的外法向量,0000{,,}r p p x x y y z z ==--- ,r r =,证明:1tu dS r n∂∂∑⎰⎰ ;(3) 设_n =(,,)n x y z 为 ∑上点(,,)p x y z 处的外法向量, 0000{,,}r p p x x y y z z ==--- ,r r =,计算积分21c o s (,)1[]4r n u u dSr r n π∂+∂∑⎰⎰ .。

温州大学_623量子力学2007--2017年_考研专业课真题试卷

2007年研究生入学考试试题考试科目：量子力学(A) 报考学科、专业：凝聚态物理、理论物第 1 页，共 2 页第 2 页，共 2 页2008年硕士研究生招生入学考试试题A科目代码及名称: 618，量子力学适用专业：凝聚态物理，理论物第1 页，共2 页第 2 页，共 2 页2009年硕士研究生入学考试试题A科目代码及名称：619量子力学适用专业：凝聚态物理，理论物第 1 页，共 2 页2009年硕士研究生入学考试试题A科目代码及名称：619 量子力学适用专业：凝聚态物理，理论2010年硕士研究生招生入学考试试题科目代码及名称: 619量子力学A 适用专业：理论物理凝聚态物第 2 页，共 2 页2011年硕士研究生入学考试试题科目代码及名称：619 量子力学A 适用专业：理论物理凝聚态第 1 页，共 3 页第 2 页，共 3 页第 3 页，共 3 页2012年硕士研究生招生入学考试试题（A）科目代码及名称: 620量子力学适用专业：理论物理、凝聚态物第 1 页，共 2 页第 2 页，共 2 页2013年硕士研究生招生入学考试试题科目代码及名称: 623 量子力学适用专业：理论物理凝聚态第 1 页，共 3 页第 2 页，共 3 页第 3 页，共 3 页2014年硕士研究生招生入学考试试题A科目代码及名称: 623 量子力学适用专业：理论物理、凝聚态物第1页，共2页第2页，共2页2015年硕士研究生招生入学考试试题A科目代码及名称: 623 量子力学适用专业：理论物理、凝聚态物理第19 页，共27 页第20 页，共27 页2016年硕士研究生招生考试试题 A科目代码及名称：623 量子力学适用专业：理论物理凝聚态第 1 页，共 2页第 2 页，共 2页2017年硕士研究生招生考试试题A 科目代码及名称: 623 量子力学适用专业：070201理论物理070205凝聚态物理页页。

2007-2008 学年第一学期大学数学分析 III 试卷及答案

.
7．设函数 z = f (x, y) 在点 (x0 , y0 ) 的某邻域内有连续的一阶、二阶
偏导数，又
fx (x0 , y0 ) = 0, f y (x0 , y0 ) = 0, A = fxx (x0 , y0 ), B = fxy (x0 , y0 ), C = f yy (x0 , y0 )
在该点两个偏导数存在.（）三：解下列各题（共 25 分）
1 将定义在[0, ] 上的函数
1 ,
f
(x)
=
1
2
,
0,
0 x h, x=h h x
（其中 0 x ）展开成正弦级数.
2 设 z = u2 ln v, u = x , v = 3x − 2 y 求 z .
y
x
3
设
x2
2007——2008 学年第一学期数学分析 III 试题 A
(应用数学系 0601,0602,0603 班)
一：填空（每空 2 分，共 20 分）
1.周期，2. − 1 ，3. f (x) ，4.5， 4
5.
f
(x,
y)dxdy
=
0
d
b
a
f
(r
cos ,
r
sin
)rdr
，
D
6. L = f (x, y, z) + 11(x, y, z) + 22 (x, y, z) ，
三：解下列各题（共 25 分）
1 解：
2
2h
bn =
f (x) sin nxdx =
0
sin nxdx
0
=
2
− cos nx n
h 0

经济数学二0706Adaan(1)

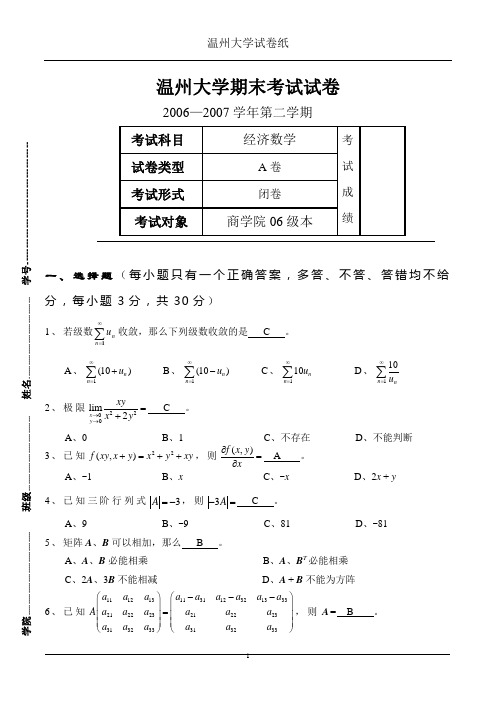
温州大学期末考试试卷2006—2007学年第二学期一、选择题（每小题只有一个正确答案，多答、不答、答错均不给分，每小题3分，共30分）1、若级数∑∞=1n n u 收敛，那么下列级数收敛的是 C 。

A 、1(10)n n u ∞=+∑ B 、1(10)n n u ∞=-∑ C 、110n n u ∞=∑ D 、110n nu ∞=∑ 2、极限2200lim2x y xyx y →→=+ C 。

A 、0B 、1C 、不存在D 、不能判断3、已知22(,)f xy x y x y xy +=++，则(,)f x y x∂=∂ A 。

A 、-1 B 、x C 、-x D 、2x + y 4、已知三阶行列式3A =-，则3A -= C 。

A 、9B 、-9C 、81D 、-81 5、矩阵A 、B 可以相加，那么 B 。

A 、A 、B 必能相乘 B 、A 、B T 必能相乘C 、2A 、3B 不能相减D 、A + B 不能为方阵6、已知1112131131123213212223212223313233313233a a a a aa aa a A a a a a aa a a a aaa ---⎛⎫⎛⎫⎪⎪= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，则A = B 。

学院-------------------------------------- 班级---------------------------------- 姓名------------------------------------- 学号-------------------------------------A 、100010101⎛⎫ ⎪ ⎪ ⎪-⎝⎭B 、101010001-⎛⎫ ⎪ ⎪ ⎪⎝⎭C 、101010001⎛⎫ ⎪ ⎪ ⎪-⎝⎭D 、100010101⎛⎫ ⎪ ⎪ ⎪-⎝⎭7、设A 为n 阶可逆矩阵，下列等式正确的是 A 。

A 、(2A )T = 2 A TB 、(2 A )-1= 2 A -1C 、0A =D 、22A A = 8、向量组n ααα ,,21线性无关，则必有 B 。

2007—数一真题、标准答案及解析

2007年考研数学一真题解析一、选择题（本题共10小题，每小题4分，满分40分，在每小题给的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后括号内）（1）当0x +→(B)A. 1-B.C. 1D.1-(2) 曲线y=1ln(1x e x++), 渐近线的条数为 (D) A.0 B.1 C.2 D.3(3)如图，连续函数y=f(x)在区间[-3，-2]，[2，3]上的图形分别是直径为1的上、下半圆周，在区间[-2，0]，[0，2]的图形分别是直径为2的上、下半圆周，设F(x)=0()xf t dt ⎰.则下列结论正确的是 (C)A. F(3)=3(2)4F -- B. F(3)=5(2)4F C. F(3)=3(2)4F + D. F(3)= 5(2)4F -- (4)设函数f （x ）在x=0处连续，下列命题错误的是 (C)A. 若0()limx f x x →存在，则f （0）=0 B. 若0()()lim x f x f x x→+- 存在，则f （0）=0C. 若0()lim x f x x → 存在，则'(0)f =0D. 若0()()lim x f x f x x→-- 存在，则'(0)f =0(5)设函数f （x ）在（0, +∞）上具有二阶导数，且"()f x o >, 令n u =f(n)=1,2,…..n, 则下列结论正确的是(D) A.若12u u >，则{n u }必收敛 B. 若12u u >，则{n u }必发散 C. 若12u u <，则{n u }必收敛 D. 若12u u <，则{n u }必发散(6)设曲线L ：f(x, y) = 1 (f(x, y)具有一阶连续偏导数），过第Ⅱ象限内的点M 和第Ⅳ象限内的点N,T 为L 上从点M 到N 的一段弧，则下列小于零的是 (B) A.(,)rx y dx ⎰ B. (,)rf x y dy ⎰C.(,)rf x y ds ⎰D.'(,)'(,)x y rf x y dx f x y dy +⎰（7）设向量组1α，2α，3α线形无关，则下列向量组线形相关的是： (A) （A ）,,122331αααααα--- （B ） ,,122331αααααα+++（C ） 1223312,2,2αααααα--- （D ）1223312,2,2αααααα+++（8）设矩阵A=211121112--⎛⎫ ⎪-- ⎪ ⎪--⎝⎭，B=100010000⎛⎫ ⎪⎪ ⎪⎝⎭,则A 于B ， (B)(A) 合同，且相似(B) 合同，但不相似 (C) 不合同，但相似(D)既不合同，也不相似（9）某人向同一目标独立重复射击，每次射击命中目标的概率为p ()01p <<，则此人第4次射击恰好第2次命中目标的概率为： (C) （A ）23(1)p p - (B)26(1)p p - (C) 223(1)p p -(D) 226(1)p p -(10) 设随即变量（X ，Y ）服从二维正态分布，且X 与Y 不相关，()X f x ，()Y f y 分别表示X ，Y 的概率密度，则在Y ＝y 的条件下，X 的条件概率密度|(|)XYf x y 为 (A)（A ）()X f x(B) ()Y f y(C) ()X f x ()Y f y(D)()()X Y f x f y 二．填空题：11－16小题，每小题4分，共24分，请将答案写在答题纸指定位置上。

2007年浙江省数学分析竞赛试题及答案

2007浙江省第六届数学分析竞赛试题一．计算题 1. 求951x dx x +⎰.解：原式()55215x d x =+⎰()232211553t dt t t C ⎛⎫=-=-+ ⎪⎝⎭⎰. 2. 求()()1120112limsin xxx x x x→+-+.解：令()()11xf x x =+，则原式()()002lim limsin x x f x f x xx x→→-=()()()0lim 22x f x f x →''=-()()()()()()00002lim lim 2lim 2lim 2x x x x f x f x f x f x f x f x →→→→''=-()()()()002lim 2lim 2x x f x f x e e f x f x →→''=-()()limx f x e f x →'=-()()2001ln 11lim lim 1x x x x x e x x →→-++=-+()0ln 1lim22x x ee x →-+=-=.3. 求p 的值，使()()220070bx p ax p edx ++=⎰.解：情形一，当a b =时，p 的值可以任意取；情形二，当a b ≠时，做变换t x p =+，则原式左边22007b pt a pt e dt ++=⎰，因为被积函数是奇函数，故当()a p b p +=-+时，即2a b p +=-时，有()()220070b x p a x p e dx ++=⎰. 4. 设(),x ∀∈-∞+∞，()0f x ''≥，且()201x f x e-≤≤-，求()f x 的表达式.解：（1）由()2011x f x e-≤≤-<，知()f x 有界；（2）下证()0f x '=，(),x ∀∈-∞+∞.假若存在()0,x ∈-∞+∞，使得()00f x '≠，则()()()()()()2000012f x f x f x x x f x x ξ'''=+-+- ()()()000f x f x x x '≥+-，若()00f x '>，则()()()()000f x f x f x x x '≥+-→+∞，()x →+∞，这与()f x 有界矛盾；若()00f x '<，则()()()()000f x f x f x x x '≥+-→+∞，()x →-∞，这与()f x 有界矛盾，因此()00f x '=，(),x ∀∈-∞+∞，()f x C =，(),x ∀∈-∞+∞；（3）由()00010f e ≤≤-=，知()00f =，因此()0f x =，(),x ∀∈-∞+∞.5. 计算()2Sxy dS +⎰⎰，其中S 为柱面224x y +=，()01z ≤≤.解：方法一因圆柱面224xy +=，()01z ≤≤的参数方程为2c o s 2s i nx uy u z v =⎧⎪=⎨⎪=⎩，故2dSEG F dudv =-，其中2224u u u E x y z =++=，0u v u v u v F x x y y z z =++=，2221v v v G x y z =++=，于是()()122224cos 2sin Sxy dS dv u u du π+=+⎰⎰⎰⎰()2224cos 2sin u u du π=+⎰20cos21882u du ππ-==⎰.方法二注意到对称性()22SSx y dS x dS +=⎰⎰⎰⎰()2212Sx y dS =+⎰⎰()1144221822S dS ππ==⋅⋅⋅⋅=⎰⎰. 二．设1211211212345632313nu n n n=+-++-+++--- ， 111123n v n n n=+++++ ，求（1）1010u v ，（2）lim n n u →∞.解：（1）因为111111232n u n n ⎛⎫=+++-+++ ⎪⎝⎭，111111232n v n n ⎛⎫=+++-+++ ⎪⎝⎭，故n n u v =，因此10101u v =，（2）方法一 2111lim lim lim 1n n n n n n k u v k n n→∞→∞→∞===+∑()22001ln 1ln31dx x x ==+=⎡⎤⎣⎦+⎰.方法二利用111ln 2n n c nε+++=++ ，其中lim 0n n ε→∞=，()()3lim lim ln3ln n n n n n u n c n c εε→∞→∞⎡⎤=++-++⎣⎦()3lim ln3n n n εε→∞=+- ln3=.三．有一个边长为4π的正方形纸（如图），C 、D 分别为AA '、BB '的中点，E 为DB '的中点.现将纸卷成圆柱形，使A 与A '重合，B 与B '重合，并将圆柱垂直放在xoy 平面上，且B 与原点O 重合，D 落在y 轴正向上.求：（1）通过C ，E 两点的直线绕z 轴旋转所得的旋转面方程；（2）此旋转面、xoy 平面和过A 点垂直于z 轴的平面所围成的立体体积. 解：()0,0,0B ，()0,4,4C π，()0,4,0D ，()2,2,0E ，通过()0,4,4Cπ和()2,2,0E 两点的直线l 方程为22224x y z π--==-，即22z x π=-，22zy π=+，（1）通过C ，E 两点的直线l 绕z 轴旋转所得的旋转面方程为22222222z z x y ππ⎛⎫⎛⎫+=-++ ⎪ ⎪⎝⎭⎝⎭，即222282z x y π+=+；（2）此旋转曲面()222228z x y π=+-，xoy 平面0z=和过A 点垂直于z 轴的平面4z π=所围成的立体体积为22224082z x y V dxdydz dzdxdy ππΩ+≤+==⎰⎰⎰⎰⎰⎰242082z dz πππ⎛⎫=+ ⎪⎝⎭⎰432086z z πππ⎛⎫=+⎪⎝⎭ 222321283233πππ=+=.四．求函数()2222,,x yz f x y z x y z+=++，在(){}222,,:14D x y z x y z =≤++≤上的最大值和最小值.解：解法一令cos x ρϕ=，cos sin y ρθϕ=，sin sin zρθϕ=，则()222221,,1sin 21sin 2x yz f x y z x y z θϕ+⎛⎫==+- ⎪++⎝⎭，其中[]0,ϕπ∈，[],θππ∈-，因()311sin 21222g θθ-≤=-≤-，且32-，12-分别是()1sin 212g θθ=-的最小值和最大值，故()2222,,x yz f x y z x y z +=++在D 上的最小值和最大值为别为31122⎛⎫+-=- ⎪⎝⎭，101+=.解法二由()()22221122y z yz y z -+≤≤+，得()()22222222213112222x y z x x yz x y z x -+++≤+≤+++， ()222222212x y z x yz x y z -++≤+≤++， ()1,,12f x y z -≤≤，且等号能达到，(),0,01f x =，()10,,2f y y -=-，故()2222,,x yz f x y z x y z +=++在D 上的最小值和最大值为别为12-，1. 五．求11limnk n k n n knC →∞=+-∑. 解：记11n n kk n n kx nC =+-=∑， ()()()22212!3!4!10112n x n n n n n n n n≤=+++++---()212!12n n n n ≤+-+()441n n n=-<，故11lim0nk n k n n knC →∞=+-=∑. 六．证明：24cos 21x x x ≤-++，20,4x π⎡⎤∈⎢⎥⎣⎦.证明：只要证()224cos 21x x x +≤+，20,4x π⎡⎤∈⎢⎥⎣⎦.该不等式等价于222cos 2cos 21x x x +≤，20,4x π⎡⎤∈⎢⎥⎣⎦，即222cos 2sin 2x x x ≤，20,4x π⎡⎤∈⎢⎥⎣⎦，令2tx =，则只要证 sin cos tt t≤，0,2t π⎡⎫∈⎪⎢⎣⎭，为此，作()sin ,cos t f t t t =-0,2t π⎡⎫∈⎪⎢⎣⎭则()31cos cos 12t t f t +'=-，0,2t π⎡⎫∈⎪⎢⎣⎭因此()31cos cos 12t t f t +'=-311cos 110cos cos t tt≥⋅-=-≥，0,2t π⎡⎫∈⎪⎢⎣⎭ 于是当02t π≤<时，()()sin 00cos tf t t f t=-≥=.结论得证.。

2006——2007学年第二学期数学分析试题B答案

2006——2007学年第二学期数学分析试题Ｂ答案（0601，0602，0603）一：填空（20分）1. 12. ≤3. 1、04. 05. ''()()x t y t 与不同时为06. ()x e C ϕ+7. 绝对收敛8. 1p >9. 充要条件 10.[,]a b 二：判断（16分）⨯∨⨯∨∨⨯⨯⨯三：计算下列各题（15分）2222212221()(3)21241)241(1) (5)22x x x x x x C ====-+⎰⎰分分分2令6x u =则原式变为523216(1)(3)16(ln |1|)326ln |1| 5u u du u u u u u C C ==-+-+=-+-++=+⎰⎰分（分）2020220020cos 3sin cos 1cos sin sin cos (3)2sin cos 11(sin cos )22sin cos (ln |sin cos |)| (4)44d d d d πππππθθθθθθθθθθθθθθθθπθθπ++-+=++=++=+=⎰⎰⎰⎰分分 (5)分四：解下列各题（28分）1、求幂级数 +++++++12531253n x x x x n )1,1(-∈x 的和函数0011,12121n n n x n n ∞∞====±++∑∑2n+1(-1)解：因且，与都是发散级数该幂级数的收敛区域为(1,1)- （4分）设3521()3521n x x x F x x n +=++++++在收敛区域||1x <内逐项微分之，得'2321()11F x x x x =+++=- （5分）注意(0)0F =，即得2011()ln (||1)121xdt xF x x t x+==<--⎰于是当||1x <时，有352111ln (||1)352121n x x x x x x n x+++++++=<+- （7分）2、计算⎰⎰⎪⎭⎫ ⎝⎛∞→x t x t x dte dt e 022022lim 解：该极限是∞∞型的不定式极限，利用洛必塔法则有 ()22222222222020lim2lim(3)2lim (5)2lim20 (7)x t xx t x xt x x xt x x xxx e dt e dte e dtee dte e xe →∞→∞→∞→∞====⎰⎰⎰⎰分分分112(1)3lim sin sin sin1(1)lim sin (3)n n n i n n n n n i n n ππππππ→∞→∞=-⎛⎫+++ ⎪⎝⎭-=⋅∑分其中的和式是()sin f x x =在区间[0,]π上的一个积分和，这里所取的是等分分割，(1),i i i x nn ππξ-∆==为小区间1,(1)[][,]i i i i x x n nππ--=的左端点，1,2,,i n =故有12(1)lim sin sin sin1sin (6)n n n n n n xdxπππππ→∞-⎛⎫+++ ⎪⎝⎭=⎰分1(cos )|2(7)x πππ=-=分4 解：为方便起见。

温州大学618数学分析2015——2018,2020年考研真题试卷试题

=
ln
x3 y2 +
z
, 求全微分du
∫ （4）求定积分 2 ln2 xdx 1
∑∞
（5）求级数和
(−1)n−1
n=1 2n ⋅ n!
（6）求 ( x − y)dx + ( x + y)dy, L是椭圆 x2 + y2 = 1, 逆时针方向。
∫ L
23
2 （每小题6分，共36分）
（1）
假设
lim
n→∞
一、（10 分）按函数极限的定义证明极限 lim x2 4 . x2
二、（10 分）求极限 lim n 1n 2n L 2017n . n
三、（10
分）求由参数方程
x
y
(t 1)et t 2et
所确定的函数
y
y(x)
的二阶导数
d2 y dx2
.
xy2
四、（15
分）设
f
(x,
八、（12 分）判别级数
(1)n1 的收敛性，并指出是条件收敛还是绝对收敛.
n1 n 1 n
第 1 页，共 2 页
2018 年硕士研究生招生考试试题
科目代码及名称: 622 数学分析
适用专业：070104 应用数学
（请考生在答题纸上答题，在此试题纸上答题无效）
九、
（10
分）求幂级数
n1
n! nn
x2n
的收敛域.
十、（10 分）证明函数项级数 (1 cos x ) 在[ , ]上一致收敛，其中 0 .
n1
n
十一、（10 分）设 f (x) 为连续的周期函数，周期为T ，证明
aT
f (x)dx

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2007 年研究生入学考试试题
考试科目：数学分析(A) 报考学科、专业：应用数学
请注意:全部答案必须写在答题纸上，否则不给分。
１．(10 分) 证明：数列 {sin n} 不收敛 .
x f ( x ) ．２．(10 分) 已知 f (0) 0 ， f (0) 存在，求极限： lim
1 1 ８．(１0 分) 判断正项级数 ln(1 ) 的敛散性． n n n 1
3 (1) n x n 的收敛半径与收敛域．９．(１0 分) 求幂级数 n n 1

n
10．(15 分) 证明函数项级数 3n sin
n 1
2
a f ( x ) dx 2 a f ( x ) dx a f ( y ) dy ． x 0 0
第２Biblioteka 页，共２页
1 在 (0, ) 中不一致收敛， 4n x
但其和函数在 (0, ) 中连续．
1 y sin 2 x y2 11．(10 分) 讨论函数 f ( x, y ) 0 , x2 y 2 0 , x2 y 2 0
在 (0, 0) 处的连续性、可导性与可微性． 12．(15 分) 设 f ( x ) 在 [0, a ] 上连续，证明等式：
x T
（1） ( x )
0
x f ( t )dt f ( t )dt 也是以 T 为周期的周期函数； T 0
1 1 （2） lim f ( x )dx x x T 0
x
f (t )dt ．
0
x
T
６．(15 分) 设 f ( x ) 在 [0， ) 连续， lim f ( x ) A 0 ，求证：
x0
n t n 1 (1 ) n dt ．３．(15 分) 计算积分 t 0
４．(15 分) 已知 f ( x ) 连续， f (0) f (1) 0 ， f ( x ) A ，求证： f ( x ) A 2 , x [0,1] ．５．(10 分) 设 f ( x ) 是以 T 为周期的连续周期函数，求证：

o
f ( x )sin xdx 发散．

７．(15 分) 设 an 是收敛的正项级数，并且 an 单调下降收敛于零．
n 1
证明： n(an an 1 ) 收敛，而且 n(an an 1 ) an ．
n 1 n 1 n 1

第１
页，共２
页
请注意:全部答案必须写在答题纸上，否则不给分。