九年级数学上册 5.1 总体平均数与方差的估计习题集训 湘教版
湘教版九上数学5.1总体平均数与方差的估计试题及答案

5.1总体平均数与方差的估计一、选择题1.为了解实验中学某班学生每天的睡眠情况,随机抽取该班10名学生,在一段时间里,每人平均每天的睡眠时间(单位:时)统计如下:6,8,8,7,7,9,10,6,9,7.由此估计该班学生平均每天的睡眠时间为() A.7小时 B.7.5小时C.7.7小时 D.8小时2.从总体中随机抽取一个样本,计算出样本方差为2,可以估计总体方差()A.一定大于2 B.约等于2C.一定等于2 D.与样本方差无关3.2016·株洲甲、乙、丙、丁四名射击队员考核赛的平均成绩(环)及方差统计如下表,现要根据这些数据,从中选出一人参加比赛,如果你是教练员,你的选择是()A.甲 B.乙 C.丙 D.丁4.张老师买了一辆汽车,为了掌握汽车的耗油情况,在连续两次加油时做了如下工作:(1)把油箱加满油;(2)记录了两次加油时的累计里程(注:“累计里程”指汽车从出厂开始累计行驶的路程),以下是张老师连续两次加油时的记录:则在这段时间内,该车每100千米平均耗油量为()A.3升 B.5升 C.7.5升 D.9升5.要估计某鱼塘中的鱼数,养鱼者首先从鱼塘中打捞了50条鱼,在每条鱼身上做好记号后把这些鱼放归鱼塘,过一段时间后,再从鱼塘中打捞出100条鱼,发现只有2条鱼是做了记号的鱼.假设鱼在鱼塘内均匀分布,那么这个鱼塘的鱼数约为()A.5000条 B.2500条C.1750条 D.1250条二、填空题6.甲、乙两台机器分别灌装每瓶质量为500克的酸奶,从甲、乙灌装的酸奶中分别随机抽取了30瓶,测得它们实际质量的方差是s甲2=4.8,s乙2=3.6,那么________(填“甲”或“乙”)机器灌装的酸奶质量较稳定.7.2017·常德彭山的枇杷大又甜,在今年5月18日“彭山枇杷节”期间,从山上5棵枇杷树上采摘到了200千克枇杷,请估计彭山近600棵枇杷树今年一共收获了枇杷________千克.三、解答题8.为保护环境,创建绿色鹰潭,某环保小组随机调查了市区30个家庭一天丢弃塑料袋的情况,统计结果如下:(1)这种调查方式属于普查还是抽样调查:____________;(2)这30个家庭一天丢弃塑料袋个数的众数是________,中位数是________;(3)鹰潭市市区人口约有44万(含余江、贵溪两县城),假设平均一个家庭有4个人.若根据30个家庭这一天丢弃塑料袋个数的平均数估算,则全市一天丢弃塑料袋总数约有多少个(写出解答过程,结果用科学记数法表示)?通过该环保小组的统计和你的估算,写出你的感想或对市民提出一条科学性的建议.9.某校九年级学生开展踢毽子比赛活动,每班派5名同学参加,按团体总分排列名次,在规定时间内每人踢100个以上(含100)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):统计发现两班总分相等,此时有同学建议,可以通过考查数据中的其他信息作为参考,请你解答下列问题:(1)计算两班的优秀率;(2)求两班比赛数据的中位数;(3)计算两班比赛数据的方差;(4)根据以上三条信息,你认为应该把冠军奖状发给哪一个班?简述理由.10.甲、乙两名队员参加射击训练,成绩分别被制成如图K-37-1所示两个统计图:图K-37-1根据以上信息,整理分析数据如下:(1)求出表格中a,b,的值;(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名队员参赛,你认为应选派哪名队员?11数学活动生活中很多矿泉水没有喝完便被扔掉,造成极大的浪费,为此数学兴趣小组的同学对某单位的某次会议所用矿泉水的浪费情况进行调查,为期半天的会议中,每人发一瓶500 mL的矿泉水,会后对所发矿泉水的情况进行统计,大致可分为四种:A.全部喝完;B.喝剩约13;C.喝剩约一半;D.开瓶但基本未喝.同学们根据统计结果绘制成如图K-37-2所示的两个统计图,根据统计图提供的信息,解答下列问题:(1)参加这次会议的有多少人?在图②中D所在扇形的圆心角是多少度?并补全条形统计图;(2)若开瓶但基本未喝算全部浪费,试计算这次会议平均每人浪费矿泉水约多少毫升(计算结果保留整数);(3)据不完全统计,该单位每年约有此类会议60次,每次会议人数约在40至60人之间,请用(2)中计算的结果,估计该单位一年中因此类会议浪费的矿泉水(500 mL/瓶)约有多少瓶(可使用科学计算器).图K-37-21.[答案] C 2.[答案] B 3.[答案] C4.[解析] C 由题意可得:两次加油间耗油30升,行驶的路程为6600-6200=400(千米), 所以该车每100千米平均耗油量为30÷(400÷100)=7.5(升). 5.[答案] B 6. [答案] 乙[解析] 方差越小,数据越稳定. 7.[答案] 24000[解析] 根据题意,得200÷5×600=24000(千克). 8.解:(1)抽样调查(2)2出现的次数最多,是11次,所以众数是2.30个数据中,中位数应是第15个和第16个的平均数,显然是3.故答案为2,3.(3)样本平均数x -=130×(1×0+1×1+11×2+7×3+5×4+4×5+1×6)=3(个),∴全市一天丢弃塑料袋总数=44×1044×3=3.3×105(个).答案不唯一,只要有实际意义即可,如感想:生活垃圾不统不知道,一统吓一跳等;建议:少用一次性塑料袋,多用健康环保袋;爱护环境,从我做起或人人有责等等.9.解:(1)甲班的优秀率是35×100%=60%;乙班的优秀率是25×100%=40%.(2)甲班5名学生比赛数据的中位数为100个;乙班5名学生比赛数据的中位数为97个. (3)x 甲= 15×500=100(个),x 乙= 15×500=100(个).s 甲2= 15 [(100-100)2+(98-100)2+(110-100)2+(89-100)2+(103-100)2]=46.8,s 乙2= 15[(89-100)2+(100-100)2+(95-100)2+(119-100)2+(97-100)2]=103.2.(4)应该把冠军奖状发给甲班.理由:因为甲班5名学生比赛数据的优秀率比乙班高、中位数比乙班大、方差比乙班小,所以应该把冠军奖状发给甲班.10.解:(1)甲的平均成绩a =5×1+6×2+7×4+8×2+9×11+2+4+2+1=7(环),∵乙射击的成绩从小到大排列为3,4,6,7,7,8,8,8,9,10, ∴乙射击成绩的中位数b =7+82=7.5(环),s乙2=110×[(3-7)2+(4-7)2+(6-7)2+2×(7-7)2+3×(8-7)2+(9-7)2+(10-7)2]=110×(16+9+1+3+4+9)=4.2.故a =7,b =7.5,c =4.2.(2)(答案合理即可)从平均成绩看,甲、乙二人的成绩相等,均为7环; 从中位数看,甲射中7环以上的次数少于乙;从众数看,甲射中7环的次数最多而乙射中8环的次数最多;从方差看,甲的成绩比乙的成绩稳定;综合以上各因素,若选派一名队员参赛,可选派乙参赛,因为乙获得高分的可能性更大. 11 解:(1)根据所给扇形统计图,可知喝剩约13的人数占总人数的50%,∴25÷50%=50(人), ∴参加这次会议的有50人. ∵550×360°=36°, ∴D 所在扇形的圆心角是36°. 补全条形统计图如图所示:(2)(25×13×500+10×500×12+5×500)÷50=275003÷50≈183(mL).答:这次会议平均每人浪费矿泉水约183 mL.(3)该单位每年参加此类会议的总人数约为2400~3600,则浪费矿泉水约为2400+36002×183÷500=1098(瓶).答:该单位一年中因此类会议浪费的矿泉水约有1098瓶.。
湘教版九年级上册数学5.1 总体平均数与方差的估计2同步练习

5.1 总体平均数与方差的估计
1.(贵港中考)一组数据1,3,0,4的方差是_____.
2.下列各组数据中,方差最小的是()
A.1,2,3,4,5 B.2,3,4,5,6 C.2,4,6,8,10 D.3,3,1,3.14,π,
3.(自贡中考)一组数据,6、4、a、3、2的平均数是5,这组数据的方差为()A.8 B.5 C.22D.3
4.(常州中考)甲、乙、丙、丁四人进行射击测试,每人10次射击成绩平均数均是9.2环,方差分别为S甲2=0.56,S乙2=0.60,S丙2=0.50,S丁2=0.45,则成绩最稳定的是()
A.甲B.乙C.丙D.丁
5.(盘锦中考)甲、乙两名学生的十次数学考试成绩的平均分分别是145和146,成绩的方差分别是8.5和60.5,现在要从两人中选择一人参加数学竞赛,下列说法正确的是()
A.甲、乙两人平均分相当,选谁都可以
B.乙的平均分比甲高,选乙
C.乙的平均分和方差都比甲高,选乙
D.两人的平均分相当,甲的方差小,成绩比乙稳定,选甲
6.(威海中考)在某中学举行的演讲比赛中,初一年级5名参赛选手的成绩如下表所示,请你根据表中提供的数据,计算出这5名选手成绩的方差()
A.2 B.6.8 C.34 D.93
7.(营口中考)小华和小苗练习射击,两人的成绩如图所示,小华和小苗两人成绩的方差分别为S12、S22,根据图中的信息判断两人方差的大小关系为
________
8.(佛山中考)甲、乙两组数据(单位:厘米)如下表
(1)根据以上数据填表
(2)那一组数据比较稳定?。
湘教版九年级数学上册同步练习:5.1总体平均数与方差的估计

5.1整体均匀数与方差的预计知识点 1用样本均匀数预计整体均匀数1.为认识实验中学某班学生每日的睡眠状况,随机选择该班10名学生进行检查.在一段时间里,均匀每人每日的睡眠时间统计以下(单位:时 ):6,8,8,7,7,9,10,6,9,7.由此预计该班学生均匀每人每日的睡眠时间为 ()A.7 小时B.7.5 小时C.7.7 小时D.8 小时2.从鱼塘中打捞出草鱼 240 尾,从中任选 9 尾,称得每尾的质量分别是 1.5,1.6,1.4,1.6,1.2,1.7,1.8,1.3,1.4(单位: kg).请估计这 240 尾草鱼的均匀质量是 ()A.1.2 kg B.1.3 kgC.1.5 kg D.1.6 kg3.饮料店为了认识本店罐装饮料上半年的销售状况,随机检查了8 天该种饮料的日销售量,结果以下(单位:听 ):33,32,28,32,25,24,31,35.(1)这 8 天的均匀日销售量是多少听?(2)依据上边的计算结果,预计上半年(按 181 天计算 )该店能销售这类饮料多少听.4.为了认识某小区居民的用水状况,随机抽查了该小区10 户家庭的月用水量,结果以下:月用水量 (吨) 10 13 14 1718户数22321(1)计算该小区每户家庭的月均匀用水量;(2)假如该小区有 500 户家庭,依据上边的计算结果,预计该小区居民每个月共用水多少吨.知识点 2用样本方差预计整体方差5.从整体中随机抽取一个样本,计算出样本方差为2,能够预计整体方差 ()A.必定大于 2 B.约等于 2C.必定等于 2 D.与样本方差没关6.为了比较甲、乙两种水稻秧苗谁出苗更齐整,每种秧苗各随机抽取 50 株,分别量出每株长度,发现两组秧苗的均匀长度同样,甲、乙两种秧苗的方差分别是 3.5,10.9,则以下说法正确的选项是() A.甲秧苗出苗更齐整B.乙秧苗出苗更齐整C.甲、乙两种秧苗出苗同样齐整D.没法确立甲、乙两种秧苗出苗谁更齐整7.某工厂为了选拔1 名车工参加直径为 5 mm 精细仪器的加工技术竞赛,随机抽取甲、乙两名车工加工的 5 个仪器,现测得的结果如下表:甲5.05 5.02 5 4.96 4.97乙55.01 5 4.97 5.02由此能够预计,甲、乙两人中技术比较稳固的是________.8.甲、乙两台机床同时生产一种部件,随机抽查了10 天的生产状况,两台机床每日出次品数分别是:甲: 0,1,0, 2,2, 0,3,1,2,4.乙: 2,3,1, 1,0, 2,1,1,0,1.预计这两台机床每日出次品数的方差.9.从整体中抽取一部分数据作为样本去预计整体的某种属性.下面表达正确的选项是 ()A.样本容量越大,样本均匀数就越大B.样本容量越大,样本的方差就越大C.样本容量越大,对整体的预计就越正确D.以上都不对10.A,B 两农场各养奶牛200 头,为了认识两农场一天牛奶的产量,任意抽取10 头奶牛,称得它们的牛奶产量以下(单位: kg):A 农场: 6.5,6.0,6.5,7.9,7.1,7.1,7.8,6.1,8.0,7.1;B 农场: 6.8,7.3,7.5,6.6,7.0,7.0,6.6,6.9,6.9,7.0.(1)依据 10 头奶牛牛奶产量的均匀数,预计A,B 两农场中200头奶牛一天的牛奶总产量;(2)假如学校要推行“学生奶”工程,你以为选择哪个农场作为学校的长久供货方较好?为何?11.甲、乙两种水稻试验品种连续 5 年每公顷的均匀产量以下(单位:吨 /公顷 ):品种第1年第2年第3年第4年第5年甲9.89.910.11010.2乙9.410.310.89.79.8为使水稻品种的产量比较稳固,依据题中所给的数据,你选择哪一种水稻品种?请说明原因.12.某学校抽查了某班级某月10 天的用电量,数据以下表 (单位:度):度数8910131415天数112312(1)这 10 天用电量的众数是 ________,中位数是 ________;(2)求这个班级均匀每日的用电量;(3)已知该校共有 20 个班级,该月合计30 天,试预计该校该月总的用电量.13.某检查小组采纳简单随机抽样方法,对某市部分中小学生一天中阳光体育运动时间进行了抽样检查,并把所得数据整理后绘制成如图 5-1-1 所示的统计图.(1)该检查小组抽取的样本容量是多少?(2)求样本中阳光体育运动时间为 1.5 小时的学生人数,并补全条形统计图;(3)请预计该市中小学生一天中阳光体育运动的均匀时间.图 5-1-11.C 2.C13.解: (1)8 天的均匀日售量是8×(33+32+28+32+25+24+31+35)=30(听).(2)30 ×181=5430(听),∴估上半年 (按 181 天算 )店能售种料5430 听.4.解:(1)小区每家庭的月均匀用水量是(10 ×2+13×2+14×3+17×2+18) ÷10=14(吨).(2)依据意,得 14×500=7000(吨).答:估小区居民每个月共用水7000 吨.5.B 6.A7.乙8. [ 分析 ] 假如本是一个随机本,那么能够用本的特点估体的特点.1解: x 甲=10×(0+1+⋯+4)= 1.5,1x 乙=10×(2+3+⋯+1)=1.2.1s 甲2=10×[2 ×(1-1.5)2+3×(2- 1.5)2+(3-1.5)2+(4-1.5)2+3×(0-1.5)2] =1.65,1s 乙2=10×[5 ×(1-1.2)2+2×(2-1.2)2+ (3- 1.2)2+2×(0-1.2)2]=0.76.9.C10.解:(1)A ,B 两抽取的 10 奶牛牛奶量的均匀数分是(6.5 + 6.0 + 6.5 + 7.9+ 7.1 + 7.1 + 7.8 + 6.1 + 8.0 + 7.1) ÷10 =7.01(kg);(6.8 + 7.3 + 7.5 + 6.6+ 7.0 + 7.0 + 6.6 + 6.9 + 6.9 + 7.0) ÷10 =6.96(kg).据此可预计 A ,B 两农场 200 头奶牛一天的牛奶总产量分别是7.01 ×200=1402(kg),6.96 ×200=1392(kg).(2)A 农场牛奶产量的方差为 0.4789,B 农场牛奶产量的方差为0.0704,因此 B 农场的牛奶产量较为稳固, 应选择 B 农场作为学校的长久供货方较好.11. 解:x 甲=(9.8+9.9+10.1+10+10.2) ÷5=10,x 乙=(9.4+10.3+ 10.8+9.7+9.8) ÷5=10.1s 甲 2=5×[(9.8-10)2+ (9.9-10)2+(10.1- 10)2+(10-10)2+(10.21-10)2] =0.02,s 乙 2=5×[(9.4-10)2+(10.3-10)2+(10.8-10)2+(9.7-10)2+(9.8-10)2]=0.244.∵ x 甲=x 乙,s 甲 2<s 乙 2,∴甲种水稻的产量比较稳固,∴选择甲种水稻.12. (1)13 度 13 度∵-=1×++ ×+ ×+ + ×= 度,(2)x10 (8 9 10 2 13 3 14 15 2) 12( )∴这个班级均匀每日的用电量为12 度.(3)∵12×20×30=7200(度),∴预计该校该月总的用电量为7200 度.13. (1)100 ÷20%=500,∴该检查小组抽取的样本容量是500.(2)500 ×24%=120(人),∴样本中阳光体育运动时间为 1.5 小时的学生共有120 人.补全条形统计图如图:1(3)500×(0.5 ×100+1×200+1.5 ×120+2×80)=1.18(时),∴预计该市中小学生一天中阳光体育运动的均匀时间为 1.18 小时.。
湘教版九年级上册数学5.1 总体平均数与方差的估计1同步练习

5.1 总体平均数与方差的估计1.(江西模拟)小芳家今年6月份头6天的用电量如下表:请你根据统计知识,估计小芳家6月份总用电量是()A.162 B.120 C.96 D.1232.(济宁中考)从总体中抽取一部分数据作为样本去估计总体的某种属性.下面叙述正确的是()A.样本容量越大,样本平均数就越大B.样本容量越大,样本的方差就越大C.样本容量越大,样本的方差就越小D.样本容量越大,对总体的估计就越准确3.(怀化模拟)李大伯在承包的果园里种植了100棵樱桃树,今年已经进入收获期,从中任意采摘了6棵树上的樱桃,分别称得每棵树的产量(单位:千克)如下表:设这组数据的中位数为m,樱桃的总产量为n,则m,n分别为()A.18,2000 B.19,1900C.18.5,1900 D.19,18504.(成都中考)在开展“国学诵读”活动中,某校为了解全校1300名学生课外阅读的情况,随机调查了50名学生一周的课外阅读时间,并绘制成如图所示的条形统计图.根据图中数据,估计该校1300名学生一周的课外阅读时间不少于7小时的人数是_____.5.为比较甲、乙两种电子钟每日走时误差的情况,从这两种电子钟中,各随机抽取10台进行测试.测试结果是两种电子钟的走时误差的平均数相同,方差分别是S甲2=6、S乙2=4.8,则走时比较稳定的是.(填“甲”、“乙”中的一个)6.甲、乙两台机床生产同一种零件,并且每天产量相等,在6天中每天生产零件中的次品数依次是:甲:3、0、0、2、0、1;乙:1、0、2、1、0、2.则甲、乙两台机床中性能较稳定的是.7.甲、乙两台包装机同时包装质量为500克的白糖,从中各随机抽出10袋,测得实际质量如下(单位:g)甲:501 500 503 506 504 506 500 498 497 495乙:503 504 502 498 499 501 505 497 502 499(1)分别计算两个样本的平均数;(2)分别计算两个样本的方差;(3)哪台包装机包装的质量较稳定?。
2021年秋湘教版九年级数学上册同步练习:5.1 总体平均数与方差的估计

5.1总体平均数与方差的估计一、选择题1.为理解实验中学某班学生每天的睡眠情况,随机抽取该班10名学生,在一段时间里,每人平均每天的睡眠时间(单位:时)统计如下:6,8,8,7,7,9,10,6,9,7.由此估计该班学生平均每天的睡眠时间为()A.7小时B.7.5小时C.7.7小时D.8小时2.从总体中随机抽取一个样本,计算出样本方差为2,可以估计总体方差()A.一定大于2 B.约等于2C.一定等于2 D.与样本方差无关3.2021·株洲甲、乙、丙、丁四名射击队员考核赛的平均成绩(环)及方差统计如下表,现要根据这些数据,从中选出一人参加比赛,假如你是教练员,你的选择是()A.甲B.乙C4.张教师买了一辆汽车,为了掌握汽车的耗油情况,在连续两次加油时做了如下工作:(1)把油箱加满油;(2)记录了两次加油时的累计里程(注:“累计里程〞指汽车从出厂开场累计行驶的路程),以下是张教师连续两次加油时的记录:那么在这段时间内,该车每100千米平均耗油量为()A.3升B.5升C.7.5升D.9升5.要估计某鱼塘中的鱼数,养鱼者首先从鱼塘中打捞了50条鱼,在每条鱼身上做好记号后把这些鱼放归鱼塘,过一段时间后,再从鱼塘中打捞出100条鱼,发现只有2条鱼是做了记号的鱼.假设鱼在鱼塘内均匀分布,那么这个鱼塘的鱼数约为()A.5000条B.2500条C.1750条D.1250条二、填空题6.甲、乙两台机器分别灌装每瓶质量为500克的酸奶,从甲、乙灌装的酸奶中分别随机抽取了30瓶,测得它们实际质量的方差是s甲2=4.8,s乙2=3.6,那么________(填“甲〞或“乙〞)机器灌装的酸奶质量较稳定.7.2021·常德彭山的枇杷大又甜,在今年5月18日“彭山枇杷节〞期间,从山上5棵枇杷树上采摘到了200千克枇杷,请估计彭山近600棵枇杷树今年一共收获了枇杷________千克.三、解答题8.为保护环境,创立绿色鹰潭,某环保小组随机调查了市区30个家庭一天丢弃塑料袋的情况,统计结果如下:(1)(2)这30个家庭一天丢弃塑料袋个数的众数是________,中位数是________;(3)鹰潭市市区人口约有44万(含余江、贵溪两县城),假设平均一个家庭有4个人.假设根据30个家庭这一天丢弃塑料袋个数的平均数估算,那么全市一天丢弃塑料袋总数约有多少个(写出解答过程,结果用科学记数法表示)?通过该环保小组的统计和你的估算,写出你的感想或对市民提出一条科学性的建议.9.某校九年级学生开展踢毽子比赛活动,每班派5名同学参加,按团体总分排列名次,在规定时间内每人踢100个以上(含100)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):统计发现两班总分相等,此时有同学建议,可以通过考察数据中的其他信息作为参考,请你解答以下问题:(1)计算两班的优秀率; (2)求两班比赛数据的中位数; (3)计算两班比赛数据的方差;(4)根据以上三条信息,你认为应该把冠军奖状发给哪一个班?简述理由.10.甲、乙两名队员参加射击训练,成绩分别被制成如图K -37-1所示两个统计图:图K -37-1根据以上信息,整理分析数据如下:(1)求出表格中,,的值;(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.假设选派其中一名队员参赛,你认为应选派哪名队员?11数学活动生活中很多矿泉水没有喝完便被扔掉,造成极大的浪费,为此数学兴趣小组的同学对某单位的某次会议所用矿泉水的浪费情况进展调查,为期半天的会议中,每人发一瓶500 mL 的矿泉水,会后对所发矿泉水的情况进展统计,大致可分为四种:A.全部喝完;B.喝剩约13;C.喝剩约一半;D.开瓶但根本未喝.同学们根据统计结果绘制成如图K -37-2所示的两个统计图,根据统计图提供的信息,解答以下问题:(1)参加这次会议的有多少人?在图②中D 所在扇形的圆心角是多少度?并补全条形统计图;(2)假设开瓶但根本未喝算全部浪费,试计算这次会议平均每人浪费矿泉水约多少毫升(计算结果保存整数);(3)据不完全统计,该单位每年约有此类会议60次,每次会议人数约在40至60人之间,请用(2)中计算的结果,估计该单位一年中因此类会议浪费的矿泉水(500 mL/瓶)约有多少瓶(可使用科学计算器).图K -37-21.[答案] C 2.[答案] B 3.[答案] C4.[解析] C 由题意可得:两次加油间耗油30升,行驶的路程为6600-6200=400(千米),所以该车每100千米平均耗油量为30÷(400÷100)=7.5(升). 5.[答案] B 6. [答案] 乙[解析] 方差越小,数据越稳定. 7.[答案] 24000[解析] 根据题意,得200÷5×600=24000(千克). 8.解:(1)抽样调查(2)2出现的次数最多,是11次,所以众数是2.30个数据中,中位数应是第15个和第16个的平均数,显然是3.故答案为2,3. (3)样本平均数x -=130×(1×0+1×1+11×2+7×3+5×4+4×5+1×6)=3(个),∴全市一天丢弃塑料袋总数=44×1044×3=3.3×105(个).答案不唯一,只要有实际意义即可,如感想:生活垃圾不统不知道,一统吓一跳等;建议:少用一次性塑料袋,多用安康环保袋;保护环境,从我做起或人人有责等等.9.解:(1)甲班的优秀率是35×100%=60%;乙班的优秀率是25×100%=40%.(2)甲班5名学生比赛数据的中位数为100个;乙班5名学生比赛数据的中位数为97个.(3)x 甲= 15×500=100(个),x 乙= 15×500=100(个).s 甲2= 15 [(100-100)2+(98-100)2+(110-100)2+(89-100)2+(103-100)2]=46.8,s 乙2= 15 [(89-100)2+(100-100)2+(95-100)2+(119-100)2+(97-100)2]=103.2.(4)应该把冠军奖状发给甲班.理由:因为甲班5名学生比赛数据的优秀率比乙班高、中位数比乙班大、方差比乙班小,所以应该把冠军奖状发给甲班.10.解:(1)甲的平均成绩a =5×1+6×2+7×4+8×2+9×11+2+4+2+1=7(环),∵乙射击的成绩从小到大排列为3,4,6,7,7,8,8,8,9,10, ∴乙射击成绩的中位数b =7+82=7.5(环), s乙2=110×[(3-7)2+(4-7)2+(6-7)2+2×(7-7)2+3×(8-7)2+(9-7)2+(10-7)2]=110×(16+9+1+3+4+9)=4.2. 故a =7,b =7.5,c =4.2.(2)(答案合理即可)从平均成绩看,甲、乙二人的成绩相等,均为7环; 从中位数看,甲射中7环以上的次数少于乙;从众数看,甲射中7环的次数最多而乙射中8环的次数最多; 从方差看,甲的成绩比乙的成绩稳定;综合以上各因素,假设选派一名队员参赛,可选派乙参赛,因为乙获得高分的可能性更大.11 解:(1)根据所给扇形统计图,可知喝剩约13的人数占总人数的50%,∴25÷50%=50(人), ∴参加这次会议的有50人.∵550×360°=36°, ∴D 所在扇形的圆心角是36°. 补全条形统计图如下图:(2)(25×13×500+10×500×12+5×500)÷50=275003÷50≈183(mL).答:这次会议平均每人浪费矿泉水约183 mL.(3)该单位每年参加此类会议的总人数约为2400~3600,那么浪费矿泉水约为2400+36002×183÷500=1098(瓶). 答:该单位一年中因此类会议浪费的矿泉水约有1098瓶.。
【教育资料】秋湘教版九年级数学上册同步练习:5.1 总体平均数与方差的估计学习精品

5.1总体平均数与方差的估计一、选择题1.为了解实验中学某班学生每天的睡眠情况,随机抽取该班10名学生,在一段时间里,每人平均每天的睡眠时间(单位:时)统计如下:6,8,8,7,7,9,10,6,9,7.由此估计该班学生平均每天的睡眠时间为()A.7小时B.7.5小时C.7.7小时D.8小时2.从总体中随机抽取一个样本,计算出样本方差为2,可以估计总体方差()A.一定大于2 B.约等于2C.一定等于2 D.与样本方差无关3.2019·株洲甲、乙、丙、丁四名射击队员考核赛的平均成绩(环)及方差统计如下表,现要根据这些数据,从中选出一人参加比赛,如果你是教练员,你的选择是()A.甲B.乙C4.张老师买了一辆汽车,为了掌握汽车的耗油情况,在连续两次加油时做了如下工作:(1)把油箱加满油;(2)记录了两次加油时的累计里程(注:“累计里程”指汽车从出厂开始累计行驶的路程),以下是张老师连续两次加油时的记录:则在这段时间内,该车每100千米平均耗油量为()A.3升B.5升C.7.5升D.9升5.要估计某鱼塘中的鱼数,养鱼者首先从鱼塘中打捞了50条鱼,在每条鱼身上做好记号后把这些鱼放归鱼塘,过一段时间后,再从鱼塘中打捞出100条鱼,发现只有2条鱼是做了记号的鱼.假设鱼在鱼塘内均匀分布,那么这个鱼塘的鱼数约为()A.5000条B.2500条C.1750条D.1250条二、填空题6.甲、乙两台机器分别灌装每瓶质量为500克的酸奶,从甲、乙灌装的酸奶中分别随机抽取了30瓶,测得它们实际质量的方差是s甲2=4.8,s乙2=3.6,那么________(填“甲”或“乙”)机器灌装的酸奶质量较稳定.7.2019·常德彭山的枇杷大又甜,在今年5月18日“彭山枇杷节”期间,从山上5棵枇杷树上采摘到了200千克枇杷,请估计彭山近600棵枇杷树今年一共收获了枇杷________千克.三、解答题8.为保护环境,创建绿色鹰潭,某环保小组随机调查了市区30个家庭一天丢弃塑料袋的情况,统计结果如下:(1)这种调查方式属于普查还是抽样调查:____________;(2)这30个家庭一天丢弃塑料袋个数的众数是________,中位数是________;(3)鹰潭市市区人口约有44万(含余江、贵溪两县城),假设平均一个家庭有4个人.若根据30个家庭这一天丢弃塑料袋个数的平均数估算,则全市一天丢弃塑料袋总数约有多少个(写出解答过程,结果用科学记数法表示)?通过该环保小组的统计和你的估算,写出你的感想或对市民提出一条科学性的建议.9.某校九年级学生开展踢毽子比赛活动,每班派5名同学参加,按团体总分排列名次,在规定时间内每人踢100个以上(含100)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):统计发现两班总分相等,此时有同学建议,可以通过考查数据中的其他信息作为参考,请你解答下列问题:(1)计算两班的优秀率; (2)求两班比赛数据的中位数; (3)计算两班比赛数据的方差;(4)根据以上三条信息,你认为应该把冠军奖状发给哪一个班?简述理由.10.甲、乙两名队员参加射击训练,成绩分别被制成如图K -37-1所示两个统计图:图K -37-1根据以上信息,整理分析数据如下:(1)(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名队员参赛,你认为应选派哪名队员?11数学活动生活中很多矿泉水没有喝完便被扔掉,造成极大的浪费,为此数学兴趣小组的同学对某单位的某次会议所用矿泉水的浪费情况进行调查,为期半天的会议中,每人发一瓶500 mL 的矿泉水,会后对所发矿泉水的情况进行统计,大致可分为四种:A.全部喝完;B.喝剩约13;C.喝剩约一半;D.开瓶但基本未喝.同学们根据统计结果绘制成如图K -37-2所示的两个统计图,根据统计图提供的信息,解答下列问题:(1)参加这次会议的有多少人?在图②中D 所在扇形的圆心角是多少度?并补全条形统计图;(2)若开瓶但基本未喝算全部浪费,试计算这次会议平均每人浪费矿泉水约多少毫升(计算结果保留整数);(3)据不完全统计,该单位每年约有此类会议60次,每次会议人数约在40至60人之间,请用(2)中计算的结果,估计该单位一年中因此类会议浪费的矿泉水(500 mL/瓶)约有多少瓶(可使用科学计算器).图K -37-21.[答案] C 2.[答案] B 3.[答案] C4.[解析] C 由题意可得:两次加油间耗油30升,行驶的路程为6600-6200=400(千米),所以该车每100千米平均耗油量为30÷(400÷100)=7.5(升). 5.[答案] B 6. [答案] 乙[解析] 方差越小,数据越稳定. 7.[答案] 24000[解析] 根据题意,得200÷5×600=24000(千克). 8.解:(1)抽样调查(2)2出现的次数最多,是11次,所以众数是2.30个数据中,中位数应是第15个和第16个的平均数,显然是3.故答案为2,3. (3)样本平均数x -=130×(1×0+1×1+11×2+7×3+5×4+4×5+1×6)=3(个),∴全市一天丢弃塑料袋总数=44×1044×3=3.3×105(个).答案不唯一,只要有实际意义即可,如感想:生活垃圾不统不知道,一统吓一跳等;建议:少用一次性塑料袋,多用健康环保袋;爱护环境,从我做起或人人有责等等.9.解:(1)甲班的优秀率是35×100%=60%;乙班的优秀率是25×100%=40%.(2)甲班5名学生比赛数据的中位数为100个;乙班5名学生比赛数据的中位数为97个. (3)x 甲= 15×500=100(个),x 乙= 15×500=100(个).s 甲2= 15 [(100-100)2+(98-100)2+(110-100)2+(89-100)2+(103-100)2]=46.8,s 乙2= 15 [(89-100)2+(100-100)2+(95-100)2+(119-100)2+(97-100)2]=103.2.(4)应该把冠军奖状发给甲班.理由:因为甲班5名学生比赛数据的优秀率比乙班高、中位数比乙班大、方差比乙班小,所以应该把冠军奖状发给甲班.10.解:(1)甲的平均成绩a =5×1+6×2+7×4+8×2+9×11+2+4+2+1=7(环),∵乙射击的成绩从小到大排列为3,4,6,7,7,8,8,8,9,10, ∴乙射击成绩的中位数b =7+82=7.5(环), s乙2=110×[(3-7)2+(4-7)2+(6-7)2+2×(7-7)2+3×(8-7)2+(9-7)2+(10-7)2]=110×(16+9+1+3+4+9)=4.2. 故a =7,b =7.5,c =4.2.(2)(答案合理即可)从平均成绩看,甲、乙二人的成绩相等,均为7环; 从中位数看,甲射中7环以上的次数少于乙;从众数看,甲射中7环的次数最多而乙射中8环的次数最多; 从方差看,甲的成绩比乙的成绩稳定;综合以上各因素,若选派一名队员参赛,可选派乙参赛,因为乙获得高分的可能性更大.11 解:(1)根据所给扇形统计图,可知喝剩约13的人数占总人数的50%,∴25÷50%=50(人), ∴参加这次会议的有50人. ∵550×360°=36°, ∴D 所在扇形的圆心角是36°. 补全条形统计图如图所示:(2)(25×13×500+10×500×12+5×500)÷50=275003÷50≈183(mL).答:这次会议平均每人浪费矿泉水约183 mL.(3)该单位每年参加此类会议的总人数约为2400~3600,则浪费矿泉水约为2400+36002×183÷500=1098(瓶).答:该单位一年中因此类会议浪费的矿泉水约有1098瓶.。
九年级数学上册 5.1 总体平均数与方差的估计习题1(无答案)(新版)湘教版
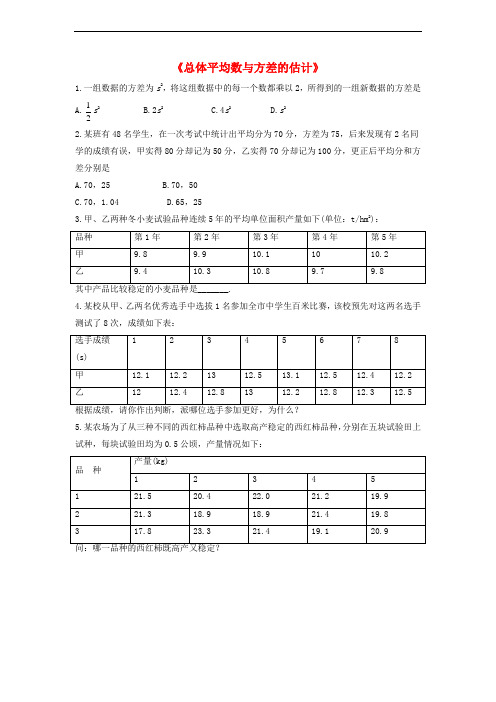
《总体平均数与方差的估计》
1.一组数据的方差为s 2
,将这组数据中的每一个数都乘以2,所得到的一组新数据的方差是 A.
2
1s 2
B.2s 2
C.4s 2
D.s 2 2.某班有48名学生,在一次考试中统计出平均分为70分,方差为75,后来发现有2名同学的成绩有误,甲实得80分却记为50分,乙实得70分却记为100分,更正后平均分和方差分别是
A.70,25
B.70,50
C.70,1.04
D.65,25
3.甲、乙两种冬小麦试验品种连续5年的平均单位面积产量如下(单位:t/hm 2
):
4.某校从甲、乙两名优秀选手中选拔1名参加全市中学生百米比赛,该校预先对这两名选手测试了8次,成绩如下表:
5.某农场为了从三种不同的西红柿品种中选取高产稳定的西红柿品种,分别在五块试验田上试种,每块试验田均为0.5公顷,产量情况如下:。
湘教版九年级数学上51总体平均数与方差的估计同步练习含试卷分析详解.docx

湘教版九年级数学上册第五章用样本推断总体5」总体平均数与方差的估计同步练习1.为了让人们感受丢弃塑料袋对环境造成的影响,某班环保小组的六名同学记录了自己家屮一周内丢弃的塑料袋的数量,结果如下(单位:个):33, 25, 28, 26, 25, 31.如果该班有45名学生,那么根据提供的数据,估计本周全班同学各家总共丢弄塑料袋的数量约()A. 900 个B. 1080 个C. 1260 个D. 1800 个2.某社区开展“节约每一滴水”活动,为了了解开展活动的一个月以来节约用水的情况,从该小区请你估计这1000个家庭一个月节约用水的总量大约是()A. 325 m3B. 330 m3C. 400 m3D. 650 m33.为了增强市民的环保意识,某校九年级(2)班的50名学生在今年6月5 口(世界环境LI)这一天请根据以上数据冋答:(1)5()户居民每天丢弃废旧塑料袋的平均个数是—个;(精确到个位)⑵该校所在的居民区有1万户,则该居民区每天丢弃的废旧塑料袋约—万个.4.某水果店购进2000箱苹果,从中任选10箱,称得质量分别是(单位:千克):16, 16.5, 14.5, 13.5, 15, 16.5, 15.5, 14, 14, 14.5,若每千克苹果的售价为4元,则利用样本平均数估计这批苹果的销售额是_________________ 元.5.从某校参加毕业会考的学生中,随机抽査了30名学生的数学成绩,分数如下:9084848687987882909368958471786194887710070978568998885929397试估计该校参加毕业考试的学生的数学平均成绩.(结果保留整数)6.某特警部队为了选拔“神枪手”,举行了1000米射击比赛,最后甲、乙两名战上进入决赛.在相同条件下,两人各射靶10次,经过统计计算,甲、乙两名战士的总成绩都是99.68环,甲的方差是0.28,乙的方差是0.01,则下列说法中,正确的是()A.甲的成绩比乙的成绩稳定B.甲、乙两人成绩的稳定性相同C.乙的成绩比甲的成绩稳定D.无法确定谁的成绩更稳定7.金华火腿遐迩闻名.某火腿公司冇甲、乙、丙三台切割包装机,同时分装质量为500克的火腿心片.现从它们分装的火腿心片中各随机抽取10盒,经称量并计算得到质量的方差如表所示,你认为包装质量最稳定的切割包装机是()A.甲B.乙C.丙D.不能确定&己知甲、乙两种棉花的纤维长度的平均数相等,若甲种棉花的纤维长度的方差5 <=1.3275,乙 种棉花的纤维长度的方差£「=1.8775,则甲、乙两种棉花质量较好的是—•9.某学校为了了解该学校七年级学生双休日上网的情况,随机调查了该学校七年级的25名学生, 得到了上周双休日上网时间的一组样木数据,其频数分布直方图如图所示,那么估计该学校七年级 每名学生双休LI 上网的平均时间是()1小2小3小4小5小6小时间10.某校九年级420名学生参加植树活动,随机调查了 50名学生植树的数量,并根据数据绘制了 如下条形统计图,请估计该校九年级学牛此次植树活动约植树 棵.第1天 第2天 第3天 第4天 第5天 第6天 第7天 路程(千米)36 29 27 40437233小辰家的轿车每月(按30天计算)要行驶多少千米?13.为了了解市场上甲、乙两种乎表U 走时误差的情况,从这两种手表中各随机抽取10块进行测 试,两H 期类型 一 二 -四 五 六 七 八 九 十 甲种手表 -3 4 2 -1 -2 -2 1 -2 2 1 乙种手表-41-2141-212-2(年种77 口 —口第1年 第2年 第3年 第4年 第5年甲 9.8 9.9 10.1 10 10.2 乙9.410.310.89.79.82 - 0 34 56棵树11•甲、乙两种水稻试验站种连续5年的平均单位面积产龟如下:(单位:吨/公顷)经计算,兀甲=1(),兀乙=10,试根据这组数据估计—种水稻晶种的产量比较稳定. A ・3.2小时 B ・3.4小时C ・3.5小时 D ・36小时2876543210人数 181713(2)你认为甲、乙两种手表中哪种手表稳定性好?说说你的理由.14・王大伯儿年前承包了甲、乙两片荒山,各栽1()()棵杨梅树,成活98%•现己挂果,经济效益初步显现,为了分析收成情况,他分別从两山上随意各采摘了4棵树上的杨梅,每棵的产量如折线统(1)分别计算甲.乙两山样本的平均数,并估算出甲.乙两山杨梅的产量总和;(2)试通过计算说明,哪个山上的杨梅产量较稳定?答案:1. C2. A3. 4 44.12 万5.解:《=舟(90 + 84 +・・・+ 97)=乍許85(分),即样本平均数为85•于是可以估计,该校参加毕业会考的学生的数学平均成绩约为85分6.C7.A8.甲9.B10.168011.甲12.解:1200千米13.解:(l)x 甲=0, x 乙=0(2)S『=4.8, S 乙" = 5.2甲种乎表走时稳定性好14.解:(l)x 甲=40(千克),x乙=40(千克),总产量为40x100x98% X 2 = 7840(千克)(2)s 2=|[(50-40)2+(36-40)2+(40-40)2+(34-40)2]=38(千克2); s z.2=|[(36-40)2+(40-40)2 +(48—40)2+(36—40円=24(千克2). Vs .t.2>s乙乙山上的杨梅产量较稳定我的写字心得体会从小开始练习写字,几年来我认认真真地按老师的要求去练习写字。
