导线网平差程序设计共86页
导线网平差及精度评定程序设计平差

导线网平差及精度评定程序设计平差问题描述背景:导线网平差及精度评定程序设计平差是在测量和测绘工作中常用的一种技术方法。
它是通过对导线网观测数据进行处理和计算,得出导线网的平差结果,并评定其精度,以确保测量结果的准确性和可靠性。
背景:导线网平差及精度评定程序设计平差是在测量和测绘工作中常用的一种技术方法。
它是通过对导线网观测数据进行处理和计算,得出导线网的平差结果,并评定其精度,以确保测量结果的准确性和可靠性。
目的:本文档旨在介绍导线网平差及精度评定程序设计平差的背景和目的。
通过对平差方法和流程的解释,使读者了解导线网平差的基本原理和操作步骤,并了解如何评定导线网平差结果的精度。
这将有助于测量和测绘工作中平差的正确实施,并对测量数据进行科学的分析和解释。
目的:本文档旨在介绍导线网平差及精度评定程序设计平差的背景和目的。
通过对平差方法和流程的解释,使读者了解导线网平差的基本原理和操作步骤,并了解如何评定导线网平差结果的精度。
这将有助于测量和测绘工作中平差的正确实施,并对测量数据进行科学的分析和解释。
目的:本文档旨在介绍导线网平差及精度评定程序设计平差的背景和目的。
通过对平差方法和流程的解释,使读者了解导线网平差的基本原理和操作步骤,并了解如何评定导线网平差结果的精度。
这将有助于测量和测绘工作中平差的正确实施,并对测量数据进行科学的分析和解释。
目的:本文档旨在介绍导线网平差及精度评定程序设计平差的背景和目的。
通过对平差方法和流程的解释,使读者了解导线网平差的基本原理和操作步骤,并了解如何评定导线网平差结果的精度。
这将有助于测量和测绘工作中平差的正确实施,并对测量数据进行科学的分析和解释。
请注意:本文档仅供参考和研究使用,不可用于商业目的或作为法律依据。
建议在实际应用中,根据具体情况和专业要求,进行适当的调整和改进。
请注意:本文档仅供参考和研究使用,不可用于商业目的或作为法律依据。
建议在实际应用中,根据具体情况和专业要求,进行适当的调整和改进。
导线平差计算方案设置-16页文档资料

导线平差计算方案设置一、导线类型:1.闭、附合导线(图1)2.无定向导线(图2)3.支导线(图3)4.特殊导线或网(见数据输入一节),该选项适用于所有的导线,但不计算闭合差。
而且该类型不需要填写未知点数目。
当点击表格最后一行时自动添加一行,计算时删除后面的空行。
5.坐标导线。
指使用全站仪直接观测坐标、高程的闭、附合导线。
6.单面单程水准测量记录计算。
指仅进行单面读数且仅进行往测而无返测的水准测量记录计算。
当数据中没有输入“中视”时可以用作五等、等外水准等的记录计算。
当输入了“中视”时可以用作中平测量等的记录计算。
说明:除“单面单程水准测量记录计算”仅用于低等级的水准测量记录计算外,其它类型选项都可以进行平面及高程的平差计算,输入了平面数据则进行平面的平差,输入了高程数据则进行高程的平差,同时输入则同时平差。
如果不需进行平面的平差,仅计算闭、附合高程路线,可以选择类型为“无定向导线”,或者选择类型为“闭附合导线”但表格中第一行及最后一行数据(均为定向点)不必输入,因为高程路线不需定向点。
二、概算1.对方向、边长进行投影改化及边长的高程归化。
2.应选择相应的坐标系统,以及Y坐标是否包含500KM。
选择了概算时,Y坐标不应包含带号。
三、平面计算设置(一)、等级:选择等级,以便根据《工程测量规范》自动进行限差等的设置。
不同的规范,或者相同的规范但不同的版本可能技术要求不同,请在软件进行自动设置后做必要的检查,如有不符,可以自行设置。
(二)、近似平差与严密平差的选择及近似平差的方位角、边长是否反算1.近似平差:程序先分配角度闭合差再分配坐标增量闭合差,即分别平差法。
2.严密平差:按最小二乘法原理平差。
3.《工程测量规范》规定:一级及以上平面控制网的计算,应采用严密平差法,二级及以下平面控制网,可根据需要采用严密或简化方法平差。
当采用简化方法平差时,应以平差后坐标反算的角度和边长作为成果。
《城市测量规范》规定:四等以下平面控制网可采用近似平差法和按近似方法评定其精度。
数据结构课程设计——导线网平差程序的设计与实现

数据结构课程设计——导线网平差程序的设计与实现设计二:导线网平差程序的设计与实现一、设计目的立足于《数据结构与测绘软件开发》这一课程的课堂教学及其实验课程设计,为着实提高学生基于计算机辅助的方式切实解决工程实际问题的动手能力,通过本实习,一方面,使学生深入了解课堂所学知识,另一方面,通过实践掌握测绘行业软件设计与开发的基本方法,深刻掌握矩阵运算、曲线/曲面拟合的数值解法,掌握不同类型的典型测绘软件设计方法,使得学生初步具备编写测绘软件常用算法的能力以及开发中小规模测绘专业软件的能力。
有导线网如图,观测了14条边长和16个转折角,已知测角精度10βδ''=,测边精度为1.0()()S S m mm δ=。
已知A 、B 、C 、D 、E 、F 点的坐标(无误差),如下表:表1 已知点数据点号 X(m) Y(m)A 5256.953 4520.068B 5163.752 4281.277C 3659.371 3621.210D 4119.879 3891.607E 4581.150 5345.292F 4851.5545316.953表2 角度观测值编号角度观测值(° ′ ″)编号角度观测值(° ′ ″)1 163 45 04 9 169 10 302 64 58 37 10 98 22 043 250 18 11 11 94 53 50 4 103 57 34 12 111 14 235 83 08 05 13 79 20 18三、关键问题描述3.1 未知点近似坐标计算平面控制网进行平差计算时需要计算未知点的近似坐标1.坐标计算公式1、2点的坐标已知,并观测了1-2、1-3的夹角,根据这些数据可以求出3号点坐标根据1、2两点的坐标,可以反算出1、2方向的方位角T12,3号点的坐标为++=++=)sin()cos(121313121313ααT S y y T S x x式子中S13为观测边长,α为观测角度 2.计算流程从读入的数据循环计算未知点的坐标,已计算出的坐标当做已知坐标的点处理参加下次计算,以此类推,逐步计算出未知点的坐标3.实现算法CMatrix CPlaneNetAdjust::XYJS() { CMatrix _XYJS(Pnumber,2); double T12; for(int i=0;i0&&xy[k2].Y>0) { T12=GetT12(k1,k2); } double s12=Gets12(k1,k2); double s13=Gets12(k1,k3); double T13=T12+guancejiao[i].Guancezhi; double dx=s13*cos(T13); double dy=s13*sin(T13); xy[k3].X=xy[k1].X+dx; xy[k3].Y=xy[k1].Y+dy; } for(int i=0;i<="" bdsfid="103" double="" p="" temp1="xy[i].X;" temp2="xy[i].Y;" {="">}return _XYJS;}3.2 误差方程列立1.理论分析平面控制网的误差方程都是非线性方程,必须引入参数近似值将误差方程线性化,取X的充分近似值 0X ,x ?是微小量,在按台劳公式展开时可以略去二次和二次以上的项,而只取至一次项,于是可对非线性平差值观测方程式线性化,于是有如下的式子对于观测角的改正数有对于边长观测值的改正数有2.实现算法如下:CMatrix CPlaneNetAdjust::B() { CMatrix _B1(Lnumber,Pnumber*2); double a; double b; double c; double d; double m; double n; double m1; double n1; for(int i=0;i<="">D A D A D B D B DA DB X X Y Y X X Y Y L ??arctan ??arctan 1-----=-=αα()()22??S AD A D Y Y X X -+-=kjkjk k jk jk j jk jkj jk jk jk y S Y x S Y y S X x S Y ?)(?)(?)(?)(?200200200200"??+??-??-??+=ρρρραδh jhjh h jh jh j jh jh j jh jh jh y S Y x S Y y S X x S Y ?)(?)(?)(?)(?200 200200200"??+??-??-??+=ρρρραδ)(?)("?)("?)("?)("?)("?)("?)(" )("00200200200200200200200200i jk jh h jh jhh jh jh j jh jh j jh jh k jk jkk jk jk j jk jk j jk jk i L y S X x S Y y S X x S Y y S X x S Y y S X xS Y v ---??+?-?-?-+?-?-?-=ααρρρρρρρρi k jkjkk jk jk j jk jk j jk jk i l y S Y x S X y S Y x S X v -?+?+?-?-=000000000jki i S L l -=2002000)()(j k j k jk Y Y X X S -+-=_B1.setValue(i,2*k1,0);_B1.setValue(i,2*k1+1,0);}else{_B1.setValue(i,2*k1,a);_B1.setValue(i,2*k1+1,b);}if(k2<knpnumber)< bdsfid="148" p=""></knpnumber)<> {_B1.setValue(i,2*k2,0);_B1.setValue(i,2*k2+1,0);}else{_B1.setValue(i,2*k2,-a);_B1.setValue(i,2*k2+1,-b);}}for(int i=0;i<tnumber;i++)< bdsfid="160" p=""></tnumber;i++)<>{const double p=206.265;int k1=cezhan[i];int k3=huoshi[i];int k2=qianshi[i];double dx12=xy[k2].X-xy[k1].X;double dy12=xy[k2].Y-xy[k1].Y;double dx13=xy[k3].X-xy[k1].X;double dy13=xy[k3].Y-xy[k1].Y;c=(p*dx13/Gets12(k1,k3)/Gets12(k1,k3)-p*dx12/Gets12(k1,k2)/Gets12(k1,k2));c=-c;d=-p*dy13/Gets12(k1,k3)/Gets12(k1,k3)+p*dy12/Gets12(k1,k2)/Get s12(k1,k2);d=-d;m=-p*dy13/Gets12(k1,k3)/Gets12(k1,k3);m=-m;n=p*dx13/Gets12(k1,k3)/Gets12(k1,k3);n=-n;m1=p*dy12/Gets12(k1,k2)/Gets12(k1,k2);m1=-m1;n1=-p*dx12/Gets12(k1,k2)/Gets12(k1,k2);n1=-n1;if(k1<knpnumber)< bdsfid="183" p=""></knpnumber)<> {_B1.setValue(i+Snumber,2*k1,0);_B1.setValue(i+Snumber,2*k1+1,0);}else if(k1>=knPnumber){_B1.setValue(i+Snumber,2*k1,c);_B1.setValue(i+Snumber,2*k1+1,d);}if(k2<knpnumber)< bdsfid="194" p=""></knpnumber)<> {_B1.setValue(i+Snumber,2*k2,0);_B1.setValue(i+Snumber,2*k2+1,0);}else if(k2>=knPnumber){ _B1.setValue(i+Snumber,2*k2,m1); _B1.setValue(i+Snumber,2*k2+1,n1); } if(k3=knPnumber) { _B1.setValue(i+Snumber,2*k3,m); _B1.setValue(i+Snumber,2*k3+1,n); } }CMatrix _B(Lnumber,2*(Pnumber-knPnumber)); for(int i=0;i<_B1.getRow();i++) { for(int j=2*knPnumber;j<2*Pnumber;j++) { double temp=_B1.getValue(i,j); _B.setValue(i,(j-2*knPnumber),temp); } } return _B;}3.3 法方程构建与解算1.理论分析误差方程系数构成法方程2.实现代码①计算LCMatrix CPlaneNetAdjust::L() { CMatrix _L(Lnumber,1); double l; double s; double s0; for(int i=0;i<="" bdsfid="209" const="" cout<<l<l x B V -=?0?=-Pl B x PB B TTmin =PV V T V L L +=?20σ20?σPV V T double A13; double A;int k1=cezhan[i]; int k2=huoshi[i]; int k3=qianshi[i];A12=GetT12(k1,k2); A13=GetT12(k1,k3); A=GetA(k1,k2,k3); l=A13-A12; if(l<0) { l=pi+l; }if(l>=pi) { l=l-pi; }l=l-A;//cout<<rad_dms(a12)<<" "<<rad_dms(a)<<"<="" "<<rad_dms(a13)<<"="" bdsfid="220" p=""></rad_dms(a12)<<">"<<rad_dms(l)<<endl;< bdsfid="222" p=""></rad_dms(l)<<endl;<>_L.setValue(i+Snumber,0,rad_dms(l));} return _L; }②计算权阵PCMatrix CPlaneNetAdjust::P() { CMatrix _P(Lnumber,Lnumber); for(int i=0;i<="" p="" {="">temp=temp=Cjwucha*Cjwucha/(1*sqrt(bianchang[i].Len))/( 1*sqrt(bianchang[i].Len)); _P.setValue(i,i,temp); } for(int i=Snumber;i<="">3.4 精度估计1.单位权中误差间接平差与条件平差虽采用了不同的函数模型,但它们是在相同的最小乘原理下进行的,所以两法的平差结果总是相等的,这是因为在满足条件下的V 是唯一确定的,故平差值不因方法不同而异。
【免费下载】导线网平差算例
闭合差计 算与检核
平差
平差报告的 生成和输出
实例 1 符合导线实例
这是一条符合导线的测量数据和简图,A、B、C 和 D 是已知坐标点,2、3 和 4 是
待测的控制点。
原始测量数据如下:
测站点 角度(°′″) 距离(米)
B
A
2
3
4
C
D
导线图如下:
85.30211
254.32322
.04333
272.20202
测站 3 的观测信息
以 4 号点为测站点,以 3 号点为定向点时,照准 C 点的数据输入如下图“测站 4 的观测信息”所示:
测站 4 的观测信息
说明:①数据为空或前面已输入过时可以不输入(对向观测例外) ②在电子表格中输入数据时,所有零值可以省略不输。
以上数据输入完后,点击菜单“文件\另存为”,将输入的数据保存为平差易数据 格式文件(格式内容详见附录 A): [STATION] (测站信息) B,10,8345.870900,5216.602100 A,10,7396.252000,5530.009000 C,10,4817.605000,9341.482000 D,10,4467.524300,8404.762400 2,00 3,00 4,00
导线网平差算例
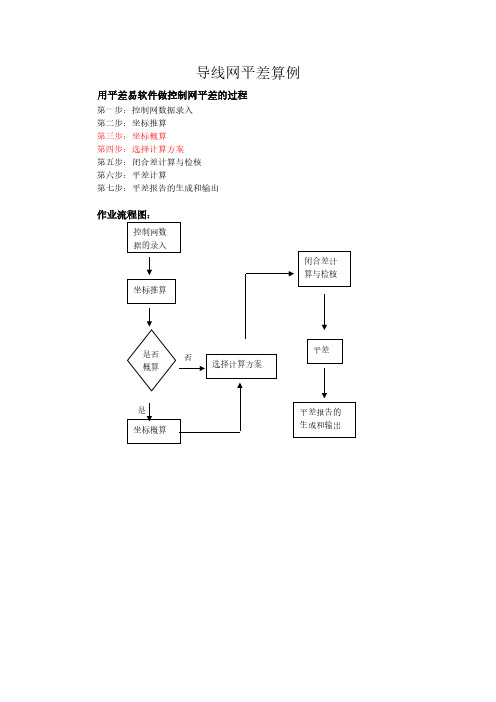
用平差易软件做控制网平差的过程
第一步:控制网数据录入 第二步:坐标推算 第三步:坐标概算 第四步:选择计算方案 第五步:闭合差计算与检核 第六步:平差计算 第七步:平差报告的生成和输出
作业流程图:
控制网数 据的录入
坐标推算
是否 概算
是 坐标概算
否 选择计算方案
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电,力根通保据过护生管高产线中工敷资艺设料高技试中术卷资,配料不置试仅技卷可术要以是求解指,决机对吊组电顶在气层进设配行备置继进不电行规保空范护载高与中带资负料荷试下卷高问总中题体资,配料而置试且时卷可,调保需控障要试各在验类最;管大对路限设习度备题内进到来行位确调。保整在机使管组其路高在敷中正设资常过料工程试况中卷下,安与要全过加,度强并工看且作护尽下关可都于能可管地以路缩正高小常中故工资障作料高;试中对卷资于连料继接试电管卷保口破护处坏进理范行高围整中,核资或对料者定试对值卷某,弯些审扁异核度常与固高校定中对盒资图位料纸置试,.卷保编工护写况层复进防杂行腐设自跨备动接与处地装理线置,弯高尤曲中其半资要径料避标试免高卷错等调误,试高要方中求案资技,料术编试交写5、卷底重电保。要气护管设设装线备备置敷4高、调动设中电试作技资气高,术料课中并3中试、件资且包卷管中料拒含试路调试绝线验敷试卷动槽方设技作、案技术,管以术来架及避等系免多统不项启必方动要式方高,案中为;资解对料决整试高套卷中启突语动然文过停电程机气中。课高因件中此中资,管料电壁试力薄卷高、电中接气资口设料不备试严进卷等行保问调护题试装,工置合作调理并试利且技用进术管行,线过要敷关求设运电技行力术高保。中护线资装缆料置敷试做设卷到原技准则术确:指灵在导活分。。线对对盒于于处调差,试动当过保不程护同中装电高置压中高回资中路料资交试料叉卷试时技卷,术调应问试采题技用,术金作是属为指隔调发板试电进人机行员一隔,变开需压处要器理在组;事在同前发一掌生线握内槽图部内 纸故,资障强料时电、,回设需路备要须制进同造行时厂外切家部断出电习具源题高高电中中源资资,料料线试试缆卷卷敷试切设验除完报从毕告而,与采要相用进关高行技中检术资查资料和料试检,卷测并主处且要理了保。解护现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
导线网平差程序设计.ppt

– 改正性维护,也就是诊断和改正在使用过程中发现的软件错误
– 适应性维护,即修改软件以适应环境的变化
– 完善性维护,即根据用户的要求改进或扩充软件使它更完善
– 预防性维护,即修改软件为将来的维护活动预先做准备。
• 1.4.4 螺旋模型
– 软件风险:
• 产品交付给用户之后用户可能不满意 • 到了预定交付日期软件而可能还没开发出来 • 实际开发成本可能超出预算 • 产品完成前一些关键的开发人员可能离开 • 产品投入市场之前已经有功能相近、价格更低的软件先行投入
– 构建原型是一种能使某些类型的风险降至最低的方法。 – 螺旋模型的基本思想:使用原型及其他方法来尽量降低风险,即
非功能需求:它描述了系统展现给用户的行为和执行的操 作等。它包括产品必须遵从的标准、规范和合约;外部界 面的具体细节;性能要求;设计或实现的约束条件及质量 属性。
需求分析的数据要求
• 任何一个软件系统本质上都是信息处理系 统,系统必须处理的信息和系统应该产生 的信息在很大程度上决定了系统的面貌, 对软件设计有深远影响。
– 在需求分析阶段确定的系统逻辑模型是以后设计和实现目标系统 的基础,因此必须准确完整地体现用户的要求。
–软件开发
④总体设计
➢这个阶段必须回答的关键问题是:“概括地说, 应该如何解决这个问题?”。总体设计阶段的 第一项主要任务就是应该考虑几种可能的解决 方案。
➢结构设计的一条基本原理就是程序应该模块化, 也就是一个大程序应该由许多规模适中的模块 按合理的层次结构组织而成。总体设计阶段的 第二项主要任务就是设计软件的结构,也就是 确定程序由哪些模块组成以及模块间的关系。 通常用层次图或结构图描绘软件的结构。
导线平差的程序设计与实现-毕业论文

山西水利职业技术学院实习报告题目导线平差的程序设计与实现姓名:孟国娇学号:专业:工程造价1139报告提交日期:山西水利职业技术学院设计任务书学院:土建工程系专业年级:工程造价2011 学生姓名:孟国娇任务下达日期:2012年 2 月20日毕业设计日期:2012年3月12日至2012年6月13日毕业设计题目:导线平差的程序设计与实现毕业设计主要内容和要求:主要内容:(1)测量平差的研究背景及意义;(2)测量平差概述;(3)Excel在单一附和导线近似平差中的应用;(4)Excel在单一附和导线条件平差中的应用;(5)导线网的间接平差理论;(6)导线网平差的结构和函数设计与实现。
设计要求:(1)毕业设计要充分发挥主观能动性,积极思考,主动实践;(2)毕业设计撰写结构要严整,叙述清楚,理论分析适当,数据可靠,研究方法合理,结论正确,论文格式符合规范;(3)研究成果要有一定的实用或参考价值。
院长签字:指导教师签字:摘要随着测绘科学技术的不断发展,在测量数据的处理中产生很多种平差的方法。
在本文中,导线网的近似平差和条件平差的一些简单计算可通过Excel表编制计算公式和编程实现,我们只需在已编好的Excel表中稍作调整和公式修改,并输入已知数据,最终就可得到所需的平差结果,这为测量的内业工作提供了服务和参考;导线网的间接平差程序是利用C++编程实现的,我们需要将导线网的已知数据信息按照特定的规则输入到dat文本中,利用C++程序读取文本数据信息后,对其进行一系列的平差计算,最终获得平差后的结果,并以dat文本的形式输出且保存,这样就可为测量工作提供一定的参考,还能为测绘数据的管理带来帮助。
关键词:导线平差;Excel;C++;程序目录1绪论...............................................................................................................................................1.1研究背景及意义.................................................................................................................1.2国内外研究状况.................................................................................................................1.3本文研究的具体内容.........................................................................................................1.4平差程序相关说明.............................................................................................................1.4.1平差程序计算特点..................................................................................................1.4.2平差程序的基本要求..............................................................................................1.4.3平差程序的结构化设计..........................................................................................1.4.4平差程序模块化......................................................................................................1.4.5平差程序的数据结构.............................................................................................. 2测量平差.......................................................................................................................................2.1测量平差概述.....................................................................................................................2.1.1测量平差..................................................................................................................2.1.2测量平差的函数模型..............................................................................................2.2最小二乘原理.....................................................................................................................2.3条件平差原理.....................................................................................................................2.3.1条件平差的数学模型..............................................................................................2.3.2条件平差原理..........................................................................................................2.3.3条件平差的计算步骤..............................................................................................2.3.4精度评定..................................................................................................................2.4间接平差原理.....................................................................................................................2.4.1间接平差的数学模型..............................................................................................2.4.2间接平差的的一般原理..........................................................................................2.4.3按间接平差法求平差值的计算步骤......................................................................2.4.4精度评定.................................................................................................................. 3Excel在导线平差中的应用.........................................................................................................3.1 Excel在平差中的应用基础...............................................................................................3.1.1 引言.........................................................................................................................3.1.2Excel在平差中的基本应用操作函数...................................................................3.1.3 核心问题的解决及技巧.........................................................................................3.1.4 三角函数在Excel中的处理方法..........................................................................3.1.5 小结.........................................................................................................................3.2Excel在附和导线近似平差中的应用..............................................................................3.2.1 单一附和导线近似平差.........................................................................................3.2.2单一附和导线近似平差实例..................................................................................3.3 Excel在导线网条件平差中的应用...................................................................................3.3.1单一附合导线条件平差..........................................................................................3.3.2边角权的确定及单位权中误差..............................................................................3.3.3单一附和导线条件平差实例.................................................................................. 4导线网的间接平差程序设计与实现 ...........................................................................................4.1矩阵的相关函数.................................................................................................................4.1.1矩阵相乘..................................................................................................................4.1.2矩阵转置..................................................................................................................4.1.3矩阵求逆..................................................................................................................4.1.4矩阵输出..................................................................................................................4.1.5设置实数输出精度..................................................................................................4.2平差中的重要函数.............................................................................................................4.2.1角度制与弧度制的相互转化..................................................................................4.2.2测量正反算函数......................................................................................................4.2.3近似坐标计算..........................................................................................................4.3导线网的平差理论.............................................................................................................4.3.1平差概述..................................................................................................................4.3.2边角网的最小二乘平差..........................................................................................4.4间接平差的结构与函数设计.............................................................................................4.4.1间接平差..................................................................................................................4.4.2结构与函数设计......................................................................................................4.5导线网平差的程序应用.....................................................................................................4.5.1平面网数据的输入格式..........................................................................................4.5.2导线网平差程序应用实例...................................................................................... 5结论与展望 ...................................................................................................................................5.1Excel在导线平差中的应用..............................................................................................5.1.1Excel在导线近似平差中的应用...........................................................................5.1.2Excel在导线网条件平差中的应用.......................................................................5.2C++在导线平差中的应用 .................................................................................................5.3测量平差的展望................................................................................................................ 参考文献........................................................................................................................................... 致谢. (54)1绪论1.1研究背景及意义测量工作是工程施工非常基础、重要的环节,对工程设计、工程施工、工程的验收都发挥着指导性、不可替代的作用。
导线网条件平差计算

感谢您的观看
汇报人:XX
实例总结和经验教训
实例分析:介绍 具体的导线网条 件平差计算实例, 包括数据来源、 计算过程和结果
分析
总结:对实例分 析的结果进行总 结,提炼出导线 网条件平差计算 的关键技术和方
法
经验教训:分享 在实例分析过程 中遇到的问题和 解决方法,以及 可以改进和优化
的地方
实例应用:探讨 实例分析结果在 实际工程中的应 用,以及如何根 据实际情况调整 和改进计算方法
精度分析和误差处理
精度分析:通过对比实际测量数据和计算结果,评估平差计算的准确性和可靠性。 误差处理:对测量过程中产生的误差进行修正,以提高平差计算的精度。 实例分析:通过具体实例展示精度分析和误差处理在导线网条件平差计算中的应用。 注意事项:强调在进行精度分析和误差处理时应注意的事项,以确保计算结果的准确性。
软件测试和性能评估
测试目的:验证软件是否符合 设计要求和功能需求
测试方法:单元测试、集成测 试、系统测试和验收测试
性能评估指标:处理速度、精 度、可靠性、可扩展性和可维 护性
评估工具:负载测试、压力测 试和性能分析工具
导线网条件平差 计算的未来发展
导线网条件平差计算技术的发展趋势和方向
智能化:随着人 工智能技术的不 断发展,导线网 条件平差计算将 更加智能化,能 够自动识别和解
决各种问题。
自动化:未来导 线网条件平差计 算将更加自动化, 减少人工干预, 提高计算效率和
精度。
精细化:随着测量 技术和数据处理技 术的发展,导线网 条件平差计算将更 加精细化,能够对 各种复杂情况进行
精确处理。
集成化:未来导 线网条件平差计 算将与其他测量 技术进行集成, 形成更加完整的 测量系统,提高 测量精度和效率。
基于Matlab的导线网平差程序设计_李建章

第29卷 第4期2010年8月兰州交通大学学报J ou rnal of Lanzh ou Jiaotong UniversityV ol.29N o.4A ug.2010 文章编号:1001-4373(2010)04-0088-03基于M atlab的导线网平差程序设计*李建章(兰州交通大学土木工程学院,甘肃兰州 730070)摘 要:导线网数据量大,网形复杂多变,其数据处理过程大多涉及到矩阵的计算.利用VC、VB等编程语言进行导线网程序的开发,算法比较复杂.基于M atlab平台,利用其强大的矩阵处理能力,设计出导线网数据结构,此基础上进行导线网平差程序的设计与开发,减小了代码编写的工作量.关键词:导线网;数据结构;平差;程序设计中图分类号:P209 文献标志码:A 导线网网形灵活多变,在城市测量中应用非常广泛.通常情况下,其外业观测数据量大,数据处理过程中大多涉及到矩阵的计算,且由于导线网网形的不确定性,因此其程序设计非常复杂[1].本文总结导线网的规律,设计出通用数据结构,并基于Matlab 强大的矩阵计算能力,编制了导线网数据处理程序. 1 导线网数据结构设计导线网由导线点、导线边和角度3类要素构成,其中导线边包括起点和终点,角度包括左边和右边.要使程序能对于任意形状的导线网进行处理,首先需要设计数据结构,以存储相关数据.这些数据包括起算数据、观测数据和网形各要素连接关系等,它们都是导线网各要素的属性值.本文用3个表来存储各要素,如表1-3所示.表1 点表数据结构Tab.1 Data structure of points序号字段类型备注1点名称整型2初始纵坐标浮点3初始横坐标浮点4已知点标志整型1为已知点,0为未知点5平差纵坐标浮点6平差横坐标浮点表2 角度数据结构Tab.2 Data structure of angles序号字段类型备注1角度编号整型2左边整型3右边整型4角度浮点度分秒表3 边数据结构Tab.3 Data structure of lines序号字段类型备注1导线边编号整型2起点整型3终点整型4边长浮点5方位浮点弧度6纵坐标增量浮点7横坐标增量浮点 表1-3中分别存储在ptTab,lineTab,angleTab 矩阵中,保存为.mat文件,程序运行时加载[2].2 近似坐标计算近似坐标的计算是导线网平差中关键的一个环节.其精度直接影响到后续平差计算的点位精度和迭代平差工作量大小.近似坐标计算包括近似方位角的计算和近似坐标的计算两个步骤.2.1 近似方位角计算近似方位角的计算以角度为单位,将已知方位传递到网中每一条边.设某角度一边方位已知,而另一边方位未知,由于两边夹角已知,可计算出未知边的方位.图1所示为4种可能情况.图1 方位角计算4种情况Fig.1 Four situation of azimuth angle calculation*收稿日期:2010-04-06作者简介:李建章(1974-),男,甘肃会宁人,讲师.第4期李建章:基于M atlab 的导线网平差程序设计假定已知左边方位角为fw 1,夹角为α,则以上4种情况下右边的方位角f w r 讨论如下.情况一:fw r =fw 1+α(1)情况二:fw r =fw 1+α(2)情况三:fw r =fw 1±π+α(3)情况四:fw r =fw 1±π+α(4)同理可得,已知右边方位角计算左边方位角的情况,也有4种可能性.程序根据角度两边的端点点名的关系判断以上8种情况,采用相应的计算公式计算未知边方位角[3].程序在获得未知边方位角后,将计算结果保存到边表相应记录中.然后在角度表中搜索相邻角度,搜索条件是:该角度的一边必须是上一角度的一边,而另一边不是上一角度的一边.查询到满足条件的角度后,判断其是否为截至角(两边方位已知),如否则计算出该角度未知边方位,重复前面的步骤直至某一截至角停止.然后在边表中查询有无近似方位未知的边,如有,再次执行以上步骤,直至边表中所有边近似方位计算完毕,这个过程可以通过一个函数自身迭代来实现.程序流程如图2所示.图2 计算近似方位流程图Fig .2 Flow chart of calculating azimuth angle计算导线边方位的子程序如下所示:functio n [ptT ab ,angleT ab ,lineT ab ,ok ]=g etfw0(pt -T ab ,ang le T ab ,lineT ab )[baindex ]=getanglebeg in (angleT ab ,line Tab );%查找起算角[ok ,ptT ab ,line T ab ,ang le T ab ]=caculateFW0(baindex ,ptT ab ,line Tab ,ang le Tab );%由起算角往前传递方位.if no t (fwisok (lineTab ))%判断有没有方位未知的导线边 [ptT ab ,ang leT ab ,lineT ab ,ok ]=getfw 0(ptT ab ,a n -gleT ab ,lineT ab ); %函数迭代计算.end end2.2 近似坐标计算通过2.1计算,所有导线边的近似方位计算完毕,此时可以利用每条边的边长和近似方位计算其坐标增量,这个过程只需要在边表中循环计算即可.然后以导线边为单位,从起始边出发,将已知坐标传递到各未知点.所谓起始边即该边一端点坐标已知,另一端点坐标未知.利用导线边坐标增量计算未知点坐标,然后查找相邻边,判断其是否为截至边(两端点坐标皆知),如否,计算未知点坐标.重复查找计算直至截至边,然后程序在点表中判断有无近似坐标未知的点,如有,则重复以上步骤,否则程序退出.这个过程和2.1中计算方位角的过程是类似的,因此不再列出程序流程图和代码.3 误差方程系数矩阵计算导线网观测值有角度和边长两种类型,一个观测值可列出一个误差方程.因此程序需分别读取角度表和导线边表中每个记录来计算误差方程系数矩阵B 、常数项矩阵l 和权阵P .3.1 利用观测角度计算误差方程系数矩阵设某角度观测值为ang le ,其左边近似方位、左边长、左边起点点名,左边起点点序号,左边终点点名,左边终点点序号,左边坐标增量分别为:lfw ,ls ,lbname ,lbindex ,lename ,leindex ,ldetx ,ldety ,同理对应右边各项为:rfw ,rs ,rbname ,rbindex ,rename ,reindex ,rdetx ,rdety .由图1可知,各观测角度两边的方向有4种情况,为简化程序,首先将其全部转化为情况1.设转换后左导线边起、终点序号分别为tem lbindex ,tem -leindex .右导线边起、终序点号分别为tem rbindex ,temreindex .如下是图1第三种情况的转换代码.if lename ==rbname temlbindex =leinde x ; temleindex =lbinde x ; tem rbindex =rbindex ; tem reindex =reindex ; lde tx =(-1)*lde tx ; lde ty =(-1)*lde ty ; rdetx =rdetx ;89兰州交通大学学报第29卷 rdety =rdety ; lfw =lfw +pi (); rfw =rfw ;end设该角度序号为index .又左边起点、终点和右边起点、终点的未知数序号分别为:lbcontrindex ,le -contrindex ,rbco ntrindex ,recontrindex .则B (index ,(2×leco ntrindex -1))=ρΔy L 1000s 2L B (index ,(2×leco ntrindex ))=-ρΔx L1000s 2L B (index ,(2×reco ntrindex -1))=-ρΔy R1000s 2RB (index ,(2×reco ntrindex ))=-ρΔx R1000s 2RB (index ,(2×lbcontrindex -1))=ρΔy R 1000s 2R -ρΔy L1000s 2L B (index ,(2×lbcontrindex ))=-ρΔx R 1000s 2R +ρΔx L1000s 2L angle 0=r f w -l f wl (index ,1)=(angle 0-ang le )×180×3600πP (index ,index )=1[4]上述各点如为已知点,则对应系数为0.未知点序号为所有待求点的排列序号,用于控制误差方程系数在B 矩阵中的列位置.3.2 利用观测边长计算误差方程系数矩阵设某观测边坐标增量为Δx ,Δy ,观测边长为S ,S 0=Δx 2+Δy 2,则B (index ,(2×lbco ntrindex -1))=-ΔxS 0(5)B (index ,(2×lbco ntrindex ))=-ΔyS 0(6)B (index ,(2×leco ntrindex -1))=ΔxS 0(7)B (index ,(2×lecontrindex ))=ΔyS 0(8)l (index ,1)=1000×(S 0-S )(9)P (index ,index )=S100[5](10)其中已知点对应项系数为0,其中index 为观测边序号,观测边序号是该边在边表中序号加上角度观测值个数.lbcontrindex 和leco ntrindex 为该边起点、终点的未知点序号.以上过程需要一个循环语句即可完成.4 结束语本文基于Matlab 开发了导线网平差程序,算法简单,编程工作量小[6].对于测绘专业类似计算问题如三角网、水准网等的程序设计有一定的借鉴意义.由于篇幅的限制,本文没有论述其他相关处理过程的算法,包括利用误差方程迭代计算获取最优解、度分秒和弧度互化、边点要素属性的查询等,这些算法在M atlab 中实现相对比较容易.参考文献:[1] 汪自军,陈圣波,臧立娟,等.导线网数据处理系统关键技术及其实践[J ].微计算机信息,2008(2):216-218.[2] 李建章.基于M a tlab 的水准网平差程序设计[J ].兰州交通大学学报,2009,28(3):29-31.[3] 武艳强,黄立人,江在森.导线网平差中近似坐标的无限定推算方法[J ].测绘通报,2006(12):12-15.[4] 武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M ].武汉:武汉大学出版社,2003:102-125.[5] 姚德新.土木工程测量学教程[M ].北京:中国铁道出版社,2003:67-68.[6] 薄志义,曹福生.程序寻找支导线网计算路径的研究[J ].测绘科学,2007(9):68-69.Adjustment Programming of Traverse Network on the Basis of MatlabLI Jian -zhang(Sch ool of Civil En gineering ,Lanzhou Jiaotong University ,Lanzh ou 730070,China )A bstract :H aving large data and complex shape ,the data pro cessing of traverse netw o rk involves matrix cal -culation .It 's mo re difficult to prog ram on o ther prog ramming lang uages like VC and VB .In the e ssay ,the data structure o f traverse netw ork is desig ned by utilizing the matrix dispo sal capability of M atlab ,and thenthe prog ram that has the adv antag es of being simple in algo rithm is finished .Key words :trave rse ne tw ork ;data structure ;adjustment ;pro gramming90。
