福建师范大学附属中学2020-2021学年上学期期中考模拟试卷高二数学(实验班)试题及答案
2020-2021学年度福建师范大学附属中学高二上学期期中考试数学试卷【含解析】
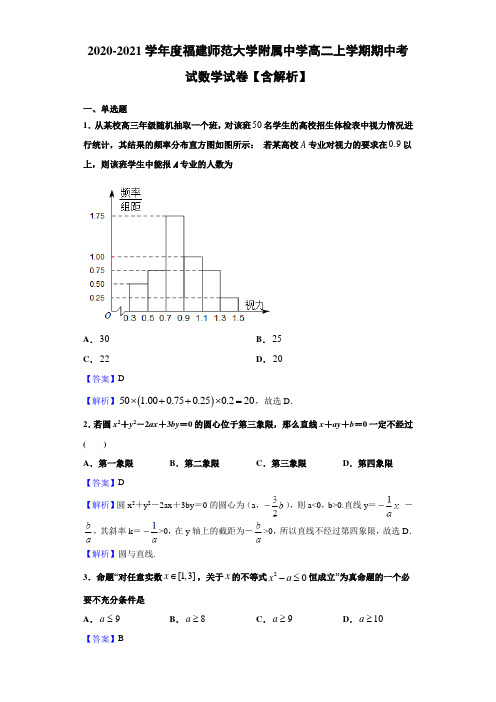
2020-2021学年度福建师范大学附属中学高二上学期期中考试数学试卷【含解析】一、单选题1.从某校高三年级随机抽取一个班,对该班50名学生的高校招生体检表中视力情况进行统计,其结果的频率分布直方图如图所示: 若某高校A 专业对视力的要求在0.9以上,则该班学生中能报A 专业的人数为A .30B .25C .22D .20【答案】D【解析】()50 1.000.750.250.220⨯++⨯=,故选D .2.若圆x 2+y 2-2ax +3by =0的圆心位于第三象限,那么直线x +ay +b =0一定不经过 ( ) A .第一象限 B .第二象限C .第三象限D .第四象限【答案】D【解析】圆x 2+y 2-2ax +3by =0的圆心为(a ,),则a<0,b>0.直线y =-,其斜率k =>0,在y 轴上的截距为->0,所以直线不经过第四象限,故选D .【解析】圆与直线.3.命题“对任意实数[1,3]x ∈,关于x 的不等式20x a -≤恒成立”为真命题的一个必要不充分条件是 A .9a ≤ B .8a ≥C .9a ≥D .10a ≥【答案】B【分析】根据题意可知,利用参数分离的方法求出使命题“对任意实数[1,3]x ∈,关于x 的不等式20x a -≤恒成立”为真命题的a 的取值范围,a 的取值范围构成的集合应为正确选项的真子集,从而推出正确结果. 【详解】命题“对任意实数[1,3]x ∈,关于x 的不等式20x a -≤恒成立”为真命题9a ∴≥根据选项满足是9a ≥的必要不充分条件只有8a ≥,故答案选B .【点睛】本题主要考查了简单的不等式恒成立问题以及求一个命题的必要不充分条件. 4.高铁、扫码支付、共享单车、网购并称中国“新四大发明”,近日对全国100个城市的共享单车和扫码支付的使用人数进行大数据分析,其中共享单车使用的人数分别为123100,,,,x x x x ,它们的平均数为x ,方差为2s ;其中扫码支付使用的人数分别为132x +,232x +,332x +,,10032x +,它们的平均数为x ',方差为2s ',则x ',2s '分别为( )A .32x +,232s +B .3x ,23sC .32x +,29sD .32x +,292s +【答案】C【分析】由样本数据的平均数和方差的公式,化简、运算,即可求解,得到答案. 【详解】由平均数的计算公式,可得数据12100,,,x x x 的平均数为1231001()100x x x x x =++++数据1210032,32,,32x x x +++的平均数为:121001210011[(32)(32)(32)][3()2100]32100100x x x x x x x ++++++=++++⨯=+, 数据12100,,,x x x 的方差为2222121001[()()()]100s x x x x x x =-+-++-,数据1210032,32,,32x x x +++的方差为:222121001{[(32)(32)[(32(32)][(32)(32)]}100x x x x x x +-+++-++++-+ 2222121001[9()9()9()]9100x x x x x x s =-+-++-= 故选C.【点睛】本题主要考查了样本数据的平均数和方差的计算与应用,其中解答中熟记样本数据的平均数和方差的计算公式,合理化简与计算是解答的关键,着重考查了推理与运算能力,属于基础题.5.设不等式224x y +≤表示的平面区域为D ,在区域D 内随机取一个点,则2x y +≤的概率是( )A .1ππ- B .2ππ- C .1πD .2π【答案】D【分析】不等式224x y +表示的平面区域为圆心为()0,0半径为2的圆内部,面积为4π;满足||||2x y +≤的平面区域的面积为8,即可得出结论.【详解】依题意得,如下图,分别画出224x y +和||||2x y +≤表示的区域, 不等式224x y +表示的平面区域D 是圆心为()0,0半径为2的圆内部,所以面积为4π; 而||||2x y +≤表示的区域为边长22的正方形内部,面积为8, 要满足||||2x y +≤且满足224x y +表示的平面区域的面积为8, 得出所求概率为824ππ=. 故选:D .【点睛】本题考查几何概型,其中运用了线性规划表示的平面区域和圆的方程,考查对图形的理解能力,正确求出面积是关键.6.已知圆M 的方程为22680x y x y +--=,过点()0,4P 的直线l 与圆M 相交的所有弦中,弦长最短的弦为AC ,弦长最长的弦为BD ,则四边形ABCD 的面积为( ) A .30 B .40C .60D .80【答案】B【分析】由题可知点()0,4P 在圆内,则最短的弦是以()0,4P 为中点的弦,过()0,4P 最长的弦BD 为直径,求出后即可求出四边形面积.【详解】圆M 的标准方程为()()223425x y -+-=,即圆是以()3,4M 为圆心,5为半径的圆,且由()()220344925-+-=<,即点()0,4P 在圆内,则最短的弦是以()0,4P 为中点的弦,所以22592AC ⎛⎫=+ ⎪⎝⎭,所以8AC =,过()0,4P 最长的弦BD 为直径,所以10BD =, 且AC BD ⊥,故而1402ABCD S AC BD =⋅⋅=. 故选:B.【点睛】本题考查直线与圆的位置关系,考查弦长的计算,属于基础题.7.在新冠肺炎疫情联防联控期间,某居委会从辖区内A ,B ,C 三个小区志愿者中各选取1人,随机安排到这三个小区,协助小区保安做好封闭管理和防控宣传工作.若每个小区安排1人,则每位志愿者不安排在自己居住小区的概率为( ) A .16B .13C .12D .23【答案】B【分析】基本事件总数336n A ==,每位志愿者不安排在自己居住小区包含的基本事件个数1112112m C C C ==,由此能求出每位志愿者不安排在自己居住小区的概率. 【详解】由题意,基本事件总数336n A ==,每位志愿者不安排在自己居住小区包含的基本事件个数1112112m C C C ==,∴每位志愿者不安排在自己居住小区的概率为2163m P n ===, 故选:B【点睛】本题考查概率的求法,考查古典概型、列举法等基础知识,考查运算求解能力,是中档题.8.平面内到两个定点的距离之比为常数(1)k k ≠的点的轨迹是阿波罗尼斯圆.已知曲线C 是平面内到两个定点1(1,0)F -和2(1,0)F 的距离之比等于常数(1)a a >的阿波罗尼斯圆,则下列结论中正确的是( ) A .曲线C 关于x 轴对称 B .曲线C 关于y 轴对称 C .曲线C 关于坐标原点对称 D .曲线C 经过坐标原点 【答案】A【分析】先根据阿波罗尼斯圆的定义求得这个曲线C 的方程,再根据所求得的方程对选项逐一进行排除,从而得出正确选项.【详解】设动点(),P x y ()()222211x y a x y ++=-+,两边平方并化简得2222221211a a x y a a ⎛⎫+⎛⎫-+= ⎪ ⎪--⎝⎭⎝⎭,故圆的圆心为221,01a a ⎛⎫+ ⎪-⎝⎭,半径为221ar a =-.由此可知圆关于x 轴对称,不关于y 轴,原点对称.B,C 选项错误,A 选项正确.由于1a >,221212a a a +>⋅=,所以2221211a aa a +>--,故圆不经过坐标原点,D选项是错误的.【点睛】本小题主要考查利用直接法求动点的轨迹方程,考查对新概念的理解,考查图形的对称性,属于中档题.二、多选题9.下列4个说法中正确的有( )①命题“若2320x x -+=,则1x =”的逆否命题为“若1x ≠则2320x x -+≠”; ②若00:0,sin 1p x x ∃≥>,则:0,sin 1p x x ⌝∀≥≤; ③若复合命题:“p q ∧”为假命题,则p ,q 均为假命题; ④“2x >”是“2320x x -+>”的充分不必要条件. A .① B .②C .③D .④【答案】ABD【分析】由命题的逆否命题的形式可判断①;由特称命题的否定是全称命题可判断②;由复合命题的真值表可判断③;由充分不必要条件的定义和二次不等式的解法可判断④,进而可得正确选项.【详解】对于①:命题“若2320x x -+=,则1x =”的逆否命题为“若1x ≠则2320x x -+≠”,故①正确;对于②:若00:0,sin 1p x x ∃≥>,则:0,sin 1p x x ⌝∀≥≤,故②正确;对于③:若复合命题:“p q ∧”为假命题,则p 、q 至少有一个是假命题;故③不正确; 对于④:2x >能推出2320x x -+>,但2320x x -+>不一定有2x >成立,1x <也成立,所以“2x >”是“2320x x -+>”的充分不必要条件,故④正确, 所以①②④正确, 故选:ABD10.(多选)已知直线l 经过点(3,4),且点(2,2),(4,2)A B --到直线l 的距离相等,则直线l 的方程可能为( ) A .23180x y +-= B .220x y --= C .220x y ++= D .2360x y -+=【答案】AB【分析】由题可知直线l 的斜率存在,所以设直线l 的方程为4(3)y k x -=-,然后利用点到直线的距离公式列方程,可求出直线的斜率,从而可得直线方程【详解】当直线l 的斜率不存在时,显然不满足题意.当直线l 的斜率存在时,设直线l 的方程为4(3)y k x -=-,即430kx y k -+-=.2211k k =++,所以2k =或23k =-, 所以直线l 的方程为220x y --=或23180x y +-=. 故选:AB【点睛】此题考查直线方程的求法,考查点到直线的距离公式的应用,属于基础题 11.以下对各事件发生的概率判断正确的是( )A .甲、乙两人玩剪刀、石头、布的游戏,则玩一局甲不输的概率是13B .从1名男同学和2名女同学中任选2人参加社区服务,则选中一男一女同学的概率为23C .将一个质地均匀的正方体骰子(每个面上分别写有数字1,2,3,4,5,6)先后抛掷2次,观察向上的点数,则点数之和是6的概率是536D .从三件正品、一件次品中随机取出两件,则取出的产品全是正品的概率是12【答案】BCD【分析】结合选项,利用树状图和列举法,求得基本事件的总数,利用古典概型的概率计算公式,逐项求解,即可求解.【详解】对于A 中, 甲、乙两人玩剪刀、石头、布的游戏,共有339⨯=种情形, 结合树状图,可得玩一局甲不输的情况,共有236⨯=种情形, 所以玩一局甲不输的概率是6293=,所以A 不正确;对于B 中,设1名男生为a ,两名女生分别为,A B ,则从这3人中选取2人包含:(,),(,),(,)a A a B A B ,共3种选法, 其中选中一男一女同学包含:(,),(,)a A a B , 所以选中一男一女同学的概率为23,所以B 正确; 对于C 中,将一个质地均匀的正方体骰子,先后抛掷2次,共有36种不同的结果, 其中点数和为6的有:(1,5),(2,4),(3,3),(4,2),(5,1),共有5种, 所以点数之和是6的概率是536,所以C 正确; 对于D 中,从三件正品、一件次品中随机取出两件,则取出的产品全是正品的概率是232412C P C ==,所以D 是正确的.故选:BCD 。
福建师范大学附属中学2021届高三上学期期中考试数学试题

福建师大附中2020-2021学年上学期期中考试高三数学试卷时间:120分钟 满分: 150分 第Ⅰ卷(选择题,共70分)一、选择题:本题共10小题,每小题5分,共50分.在每小题给出的选项中,只有一项是符合题目要求的.-1. 已知等差数列{}n a 的前n 项和为n S ,若1512,90a S ==,则等差数列{}n a 公差d =( ) A. 2 B.32C. 3D. 4C根据等差数列的求和公式即可得出. ∵a 1=12,S 5=90, ∴5×12+542⨯ d=90, 解得d=3.故选C .2. 已知直线a ,b 和平面α,β,满足 a α⊂,b β⊂,则“a 和b 相交”是“a 和β相交”的( ) A. 充分不必要条件 B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件 A由充分条件和必要条件的定义判断即可解:若a 和b 相交于点O ,则,O a O b ∈∈,因为 a α⊂,b β⊂,所以,O O αβ∈∈,所以a 和β相交,若a 和β相交于直线l ,当a α⊂,b β⊂时,a 和b 可能相交,可能平行,可能异面, 所以“a 和b 相交”是“a 和β相交”的充分不必要条件,故选:A 3. 已知复数z 的共轭复数为z ,且满足232z z i +=+,则||z =( )A. B. C. 3D. 5B设复数(,)z a bi a b R =+∈,则z a bi =-,代入232z z i +=+中求出,a b 的值,再根据复数模公式求得结果.设(,)z a bi a b R =+∈,则z a bi =-, 又因为232z z i +=+,即332a bi i +=+, 所以1,2a b ==,所以|z |5=,故选:B. 4. 已知数列{}n a 满足2112n n n a a a +=+-,且112a =,则该数列前2016项的和为( ) A. 2015 B. 2016 C. 1512 D. 30252C通过计算出数列的前几项确定数列{}n a 是以2为周期的周期数列,进而计算可得结论. 依题意,112a =, 22112111112222a a a =+-=+-=, 2232211111222a a a =+-=+-=, ⋯从而数列{}n a 是以2为周期的周期数列, 于是所求值为20161(1)151222⨯+=,故选:C 5. 如图为某几何体的三视图,则其体积为( )A. 43π+B. 2π+C. 23π+D. 223π+A根据三视图还原几何体可得该几何体是由一个半圆柱和一个四棱锥组合而成,由此可求出其体积.如图,根据三视图还原几何体可得该几何体是由一个半圆柱和一个四棱锥组合而成,根据三视图可知,半圆柱的底面半径为1,高为2,四棱锥的底面是边长为2的正方形,高为1,所以该几何体的体积211412221233V ππ=⨯⨯⨯+⨯⨯⨯=+.故选:A.6. 已知ABC 是边长为2的等边三角形,且AE EB =,2AD DC =,则BD CE ⋅=( ) A. 3- B. 2- C. 1- D. 3B由平面向量的线性运算可得2132BD CE AC AB AB AC ⎛⎫⎛⎫⋅=-⋅- ⎪ ⎪⎝⎭⎝⎭,再由平面向量数量积的运算即可得解.由题意画出图形,如图,因为AE EB =,2AD DC =,所以12AE AB =,23AD AC =,所以()()2132BD CE AD AB AE AC AC AB AB AC ⎛⎫⎛⎫⋅=-⋅-=-⋅- ⎪ ⎪⎝⎭⎝⎭22241241422cos6042332332AC AC AB AB =-+⋅-=-⨯+⨯⨯-⨯=-.故选:B. 7. 在正方体1111ABCD A B C D -中,记平面11CB D 为α,若α平面ABCD m =,α⋂平面11ABB A n =,则m ,n 所成角的余弦值为( )A. 32B.62C.33D.12D由线面平行的性质可得出1A BD ∠即为m ,n 所成角,则求出即可.如图,连接11,,BD A B A D ,可得在正方体中,111B B CC DD ,即四边形11BB D D 是平行四边形,11//B D BD ∴,BD ⊂平面ABCD ,11B D ⊄平面ABCD ,∴11//B D 平面ABCD ,又α平面ABCD m =,11B D α⊂,11//B D m ∴,//BD m ∴,同理可得1//CD 平面11ABB A ,α⋂平面11ABB A n =,1CD α⊂, 1//CD n ∴,1//A B n , 1A BD ∴∠即为m ,n 所成角,1A BD 为等边三角形,160A BD ∴∠=,11cos 2A BD ∴∠=.故选:D.8. 在四面体ABCD 中,22BD AC ==,2AB BC AD ===,AD BC ⊥,则四面体ABCD 的外接球的体积为( ) A. 2πB. 43πC. 162πD. 163πB由题可得四面体ABCD 可还原成棱长为2的正方体,即可由此求出外接球半径,得出体积.2,22AB AD BD ===,满足222AB AD BD +=,AB AD ∴⊥,由AD BC ⊥,∴四面体ABCD 可还原成棱长为2的正方体,设外接球的半径为R ,则222222223R =++=3R =∴外接球的体积343433V.故选:B.9. 已知函数3,0,(),0.x x f x x x ⎧=⎨-<⎩若函数2()()2()g x f x kx xk =--∈R 恰有4个零点,则k 的取值范围是( )A. 1,(22,)2⎛⎫-∞-+∞ ⎪⎝⎭B. 1,(0,22)2⎛⎫-∞- ⎪⎝⎭C. (,0)(0,22)-∞D. (,0)(22,)-∞+∞D由(0)0g =,结合已知,将问题转化为|2|y kx =-与()()||f x h x x =有3个不同交点,分0,0,0k k k =<>三种情况,数形结合讨论即可得到答案. 注意到(0)0g =,所以要使()g x 恰有4个零点,只需方程()|2|||f x kx x -=恰有3个实根 即可, 令()h x =()||f x x ,即|2|y kx =-与()()||f x h x x =的图象有3个不同交点.因2,0()()1,0x x f x h x x x ⎧>==⎨<⎩,当0k =时,此时2y =,如图1,2y =与()()||f x h x x =有1个不同交点,不满足题意; 当0k <时,如图2,此时|2|y kx =-与()()||f x h x x =恒有3个不同交点,满足题意; 当0k >时,如图3,当2y kx =-与2yx 相切时,联立方程得220x kx -+=,令0∆=得280k -=,解得22k =(负值舍去),所以22k >. 综上,k 的取值范围为(,0)(22,)-∞+∞.故选:D .【点晴】本题主要考查函数与方程的应用,考查数形结合思想,转化与化归思想,是一道中档题.10. 已知1234,,,a a a a 成等比数列,且1234123ln()a a a a a a a +++=++.若11a >,则( ) A. 1324,a a a a << B. 1324,a a a a ><C. 1324,a a a a <>D. 1324,a a a a >>B先证不等式ln 1x x ≥+,再确定公比的取值范围,进而作出判断.令()ln 1,f x x x =--则1()1f x x'=-,令()0,f x '=得1x =,所以当1x >时,()0f x '>,当01x <<时,()0f x '<,因此()(1)0,ln 1f x f x x ≥=∴≥+,若公比0q >,则1234123123ln()a a a a a a a a a a +++>++>++,不合题意;若公比1q ≤-,则212341(1)(1)0,a a a a a q q +++=++≤ 但212311ln()ln[(1)]ln 0a a a a q q a ++=++>>,即12341230ln()a a a a a a a +++≤<++,不合题意; 因此210,(0,1)q q -<<∈,22113224,0a a q a a a q a ∴>=<=<,选B.11. 在公比为q 等比数列{}n a 中,n S 是数列{}n a 的前n 项和,若521127,==a a a ,则下列说法正确的是( ) A. 3q = B. 数列{}2n S +是等比数列 C. 5121S = D. ()222lg lg lg 3n n n a a a n -+=+≥ACD根据等比数列的通项公式,结合等比数列的定义和对数的运算性质进行逐一判断即可. 因为521127,==a a a ,所以有431127273q a q q q a ⋅=⋅⇒=⇒=,因此选项A 正确;因为131(31)132n n n S -==--,所以131+2+2(3+3)132nn n S -==-, 因为+1+111(3+3)+222=1+1+21+3(3+3)2n nn n n S S -=≠常数, 所以数列{}2n S +不是等比数列,故选项B 不正确; 因为551(31)=1212S =-,所以选项C 正确; 11130n n n a a q --=⋅=>,因为当3n ≥时,22222lg lg =lg()=lg 2lg n n n n n n a a a a a a -+-++⋅=,所以选项D 正确.故选:ACD12. 已知曲线1C :cos y x =,2C :2sin 23y x π⎛⎫=+⎪⎝⎭,则下面结论正确的是( )A. 把曲线1C 向左平移6π个单位长度,再把得到的曲线上各点的横坐标缩短到原来的12倍(纵坐标不变),得到曲线2C B. 把曲线1C 向左平移3π个单位长度,再把得到的曲线上各点的横坐标伸长到原来的2倍(纵坐标不变),得到曲线2CC. 把曲线1C 上各点的横坐标缩短到原来的12倍(纵坐标不变),再把得到的曲线向左平移6π个单位长度,得到曲线2CD. 把曲线1C 上各点的横坐标缩短到原来的12倍(纵坐标不变),再把得到的曲线向左平移12π个单位长度,得到曲线2C AD先利用诱导公式把2sin 23y x π⎛⎫=+⎪⎝⎭化简得,2sin 2cos 236y x x ππ⎛⎫⎛⎫=+=+ ⎪ ⎪⎝⎭⎝⎭,然后利用三角函数图像变换规律求解即可解:2sin 2sin 2cos 23266y x x x ππππ⎛⎫⎛⎫⎛⎫=+=++=+⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,所以将曲线1C :cos y x =向左平移6π个单位长度,得cos 6⎛⎫=+ ⎪⎝⎭y x π,再把得到的曲线上各点的横坐标缩短到原来的12倍(纵坐标不变),得到曲线cos 26y x π⎛⎫=+ ⎪⎝⎭; 或将曲线1C :cos y x =上各点的横坐标缩短到原来的12倍(纵坐标不变),得到cos 2y x =,再把得到的曲线向左平移12π个单位长度,得到cos 2cos 2126y x x ππ⎡⎤⎛⎫⎛⎫=+=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,故选:ADA.∵OB β⊥,∴OB AB ⊥,∴OA =,∴点A 在以O 的球面运动,A 正确;B .由题意知A 在平面β内绕点B 作圆周运动,当AB 垂直于水平面时,投影长度为0,当AB 平行于水平面时,投影长度为AB ,∴线段AB 在水平地面上的正投影长度范围为[0,]AB ,B 错误;C .当AB α⊥时,直线OA 与平面α的所成的角的正弦值为最大值,此时线面角为AOB ∠,37sin 3737AB AOB OA AB∠===,C 正确. D .画出该模型的直观图,∵β与水平面所成的角为θ,且02πθ<<,∴DCE θ∠=,∵直线OB 与水平面所成的角为δ,且//FC OB , ∴FCG δ∠=,∵OB CD ⊥,∴FC CD ⊥,∴2FCG DCE π∠+∠=,即θδ+为定值,定值为2π,D 正确.故选:ACD . Ⅱ卷(非选择题,共80分)三、填空题:本题共6小题,每小题5分,共30分. 15. 已知向量()1,2a =,(),1b t =,若a ,b 5,则实数t 的值为____. 34-. 根据向量夹角的坐标公式求解即可. 因为,a b 夹角的余弦值为5,所以25551t =⋅+,即221t t +=+,22441t t t ++=+.解得34t =-.故答案为:34-16. 函数f (x )=sin 22x 的最小正周期是__________.2π.将所给的函数利用降幂公式进行恒等变形,然后求解其最小正周期即可.函数()2sin 2f x x ==142cos x-,周期为2π 17. 16/17世纪之交,随着天文、航海、工程、贸易以及军事的发展,改进数字计算方法成了当务之急,约翰•纳皮尔正是在研究天文学的过程中,为了简化其中的计算而发明了对数.后来天才数学家欧拉发现了对数与指数的关系,即b a N = ⇔ log a b N =. 现在已知23a =, 34b =,则ab =__________. 2先根据要求将指数式转为对数式,作乘积运算时注意使用换底公式去计算. ∵23a =, 34b = ∴2log 3a =, 3log 4b = ∴23ln3ln4ln4log 3log 42ln2ln3ln2ab =⋅=⋅== 故答案为218. 设12(21)(21)n n n n b +=--,n T 为{}n b 的前n 项和,则使得20152016n T >成立的n 的最小值是______. 10利用裂项相消法求出n T ,然后解不等式20152016n T >即可得答案 解:因为11211(21)(21)2121n n nn n n b ++==----- , 所以12231111111212121212121n n n T +=-+-+⋅⋅⋅+-------, 11121n +=--, 要使20152016n T >,只要1120151212016n +->-,即11111212016n +->--, 122017n +>,所以111n +≥,即10n ≥, 所以n 的最小值是10, 故答案为:1019. 已知函数()()sin cos 0f x x x ωωω=+>,x R ∈,若函数()f x 在区间(),ωω-内单调递增,且函数()f x 的图像关于直线x ω=对称,则ω的值为 .由()f x 在区间(),ωω-内单调递增,且()f x 的图像关于直线x ω=对称,可得π2ωω≤,且()222πsin cos sin 14f ωωωω⎛⎫=+=+= ⎪⎝⎭,所以2ππ42ωω+=⇒=20. 设n S 为数列{}n a 的前n 项和,1(1),,2n n n n S a n N *=--∈则 (1)3a =_____;(2)12100S S S ++⋅⋅⋅+=___________.116-;10011(1)32-. (1)令1n =,114a =-;443311,,168S a S a =-=--两式对减得到3116=-a ; (2)由1(1),,2n n n n S a n N *=--∈可得1(1(1),,)22n n n nn S n N n S S -*=--∈≥- 当n 为偶数时,可得222121,2k k k k S S S -=--整理得2121,2k k S --=当n 为奇数时,可得21212211(,2)k k k k S S S +++-=--整理得221212221111202222k k k k k S S ++++=-+⨯+==,所以501210013991001114411(1)13214S S SS S S ⎡⎤⎛⎫--⎢⎥ ⎪⎝⎭⎢⎥⎣⎦++⋅⋅⋅+=++⋅⋅⋅+==--.四、解答题:本题共4小题,共50分.解答应写出文字说明、证明过程或演算步骤.21. 在①112n n a a +=-,②116n n a a +-=-,③18n n a a n +=+-这三个条件中任选一个,补充在下面的问题中,并解答.问题:设n S 是数列{}n a 的前n 项和,且14a =,______________,求{}n a 的通项公式,并判断n S 是否存在最大值,若存在,求出最大值;若不存在,说明理由.选①,312n n a -⎛⎫=- ⎪⎝⎭,n S 存在最大值,且最大值为4;选②,12566n a n =-+,n S 存在最大值,且最大值为50;选③,217242n n n a -+=,n S 不存在最大值,理由见解析.选①先判断{}n a 是首项为4,公比为12-的等比数列,再求n a ,最后分n 为奇数和n 为偶讨论,分别判断n S 存在最大值并求出最大值即可;选②先判断{}n a 是首项为4,公差为16-的等差数列,再求出12566n a n =-+,最后判断n S 存在最大值并求出n S 的最大值;选③先求出217242n n n a -+=,再判断n S 不存在最大值. 解:选①:因为112n n a a +=-,14a =,所以{}n a 是首项为4,公比为12-的等比数列. 所以1311422n n n a --⎛⎫⎛⎫=⨯-=- ⎪⎪⎝⎭⎝⎭.当n 为奇数时,141281113212n n nS ⎡⎤⎛⎫--⎢⎥ ⎪⎝⎭⎢⎥⎛⎫⎣⎦==+ ⎪⎝⎭+, 因为81132n⎛⎫+ ⎪⎝⎭随着n 的增大而减小,所以此时n S 的最大值为14S =; 当n 为偶数时,141281113212n n nS ⎡⎤⎛⎫--⎢⎥ ⎪⎝⎭⎢⎥⎛⎫⎣⎦==- ⎪⎝⎭+,且81814323n n S ⎛⎫=-<< ⎪⎝⎭, 综上,n S 存在最大值,且最大值为4.选②:因为116n n a a +-=-,14a =,所以{}n a 是首项为4,公差为16-的等差数列.所以()112541666n a n n ⎛⎫=+-⋅-=-+ ⎪⎝⎭,由于125066n -+≥,得25n ≤,所以n S 存在最大值,且最大值为25S 或24S , 因为25252414255026S ⨯⎛⎫=⨯+⨯-= ⎪⎝⎭,所以n S 的最大值为50.选③:因为18n n a a n +=+-,所以18n n a a n +-=-, 所以217a a -=-,326a a -=-,…,19n n a a n --=-, 所以()()()()()2111221791171622n n n n n n n n n a a a a a a a a ----+---+-=-+-+⋅⋅⋅+-==,又14a =,所以217242n n n a -+=,当16n ≥时,0n a >,故n S 不存在最大值.22. 如图,单位圆O 与,x y 轴正半轴的交点分别为,A D ,圆O 上的点C 在第一象限.(1)若点C 的坐标为31,22⎛⎫⎪ ⎪⎝⎭,延长CD 至点B ,使得2DB =,求OB 的长;(2)圆O 上的点E 在第二象限,若23EOC π∠=,求四边形OCDE 面积的最大值.(1) 7OB =;(2)32. 试题分析:⑴由点312C ⎫⎪⎪⎝⎭,可得30AOC ∠=︒,故60COD ∠=︒,所以120CDB ∠=︒,由余弦定理求出OB 的长;⑵设62COD ππθθ⎛⎫∠=<< ⎪⎝⎭,则23DOE πθ∠=-,从而可得四边形OCDE 的面积()S θ,由θ的取值范围得当3πθ=时,四边形OCDE 的面积有最大值,且最大值为32解析:(1)由点31,2C ⎛⎫ ⎪ ⎪⎝⎭在单位圆上,可知30AOC ︒∠=, 由图像可得60COD ︒∠=;在CDB ∆中,1OD =,120CDB ︒∠=,2DB =; 由余弦定理得222OB OD DB =+ 2cos120OD OB ︒-⋅⋅; 解得7OB =;(2)设62COD ππθθ⎛⎫∠=<< ⎪⎝⎭,23DOE πθ∠=- 1sin 2COD S θ∆=,12sin 23EOD S πθ∆⎛⎫=-⎪⎝⎭四边形OCDE 的面积()EOD CODS S S θ∆∆=+ 112sin sin 223πθθ⎛⎫=+- ⎪⎝⎭ 62ππθ⎛⎫<< ⎪⎝⎭131sin sin 22θθθ⎡⎤=+⎢⎥⎣⎦33sin 4θθ= 36πθ⎛⎫=+ ⎪⎝⎭62ππθ<<,2363πππθ∴<+<当62ππθ+=,即3πθ=时,四边形OCDE 的面积S 的最大值为3. 【详解】23. 如图,在棱柱ABCD A B C D ''''-中,底面ABCD 为平行四边形,4DD CD '==,2AD =,3BAD π∠=,且D 在底面上的投影H 恰为CD 的中点.(1)过D H '作与 BC 垂直的平面α,交棱BC 于点N ,试确定点N 的位置,并说明理由; (2)在线段D C ''上是否存在点P ,使二面角P BH A --为34π?若存在,请确定点P 的位置;若不存在,请说明理由.(1)N 为棱BC 的中点;理由见解析;(2)存在,P 的位置与C '重合.(1)取BC 中点N ,利用余弦定理求得NH ,可证明NH BC ⊥,从而可证得得BC ⊥平面D HN '; (2)由(1)得AD BD ⊥,分别以DA ,DB 为x ,y 轴的正方向,以过D 点垂直于平面ABCD 的方向为z 轴,建立空间直角坐标系D xyz -,设D P D C λ'''=,由向量法求二面角P BH A --,由二面角的大小可求得λ,得P 点位置.解:(1)当点N 为棱BC 的中点时,符合题目要求,证明如下: 分别连结NH ,ND '.在HNC △中,222cos 33NH NC CH NC CH π=+-⋅⋅=所以222HC NC HN =+,因此2HNC π∠=,即NH BC ⊥,因为D 在底面上的投影H 恰为CD 的中点,所以D H '⊥平面ABCD , 又BC ⊂平面ABCD ,所以D H BC '⊥, 又NH BC ⊥,D H NH H '=,D H ',NH ⊂平面D HN ',所以BC ⊥平面D HN ',因此,点N 即所求,平面D HN '即为α.(2)存在满足条件的点P ,且P 的位置与C '重合.证明如下: 由(1)知可得HN BC ⊥,//HN DB ,//AD BC ,所以AD BD ⊥,分别以DA ,DB 为x ,y 轴的正方向,以过D 点垂直于平面ABCD 的方向为z 轴,建立空间直角坐标系D xyz -,23HD '=,(0,0,0)D ,()1,3,0H -,()0,23,0B ,()1,3,23D '-,()2,23,0C -,()3,33,23C '-,设()()2,23,02,23,0D P D C λλλλ'''==-=- 易得平面AHB 的一个法向量为()0,0,1m =,()1,3,0HB =,(0,0,23HD '=,(2,233HP HD D P λλ''=+=-, 设(,,)n x y z =为平面PBH 的一个法向量,则:00n HB n HP ⎧⋅=⎨⋅=⎩,即得30223230x y x y z λλ⎧+=⎪⎨-++=⎪⎩, 令3x =,得()3,1,2n λ=-,因为二面角P BH A --为34π, 所以3cos ,cos4m n π<>=,即22m n m n ⋅=-⋅22244λλ=+, 又因为二面角P BH A --的大小为钝角,故1λ=. 24. 已知函数2()2ln f x x x a x =--,()g x ax =. (1)讨论函数()()()F x f x g x =+的单调性; (2)若不等式sin ()2cos xg x x≤+对任意0x ≥恒成立,求a 的取值范围.(1)答案见解析;(2)1,3⎡⎫+∞⎪⎢⎣⎭.(1)求导数()F x ',分类讨论确定其正负,得()F x 的单调性;(2)设sin ()(0)2cos x h x ax x x=-≥+,求出212cos ()(2cos )x h x a x +'=-+,然后用换元法, 设cos t x =,求出212()(2)t t t ϕ+=+的取值范围11,3⎡⎤-⎢⎥⎣⎦,由根据a 的范围分类讨论,确定的正负,13a ≥与0a ≤都易得结论,当103a <<时,对于02x π<<,由不等式性质得sin ()3x h x ax <-,令sin ()3xT x ax =-,用导数研究它的单调性得不可能恒成立,从而得a 的范围.(1)2()2ln F x x x a x ax =--+,定义域为(0,)+∞.22(2)(2)(1)()x a x a x a x F x x x'+--+-==, ①02a-≤即0a ≥时,()F x 在(0,1)上递减,()F x 在(1,)+∞上递增, ②012a <-<即20a -<<,()F x 在0,2a ⎛⎫- ⎪⎝⎭和(1,)+∞上递增,在,12a ⎛⎫- ⎪⎝⎭上递减,③12a-=即2a =-时,()F x 在(0,)+∞上递增. ④12a ->即2a <-时,()F x 在(0,1)和,2a ⎛⎫-+∞ ⎪⎝⎭上递增,()F x 在1,2a ⎛⎫- ⎪⎝⎭上递减,(2)设sin ()(0)2cos xh x ax x x=-≥+,则212cos ()(2cos )x h x a x +'=-+,设cos t x =,则[]1,1t ∈-,212()(2)t t t ϕ+=+,432(2)(1)2(1)()0(2)(2)t t t t t t ϕ-+---'==≥++, ()t ϕ∴在[]1,1-上递增,()t ϕ∴的值域为11,3⎡⎤-⎢⎥⎣⎦,①当13a ≥时,()0h x '≥,()h x 为[]0,+∞上的增函数,()(0)0h x h ∴≥=,适合条件.②当0a ≤时,10222h a ππ⎛⎫=⋅-< ⎪⎝⎭,∴不适合条件.③当103a <<时,对于02x π<<,sin ()3x h x ax <-,令sin ()3x T x ax =-,cos ()3xT x a '=-,存在00,2x π⎛⎫∈ ⎪⎝⎭,使得()00,x x ∈时,()0T x '<,()T x ∴在()00,x 上单调递减,()0(0)0T x T ∴<<,即在()00,x x ∈时,()0h x <,∴不适合条件.综上,a 的取值范围为1,3⎡⎫+∞⎪⎢⎣⎭.。
2024学年福建师大附中高二数学上学期期中考试卷附答案解析

2024学年福建师大附中高二数学上学期期中考试卷时间:120分钟满分:150分试卷说明:(1)本卷共四大题,19小题,解答写在答卷的指定位置上,考试结束后,只交答卷.(2)考试过程中不得使用计算器或具有计算功能的电子设备.第Ⅰ卷(选择题,共58分)一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的选项中,只有一项是符合题目要求的.1.经过点(2,2)-,倾斜角是120的直线方程是()A.2(2)3y x -=-+ B.22)y x -=+C.32(2)3y x -=+ D.22)y x -=+2.已知方程22122x y k k+=+-表示焦点在y 轴上的椭圆,则实数k 的取值范围为()A.()2,0- B.()0,2 C.()2,2- D.()()2,00,2-⋃3.在圆222210x y x y +---=的所有经过坐标原点的弦中,最短的弦的长度为()A.1B.2C. D.44.如图,在直三棱柱111ABC A B C -中,13AA AC BC ===,90ACB ∠= ,点D 是线段1AA 上靠近1A 的三等分点,则直线1C D 与1B C 所成角的余弦值为()A.510-B.10-C.510D.10105.已知实数,x y 满足224240x y x y +---=,则13y x -+的最大值是()A.12B.2C.34D.6.光线通过点()2,3A ,在直线:10l x y ++=上反射,反射光线经过点()2,2B ,则反射光线所在直线方程为()A.6520x y --= B.65220x y +-=C.5620x y -+= D.56220x y +-=7.若直线y x b =+与曲线3y =有公共点,则实数b 的取值范围是()A.1⎡⎤-⎣⎦B.1⎡-+⎣C.)1⎡-⎣D.(1-+8.设1F ,2F 是椭圆2222:1x y C a b+=(0a b >>)的左、右焦点,过1F 的直线与C 交于A ,B 两点,若22AF BF ⊥,53aAB =,则C 的离心率为()A.5B.35C.25D.5二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.已知圆()2222212:1,:(3)(3)0C x y C x y r r +=-+-=>,则下列说法正确的是()A.当1r =时,圆1C 与圆2C 有2条公切线B.当2r =时,1y =是圆1C 与圆2C 的一条公切线C.当3r =时,圆1C 与圆2C 相交D.当4r=时,圆1C 与圆2C 的公共弦所在直线的方程为12y x =-+10.如图,边长均为1的两个正方形ABCD 和正方形ABEF 所在的平面互相垂直,动点M ,N 分别在正方形对角线AC 和BF 上移动,且(0CM BN a a ==<<,则下列说法正确的是()A.(a ∃∈,使12MN CE=B.线段MN 存在最小值,最小值为23C.直线MN 与平面ABEF 所成的角恒为45D.(a ∀∈,都有MN ,BC ,BE共面11.平面直角坐标系中,若点()11,A x y ,点()22,B x y ,则称()1212,d A B x x y y =-+-为点A 到点B的“曼哈顿距离”.已知点O 为坐标原点,点P 在圆221x y +=上,点Q 在直线20x y +-=上,则下列说法正确的是()A.若点P 的横坐标为35-,则()7,5d O P =B.(),d O PC.(),d O Q 的最小值是2D.(),d Q P 的最小值是2Ⅱ卷(非选择题,共92分)三、填空题:本题共3小题,每小题5分,共15分.12.圆224x y +=与圆22+44120x y x y -+-=交于A ,B 两点,则线段AB 的垂直平分线的方程为____________.13.在空间直角坐标系中已知()1,2,1A ,()1,0,2B ,()1,1,4C -,CD 为三角形ABC 边AB 上的高,则CD =__________.14.在对角线1||6AC =的正方体1111ABCD A B C D -中,正方形11BCC B 所在平面内的动点P 到直线11D C 、DC 的距离之和为4,则1PC PC ⋅的取值范围是_________.四、解答题:5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.已知直线经过点()1,2A ,求满足下列条件的直线方程.(1)直线与直线123x y-=平行;(2)直线在两坐标轴上的截距相等.16.如图,已知四棱锥P ABCD -的底面ABCD 是直角梯形,,2AD BC AD =∥,90ABC ∠=︒,且PA ⊥平面,1ABCD PA AB BC ===.求:(1)求平面PCD 与平面PBA 夹角的余弦值;(2)点A 到平面PCD 的距离.17.已知圆M 经过两点()2,2A 、()4,2B ,且圆M 的圆心在直线0x y -=上.(1)求圆M 的方程;(2)若点P 为直线:20x y +-=上的动点,过点P 作圆M 的切线PQ 、PR ,切点为Q 、R ,求四边形PQMR 面积的最小值,并出此时点P 的坐标.18.如图1,在直角ABC V 中,AB BC =,点D ,E 分别为边AB ,AC 的中点,将ADE V 沿着DE 折起,使得点A 到达点P 的位置,如图2,且二面角P DE C --的大小为60o .(1)求证:平面PBC ⊥平面PBD ;(2)在棱PE 上是否存在点G ,使得BG 与平面PDE 所成角的正弦值为8?若存在,求PG PE 的值;若不存在,请说明理由.19.已知椭圆C :()222210+=>>x y a b a b ,连接椭圆上任意两点的线段叫作椭圆的弦,过椭圆中心的弦叫做椭圆的直径.若椭圆的两直径的斜率之积为22b a-,则称这两直径为椭圆的共轭直径.特别地,若一条直径所在的斜率为0,另一条直径的斜率不存在时,也称这两直径为共轭直径.现已知椭圆E :22143x y +=.(1)已知点31,2A ⎛⎫ ⎪⎝⎭,31,2B ⎛⎫-- ⎪⎝⎭为椭圆E 上两定点,求AB 的共轭直径的端点坐标.(2)过点()作直线与椭圆E 交于1A 、1B 两点,直线1AO 与椭圆E 的另一个交点为2A ,直线1B O 与椭圆E 的另一个交点为2B .当11A OB △的面积最大时,直径12A A 与直径12B B 是否共轭,请说明理由.(3)设CD 和MN 为椭圆E 的一对共轭直径,且线段CM 的中点为T .已知点P 满足:OP OT λ=,若点P 在椭圆E 的外部,求λ的取值范围.2024学年福建师大附中高二数学上学期期中考试卷时间:120分钟满分:150分试卷说明:(1)本卷共四大题,19小题,解答写在答卷的指定位置上,考试结束后,只交答卷.(2)考试过程中不得使用计算器或具有计算功能的电子设备.第Ⅰ卷(选择题,共58分)一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的选项中,只有一项是符合题目要求的.1.经过点(2,2)-,倾斜角是120的直线方程是()A.2(2)3y x -=-+ B.22)y x -=+C.2(2)3y x -=+ D.22)y x -=+【答案】B 【解析】【分析】根据题意,求得直线的斜率为k =.因为所求直线的倾斜角为120 ,可得直线的斜率为tan120k == ,又因为所求直线经过点(2,2)-,可得直线的方程为22)y x -=+.故选:B2.已知方程22122x y k k+=+-表示焦点在y 轴上的椭圆,则实数k 的取值范围为()A.()2,0- B.()0,2 C.()2,2- D.()()2,00,2-⋃【答案】A 【解析】【分析】根据给定的方程及椭圆焦点位置,列出不等式求解即得.由方程22122x y k k+=+-表示焦点在y 轴上的椭圆,得220k k ->+>,解得20k -<<,所以实数k 的取值范围为()2,0-.故选:A3.在圆222210x y x y +---=的所有经过坐标原点的弦中,最短的弦的长度为()A.1 B.2C. D.4【答案】B【分析】利用配方法化简圆的方程,结合垂径定理与勾股定理,可得答案.由222210x y x y +---=,则圆的标准方程为()()22113x y -+-=,如下图:图中AB MO ⊥,MB MO ==,M 为圆222210x y x y +---=的圆心,,A B 为直线AB 与圆的交点,易知AB 为所有经过坐标原点的弦中的最短弦,2AB ===.故选:B.4.如图,在直三棱柱111ABC A B C -中,13AA AC BC ===,90ACB ∠= ,点D 是线段1AA 上靠近1A 的三等分点,则直线1C D 与1B C 所成角的余弦值为()A.510-B.1010-C.510D.1010【答案】C 【解析】【分析】根据题意,可以用正方体模型补形解题,通过平移找出线线所成的角度借助余弦定理解题即可.根据题意,可以补充成一个棱长为3的正方体.如图所示.取NM 的三等分点1D ,连接11B D ,根据正方体性质,知道111//B D C D .则11CB D ∠为直线1C D 与1B C 所成角或补角.连接1CD ,CM .根据正方体性质,知道1MD CM ⊥.22223332CM BM CB =+=+=2222112(32)22CD D M CM =+=+2222113332CB BC BB =+=+=222211111310D B ND NB =+=+=在11D B C △中,余弦定理知道,2221111111115cos 21021032125D B CB CD D B C D B CB +-∠====⨯⨯⨯,则直线1C D 与1B C所成角的余弦值为10.故选:C .5.已知实数,x y 满足224240x y x y +---=,则13y x -+的最大值是()A.12B.2C.34D.【答案】C 【解析】【分析】将问题转化为圆()()22219x y -+-=上的点与()3,1-连线的斜率,利用圆的切线方程的求法可求得斜率的取值范围,进而得到最大值.由224240x y x y +---=得:()()22219x y -+-=,∴点(),x y 的轨迹是以2,1为圆心,3为半径的圆,13y x -∴+的几何意义为该圆上的点(),x y 与()3,1-连线的斜率,当过点()3,1-的直线斜率不存在,即为3x =-时,与圆显然不相切;设过点()3,1-的圆的切线为()13y k x -=+,即310kx y k -++=,∴圆心到切线的距离3d ==,解得:34k =±,133,344y x -⎡⎤∴∈-⎢⎥+⎣⎦,则13y x -+的最大值为34.故选:C.6.光线通过点()2,3A ,在直线:10l x y ++=上反射,反射光线经过点()2,2B ,则反射光线所在直线方程为()A.6520x y --=B.65220x y +-=C.5620x y -+=D.56220x y +-=【答案】C 【解析】【分析】先求出()2,3A 关于直线的对称点,从而得到反射光线所在直线经过点()2,2B 和对称点,从而得到反射光线所在直线方程.设点()2,3A 关于直线的对称点为()00,A x y ',则0000231022312x y y x ++⎧++=⎪⎪⎨-⎪=-⎪⎩,解得004,3x y =-=-,故()4,3A '--.由于反射光线所在直线经过点()4,3A '--和()2,2B ,所以反射光线所在直线的方程为()232224y x +-=-+,即5620x y -+=.故选:C.7.若直线y x b =+与曲线3y =有公共点,则实数b 的取值范围是()A.1⎡⎤-⎣⎦B.1⎡-+⎣C.)1⎡-⎣D.(1-+【答案】A 【解析】【分析】根据曲线3y =-即为()()()222343x y y -+-=≤,利用直线与圆的位置关系求解.解:曲线3y =-即为()()()222343x y y -+-=≤,表示以()2,3为圆心,以2为半径的半圆,其图象如图所示:由圆心到直线的2=,解得1b =+1b =-当直线过点()0,3时,3b =,因为直线y x b =+与曲线3y =有公共点,所以实数b的取值范围是1⎡⎤-⎣⎦,故选:A8.设1F ,2F 是椭圆2222:1x y C a b+=(0a b >>)的左、右焦点,过1F 的直线与C 交于A ,B 两点,若22AF BF ⊥,53aAB =,则C 的离心率为()A.5B.35C.25D.5【答案】D 【解析】【分析】设1AF x =,1BF y =,()0x y <<,根据椭圆的定义及勾股定理求出x 、y ,即可求出2BF 、2AF ,再由余弦定理求出a 与c 的关系,即可求出离心率.不妨设1AF x =,1BF y =,()0x y <<,则22AF a x =-,22BF a y =-.又22AF BF ⊥,所以()()()22222a x a y x y -+-=+,化简得()224xy a x y a ++=,显然53a x y AB +==,所以223a xy =,解得23a x =,y a =,所以243a AF =,2BF a =,故()2221224233cos 2223a a c c AF F a a c ⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭∠=-=⨯⨯,解得a =,故C的离心率为5.故选:D二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.已知圆()2222212:1,:(3)(3)0C x y C x y r r +=-+-=>,则下列说法正确的是()A.当1r =时,圆1C 与圆2C 有2条公切线B.当2r =时,1y =是圆1C 与圆2C 的一条公切线C.当3r =时,圆1C 与圆2C 相交D.当4r=时,圆1C 与圆2C 的公共弦所在直线的方程为12y x =-+【答案】BD 【解析】【分析】由两圆的标准方程可得它们的圆心和半径,再根据圆心距与半径的关系判断出两圆的位置关系,即可得出公切线条数,可判断AC 错误;利用圆心到直线的距离与半径的关系可得B 正确,将两圆方程相减可得它们的公共弦所在直线的方程为12y x =-+,即D 正确.由221:1C x y +=可知圆心为()10,0C ,半径为1;由()2222:(3)(3)0C x y rr -+-=>可知圆心为()23,3C ,半径为r ,两圆圆心距为12C C =;对于A ,当1r =时,1212r C C +=<=,圆1C 与圆2C 相离,有4条公切线,所以A 错误;对于B ,当2r =时,1y =与圆1C 相切,圆心()23,3C 到1y =的距离为2,即1y =与圆2C 也相切,所以1y =是圆1C 与圆2C 的一条公切线,即B 正确;对于C ,当3r =时,1214r C C +=<=,圆1C 与圆2C 相离,即C 错误;对于D ,当4r=时,121315r C C r -=<=<+=,此时两圆相交,圆2C 的一般方程为226620x y x y +--+=,与圆1C 的方程相减可得2210x y +-=,化简可得圆1C 与圆2C 的公共弦所在直线的方程为12y x =-+,即D 正确.故选:BD10.如图,边长均为1的两个正方形ABCD 和正方形ABEF 所在的平面互相垂直,动点M ,N 分别在正方形对角线AC 和BF 上移动,且(0CM BN a a ==<<,则下列说法正确的是()A.(a ∃∈,使12MN CE=B.线段MN 存在最小值,最小值为23C.直线MN 与平面ABEF 所成的角恒为45D.(a ∀∈,都有MN ,BC ,BE共面【答案】AD 【解析】【分析】以,,BA BE BC 为,,x y z 轴建立如图所示的空间直角坐标系,写出各点坐标,用空间向量法判断各选项.由已知⊥BC 平面ABEF ,以,,BA BE BC 为,,x y z 轴建立如图所示的空间直角坐标系,则(1,0,0)A ,(1,1,0)F ,(0,0,1)C ,(0,1,0)E ,在坐标平面xBy 上,直线BF 的方程为0x y -=,BN a =,则22,,0)22N a a ,在坐标平面xBz 上,直线AC 的方程为1x z +=,CM a =,则,0,1)22M a a -,)(0,1,1CE =- ,(0,,1)22MN a a =- ,易知,当2a =时,111(0,,222MN CE =-= ,A 正确;MN === ,所以2a =时,min 2MN = ,B 错;平面ABEF 的一个法向量是(0,0,1)m =,12cos ,a m MN m MN m MN-⋅==,所以CE 与平面ABEF12a -,这个值不是恒为22,因此角的大小不可能恒为45︒,C 错;(0,0,1),(0,1,0)BC BE ==,(0,,1)22MN a a =-1)22a BC aBE =-+(,所以MN ,BC ,BE共面,D 正确,故选:AD.11.平面直角坐标系中,若点()11,A x y ,点()22,B x y ,则称()1212,d A B x x y y =-+-为点A 到点B 的“曼哈顿距离”.已知点O 为坐标原点,点P 在圆221x y +=上,点Q在直线20x y +-=上,则下列说法正确的是()A.若点P 的横坐标为35-,则()7,5d O P =B.(),d O PC.(),d O Q 的最小值是2D.(),d Q P 的最小值是52【答案】ABD 【解析】【分析】对于A ,求出点P 的坐标即可判断;对于B ,利用基本不等式即可判断;对于C ,D ,利用绝对值放缩和绝对值不等式性质应用即可判断.对于A ,把35x =-代入221x y +=中,可得45y =±,则()347,555d O P =-+±=,故A 正确;对于B ,设(,)P x y ,则221x y +=,于是(),d O P x y =+===≤=当且仅当||||2x y ==时等号成立,即(),d O P B 正确;对于C ,设点(,2)Q m m ,则(),2d O Q m m m m=+=+|||||m m m m ≥+-≥-=m =时,等号成立,即(),d O Q ,故C 错误;对于D ,设点(cos ,sin )P θθ,[0,2π]θ∈,(,2)Q m m -,则()sin ,cos sin 2cos 22d Q P m m m m θθθθ=-+-+=-+-sin sin sin |cos ||||cos ||cos222m m m m θθθθθθ≥-+≥-++=+sin 5(cos )|sin()22θθθϕ=-+=-+,其中sin 55ϕϕ==,故只需当sin ,cos 55θθ==时,(),d Q P 取得最小值为2,此时10m =,故D 正确.故选:ABD.【点睛】关键点点睛:本题的关键之一是对“曼哈顿距离”的理解,根据新定义,写出曼哈顿距离;关键之二是含有绝对值的式子的处理,可根据绝对值的放缩和绝对值不等式,去掉绝对值的符号再求相关最值.Ⅱ卷(非选择题,共92分)三、填空题:本题共3小题,每小题5分,共15分.12.圆224x y +=与圆22+44120x y x y -+-=交于A ,B 两点,则线段AB 的垂直平分线的方程为____________.【答案】0x y +=【解析】【分析】线段AB 的垂直平分线的方程即为两圆圆心所在直线的方程,求出两圆圆心坐标,即可求出直线方程.圆224x y +=圆心坐标为0,0,圆22+44120x y x y -+-=化成标准方程为()()222+220x y -+=,圆心坐标为()2,2C -,两圆公共弦的垂直平分线恰为过两圆圆心的直线CO ,由20120CO k --==--,则直线CO 的方程为y x =-,即0x y +=.故答案为:0x y +=.13.在空间直角坐标系中已知()1,2,1A ,()1,0,2B ,()1,1,4C -,CD 为三角形ABC 边AB 上的高,则CD =__________.【答案】3【解析】【分析】应用空间向量法求点到直线距离.()2,1,3AC =-- ,()0,2,1AB =-,则AC =AC AB AD AB⋅=== ,所以3CD ===,故答案为:314.在对角线1||6AC =的正方体1111ABCD A B C D -中,正方形11BCC B 所在平面内的动点P 到直线11D C 、DC 的距离之和为4,则1PC PC ⋅的取值范围是_________.【答案】[2,1]-【解析】【分析】将点P 到直线11D C 、DC 的距离转化为1||PC 和||PC ,可得1||||4PC PC +=,结合椭圆的定义可得点P 的轨迹是以1,C C 为焦点的椭圆,建立平面直角坐标系得椭圆的标准方程,根据椭圆方程和平面向量数量积坐标表示可求出结果.因为1||6AC =,所以1||CC =,在正方体1111ABCD A B C D -中,11D C ⊥平面11BCC B ,DC ⊥平面11BCC B ,因为1,PC PC ⊂平面11BCC B ,所以111D C PC ⊥,DC PC ⊥,所以1||||4PC PC +=,且14||CC >=,所以点P 的轨迹是以1,C C 为焦点的椭圆,这里24a =,2c =2a =,c =,2221b a c =-=,以1CC 的中点O 为原点,1OC 为x 轴,1CC 的中垂线为y 轴建立平面直线坐标系,所以点P 的轨迹方程为2214x y +=,设(,)P x y ,因为()0C ,1(C ,则()PC x y =+,1()PC x y = ,所以221()()3PC PC x y x y x y ⋅=+⋅=-+ 222331244x x x =-+-=-,因为22x -≤≤,204x ≤≤,121PC PC -≤⋅≤.故答案为:[2,1]-四、解答题:5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.已知直线经过点()1,2A ,求满足下列条件的直线方程.(1)直线与直线123x y-=平行;(2)直线在两坐标轴上的截距相等.【答案】(1)3210x y -+=(2)3x y +=或20x y -=【解析】【分析】(1)由直线平行,设直线方程为23x ym -=,代入点A 可得解;(2)当直线不过坐标原点时,设直线方程为1x ya a+=,代入点A 即可,,当直线过坐标原点时,可得直线方程为21y x =.【小问1详解】由已知直线与直线123x y-=平行,则设直线():123x yl m m -=≠,又直线过点()1,2A ,即1223m -=,解得16m =-,则直线方程为1236x y -=-,即3210x y -+=;【小问2详解】当直线不过坐标原点时,设直线方程为1x ya a+=,则121a a+=,解得3a =,即直线方程为133x y+=,即3x y +=;当直线过坐标原点时,直线方程为21y x =,即20x y -=,综上所述直线方程为3x y +=或20x y -=.16.如图,已知四棱锥P ABCD -的底面ABCD 是直角梯形,,2AD BC AD =∥,90ABC ∠=︒,且PA ⊥平面,1ABCD PA AB BC ===.求:(1)求平面PCD 与平面PBA 夹角的余弦值;(2)点A 到平面PCD 的距离.【答案】(1)6(2)63【解析】【分析】(1)直接建立空间直角坐标系,先求法向量,再求两法向量夹角的余弦值,再求正弦值即可;(2)直接用空间向量法求点到面的距离.【小问1详解】以A 为坐标原点,AB 所在直线为x 轴,AD 所在直线为y 轴,AP 所在直线为z 轴建立如图所示的空间直角坐标系,(0,0,0)A ,(1,0,0)B ,()1,1,0C ,(0,2,0)D ,(0,0,1)P ,所以(0,2,1)PD =-,(1,1,1)PC =- ,设平面PCD 的法向量(,,)n x y z = ,则·20·0n PD y z n PC x y z ⎧=-=⎪⎨=+-=⎪⎩,令2z =,则1y =,1x =,所以(1,1,2)n = ,取平面PBA 法向量为(0,1,0)m =,所以6m n m n ⋅==,故面PCD 与面PBA 夹角的余弦值为66;【小问2详解】因为(0,2,0)AD = ,平面PCD 法向量为(1,1,2)n =,所以点A 到平面PCD 的距离||6||3d AD n n =⋅=uuu r r r.17.已知圆M 经过两点()2,2A 、()4,2B ,且圆M 的圆心在直线0x y -=上.(1)求圆M 的方程;(2)若点P 为直线:20x y +-=上的动点,过点P 作圆M 的切线PQ 、PR ,切点为Q 、R ,求四边形PQMR 面积的最小值,并出此时点P 的坐标.【答案】(1)()()22332x y -+-=(2);()1,1P 【解析】【分析】(1)根据圆上的两个已知点求得其对称轴,联立方程求得圆心,利用两点距离公式,可得答案;(2)根据题意,作图,结合切线的性质以及动点与直线的性质,可得答案.【小问1详解】由()2,2A 与()4,2B ,则直线AB 的斜率22042AB k -==-,其中点坐标为()3,2,所以,A B 的对称轴为直线3x =,易知圆心M 在直线3x =上,联立30x x y =⎧⎨-=⎩,解得33x y =⎧⎨=⎩,则()3,3M ,半径r AM ===,所以圆M 的标准方程为()()22332x y -+-=.【小问2详解】根据题意,作图如下:由图可知:四边形PQMR 的面积为MRP MQP S S +V V ,且MRP MQP ≅V V ,MR PR ⊥,在Rt MRP V 中,222PR MP MR =-,因为MR =,所以当PR 最小时,MRP S V 最小,当MP l ⊥时,MP 最小,此时PR 最小,此时MP ==PR =,12MRP S PR MR =⋅⋅= ,所以四边形PQMR 面积的最小值为由直线:20+-=l x y ,则其斜率1k =-,直线MP 的斜率11MP k k-==,则直线MP 的方程为33y x -=-,整理可得y x =,联立20y x x y =⎧⎨+-=⎩,解得11x y =⎧⎨=⎩,则()1,1P .18.如图1,在直角ABC V 中,AB BC =,点D ,E 分别为边AB ,AC 的中点,将ADE V 沿着DE 折起,使得点A 到达点P 的位置,如图2,且二面角P DE C --的大小为60o .(1)求证:平面PBC ⊥平面PBD ;(2)在棱PE 上是否存在点G ,使得BG 与平面PDE 所成角的正弦值为8?若存在,求PG PE 的值;若不存在,请说明理由.【答案】(1)证明见解析;(2)16或13.理由见解析.【解析】【分析】(1)证明DE ⊥平面PBD ,由平行得证⊥BC 平面PBD ,再由面面垂直的判定定理得证面面垂直;(2)先证明PDB ∠是已知二面角的平面角,得60PBD ∠=︒,取BD 中点O ,证明⊥PO 平面BCED ,然后以O 为原点,,OB OP 为,x z 轴,过O 平行BC 的直线为y ,建立如图所示的空间直角坐标系,设2AB BC ==,得各点坐标,求出平面PDE 的一个法向量,设13(,,)(01)22PG k PE k k k k ==--≤≤ ,求得BG ,再根据线面角的向量求法求线面角,从而可得结论.【小问1详解】由题意,PD DE BD DE ⊥⊥,PD BD D ⋂=,,PD BD ⊂平面PBD ,所以DE ⊥平面PBD ,又因为图1中,,D E 分别是,AB AC 中点,所以//DE BC ,所以⊥BC 平面PBD ,而⊂BC 平面PBC ,所以平面PBC ⊥平面PBD ;【小问2详解】由题意,PD DE BD DE ⊥⊥,所以ADB ∠是二面角P DE C --的平面角,二面角P DE C --的大小为60o .则60PDB ∠=︒,又由已知PD BD =,所以PBD △等边三角形,取BD 中点O ,连接OP ,则PO BD ⊥,由(1)知⊥BC 平面PBD ,而PO ⊂平面PBD ,所以BC PO ⊥,BC BD B = ,,BC BD ⊂平面BCED ,所以⊥PO 平面BCED ,以O 为原点,,OB OP 为,x z 轴,过O 平行BC 的直线为y ,建立如图所示的空间直角坐标系,设2AB BC ==,则112DE BC ==,1BD AD ==,2PO =,1(,0,0)2B ,32P ,1(,0,0)2D -,1(,1,0)2E -,1(,1,),(0,1,0)22PE DE =--= ,设平面PDE 的一个法向量为(,,)n x y z = ,则10220n PE x y z nDE y ⎧⋅=-+-=⎪⎨⎪⋅==⎩,取x =1)n =- ,设13(,,)(01)22PG k PE k k k k ==--≤≤,1(,0,22BP =-,11(,,2222BG BP PG k k k =+=---+ ,BG 与平面PDE所成角的正弦值为8,则cos ,8BG n BG n n BG ⋅== ,解得16k =或13k =.所以PG PE 的值为16或13.19.已知椭圆C :()222210+=>>x y a b a b ,连接椭圆上任意两点的线段叫作椭圆的弦,过椭圆中心的弦叫做椭圆的直径.若椭圆的两直径的斜率之积为22b a-,则称这两直径为椭圆的共轭直径.特别地,若一条直径所在的斜率为0,另一条直径的斜率不存在时,也称这两直径为共轭直径.现已知椭圆E :22143x y +=.(1)已知点31,2A ⎛⎫ ⎪⎝⎭,31,2B ⎛⎫-- ⎪⎝⎭为椭圆E 上两定点,求AB 的共轭直径的端点坐标.(2)过点()作直线与椭圆E 交于1A 、1B 两点,直线1AO 与椭圆E 的另一个交点为2A ,直线1B O 与椭圆E 的另一个交点为2B .当11A OB △的面积最大时,直径12A A 与直径12B B 是否共轭,请说明理由.(3)设CD 和MN 为椭圆E 的一对共轭直径,且线段CM 的中点为T .已知点P 满足:OP OT λ=,若点P 在椭圆E 的外部,求λ的取值范围.【答案】(1)2⎫-⎪⎪⎭和2⎛⎫ ⎪ ⎪⎝⎭;(2)直径12A A 与直径12B B 共轭,理由见解析;(3)λ>或λ<【解析】【分析】(1)设所求直线方程为:y kx =依题意可得12k =-,即可得到直线方程,再联立直线与椭圆方程求出交点坐标即可;(2)设:x my =()111,A x y 、()122,B x y,联立直线与椭圆方程,消元、列出韦达定理,则12S y y =-,再利用基本不等式求出面积最大值,即可求出参数m 的值,即可判断;(3)设点()11,C x y ,()22,M x y ,设CD l :y kx =,则MN l :34y x k=-,联立直线与椭圆方程,求出交点坐标,从而得到P 点坐标,再由P 在椭圆内部,即可得到不等式,解得即可;解:(1)由题设知32AB k =,设所求直线方程为:y kx =,则34AB k k ⋅=-,则12k =-.故共轭直径所在直线方程为:12y x =-.联立椭圆与12y x =-,即2212143y x x y ⎧=-⎪⎪⎨⎪+=⎪⎩可得:23x =,x =.故端点坐标为2⎫-⎪⎪⎭和2⎛⎫⎪⎪⎝⎭.(2)由题设知,不与x轴重合,故设:x my=,()111,A x y、()122,B x y联立方程:()22223430143x mym yx y⎧=-⎪⇒+--=⎨+=⎪⎩,则1226334y ym+=+,122334y ym-=+,2122121234mx xm-=+,122223434S ym m=-=⋅=++63=≤=.当且仅当2313m+=,即223m=时取等号,此时121221222123312124A AB By y bk kx x m a-⋅===-=--,故直径12A A与直径12B B共轭.(3)设点()11,C x y,()22,M x y,当CD不与坐标轴重合时,设CDl:y kx=,则MNl:34y xk=-.联立2222211221212,3434143y kxkx yx y k k=⎧⎪⇒==⎨+++=⎪⎩.同理可得:22221634kxk=+,222934yk=+.由椭圆的对称性,不妨设C在第一象限,则M必在第二象限或第四象限,则1x=,1y=若M在第二象限,则2x=,2y=,从而T⎪⎝⎭,则P ⎫⎪⎪⎪ ⎪⎝⎭.又P在椭圆外,则223412⎛⎫ ⎪ ⎪+> ⎪ ⎪ ⎪⎝⎭⎝⎭,化简可得:22λ>,即λ>λ<.若M 在第四象限,同理可得22λ>,即λ>λ<当CD 与x 轴垂直或重合时,由椭圆的对称性,不妨取()2,0C,(M ,则3,2P λλ⎛⎫⎪ ⎪⎝⎭.又P 在椭圆外,则2223341224λλλ+⋅>⇒>,即λ>,或λ<,综上:λ>或λ<.【点睛】解决直线与椭圆的综合问题时,要注意:(1)注意观察应用题设中的每一个条件,明确确定直线、椭圆的条件;(2)强化有关直线与椭圆联立得出一元二次方程后的运算能力,重视根与系数之间的关系、弦长、斜率、三角形的面积等问题.。
福建师范大学附属中学2020-2021学年上学期期中考模拟试卷高二数学(实验班)试题及答案

绝密★启用前福建师大附中2020-2021 学年上学期期中考模拟试卷高二数学(实验班)第I 卷(选择题,共64 分)一、单项选择题:每小题6 分,共48 分.在每小题给出的选项中,只有一个选项是正确的.1. 已知α, β∈ (0, π),则“sin α + sin β < 1”是“sin(α + β) < 1”的( ▲)3 3A. 充分不必要条件B. 必要不充分条件C. 充分且必要条件D. 既不充分也不必要条件2. 已知直线l: x sin α + y cos α = 1 (0 ≤ α < 2π) 与圆C: (x− 2)2 + (y− √5)2 = 4 相切,则满足条件的α的个数为( ▲)A. 1B. 2C. 3D. 43. 已知圆C : (x + 2a)2+ y2 = 4 与圆C : x2 + (y− b)2= 1 有且仅有1 条公切线,则 1 + 1的最小1 2值为( ▲)a2b2A. 6B. 7C. 8D. 94. 已知点M(x, y) 在曲线C: x2 + y2− 4x− 21 = 0 上运动,设t = x2 + y2 + 12x− 12y− 150 − a,且t的最大值为b,若a, b > 0,则 1 + 1a+1 b的最小值为( ▲)A. 1B. 2C. 3D. 45. 如图所示,两半径相等的圆A, B相交,CD为它们的公切线段,且两块阴影部分面积相等,在线段AB上任取一点M,则M在线段EF上的概率为( ▲)A. 1 −π4 B. 2 − π2C. 2− 1D. 4− 1ππx + y− 2 ≤ 06. 已知区域D = {(x, y)| { x− y + 2 ≤ 0 },给定下列四个命题:3x− y + 6 ≥ 0p1: ∀(x, y) ∈ D, x + y + 1 ≥ 0 p2: ∀(x, y) ∈ D, 2x− y + 2 ≤ 0 p : ∃(x, y) ∈ D, y+1 ≤−4 p : ∃(x, y) ∈ D, x2 + y2≤ 23 x−1 4则下列选项中是真命题的为( ▲)A. p1 ∧p3B. p2 ∧p4C. p1 ∧p4D. p2 ∧p37. 已知在△ ABC内有一点O满足∠OAB = ∠OAC = ∠OBC = ∠OCA = α,给定下列两个命题:p: 存在点O使得α≥ 36°q: 对于任意的点O总有c, a, b成等比数列则下列选项中是真命题的为( ▲)A. p∧qB. p∧(¬q)C. (¬p) ∧qD. (¬p) ∧(¬q)8. 在平面直角坐标系中,定义d(A, B) = max{|x1 −x2|, |y1 −y2|} 为两点A(x1, y1), B(x2, y2) 的“切比雪夫距离”,并对于点P与直线l上任意一点Q,称d(P, Q) 的最小值为点P与直线l间的“切比雪夫距离”,记作d(P, l),给定下列四个命题:p1: 对于任意的三点A, B, C,总有d(C, A) + d(C, B) ≥ d(A, B)p : 若点P(3, 1),直线l: 2x− y− 1 = 0,则d(P, l) = 42 3p3: 满足d(O, M) = C(C > 0) 的点M的轨迹为正方形p4: 若点F1(−c, 0), F2(c, 0),则满足|d(P, F1) −d(P, F2)| = 2a(2c > 2a > 0) 的点M的轨迹与直线y = k (k为常数) 有且仅有2 个公共点则下列选项中真命题的个数为( ▲)A. 1B. 2C. 3D. 4二、多项选择题:每小题6 分,共12 分.在每小题给出的选项中,正确选项不少于2 个,全部选对得6 分,选对但不全得3 分,有选错得0 分.9.在平面直角坐标系中,直线l: y = k(x− 2) + 3 与坐标轴分别交于点A, B,则下列选项中是真命题的有( ▲ )A.存在正实数m使得△ OAB面积为m的直线l恰有一条B.存在正实数m使得△ OAB面积为m的直线l恰有二条C.存在正实数m使得△ OAB面积为m的直线l恰有三条D.存在正实数m使得△ OAB面积为m的直线l恰有四条10.下列选项中说法正确的有( ▲ )A. “若点(2, 1) 在圆x2 + y2 + kx + 2y + k2− 15 = 0 外,则k < −4 或k > 2”的否命题B. 已知直线y = kx与圆(x + cos θ)2+ (y− sin θ)2= 1,∀θ∈ ℝ,总有k使得直线与圆恒相切C. 已知直线y = kx与圆(x + cos θ)2+ (y− sin θ)2= 1,∀k∈ ℝ,总有θ使得直线与圆恒相切D. 过直线2x + y + 4 = 0 上的动点P引圆C: x2 + y2− 2y = 1 的两条切线,A, B为切点,则四边形PACB面积的最小值为2√2第II 卷(非选择题,共86 分)三、填空题:每小题 6 分,共24 分.11.已知五个互不相等的样本x1, x2, x3, x4, x5 ∈ℕ,它们的平均数为7,标准差为2,则样本数据中最大值为▲.12. 已知点A(x1, y1), B(x2, y2) 是曲线x2 + y2− 2x + 4y = 0 上的两点,则|x1y2 −x2y1| 的最大值为▲.13. 已知区域D表示不在直线(1 − m2)x + 2my = 2 + 2√3m(m∈ ℝ) 上的点构成的集合,在区域D内任取一点P(x, y),则√x+的取值范围为▲.√x2+y214. 已知在平面内有P1, P2, … , P n共n个点,若在该平面内有点P到P1, P2, … , P n的距离之和最小,则称点P为点P1, P2, … , P n的一个“中位点”,给定下列四个命题:p1: 若三点A, B, C共线,且C在线段AB上,则C是A, B, C的“中位点”p2: 若四点A, B, C, D共线,则它们的“中位点”存在且唯一p3: 直角三角形的斜边中点是该直角三角形三个顶点的“中位点”p4: 梯形对角线交点是梯形四个顶点的唯一“中位点”则上述命题中真命题有▲.(写出所有真命题的序号)四、解答题:4 小题,共66 分.解答应写出文字说明、证明过程或演算步骤.15. (16 分)已知圆M: (x− 2)2+ y2 = 1,过直线l: x = −1 上一动点P作圆的两条切线,切点分别为A, B.(I)当有一条切线于坐标轴平行时,求另一条切线的方程;(II)当圆切点弦所对的圆心角最小时,求|AB| 的值;(III) 记切线PA, PB分别交y轴于点S, T,求|ST| 的最小值.16. (16 分)若过点P的两直线l1, l2斜率之积为λ(λ≠ 0),则称直线l1, l2是一组“Pλ共轭线对”.(I) 若直线l1, l2是一组“O−3共轭线对”,当两直线夹角最小时,求两直线倾斜角;(II) 若点A(0, 1), B(−1, 0), C(1, 0) 分别是直线PQ, QR, RP上的点(A, B, C, P, Q, R均不重合),且直线PR, PQ是一组“P1 共轭线对”,直线QP, QR是一组“Q4 共轭线对”,直线RP, RQ是一组“R9 共轭线对”,求点P的坐标;(III) 若直线l1, l2是一组“M−2共轭线对”,其中点M(−1, −√2),当两直线旋转时,求原点到两直线距离之积的取值范围.17. (18 分)疫苗能够使人体获得对病毒的免疫力,是保护健康人群最有效的手段.新冠肺炎疫情发生以来, 军事医学科学院陈薇院土领衔的团队开展应急科研攻关,研制的重组新型冠状病毒疫苗(腺病毒载体),于 4 月 12 日开始招募志愿者,进入二期临床试验.根据普遍规律,志愿者接种疫苗后体内会产生抗体, 人体中检测到抗体,说明有抵御病毒的能力.科研人员要定期从接种疫苗的志愿者身上采集血液样本, 检测人体中抗体含量水平(单位:miu /mL ,百万国际单位/毫升).(I) IgM 作为人体中首先快速产生的抗体,是人体抗感染免疫的“先头部队”.经采样分折,志愿者身体中 IgM 含量水平 y (miu /mL ) 与接种天数 x (接种后每满 24 小时为一天,x ∈ ℕ∗)近似满足函数 关系:y = { 0.1x , x ≤ 10.经研究表明,IgM 含量水平不低于 0.2miu /mL 时是免疫的有效时段,试e 10−x , x > 10 估计接种一次后IgM 含量水平有效时段可经历的时间(向下取整).(参考数据:e ≈ 2.718) (II) IgG 虽然是接种后产生比较慢的抗体,却是血清和体液中含量最高的抗体,也是亲和力最强、人体内分布最广泛、具有免疫效应的抗感染“主力军”.科研人员每间隔 3 天检测一次(检测次数依次记为 t i , i = 1, 2, 3, 4, 5, 6, 7)某志愿者人体中 IgG 的含量水平,记作 z i (miu /mL ) (i = 1, 2, 3, 4, 5, 6, 7),得到相关数据如下表:(i) 请画出散点图,并根据散点图判断,线性拟合模型 z = a + bt 与指数拟合模型 z = c ∙ d t 哪种更适合拟合 z 与 t 的关系(不必说明理由);(ii) 研究人员发现,上述数据中存在一组异常数据应当予以剔除.试根据余下的六组数据,利用(i)中选择的拟合模型计算回归方程,并估计原异常数据对应的 z i 值.(回归系数与估计值均保留两位小数,由七组数据计算出的参考数据见下表,其中 u = ln z )参考公式:线性回归直线 y = a + bx 的斜率和截距的最小二乘估计分别为 b= ∑(x i − x̅)(y i − y ),a = y − bx̅ ∑(x i − x̅)218. (16 分)某科研团队发现了一种新型单细胞生物,在长时间观测后,科研团队发现每个活细胞在每一分钟内都会独立且等可能地发生以下四件事中的一件:①死亡;②保持原状;③分裂成两个活细胞;④分裂成三个活细胞.若初始时在一条件适宜的孤立系统中放置两个活细胞,试计算理论上在无限长时间后该系统中仍有活细胞存活的概率.( )绝密★启用前福建师大附中 2020-2021 学年上学期期中考模拟试卷高二数学(实验班)答案第 I 卷(选择题,共 64 分)一、单项选择题:每小题 6 分,共 48 分.在每小题给出的选项中,只有一个选项是正确的.二、多项选择题:每小题 6 分,共 12 分.在每小题给出的选项中,正确选项不少于 2 个,全部选对得 6 分,选对但不全得 3 分,有选错得 0 分.第 II 卷(非选择题,共 86 分)三、填空题:每小题 6 分,共 24 分.四、解答题:4 小题,共 66 分.解答应写出文字说明、证明过程或演算步骤.15. 解:(I) 3x + 4y − 1 = 0 或 3x − 4y − 1 = 0(II) |AB |min =4√23(III) |ST |min =√2216. 解:(I)π , 2π(II) P (3, 3) 或 P 3 ,3(III) d d∈ [0, √2)3 35 51 217. 解:(I) 9 天(II) (i) 指数拟合模型 z = c ∙ d t(ii) ẑ = 0.06 × 2.27t ;z 4 = 1.5518. 解:2√2 − 2。
2021-2022学年福建师范大学附属中学高二上学期期中考试数学试题(解析版)

2021-2022学年福建师范大学附属中学高二上学期期中考试数学试题一、单选题1.经过点(1,-1)且一个方向向量为(1,32-)的直线l 的方程是( ) A .3x +2y -1=0B .3x +2y +1=0C .2x +3y +1=0D .x -2y -3=0【答案】A 【分析】根据直线的方向向量求出直线的斜率k 的值,代入点斜式方程,求出直线方程即可.【详解】直线l 的一个方向向量为(1,32-),且经过(1,-1), 故直线l 的斜率k =32-, 故直线方程为:y +1=32-(x -1),即3x +2y -1=0, 故选:A.2.圆()22:39A x y -+=与圆22:812270B x y x y +--+=的位置关系是( )A .内切B .外切C .相交D .相离 【答案】C【分析】求出圆心距,与两半径的和差比较可得.【详解】圆心A ,圆心为(3,0)A ,半径为3r =,圆B 标准方程为22(4)(6)25x y -+-=,圆心为(4,6)B ,半径为5R =.AB ,显然5353-<+,所以两圆相交.故选:C .3.已知直线1:(2)20l ax a y +++=与2:10l x ay ++=平行,则实数a 的值为A .-1或2B .0或2C .2D .-1【答案】D【分析】根据两直线平行,列方程,求的a 的值.【详解】已知两直线平行,可得a•a -(a+2)=0,即a 2-a-2=0,解得a=2或-1.经过验证可得:a=2时两条直线重合,舍去.∴a=-1.故选D【点睛】对于直线1111222200l A x B y C l A x B y C ++=++=:,:,若直线12122112211221000l l A B A B AC A C B C B C ⇔-=-≠-≠且(或); 4.设函数f (x )=sin2x ,x ∈R ,若π0,2θ⎡⎫∈⎪⎢⎣⎭,函数()f x θ+是偶函数,则θ的值为( ) A .12π B .6π C .4π D .3π 【答案】C【分析】由诱导公式和余弦函数为偶函数,可得ππ24k θ=+(Z k ∈),再由θ的范围,可得所求值. 【详解】函数f (x )=sin2x ,x ∈R ,函数f (x +θ)=sin2(x +θ)=sin (2x +2θ), 由于f (x +θ)是偶函数,可得2θ=k π+π2(k ∈Z ), 即ππ24k θ=+(k ∈Z ), 由θ∈[0,π2),可得θ的值为π4. 故选:C.5.正方体中,M 是1DD 的中点,O 为底面ABCD 的中心,P 为棱11A B 上的任意一点,则直线OP 与直线AM 所成的角为A .45B .60C .90D .与点P 的位置有关【答案】C【详解】试题分析:如下图所示建立空间直角坐标系,不妨设正方体的棱长为2,设(,0,0)P x ,(1,1,2)O ,(0,2,1)M ,(0,0,2)A ,∴(1,1,2)OP x =---,(0,2,1)AM =-,∴(1)012(2)(1)0OP AM x ⋅=-⋅-⨯+-⨯-=,即OP AM ⊥,故夹角为2π,故选C. 【解析】异面直线的夹角.【名师点睛】探求常规的异面直线所成角的问题,首先要理清求角的基本步骤为“一作,二证,三求”,通过平行线或补形平移法把异面直线转化为相交直线进而求其夹角,其中空间选点任意但要灵活,如常选择“端点,中点,等分点”,通过三角形的中位线平行于底边,长方体对面上的平行线进行平移等.这是研究空间图形的一种基本思路,即把空间图形问题转化为平面图形问题.6.直线y =x +b 与曲线21x y =--有且仅有一个公共点,则实数b 的取值范围是( )A .b =±2B .-1<b ≤1或b =2-C .-1≤b <1或b =2D .-2≤b ≤2【答案】C【分析】把曲线方程整理后可知其图像为半圆,进而画出图像来,要使直线与曲线有且仅有一个交点,那么很容易从图上看出其三个极端情况分别是:直线在第二象限与曲线相切,交曲线于(0,1)和(-1,0),及与曲线交于点(0,-1),分别求出b ,则b 的范围可得.【详解】曲线21x y =--有即 x 2+y 2=1 (x ≤0),表示一个半圆(单位圆位于x 轴及x 轴左侧的部分).如图,则A (0,1)、B (-1,0)、C (0,-1),当直线y =x +b 经过点C 时,-1=0+b ,求得 b =-1;当直线y =x +b 经过点B 、点A 时,0=-1+b ,求得b =1;当直线y =x +b 和半圆相切时,由圆心到直线的距离等于半径,可得12b =b 2,或 b =2(舍去),故要求的实数b 的范围为-1≤b <1或b =2,故选:C. 7.已知A ,B ,C ,D 在球O 的表面上,ABC 为等边三角形且其面积为334,AD ⊥平面ABC ,AD =2,则球O 的表面积为( )A .πB .2πC .4πD .8π 【答案】D【分析】由正弦定理可得ABC 外接圆的半径,作图利用勾股定理可得四面体D ABC -的外接球的半径,即可求出球O 的表面积. 【详解】因为ABC 为等边三角形且其面积为22133324sin 60a =, 所以ABC 3ABC 外接圆的半径为r , 由正弦定理可得32260r ==,1r =,取底面中心为1O ,即11O A = ∵AD ⊥平面ABC ,AD =2,过1O 作1//O O AD ,且取11=2O O AD , 则O 即是四面体D ABC -外接球的球心,半径R OA =,在1Rt O OA △中,2222211122AD OA O O O A ⎛⎫=+=+= ⎪⎝⎭,则2R OA == 所以球O 的表面积为24π8πR =.故选:D.8.已知点F 是椭圆22221(0)y x a b a b +=>>的上焦点,点P 在椭圆E 上,线段PF 与圆222()216c b x y +-=相切于点Q ,O 为坐标原点,且()0OP OF FP +⋅=,则椭圆E 的离心率为( )A 6B 5C .23 D .12 【答案】B【分析】根据()0OP OF FP +⋅=可得1PF PF ⊥,结合圆的相切关系可得1PF b =,然后利用椭圆的定义及勾股定理可求离心率. 【详解】设椭圆的下焦点为1F ,圆222()216c b x y +-=的圆心为A ,线段PF 的中点为B , 因为()0OP OF FP +⋅=,所以()()0OP OF OP OF +⋅-=,即OP OF c ==;所以OB PF ⊥,由于1//OB PF ,所以1PF PF ⊥;因为线段PF 与圆222()216c b x y +-=相切于点Q , 所以AQ PF ⊥,所以1//PF AQ ,所以11AQ AF PF FF =; 因为12,,42b c FF c AQ AF ===,所以1PF b =; 根据椭圆定义可得2PF a b =-,所以有()22224a b b c -+=,整理得23b a =, 所以离心率2513c b e a a ⎛⎫==-= ⎪⎝⎭. 故选:B.【点睛】本题主要考查椭圆的离心率的求解,根据题意构建关于,,a b c 的关系式是求解的关键,侧重考查数学运算的核心素养.二、多选题9.已知F 1,F 2分别是椭圆C :22195x y +=的左,右焦点,P 为椭圆C 上异于长轴端点的动点,则下列结论正确的是( )A .1PF F 的周长为10B .1PF F 面积的最大值为25C .1||PF 的最小值为1D .椭圆C 的焦距为6【分析】根据椭圆的方程求出,,a b c ,再结合椭圆定义与椭圆的几何性质即可分别判断正误求解.【详解】∵椭圆C 方程为:22195x y +=, 3,5,2a b c ∴===12PF F ∴△的周长为1212||||||2210PF PF F F a c ++=+=,∴A 正确;∴△PF 1F 2面积的最大值为12252c b ⋅⋅=,此时P 位于短轴的端点,∴B 正确; P 在椭圆的左顶点时,|PF 1|的最小值为a -c =1,又P 为椭圆C 上异于长轴端点的动点,∴C 错误; 椭圆C 的焦距为2c =4,∴D 错误.故选:AB.10.某同学在研究函数()211f x x x =++-的最值时,联想到两点间的距离公式,从而将函数变形为()()()()()2222001100f x x x =-+-+-+-,则下列结论正确的是( )A .函数()f x 的最小值为22B .函数()f x 的最小值为2C .函数()f x 没有最大值D .函数()f x 有最大值 【答案】BC【分析】由题意画出图形,利用动点到两定点距离和的变化求出最小值判断AB ,分析无最大值判断CD .【详解】设2222()(0)(01)(1)(00)f x x x =-+-+-+-,可理解为动点(,0)P x 到两个定点(0,1)A ,(1,0)B 的距离和.如图:由三角形三边关系可得2PA PB AB +≥当点P 和点B 重合时,等号成立,PA PB +无最大值,所以函数()f x 2.11.已知点F 1,F 2分别是椭圆()222210x y a b a b +=>>的左、右焦点,点P 是椭圆上的一点(异于左、右顶点),若存在以22c 为半径的圆内切于12PF F △,则该椭圆的离心率可能为( ) A .22 B .12 C .13 D .14【答案】CD【分析】根据题意可得12122PF F S c b ≤⨯⨯,从而可得()121222222a c c cb ⨯+⨯≤⨯⨯,再化简转化为关于e 的不等式,解不等式即可求解.【详解】由椭圆性质可得:12PF F △的面积满足12122PF F Sc b ≤⨯⨯, 又存在以22c 为半径的圆内切于12PF F △, ∴()12121222222PF F S a c c c b =⨯+⨯≤⨯⨯, ∴a +c ≤2b ,∴(a +c )2≤2b 2=2(a 2-c 2),∴3c 2+2ac -a 2≤0,∴3e 2+2e -1≤0,∴ 113e -≤≤ 又01e <<,解得103e <≤, 故选:CD.12.如图,矩形ABCD 中,22AB AD ==,E 为边AB 的中点,将△ADE 沿直线DE 翻折成△A 1DE (点A 不落在底面BCDE 内),若M 为线段A 1C 的中点,则在△ADE 翻转过程中,以下命题正确的是( )A .四棱锥1A BCDE -2B .线段BM 长度是定值C .MB ∥平面A 1DE 一定成立D .存在某个位置,使1DE A C ⊥【答案】ABC 【分析】对选项A ,取DE 的中点O ,连接1A O ,根据题意得到当平面1A DE ⊥平面BCDE 时,1A 到平面BCDE 的距离最大,再计算四棱锥1A BCDE -体积即可判断A 正确.对选项B ,对选项B ,取CD 的中点F ,连接MF ,BF ,根据等角定理得到145A DE MFB ∠=∠=,再利用余弦定理即可判断B 正确.对选项C ,首先根据题意易证平面//MBF 平面1A DE ,再利用面面平行的性质即可判断C 正确,对选项D ,连接AC ,根据1A C 在平面BCDE 的射影在AC 上,DE 与AC 不垂直,即可判断D 错误.【详解】对选项A ,取DE 的中点O ,连接1A O ,如图所示:当平面1A DE ⊥平面BCDE 时,1A 到平面BCDE 的距离最大.因为1A D AE =,O 为DE 中点,所以1AO DE ⊥. 又因为平面1A DE ⋂平面BCDE DE =,所以1A O BCDE ⊥. 22112DE =+=,所以22122122AO ⎛⎫=-= ⎪ ⎪⎝⎭. 所以四棱锥1A BCDE -体积最大值为()1211223224+⨯⨯⨯=,故A 正确. 对选项B ,取CD 的中点F ,连接MF ,BF ,如图所示:因为,M F 分别为1,A C AB 的中点,22AB AD ==,所以四边形DEBF 为菱形,所以1//A D MF ,//DE BF ,所以145A DE MFB ∠=∠=,11122MF A D ==,2BF DE ==, 所以()2211252222222MB ⎛⎫=+-⨯⨯⨯= ⎪⎝⎭,故B 正确. 对选项C ,因为1//MF A D ,1A D ⊂平面1A DE ,所以//MF 平面1A DE ,因为//FB DE ,DE ⊂平面1A DE ,所以//BF 平面1A DE ,又因为MF BF F ⋂=,,MF BF ⊂平面MBF ,所以平面//MBF 平面1A DE ,又因为MB ⊂平面MBF ,所以//MB 平面1A DE ,故C 正确.对选项D ,连接AC ,如图所示:因为1A C 在平面BCDE 的射影在AC 上,45DEA =∠,1tan 2CAB ∠=,所以DE 与AC 不垂直, 所以DE 与1A C 不垂直,故D 错误.故选:ABC三、填空题13.求过点3(4,)P -且与圆()()22139x y -+-=相切的直线方程为______.【答案】x =4或3x +4y =0【分析】先考虑直线的斜率是否存在,然后结合点到直线的距离公式即可求解.【详解】当直线的斜率存在时,可设直线方程为y +3=k (x -4),即kx -y -4k -3=0, 234331k k k ---=+,解得k =34-,此时直线方程为3x +4y =0, 当直线的斜率不存在时,直线方程为x =4此时圆心(1,3) 到直线x =4的距离为3,所以直线与圆相切,符合题意.故答案为:x =4或3x +4y =0.14.如图,在三棱柱ABC -A 1B 1C 1中,所有棱长均为1,且AA 1⊥底面ABC ,则点B 1到平面ABC 1的距离为______.21 【分析】建立合适的空间直角坐标系,求出所需点的坐标和向量的坐标,利用待定系数法求出平面ABC 1的法向量,再由点到平面的距离公式求解即可.【详解】以点C 为坐标原点,建立空间直角坐标系如图所示, 则()()()1131,0,0,1,0,0,1,1,0,0,12A B B C ⎫⎪⎪⎝⎭, 所以131,122C A ⎛⎫=- ⎪ ⎪⎝⎭,()10,1,1C B =-, ()110,1,0C B =, 设平面ABC 1的法向量为(,,)n x y z =,则1100n C A n C B ⎧⋅=⎪⎨⋅=⎪⎩,即31020y z y z ⎧+-=⎪⎪-=⎩, 令1x =,则3y z ==(1,3,3)n =,所以点B 1到平面ABC 1的距离为113217133C B n n ⋅==++. 217..15.已知直线l :kx ﹣y ﹣2k +2=0与圆C :x 2+y 2﹣2x ﹣6y +6=0相交于A ,B 两点,则|AB |的最小值为______________. 【答案】2【分析】根据题意,分析圆C 的圆心与半径,将直线l 的方程变形为y ﹣2=k (x ﹣2),恒过定点M (2,2),分析可得M 在圆C 内部,分析可得:当直线l 与CM 垂直时,弦|AB |最小,求出此时|CM |的值,由勾股定理分析可得答案.【详解】解:根据题意,圆C :x 2+y 2﹣2x ﹣6y +6=0即(x ﹣1)2+(y ﹣3)2=4, 圆心C 的坐标为(1,3),半径r =2,直线l :kx ﹣y ﹣2k +2=0,即y ﹣2=k (x ﹣2),恒过定点M (2,2), 又由圆C 的方程为(x ﹣1)2+(y ﹣3)2=4,则点M (2,2)在圆内, 分析可得:当直线l 与CM 垂直时,弦|AB |最小, 此时|CM |22(21)(23)-+-2 则|AB |的最小值为42-22 故答案为:22四、双空题16.17世纪,笛卡尔在《几何学》中,通过建立坐标系,引入点的坐标的概念,将代数对象与几何对象建立关系,从而实现了代数问题与几何问题的转化,打开了数学发展的新局面,创立了新分支——解析几何.我们知道,方程1x =在一维空间中,表示一个点;在二维空间中,它表示一条直线,那么在三维空间中,它表示______,过点(1,1,2)-P 且法向量为(1,2,3)=v 的平面的方程是______. 【答案】 一个平面 2350x y z ++-=【分析】根据空间直角坐标系的特征判断即可,再由在空间直角坐标系中,若法向量为(),,n A B C =,且平面过点()000,,x y z ,那么平面方程为()()()0000A x x B y y C z z -+-+-=计算可得;【详解】解:依题意可得1x =在三维空间中,它表示一个平面,在这个平面上所有点的横坐标都为1, 过点(1,1,2)-P 且法向量为(1,2,3)=v 的平面的方程为()()()1121320x y z -+++-=,整理得2350x y z ++-=故答案为:一个平面;2350x y z ++-=五、解答题17.在①sin cos 6a C c A π⎛⎫=+ ⎪⎝⎭,②2c cos A =a cos B +b cos A ,③b 2+c 2=a 2+bc ,这三个条件中任选一个,补充在下面问题中,并解决该问题.问题:在△ABC 中,内角A ,B ,C 的对边分别是a ,b ,c ,若已知b =6,ABCS=______,求a 的值.【答案】选①:a =②:a =③:a =【分析】选条件①时,直接利用正弦定理和三角函数的关系式的变换及三角形的面积公式和余弦定理,求出a 的值;选条件②时,直接利用三角函数的关系式的变换及三角形的面积公式和余弦定理,求出a 的值; 选条件③时,直接利用余弦定理及三角形的面积公式,求出结果. 【详解】若选①:因为πsin cos 6a C c A ⎛⎫=+ ⎪⎝⎭,所以πsin sin sin cos 6A C C A ⎛⎫=+ ⎪⎝⎭,因为0<C <π,所以sin C ≠0所以1sin cos sin 62A A A A π⎛⎫=+=- ⎪⎝⎭,即3sin 2A A =,所以tan A = 因为0<A <π,所以π6A =.所以1113sin 62222ABCSbc A c c ==⨯⨯==所以c =,由余弦定理有(222222cos 62612a b c bc A =+-=+-⨯⨯=,所以a =若选②:因为2c cos A =a cos B +b cos A , 所以2sin C cos A =sin A cos B +sin B cos A ,所以2sin C cos A =sin (A +B )=sin (π-C )=sin C 因为0<C <π,所以sin C ≠0,所以1cos 2A =, 因为0<A <π,所以3A π=,所以11sin 622ABCSbc A c ==⨯== 所以c =2,由余弦定理有2222212cos 62262282a b c bc A =+-=+-⨯⨯⨯=,所以a =若选③:因为b 2+c 2=a 2+bc ,所以b 2+c 2-a 2=bc ,所以2221cos 22b c a A bc +-==, 因为0<A <π,所以π3A =,所以11sin 622ABCSbc A c ==⨯== 所以c =2,由余弦定理有2222212cos 62262282a b c bc A =+-=+-⨯⨯⨯=,所以a =故答案为:18.在平面直角坐标系xOy 中,已知点Q0),直线l :x =P 满足到点Q 的距离与到直线l . (1)求动点P 的轨迹C 的方程;(2)若直线m :x -y -1=0与曲线C 交于A ,B 两点,求|AB |.【答案】(1)22163x y +=【分析】(1)设P 的坐标,由题意可得P 的横纵坐标的关系,进而求出P 的轨迹方程. (2)联立直线与曲线方程,写出韦达定理,利用弦长公式计算即可 可求弦|AB |的长.【详解】(1)设P (x ,y ),由题意可得222(3)232x y x -+=-, 整理可得:22163x y +=;所以P 的轨迹C 的方程为:22163x y +=.(2)设直线m :x -y -1=0与曲线C 交于A (x 1,y 1),B (x 2,y 2),由2216310x y x y ⎧+=⎪⎨⎪--=⎩,消去y 得x 2+2(x -1)2=6,整理得3x 2-4x -4=0, 由()Δ163440=-⨯-⨯>所以x 1+x 2=43,x 1x 2=43-,,所以()()221212(1)4AB k x x x x ⎡⎤=++-⎣⎦.224482(11)4333⎡⎤⎛⎫⎛⎫=+--=⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦19.如图,正方形ABCD 的中心为O ,四边形OBEF 为矩形,平面OBEF ⊥ 平面ABCD ,点G 为AB 的中点,2AB BE == .(1)求证:EG ∥ 平面ADF ; (2)求点D 到直线EG 的距离. 【答案】(1)证明见解析; 230【分析】(1)取AD 的中点M ,连接MG OD FM G ,,, 为线段AB 的中点,根据三角形的中位线定理、矩形的性质、平行四边形的判断定理、线面平行的判定定理即可证明结论.(2)连接ED ,根据面面垂直的性质定理可得EB ⊥平面ABCD ,建立空间直角坐标系,求得直线EG 的单位方向向量EGe EG=,可得点D 到直线EG 的距离22()d ED ED e =-⋅.【详解】(1)证明:取AD 的中点M ,连接,,MG OD FM ,正方形ABCD 的中心为O ,则,,B O D 共线,又G 为线段AB 的中点,则MG BD MG OB =∥, ,∵四边形OBEF 为矩形,则,,EF OB EF OB EF MG EF MG =∴=∥,∥ , ∴四边形EFMG 为平行四边形,∴EG FM ∥ ,而FM ⊂平面AFD ,而EG ⊄平面AFD , ∴EG ∥平面AFD . (2)连接ED ,∵四边形OBEF 为矩形,则EB BO ⊥,平面OBEF ⊥平面ABCD , 平面OBEF平面ABCD BO =,EB ⊂平面OBEF ,∴EB ⊥平面ABCD ,故以B 为坐标原点,以,,BC BA BE 为,,x y z 轴, 建立如图所示的空间直角坐标系B xyz - ,则()()()2,2,0,0,1,0,0,0,2D G E ,()2,2,2ED =-,0,1,2)EG -=(,直线EG 的单位方向向量150,1,2)EG e EG-==, ∴65EG ED e ED EG⋅=⋅=∴点D 到直线EG 的距离2236230()125d ED ED e =-⋅=-=20.已知函数()23sin 3cos 2f x x x x =+.(1)求()f x 的单调递减区间;(2)0,2x π⎛⎫∀∈ ⎪⎝⎭,cos 03a x f x π⎛⎫+-> ⎪⎝⎭,求a 的取值范围.【答案】(1),36k k ππππ⎡⎤-+⎢⎥⎣⎦(Z k ∈);(2)()22,-+∞.【分析】(1)先通过降幂公式和辅助角公式将函数化简,进而求出单调递减区间; (2)先用诱导公式将函数化简,进而进行换元,然后通过参变分离解得答案. 【详解】(1)()23sin 3sin cos 2f x x x x =-+1133cos 2sin 22222x x =--+ sin 226x π⎛⎫=-++ ⎪⎝⎭.令222262k x k πππππ-+≤+≤+,Z k ∈,解得36k x k ππππ-+≤≤+,Z k ∈.故()f x 的单调递减区间是,36k k ππππ⎡⎤-+⎢⎥⎣⎦(Z k ∈).(2)()sin 226f x x π⎛⎫=-++ ⎪⎝⎭,2sin 22cos 222cos 132f x x x x ππ⎛⎫⎛⎫-=--+=+=+ ⎪ ⎪⎝⎭⎝⎭,则2cos cos 2cos 103a x f x a x x π⎛⎫+-=++> ⎪⎝⎭.令cos t x =,0,2x π⎛⎫∈ ⎪⎝⎭,则01t <<,即2210at t ++>,可得12a t t ⎛⎫>-+ ⎪⎝⎭.因为1122222t t t t +≥⋅=,当且仅当12t t =,即22t =,4x π=时取等号,所以1222t t ⎛⎫-+≤- ⎪⎝⎭.故22a >-,即a 的取值范围是()22,-+∞.21.如图所示,正方形ABCD 所在平面与梯形ABMN 所在平面垂直,//MB AN ,2NA AB ==,4BM =,23CN =.(1)证明:MB ⊥平面ABCD ;(2)在线段CM (不含端点)上是否存在一点E ,使得二面角E BN M --的余弦值为33,若存在求出的CEEM值,若不存在请说明理由. 【答案】(1)证明见解析. (2)存在;12CE EM =.【分析】(1)由面面垂直的性质可得BC BM ⊥,再得出BM AB ⊥即可证明;(2)设CE CM λ=,求出平面BEN 和平面BMN 的法向量,利用向量关系建立方程求出λ即可得出. 【详解】(1)正方形ABCD 中,BC AB ⊥,平面ABCD ⊥平面ABMN ,平面ABCD ⋂平面ABMN AB =,BC ⊂平面ABCD ,BC ∴⊥平面ABMN ,BC ∴⊥BM ,且BC BN ⊥,又2,23BC CN ==,2222BN CN BC ∴=-=,又2AB AN ==,222BN AB AN ∴=+AN AB ∴⊥,又//AN BM ,BM AB ∴⊥,BCBA B =,∴BM ⊥平面ABCD ;(2)由(1)知,BM ⊥平面ABCD ,BM AB ⊥以B 为坐标原点,,,BA BM BC 所在直线分别为,,x y z 轴建立空间直角坐标系, 则()()()0,0,0,2,0,0,0,0,2B A C ,()()()2,0,2,2,2,0,0,4,0D N M , 设点(),,E x y z ,CE CM λ=,()(),,20,4,2x y z λ∴-=-,()04,0,4,2222x y E z λλλλ=⎧⎪∴=∴-⎨⎪=-⎩, ()()2,2,0,0,4,22BN BE λλ∴==-,设平面BEN 的法向量为(),,m x y z =,()2204220BN m x y BE m y z λλ⎧⋅=+=⎪∴⎨⋅=+-=⎪⎩,令221,1,,1,1,11x y z m λλλλ⎛⎫=∴=-=∴=- ⎪--⎝⎭, 显然,平面BMN 的法向量为()0,0,2BC =,cos ,2BC m BC m BC m⋅∴<>===⋅== 即23210λλ+-=,解得13λ=或1-(舍),则存在一点E ,且12CE EM =. 22.在平面直角坐标系中,已知椭圆C :()222210x y a b a b+=>>的左右焦点分别为1F ,2F ,点P 为椭圆C 上的动点,△12F PF 3450x y -+=相切.(1)求精圆C 的方程;(2)若直线l 过定点()1,0且与椭圆C 交于不同的两点A ,B ,点M 是椭圆C 的右顶点,直线AM ,BM 分别与y 轴交于P ,Q 两点,试问:以线段PQ 为直径的圆是否过x 轴上的定点?若是,求出定点坐标;若不是,说明理由.【答案】(1)2214x y +=;(2)是,()T .【分析】(1)由题设可得c b ⋅=3450x y -+=的距离为b ,即可求椭圆参数,进而写出椭圆方程.(2)法一:讨论斜率的存在性分别研究定点,且斜率存在时设()1y k x =-、()11,A x y 、()22,B x y ,联立椭圆方程,应用韦达定理求12x x +、12x x ;法二:设1x my =+,联立椭圆方程应用韦达定理求12y y +、12y y ;(两种方法后续过程)求直线AM 、BM 方程进而确定P ,Q 坐标,设定点N 坐标,则有0PN QN ⋅=,利用向量数量积的坐标表示列方程求N 坐标即可;【详解】(1)由△12F PF3450x y -+=相切.∴121221PF F S c b b ⎧=⋅⋅=⎪⎪⎨⎪==⎪⎩,解得1b =,c =2a =,则椭圆C 的方程是2214x y +=.(2)以线段PQ 为直径的圆过x 轴上的定点.法一:当直线l 斜率不存在时,以PQ 为直径的圆的方程为:223x y +=,恒过定点30,.当直线l 斜率存在时,设()1y k x =-,()0k ≠. 由()22114y k x x y ⎧=-⎪⎨+=⎪⎩得:()2222148440k x k x k +-+-=. 设()11,A x y ,()22,B x y ,则有2122814k x x k +=+,21224414k x x k -=+. 又M 是椭圆C 的右顶点,则()2,0M . 由题意知:直线AM 为()1122y y x x =--,故11(0,2)2y x P --. 直线BM 为:()2222y y x x =--,故2220,2y Q x ⎛⎫- ⎪-⎝⎭. 若以PQ 为直径的圆过x 轴上的定点()0,0N x ,则等价于0PN QN ⋅=恒成立.又1012,2y PN x x ⎛⎫= ⎪-⎝⎭,2022,2y QN x x ⎛⎫= ⎪-⎝⎭,∴21201222022y y PN QN x x x ⋅=+⋅=--恒成立. 又()()()2221212122224484222424141414k k k x x x x x x k k k ---=-++=-⨯+=+++ ()()()222221212121222244831111141414k k k y y k x k x k x x x x k k k k ⎛⎫--=--=-++=-+= ⎪+++⎝⎭. ∴()()22222120002122124143042214k y y k x x x k x x k -++=+=-=--+,解得0x =故以PQ 为直径的圆过x 轴上的定点30,.法二:设1x my =+,代入2214x y +=得()224230m y my ++-=.12224m y y m +=-+,12234y y m =-+直线AM :()1122y y x x =--,令0x =得11112221y y y x my --==+-,即1120,1y P my ⎛⎫- ⎪-⎝⎭,同理得2220,1y Q my ⎛⎫- ⎪-⎝⎭ 设以线段PQ 为直径的圆过x 轴上的定点(),0T t ,有PT QT ⊥,即0PT QT ⋅=,则()21221212401y y t m y y m y y +=-++,将12y y +、12y y 代入得230t,t =()T .【点睛】关键点点睛:第二问,设直线及交点坐标,联立椭圆方程并整理,应用韦达定理求12x x +、12x x 或12y y +、12y y ,再根据已知确定P ,Q 坐标,并设N 坐标易知0PN QN ⋅=,利用向量数量积坐标公式求N 坐标即可.。
福建师大附中2022-2022学年高二数学第一学期期中(模块)考试卷【名校特供】

福建师大附中2021-2021学年第一学期高二数学模块考试卷必修5(理科)〔总分值:150分,时间:120分钟〕说明:试卷分第I 卷和第II 卷两局部,请将答案填写在答卷上,考试结束后只交答案卷.第I 卷 共100分一、选择题:〔每题5分,共50分,在每题给出的四个选项中,只有一项符合要求〕1、设2(2),(1)(3),M a a N a a =-=+-那么有〔 **** 〕A .M N >B .M N ≥ 〔等号定能取到〕C .M N <D .M N ≤ 〔等号定能取到〕2、在等差数列}{n a 中,69327a a a -=+,n S 表示数列}{n a 的前n 项和,那么=11S ( **** )A .18B .99C .198D .2973、假设,,a b c 为实数,那么以下命题正确的选项是〔****〕A .假设a b >,那么22ac bc >B .假设0a b <<,11a b<则 C .假设0a b <<,b a a b>则 D .假设0a b <<,那么22a ab b >> 4、以下函数中,最小值为4的是 〔**** 〕A . 4y x x =+ 〔3x ≥〕B . 4sin sin y x x=+ (0)x π<< C . e 4e x x y -=+ D .3log 4log 3x y x =+5、ABC ∆满足sin 2cos sin C B A =,那么ABC ∆的形状是〔 **** 〕 A .等腰三角形 B .直角三角形 C .等边三角形 D .等腰三角形或直角三角形6、记等比数列{}n a 的前n 项和为S n ,假设S 3=2,S 6=18,那么105S S 等于〔 **** 〕 A . 3- B . 5 C . -31 D .337、符合以下条件的三角形有且只有一个的是〔 **** 〕A . a=1,b=2 ,c=3B . a=1,b=2 ,∠A=30°C . a=1,b=2,∠A=100°D . b=c=1, ∠B=45°8、北京2021年第29届奥运会开幕式上举行升旗仪式,在坡度15°的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为,那么旗杆的高度为( **** )A .10米B .30米 C. D.9、假设不等式组0024x y y x y x s≥⎧⎪≥⎪⎨+≤⎪⎪+≤⎩表示的平面区域是一个三角形,那么s 的取值范围是 ( **** )A .0<s ≤2或s ≥4B .0<s ≤2C .2≤s ≤4D .s ≥410、如果数列{}n a 满足:121321,,,...,,...n n a a a a a a a ----是首项为1,公比为2的等比数列,那么n a 等于〔 **** 〕。
福建省福州市仓山区福建师范大学附属中学2020-2021学年高二数学上学期期末考试试题(含解析)

福建师大附中2020-2021学年上学期期末考试高二数学试卷第Ⅰ卷(选择题,共70分)一、单项选择题:每小题5分,共50分.在每小题给出的选项中,只有一个选项是正确的. 1.已知空间向量()1,2,31a λμ=+-,()6,2,0b λ=共线,则实数λ的值是( ) A. -3 B. 2C. -3或2D. 3或-2【答案】C 【解析】 【分析】由向量共线定理求解.【详解】由题意存在实数k ,使得a kb =,即(1,2,31)(6,2,0)k λμλ+-=,∴1622310k k λλμ+=⎧⎪=⎨⎪-=⎩,解得21213k λμ⎧⎪=⎪⎪=⎨⎪⎪=⎪⎩或31313k λμ⎧⎪=-⎪⎪=-⎨⎪⎪=⎪⎩.故选:C.【点睛】本题考查空间向量共线,掌握空间向量共线定理是解题基础. 2.设()f x 是可导函数,且()()000lim 2x f x f x x x∆→--∆=∆,则()0f x '=( )A. 2B. -1C. 1D. -2【答案】A 【解析】 【分析】根据导数的定义求解. 【详解】()()()0000000[()]lim lim ()2x x f x f x x f x x f x f x x x∆→∆→--∆+-∆-'===∆-∆. 故选:A.【点睛】本题考查导数的定义,()()0000()lim x f x x f x f x x∆→+∆-'=∆,注意极限中形式的一致性.3.正方体1111ABCD A B C D -中,M 是1DD 的中点,O 是底面ABCD 的中心,P 是棱11A B 上任意一点,则直线OP 与直线AM 所成的角是( ) A.4π B.3π C.2π D. 与P 点的位置有关 【答案】C 【解析】 【分析】建立空间直角坐标系,用向量法求解.【详解】如图,以1,,DA DC DD 为,,x y z 轴建立空间直角坐标系,设正方体棱长为2,则(2,0,0),(0,0,1),(1,1,0)A M O ,设(2,,2)P m , (2,0,1),(1,1,2)AM OP m =-=-,∴210(1)120AM OP m ⋅=-⨯+⨯-+⨯=,∴AM OP ⊥,即AM OP ⊥. ∴直线OP 与直线AM 所成的角为2π. 故选:C.【点睛】本题考查异面直线所成的角,解题关键是建立空间直角坐标系,用空间向量法求解.4.已知正四面体D ABC -的各棱长为1,点E 是AB 的中点,则EC AD ⋅的值为( ) A.14B. 14-C.3 D. 3-【答案】A 【解析】 【分析】把EC 表示为AC AE -,然后再求数量积.【详解】由题意,四面体D ABC -是正四面体,每个面都是正三角形, ∴EC AD ⋅()AC AE AD AC AD AE AD =-⋅=⋅-⋅1111cos601cos6024=⨯⨯︒-⨯⨯︒=. 故选:A.【点睛】本题考查向量的数量积,解题关键是把EC 表示为AC AE -,然后计算即可. 5.在长方体1111ABCD A B C D -中,2AB BC ==,11AA =,则1AB 与平面11ABC D 所成角的正弦值为( ) A.25B.25C.10 D.12【答案】B 【解析】 【分析】做出线面角,在直角三角形中解角的正弦值.【详解】做11B H BC ⊥于H 点,连接AH ,因为1AB CB ⊥面,1AB B H ∴⊥,又因为111,B H BC BC AB B ⊥⋂=,111B H ABC D ∴⊥面,根据线面角的定义得到1B AH ∠为所求角,在11BB C 中,1111,2,BB B C ==由等面积法得到1,5B H =15AB =,线面角的正弦值为:112.5HB AB = 故答案为B.【点睛】这个题目考查了空间中的直线和平面的位置关系,线面角的求法.求线面角,一是可以利用等体积计算出直线的端点到面的距离,除以线段长度就是线面角的正弦值;还可以建系,用空间向量的方法求直线的方向向量和面的法向量,再求线面角即可. 6.函数y =2x 2–e |x |在[–2,2]的图像大致为( )A. B. C. D.【答案】D 【解析】试题分析:函数f (x )=2x 2–e |x|在[–2,2]上是偶函数,其图象关于y 轴对称,因为22(2)8,081f e e =-<-<,所以排除,A B 选项;当[]0,2x ∈时,4x y x e '=-有一零点,设为0x ,当0(0,)x x ∈时,()f x 为减函数,当0(,2)x x ∈时,()f x 为增函数.故选D7.若函数()()sin xf x e x a =+在[]0,π上单调递增,则实数a 的取值范围是( )A. ()2,+∞B. ()1,+∞C. )2,⎡-+∞⎣D. [)1,+∞ 【答案】D 【解析】 分析】()0f x '≥在[]0,π恒成立,再转化为求函数最值.【详解】()(sin cos ))]4x xf x e x a x e x a π'=++=++,由题意)]04xe x a π++≥在[0,]x π∈恒成立,即)4a x π≥+在[0,]x π∈恒成立,[0,]x π∈时,5[,]444x πππ+∈,sin()[42x π+∈-,所以)14x π≤+≤,所以1a ≥. 故选:D.【点睛】本题考查用导数研究函数的单调性,函数在区间[]0,π上单调递增,转化为()f x '≥在区间[]0,π上恒成立,不等式恒成立又可转化为求函数最值.本题对学生的转化与化归能力有一定的要求.8.在空间直角坐标系O xyz -中,四面体ABCD 的顶点坐标分别是()0,0,2A ,()2,2,0B ,()1,2,1C ,()2,2,2D .则点B 到面ACD 的距离是( )A.3B.3C.3D.3【答案】A 【解析】 【分析】求出平面ACD 的一个法向量n ,再求出BD 在n 方向上的投影的绝对值即可. 【详解】由题意(2,2,0),(1,0,1),(0,0,2)AD CD BD ===, 设平面ACD 的一个法向量为(,,)n x y z =,则220n AD x y n CD x z ⎧⋅=+=⎨⋅=+=⎩,取1x =,则(1,1,1)n =--,∴233BD n n⋅-==,即B 到平面ACD故选:A.【点睛】本题考查用空间向量法求点到平面的距离.设n 是平面α的一个法向量,Q 是平面α内任一点,则P 到平面α的距离是PQ n n⋅.9.已知函数()22,02,0x x x a x f x ae x a x ⎧++<=⎨--≥⎩恰有两个零点,则实数a 的取值范围是( )A. (][),01,-∞⋃+∞B. (](),01,-∞+∞C. (]{},01-∞D. (],0-∞【答案】C 【解析】 【分析】分别讨论0x <时,2()2f x x x a =++的零点个数,0x ≥时,()2xf x ae x a =--的零点个数,综合后可得结论.【详解】0x ≥时,()2xf x ae x a =--,()1x f x ae '=-, (0)f a =-,当0a ≤,()0f x '≤,()f x 递减,(0)0f a =-≥,(ln 2)ln 20f =-<,因此()f x 在[0,)+∞上有且只有一个零点.当1a ≥时,()0f x '≥,()f x 递增,(0)0f a =-<,(ln 4)2ln 40f a =->,因此在()f x 在[0,)+∞上有且只有一个零点,01a <<时,,1()1()x xf x ae a e a '=-=-,1(ln )0f a '=,1[0,ln )x a∈时,()f x 递减,1(ln ,)x a ∈+∞时,()f x 递增,(0)0f a =-<, x →+∞时,2x ae x a --→+∞,()f x 在[0,)+∞上有一个零点,∴a R ∈,()f x 在[0,)+∞上有一个零点,0x <时,22()2(1)1f x x x a x a =++=++-,若0a ≤或1a =,()f x 有一个零点,若1a >,()f x 无零点,若01a <<,()f x 有两个零点. 因此满足题意的a 的取值范围是 (,0]{1}-∞ 故选:C.【点睛】本题考查函数的零点个数,对分段函数来讲要分段讨论,对于复杂的函数一般可通过导数研究函数的单调性与最值,结合零点存在定理确定零点个数. 10.已知()f x 是定义在,00,22ππ⎛⎫⎛⎫-⋃ ⎪ ⎪⎝⎭⎝⎭上的偶函数,且当02x π<<时,有()()'cos sin 0f x x f x x +>,则不等式()2cos 3f x f x π⎛⎫< ⎪⎝⎭的解集为( )A. ,0,233πππ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭B. ,0,332πππ⎛⎫⎛⎫-⋃ ⎪ ⎪⎝⎭⎝⎭C. ,00,33ππ⎛⎫⎛⎫-⎪ ⎪⎝⎭⎝⎭D. ,32ππ⎛⎫ ⎪⎝⎭【答案】C 【解析】 【分析】构造新函数()()cos f x g x x =,确定它的单调性后结合偶函数性质可解题中不等式. 【详解】设()()cos f x g x x =,则2()cos ()sin ()cos f x x f x xg x x'+'=,∵当02x π<<时,有()()'cos sin 0f x x f x x +>,∴()0g x '>,∴()g x 在(0,)2π上单调递增.又()f x 是定义在,00,22ππ⎛⎫⎛⎫-⋃ ⎪ ⎪⎝⎭⎝⎭上的偶函数,∴()g x 也是定义在,00,22ππ⎛⎫⎛⎫-⋃ ⎪ ⎪⎝⎭⎝⎭上的偶函数(因为()()()()cos()cos f x f x g x g x x x--===-),不等式()2cos 3f x f x π⎛⎫< ⎪⎝⎭可化为()()3cos cos 3f f x x ππ<,即()()3g x g π<,()()3g x g π< ∴03x π<<,03x π-<<或03x π<<. 故选:C.【点睛】本题考查用导数解不等式,解题关键是构造新函数()()cos f x g x x=,确定它的奇偶性和单调性.二、多项选择题:每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.11.定义在R上的可导函数()y f x=的导函数的图象如图所示,以下结论正确的是()A. -3是()f x的一个极小值点;B. -2和-1都是()f x的极大值点;C. ()f x的单调递增区间是()3,-+∞;D. ()f x的单调递减区间是(),3-∞-.【答案】ACD 【解析】【分析】由导函数与单调性、极值的关系判断.【详解】当3x<-时,()0f x'<,(3,)x∈-+∞时()0f x'≥,∴3-是极小值点,无极大值点,增区间是()3,-+∞,减区间是(),3-∞-.故选:ACD.【点睛】本题考查导数与函数单调性、极值的关系,一定要注意极值点两侧导数的符号相反.12.定义在R的函数()f x,已知()00x x≠是它的极大值点,则以下结论正确的是()A. 0x-是()f x-的一个极大值点B. 0x-是()f x-的一个极小值点C.x是()f x-的一个极大值点D. 0x-是()f x--的一个极小值点【答案】AD【解析】【分析】由()f x '确定()f x -的导数的性质,从而可确定()f x -的性质.再根据()y f x =-与()y f x =的图象关于x 轴对称作答.【详解】()000x x ≠是()f x 的极大值点,就是存在正数m ,使得在00(,)x m x -上,()0f x '>,在00(,)x x m +上,()0f x '<. 设()()g x f x =-,()()g x f x ''=--,当00x x x m -<<-+时,00x m x x -<-<,()0f x '->,()0g x '<,同理00x m x x --<<-时,()0g x '>,∴0x -是()f x -的一个极大值点,从而0x -是()f x --的一个极小值点,0x 是()f x -的一个极小值点.不能判定0x -是不是()f x -的极值点. 故选:AD.【点睛】本题考查导数与函数单调性、极值的关系,一定要注意极值点两侧导数的符号相反. 13.设()30,x ax b a b R ++=∈,下列条件中,使得该三次方程仅有一个实根的是( )A. 3a =-,2b =B. 3a =-,3b =-C. 3a =-,2b >D. 1a =,2b =【答案】BCD 【解析】 【分析】把各选项代入函数式检验,能求出实根的解出实根,不能求出实根的用函数的性质判断. 详解】记3()f x x ax b =++,3a =-,2b =时,32()32(1)(2)0f x x x x x =-+=-+=,1x =或2x =-,不满足题意;3a =-,3b =-时,3()33f x x x =--,2()333(1)(1)f x x x x '=-=+-,()f x 在(,1)-∞-和(1,)+∞是递增,在(1,1)-上递减,而()(1)10f x f =-=-<极大值,()f x 只有一个零点,即()0f x =只有一个实根,同理3a =-,2b >时,()f x 在(,1)-∞-和(1,)+∞是递增,在(1,1)-上递减,而()(1)20f x f b ==->极小值,()f x 只有一个零点,即()0f x =只有一个实根,1a =,2b =时,32()2(1)(2)0f x x x x x x =++=+-+=,只有一个实根1-,故选:BCD.【点睛】本题考查方程实根个数问题,对于方程根无法解出的情况可以通过研究函数的极值与单调性确定函数零点即方程根的个数.14.如图,矩形ABCD 中,22AB AD ==,E 为边AB 的中点.将ADE ∆沿直线DE 翻折成1A DE ∆(点1A 不落在底面BCDE 内).若M 为线段1A C 的中点,则在ADE ∆翻转过程中,以下命题正确的是( )A. 四棱锥1A BCDE -体积最大值为24B. 线段BM 长度是定值;C. //MB 平面1A DE 一定成立;D. 存在某个位置,使1DE A C ⊥; 【答案】ABC 【解析】 【分析】平面1A DE ⊥平面BCDE 时,1A 到平面BCDE 的距离最大,求出这个最大值,即能求出最大体积知A 是否正确,取CD 中点N ,连接,MN BN ,可得145MNB A DE ∠=∠=︒,平面//BMN 平面1A DE ,从而可得B 、C 是否正确,对D ,假设有1DE A C ⊥,推导出矛盾结论,说明D 错误.【详解】ADE ∆是等腰直角三角形,A 到DE 的距离是22,当平面1A DE ⊥平面BCDE 时,1A 到平面BCDE 的距离最大为22,又13211122BCDE S =⨯-⨯⨯=,∴132232V =⨯⨯=最大.A 正确; 取CD 中点N ,连接,MN BN ,∵M 是1A C 的中点,∴1//MN A D ,而MN ⊄平面1A DE ,DE ⊂平面1A DE ,∴//MN 平面1A DE ,由DN 与EB 平行且相等得DNBE 是平行四边形,//BN DE ,同理得//BN 平面1A DE , 而BN MN N ⋂=,∴平面//BMN 平面1A DE ,BM ⊂平面BMN ,∴//MB 平面1A DE ,C 正确,在上述过程中得145MNB A DE ∠=∠=︒,又1112,22BN DE MN A D ====,∴22115(2)()22cos 45222BM =+-⨯⨯︒=为定值,B 正确;假设存在某个位置,使1DE A C ⊥,取DE 中点O ,连接1,A O CO ,显然1AO DE ⊥,而111A OA C A =,∴DE ⊥平面1A OC ,OC ⊂平面1A OC ,∴ DE OC ⊥,则CE CD =,但2CE =2CD =,不可能相等,所以不可能有1DE A C ⊥.D 错. 故选:ABC.【点睛】本题考查空间折叠问题,考查空间线面的位置关系,解题时对体积,平行、垂直都要有充分的认识.对一个命题说明它为假时可以通过反证法证明.第Ⅱ卷(非选择题,共80分)三、填空题:每小题5分,共20分.15.已知函数()()2'35f x f x x =+,则()'1f =______.【答案】3 【解析】 【分析】先求出导函数()f x ',令3x =,求出(3)f '后再求'(1)f .【详解】由题意()2(3)5f x f x ''=+,(3)2(3)35f f ''=⨯+,(3)1f '=-,即()25f x x '=-+, ∴(1)253f '=-+=. 故答案为:3.【点睛】本题考查导数的运算,属于基础题. 16.过原点与曲线2xy e =相切的直线方程为______. 【答案】2y ex = 【解析】 【分析】设切点坐标,写出切线方程,由切线过原点,再求出切点坐标,从而得切线方程 【详解】设切点为00(,)P x y ,由于2xy e '=,∴ 切线斜率为02x k e =, 切线方程为00022()x x y ee x x -=-,∵切线过原点,∴00022x x e x e -=-.01x =,所以切线方程为22(1)y e e x -=-,即2y ex =. 故答案为:2y ex =.【点睛】本题考查导数的几何意义.求过某点的切线,应先设切点坐标,由导数的几何意义写出切线方程,代入所过点的坐标求出切点坐标,从而得出切线方程.17.若函数()33=-f x x x 在区间()1,a a -上有最小值,则实数a 的取值范围是______.【答案】(1,0)- 【解析】 【分析】先求()f x 的极小值点,()f x 的极小值点在区间(1,)a a -上,由此可得a 的范围.【详解】2()333(1)(1)f x x x x '=-=--+,当1x <-或1x >时,()0f x '<,当11x -<<时,()0f x '>,∴1x =-是函数()f x 的极小值点.∵函数()33=-f x x x 在区间()1,a a -上有最小值,即为极小值.∴11a a -<-<,解得10a -<<. 故答案为:(1,0)-.【点睛】本题考查导数与最值的关系.连续函数在(,)a b 的最小值就是极小值,最大值就是极大值.但在[,]a b 是的最值不一定是极值.18.已知三棱锥的四个面都是腰长为2的等腰三角形,该三棱锥的正视图如图所示,则该三棱锥的体积是______,该几何体的外接球半径为______.【答案】 (1). 335【解析】 【分析】由正视图知三棱锥两个面垂直,如图平面ABD ⊥平面CBD ,H 是BD 中点,则1AH =,3BH DH ==ABD ∆和CBD ∆的外心,由三角形的外心找到三棱锥外接球球心.【详解】由正视图,知平面ABD ⊥平面CBD ,如图,H 是BD 中点,则1AH =为三棱锥A BCD -的高,3BH DH ==1CH AH ==,123132CBD S ∆=⨯=13313ABCD V ==分别延长,CH AH 至,M N ,使1HM HN ==,则可得,M N 分别是,ABD CBD ∆∆的外心,作OM ⊥平面ABD ,作ON ⊥平面CBD ,,OM ON 交于点O (这两条直线都在平面ACH 内,因此它们相交,也可作//,//OM CH ON AH 得结论),则O 为三棱锥A BCD -外接球球心.OMHN 是正方形,1OM HN ==,2222215OA AM OM =+=+=.35 【点睛】本题考查三视图,考查棱锥的体积及棱锥的外接球.解题关键是由正视图得出三棱锥中的线面间的位置关系及线段长度.难点是寻找外接球球心.掌握如下结论就容易找到球心:多面体的外接球球心一定在过各面外心且与此面垂直的直线上. 四、解答题:5小题,共60分.解答应写出文字说明、证明过程或演算步骤. 19.已知函数()2f x ax blnx =+在1x =处有极值12. (1)求a,b 的值; (2)求()f x 的单调区间.【答案】(1)12a =,1b =-.(2) 单调减区间是()0,1,单调增区间是()1,+∞. 【解析】 【分析】(1)先对函数求导,得到()2bf x ax x'=+,再由题意,列出方程组,求解,即可得出结果; (2)由(1)的结果,得到()212f x x lnx =-,对其求导,解对应的不等式,即可得出单调区间.【详解】解:(1)()'2.b f x ax x =+又()f x 在1x =处有极值12,()()112'10ff⎧=⎪∴⎨⎪=⎩即1220aa b⎧=⎪⎨⎪+=⎩解得12a=,1b=-.(2)由(1)可知()212f x x lnx=-,其定义域是()0,∞+,()()()111'x xf x xx x+-=-=.由()'0f x<,得01x<<;由()'0f x>,得1x>.∴函数()y f x=的单调减区间是()0,1,单调增区间是()1,+∞.【点睛】本题主要考查由函数极值求参数,以及导数的方法求单调区间的问题,通常需要对函数求导,利用导数的方法求解即可,属于常考题型.20.如图,三棱柱ADE BCG-中,四边形ABCD是矩形,F是EG的中点,EA AB⊥,1AD AE EF===,平面ABGE⊥平面ABCD.(1)求证:AF⊥平面FBC;(2)求锐二面角B FC D--的平面角的大小.【答案】(1)见解析(2)3π【解析】【分析】(1)先由已知面面垂直证明BC⊥平面ABGE,得BC AF⊥,再在矩形ABGE中由勾股定理逆定理证明AF BF⊥,从而可得线面垂直;(2)由(1)知AD,AB,AE两两垂直,以它们为坐标轴建立空间直角坐标系,写出各点坐标,求出平面的法向量,用向量法求二面角.【详解】解:(1)证明:∵平面ABGE⊥平面ABCD,平面ABGE平面ABCD AB=,又由四边形ABCD是矩形知,BC AB⊥,BC⊂平面ABCD,∴BC⊥平面ABGE,∵AF ⊂平面ABGE , ∴BC AF ⊥.在AFB ∆中,2AF BF ==,2AB =,∴222AF BF AB +=,即AF BF ⊥,又BF BC B ⋂=, ∴AF ⊥平面FBC .(2)由(1)知AD ,AB ,AE 两两垂直,分别以AD ,AB ,AE 所在直线为x 轴,y 轴,z 轴建立空间直角坐标系,则()0,0,0A ,()1,0,0D ,()1,2,0C,()0,0,1E ,()0,2,0B ,()0,1,1F ,∴()1,0,1DE =-,()0,2,0DC =,设()1,,n x y z =为平面CDEF 的法向量,则1100n DC n DE ⎧⋅=⎪⎨⋅=⎪⎩,即200y x z =⎧⎨-+=⎩,令1x =,得1z =,即()11,0,1n =,取()20,1,1n AF ==为平面BCF 的一个法向量, ∴1212121cos ,2n n n n n n ⋅==, ∴锐二面角B FC D --的平面角的大小是3π.【点睛】本题考查线面垂直的证明,考查向量法求二面角.掌握证明线面垂直的判定定理及面面垂直的性质定理是解答本题的关键.在求空间角时,一般都是建立空间直角坐标系,用空间向量法求角.21.如图,有一块半径为20米,圆心角23AOB π∠=的扇形展示台,展示台分成了四个区域:三角形OCD ,弓形CMD ,扇形AOC 和扇形BOD (其中AOC BOD ∠=∠).某次菊花展依次在这四个区域摆放:泥金香、紫龙卧雪、朱砂红霜、朱砂红霜.预计这三种菊花展示带来的日效益分别是:泥金香50元/米2,紫龙卧雪30元/米2,朱砂红霜40元/米2.(1)设COD θ∠=,试建立日效益总量y 关于θ的函数关系式; (2)试探求θ为何值时,日效益总量达到最大值. 【答案】(1)y 160004000sin 20003πθθ=+⋅-,其中,203πθ<<.(2)当3πθ=时,日效益总量可取得最大值. 【解析】 【分析】(1)利用扇形面积公式可求出四个区域的面积,从而可计算出日收益. (2)利用导数可求得日收益的最大值.【详解】(1)依题意得,23232AOC πθπθ-∠==-,则22112040220sin 502322y πθθ⎛⎫=⋅-⋅⋅+⋅⋅⋅ ⎪⎝⎭22112020sin 3022θθ⎛⎫+⋅⋅-⋅⋅⋅ ⎪⎝⎭1600010000sin 60006000sin 32πθθθθ⎛⎫=⋅-+⋅+- ⎪⎝⎭160004000sin 20003πθθ=+⋅-,其中,203πθ<<. (2)'4000cos 2000y θ=⋅-, 令'0y =,得3πθ=,当π0θ3,'0y >,当233ππθ<<时,'0y <,所以,3πθ=是函数的极大值点,且唯一;从而当3πθ=时,日效益总量可取得最大值.【点睛】本题考查三角函数模型的应用,考查导数在实际问题中的应用.解题关键是根据题意列式,求出函数表达式,然后再利用导数知识可求得最大值.22.在如图所示的六面体中,面ABCD 是边长为2的正方形,面ABEF 是直角梯形,90FAB ∠=,//AF BE ,24BE AF ==.(Ⅰ)求证:AC //平面DEF ;(Ⅱ)若二面角E AB D --为60,求直线CE 和平面DEF 所成角的正弦值.【答案】(1)证明见解析. 7. 【解析】试题分析:(1)连接,AC BD 相交于点O ,取DE 的中点为G ,连接,FG OG ,易证四边形AOGF 是平行四边形,从而可得结论;(2)以C 为坐标原点,CB 为x 轴、CD 为y 轴、CE 为z 轴建立空间直角坐标系.则()()((0,0.0,0,2,0,3,3C D E F ,计算法向量,根据公式sin cos ,CE n θ=即可求出. 试题解析:(1):连接,AC BD 相交于点O ,取DE 的中点为G ,连接,FG OG .ABCD 是正方形,O ∴是BD 的中点,1,2OG BE OG BE ∴=, 又因为1//,2AF BE AF BE =,所以OG AF 且OG AF =, 所以四边形AOGF 是平行四边形,//AC FG ∴,又因为FG ⊂平面,DEF AC ⊄平面DEF AC//∴平面DEF(2)ABCD ∴是正方形,ABEF 是直角梯形,FAB 90∠=︒,DA AB,FA AB ∴⊥⊥4AD AF ∴⋂=,AB ⊥平面AFD ,同理可得AB ⊥平面EBC .又AB ⊂平面ABCD ,所以平面AFD ⊥平面ABCD,又因为二面角E AB D --为60°,所以60,2 4.2FAD EBC BE AF BC ∠=∠=︒===,由余弦定理得EC 23=, 所以EC BC ⊥,因为AB ⊥半面EBC ,EC AB ∴⊥,所以EC ⊥平面ABCD ,以C 为坐标原点,CB 为x 轴、CD 为y 轴、CE 为z 轴建立空间直角坐标系. 则()()()()0,0.0,0,2,0,0,0,23,1,2,3C D E F , 所以()()()0,0,23,1,0,3,1,2,3CE DF F ==,设平面DEF 的一个法向量为(),,n x y z =,则00n DF n EF ⎧⋅=⎪⎨=⎪⎩即30230x z x y z ⎧+=⎪⎨+-=⎪⎩令3z =,则33x y =-⎧⎨=⎩,所以()3,3,3n =-设直线CE 和平面DEF 所成角为θ, 则7sin cos ,2321CE n θ===⨯23.已知函数()()1ln 1f x a x =+,()32g x x x =-+.(1)当1a =时,试讨论方程()()21f x k k R =-∈的解的个数;(2)若曲线()()211y f x e x e =-<<-和()()0y g x x =<上分别存在点A ,B ,使得AOB ∆是以原点O 为直角顶点的直角三角形,且斜边AB 的中点在y 轴上,求实数a 的取值范围.【答案】(1)见解析(2)2 ,2ee⎛⎫⎪⎝⎭【解析】【分析】(1)求出导函数()f x',由导函数确定函数的单调性,作出函数的大致图象,通过图象确定方程()()21f x k k R=-∈解的个数;(2)设()11,A x y,()22,B x y,由1202x x+=,21x x=-,32211y x x=+,题意说明1212OA OB x x y y⋅=+=,代入得()()()32111111ln1x x x xa x-+⋅+=+,化简后有()11110ln1xa x+-=+,从而()111ln1xax+=+,只要求得()()1ln1xh xx+=+(211e x e-<<-)的值域即得a的范围.【详解】(1)当1a=,()()1ln1f xx=+,()()()()()221111ln1ln'1x xxx xf--++==++;又()f x的定义域为()()1,00,-+∞;当1x>-时,()'0f x<恒成立.所以,()f x在()1,0-上单调递减,在()0,∞+也单调递减,图象如图所示.因此,当210k-=即1k=±时,方程无解;当210k-≠即1k≠±时,方程有唯一解.(2)设()11,A x y ,()()1111ln 1f x a y x ==+,()22,B x y ,()()3222220y g x x x x ==-+<, 则1202x x +=,21x x =-,∴32211y x x =+. ()11,OA x y =,()22,OB x y =,由题意,12120OA OB x x y y ⋅=+=,即()()()321111110ln 1x x x x a x -+⋅+=+, ∴()2111110ln 1x x a x ⎡⎤+-+=⎢⎥+⎣⎦, ∵2111e x e -<<-,∴()11110ln 1x a x +-=+, 则()111ln 1x a x +=+. 设()()1ln 1x h x x +=+,则()()()2ln 11'ln 1x h x x +-=+, ∵211e x e -<<-,∴()'0h x >,即函数()()1ln 1x h x x +=+在()211e x e -<<-上为增函数, 则()()221111ln 11ln 11e e a e e -+-+<<-+-+, 即22e e a <<. ∴实数a 的取值范围是2,2e e ⎛⎫ ⎪⎝⎭. 【点睛】本题考查用导数研究方程根的个数,求函数值域问题.解题关键是问题的转化.方程根的个数可通过函数图象与直线的交点个数来研究,而题中第(2)个问题,通过,A B 两点的关系,转化为()()()321111110ln 1x x x x a x -+⋅+=+,即()11110ln 1x a x +-=+有解,然后再转化为求函数值域.本题对学生的转化与化归能力要求较高,对运算求解能力要求较高.。
2020-2021学年福建省福州教育学院第二附属中学高二上学期期中考试数学试题 word版

福建省福州教育学院第二附属中学2020-2021学年高二上学期期中考试数学试题一、选择题(本大题共11小题,共55)1. 若一组数据12345,,,,x x x x x 的平均数为5,方差为2,则12323,23,23x x x ---,4523,23x x --的平均数和方差分别为( )A. 7,-1B. 7,1C. 7,2D. 7,82. 质监部门对2辆新能源汽车和3辆燃油汽车进行质量检测,现任取2辆,则选中的2辆都为燃油汽车的概率为( ) A. 0.6B. 0.5C. 0.4D. 0.33. 某同学用如下方式估算圆周率,他向图中的正方形中随机撒豆子100次,其中落入正方形的内切圆内有68次,则他估算的圆周率约为( )A. 3.15B. 2.72C. 1.47D. 3.844. 命题“若21x ≤,则11x -≤≤”的逆否命题是( ) A. 若21x ≥,则1≥x ,或1x ≤- B. 若11x -<<,则21x < C. 若1≥x 或1x ≤-,则21x ≥D. 若1x >或1x <-,则21x > 5. 命题“若a b >,则a c b c +>+”的否命题为( ) A. 若a b <,则a c b c +<+ B. 若a b ≤,则a c b c +≤+ C. 若a c b c +<+,则a b <D. 若a c b c +≤+,则a b ≤6. 与双曲线22154x y -=3 )A. 22154x y +=B. 221123x y +=C. 221167x y +=D.221128x y += 7. 椭圆221259x y +=和椭圆221925x y k k+=--(09k <<)有( )A. 等长的长轴B. 相等的焦距C. 相等的离心率D. 等长的短轴8. 椭圆22217x y b+=,过原点O C ,D ,若||4CD =,则椭圆的标准方程为( )A. 22174x y +=B. 22173x y +=C. 22176x y +=D. 222177x y +=9. 已知椭圆E :221112x y +=与双曲线C :()222105x y a a -=>有相同的焦点,则双曲线C 的渐近线方程为( )A. 5y x =±B. 3y x =±C. 5y x =±D.y x =10. 设双曲线C :22221x y a b-=(a >0,b >0)的左、右焦点分别为F 1,F 2.P是C 上一点,且F 1P ⊥F 2P .若△PF 1F 2的面积为4,则a =( ) A. 1B. 2C. 4D. 811. 过抛物线y 2=4x 的焦点F 的直线交抛物线于A ,B 两点,若线段AB 的中点M 到y 轴的距离为2,则|AB |=( ) A. 8B. 6C. 5D. 4二、不定项选择题(本大题共1小题,共5)12. 已知抛物线2:2C y px =过点(1,1)P 则下列结论正确是( )A. 点P 到抛物线焦点的距离为32B. 过点P 作过抛物线焦点的直线交抛物线于点Q ,则△OPQ 的面积为532C. 过点P 与抛物线相切的直线方程为210x y -+=D. 过点P 作两条斜率互为相反数的直线交抛物线于M ,N 点则直线MN 的斜率为定值三、填空题(本大题共4小题,共20)13. 椭圆222120x y a +=的焦点在x 轴上,焦距为8,则该椭圆的离心率为_______.14. 已知不等式2121xx ->-的解集为A ,()22100x x m m ++-≤>的解集为B ,若“x A ∈”是“x B ∈”的充分不必要条件,那么实数m 的取值范围是________.15. 从0,2,4,6,8这5个数中任取两个数作差,则差值恰好为2的概率是______.16. 已知椭圆22:14x M y +=,直线l 与椭圆M 相交于,A B 两点,点1(1,)2D 是弦AB 的中点,则直线l 的方程为__________.四、解答题(本大题15小题,共70)17. 已知命题p :方程22112x y m m +=--表示焦点在x 轴上的双曲线;命题q :关于x 的不等式220x x m -+>的解集为R ;若“p q ∨”是真命题,求实数m 的取值范围.18. 已知椭圆()222210x y C a b a b +=>>:3()2,0A 是椭圆的右顶点.(1)求椭圆的方程;(2)过点()1,0G 且斜率为12的直线l 与曲线C 相交于不同的两点M ,N ,求AMN 的面积.19. 双曲线C :2213y x -=,过点()2,1P ,作一直线交双曲线于A 、B 两点,若P 为AB 的中点. (1)求直线AB方程;(2)求弦AB 的长20. 已知抛物线22(0)x py p =>与直线3210x y -+=交于,A B 两点,5138AB =,点M 在抛物线上,MA MB ⊥.(Ⅰ) 求p 的值; (Ⅱ) 求点M 的坐标.21. 2020年5月28日,十三届全国人大三次会议表决通过了《中华人民共和国民法典》,此法典被称为“社会生活的百科全书”,是新中国第一部以法典命名的法律,在法律体系中居于基础性地位,也是市场经济的基本法.民法典与百姓生活密切相关,某大学为了解学生对民法典的认识程度,选取了120人进行测试,测试得分情况如图所示.(1)试求出图中实数a 的值,并求出成绩落在[]90,100的人数;(2)如果抽查的测试平均分超过75分,就表示该学校通过测试.试判断该校能否通过测试; (3)如果在[)80,90中抽取3人,在[]90,100中抽取2人,再从抽取的5人中选取2人进行民法典的宣传,那么选取的2人中恰好1人成绩落在[]90,100的概率是多少?福州教育学院第二附属中学20-21学年第一学期期中考高二数学试卷(答案)一、选择题(本大题共11小题,共55)1. 若一组数据12345,,,,x x x x x 的平均数为5,方差为2,则12323,23,23x x x ---,4523,23x x --的平均数和方差分别为( )A. 7,-1B. 7,1C. 7,2D. 7,8【答案】D2. 质监部门对2辆新能源汽车和3辆燃油汽车进行质量检测,现任取2辆,则选中的2辆都为燃油汽车的概率为( ) A. 0.6 B. 0.5C. 0.4D. 0.3【答案】D3. 某同学用如下方式估算圆周率,他向图中的正方形中随机撒豆子100次,其中落入正方形的内切圆内有68次,则他估算的圆周率约为( )A. 3.15B. 2.72C. 1.47D. 3.84【答案】B4. 命题“若21x ≤,则11x -≤≤”的逆否命题是( ) A. 若21x ≥,则1≥x ,或1x ≤- B. 若11x -<<,则21x < C. 若1≥x 或1x ≤-,则21x ≥ D. 若1x >或1x <-,则21x > 【答案】D5. 命题“若a b >,则a c b c +>+”的否命题为( ) A. 若a b <,则a c b c +<+ B. 若a b ≤,则a c b c +≤+ C. 若a c b c +<+,则a b < D. 若a c b c +≤+,则a b ≤【答案】B6. 与双曲线22154x y -=的焦点相同,且离心率为32的椭圆的标准方程为( )A. 22154x y +=B. 221123x y +=C. 221167x y +=D.221128x y += 【答案】B7. 椭圆221259x y +=和椭圆221925x y k k+=--(09k <<)有( )A. 等长的长轴B. 相等的焦距C. 相等的离心率D. 等长的短轴 【答案】B8. 椭圆22217x y b+=,过原点O C ,D ,若||4CD =,则椭圆的标准方程为( )A. 22174x y +=B. 22173x y +=C. 22176x y +=D. 222177x y +=【答案】D9. 已知椭圆E :221112x y +=与双曲线C :()222105x y a a -=>有相同的焦点,则双曲线C 的渐近线方程为( )A. y x =B. y x =C. y x =D.2y x =±【答案】D10. 设双曲线C :22221x y a b-=(a >0,b >0)的左、右焦点分别为F 1,F 2.P是C 上一点,且F 1P ⊥F 2P .若△PF 1F 2的面积为4,则a =( ) A. 1B. 2C. 4D. 8【答案】A11. 过抛物线y 2=4x 的焦点F 的直线交抛物线于A ,B 两点,若线段AB 的中点M 到y 轴的距离为2,则|AB |=( ) A. 8 B. 6C. 5D. 4【答案】B二、不定项选择题(本大题共1小题,共5)12. 已知抛物线2:2C y px =过点(1,1)P 则下列结论正确的是( ) A. 点P 到抛物线焦点的距离为32B. 过点P 作过抛物线焦点的直线交抛物线于点Q ,则△OPQ 的面积为532C. 过点P 与抛物线相切的直线方程为210x y -+=D. 过点P 作两条斜率互为相反数的直线交抛物线于M ,N 点则直线MN 的斜率为定值 【答案】BCD三、填空题(本大题共4小题,共20)13. 椭圆222120x y a +=的焦点在x 轴上,焦距为8,则该椭圆的离心率为_______.【答案】23. 14. 已知不等式2121xx ->-的解集为A ,()22100x x m m ++-≤>的解集为B ,若“x A ∈”是“x B ∈”的充分不必要条件,那么实数m 的取值范围是________. 【答案】[)4,+∞15. 从0,2,4,6,8这5个数中任取两个数作差,则差值恰好为2的概率是______. 【答案】15; 16. 已知椭圆22:14x M y +=,直线l 与椭圆M 相交于,A B 两点,点1(1,)2D 是弦AB 的中点,则直线l 的方程为__________. 【答案】220x y +-=四、解答题(本大题15小题,共70)17. 已知命题p :方程22112x y m m +=--表示焦点在x 轴上的双曲线;命题q :关于x 的不等式220x x m -+>的解集为R ;若“p q ∨”是真命题,求实数m 的取值范围. 【答案】1m18. 已知椭圆()222210x y C a b a b +=>>:的离心率为32,()2,0A 是椭圆的右顶点. (1)求椭圆的方程; (2)过点()1,0G 且斜率为12的直线l 与曲线C 相交于不同的两点M ,N ,求AMN 的面积.【答案】(1)2214x y +=;(2)74. 19. 双曲线C :2213y x -=,过点()2,1P ,作一直线交双曲线于A 、B 两点,若P 为AB 的中点. (1)求直线AB的方程;(2)求弦AB 的长【答案】(1)611y x =-;(2)4244233. 20. 已知抛物线22(0)x py p =>与直线3210x y -+=交于,A B 两点,5138AB =,点M 在抛物线上,MA MB ⊥.(Ⅰ) 求p 的值;(Ⅱ) 求点M 的坐标.【答案】(Ⅰ)14p =;(Ⅱ)M 的坐标为(0,0)或39(,)48-. 21. 2020年5月28日,十三届全国人大三次会议表决通过了《中华人民共和国民法典》,此法典被称为“社会生活的百科全书”,是新中国第一部以法典命名的法律,在法律体系中居于基础性地位,也是市场经济的基本法.民法典与百姓生活密切相关,某大学为了解学生对民法典的认识程度,选取了120人进行测试,测试得分情况如图所示.(1)试求出图中实数a 的值,并求出成绩落在[]90,100的人数;(2)如果抽查的测试平均分超过75分,就表示该学校通过测试.试判断该校能否通过测试; (3)如果在[)80,90中抽取3人,在[]90,100中抽取2人,再从抽取的5人中选取2人进行民法典的宣传,那么选取的2人中恰好1人成绩落在[]90,100的概率是多少? 【答案】(1)0.05a =,12人;(2)能够通过;(3)35。
