《中心投影与平行投影》习题
课时作业24:1.2.1 中心投影与平行投影~1.2.2 空间几何体的三视图

§1.2空间几何体的三视图和直观图1.2.1中心投影与平行投影1.2.2空间几何体的三视图基础过关1.一个几何体的三视图如图所示,则该几何体可以是()A.棱柱B.棱台C.圆柱D.圆台解析先观察俯视图,再结合正视图和侧视图还原空间几何体.由俯视图是圆环可排除A,B,由正视图和侧视图都是等腰梯形可排除C,故选D.答案D2.某空间几何体的正视图是三角形,则该几何体不可能是()A.圆柱B.圆锥C.四面体D.三棱柱解析由三视图知识,知圆锥、四面体、三棱柱(放倒看)都能使其正视图为三角形,而圆柱的正视图不可能为三角形,故选A.答案A3.一个长方体去掉一个小长方体,所得几何体的正视图与侧视图分别如图所示,则该几何体的俯视图为()解析正视图中小长方形在左上方,对应俯视图应该在左侧,排除B,D,侧视图中小长方形在右上方,排除A,故选C.答案C4.下列物品:①探照灯;②车灯;③太阳;④月亮;⑤台灯中,所形成的投影是中心投影的是________(填序号).解析探照灯、车灯、台灯的光线是由光源发出的光线,是中心投影;太阳、月亮距离地球很远,我们认为是平行光线,因此不是中心投影,故答案为①②⑤.答案①②⑤5.一几何体的直观图如图所示,下列给出的四个俯视图中正确的是________(填序号).解析该几何体是组合体,上面的几何体是一个五面体,下面是一个长方体,且五面体的一个面即为长方体的一个面,五面体最上面的棱的两端点在底面的射影距左右两边距离相等,因此填②.答案②6.根据以下三视图想象物体原形,并画出物体的实物草图.解(1)此几何体上面为圆柱,下面为圆台,实物草图如图①.(2)此几何体上面为圆锥,下面为圆柱,实物草图如图②.能力提升7.某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为()A.32B.23C.22D.2解析由三视图知可把四棱锥放在一个正方体内部,四棱锥为D-BCC1B1,最长棱为DB1=DC2+BC2+BB21=4+4+4=2 3.故选B.答案B8.如图,E,F分别为正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E 在该正方体的面上的射影可能是()A.①②③B.②③C.①②④D.②④解析因为正方体是对称的几何体,所以四边形BFD1E在该正方体的面上的射影可分为:自上而下、自左至右、由前及后三个方向的射影,也就是在面ABCD、面BCC1B1、面DCC1D1上的射影.四边形BFD1E在面ABCD和面DCC1D1上的射影相同,如图②所示;四边形BFD1E在该正方体的对角面ABC1D1内,它在面BCC1B1上的射影显然是一条线段,如图③所示.故②③正确.答案B9.如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的正视图与侧视图的面积的比值为________.解析依题意得三棱锥P-ABC的正视图与侧视图分别是一个三角形,且这两个三角形的底边长都等于正方体的棱长,底边上的高也都等于正方体的棱长,因此三棱锥P-ABC的正视图与侧视图的面积的比值为1.答案110.某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在侧视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为________.解析由三视图可知,该几何体为如图①所示的圆柱,该圆柱的高为2,底面周长为16.画出该圆柱的侧面展开图,如图②所示,连接MN,则MS=2,SN=4,则从M到N的路径中,最短路径的长度为MS2+SN2=22+42=2 5.答案2511.画出下列几何体的三视图.解题图①为正六棱柱,可按棱柱的画法画出,其三视图如图a;题图②为一个圆锥与一个圆台的组合体,按圆锥、圆台的三视图画出它们的组合形状,其三视图如图b.创新突破12.一个物体由几块相同的小正方体组成,其三视图如图所示,试据图回答下列问题:(1)该物体有多少层?(2)该物体的最高部分位于哪里?(3)该物体一共由几个小正方体构成?解(1)该物体一共有两层,从正视图和侧视图都可以看出来.(2)该物体最高部分位于左侧第一排和第二排.(3)从侧视图及俯视图可以看出,该物体前后一共三排,第一排左侧2个,右侧1个;第二排左侧2个,右侧没有;第三排左侧1个,右侧1个.该物体一共由7个小正方体构成.。
专训1 平行投影、中心投影、正投影间的关系

4.如图①②分别是两棵树及其影子的情形.
(1)哪个图反映了阳光下的情形?哪个图反映了路灯 下的情形?
(2)你是用什么方法判断的? (3)请分别画出图中表示小丽影子的线段.
解:(1)题图②反映了阳光下的情形,题图①反映了路灯下 的情形.
(2)题图①中过影子顶端与树顶端的直线相交于一点, 符合中心投影的特点,因此题图①反映了路灯下的 情形;题图②中过影子顶端与树顶端的直线平行, 符合平行投影的特点,因此题图②反映了阳光下的 情形.
•
9、有时候读书是一种巧妙地避开思考 的方法 。2021 /8/620 21/8/6F riday, August 06, 出 的人谈 话。202 1/8/62 021/8/6 2021/8 /68/6/2 021 4:44:34 PM
•
11、越是没有本领的就越加自命不凡 。2021/ 8/6202 1/8/620 21/8/6 Aug-21 6-Aug-2 1
(3)路灯下小丽的影子如图①所示,表示影子的线段为 AB;阳光下小丽的影子 如图②所示,表示影子 的线段为CD.
误区诊断:平行投影和中心投影对应的光线是不同的,形 成平行投影的光源发出的光线是平行光线,而 形成中心投影的光源发出的光线交于一点;同 一时刻,平行投影下的影子的方向总是在同一 方向,而中心投影下的影子可能在同一方向, 也可能在不同方向.
14、意志坚强的人能把世界放在手中 像泥块 一样任 意揉捏 。2021 年8月6 日星期 五2021/ 8/6202 1/8/620 21/8/6
•
15、最具挑战性的挑战莫过于提升自 我。。2 021年8 月2021 /8/620 21/8/62 021/8/ 68/6/20 21
•
16、业余生活要有意义,不要越轨。2 021/8/ 62021/ 8/6Aug ust 6, 2021
中心投影练习题

中心投影练习题在工程图纸上,中心投影是一种常用的投影方法,通过将三维物体的主要视图投影到平面上,使得观察者可以更清楚地理解物体的形状和尺寸。
为了帮助大家更好地掌握中心投影的技巧,下面将给出一些中心投影练习题,供大家练习。
练习一:正方体的中心投影1. 将一个边长为10cm的正方体的主要视图绘制出来。
解答:首先,在图纸上绘制一个正方形,边长为10cm,作为正方体的底面。
然后,通过绘制与底面平行的线段,以及连接底面上对应点的线段,绘制出正方体的主要视图。
最后,根据中心投影的原理,将立方体的各个顶点与底面上对应点的连线伸长,直到与底面的平行线相交,即可得到中心投影。
练习二:圆柱体的中心投影1. 绘制一个底面直径为10cm、高度为15cm的圆柱体的主要视图。
解答:首先,在图纸上绘制一个直径为10cm的圆作为圆柱体的底面。
然后,通过绘制一条与底面直径垂直的线段,再绘制一条连接底面两个端点的线段,可以得到圆柱体的主要视图。
最后,根据中心投影的原理,将圆柱体的各个底面上的点与主要视图中对应点的连线伸长,直到与主要视图的平行线相交,即可得到中心投影。
练习三:球体的中心投影1. 绘制一个直径为8cm的球体的主要视图。
解答:由于球体的形状是圆形的,所以它的中心投影在二维平面上是一个圆。
首先,在图纸上绘制一个直径为8cm的圆,作为球体的主要视图。
然后,根据中心投影的原理,将球体的各个点与主要视图中对应点的连线伸长,直到与主要视图的圆形相交,即可得到中心投影。
通过以上练习题的实践,相信大家对中心投影的方法和技巧有了更深入的理解。
同时,不同形状的物体在进行中心投影时需要采取不同的绘制方法和步骤,所以在实际的工程图纸中需要根据具体情况进行处理。
通过不断地练习和实践,我们可以更加熟练地运用中心投影的技巧,提高自己的工程图纸能力。
祝大家取得良好的学习效果!。
中心投影与平行投影(数学鲁教版九年级上册)

中心投影与平行投影
1. 中心投影
例1 在操场上的路灯下,旗杆(线段AB )和竹竿(线段DE )的影子如图1所示,在点M 处有一棵小树,它的影子是线段MN .请你在图中确定路灯的位置(用点P 表示),并画出表示小树的线段.
思路点拨:根据中心投影的性质确定点P 的位置,连接PN 并过点M 作垂线即可画出表示小树的线段.
解:
2. 平行投影
例2 一天早上,小茗陪爷爷晒太阳,如图,小茗(线段AB )和爷爷(线段CD )在同一平面上站立,其中小茗在太阳光下的影子为线段BE ,请你在图中画出爷爷的影子.
思路点拨:连接AE ,根据平行投影的性质,分别过点C ,D 作AE ,BE 的平行线即可画出爷爷的影子.
解:
3. 区分两种投影
例3 如图3所示的分别是两棵树及其影子的情形.
(1)哪个图反映了阳光下的情形?哪个图反映了路灯下的情形?
(2)请分别画出图中表示小丽影长的线段.
思路点拨:根据中心投影和平行投影的性质及它们的区别,很容易确定表示小丽影长的线段.我们可以借助图①,②深入研究两种投影中构造的相似三角形的区别,请同学们在图②中过表示路灯的点作垂线,并小组交流两图中的相似三角形有哪几对!
解:
参考答案
①
②
图3 图2 图1
例1 如图1,点P 即为所求,线段HM 为表示小树的线段.
例2 如图2,线段DF 即为所求.
例3 (1)图①反映了阳光下的情形,图②反映了路灯下的情形.
(2)如图3,线段AB ,CD 是表示小丽影长的线段. 图 1
图2
①
② 图3。
中心投影与平行投影和空间几何体的三视图7

中心投影与平行投影 空间几何体的三视图1、有一个几何体的三视图如下图所示,这个几何体应是一个( )A 、棱台B 、棱锥C 、棱柱D 、都不对2.三视图的正视图、俯视图、侧视图分别是从 、 、 观察同一个几何体,画出的空间几何体的图形. 答案:正前方,正上方,正左方3.圆台的正视图、侧视图都是 ,俯视图是 .答案:全等的等腰梯形,两个同心圆. 4.给出下列命题:① 如果一个几何体的三视图是完全相同的,则这个几何体是正方体;② 如果一个几何体的正视图和俯视图都是矩形,则这个几何体是长方体;主视图 左视图 俯视图③如果一个几何体的三视图都是矩形,则这个几何体是长方体;④如果一个几何体的正视图和侧视图都是等腰梯形,则这个几何体是圆台.其中正确命题的个数是()A.0B.1C.2D.3答案:B.5.若一个几何体的正视图和侧视图都是等腰三角形,俯视图是圆,则这个几何体可能是()A.圆柱B.三棱柱C.圆锥D.球体答案:C.6.三视图均相同的几何体有()A.球B.正方体C.正四面体D.以上都对答案:D.7.答案:三视图如图:8.画出图中3个图形的指定三视图(之一).答案:9.若一个几何体的正视图和侧视图都是等腰三角形,俯视图是圆,则这个几何体可能是( ).A.圆柱 B.三棱柱 C.圆锥 D.球体 答案:C.长方体的左视图 五棱柱的主视图 圆柱的俯视图画左视图画主视图画俯视图10.如图1所示,空心圆柱体的正视图是( )答案:C.11.如图,E ,F 分别是正方体1AC 的面11ADD A 和面11BCC B 的中心,则四边形1BFD E 在该正方体的面上的正投影(投射线垂直于投影面的投影)可能是 . (把所有可能图形的序号都填上)答案:(2)(3).12. 有一个几何体的三视图如下图所示,这个几何体应是一个A.棱台B.棱锥C.棱柱D.都不对 答案:A.13. 图(1)为长方体积木块堆成的几何体的三视图,此几何体共由________块木块堆成;图(2)中的三视图表示的实物为_____________侧视图俯视图图(1)图(2)答案:(1)4 (2)圆锥.14. 若一个几何体的正视图和侧视图都是等腰三角形,俯视图是圆,则这个几何体可能是( ).A.圆柱 B.三棱柱 C.圆锥 D.球体 答案:C.15. 画出右图的三视图.答案:解:正视图16. 如图1所示,空心圆柱体的正视图是( )答案:C.。
中心投影、平行投影专项练习题
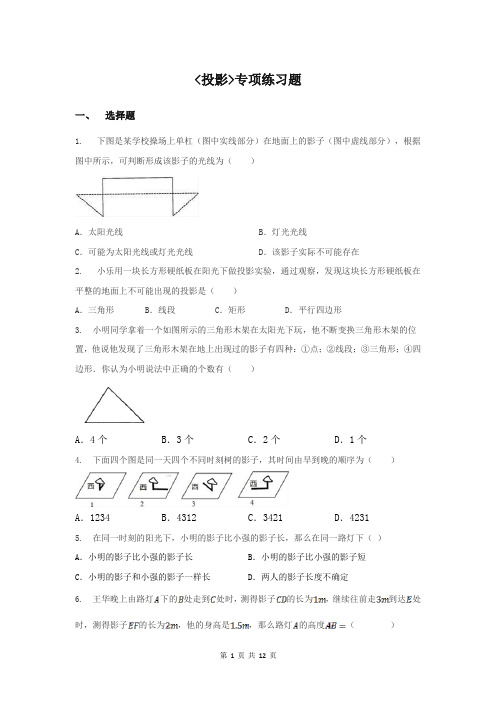
<投影>专项练习题一、选择题1.下图是某学校操场上单杠(图中实线部分)在地面上的影子(图中虚线部分),根据图中所示,可判断形成该影子的光线为()A.太阳光线 B.灯光光线C.可能为太阳光线或灯光光线 D.该影子实际不可能存在2.小乐用一块长方形硬纸板在阳光下做投影实验,通过观察,发现这块长方形硬纸板在平整的地面上不可能出现的投影是()A.三角形 B.线段 C.矩形D.平行四边形3. 小明同学拿着一个如图所示的三角形木架在太阳光下玩,他不断变换三角形木架的位置,他说他发现了三角形木架在地上出现过的影子有四种:①点;②线段;③三角形;④四边形.你认为小明说法中正确的个数有()A.4个B.3个C.2个D.1个4. 下面四个图是同一天四个不同时刻树的影子,其时间由早到晚的顺序为()A.1234B.4312C.3421D.42315. 在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下()A.小明的影子比小强的影子长B.小明的影子比小强的影子短C.小明的影子和小强的影子一样长D.两人的影子长度不确定6. 王华晚上由路灯下的处走到处时,测得影子的长为,继续往前走到达处时,测得影子的长为,他的身高是,那么路灯的高度()A.8m B.7.2m C.6m D.4.5m7. 如图,路灯距地面8m,身高1.6m的小明从点A处沿AO所在的直线行走14m到点B时,人影长度()A.变长3.5m B.变长2.5m C.变短3.5m D.变短2.5m8. 小阳和小明两人从远处沿直线走到路灯下,他们规定:小阳在前,小明在后,两人之间的距离始终与小阳的影长相等.在这种情况下,他们两人之间的距离()A.始终不变B.越来越远C.时近时远D.越来越近9.如图,夜晚路灯下有一排同样高的旗杆,离路灯越近,旗杆的影子()A.越长 B.越短 C.一样长 D.随时间变化而变化10. 如图,在一间黑屋子里用一盏白炽灯照一个球,球在地面上的阴影的形状是一个圆,当把白炽灯向上远移时,圆形阴影的大小的变化情况是()A.越来越小B.越来越大C.大小不变D.不能确定11. 下列四幅图形中,表示两棵小树在同一时刻阳光下的影子的图形可能是( ) A.B.C.D.12. 在同一平面内的影子如图所示,此时,第三根木棒的影子表示正确( ) A.B.C.D.13.在太阳光下,转动一个正方体,观察正方体在地上投下的影子,那么这个影子最多可能是几边形( )A.四边形 B.五边形C.六边形D.七边形二、填空题14. 如图是一幢建筑物和一根旗杆在一天中四个不同时刻的影子.将四幅图按先后顺序排列应为________.15. 人在灯光下走动时,其自身的影子通常会发生变化,当人走近灯光时,其影子的长度就会________;当人远离灯光时,其影子的长度就会________.16. 在路灯下的甲、乙两人影长相等,那么两人的身高为________.(相等,不相等,不一定相等)17. 平行于投影面的平行四边形的面积与它的正投影的面积的大小关系是________.18. 如图,一只小猫在一片废墟中玩耍,一只老鼠呆在________处才不会被小猫发现.19. 两根不一样长的木杆垂直竖立在地面上,若它们的影长相等,则此时的投影是____ _.(填写“平行投影”或“中心投影”)20. 如图,小明晚上由路灯A下的B处走到C处时,测得影长CD的长为1m,从C处继续往前走3m达到E处时,测得影子EF的长为2m,已知小明的身高时1.5m,那么路灯A的高度AB等于_____m.21.如图,电影胶片上每一个图片的规格为3.5cm×3.5cm,放映屏幕的规格为2m×2m,若放映机的光源S距胶片20cm,那么光源S距屏幕________ 米时,放映的图象刚好布满整个屏幕.22. 如图是四个直立在地面上的艺术字母的投影(阴影部分)效果,在艺术字母“L,K,C”的投影中,与艺术字母“N”属于同一种投影的有________ .23. 如图所示是两棵小树在同一时刻的影子,可以断定这是_____投影.24.如图,当太阳光与地面上的树影成45°角时,树影投射在墙上的影子CD等于2米,若树底部到墙的距离BC等于8米,则树高AB等于________米.25.如图是测得的两根木杆在同一时间的影子,那么它们是由________形成的投影(填“太阳光”或“灯光”).26. 皮影戏中的皮影是由投影得到的;太阳光线可以看成投影.三、作图题27. 如图,在路灯的同侧有两根高度相同的木棒,请分别画出这两根木棒的影子.28. 三根垂直地面的木杆甲、乙、丙,在路灯下乙、丙的影子如图所示.试确定路灯灯泡的位置,再作出甲的影子.(不写作法,保留作图痕迹)29. 如图,楼房和旗杆在路灯下的影子如图所示.(1)试确定路灯灯炮的位置;(2)再作出小树在路灯下的影子.(用线段表示,不写作法,保留作图痕迹)四、解答题30.假山具有多方面的造景功能,与建筑、植物等组合成富于变化的景致.某公园有一座假山,小亮、小慧等同学想用一些测量工具和所学的几何知识测量这座假山的高度来检验自己掌握知识和运用知识的能力,如图,在阳光下,小亮站在水平地面的D处,此时小亮身高的影子顶端与假山的影子顶端E重合,这时小亮身高CD的影长DE=2米,一段时间后,小亮从D点沿BD的方向走了3.6米到达G处,此时小亮身高的影子顶端与假山的影子顶端H重合,这时小亮身高的影长GH=2.4米,已知小亮的身高CD=FG=1.5米,点G,E,D均在直线BH上,AB⊥BH,CD⊥BH,GF⊥BH,请你根据题中提供的相关信息,求出假山的高度AB.31.如图,是小亮晚上在广场散步的示意图,图中线段表示站立在广场上的小亮,线段表示直立在广场上的灯杆,点表示照明灯的位置.在小亮由处沿所在的方向行走到达处的过程中,他在地面上的影子长度越来越___ _____(用“长”或“短”填空);请你在图中画出小亮站在处的影子;当小亮离开灯杆的距离时,身高为的小亮的影长为,①灯杆的高度为多少?②当小亮离开灯杆的距离时,小亮的影长变为多少?32.某数学兴趣小组,利用树影测量树高,如图①,已测出树AB的影长AC为12 m,并测出此时太阳光线与地面成30°夹角.(1)求出树AB的高;(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变.求树的最大影长(用图②解答).①②33.小红想利用阳光下的影长测量学校旗杆AB的高度.如图,他在某一时刻在地面上竖直立一个2米长的标杆CD,测得其影长DE=0.4米.(1)请在图中画出此时旗杆AB在阳光下的投影BF.(2)如果BF=1.6,求旗杆AB的高.34.如图,边长为acm的正方体其上下底面的对角线AC、A1C1与平面H垂直.(1)指出正方体六个面在平面H上的正投影图形;(2)计算投影MNPQ的面积.35.小明和小丽在操场上玩耍,小丽突然高兴地对小明说:“我踩到你的‘脑袋’了.”如图即表示此时小明和小丽的位置.(1)请画出此时小丽在阳光下的影子;(2)若已知小明的身高为1.60m,小明和小丽之间的距离为2m,而小丽的影子长为1.75m,求小丽的身高.36.如图,灯杆AB与墙MN的距离为18米,小丽在离灯杆(底部)9米的D处测得其影长DE为3m,设小丽身高为1.6m.(1)求灯杆AB的高度;(2)小丽再向墙走7米,她的影子能否完全落在地面上?若能,求此时的影长;若不能,求落在墙上的影长.37.如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC 所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.38.如图,在一间黑屋里用一白炽灯照射一个球,(1)球在地面上的阴影是什么形状?(2)当把白炽灯向上移时,阴影的大小会怎样变化?(3)若白炽灯到球心距离为1米,到地面的距离是 3米,球的半径是0.2米,求球在地面上阴影的面积是多少?39.如图,某一广告墙PQ旁有两根直立的木杆AB和CD,某一时刻在太阳光下,木杆CD 的影子刚好不落在广告墙PQ上.(1)请在图中画出此时的太阳光线CE及木杆AB的影子BF;(2)若AB=5米,CD=3米,CD到PQ的距离DQ的长为4米,求此时木杆AB的影长.40.如图所示,小鹏准备测量学校旗杆的高度,他发现斜坡正对着太阳时,旗杆AB影子恰好落在水平地面BC和斜坡坡面CD上,测得旗杆在水平地面上的影长BC="20" m,在斜坡坡面上的影长CD="8" m,太阳光线AD与水平地面成30°角,且太阳光线AD与斜坡坡面CD 互相垂直,请你帮小鹏求出旗杆AB的高度.(精确到1 m)41.路边有一根电线杆AB和一块正方形广告牌.有一天,小明突然发现,在太阳光照射下,电线杆顶端A的影子刚好落在正方形广告牌的上边中点G处,而正方形广告牌的影子刚好落在地面上E点(如图),已知BC=5米,正方形边长为3米,•DE=4米.(1)求电线杆落在广告牌上的影长;(2)求电线杆的高度(精确到0.1米).42.如图,晚上,小亮在广场上乘凉.图中线段AB表示站在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯.(1)请你在图中画出小亮在照明灯(P)照射下的影子;(2)如果灯杆高PO=12m,小亮的身高AB=1.6m,小亮与灯杆的距离BO=13m,请求出小亮影子的长度.43.学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图所示,在同一时间,身高为1.6 m的小明(AB)的影子BC长是3m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB=6m.(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置G;(2)求路灯灯泡的垂直高度GH;(3)如果小明沿线段BH向小颖(点H)走去,当小明走到BH中点B1处时,求其影子B1C1的长;当小明继续走剩下的路程的到B2处时,求其影子B2C2的长;当小明继续走剩下路程的到B3处时,……按此规律继续走下去,当小明走剩下路程的到处时,其影子的长为________m(直接用含n的代数式表示).。
2024九年级数学下册第3章投影与视图3.1投影3.1.1平行投影与中心投影习题课件新版湘教版

12 如图①,某人的一器官后面A处长了一个新生物,现需 检测其到皮肤的距离,为避免伤害器官,可利用一种新 型检测技术,检测射线可避开器官从侧面测量.某医疗 小组制定方案,通过医疗仪器的测量获得相关数据,并 利用数据计算出新生物到皮肤的距离方案如下:
课题 工具
检测新生物到皮肤的距离 医疗仪器等
示意图
【点拨】 如图,延长 PA,PB 分别交 x 轴于 A′,B′,作 PE⊥x
轴于 E,交 AB 于 D. ∵P(2,3),A(-1,1),B(3,1),
∴PD=2,PE=3,AB=4. ∵AB∥A′B′, ∴△PAB∽△PA′B′,∴AA′BB′=PPDE,即 A′4B′=23,∴A′B′=6,故选 D. 【答案】D
说明
如图②,新生物在A处,先在皮肤上选择最大限度地 避开器官的B处照射新生物,检测射线与皮肤MN的 夹角为∠DBN;再在皮肤上选择距离B处9 cm的C处 照射新生物,检测射线与皮肤MN的夹角为∠ECN
测量数据
∠DBN=35°,∠ECN=22°,BC=9 cm
请你根据上表中的测量数据,计算新生物A处到皮肤的距离 (结果精确到0.1 cm;参考数据:sin 35°≈0.57,cos 35°≈ 0.82 , tan 35°≈0.70 , sin 22°≈0.37 , cos 22°≈0.93 , tan 22°≈0.40).
【答案】D
10 如图,下列判断正确的是( )
A.图①是在阳光下的影子,图②是在灯光下的影子 B.图②是在阳光下的影子,图①是在灯光下的影子 C.图①和图②都是在阳光下的影子 D.图①和图②都是在灯光下的影子
【点拨】 题图①中影子的方向不同,是在灯光下的影子;题
图②中影子的方向相同,且影长与树高成正比例,是在阳 光下的影子.
中心投影与平行投影(基础)(含答案)

中心投影与平行投影(基础)一、单选题(共10道,每道10分)1.下列现象不属于投影的是( )A.皮影B.素描画C.手影D.树影答案:B解题思路:试题难度:三颗星知识点:略2.下列关于投影的说法正确的是( )A.投影面是一个垂直于投射线的平面B.正投影是一种平行投影C.矩形的正投影一定是矩形D.中心投影的投影线是相互平行的答案:B解题思路:试题难度:三颗星知识点:略3.同一灯光下两个物体的影子可以是( )A.同一方向B.不同方向C.相反方向D.以上皆有可能答案:D解题思路:试题难度:三颗星知识点:略4.如图,晚上小亮在路灯下散步,在小亮由A处走到B处这一过程中,他在地上的影子( )A.逐渐变短B.逐渐变长C.先变长后变短D.先变短后变长答案:D解题思路:试题难度:三颗星知识点:略5.如图,在一间黑屋子里用一盏白炽灯照一个球,球在地面上的阴影的形状是一个圆,当把球向远离灯的位置移动时,圆形阴影面积的大小的变化情况是( )A.越来越小B.越来越大C.大小不变D.不能确定答案:A解题思路:试题难度:三颗星知识点:略6.如图,路灯距地面8米,身高1.6米的小明从点A处沿AO所在的直线行走14m到点B时,人影长度( )A.变长3.5mB.变长2.5mC.变短3.5mD.变短2.5m答案:C解题思路:试题难度:三颗星知识点:略7.在阳光照射下的升旗广场的旗杆从上午九点到十一点的影子长的变化规律为( )A.逐渐变长B.逐渐变短C.影子长度不变D.影子长短变化无规律答案:B解题思路:试题难度:三颗星知识点:略8.若线段CD是线段AB的正投影,则AB与CD的大小关系为( )A.AB>CDB.AB<CDC.AB=CDD.AB≥CD答案:D解题思路:试题难度:三颗星知识点:略9.如图①②③④是一天中四个不同时刻的木杆在地面上的影子,将它们按时间先后顺序排列正确的一项是( )A.④③①②B.①②③④C.②③①④D.③①④②答案:A解题思路:试题难度:三颗星知识点:略10.同一时刻,小明在阳光下的影长为2米,与他邻近的旗杆的影长为6米,小明的身高为1.6米,则旗杆的高为( )A.3.2米B.4.8米C.5.2米D.5.6米答案:B解题思路:试题难度:三颗星知识点:略。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《中心投影与平行投影》习题
一、基础题型
1.皮影戏是在哪种光照射下形成的( )
A .灯光
B .太阳光
C .平行光
D .都不是2.下列各种现象属于中心投影现象的是( )
A .上午10点时,走在路上的人的影子
B .晚上10点时,走在路灯下的人的影子
C .中午用来乘凉的树影
D .升国旗时,地上旗杆的影子
3.小刚走路时发现自己的影子越走越长,这是因为( )
A .从路灯下走开,离路灯越来越远
B .走到路灯下,离路灯越来越近
C .人与路灯的距离与影子长短无关
D .路灯的灯光越来越亮
4.两个物体映在地上的影子有时在同侧,有时在异侧,则这可能是________投影.5._______和_______都是在灯光照射下形成的影子.
6.如图,AB 和D E 是直立在地面上的两根立柱,AB =5米,某一时刻AB 在阳光下的投影BC =3米,在测量AB 的投影时,同时测量出D E 在阳光下的投影长为6米,则D E 的长为_______.7.说出平行投影与中心投影的异同.
8.点光源发出的光线照射到物体上,会形成影子,那么在手术室里有4位医生,会有几个
影子?说明你的理由.
二、提高训练
9.如图,AB , CD 是两根木杆,它们在同一平面内的同一直
线
MN 上,则下列有关叙述正确的是( )
A .若射线
B N 正上方有一盏路灯,则AB ,CD 的影子都在射线B N 上;
B .若线段BD 正上方有一盏路灯,则AB 的影子在射线B M 上,CD 的影子在射线D N 上;
C .若在射线
D N 正上方有一盏路灯,则AB ,CD 的影子都在射线B N 上;
D .若太阳处在线段BD 的正上方,则AB , CD 的影子位置与选项B 中相同.10.在一盏路灯的周围有一圈栏杆,则下列叙述中不正确的是( )A .若栏杆的影子落在围栏里,则是在太阳光照射下形成的B
.若这盏路灯有影子,则说明是在白天形成的影子
C .若所有的栏杆的影子都在围栏外,则是在路灯照射下形成的
D .若所有的栏杆的影子都在围栏外,则是在太阳光照射下形成的
11.如图,BE ,DF
是甲,乙两人在路灯下形成的影子, 请在图中画出灯泡的位置.
12.如图,在圆桌的正上方有一盏吊灯,在灯光下,圆桌在地板上的投影是面积为4m 2
的圆.已知圆桌的高度为1m ,圆桌面的半径为0.5m
, 试求吊灯距圆桌面的距离.
参考答案
1.A 2.B 3.A 4.中心 5.皮影,手影等 6.10m
7.相同点:都是在光线照射下形成的影子;不同点:平行投影是平行光源,中心投影是点光源;形成的影子情况不同
8.没有影子,手术室里用的是无影灯
9.B 10.D 11.连结E A ,F C , 它们的延长线的交点即为灯泡的位置
12.m
13。
