节约里程法应用案例
节约里程法的应用

节约里程法的应用1.基本资料介绍①宝洁公司是广州配送中心最大的服务商,为其配送的客户和货量见下表,我们以广州配送中心为例来说明有装载限制的车辆调度的优化方法。
公司客户分布在全国各地,这里主要以广东省内7家客户及省外一家特殊客户的一次配送为例。
城市和货运量②广州配送中心为这次配送提供了三种车型,载重量分别为2吨、5吨和8吨,不同车型的运输单价不一样,具体见运输单价表。
配送中心的配送是由外协商提供车辆,因此汽车的数量没有限制。
运输单价表2.步骤第一步:各城市之间的距离见上表。
第二步:计算连接城市到同一线路上的距离节约值,具体见下表。
第三步:确定初始方案的运输线路及运输费用,现安排4辆2吨、4辆5吨的车给每个客户送货。
运输线路及运输费用见下表所示。
运输线路及运输费用运输路线车型距离单价运费广州-东莞5T 50 2.7 135广州-江门2T 53 2.4 127.2广州-惠州2T 116 2.4 278.4广州-阳江5T 173 2.7 467.1广州-汕尾5T 221 2.7 596.7广州-揭阳5T 333 2.7 899.1广州-汕头2T 344 2.4 825.6广州-漳州2T 478 2.4 1147.2合计1768 4476.3第四步:进行线路第一次优化。
第一次修改后的车辆调度结果运输路线车型距离单价运费广州-东莞5T 50 2.7 135 广州-江门2T 53 2.4 127.2 广州-惠州2T 116 2.4 278.4 广州-阳江5T 173 2.7 467.1 广州-汕尾5T 221 2.7 596.7 广州-揭阳5T 333 2.7 899.1 广州-汕头-漳州5T 502 2.7 1355.4 合计1148 3858.9第五步:继续进行线路优化。
第二次修改后的车辆调度结果运输路线车型距离单价运费广州-东莞5T 50 2.7 135广州-江门2T 53 2.4 127.2广州-惠州2T 116 2.4 278.4广州-阳江5T 173 2.7 467.1广州-汕尾5T 221 2.7 596.7 广州-揭阳-汕头-漳州8T 526 3.65 1919.19 合计1139 3523.59从表中可以看出,广州-惠州-揭阳-汕头-漳州路线上的总货运量达到7.9吨,再连接任何一个城市都将使货运量超过最高限制(8吨),则不能继续配载,所以可以首先确定的是这一条线路。
运输的优化求解、运输问题—节约里程法

1、列运输平衡表
列表时要求表内供销平衡,并将运费标入表内空格。
需
供
B1
B2
B3
A1
x11 90 x12 70 x13 100
供应量 200
A2
x21 80 x22 65 x23 80
250
需求量 100 150
200
250
需求量 100 150
200
450
由于上表中有负检验数,故需继续 进行调整,得新运输方案表。
新运输方案2表
需
供
B1
B2
B3
A1
100 90 100 70
100
A2
80 50 65 200 80
需求量 100
150
200
供应量 200 250 450
对新运输方案表进行检验。
新运输方案2检验表
其需量等于总供量与总需量之差,并设其相应运价为0。这
样,就可以用表上作业法求解产大于销的运输问题。
2、销大于产的运输问题 n m
对于销量大于产量,即 bj ai 的运输问题,必
j 1
i 1
然有一些销地不能得到满足,发生缺货,此时引入虚拟供
应点,并设其相应运价为0。这样,就可以用产销平衡的表
上作业法求解销大于产的运输问题。
450
2、建立初始调运方案
采用最小元素法,即在平衡表中挑取运价最小或
较小的供需点格子尽量优先分配的调运方法。
需
供
B1
A1
0 90
B2
B3
供应量
节约里程法路径优化

节约里程法路径优化节约里程法是一种用于路径优化的方法,通过选择最短路径来减少行程中的里程数。
在现实生活中,我们经常需要规划行程,比如出差、旅行或者日常的通勤。
而选择最优路径可以节省时间和精力,提高效率。
下面我将以一个出差的例子来说明如何使用节约里程法进行路径优化。
假设我需要从A市出差到B市,那么我可以通过多种交通方式进行选择,比如飞机、火车、汽车等。
为了节约里程,我需要考虑以下几个因素:距离、时间、费用和舒适度。
我可以考虑乘坐飞机。
飞机通常是最快的交通工具,可以快速到达目的地。
然而,飞机票价格较高,且需要提前预订。
如果我需要频繁出差,花费较多的机票费用可能会对我的财务造成一定的压力。
我可以选择乘坐火车。
火车通常比汽车更舒适,且价格相对较低。
但是,火车的速度可能较慢,行程可能需要更长的时间。
如果我需要在短时间内到达目的地,乘坐火车可能不是最佳选择。
我可以选择乘坐汽车。
汽车的灵活性较高,我可以根据需要随时停下来休息或处理其他事务。
然而,长途驾驶可能会让我感到疲劳,而且汽车的油费和路桥费用也需要考虑。
综合考虑以上因素,我可以做出最优选择。
如果时间充裕且预算充足,我可以选择乘坐飞机,以最快的速度到达目的地。
如果时间有限,但预算有限,我可以选择乘坐火车,虽然时间稍长,但价格相对较低。
如果我喜欢自驾旅行或者需要灵活性,我可以选择乘坐汽车。
节约里程法可以帮助我在出差或旅行时选择最优路径。
通过综合考虑距离、时间、费用和舒适度等因素,我可以做出最合适的决策。
这样不仅可以节约里程,还可以提高出差或旅行的效率和体验。
希望这种方法能对大家在路径优化方面提供一些参考和帮助。
节约里程法应用案例
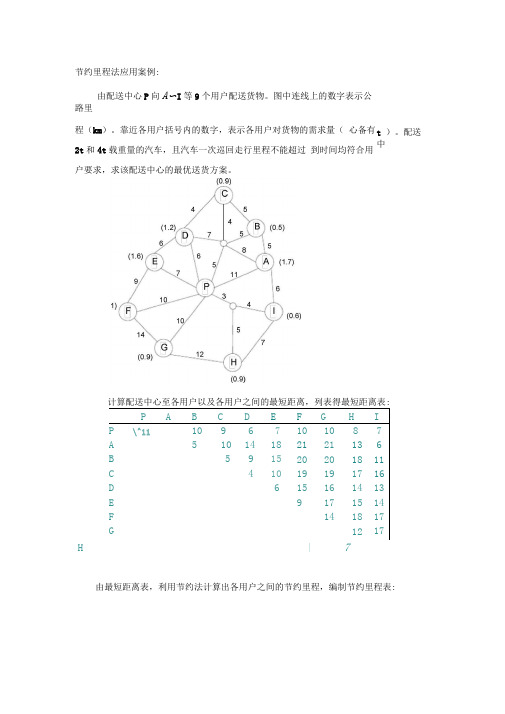
节约里程法应用案例:
由配送中心P向A〜I等9个用户配送货物。
图中连线上的数字表示公
路里
程(km)。
靠近各用户括号内的数字,表示各用户对货物的需求量(心备有
2t和4t载重量的汽车,且汽车一次巡回走行里程不能超过到时间均符合用
户要求,求该配送中心的最优送货方案。
计算配送中心至各用户以及各用户之间的最短距离,列表得最短距离表:
P A B C D E F G H I P \^1110 9 6 710 10 8 7
A 5 10 14 18 2121 136
B 5 9 1520 20 1811
C 4 1019 19 17 16
D 6 15 16 14 13
E 9 17 15 14
F 14 18 17
G 12 17
H \ 7
由最短距离表,利用节约法计算出各用户之间的节约里程,编制节约里程表:
t )。
配送
中
A B c D E F G H I
A 16 10 3 0 0 0 6 12
B14 7 2 0 0 0 6
C 11 6 0 0 0 0
D 7 10 0 0
E -8 0 00
F 6 00
G 6 0
H8
1
根据节约里程表中节约里程多少的顺序,由大到小排列,编制节约里程顺序表,以便尽量使节约里程最多的点组合装车配送。
束条件,渐进绘出配送路径:
6
A
B
6
D
o
- 1
E
6
6
c
9
A
径 B
径 c
径
1 1
9) a。
节约里程法典型实例

物流方案设计(最优运输路线决策-节约里程法)典型实例:已知配送中心P O向5个用户P j配送货物,其配送路线网络、配送中心与用户的距离以及用户之间的距离如下图与表所示:图中括号内的数字表示客户的需求量(单位:吨),线路上的数字表示两结点之间的距离,配送中心有3台2t卡车和2台4t两种车辆可供使用,1、试利用节约里程法制定最优的配送方案?2、设卡车行驶的速度平均为40公里/小时,试比较优化后的方案比单独向各用户分送可节约多少时间?第(1)步:作运输里程表,列出配送中心到用户及用户间的最短距离。
得初始方案配送距离=39X 2=78KM第(5)步:根据载重量约束与节约里程大小,将各客户结点连接起来,形成二个配送路线。
即A B 两配送方案。
序号 路线 节约里程 序号 路线 节约里程1 P 2P 3 10 6 P i F 52 2 P 3P 4 8 7 P i P3 1 3 P 2P4 6 8 F 2F5 0 4 P 4P 5 5 9 F 3F 5 0 5P l P 2410P i F 4第(2)步:由运输里程表、按节约里程公式,求得相应的节约里程数,如上表( 第(3)步:将节约里程 sij 进行分类,按从大到小顺序排列第(4)步:确定单独送货的配送线路)内。
(1.5)①配送线路A:P0-P2-P3-P4- P 0 运量q A= q 2+q3+q4 = 1.7+0.9+1.4 = 4t 用一辆4t 车运送节约距离S A =10 +8 = 18km②配送线路B: P 0-P5 -P 1-P0 运量q B =q 5+q1=2.4+1.5=3.9t<4t 车用一辆4t 车运送节约距离S B=2km第(6)步:与初始单独送货方案相比,计算总节约里程与节约时间总节约里程:△ S= S A+S B= 20 km与初始单独送货方案相比,可节约时间:△T = △ S/V=20/40=0.5小时。
物流方案设计(最优运输路线决策-节约里程法)典型实例

物流方案设计(最优运输路线决策-节约里程法)典型实例:已知配送中心P O向 5 个用户 P j配送货物,其配送路线网络、配送中心与用户的距离以及用户之间的距离如下图与表所示:图中括号内的数字表示客户的需求量(单位:吨),线路上的数字表示两结点之间的距离,配送中心有 3 台 2t 卡车和 2 台 4t 两种车辆可供使用,1、试利用节约里程法制定最优的配送方案?2、设卡车行驶的速度平均为40 公里 / 小时,试比较优化后的方案比单独向各用户分送可节约多少时间?( 0.9)P3 4( 1.7)5P2 6128( 1.4)12 P4 7 P0 1312 10 8P5 16P1 ( 1.5)需要量P0( 2.4)1.5 8 P11.7 8 12 P20.9 6 13 4 P31.4 7 15 9 5 P42.4 10 16 18 16 12 P5第( 1)步:作运输里程表,列出配送中心到用户及用户间的最短距离。
需要量0 P1.5 8 P11.7 8 ( 4)P12 20.9 6 (1)( 10)P3 13 41.4 7 (0)(6)(8)4 15 9 5 P2.4 10(2)(0)(0)(5)16 18 16 P512第( 2)步:由运输里程表、按节约里程公式,求得相应的节约里程数,如上表()内。
第( 3)步:将节约里程sij 进行分类,按从大到小顺序排列序号路线节约里程序号路线节约里程1 P2P3 10 6 P1 P5 22 P P 8 7 P P 13 4 1 33 P P 6 8 P P 02 4 2 54 P4P5 5 9 P3 P5 05 P1P2 4 10 P1 P4 0第( 4)步:确定单独送货的配送线路(0.9)P3 ( 1.7 )P268( 1.4)P4 7P0108P5P1(1.5)(2.4 )得初始方案配送距离 =39× 2=78KM第( 5)步:根据载重量约束与节约里程大小,将各客户结点连接起来,形成二个配送路线。
物流工程——节约里程法

练习题
某连锁零售店,下设有一个配送中心P和10个连 锁分店A~J,配送中心和各连锁分店及各连锁分店之 间的位置关系如下图1所示,两点间连线上的数字为 两点间的路线长度(单位:公里)。各连锁分店对某 种商品的需求量见表1,该商品由配送中心统一采购 并进行配送。配送中心备用2t和4t的货车,限定送货 车辆一次巡回距离不超过35公里,设送到时间均符合 用户要求,求配送中心的最优送货方案。
节约里程法
第二步:计算连接城市到同一线路上的距离节约值
节约里程法
第三步:确定初始方案的运输线路及运输费用,现安排4辆2吨、4辆5吨的车给 每个客户送货。运输线路及运输费用见下表所示。
节约里程法
第四步:进行线路第一次优化。
节约里程法
第一次修改后的车辆调度结果:
节约里程法
第五步:继续进行线路优化。
P3
5 6
4 (1.7)
P2
8 12
(1.4)
P4
7
12
P0
13
12
10
8
16
P5
( 2.4 )
P1 (1.5 )
节约里程法
• 第1 步:作运输里程表,列出配送中心到用户 及用户间的最短距离。
需求量 P0
P1
1.5
8
P1
P2
1.7
8
12
P2
P3
0.9
6
13
4
P3
P4
1.4
7
15
9
5
P4
P5
2.4
10
节约里程法
第六步:最终方案的确定。
节约里程法
• 最终修改后的车辆调度结果:
节约里程法
节约里程法应用案例
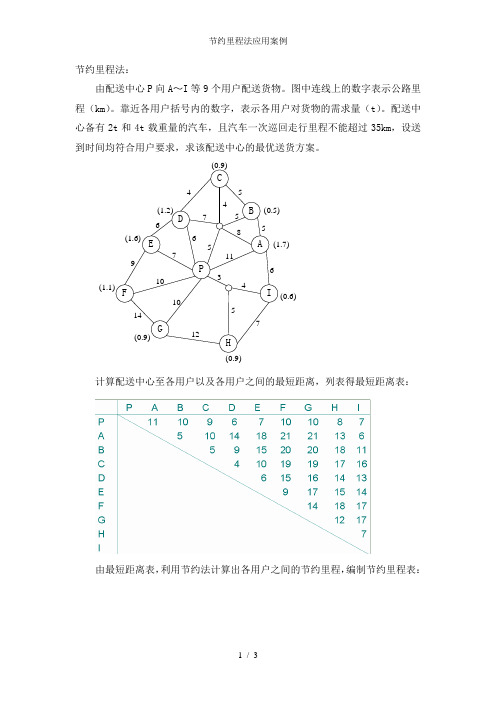
节约里程法:
由配送中心P 向A ~I 等9个用户配送货物。
图中连线上的数字表示公路里程(km )。
靠近各用户括号内的数字,表示各用户对货物的需求量(t )。
配送中心备有2t 和4t 载重量的汽车,且汽车一次巡回走行里程不能超过35km ,设送到时间均符合用户要求,求该配送中心的最优送货方案。
计算配送中心至各用户以及各用户之间的最短距离,列表得最短距离表:
由最短距离表,利用节约法计算出各用户之间的节约里程,编制节约里程表:
A
B C
D
E
F
G
H
I P
(0.9)
(1.2)(1.6)(0.9)
(0.9)
(0.6)
(1.7)(0.5)4
44
5
555
5
66
6
3
77
7
8
9
1010
1112
14
根据节约里程表中节约里程多少的顺序,由大到小排列,编制节约里程顺序表,以便尽量使节约里程最多的点组合装车配送。
根据节约里程排序表和配车(车辆的载重和容积因素)、车辆行驶里程等约束条件,渐进绘出配送路径:
(0.9)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
节约里程法应用案例:
由配送中心P 向A ~I 等9个用户配送货物。
图中连线上的数字表示公路里程(km )。
靠近各用户括号内的数字,表示各用户对货物的需求量(t )。
配送中心备有2t 和4t 载重量的汽车,且汽车一次巡回走行里程不能超过35km ,设送到时间均符合用户要求,求该配送中心的最优送货方案。
计算配送中心至各用户以及各用户之间的最短距离,列表得最短距离表:
由最短距离表,利用节约法计算出各用户之间的节约里程,编制节约里程表:
A
B C
D
E
F
G
H
I P
(0.9)
(1.2)(1.6)
(0.9)
(0.9)
(0.6)
(1.7)(0.5)4
44
5
555
5
66
6
3
77
7
8
9
10
10
1112
14
根据节约里程表中节约里程多少的顺序,由大到小排列,编制节约里程顺序表,以便尽量使节约里程最多的点组合装车配送。
根据节约里程排序表和配车(车辆的载重和容积因素)、车辆行驶里程等约束条件,渐进绘出配送路径:
(0.9)。
