(3、4)第二章 2.2热力学第一定律 上
合集下载
第二章_热力学第一定律

6
“热力学之父”开尔文
• 上帝要给人类科学,于是“牛顿”走上了历史的舞台; 上帝要给人类工程,于是来了“开尔文”,从此产生 了电机工程、资讯工程与机械工程。 • 开尔文是位天才,10岁进大学,22岁剑桥大学就想聘 他去当物理系主任,绝对温度 K 就来自于他姓氏的缩 写。他提出了热力学第二定律,他首先压缩制出液氮, 他铺设了环球信息的第一条电缆,发明了电子检流器, 最先提出同位素放射理论的。因为他的发现,世界上 每一个学习工程与理科的学生,打开课本,就会发现 “能量”的观念贯穿了每一个物理与化学的公式,解 释了每一个热、电、磁的运动,成为近代科技的基石。
开尔文的哥哥—詹姆斯· 汤姆生 (James Thomson, 1822~1892, 英国)首次使用“热力学(thermodynamics)”这个名词(1849)
克劳修斯 (Rudolf Clausius, 1822~1888,德国) 提出热力学第二定律(1850), 首次引入平均自由程 概念(1858),首次定义“熵”(1854),提出 “熵增原理”(1865);首次用统计方法导出压力 公式(1851),引进自由程概念(1858),获科普利 奖。 能斯特(Walther Nernst, 1864~1941,德国) 提出热力学第三定律(1906),于1920年获Nobel物 理奖。
W pambdV
16
不同过程体积功的计算
一般过程:
W pambdV
恒压过程: W pdV p dV pV
恒外压过程:
W pamb V
理想气体可逆过程:
nRT W pambdV pdV dV V
功是“非状态函数”(与途径相关) W
18
§2.3 恒容热、恒压热,焓
“热力学之父”开尔文
• 上帝要给人类科学,于是“牛顿”走上了历史的舞台; 上帝要给人类工程,于是来了“开尔文”,从此产生 了电机工程、资讯工程与机械工程。 • 开尔文是位天才,10岁进大学,22岁剑桥大学就想聘 他去当物理系主任,绝对温度 K 就来自于他姓氏的缩 写。他提出了热力学第二定律,他首先压缩制出液氮, 他铺设了环球信息的第一条电缆,发明了电子检流器, 最先提出同位素放射理论的。因为他的发现,世界上 每一个学习工程与理科的学生,打开课本,就会发现 “能量”的观念贯穿了每一个物理与化学的公式,解 释了每一个热、电、磁的运动,成为近代科技的基石。
开尔文的哥哥—詹姆斯· 汤姆生 (James Thomson, 1822~1892, 英国)首次使用“热力学(thermodynamics)”这个名词(1849)
克劳修斯 (Rudolf Clausius, 1822~1888,德国) 提出热力学第二定律(1850), 首次引入平均自由程 概念(1858),首次定义“熵”(1854),提出 “熵增原理”(1865);首次用统计方法导出压力 公式(1851),引进自由程概念(1858),获科普利 奖。 能斯特(Walther Nernst, 1864~1941,德国) 提出热力学第三定律(1906),于1920年获Nobel物 理奖。
W pambdV
16
不同过程体积功的计算
一般过程:
W pambdV
恒压过程: W pdV p dV pV
恒外压过程:
W pamb V
理想气体可逆过程:
nRT W pambdV pdV dV V
功是“非状态函数”(与途径相关) W
18
§2.3 恒容热、恒压热,焓
热力学第一定律1完整ppt课件

南京大学精品课程 物理化学→ 网络课程→辅导答疑→第几章→
完整版PPT课件
3
物理化学电子教案—第二章
ΔU=Q+W
完整版PPT课件
4
第二章热力学第一定律
2.1基本概念及术语 2.2热力学第一定律 2.3恒容热、恒压热及焓 2.4摩尔热容 2.5相变焓 2.7.化学反应焓 2.8标准摩尔反应焓的计算 2.10可逆过程与可逆体积功 2.11节流膨胀与焦耳-汤姆逊实验
物理化学
主讲: 化学学院 周建敏
祝大家学习愉快,天天进步!
联系电话:
短号:69779 办电:2923571 宅电:2981088
电子邮箱: mmczjm@
QQ: 530018104
完整版PPT课件
1
热力学第一定律
完整版PPT课件
2
物理化学
/jingpin/wlhx/index.htm
(ⅲ)定容过程 V1=V2 (iv )绝热过程 Q=0
气体 真空
(v)循环过程 所有状态函数改变量为零
(vi) 对抗恒定外压过程 pamb=常数。
(vii)自由膨胀过程(向真空膨胀过程)。Pamb=0
完整版PPT课件
17
§2.1- 4功和热
功由于系统与环境间除热外而引起的能量传递形式。 用符号W 表示。单位:J KJ
环境对系统作功 W >0;系统对环境作功W <0
注意: W与变化的过程有关, W是途径函数,不能以全微
分表示,微小变化过程的功,不能用dW,用δW 表示
体积功 系统因体积变化时与环境传递的功;
功 非体积功
体积功以外的其它功, 以W' 表示 ,如,
电功,表面功等。
完整版PPT课件
完整版PPT课件
3
物理化学电子教案—第二章
ΔU=Q+W
完整版PPT课件
4
第二章热力学第一定律
2.1基本概念及术语 2.2热力学第一定律 2.3恒容热、恒压热及焓 2.4摩尔热容 2.5相变焓 2.7.化学反应焓 2.8标准摩尔反应焓的计算 2.10可逆过程与可逆体积功 2.11节流膨胀与焦耳-汤姆逊实验
物理化学
主讲: 化学学院 周建敏
祝大家学习愉快,天天进步!
联系电话:
短号:69779 办电:2923571 宅电:2981088
电子邮箱: mmczjm@
QQ: 530018104
完整版PPT课件
1
热力学第一定律
完整版PPT课件
2
物理化学
/jingpin/wlhx/index.htm
(ⅲ)定容过程 V1=V2 (iv )绝热过程 Q=0
气体 真空
(v)循环过程 所有状态函数改变量为零
(vi) 对抗恒定外压过程 pamb=常数。
(vii)自由膨胀过程(向真空膨胀过程)。Pamb=0
完整版PPT课件
17
§2.1- 4功和热
功由于系统与环境间除热外而引起的能量传递形式。 用符号W 表示。单位:J KJ
环境对系统作功 W >0;系统对环境作功W <0
注意: W与变化的过程有关, W是途径函数,不能以全微
分表示,微小变化过程的功,不能用dW,用δW 表示
体积功 系统因体积变化时与环境传递的功;
功 非体积功
体积功以外的其它功, 以W' 表示 ,如,
电功,表面功等。
完整版PPT课件
热力学第一定律

2014-12-2 29
3、分析
机械能的增量 流动功
1 2 q u c f gz ( pv ) wi 2 18 2
容积变化功 机械能可以全 部转变为功 工质对机器作的功
说明:
(1)工质在状态变化过程中从热能转变而来的机械能 总等于膨胀功 。
1 2 (2)2 c f 、gz、wi
1、热力学第一定律的第二解析式
引进技术功概念后,稳定流动能量方程式(2-16)可写为
Q H Wt 2 23a
对于微元过程,有
q h wt 2 23
q dh wt 2 23b Q dH Wt 2 23c
若过程可逆,则
q h vdp, q dh vdp2 23d
1、开口系统能量方程式 2、稳定流动能量方程式 3、分析
2014-12-2
22
1、开口系统能量方程式
如图所示,一开口系统在dτ时间内进行一个微元过程:
2014-12-2
23
考察该系统微元过程的能量平衡:
进入系统的能量 离开系统的能量 控制容积的储存能增量
dE1 p1dV 1 Q
dE2 p2dV2 Wi
2014-12-2
15
一、推动功和流动功
推动功—工质在开口 系统中流动而传递的功。
mkg工质的推动功等于
pAl pV mpv
1kg工质的推动功等于
2014-12-2
pv
16
说明:
(1)推动功只有在工质移动位置时才起作用。 (2)工质在传递推动功时没有热力状态的变化,也 没有能量形态的变化。 (3)工质的作用只是单纯地运输能量。
2 1
2014-12-2
3、分析
机械能的增量 流动功
1 2 q u c f gz ( pv ) wi 2 18 2
容积变化功 机械能可以全 部转变为功 工质对机器作的功
说明:
(1)工质在状态变化过程中从热能转变而来的机械能 总等于膨胀功 。
1 2 (2)2 c f 、gz、wi
1、热力学第一定律的第二解析式
引进技术功概念后,稳定流动能量方程式(2-16)可写为
Q H Wt 2 23a
对于微元过程,有
q h wt 2 23
q dh wt 2 23b Q dH Wt 2 23c
若过程可逆,则
q h vdp, q dh vdp2 23d
1、开口系统能量方程式 2、稳定流动能量方程式 3、分析
2014-12-2
22
1、开口系统能量方程式
如图所示,一开口系统在dτ时间内进行一个微元过程:
2014-12-2
23
考察该系统微元过程的能量平衡:
进入系统的能量 离开系统的能量 控制容积的储存能增量
dE1 p1dV 1 Q
dE2 p2dV2 Wi
2014-12-2
15
一、推动功和流动功
推动功—工质在开口 系统中流动而传递的功。
mkg工质的推动功等于
pAl pV mpv
1kg工质的推动功等于
2014-12-2
pv
16
说明:
(1)推动功只有在工质移动位置时才起作用。 (2)工质在传递推动功时没有热力状态的变化,也 没有能量形态的变化。 (3)工质的作用只是单纯地运输能量。
2 1
2014-12-2
第二章热力学第一定律

敞开系统 系 统
所研究的 物质对象
系统与环境
物质进出 能量得失 √ √
封闭系统 隔离系统
√
状态及状态函数
系统有p, V, T, 组成, 内能等等宏观性质, 系统内的每个粒子 又有结构, 运动情况和粒子间相互作用等微观性质. 系统的宏观 性质有些是各粒子微观性质的某种平均作用, 如温度是分子热 运动的平均强度; 有些则是粒子微观性质的总体表现, 如压力是 分子运动碰撞容器壁面时对单位面积壁面的总垂直力.
状态及状态函数
系统的状态 是系统所有宏观性质的综合表现. 具有单值对应的函数关系 (a) 系统所有的性质一定, 状态就一定; (实际上当系统中物质量及组成, 温度, 压力(或体积) 一定时, 状态便可确定) (b) 状态一定, 系统所有的性质均一定. 因此, 宏观性质又称为状态函数 状态函数的基本性质——状态函数法的基础. • 其微小变化值可用数学上的全微分表示,如dT, dp, dV… • 其增量只与系统的始态和终态有关, 与具体变化途径无关
系统的宏观性质简称性质, 有的可以测量, 有的不可以测量. 性质可分为如下两大类:
系统的性质
{ 强度性质 无空间上的加和性: T,
T p T p
广延性质 有空间上的加和性: n, V ,U, H ,S ,G …
p ,Vm , Um …
nL VL UL SL nR VR UR SR
两者的关系:广延性质的 摩尔量是(准)强度性质, 如:摩尔体积 Vm 等.
{p
su
}
W
p始
一粒粒取走砂粒 (剩 余 砂 粒 相 当 前 述 一个重物)
V终
p始
V始
所研究的 物质对象
系统与环境
物质进出 能量得失 √ √
封闭系统 隔离系统
√
状态及状态函数
系统有p, V, T, 组成, 内能等等宏观性质, 系统内的每个粒子 又有结构, 运动情况和粒子间相互作用等微观性质. 系统的宏观 性质有些是各粒子微观性质的某种平均作用, 如温度是分子热 运动的平均强度; 有些则是粒子微观性质的总体表现, 如压力是 分子运动碰撞容器壁面时对单位面积壁面的总垂直力.
状态及状态函数
系统的状态 是系统所有宏观性质的综合表现. 具有单值对应的函数关系 (a) 系统所有的性质一定, 状态就一定; (实际上当系统中物质量及组成, 温度, 压力(或体积) 一定时, 状态便可确定) (b) 状态一定, 系统所有的性质均一定. 因此, 宏观性质又称为状态函数 状态函数的基本性质——状态函数法的基础. • 其微小变化值可用数学上的全微分表示,如dT, dp, dV… • 其增量只与系统的始态和终态有关, 与具体变化途径无关
系统的宏观性质简称性质, 有的可以测量, 有的不可以测量. 性质可分为如下两大类:
系统的性质
{ 强度性质 无空间上的加和性: T,
T p T p
广延性质 有空间上的加和性: n, V ,U, H ,S ,G …
p ,Vm , Um …
nL VL UL SL nR VR UR SR
两者的关系:广延性质的 摩尔量是(准)强度性质, 如:摩尔体积 Vm 等.
{p
su
}
W
p始
一粒粒取走砂粒 (剩 余 砂 粒 相 当 前 述 一个重物)
V终
p始
V始
第二章 热力学第一定律

闭口与稳流开口的能量方程
闭口 稳流开口
q = ∆u + w
q = ∆h + wt
等价
容积变化功w 技术功wt 轴功ws 推进功∆ 推进功∆(pv) 几种功的关系? 几种功的关系?
几种功的关系
1 2 wt = ∆cf + g∆z + ws 2
q = ∆h + wt = ∆u +∆( pv) + w t
1 2 2 Q = (U2 −U1) + ( p2V2 − pV1) + m(cf 2 − cf 2 ) + mg(z2 − z1) +Ws 1 2
焓(Enthalpy) 的引入 )
定义: 定义:h = u + pv H = U + pV
1、焓是状态量 、 2、一般焓只计算其变化量△h 、 3、对流动工质,焓代表能量(内能 推进功 、对流动工质, 代表能量 内能 推进功) 内能+推进功 对静止工质, 不代表能量 对静止工质,焓不代表能量 4、物理意义:开口系中随工质流动而携带 物理意义:开口系中随工质流动而携带 取决于热力状态的能量 能量。 的、取决于热力状态的能量。
可逆(准静态 过程闭口系能量方程 可逆 准静态)过程闭口系能量方程 准静态
可逆过程容 可逆过程容 积变化功: 积变化功: 闭口系统能 量方程: 量方程:
δw = pdv δq = du + δw
δq = du + pdv q = ∆ u + ∫ pdv
注意公式应用条件
例2 - 1 如图所示,闭口系内的一定量气体由状态1 如图所示 , 闭口系内的一定量气体由状态 1 经 1a2 变化至状态2 吸热70kJ, 同时对外做功25kJ,, 70kJ 25kJ 变化至状态 2 , 吸热 70kJ , 同时对外做功 25kJ ,, 试问: 工质若由1 变化到2 试问:(1)工质若由1经1b2变化到2时,吸热为 90kJ 则对外做功是多少? kJ, 90kJ , 则对外做功是多少 ? ( 2 ) 若外界对气体 做功30kJ, 迫使它从状态2 30kJ 返回到状态1 做功 30kJ , 迫使它从状态 2 经 2c1 返回到状态 1 , 则此返回过程是吸热过程还是放热过程? 则此返回过程是吸热过程还是放热过程?其值为 多少? 多少?
第二章 热力学第一定律

1 2 ws m u2 p2v2 cf2 gz2 0 2
令
u pv h
U pV H
,h 称为比焓。
, H 称为焓
焓的定义:焓=热力学能+推动功。
2-4 开口系统的稳定流动能量方程式
由于p、v 、u都是状态参数,所以焓也是工质的一个
1 2 Ws m u2 cf2 gz2 mp2v2 2 1 2 Ws m u2 cf2 gz2 p2v2 2
2-4 开口系统的稳定流动能量方程式
根据热力学第一定律可得
1 2 Q m u1 p1v1 2 cf1 gz1
本章主要内容
1 2 3 4 5
热力系统的储存能 热力学第一定律的实质 闭口系统的热力学第一定律表达式 开口系统的稳定流动能量方程式 稳定流动能量方程式的应用
2-1 热力系统的储存能
热力学能
热力学储存能
U
宏观动能与宏观位能
热力学能的定义:
Ek , E p
物体因热运动而具有的能量 , 是存储于物体内部的能量 。 内动能 内位能 原子能 化学能
对于单位质量工质的可逆过程 ,
q du pdv
q u pdv
1
2
2-3 闭口系统的热力学第一定律表达式
适用条件:
闭口系;可逆、不可逆; 理想和实际气体;初、终态为平衡态
符号规定:
吸热q为正,放热为负 系统对外作功为正,反之为负
系统内能增大 U为正,反之为负
2-3 闭口系统的热力学第一定律表达式
热力学能(内能)
2-3 闭口系统的热力学第一定律表达式
Q ΔU
令
u pv h
U pV H
,h 称为比焓。
, H 称为焓
焓的定义:焓=热力学能+推动功。
2-4 开口系统的稳定流动能量方程式
由于p、v 、u都是状态参数,所以焓也是工质的一个
1 2 Ws m u2 cf2 gz2 mp2v2 2 1 2 Ws m u2 cf2 gz2 p2v2 2
2-4 开口系统的稳定流动能量方程式
根据热力学第一定律可得
1 2 Q m u1 p1v1 2 cf1 gz1
本章主要内容
1 2 3 4 5
热力系统的储存能 热力学第一定律的实质 闭口系统的热力学第一定律表达式 开口系统的稳定流动能量方程式 稳定流动能量方程式的应用
2-1 热力系统的储存能
热力学能
热力学储存能
U
宏观动能与宏观位能
热力学能的定义:
Ek , E p
物体因热运动而具有的能量 , 是存储于物体内部的能量 。 内动能 内位能 原子能 化学能
对于单位质量工质的可逆过程 ,
q du pdv
q u pdv
1
2
2-3 闭口系统的热力学第一定律表达式
适用条件:
闭口系;可逆、不可逆; 理想和实际气体;初、终态为平衡态
符号规定:
吸热q为正,放热为负 系统对外作功为正,反之为负
系统内能增大 U为正,反之为负
2-3 闭口系统的热力学第一定律表达式
热力学能(内能)
2-3 闭口系统的热力学第一定律表达式
Q ΔU
第二章 热力学第一定律

(二)热力学第一定律
热力学第一定律实质就是能量守恒和转换 定律在热现象上的应用。 表述1:热可以变为功,功也可以变为热;一 定量的热消灭,必产生一定量的功;消耗一 定量的功时,必出现与之相应数量的热。
表述2:第一类永动机是造不成的
First Law of Thermodynamics
In 1843, at the age of 25, James Prescott Joule did a series of careful experiments to prove the equivalence of heat and work.
A p V
dl
对推进功的说明
1、与宏观流动有关,流动停止,推进功不存在 2、作用过程中,工质仅发生位置变化,无状态变化
3、w推=pv与所处状态有关,是状态量 4、并非工质本身的能量(动能、位能)变化引起, 而由外界(泵与风机)做出,流动工质所携带的能量
可理解为:由于工质的进出,外界与系统之
间所传递的一种机械功,表现为流动工质进 出系统使所携带和所传递的一种能量
4、物理意义:开口系中随工质流动而携带的、取决 于热力状态的能量。
三、稳定流动能量方程
Energy balance for steady-flow systems
稳定流动条件
(P22)
1、
•
•
•
mout min m
2、
•
Q Const
min
uin 1 2
c
2 in
gzin
3、
•
•
Wnet ConstWs
三、总能
热力系统的储存能: 储存于热力系统的能量。 (1)内部储存能———热力学能 (2)外部储存能———宏观动能,宏观位能。
第二章 热力学第一定律2010-11-15
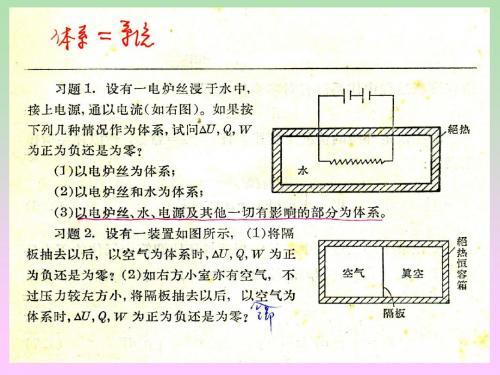
三、焦耳实验 1. 实验装置: 实验装置: 2. 实验过程: 实验过程: 3. 实验结果: 实验结果: 4. 实验结果推论: 实验结果推论: 5. 理想气体的热力学能和焓 理想气体的热力学能和焓: U = f (T) H = f (T)
四、理想气体恒温过程Q、W、△U、△H 的计算 理想气体恒温过程 、 、 五、盖斯定律 1.表述: 表述: 表述 2.应用:例题 应用: 应用
研究正在喷射气体的钢瓶中剩余气体的性质; 、研究正在喷射气体的钢瓶中剩余气体的性质; 注意:系统与环境之间总存在一个界面(实际的或假想的)。 注意:系统与环境之间总存在一个界面(实际的或假想的)。
2. 系统分类:⑴敞开系统;⑵封闭系统;⑶隔离系统 系统分类: 敞开系统; 封闭系统; 例: 二、系统性质 1.定义:由大量粒子构成的系统的一切宏观性质叫系统性质。 定义: 系统性质。 定义 由大量粒子构成的系统的一切宏观性质叫系统性质 例如:T,P,ρ,η,V,m,n, U, H, S…… 例如: 2. 分类: 分类:
硫酸溶于水的过程。 例1. 硫酸溶于水的过程。
若在烧杯中进行, < 。 若在烧杯中进行,Q<0。 若在保温瓶中进行(视为绝热过程) 若在保温瓶中进行(视为绝热过程) ,Q = 0。 。
00-7-23
6
例2.
途径a: 途径 : Q = 0; ; 途径b: 途径 : Q>0; > ; 注意:这里 注意:这里H2视为理想气体
五、过程与途径
1.定义:系统从某一状态(始态)变至另一状态(末态),称为过程。 定义:系统从某一状态(始态)变至另一状态(末态),称为过程。 定义 ),称为过程 实现这一过程的具体步骤称为途径 途径。 实现这一过程的具体步骤称为途径。 2.过程分类:⑴单纯 过程分类: 单纯PVT变化过程;⑵相变化过程;⑶化学反应过程 变化过程; 相变化过程; 过程分类 变化过程 各举一例: 各举一例: 3. 常见的热力学过程: 常见的热力学过程: 恒温过程; 恒温过程; 恒压过程; 恒压过程; 恒容过程; 恒容过程; 绝热过程; 绝热过程; 循环过程; 7-23
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3
虽然右边每个 球产生的力矩 大,但是球的 个数少,左边 每个球产生的 力矩虽小,但 是球的个数多。 于是,轮子不 会持续转动下 去而对外做功, 只会摆动几下, 便停在右图中 所画的位置上。
4
1. 热力系统的储存能
热力系统总储存能 (1) 热力学能
(内能)热力学能
(外部储存能)宏观 动能、宏观位能
不涉及化学变化和核反应时的物质分子热
第二章 热能转换的基 本概念 和基本定律
2.2 热力学第一定律
热力学第一定律就是一切热力过程所必须遵 循的能量转换与守恒定律。本小节重点阐述热力 学第一定律的实质与数学描述,为热力过程计算 奠定理论基础。
1
第一类永动机:
某物质循环一周回复到初始状态,不吸热而向外 放热或作功,这叫“第一类永动机”。这种机器 不消耗任何能量,却可以源源不断的对外做功。
6
1
(2)外部储存能:
. 宏观动能 :Ek Ek= mc2/2 . 宏观位能: Ep Ep= mgz
机械能
(3) 总储存能:E ,单位为 J 或 kJ
E = U + Ek + Ep 比总储存能:e ,单位为 J/kg 或 kJ /kg
e = u + ek + ep
7
2. 热力学第一定律的实质
热力学第一定律实质就是热力过程中的 能量守恒和转换定律 ,可表述为 :
对于单位质量工质,
流动功是由泵或风机加给被输送工质并随 工质流动向前传递的一种能量,非工质本身具 有的能量。
12
2
(2)开口系统的稳定流动能量方程 在 时间内,
进口质量 m1、 流 速 cf1、 标 高 z1 出口质量 m2、 流 速 cf2、 标 高 z2
稳定流动:
13
根据热力学第一定律可得
在 时间内进入系统的能量 在 时间内离开系统的能量
(2)对于流动工质,流动功等于pv,比 焓表示单位质量工质沿流动方向向前传递 的总能量中取决于热力状态的部分 ;
(3)对于不流动工质,不存在流动功, 比焓也不表示能量,仅是状态参数。
(4)工程上一般只需要计算工质经历某 一过程后焓的变化量,而不是其绝对值,所 以焓值的零点可人为地规定。
18
3
(3)技术功 定义:在工程热力学中,将工程技术上可 以直接利用的动能差、位能差及轴功三项之和 称为技术功,用Wt 表示
14
上式可整理成
令
,h 称为比焓。
比焓的物理意义: 比焓是状态参数;对于流动工质,比焓
令
,上式改成
表示每千克工质沿流动方向向前传递的总能
量中取决于热力状态的部分。
15
16
对于单位质量工质, 以上两式称为开口系统的稳定流动能量方程。
对于微元过程 ,稳定流动能量方程写成
17
注意:
(1)无论对于流动工质还是不流动工 质,比焓都是状态参数;
在热能与其它形式能的互相转换过程中, 能的总量始终不变。
不花费能量就可以产生功的第一类永动机 是不可能制造成功的。
进入系统的能量-离开系统的能量 = 系统储存能量的变化
8
3. 闭口系统的热力学第一定律表达式
Q
W
ΔU
对于微元过程,
9
对于可逆过程, 对于单位质量工质, 对于单位质量工质的可逆过程 ,
10
对于单位质量工质 ,
19
开口系统的稳定流动能量方程式可改写为
对于微元过程 ,
对于开口系统的稳定流动过程,系统内各 点的状态都不随时间而变化,所以可以将质量 为 m 的工质作为闭口系统来研究。
20
可以假定质量为m的工质从进口截面处的 状态1变化到出口截面处的状态2,从外界吸收 了热量Q,作了膨胀功W 。
4. 开口系统的稳定流动能量方程式
(1) 稳定流动与流动功
(a) 稳定流动 流动状况不随时间而改变的流动。即任一
流通截面上工质的状态都不随时间而改变。
稳定流动的实现条件:
1)系统和外界交换的能量(功量和热量) 与质量不随时间而变;
2)进、出口截面的状态参数不随时间而 变。
11
(b)流动功 推动工质流动所作的功,也称为推进功。
运动动能和分子之间的位能之和(热能)。
热力学能符号:U,单位:J 或kJ 。
5
比热力学能:
单位质量工质的热力学能 。符号:u;单 位:J/kg 或kJ/kg。比热力学能是状态参数。
气体工质的比热力学能可表示为
u f T , v
任何状态下系统热力学能的数值不可能为 零。由于在工程热力学中只计算工质在状态变 化中的热力学能的变化量,因此热力学能的零 点可以人为地规定,例如,通常取0K时气体 的热力学能为零。
2
欧洲,早期最著名的一个永动机设计 方案是十三世纪时一个叫边缘安 装着12个可活动的短杆,每个短杆的 一端装有一个铁球。方案的设计者认 为,右边的球比左边的球离轴远些, 因此,右边的球产生的转动力矩要比 左边的球产生的转动力矩大。这样轮 子就会永无休止地转动下去,并且带 动机器转动。这个设计被不少人以不 同的形式复制出来,但从未实现不停 息的转动。
根据闭口系统的热力学第一定律表达式
对比开口系统的稳定流动能量方程式
可得
21
对可逆过程,
式中,v 恒为正值,负号表示技术功的正负 与dp 相反。
22
将上式代入开口系统的稳定流动能量方程式 (适用于一般过程)
可得
(适用于可逆过程)
对于微元可逆过程,
技术功的图形表示
23
4
虽然右边每个 球产生的力矩 大,但是球的 个数少,左边 每个球产生的 力矩虽小,但 是球的个数多。 于是,轮子不 会持续转动下 去而对外做功, 只会摆动几下, 便停在右图中 所画的位置上。
4
1. 热力系统的储存能
热力系统总储存能 (1) 热力学能
(内能)热力学能
(外部储存能)宏观 动能、宏观位能
不涉及化学变化和核反应时的物质分子热
第二章 热能转换的基 本概念 和基本定律
2.2 热力学第一定律
热力学第一定律就是一切热力过程所必须遵 循的能量转换与守恒定律。本小节重点阐述热力 学第一定律的实质与数学描述,为热力过程计算 奠定理论基础。
1
第一类永动机:
某物质循环一周回复到初始状态,不吸热而向外 放热或作功,这叫“第一类永动机”。这种机器 不消耗任何能量,却可以源源不断的对外做功。
6
1
(2)外部储存能:
. 宏观动能 :Ek Ek= mc2/2 . 宏观位能: Ep Ep= mgz
机械能
(3) 总储存能:E ,单位为 J 或 kJ
E = U + Ek + Ep 比总储存能:e ,单位为 J/kg 或 kJ /kg
e = u + ek + ep
7
2. 热力学第一定律的实质
热力学第一定律实质就是热力过程中的 能量守恒和转换定律 ,可表述为 :
对于单位质量工质,
流动功是由泵或风机加给被输送工质并随 工质流动向前传递的一种能量,非工质本身具 有的能量。
12
2
(2)开口系统的稳定流动能量方程 在 时间内,
进口质量 m1、 流 速 cf1、 标 高 z1 出口质量 m2、 流 速 cf2、 标 高 z2
稳定流动:
13
根据热力学第一定律可得
在 时间内进入系统的能量 在 时间内离开系统的能量
(2)对于流动工质,流动功等于pv,比 焓表示单位质量工质沿流动方向向前传递 的总能量中取决于热力状态的部分 ;
(3)对于不流动工质,不存在流动功, 比焓也不表示能量,仅是状态参数。
(4)工程上一般只需要计算工质经历某 一过程后焓的变化量,而不是其绝对值,所 以焓值的零点可人为地规定。
18
3
(3)技术功 定义:在工程热力学中,将工程技术上可 以直接利用的动能差、位能差及轴功三项之和 称为技术功,用Wt 表示
14
上式可整理成
令
,h 称为比焓。
比焓的物理意义: 比焓是状态参数;对于流动工质,比焓
令
,上式改成
表示每千克工质沿流动方向向前传递的总能
量中取决于热力状态的部分。
15
16
对于单位质量工质, 以上两式称为开口系统的稳定流动能量方程。
对于微元过程 ,稳定流动能量方程写成
17
注意:
(1)无论对于流动工质还是不流动工 质,比焓都是状态参数;
在热能与其它形式能的互相转换过程中, 能的总量始终不变。
不花费能量就可以产生功的第一类永动机 是不可能制造成功的。
进入系统的能量-离开系统的能量 = 系统储存能量的变化
8
3. 闭口系统的热力学第一定律表达式
Q
W
ΔU
对于微元过程,
9
对于可逆过程, 对于单位质量工质, 对于单位质量工质的可逆过程 ,
10
对于单位质量工质 ,
19
开口系统的稳定流动能量方程式可改写为
对于微元过程 ,
对于开口系统的稳定流动过程,系统内各 点的状态都不随时间而变化,所以可以将质量 为 m 的工质作为闭口系统来研究。
20
可以假定质量为m的工质从进口截面处的 状态1变化到出口截面处的状态2,从外界吸收 了热量Q,作了膨胀功W 。
4. 开口系统的稳定流动能量方程式
(1) 稳定流动与流动功
(a) 稳定流动 流动状况不随时间而改变的流动。即任一
流通截面上工质的状态都不随时间而改变。
稳定流动的实现条件:
1)系统和外界交换的能量(功量和热量) 与质量不随时间而变;
2)进、出口截面的状态参数不随时间而 变。
11
(b)流动功 推动工质流动所作的功,也称为推进功。
运动动能和分子之间的位能之和(热能)。
热力学能符号:U,单位:J 或kJ 。
5
比热力学能:
单位质量工质的热力学能 。符号:u;单 位:J/kg 或kJ/kg。比热力学能是状态参数。
气体工质的比热力学能可表示为
u f T , v
任何状态下系统热力学能的数值不可能为 零。由于在工程热力学中只计算工质在状态变 化中的热力学能的变化量,因此热力学能的零 点可以人为地规定,例如,通常取0K时气体 的热力学能为零。
2
欧洲,早期最著名的一个永动机设计 方案是十三世纪时一个叫边缘安 装着12个可活动的短杆,每个短杆的 一端装有一个铁球。方案的设计者认 为,右边的球比左边的球离轴远些, 因此,右边的球产生的转动力矩要比 左边的球产生的转动力矩大。这样轮 子就会永无休止地转动下去,并且带 动机器转动。这个设计被不少人以不 同的形式复制出来,但从未实现不停 息的转动。
根据闭口系统的热力学第一定律表达式
对比开口系统的稳定流动能量方程式
可得
21
对可逆过程,
式中,v 恒为正值,负号表示技术功的正负 与dp 相反。
22
将上式代入开口系统的稳定流动能量方程式 (适用于一般过程)
可得
(适用于可逆过程)
对于微元可逆过程,
技术功的图形表示
23
4
