高中立体几何经典题型练习题(含答案)
高三数学立体几何专项练习题及答案

高三数学立体几何专项练习题及答案一、选择题1. 下列哪个几何体的所有面都是三角形?A. 正方体B. 圆柱体C. 正六面体D. 球体答案:C2. 一个有8个面的多面体,其中6个面是正方形,另外2个面是等边三角形,它的名字是?A. 正八面体B. 正十二面体C. 正二十面体D. 正二十四面体答案:C3. 空间中任意一点到四个角落连线的垂直距离相等的四棱锥称为?A. 正四棱锥B. 圆锥台C. 四棱锥D. 无法确定答案:C4. 任意多面体的面数与顶点数、棱数的关系是?A. 面数 + 顶点数 = 棱数 + 2B. 面数 + 棱数 = 顶点数 + 2C. 顶点数 + 棱数 = 面数 + 2D. 顶点数 + 面数 = 棱数 + 2答案:A5. 求下列多面体的棱数:(1)正六面体(2)正八面体(3)正十二面体答案:(1)正六面体的棱数为 12(2)正八面体的棱数为 24(3)正十二面体的棱数为 30二、填空题1. 下列说法正确的是:一棱锥没有底面时,它的底面是一个______。
答案:点2. 铅垂线是指从一个多面体的一个顶点到与它相对的棱上所作的垂线,它与该棱垂足的连线相交于该多面体的______上。
答案:中点3. 对正八面体,下列说法不正确的是:_____条对角线与_____两两垂直。
答案:六,相邻面三、计算题1. 一个棱锥的底面是一个边长为6cm的正三角形,其高为8cm。
求棱锥体积。
解答:底面积 S = (1/2) ×底边长 ×高 = (1/2) × 6 × 8 = 24 cm²棱锥体积 V = (1/3) × S ×高 = (1/3) × 24 × 8 = 64 cm³所以,棱锥的体积为64 cm³。
2. 一个正四棱锥的底面是一个边长为10cm的正方形,其高为12cm。
求四棱锥的体积。
解答:底面积 S = 边长² = 10² = 100 cm²四棱锥体积 V = (1/3) × S ×高 = (1/3) × 100 × 12 = 400 cm³所以,四棱锥的体积为400 cm³。
高中数学立体几何专项练习题及答案

高中数学立体几何专项练习题及答案一、选择题1. 下面哪个选项不是描述柱体的特点?A. 体积恒定B. 底面形状不限C. 侧面是矩形D. 顶面和底面平行答案:A2. 如果一个四面体的一个顶点的对边垂直于底面,那么这个四面体是什么类型?A. 正方形四面体B. 倒立四面体C. 锥体D. 正方锥体答案:C3. 以下哪个选项正确描述了一个正方体的特点?A. 全部面都是正方形B. 12 条棱长度相同C. 8 个顶点D. 6 个面都是正方形答案:D4. 若长方体的高度是 6cm,底面积是 5cm²,底面对角线长为 a cm,那么 a 的值为多少?A. √11B. √29C. √31D. √41答案:C二、填空题1. 一个正方体的棱长为 4cm,它的体积是多少?答案:64cm³2. 一个球的表面积是100π cm²,那么它的半径是多少?答案:5cm3. 一个圆柱体的底面半径为 3cm,高度为 8cm,它的体积是多少?答案:72π cm³4. 一个圆锥的底面半径为 6cm,高度为 10cm,它的体积是多少?答案:120π cm³三、计算题1. 一个四棱锥的底面是边长为 5cm 的正方形,高度为 8cm,它的体积是多少?答案:单位为 cm³,计算过程如下:首先计算底面积:5cm * 5cm = 25cm²再计算体积:25cm² * 8cm / 3 = 200cm³2. 一个圆柱体的底面直径为 12cm,高度为 15cm,它的体积是多少?答案:单位为 cm³,计算过程如下:首先计算底面半径:12cm / 2 = 6cm再计算底面积:π * 6cm * 6cm = 36π cm²最后计算体积:36π cm² * 15cm = 540π cm³3. 一个球的直径为 8cm,它的体积是多少?答案:单位为 cm³,计算过程如下:首先计算半径:8cm / 2 = 4cm再计算体积:4/3 * π * 4cm * 4cm * 4cm = 268.08π cm³4. 一个圆锥的底面半径为 10cm,高度为 20cm,它的体积是多少?答案:单位为 cm³,计算过程如下:首先计算底面积:π * 10cm * 10cm = 100π cm²最后计算体积:100π cm² * 20cm / 3 = 2000π cm³四、解答题1. 若一个长方体的长度、宽度、高度分别为 a、b、c,它的表面积为多少?答案:单位为 cm²,计算过程如下:首先计算侧面积:2 * (a * b + a * c + b * c)再计算底面积:a * b最后计算表面积:2 * (a * b + a * c + b * c) + a * b2. 一个四棱锥的底面为边长为 a 的正三角形,高度为 h,求这个四棱锥的体积。
高三立体几何习题(含答案)

CBAC1B1A1高三立体几何习题一、填空题1.已知AB是球O的一条直径,点1O是AB上一点,若14OO=,平面α过点1O且垂直AB,截得圆1O,当圆1O的面积为9π时,则球O的表面积是.【答案】100p2.把一个大金属球表面涂漆,共需油漆2.4公斤.若把这个大金属球熔化制成64个大小都相同的小金属球,不计损耗,将这些小金属球表面都涂漆,需要用漆公斤.【答案】9.63.已知球的表面积为64π2cm,用一个平面截球,使截面圆的半径为2cm,则截面与球心的距离是cm【答案】234.一个圆锥与一个球体积相等且圆锥的底面半径是球半径的2倍,若圆锥的高为1,则球的表面积为.【答案】4p5.一个底面置于水平面上的圆锥,若主视图是边长为2的正三角形,则圆锥的侧面积为.【答案】4p6.如图所示:在直三棱柱111ABC A B C-中,AB BC⊥,1AB BC BB==,则平面11A B C与平面ABC所成的二面角的大小为.【答案】4π二、选择题1.如图,已知圆锥的底面半径为10r=,点Q为半圆弧AB的中点,点P为母线SA的中点.若PQ与SO所成角为4π,则此圆锥的全面积与体积分别为()A.100051006,3ππB.10005100(16),3ππ+C.100031003,3ππD.10003100(13),3ππ+【答案】B2.如图,取一个底面半径和高都为R的圆柱,从圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥,把所得的几何体与一个半径为R的半球放在同一水平面α上.用一平行于平面α的平面去截这两个几何体,截面分别为圆面和圆环面(图中阴影部分).设截面面积分别为S圆和S圆环,那么()A.S圆>S圆环 B.S圆<S圆环 C.S圆=S圆环 D.不确定3.如图所示,PAB∆所在平面α和四边形ABCD所在的平面β互相垂直,且ADα⊥,BCα⊥,4AD=,8BC=,6AB=,若tan2tan1ADP BCP∠-∠=,则动点P在平面α内的轨迹是()A.线段B.椭圆的一部分C.抛物线D.双曲线的一部分PSAQOBβαPBADC【答案】D4.在空间中,下列命题正确的是( )A .若两直线,a b 与直线l 所成的角相等,那么//a bB .空间不同的三点A 、B 、C 确定一个平面C. 如果直线//l 平面α且//l 平面β,那么//αβ D .若直线a 与平面M 没有公共点,则直线//a 平面M 【答案】D5.如图,已知直线l ⊥平面α,垂足为O ,在ABC △中,2,2,22BC AC AB ===,点P 是边AC 上的动点.该三角形在空间按以下条件作自由移动:(1)A l ∈,(2)C α∈.则OP PB +的最大值为( ) (A) 2. (B) 22. (C) 15+. (D) 10. 【答案】C6.平面α上存在不同的三点到平面β的距离相等且不为零,则平面α与平面β的位置关系为( ))(A 平行 )(B 相交)(C 平行或重合 )(D 平行或相交 【答案】D7.a b c 、、表示直线,α表示平面,下列命题正确的是( )A .若//,//αa b a ,则//αbB . 若,α⊥⊥a b b ,则α⊥aC .若,⊥⊥a c b c ,则//a bD .若,αα⊥⊥a b ,则//a b 【答案】D8.下列命题中,正确的个数是【 】① 直线上有两个点到平面的距离相等,则这条直线和这个平面平行; ② a 、b 为异面直线,则过a 且与b 平行的平面有且仅有一个; ③ 直四棱柱是直平行六面体;④ 两相邻侧面所成角相等的棱锥是正棱锥.A 、0B 、1C 、2D 、3 【答案】B9.在四棱锥ABCD V -中,1B ,1D 分别为侧棱VB ,VD 的中点,则四面体11CD AB 的体积与四棱锥 ABCD V -的体积之比为( )A .6:1B .5:1C .4:1D .3:1【答案】C三、解答题1.(本题满分14分)本题共有2小题,第(1)小题满分6分,第(2)小题满分8分. 如图,在长方体1111ABCD A B C D -中,11AD AA ==,2AB =,点E 在棱AB 上移动. (1)证明:11D E A D ⊥;(2)AE 等于何值时,二面角1D EC D --的大小为4π. 【答案】解:(1)在如图所示的空间直角坐标系中,11(1,0,1),(0,0,0),(0,0,1)A D D设(1,,0)([0,2])E y y ∈ 则11(1,,1),(1,0,1)D E y DA =-=…所以110D E DA ⋅=……所以11D E A D ⊥……(2)方法一:设(,,)n u v w =为平面1D CE 的一个法向量 D 1 C 1A 1AE D B 1B C Oxy zABl CαNPO由1100n CD n D E ⎧⋅=⎪⎨⋅=⎪⎩,得200v w u yv w -+=⎧⎨+-=⎩,所以(2)2u y vw v =-⎧⎨=⎩…因为二面角1D EC D --的大小为4π,所以2222(0,0,1)(,,)22cos||42(2)5u v w u v w y π⋅===++-+又[0,2]y ∈,所以23y =-,即当23AE =-时二面角1D EC D --的大小为4π2.(本题满分14分)本题共有2小题,第(1)小题满分6分,第(2)小题满分8分. 如图,在长方体1111ABCD A B C D -中,11AD AA ==,2AB =,点E 在棱AB 上移动. (1)当E 为AB 的中点时,求四面体1E ACD -的体积; (2)证明:11D E A D ⊥. 【答案】解:(1)1122ACE S AE BC ∆=⋅=…因为1D D ACE⊥平面,所以1111136E ACD D ACEACE V V S D D --∆==⋅=… (2)正方形11ADD A 中,11A D AD ⊥……因为11AB ADD A ⊥平面,所以1AB A D ⊥…所以11A D AD E ⊥平面…所以11D E A D ⊥……3.三棱柱111C B A ABC -中,它的体积是315,底面ABC ∆中,090=∠BAC ,3,4==AC AB ,1B 在底面的射影是D ,且D 为BC 的中点.(1)求侧棱1BB 与底面ABC 所成角的大小;(7分) (2)求异面直线D B 1与1CA 所成角的大小.(6分)【答案】解:(1)依题意,⊥D B 1面ABC ,BD B 1∠就是侧棱1BB 与底面ABC 所成的角θ 2分111111431532ABC A B C ABC V S B D B D -∆=⋅=⨯⨯⨯=4分1532B D =5分计算25=BD ,θθtan 25tan 1==BD D B , tan 3,3πθθ=∴= 7分 (2)取11C B 的中点E ,连E A EC 1,,则1ECA ∠(或其补角)为所求的异面直线的角的大小 9分 ⊥D B 1面ABC ,D B 1‖CE ,面ABC ‖面111C B A ⊥∴CE 面111C B A ,E A CE 1⊥∴ 11分33325tan 251===∠EC AE CE A 12分 所求异面直线D B 1与1CA 所成的角6π13分 D 1C 1A 1A EDB 1BC1A(第20题图)D 1C 1B 1BCDA 1A4.在如图所示的几何体中,四边形CDPQ 为矩形,四边形ABCD 为直角梯形,且90BAD ADC ∠=∠=,平面CDPQ ⊥平面ABCD ,112AB AD CD ===,2PD =.(1)若M 为PA 的中点,求证:AC //平面DMQ ;(2)求平面PAD 与平面PBC 所成的锐二面角的大小.【答案】解:(1)如图,设CP 与M 的交点为N ,连接MN .易知点N 是CP 的中点,又M 为PA 的中点,故//AC MN .…4分 于是,由MN ∉平面DMQ ,得//AC 平面DMQ .……………6分(2)如图,以点D 为原点,分别以DA DB DC 、、为x 轴,y 轴,z 轴,建立空间直角坐标系,则(0,0,0),(1,0,0),(1,1,0),(0,2,0),(0,0,2)D A B C P .易知1(0,1,0)n =为平面PAD 的一个法向量,设2(,,)n x y z =为平面PBC 的一个法向量. 则220220n BC x y n PC y z ⎧=-+=⎪⎨=-=⎪⎩2x yz y =⎧⎪⇒⎨=⎪⎩,令1y =,得2(1,1,2)n =.…………………10分 设平面PAD 与平面PBC 所成的锐二面角为θ,则12121cos 2n n n n θ==,…………………12分 故平面PAD 与平面PBC 所成的锐二面角的大小为3π.………………………………………14分5.(本题满分14分) 本题共2个小题,第1小题6分,第2小题8分. 在如图所示的直四棱柱1111ABCD A B C D -中,底面ABCD 是边长为2的 菱形,且60,BAD ∠=︒1 4.AA =(1)求直四棱柱1111ABCD A B C D -的体积; (2)求异面直线11AD BA 与所成角的大小.【答案】解:(1)因菱形ABCD 的面积为2sin6023,AB ⋅︒= ……2分故直四棱柱1111ABCD A B C D -的体积为:12348 3.ABCD S AA ⋅=⨯=底面……6分(2)连接111BC A C 、,易知11//BC AD ,故11A BC ∠等于异面直线11AD BA 与所成角. ……8分由已知,可得111125,23,A B BC AC === ……10分 则在11A BC ∆中,由余弦定理,得222111111117cos .210A B BC AC A BC A B BC +-∠==⋅……12分 故异面直线11AD BA 与所成角的大小为7cos.10arc……14分 6.(本题满分12分)本题共2小题,第1小题满分6分,第2小题满分6分.在长方体1111ABCD A B C D -中,2AB BC ==,13AA =,过11,,A C B 三点的平面截去长方体的一个角后,得到如下所示的几何体111ABCD AC D -.(1)若11A C 的中点为1O ,求求异面直线1BO 与11A D 所成角的大小(用反三角函数值表示); (2)求点D 到平面11A BC 的距离d .【答案】解:(1)按如图所示建立空间直角坐标系.由题知,可得点D(0,0,0)、(2,2,0)B 、1(0,0,3)D 、1(2,0,3)A 、1(0,2,3)C .ABCQP D M CD1A 1C 1D由1O 是11A C 中点,可得1(1,1,3)O . 于是,111(1,1,3),(2,0,0)BO A D =--=-. 设异面直线1BO 与11A D 所成的角为θ,则111111211cos 11||||211BO A D BO A D θ⋅===.因此,异面直线1BO 与11A D 所成的角为11arccos 11. (2)设(,,)nx y z =是平面ABD 的法向量. ∴110,0.n BA n BC ⎧⋅=⎪⎨⋅=⎪⎩ 又11(0,2,3),(2,0,3)BA BC =-=-,∴230,230.y z x z -+=⎧⎨-+=⎩ 取2z =, 可得3,3,2.x y z =⎧⎪=⎨⎪=⎩即平面11BA C 的一个法向量是(3,3,2)n =. ∴||n DB d n ⋅=62211=. 7.(本题满分12分)本题共有2个小题,第1小题满分6分,第2小题满分6分.在长方体1111ABCD A B C D -中,2AB BC ==,13AA =,过1A 、1C 、B 三点的平面截去长方体的 一个角后,得到如下所示的几何体111ABCD AC D -.(1)求几何体111ABCD AC D -的体积,并画出该几何体的左视图(AB 平行主视图投影所在的平面); (2)求异面直线1BC 与11A D 所成角的大小(结果用反三角函数值表示). 【答案】解:2AB BC ==,13AA =,左视图如右图所示. (2)依据题意,有11,A D AD AD BC ,即11A D BC .∴1C BC ∠就是异面直线1BC 与11A D 所成的角. 又1C C BC ⊥,∴113tan 2C C C BC BC ∠==.∴异面直线1BC 与11A D 所成的角是3tan2arc . 8. (本题满分12分)本题共有2个小题,第1小题满分4分,第2小题满分8分.如图,在直三棱柱111C B A ABC -中,已知21===AB BC AA ,AB ⊥BC . (1)求四棱锥111A BCC B -的体积; (2)求二面角111C C A B --的大小.【答案】解:(1)因为AB ⊥BC ,三棱柱111C B A ABC -是直三棱柱,所以11AB BCC B ⊥, 从而11A B 是四棱锥111A BCC B -的高. ……………………………………2分 四棱锥111A BCC B -的体积为1822233V =⨯⨯⨯=…………………………4分 (2)如图(图略),建立空间直角坐标系.则A (2,0,0),C (0,2,0),A 1(2,0,2),B 1(0,0,2),C 1(0,2,2), …………………………………………………6分 设AC 的中点为M ,,,1CC BM AC BM ⊥⊥)0,1,1(11=⊥∴BM C ,C A BM 即平面是平面A 1C 1C 的一个法向量.ABCD1A 1C 1D CBAC 1B 1A 1PSAQOB设平面A 1B 1C 的一个法向量是),,(z y x n =,)0,0,2(),2,2,2(11-=--=B A AC …8分 令z=1,解得x=0,y=1.)1,1,0(=∴n , …………………………………………9分 设法向量n 与BM 的夹角为ϕ,二面角B 1—A 1C —C 1的大小为θ,显然θ为锐角.111.3B AC C π∴--二面角的大小为………………………………………………12分9. (本题满分12分)本题共有2个小题,第1小题满分4分,第2小题满分8分.如图,在正三棱柱111C B A ABC -中,已知16AA =, 三棱柱111C B A ABC -的体积为183. (1)求正三棱柱111C B A ABC -的表面积; (2)求异面直线1BC 与1AA 所成角的大小.【答案】解:(1)因为三棱柱的体积为183,16AA =,从而23334ABC S BC ∆==, 因此23BC =. ………………………2分 该三棱柱的表面积为2+=63+363423ABC S S S ∆=⋅=全侧. ………4分(2)由(1)可知23BC =因为1CC //1AA .所以1BC C ∠为异面直线1BC 与1AA 所成的角, ………8分 在Rt 1BC C ∆中,1233tan 63BC C ∠==, 所以1BC C ∠=6π. 异面直线1BC 与1AA 所成的角6π……………………………………………12分 10.如图,已知圆锥的底面半径为10r =,点Q 为半圆弧AB 的中点,点P 为母线SA 的中点.若直线PQ 与SO 所成的角为4π,求此圆锥的表面积.【答案】解:取OA 的中点M ,连接PM ,又点P 为母线SA 的中点 所以//PM OS ,故MPQ ∠为PQ 与SO 所成的角.………………………2分在Rt MPQ △中,4MPQ π∠=,PM QM =,………………………4分由点Q 为半圆弧AB 的中点知 OQ AB ⊥,在Rt MOQ △中,10,555OQ OM MQ ==⇒=故55PM =,所以105OS =,=106SA . ………………………8分 所以2S 100r ππ==底,101061006S r SA πππ=⋅=⨯⨯=侧………………10分1001006100(16)S S S πππ=+=+=+全底侧.…………………………………12分11.(本大题共有2个小题,满分14分)第(1)小题满分7分,第(2)小题满分7分. 如图,在四棱锥P ABCD -中,底面正方形ABCD 为边长为2,PA ⊥底面ABCD , E 为BC 的中点,PC 与平面PAD 所成的角为2arctan 2.(1)求异面直线AE 与PD 所成角的大小(结果用反三角函数表示); (2)求点B 到平面PCD 的距离.【答案】解:方法1,(1)因为底面ABCD 为边长为2的正方形,⊥PA 底面ABCD ,P S AQ O BMPABCD则 ⊥⇒⎪⎭⎪⎬⎫=⊥⊥CD A PA AD PA CD ADCD 平面PAD ,所以CPD ∠就是CP 与平面PAD 所成的角.………………2分在CDP Rt ∆中,由22tan ==∠PD CD CPD ,得22=PD ,…………………………3分 在PAD Rt ∆中,2=PA .分别取AD 、PA 的中点M 、N ,联结MC 、NC 、MN , 则NMC ∠异面直线AE 与PD 所成角或补角.……………4分 在MNC ∆中,2=MN ,5MC =,3NC =,由余弦定理得,()()22225310cos 10225NMC +-∠==-⋅, 所以10arccos10NMC π∠=-,………6分 即异面直线AE 与PD 所成角的大小为1010arccos .……7分(2)设点B 到平面PCD 的距离为h ,因为BCD P PCD B V V --=,…………………………9分 所以,11113232CD PD h BC CD PA ⨯⋅⋅=⨯⋅⋅,得2h =.……………………………14分 方法2,(1) 如图所示,建立空间直角坐标系,同方法1,得2=PA ,……………3分 则有关点的坐标分别为()0,0,0A ,()2,1,0E ,()0,2,0D ,()2,0,0P .………………5分 所以()2,1,0AE =,()2,2,0-=PD .设θ为异面直线AE 与PD 所成角, 则()101085202102cos =⨯-⨯+⨯+⨯=θ,所以,1010arccos =θ,即异面直线AE 与PD 所成角的大小为1010arccos.…………………………………7分 (2)因为()2,2,0-=PD ,()0,0,2=CD ,()0,2,0=BC ,设()w v u n ,,=, 则由⎩⎨⎧==⇒⎪⎩⎪⎨⎧==⋅=-=⋅w v u u CD n w v PD n 002022,………………………………………………11分 可得()1,1,0=n ,所以222n BC d n⋅===.……………………………………14分 12.(本题共有2个小题,满分14分);第(1)小题满分7分,第(2)小题满分7分.如图,在四棱锥ABCD P -中,底面ABCD 为边长为2的正方形,P ABCD EMNPAB CD Exyz PABCD⊥PA 底面ABCD , 2=PA .(1)求异面直线PC 与BD 所成角的大小; (2)求点A 到平面PBD 的距离.【答案】解:(1)联结AC 与BD 交于点M ,取PA 的中点N ,联结MN ,则CP MN //, 所以NMB ∠为异面直线PC 与BD 所成角或补角.……………………2分 在BMN ∆中,由已知条件得,5=BN ,2=BM ,3=MN ,…………5分所以222MN BM BN +=,2π=∠BMN ,所以异面直PC 与BD 所成角为2π.…7分 (或用线面垂直求异面直线PC 与BD 所成角的大小)(2)设点A 到平面PBD 的距离为h ,因为ABD P PBD A V V --=,……………9分所以,11113232BD PM h BC CD PA ⨯⋅⋅=⨯⋅⋅,得332=h .(或在MAN Rt ∆中求解)………14分 13.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.在正方体1111-ABCD A B C D 中,E 是棱1DD 的中点.(1)求直线BE 与平面11ABB A 所成的角的大小(结果用反三角函数值表示); (2)在棱11C D 上是否存在一点F ,使得1//B F 平面1A BE ,若存在,指明点F 的位置;若不存在,说明理由.【答案】解:(1)以A 为坐标原点,以射线1AB AD AA 、、分别为x y z 、、轴,建立空间 直角坐标系,如图所示.不妨设正方体1111ABCD A B C D -的棱长为a (0a >),则(,0,0),(0,,)2aB a E a ,于是(,,)2a BE a a =- 3分 根据正方体的性质,可知11DA ABB A ⊥平面,故11AD ABB A 是平面的一个法向量且AD =(0,,0)a 4分设直线BE 与平面11ABB A 所成的较为θ,则22sin 0332BE AD a BE ADa a θ===>⨯ 5分 所以2arcsin3θ=,故直线BE 与平面11ABB A 所成的角的大小为2arcsin 3. 6分(2)假设在棱11C D 上是存在一点F ,使得11//B F A BE 平面,设(,,)F x a a (其中0x a ≤≤)111(,0,0),(0,0,),(,0,),(,,0)B a A a BA a a B F x a a =-=- 8分根据(1)可知,(,,)2aBE a a =- 9分设(,,)n x y z =平面1A BE 的一个法向量,则100n BA n BE ⎧=⎪⎨=⎪⎩,即002ax az aax ay z -=⎧⎪⎨--=⎪⎩, 10分 取2z =,则(2,1,2)n =,由于直线11//B F A BE 平面,所以10B F n = 11分NPAB CDMBCDAO zxy即(,,0)(2,1,2)0x a a -=,化简得2()0x a a -+=,解得2ax = 12分 故在棱11C D 上是存在一点F ,使得11//B F A BE 平面,且点F 是棱11C D 的中点. 14分14.在正方体1111-ABCD A B C D 中,E 是棱1DD 的中点. 求直线BE 与11B A 所成的角的大小(结果用反三角函数值表示); 【答案】解:设正方体的棱长为a ,根据正方体的性质可得: 四棱锥E ABCD -的底面积2ABCD S a =,高2aED =2分21143323ABCD a V S ED a =⨯⨯=⨯=,解得2a = 5分因为11//AB A B ,所以ABE ∠即为异面直线BE 与11B A 所成角 或其补角, 8分在ABE 中,2,5,3AB AE BE ===,由余弦定理可得4952cos 02233ABE +-∠==>⨯⨯,即2arccos 3ABE ∠= 11分所以异面直线BE 与11B A 所成的较的大小为2arccos 3ABE ∠=. 12分15.(本题满分12分) 本题共有2个小题,第1小题满分6分,第2小题满分6分. 如图,在Rt AOB ∆中,6OAB π∠=,斜边4AB =,D 是AB 的中点.现将Rt AOB ∆以直角边AO 为轴旋转一周得到一个圆锥,点C 为圆锥底面圆周上的一点,且2BOC π∠=.(1)求该圆锥的全面积;(2)求异面直线AO 与CD 所成角的大小.(结果用反三角函数值表示)【答案】解:(1)在Rt AOB ∆中,2OB =,即圆锥底面半径为2圆锥的侧面积8S rl ππ==侧………………..4’故圆锥的全面积=+8+412S S S πππ==全侧底……………….6’(2)解法一:如图建立空间直角坐标系.则(0,0,23),(2,0,0),(0,1,3)A C D(0,0,23),(2,1,3)AO CD ∴=-=-………………..8’设AO 与CD 所成角为θ,则66cos 42322AO CD AO CDθ⋅-===-⋅⋅………………..10’∴异面直线AO 与CD 所成角为6arc cos4………………..12’ 解法二:过D 作//DM AO 交BO 于M ,连CM则CDM ∠为异面直线AO 与CD 所成角………………..8’ 在Rt AOB ∆中,23AO = 3DM ∴= D Q 是AB 的中点 M ∴是OB 的中点 1OM ∴=5CM ∴=在Rt CDM ∆中,515tan 33CDM ∠==,………………..10’ ED 1C 1A 1B 1CDBA15arctan3CDM ∴∠=,即异面直线AO 与CD 所成角的大小为15arctan 3……………….12’ 16.在棱长为1的正方体1111ABCD A B C D -中,点E 是棱BC 的中点,点F 是棱CD 上的动点. (1)试确定点F 的位置,使得1D E ⊥平面1AB F ;(2)当1D E ⊥平面1AB F 时,求二面角1C EF A --的大小(结果用反三角函数表示). 【答案】解:(1)如图建系,设 ),10(≤≤=x x DF 1分则)0,1,()0,21,1()1,1,0()1,0,1(),0,1,0(),0,0,1(),0,0,0(11x F E D B D B A 2分)0,1,(),1,0,1(),1,21,1(11x AF AB E D ==--=∴, 3分1111,011AB E D AB E D ⊥∴=-=⋅ 4分 由AF E D F AB E D ⊥∴⊥111,平面 5分21,01=⇒=⋅∴x AF E D 6分)0,1,21(F ∴,即F 为CD 中点时F AB E D 11平面⊥。
高中几何体试题及答案

高中几何体试题及答案试题一:正方体的体积和表面积计算某正方体的边长为a,求该正方体的体积和表面积。
解答:正方体的体积 V = a³正方体的表面积 S = 6a²试题二:圆柱的体积和表面积计算已知圆柱的底面半径为r,高为h,求圆柱的体积和表面积。
解答:圆柱的体积V = πr²h圆柱的表面积S = 2πrh + 2πr²试题三:圆锥的体积和表面积计算已知圆锥的底面半径为r,高为h,求圆锥的体积和表面积。
解答:圆锥的体积V = (1/3)πr²h圆锥的表面积 S = πr(r + l),其中l是圆锥的斜高,可通过勾股定理计算:l = √(r² + h²)试题四:球的体积和表面积计算已知球的半径为R,求球的体积和表面积。
解答:球的体积V = (4/3)πR³球的表面积S = 4πR²试题五:棱锥的体积计算已知一个正四棱锥的底面边长为a,高为h,求棱锥的体积。
解答:正四棱锥的体积 V = (1/3)ah²试题六:棱柱的体积和表面积计算已知一个正六棱柱的底面边长为a,高为h,求棱柱的体积和表面积。
解答:正六棱柱的体积 V = 6a²h正六棱柱的表面积S = 6a(a + √3h)试题七:椭圆的面积计算已知椭圆的长轴为2a,短轴为2b,求椭圆的面积。
解答:椭圆的面积A = πab试题八:双曲线的面积计算已知双曲线的实轴为2a,虚轴为2b,求双曲线的面积。
解答:双曲线的面积A = πa(b + a)结束语:以上试题涵盖了高中几何体的常见体积和面积计算问题,希望同学们能够熟练掌握这些基本公式,并能够灵活运用到实际问题中去。
通过不断的练习和思考,相信你们能够在几何学领域取得优异的成绩。
高中几何体试题及答案解析

高中几何体试题及答案解析试题一:立体几何基础题题目:已知一个长方体的长、宽、高分别为a、b、c,求该长方体的体积。
解析:长方体的体积可以通过其三个维度的乘积来计算,即体积V = a × b × c。
答案:V = abc。
试题二:空间向量在立体几何中的应用题目:在空间直角坐标系中,点A(1, 0, 0),点B(0, 1, 0),点C(0, 0, 1),求三角形ABC的面积。
解析:空间直角坐标系中,三角形的面积可以通过向量叉乘来求解。
设向量AB = (-1, 1, 0),向量AC = (-1, 0, 1),向量AB与向量AC 的叉乘结果为向量AB × AC = (1, -1, 1)。
该向量的模即为三角形ABC的面积的两倍。
答案:三角形ABC的面积为√3。
试题三:圆锥体的体积计算题目:已知圆锥的底面半径为r,高为h,求圆锥的体积。
解析:圆锥的体积可以通过公式V = (1/3)πr²h来计算。
答案:V = (1/3)πr²h。
试题四:球体的表面积与体积题目:已知球体的半径为R,求球体的表面积和体积。
解析:球体的表面积可以通过公式A = 4πR²来计算,球体的体积可以通过公式V = (4/3)πR³来计算。
答案:球体的表面积A = 4πR²,球体的体积V = (4/3)πR³。
试题五:旋转体的体积题目:已知圆柱的底面半径为r,高为h,求圆柱的体积。
解析:圆柱的体积可以通过公式V = πr²h来计算。
答案:V = πr²h。
结束语:通过上述试题及答案解析,我们可以看到高中几何体的计算涉及体积、面积和表面积等概念,这些计算在数学和物理等多个领域都有广泛的应用。
掌握这些基础知识对于解决更复杂的几何问题至关重要。
希望这些试题和解析能够帮助学生加深对立体几何概念的理解,并在解题过程中培养空间想象能力。
高三精选立体几何大题30题(含详细解答)
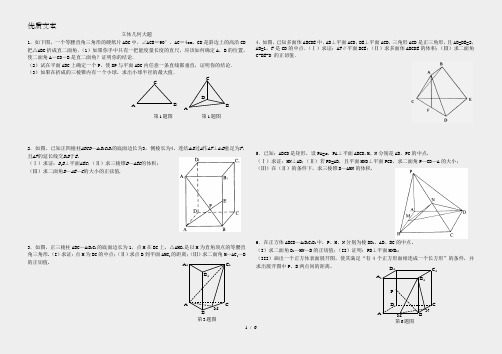
A BC第1题图ABCD第1题图立体几何大题1.如下图,一个等腰直角三角形的硬纸片ABC中,∠ACB=90°,AC=4cm,CD是斜边上的高沿CD 把△ABC折成直二面角.(1)如果你手中只有一把能度量长度的直尺,应该如何确定A,B的位置,使二面角A-CD-B是直二面角?证明你的结论.(2)试在平面ABC上确定一个P,使DP与平面ABC内任意一条直线都垂直,证明你的结论.(3)如果在折成的三棱锥内有一个小球,求出小球半径的最大值.2.如图,已知正四棱柱ABCD—A1B1C1D1的底面边长为3,侧棱长为4,连结A1B过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E。
(Ⅰ)求证:D1B⊥平面AEC;(Ⅱ)求三棱锥B—AEC的体积;(Ⅲ)求二面角B—AE—C的大小的正弦值.3.如图,正三棱柱ABC—A1B1C1的底面边长为1,点M在BC上,△AMC1是以M为直角顶点的等腰直角三角形.(I)求证:点M为BC的中点;(Ⅱ)求点B到平面AMC1的距离;(Ⅲ)求二面角M—AC1—B 的正切值. 4.如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1,F是CD的中点.(Ⅰ)求证:AF∥平面BCE;(Ⅱ)求多面体ABCDE的体积;(Ⅲ)求二面角C-BE-D 的正切值.5.已知:ABCD是矩形,设PA=a,PA⊥平面ABCD.M、N分别是AB、PC的中点.(Ⅰ)求证:MN⊥AB;(Ⅱ)若PD=AB,且平面MND⊥平面PCD,求二面角P—CD—A的大小;(Ⅲ)在(Ⅱ)的条件下,求三棱锥D—AMN的体积.6.在正方体ABCD—A1B1C1D1中,P、M、N分别为棱DD1、AB、BC的中点。
(I)求二面角B1—MN—B的正切值;(II)证明:PB⊥平面MNB1;(III)画出一个正方体表面展开图,使其满足“有4个正方形面相连成一个长方形”的条件,并求出展开图中P、B两点间的距离。
高中数学立体几何经典题型专题训练试题(含答案)

高中数学立体几何经典题型专题训练试题姓名 班级 学号 得分说明:1、本试卷包括第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
满分100分。
考试时间120分钟。
2、考生请将第Ⅰ卷选择题的正确选项填在答题框内,第Ⅱ卷直接答在试卷上。
考试结束后,只收第Ⅱ卷第Ⅰ卷(选择题)评卷人得 分一.单选题(共10小题,每题3分,共30分)1、如图,在正方体中ABCD-A1B1C1D1,M为BC的中点,点N在四边形CDD1C1及其内部运动.⊥1C1,则N点的轨迹为( )若MN AA.线段B.圆的一部分C.椭圆的一部分D.双曲线的一部分2、如图,正方体ABCD-A1B1C1D1的棱长为1,过点A作平面A1BD的垂线,垂足为H,则以下命题中,错误的是( )A.点H是△A1BD的垂心B.直线AH与CD1的成角为900C.AH的延长线经过点C1D.直线AH与BB1的成角为4503、如图,正方体ABCD-A1B1C1D1中,点P为线段AD1上一动点,点Q为底面ABCD内(含边界)一动点,M为PQ的中点,点M构成的点集是一个空间几何体,则该几何体为( )A.棱柱B.棱锥C.棱台D.球4.下列说法中正确的是( )A.棱柱的面中,至少有两个面互相平行B.棱柱中两个互相平行的平面一定是棱柱的底面C.棱柱中一条侧棱就是棱柱的高D.棱柱的侧面一定是平行四边形,但它的底面一定不是平行四边形5.用一个平面去截一个正方体,所得截面不可能是(1)钝角三角形;(2)直角三角形;(3)菱形;(4)正五边形;(5)正六边形.下述选项正确的是( )A.(1)(2)(5)B.(1)(2)(4)C.(2)(3)(4)D.(3)(4)(5)6、如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=,则下列结论中错误的是( )⊥A.AC BEB.A1C⊥平面AEFC.三棱锥A-BEF的体积为定值D.异面直线AE、BF所成的角为定值7.已知一个正六棱锥的体积为12,底面边长为2,则它的侧棱长为( )A.4B.C.D.28.一正四棱锥的高为2,侧棱与底面所成的角为45°,则这一正四棱锥的斜高等于()A.2B.C.2D.29、如图,正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,M为棱BB1的中点,则下列结论中错误的是( )A.D1O∥平面A1BC1B.D1O⊥平面AMCC.异面直线BC1与AC所成的角等于60°D.点B到平面AMC的距离为10.如图,E为正方体的棱AA1的中点,F为棱AB上的一点,且∠C1EF=90°,则AF:FB=()A.1:1B.1:2C.1:3D.1:4第Ⅱ卷(非选择题)评卷人得 分二.填空题(共14小题,每题3分,共42分)11、正方体ABCD-A1B1C1D1中,M,N分别是AA1和BB1的中点,G是BC上一点,使⊥,则∠D1NG=______.C1N MG12、已知如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为棱DD1,AB上的点(不含顶点).则下列说法正确的是______.①A1C⊥平面B1EF;②△B1EF在侧面上的正投影是面积为定值的三角形;③在平面A1B1C1D1内总存在与平面B1EF平行的直线;④平面B1EF与平面ABCD所成的二面角(锐角)的大小与点E位置有关,与点F位置无关;⑤当E,F分别为中点时,平面B1EF与棱AD交于点P,则三棱锥P-DEF的体积为.⊥,∠BAC=θ(0<θ≤),且13、如图,三棱锥A-BCD中,AB AD⊥,AC ADAB=AC=AD=2,E、F分别为AC、BD的中点,则EF的最大值为______.14、如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记,,那么M,N的大小关系是______.15.若空间四边形ABCD的两条对角线AC,BD的长分别为4,6,过AB的中点E且平行BD,AC的截面四边形的周长为______.⊥1D则EF和BD1的关系是______.16、正方体ABCD-A1B1C1D1中,EF AC⊥,EF A17、已知正方体AC1的棱长为1,点P是面AA1D1D的中心,点Q是面A1B1C1D1的对角线B1D1上一点,且PQ∥平面AA1B1B,则线段PQ的长为______.18、如图,正方体ABCD-A1B1C1D1中,E,F分别为棱DD1,AB上的点.已知下列判断:①A1C⊥平面B1EF;②△B1EF在侧面BCC1B1上的正投影是面积为定值的三角形;③在平面A1B1C1D1内总存在与平面B1EF平行的直线;④平面B1EF与平面ABCD所成的二面角(锐角)的大小与点E的位置有关,与点F的位置无关.其中正确结论的序号为______(写出所有正确结论的序号).19、如图,正方体ABCD-A1B1C1D1的棱长为4,E,F分别是棱CD、C1D1的中点,长为2的线段MN的一个端点M在线段EF上运动,另一个端点N在底面A1B1C1D1上运动,则线段MN 的中点P的轨迹(曲面)与二面角D-C1D1-B1所围成的几何体的体积为______.∈1,且AM=BN,有以下四个结论:20、如图,正方体ABCD-A1B1C1D1中,点M AB∈1,N BC⊥;①AA1MN∥;②A1C1MN③MN与面A1B1C1D1成0°角;④MN与A1C1是异面直线.其中正确结论的序号是______.21、在正方体ABCD-A1B1C1D1中,过对角线BD1的一个平面交AA1于点E,交CC1于F,①四边形BFD1E一定是平行四边形②四边形BFD1E有可能是正方形③四边形BFD1E在底面ABCD内的投影一定是正方形④四边形BFD1E点有可能垂直于平面BB1D以上结论正确的为______(写出所有正确结论的编号)22、如图,正方体ABCD-A1B1C1D1中,对角线BD1与过A1、D、C1的平面交于点M,则=______.23.设A是自然数集的一个非空子集,如果k2A∉,且A,那么k是A的一个“酷元”,⊆,且集合M中的两个元素都是“酷元”那么这样的结给定S={0,1,2,3,4,5},设M S合M有______个.24、如图,AC为圆O的直径,B为圆周上不与A、C重合的点,SA⊥圆O所在的平面,连接SB、SC、AB、BC,则图中直角三角形的个数是______.评卷人得 分三.简答题(共28分)25、四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,点P为平面ABCD所在平面外的⊥.一点,若△PAD为等边三角形,求证:PB AD26、如图,设三棱锥S-ABC的三个侧棱与底面ABC所成的角都是60°,又∠BAC=60°,且⊥.SA BC(1)求证:S-ABC为正三棱锥;(2)已知SA=a,求S-ABC的全面积.27、如图,E、F、G、H分别是空间四边形ABCD四边上的中点.(1)若BD=2,AC=6,则EG2+HF2等于多少?(2)若AC与BD成30°的角,且AC=6,BD=4,则四边形EFGH的面积等于多少?28、已知三棱锥S-ABC的三条侧棱SA、SB、SC两两互相垂直且长度分别为a、b、c,设O 为S在底面ABC上的射影.求证:(1)O为△ABC的垂心;(2)O在△ABC内;(3)设SO=h,则++=.29.已知正三棱锥的高为1,底面边长为2,其内有一个球和该三棱锥的四个面都相切,求:(1)棱锥的全面积;(2)球的半径R.30、如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC 的中点,F在棱AC上,且AF=3FC.(1)求三棱锥D-ABC的表面积;(2)求证AC⊥平面DEF;(3)若M为BD的中点,问AC上是否存在一点N,使MN∥平面DEF?若存在,说明点N 的位置;若不存在,试说明理由.参考答案评卷人得 分一.单选题(共__小题)1、如图,在正方体中ABCD-A1B1C1D1,M为BC的中点,点N在四边形CDD1C1及其内部运动.⊥1C1,则N点的轨迹为( )若MN AA.线段B.圆的一部分C.椭圆的一部分D.双曲线的一部分答案:A解析:解:正方体中ABCD-A1B1C1D1中,M为BC的中点,点N在四边形CDD1C1及其内部运动;如图所示,取CD、C1D1的中点Q、P,连接PQ,⊥1C1;当点N在线段PQ上时,MN A因为正方体ABCD-A1B1C1D1中,⊥1D1,连接B1D1,交A1C1于点O,∴B1D1A取B1C1的中点E,连接PE,则PE B∥1D1,⊥1C1;∴PE A∥1,又CC1⊥平面A1B1C1D1,PQ CC∴PQ⊥平面A1B1C1D1,∵A1C1⊂平面A1B1C1D1,⊥1C1;∴PQ A且PQ∩PE=P,∴A1C1⊥平面PQME,PQ⊂平面PQME,⊥;∴A1C1PQ∴N点的轨迹为线段PQ.故选:A.2、如图,正方体ABCD-A1B1C1D1的棱长为1,过点A作平面A1BD的垂线,垂足为H,则以下命题中,错误的是( )A.点H是△A1BD的垂心B.直线AH与CD1的成角为900C.AH的延长线经过点C1D.直线AH与BB1的成角为450答案:D解析:解:由ABCD-A1B1C1D1是正方体,得A-A1BD是一个正三棱锥,因此A点在平面A1BD上的射影H是三角形A1BD的中心,故A正确;⊥1B,又CD1A∥1B,可得直线AH与CD1的成角为90°,故B正确;∵AH⊥面A1BD,∴AH A连接AC1,由三垂线定理及线面垂直的判定可得AC1⊥面A1DB,再由过一点与已知平面垂直的直线有且只有一条可得AH与AC1重合,可得C正确;直线AH与BB1所成的角,即为AH与AA1所成的角,设为θ,由正方体棱长为1,可得正三棱锥的底面边长为,从而求得AH=,则cos,∴D错误.故选:D.3、如图,正方体ABCD-A1B1C1D1中,点P为线段AD1上一动点,点Q为底面ABCD内(含边界)一动点,M为PQ的中点,点M构成的点集是一个空间几何体,则该几何体为( )A.棱柱B.棱锥C.棱台D.球答案:A解析:解:∵Q点不能超过边界,若P点与A点重合,设AB中点E、AD中点F,移动Q点,则此时M点的轨迹为:以AE、AF为邻边的正方形;下面把P点从A点向上沿线段AD1移动,在移动过程中可得M点轨迹为正方形,…,最后当P点与D1点重合时,得到最后一个正方形,故所得几何体为棱柱,故选:A4.下列说法中正确的是( )A.棱柱的面中,至少有两个面互相平行B.棱柱中两个互相平行的平面一定是棱柱的底面C.棱柱中一条侧棱就是棱柱的高D.棱柱的侧面一定是平行四边形,但它的底面一定不是平行四边形答案:A解析:解:棱柱的定义是,有两个面互相平行,其余各面都是四边形,相邻的公共边互相平行,有这些面围成的几何体是棱柱;可以判断A正确;B不正确,例如正六棱柱的相对侧面;C 不正确,只有直棱柱满足C的条件;D不正确,例如长方体.故选A5.用一个平面去截一个正方体,所得截面不可能是(1)钝角三角形;(2)直角三角形;(3)菱形;(4)正五边形;(5)正六边形.下述选项正确的是( )A.(1)(2)(5)B.(1)(2)(4)C.(2)(3)(4)D.(3)(4)(5)答案:B解析:解:如图所示截面为三角形ABC,OA=a,OB=b,OC=c,AC2=a2+c2,AB2=a2+b2,BC2=b2+c2∠=>0,∴cos CAB=∴∠CAB为锐角,同理∠ACB与∠ABC也为锐角,即△ABC为锐角三角形;如右图,取相对棱的中点,得到的四边形是菱形;正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,如图为正六边形;经过正方体的一个顶点去切就可得到5边形.但此时不可能是正五边形.故不可能是(1)(2)(4).故选:B.6、如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=,则下列结论中错误的是( )⊥A.AC BEB.A1C⊥平面AEFC.三棱锥A-BEF的体积为定值D.异面直线AE、BF所成的角为定值答案:D解析:解:∵AC⊥平面BB1D1D,又BE⊂平面BB1D1D,⊥.故A正确.∴AC BE∵EF垂直于直线AB1,AD1,∴A1C⊥平面AEF.故B正确.C中由于点B到直线B1D1的距离不变,故△BEF的面积为定值.又点A到平面BEF的距离为,故V A-BEF为定值.C正确当点E在D1处,F为D1B1的中点时,异面直线AE,BF所成的角是∠FBC1,当E在上底面的中心时,F在C1的位置,异面直线AE,BF所成的角是∠EAA1显然两个角不相等,D不正确.故选D.7.已知一个正六棱锥的体积为12,底面边长为2,则它的侧棱长为( )A.4B.C.D.2答案:A解析:解:由于正六棱锥可知底面是六个正三角形组成,∴底面积S=6×=6,∴体积V==12,∴h=,夺直角三角形SOB中,侧棱长为SB=.故选A.8.一正四棱锥的高为2,侧棱与底面所成的角为45°,则这一正四棱锥的斜高等于()A.2B.C.2D.2答案:C解析:解:如图PO⊥底面ABCD,连接OA,取AD的中点E,连接OE,PE,则PE为斜高.∠PAO为侧棱与底面所成的角,且为45°,在直角△PAO中,PO=2,AO=2,PA=4,在直角△AEO中,AE=2,故在直角△PEA中,PE==2.故选C.9、如图,正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,M为棱BB1的中点,则下列结论中错误的是( )A.D1O∥平面A1BC1B.D1O⊥平面AMCC.异面直线BC1与AC所成的角等于60°D.点B到平面AMC的距离为答案:D解析:解:如图,∥,连接B1D1,交A1C1于N,则可证明OD1BN由OD1⊄面A1BC1,BN⊂面A1BC1,可得D1O∥面A1BC1,A正确;⊥,由三垂线定理的逆定理可得OD1AC设正方体棱长为2,可求得OM2=3,,,⊥,由线面垂直的判定可得D1O⊥平面AMC,B正确;则,有OD1OM由正方体的面对角线相等得到△A1BC1为正三角形,即∠A1C1B=60°,∴异面直线BC1与AC所成的角等于60°,C正确;设点B到平面AMC的距离为d,正方体的棱长为2a,则,,由V B-AMC=V A-BCM,得,即,解得:d=,D错误.故选:D.10.如图,E为正方体的棱AA1的中点,F为棱AB上的一点,且∠C1EF=90°,则AF:FB=()A.1:1B.1:2C.1:3D.1:4答案:C解析:解:解:设正方体的棱长为:2,由题意可知C1E==3,∠C1EF=90°,所以设AF=x,12+x2+C1E2=22+22+(2-x)2,解得:x=,所以AF:FB=:=1:3;故选:C.评卷人得 分二.填空题(共__小题)11、正方体ABCD-A1B1C1D1中,M,N分别是AA1和BB1的中点,G是BC上一点,使⊥,则∠D1NG=______.C1N MG答案:90°解析:解:连接MN,∵M,N分别是AA1和BB1的中点,∥1D1,由正方体的几何特征可得MN C在正方体ABCD-A1B1C1D1中,D1C1⊥平面B1C1CB∵C1N⊂平面B1C1CB⊥1N∴D1C1C⊥1N∴MN C⊥,MN∩MG=M,MD1,MG⊂平面MNG又∵C1N MG∴C1N⊥平面MNG又∵NG⊂平面MNG⊥∴C1N NG故∠D1NG=90°故答案为:90°12、已知如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为棱DD1,AB上的点(不含顶点).则下列说法正确的是______.①A1C⊥平面B1EF;②△B1EF在侧面上的正投影是面积为定值的三角形;③在平面A1B1C1D1内总存在与平面B1EF平行的直线;④平面B1EF与平面ABCD所成的二面角(锐角)的大小与点E位置有关,与点F位置无关;⑤当E,F分别为中点时,平面B1EF与棱AD交于点P,则三棱锥P-DEF的体积为.答案:②③⑤解析:解:对于①A1C⊥平面B1EF,不一定成立,因为A1C⊥平面AC1D,而两个平面面B1EF与面AC1D不一定平行.对于②△B 1EF 在侧面BCC 1B 1上 的正投影是面积为定值的三角形,此是一个正确的结论,因为其投影三角形的一边是棱BB 1,而E 点在面上的投影到此棱BB 1的距离是定值,故正确;对于③在平面A 1B 1C 1D 1内总存在与平面B 1EF 平行的直线,此两平面相交,一个面内平行于两个平面的交线一定平行于另一个平面,此结论正确;对于④平面B 1EF 在平面ABCD 中的射影为△DFB ,面积为定值,但△B 1EF 的面积不定,故不正确;对于⑤由面面平行的性质定理可得EQ B ∥1F ,故D 1Q=,B 1Q PF ∥,故AP=,所以三棱锥P-DEF 的体积为,故正确故答案为:②③⑤.13、如图,三棱锥A-BCD 中,AB AD ⊥,AC AD ⊥,∠BAC=θ(0<θ≤),且AB=AC=AD=2,E 、F 分别为AC 、BD 的中点,则EF 的最大值为______.答案:解析:⊥,垂足为G,连接GE,解:过F作FG AB⊥,∵AD AB∥,∴G为AB的中点,∴AD FG∴FG=1,AG=1,∵E为AC的中点,∴AE=1,∠BAC=θ,∴EG=∵AD⊥平面ABC,∴FG⊥平面ABC,△中,EF===,在Rt FGE∵0,∴EF≤.故答案是.14、如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记,,那么M,N的大小关系是______.答案:M=N解析:解:根据平面中直角三角形的勾股定理类比得,S ABC△2=S PAB△2+S PBC△2+S PAC△2①,由等体积法得,∴②,①÷②整理得M=N.故答案为:M=N.15.若空间四边形ABCD的两条对角线AC,BD的长分别为4,6,过AB的中点E且平行BD,AC的截面四边形的周长为______.答案:10解析:解:设截面四边形为EFGH,F、G、H分别是BC、CD、DA的中点,∴EF=GH=2,FG=HE=3,∴周长为2×(2+3)=10.故答案为:10.16、正方体ABCD-A1B1C1D1中,EF AC⊥,EF A⊥1D则EF和BD1的关系是______.答案:平行解析:解:法一:根据图象可知:⊥,AC∩B1C=C,⊥1D,A1D B∥1C,B1C EFEF AC⊥,EF A∥.∴EF⊥面AB1C,而BD1⊥面AB1C,即BD1EF法二:建立以D1为原点的空间直角坐标系D1-xyz,且设正方形的边长为1所以就有D1(0,0,0),B(1,1,0),A1(1,0,0),D(0,0,1),A(1,0,1),C(0,1,1)所以=(-1,0,1),=(-1,1,0),=(-1,-1,1)⊥1,所以•=-1+1=0 所以A1D BD⊥1,•=1-1=0 所以AC BD所以BD1与A1D和AC都垂直又∵EF是AC、A1D的公共垂线,∥.∴BD1EF故答案为:平行.17、已知正方体AC1的棱长为1,点P是面AA1D1D的中心,点Q是面A1B1C1D1的对角线B1D1上一点,且PQ∥平面AA1B1B,则线段PQ的长为______.答案:解析:解:∵正方体AC1的棱长为1,点P是面AA1D1D的中心,点Q是面A1B1C1D1的对角线B1D1上一点,且PQ∥平面AA1B1B,连结AD1,AB1,∴由正方体的性质,得:AD1∩A1D=P,P是AD1的中点,∥1,PQ AB∴PQ=AB1==.故答案为:.18、如图,正方体ABCD-A1B1C1D1中,E,F分别为棱DD1,AB上的点.已知下列判断:①A 1C ⊥平面B 1EF ;②△B 1EF 在侧面BCC 1B 1上的正投影是面积为定值的三角形;③在平面A 1B 1C 1D 1内总存在与平面B 1EF 平行的直线;④平面B 1EF 与平面ABCD 所成的二面角(锐角)的大小与点E 的位置有关,与点F 的位置无关.其中正确结论的序号为______(写出所有正确结论的序号).答案:②③解析:解:若A 1C ⊥平面B 1EF ,则A 1C B ⊥1F ,由三垂线逆定理知:B 1F A ⊥1B ,又当F 与A 不重合时,B 1F 与A 1B 不垂直,∴①错误;∵E 在侧面BCC 1B 1上的投影在CC 1上,F 在侧面BCC 1B 1上的投影是B ,∴△B 1EF 在侧面BCC 1B 1上的正投影是三角形,三角形的面积S=×棱长×棱长为定值.∴②正确;设平面A 1B 1C 1D 1∩平面B 1EF=l ,∵平面A 1B 1C 1D 1内总存在与l 平行的直线,由线面平行的判定定理得与l 平行的直线,与平面B 1EF 平行,∴③正确;设E 与D 重合,F 位置变化,平面B 1EF 与平面ABCD 所成的二面角(锐角)的大小也在变化,∴④错误.故答案为:②③.19、如图,正方体ABCD-A 1B 1C 1D 1的棱长为4,E ,F 分别是棱CD 、C 1D 1的中点,长为2的线段MN 的一个端点M 在线段EF 上运动,另一个端点N 在底面A 1B 1C 1D 1上运动,则线段MN 的中点P 的轨迹(曲面)与二面角D-C 1D 1-B 1所围成的几何体的体积为______.答案:解析:解:依题意知|FP|=|MN|=1,因此点P的轨迹是以点F为球心、1为半径的球的.∴所求几何体的体积是×π×13=.故答案为:.∈1,且AM=BN,有以下四个结论:∈1,N BC20、如图,正方体ABCD-A1B1C1D1中,点M AB⊥;①AA1MN∥;②A1C1MN③MN与面A1B1C1D1成0°角;④MN与A1C1是异面直线.其中正确结论的序号是______.答案:①③解析:解:当M 为A ,N 为B ,排除②;当M 为B 1,N 为C 1,排除④.作MM′A ⊥1B 1于M′,作NN′B ⊥1C 1于N′,易证|MM′|=|NN′|,MM′NN′∥∴MN M′N′∥,由此知①③正确.故答案为:①③21、在正方体ABCD-A 1B 1C 1D 1中,过对角线BD 1的一个平面交AA 1于点E ,交CC 1于F ,①四边形BFD 1E 一定是平行四边形②四边形BFD 1E 有可能是正方形③四边形BFD 1E 在底面ABCD 内的投影一定是正方形④四边形BFD 1E 点有可能垂直于平面BB 1D以上结论正确的为______(写出所有正确结论的编号)答案:①③④解析:解:如图:①由平面BCB 1C 1∥平面ADA 1D 1,并且B 、E 、F 、D 1四点共面,∴ED 1BF ∥,同理可证,FD 1EB ∥,故四边形BFD 1E 一定是平行四边形,故①正确;②若BFD 1E 是正方形,有ED 1BE ⊥,这个与A 1D 1BE ⊥矛盾,故②错误;③由图得,BFD 1E 在底面ABCD 内的投影一定是正方形ABCD ,故③正确;④当点E 和F 分别是对应边的中点时,平面BFD 1E ⊥平面BB 1D 1,故④正确.故答案为:①③④.22、如图,正方体ABCD-A 1B 1C 1D 1中,对角线BD 1与过A 1、D 、C 1的平面交于点M ,则=______.答案:2解析:解:由正方体的性质可得:D 1B ⊥平面DA 1C 1,∴D 1M 是三棱锥D 1-A 1DC 1的高.不妨设正方体的棱长为1.∵=,∴=,解得D 1M==.∴=2.故答案为:2.∉,且A,那么k是A的一个“酷元”,23.设A是自然数集的一个非空子集,如果k2A⊆,且集合M中的两个元素都是“酷元”那么这样的结给定S={0,1,2,3,4,5},设M S合M有______个.答案:5解析:解:∵S={0,1,2,3,4,5},由题意可知:集合M不能含有0,1,也不能同时含有2,4故集合M可以是{2,3}、{2,5}、{3,5}、{3,4}、{4,5},共5个故答案为:524、如图,AC为圆O的直径,B为圆周上不与A、C重合的点,SA⊥圆O所在的平面,连接SB、SC、AB、BC,则图中直角三角形的个数是______.答案:4解析:解:题题意SA⊥圆O所在的平面,AC为圆O的直径,B为圆周上不与A、C重合的点,可得出AB,BC垂直由此两个关系可以证明出CB垂直于面SAB,由此可得△ADB,△SAC,△ABC,△SBC都是直角三角形故图中直角三角形的个数是4个故答案为:4.评卷人得 分三.简答题(共__小题)25、四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,点P为平面ABCD所在平面外的⊥.一点,若△PAD为等边三角形,求证:PB AD答案:证明:如图,连结BD ,取AD 的中点E ,连结PE ,BE ;从而易知△ABD 也是等边三角形,又∵△PAD 为等边三角形,∴AD PE ⊥,AD BE ⊥,又∵PE∩BE=E ;故AD ⊥平面PBE ;故AD PB ⊥.解析:证明:如图,连结BD ,取AD 的中点E ,连结PE ,BE ;从而易知△ABD 也是等边三角形,又∵△PAD 为等边三角形,∴AD PE ⊥,AD BE ⊥,又∵PE∩BE=E ;故AD ⊥平面PBE ;故AD PB ⊥.26、如图,设三棱锥S-ABC 的三个侧棱与底面ABC 所成的角都是60°,又∠BAC=60°,且SA BC ⊥.(1)求证:S-ABC 为正三棱锥;(2)已知SA=a ,求S-ABC 的全面积.答案:(1)证明:正棱锥的定义中,底面是正多边形;顶点在底面上的射影是底面的中心,两个条件缺一不可.作三棱锥S-ABC 的高SO ,O 为垂足,连接AO 并延长交BC 于D .因为SA BC ⊥,所以AD BC ⊥.又侧棱与底面所成的角都相等,从而O 为△ABC 的外心,OD 为BC 的垂直平分线,所以AB=AC .又∠BAC=60°,故△ABC 为正三角形,且O 为其中心.所以S-ABC 为正三棱锥.(2)解:在Rt SAO △中,由于SA=a ,∠SAO=60°,所以SO=a ,AO=a .因O 为重心,所以AD=AO=a ,BC=2BD=2ADcot60°=a ,OD=AD=a .在Rt SOD △中,SD 2=SO 2+OD 2=(a )2+(a )2=,则SD=a .于是,(S S-ABC )全=•(a )2sin60°+3••a•a=a 2.解析:(1)证明:正棱锥的定义中,底面是正多边形;顶点在底面上的射影是底面的中心,两个条件缺一不可.作三棱锥S-ABC 的高SO ,O 为垂足,连接AO 并延长交BC 于D .因为SA BC ⊥,所以AD BC ⊥.又侧棱与底面所成的角都相等,从而O 为△ABC 的外心,OD 为BC 的垂直平分线,所以AB=AC .又∠BAC=60°,故△ABC 为正三角形,且O 为其中心.所以S-ABC 为正三棱锥.(2)解:在Rt SAO △中,由于SA=a ,∠SAO=60°,所以SO=a ,AO=a .因O 为重心,所以AD=AO=a ,BC=2BD=2ADcot60°=a ,OD=AD=a .在Rt SOD △中,SD 2=SO 2+OD 2=(a )2+(a )2=,则SD=a .于是,(S S-ABC )全=•(a )2sin60°+3••a•a=a 2.27、如图,E 、F 、G 、H 分别是空间四边形ABCD 四边上的中点.(1)若BD=2,AC=6,则EG 2+HF 2等于多少?(2)若AC 与BD 成30°的角,且AC=6,BD=4,则四边形EFGH 的面积等于多少?答案:解:(1)∵E 、F 、G 、H 分别是空间四边形ABCD 四边上的中点,∴EH BD ∥,且EH=BD ;FG BD ∥,且FG=BD ;∴EH FG ∥,且EH=FG ,∴四边形EFGH 是平行四边形;又BD=2,AC=6,∴EH=BD=1,EF=AC=3,在△EFG 和△HFG 中,由余弦定理得,EG 2=EF 2+FG 2-2EF•FG•cos EFG∠=32+12-2×3×1×cos EFG∠=10-6cos EFG ∠,HF 2=HG 2+FG 2-2HG•FG•cos FGH∠=32+12-2×3×1×cos (π-EFG ∠)=10+6cos EFG ∠,∴EG 2+HF 2=20;(2)∵AC 与BD 成30°的角,且EF AC ∥,FG BD ∥,∴∠EFG=30°,又AC=6,BD=4,∴EF=AC=3,FG=BD=2;∠.∴四边形EFGH的面积为S=EF•FG•sin EFG=3×2×sin30°=3解析:解:(1)∵E、F、G、H分别是空间四边形ABCD四边上的中点,∥,且EH=BD;∴EH BDFG BD∥,且FG=BD;∥,且EH=FG,∴EH FG∴四边形EFGH是平行四边形;又BD=2,AC=6,∴EH=BD=1,EF=AC=3,在△EFG和△HFG中,由余弦定理得,∠EG2=EF2+FG2-2EF•FG•cos EFG∠=32+12-2×3×1×cos EFG∠,=10-6cos EFG∠HF2=HG2+FG2-2HG•FG•cos FGH∠)=32+12-2×3×1×cos(π-EFG=10+6cos EFG∠,∴EG2+HF2=20;(2)∵AC 与BD 成30°的角,且EF AC ∥,FG BD ∥,∴∠EFG=30°,又AC=6,BD=4,∴EF=AC=3,FG=BD=2;∴四边形EFGH 的面积为S=EF•FG•sin EFG=3×2×sin30°=3∠.28、已知三棱锥S-ABC 的三条侧棱SA 、SB 、SC 两两互相垂直且长度分别为a 、b 、c ,设O 为S 在底面ABC 上的射影.求证:(1)O 为△ABC 的垂心;(2)O 在△ABC 内;(3)设SO=h ,则++=.答案:证明:(1)∵SA SB ⊥,SA SC ⊥,∴SA ⊥平面SBC ,BC ⊂平面SBC .∴SA BC ⊥.而AD 是SA 在平面ABC 上的射影,∴AD BC ⊥.同理可证AB CF ⊥,AC BE ⊥,故O 为△ABC 的垂心.(2)证明△ABC 为锐角三角形即可.不妨设a≥b≥c ,则底面三角形ABC 中,AB=为最大,从而∠ACB 为最大角.用余弦定理求得cos ACB=∠>0,∴∠ACB 为锐角,△ABC 为锐角三角形.故O 在△ABC 内.(3)SB•SC=BC•SD ,故SD=,=+,又SA•SD=AD•SO ,∴===+=++=.解析:证明:(1)∵SA SB ⊥,SA SC ⊥,∴SA ⊥平面SBC ,BC ⊂平面SBC .∴SA BC ⊥.而AD 是SA 在平面ABC 上的射影,∴AD BC ⊥.同理可证AB CF ⊥,AC BE ⊥,故O 为△ABC 的垂心.(2)证明△ABC 为锐角三角形即可.不妨设a≥b≥c ,则底面三角形ABC 中,AB=为最大,从而∠ACB 为最大角.用余弦定理求得cos ACB=∠>0,∴∠ACB 为锐角,△ABC 为锐角三角形.故O 在△ABC 内.(3)SB•SC=BC•SD ,故SD=,=+,又SA•SD=AD•SO ,∴===+=++=.29.已知正三棱锥的高为1,底面边长为2,其内有一个球和该三棱锥的四个面都相切,求:(1)棱锥的全面积;(2)球的半径R.答案:解:(1)设正三棱锥的底面中心为H,由题意知PH=1,边长BC=2,取BC中点E,连接HE、PE,则HE=S全=3×=9⊥于点G,(2)过O作OG PE∽△,且OG=OH=R,则△POG PEH∴,∴R=解析:解:(1)设正三棱锥的底面中心为H,由题意知PH=1,边长BC=2,取BC中点E,连接HE、PE,则HE=S全=3×=9⊥于点G,(2)过O作OG PE∽△,且OG=OH=R,则△POG PEH∴,∴R=30、如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC 的中点,F在棱AC上,且AF=3FC.(1)求三棱锥D-ABC 的表面积;(2)求证AC ⊥平面DEF ;(3)若M 为BD 的中点,问AC 上是否存在一点N ,使MN ∥平面DEF ?若存在,说明点N 的位置;若不存在,试说明理由.答案:解:(1)∵AB ⊥平面BCD ,∴AB BC ⊥,AB BD ⊥.∵△BCD 是正三角形,且AB=BC=a ,∴AD=AC=.设G 为CD 的中点,则CG=,AG=.∴,,.三棱锥D-ABC 的表面积为.(2)取AC 的中点H ,∵AB=BC ,∴BH AC ⊥.∵AF=3FC ,∴F 为CH 的中点.∵E 为BC 的中点,∴EF BH ∥.则EF AC ⊥.∵△BCD 是正三角形,∴DE BC ⊥.∵AB ⊥平面BCD ,∴AB DE ⊥.∵AB∩BC=B ,∴DE ⊥平面ABC .∴DE AC ⊥.∵DE∩EF=E ,∴AC ⊥平面DEF .(3)存在这样的点N ,当CN=时,MN ∥平面DEF .连CM ,设CM∩DE=O ,连OF .由条件知,O 为△BCD 的重心,CO=CM .∴当CF=CN 时,MN OF ∥.∴CN=.解析:解:(1)∵AB ⊥平面BCD ,∴AB BC ⊥,AB BD ⊥.∵△BCD 是正三角形,且AB=BC=a ,∴AD=AC=.设G 为CD 的中点,则CG=,AG=.∴,,.三棱锥D-ABC 的表面积为.(2)取AC 的中点H ,∵AB=BC ,∴BH AC ⊥.∵AF=3FC ,∴F 为CH 的中点.∵E 为BC 的中点,∴EF BH ∥.则EF AC ⊥.∵△BCD 是正三角形,∴DE BC ⊥.∵AB ⊥平面BCD ,∴AB DE ⊥.∵AB∩BC=B ,∴DE ⊥平面ABC .∴DE AC ⊥.∵DE∩EF=E ,∴AC ⊥平面DEF .(3)存在这样的点N ,当CN=时,MN ∥平面DEF .连CM ,设CM∩DE=O ,连OF .由条件知,O 为△BCD 的重心,CO=CM .∴当CF=CN 时,MN OF ∥.∴CN=.。
高中立体几何试题(答案)

高中立体几何试题1. 在正方体1111D C B A ABCD -中,求二面角111C BD A --的大小.解析:如图9-43,在平面B C D 11内作11BD E C ⊥,交1BD 于E .连结E A 1,设正方体棱长为a ,在△11BD A 和△11BD C 中,a D C D A ==1111,a B C B A 211==,11BD BD =a 3=,∴ △11BD A ≌△11BD C ,∵ 11BD E C ⊥,∴ 11BD E A ⊥,∴ 11EC A ∠ 二面角111C BD A --的平面角.在Rt △11D BC中,︒=∠9011B C D ,∴ 111112121BD E C BC D C ⋅=⋅,∴ a aa a E C 32321=⋅=,在△11EC A 中,==E C E A 11 a 32,a C A 211=,2132322)2(3232cos 22211-=⋅-⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=∠a a a a a EC A ,110 EC A ∠︒< ︒180<,︒=∠∴120 11EC A2. 如图9-50,点A 在锐二面角-MN -的棱MN 上,在面内引射线AP ,使AP 与MN 所成的∠P AM 为45°,与面所成的角为30°,求二面角-MN -的大小.解析:如图答9-44,取AP 上一点B ,作BH ⊥于H ,连结AH ,则∠BAH 为射线AP 与平面所成的角,∴ ∠BAH =30°,再作BQ ⊥MN ,交MN 于Q ,连结HQ ,则HQ 为BQ 在平面内的射影.由三垂线定理的逆定理,HQ ⊥MN ,∴ ∠BQH 为二面角-MN -的平面角.图答9-44设BQ =a ,在Rt △BAQ 中,∠BQA =90°,∠BAM =45°,∴ a AB 2=,在Rt △BAH 中∠BHA =90°,∠BAH =30°,∴ a BH 22=.在Rt △BHQ 中,∠BHQ =90°,BQ =a ,a BH 22=,∵ ∠BQH 是锐角,∴ ∠BQH =45 即二面角-MN -等于45°. 3. 如图,四棱锥P —ABCD 的底面是直角梯形,AB ∥DC ,AB ⊥BC ,且AB =21CD ,侧棱PB ⊥底面ABCD ,PC =5,BC =3,ΔPAB 的面积等于6,若平面DPA 与平面CPB 所成的二面角为α,求α.解析:平面DPA 与平面CPB 有一公共点P ,要画出它们构成的二面角的平面角必须确定它们公共交线,DA 和CB 的延长线的交点E 是它们的另一公共点.由公理二,PE 就是二面角的公共棱.有了公共棱,二面角的平面角就生了根.解 延长DA 交CB 的延长线于E ,连PE ,则PE 就是平面DPA 和平面CPB 的交线. ∵AB ∥DC ,AB ⊥BC ,∴DC ⊥BC ,PB ⊥底面ABCD.∴PB ⊥DC ,∴DC ⊥平面PCE.作CF ⊥PE 于F ,连DF 由三垂线定理得PE ⊥DF ,∴∠DFC =α.∵AB =21CD ,PC =5,BC =3,∴PB =4. S ΔPAB =6,∴AB =3,CD =6,DC AB =EC EB =21. ∴EB =3,PE =5.∵PB·EC =CF·PE ,∴CF =524.在直角ΔDCF 中,tanα=CFDC =5246=45. α=antan 45. 4. 在正方体ABCD —A 1B 1C 1D 1中,其棱长为a.(1)求证BD 1⊥截面AB 1C ;(2)求点B 到截面AB 1C 的距离;(3)求BB 1与截面AB 1C 所成的角的余弦值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学立体几何练习题精选试卷姓名班级学号得分说明:1、本试卷包括第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
满分100分。
考试时间90分钟。
2、考生请将第Ⅰ卷选择题的正确选项填在答题框内,第Ⅱ卷直接答在试卷上。
考试结束后,只收第Ⅱ卷第Ⅰ卷(选择题)一.单选题(每题2分,共40分)1.设直线l,m和平面α,β,下列条件能得到α∥β的有()①l⊂α,m⊂α,且l∥β,m∥β;②l⊂α,m⊂α且l∥m;③l∥α,m∥β且l∥m.A.1个B.2个C.3个D.0个2.一个四面体中如果有三条棱两两垂直,且垂足不是同一点,这三条棱就象中国武术中的兵器--三节棍,所以,我们常把这类四面体称为“三节棍体”,三节棍体ABCD四个顶点在空间直角坐标系中的坐标分别为A(0,0,0)、B(0,4,0)、C(4,4,0)、D(0,0,2),则此三节棍体外接球的表面积是()A.36πB.24πC.18πD.12π3.一个圆锥的侧面展开图的圆心角为90°,它的表面积为a,则它的底面积为()A.B.C.D.4、如图,三棱柱ABC-A1B1C1的侧棱长和底面边长均为4,且侧棱AA1⊥底面ABC,其主视图是边长为4的正方形,则此三棱柱的侧视图的面积为()A.16B.2C.4D.5.三棱锥P-ABC的侧棱PA,PB,PC两两互相垂直,且PA=PB=PC=2,则三棱锥P-ABC的外接球的体积是()A.2πB.4πC.πD.8π6.在正方体ABCD-A′B′C′D′中,过对角线BD‘的一个平面交AA′于点E,交CC′于点F.则下列结论正确的是()①四边形BFD′E一定是平行四边形②四边形BFD′E有可能是正方形③四边形BFD′E在底面ABCD的投影一定是正方形④四边形BFD′E有可能垂于于平面BB′D.A.①②③④B.①③④C.①②④D.②③④7.如图,在四面体A-BCD中,AB⊥平面BCD,BC⊥CD,若AB=BC=CD=1,则AD=()A.1B.C.D.28.已知a,b是空间两条异面直线,它们所成的角为80°,过空间一点P作直线l,使l与a,b所成角均为50°,这样的l有()A.1条B.2条C.3条D.4条9.满足下面哪一个条件时,可以判定两个不重合的平面α与β平行()A.α内有无数个点到平面β的距离相等B.α内的△ABC与β内的△A"B"C"全等,且AA"∥BB"∥CC"C.α,β都与异面直线a,b平行D.直线l分别与α,β两平面平行10.已知两个不同的平面α,β和两条不重合的直线m,n,有下列四个命题:①若m∥n,n⊂α,则m∥α;②若m∥α,n∥α,且m⊂β,n⊂β,则α∥β;③若m∥α,n⊂α,则m∥n;④若α∥β,m⊂α,则m∥β.其中正确命题的个数是()A.1个B.2个C.3个D.4个11.在直二面角α-AB-β的棱AB上取一点P,过P分别在α、β两个平面内作与棱成45°的斜线PC、PD,那么∠CPD的大小为()A.45°B.60°C.120°D.60°或120°12、如图,将边长为1的正方形ABCD ,沿对角线BD 折起来,使平面ABD ⊥平面C ′BD ,则AC ′=( )A .1B .C .D .13.一个正四棱锥的底面面积为Q ,则它的中截面(过各侧棱的中点的截面)的边长是( ) A .B .C .D .14.某几何体的三视图如图实数,则当x+y 取最大值时,该几何体的体积为( )A .B .C .D .15.空间三条直线a ,b ,c 中,b 和c 是一对异面直线,取三条直线中某两条直线确定平面,那么可以确定平面个数是( ) C /A BC D 正视图 侧视图 俯视图xyξ6 11A.0或1B.1或2C.0或2D.0或1或216.已知二面角α-l-β的大小为60°,且m⊥α,n⊥β,则异面直线m,n所成的角为()A.30°B.120°C.90°D.60°17.设α、β表示平面,l表示不在α内也不在β内的直线,给出下列命题:①若l⊥α,l∥β,则α⊥β;②若l∥β,α⊥β,则l⊥α;③若l⊥α,α⊥β,则l∥β.其中正确的命题是()A.①③B.①②C.②③D.①②③18.三棱锥P-ABC中,PA=PB=PC=AC=1,△ABC是等腰直角三角形,∠ABC=90°.若E为PC 中点,则BE与平面PAC所成的角的大小等于()A.30°B.45°C.60°D.90°19.在正方体A1C中,对角线A1C与平面B1BCC1所成的角是()A.∠A1CB1B.∠A1CC1C.∠A1CB D.∠A1B1C20.若m、n是两条不同的直线,α、β、γ是三个不同的平面,则下列命题中真命题是()A.若m⊥β,m∥α,则α⊥βB.若α∩γ=m,β∩γ=n,m∥n,则α∥βC.若m⊂β,α⊥β,则m⊥αD.若α⊥γ,α⊥β,则β⊥γ二.填空题(每题3分,共15分)21.将边长为a的正方形ABCD沿对角线AC折起,使得BD=a,则三棱锥D-ABC的体积是______.22.如图,图①、②、③是图④表示的几何体的三视图,其中图①是______,图②是______,图③是______(说出视图名称).23.若空间四边形ABCD的两条对角线AC,BD的长分别为4,6,过AB的中点E且平行BD,AC的截面四边形的周长为______.24、如图,以等腰直角三角形斜边BC上的高AD为折痕,把△ABD与△ACD折成互相垂直的两个平面后,某学生得出下列四个结论:①;②∠BAC=60°;③三棱锥D-ABC是正三棱锥;④平面ADC的法向量和平面ABC的法向量互相垂直.其中正确结论的序号是______.(请把正确结论的序号都填上)25.直角三角形ABC中,CA=CB=,M为AB的中点,将△ABC沿CM折叠,使A、B之间的距离为1,则三棱锥M-ABC外接球的体积为______.三.简答题(每题9分,共45分)如图,多面体ABCDEFG中,AB,AC,AD两两垂直,平面ABC∥平面DEFG,平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1.(1)证明四边形ABED是正方形;(2)判断点B,C,F,G是否四点共面,并说明为什么?(3)连接CF,BG,BD,求证:CF⊥平面BDG.27、如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD为梯形,AB平行于CD,,AD1⊥A1C,E是A1B1中点.(1)求证:CD⊥A1D1.(2)求二面角C-D1E-B1的大小.28、如图,直三棱柱ABC-A1B1C1中,AC=BC,AA1=AB,D为BB1的中点,E为AB1上的一点,AE=3EB1.(Ⅰ)证明:DE为异面直线AB1与CD的公垂线;(Ⅱ)设异面直线AB1与CD的夹角为45°,求二面角A1-AC1-B1的大小.29.按下列叙述画出图形(不必写作法):直线a,b相交于点M,点N不在直线a,b上,点N分别与直线a,b确定平面α,β.30、如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,ABCD是直角梯形,AD∥BC,∠BAD=90°,BC=2AD.(1)求证:AB⊥PD;(2)在线段PB上是否存在一点E,使AE∥平面PCD,若存在,指出点E的位置并加以证明;若不存在,请说明理由.参考答案一.单选题(共__小题)1.设直线l,m和平面α,β,下列条件能得到α∥β的有()①l⊂α,m⊂α,且l∥β,m∥β;②l⊂α,m⊂α且l∥m;③l∥α,m∥β且l∥m.A.1个B.2个C.3个D.0个答案:D解析:解:对于①,∵l⊂α,m⊂α,且l∥β,m∥β,当直线l与直线m相交时,α∥β,故①错误;对于②,l⊂α,m⊂α且l∥m,不能得到α∥β,故②错误;对于③,如图,l∥α,m∥β且l∥m,α∩β=n,故③错误;故选:D.2.一个四面体中如果有三条棱两两垂直,且垂足不是同一点,这三条棱就象中国武术中的兵器--三节棍,所以,我们常把这类四面体称为“三节棍体”,三节棍体ABCD四个顶点在空间直角坐标系中的坐标分别为A(0,0,0)、B(0,4,0)、C(4,4,0)、D(0,0,2),则此三节棍体外接球的表面积是()A.36πB.24πC.18πD.12π答案:A解析:解:由题意,可补成长方体,同一顶点的三条棱长分别为2,4,4,其对角线长为=6,∴三节棍体外接球的半径为3,∴三节棍体外接球的表面积是4π×32=36π,故选:A.3.一个圆锥的侧面展开图的圆心角为90°,它的表面积为a,则它的底面积为()A.B.C.D.答案:A解析:解:设圆锥的母线为l,所以圆锥的底面周长为:,底面半径为:=,底面面积为:.圆锥的侧面积为:,所以圆锥的表面积为:+=a,底面面积为:=.故选A.4、如图,三棱柱ABC-A1B1C1的侧棱长和底面边长均为4,且侧棱AA1⊥底面ABC,其主视图是边长为4的正方形,则此三棱柱的侧视图的面积为()A.16B.2C.4D.答案:D解析:解:根据题中的直观图和三视图,结合题意可得∵主视图是边长为4的正方形,∴三棱柱的侧棱与底面垂直,底面是边长为4的等边三角形,作出底面等边三角形的高,可得等边三角形的高为4sin60°=2,∵侧视图是以侧棱长为一边、底面三角形的高为另一边的矩形∴侧视图的面积S=4×=故选:D5.三棱锥P-ABC的侧棱PA,PB,PC两两互相垂直,且PA=PB=PC=2,则三棱锥P-ABC的外接球的体积是()A.2πB.4πC.πD.8π答案:B解析:解:以PA、PB、PC为过同一顶点的三条棱,作长方体如图则长方体的外接球同时也是三棱锥P-ABC外接球.∵长方体的对角线长为2,∴球直径为2,半径R=,因此,三棱锥P-ABC外接球的体积是πR3=π×()3=4π故选:B.6.在正方体ABCD-A′B′C′D′中,过对角线BD‘的一个平面交AA′于点E,交CC′于点F.则下列结论正确的是()①四边形BFD′E一定是平行四边形②四边形BFD′E有可能是正方形③四边形BFD′E在底面ABCD的投影一定是正方形④四边形BFD′E有可能垂于于平面BB′D.A.①②③④B.①③④C.①②④D.②③④答案:B解析:解:①∵四边形BFD′E与面BCC′B′的交线为BF,与面ADD′A′的交线为D′E,且面BCC′B′∥面ADD′A′的交线为D′E,∴BF∥D′E,同理可证明出BE∥D′F,∴四边形BFD′E一定是平行四边形,故结论①正确.②当F与C′重合,E与A点重合时,BF显然与EB不相等,不能是正方形,当这不重合时,BF和BE不可能垂直,综合可知,四边形BFD′E不可能是正方形结论②错误.③∵四边形BFD′E在底面ABCD的投影是四边形A′B′C′D′,故一定是正方形,③结论正确.④当E,F分别是AA′,CC′的中点时,EF∥AC,AC⊥BD,∴EF⊥BD,BB′⊥面ABCD,AC⊂面ABCD,∴BB′⊥AC,∴BB′⊥EF,∵BB′⊂面BDD′B′,BD⊂面BDD′B′,BD∩BB′=B,∴EF⊥面BDD′B′,∵EF⊂四边形BFD′E,平面BB′D⊂面BDD′B′,∴面形BFD′E⊥面BDD′B′.故结论④正确.故选:B.7.如图,在四面体A-BCD中,AB⊥平面BCD,BC⊥CD,若AB=BC=CD=1,则AD=()A.1B.C.D.2答案:C解析:解:∵AB⊥平面BCD,CD⊂面BCD,∴AB⊥CD,又CD⊥BC,∴CD⊥面ABC,∴CD⊥AC,又AB=BC=CD=1,∴AD2=AC2+CD2=AB2+BC2+CD2=3,∴AD=.故选C.8.已知a,b是空间两条异面直线,它们所成的角为80°,过空间一点P作直线l,使l与a,b所成角均为50°,这样的l有()A.1条B.2条C.3条D.4条答案:C解析:解:在空间取一点P,经过点P分别作a∥a‘,b∥b',设直线a'、b'确定平面α,当直线PM满足它的射影PQ在a'、b'所成角的平分线上时,PM与a'所成的角等于PM与b'所成的角因为直线a,b所成的角为80°,得a'、b'所成锐角等于80°所以当PM的射影PQ在a'、b'所成锐角的平分线上时,PM与a'、b'所成角的范围是[40°,90°).这种情况下,过点P有两条直线与a',b'所成的角都是50°当PM的射影PQ在a'、b'所成钝角的平分线上时,PM与a'、b'所成角的范围是[50°,90°).这种情况下,过点P有且只有一条直线(即PM⊂α时)与a',b'所成的角都是50°综上所述,过空间任意一点P可作与a,b所成的角都是50°的直线有3条故选:C.9.满足下面哪一个条件时,可以判定两个不重合的平面α与β平行()A.α内有无数个点到平面β的距离相等B.α内的△ABC与β内的△A"B"C"全等,且AA"∥BB"∥CC"C.α,β都与异面直线a,b平行D.直线l分别与α,β两平面平行答案:C解析:解:A错,若α∩β=a,b⊂α,a∥b,α内直线b上有无数个点到平面β的距离相等,则不能断定α∥β;B错,若α内的△ABC与β内的△A‘B'C'全等,如图,在正三棱柱中构造△ABC与△A'B'C'全等,但不能断定α∥β;C正确,因为分别过异面直线a,b作平面与平面α,β相交,可得出交线相互平行,从而根据面面平行的判定定理即可得出平面α与β平行;D错,若直线l分别与α,β两相交平面的交线平行,则不能断定α∥β;故选C.10.已知两个不同的平面α,β和两条不重合的直线m,n,有下列四个命题:①若m∥n,n⊂α,则m∥α;②若m∥α,n∥α,且m⊂β,n⊂β,则α∥β;③若m∥α,n⊂α,则m∥n;④若α∥β,m⊂α,则m∥β.其中正确命题的个数是()A.1个B.2个C.3个D.4个答案:A解析:解:①若m∥n,n⊂α,则m∥α或m⊂α,故原命题不正确;②若m∥α,n∥α,且m⊂β,n⊂β,则α∥β,对照面面平行的判定定理可知缺少条件“相交直线”,故不正确;③若m∥α,n⊂α,则m与n平行或异面或相交,故不正确;④若α∥β,m⊂α,则m∥β,根据面面平行的性质可知正确;故正确命题的个数是1个故选:A11.在直二面角α-AB-β的棱AB上取一点P,过P分别在α、β两个平面内作与棱成45°的斜线PC、PD,那么∠CPD的大小为()A.45°B.60°C.120°D.60°或120°答案:D解析:解:如图,当两斜线PC,PD同向时,在PC上取点C,过C作CG⊥AB于G,在平面β内过G作GD⊥AB,交PD于D,连结CD.∵二面角α-AB-β为直二面角,∴CG⊥β,则CG⊥GD.在Rt△CGP中,∵∠CPG=45°,设CG=a,则PG=a,∴PC=.在Rt△DGP中,∵∠DPG=45°,∴DG=PG=a,则PD=.在Rt△DGC中,∵CG=DG=a,∴CD=.∴△PCD是等边三角形,∴PC和PD所成角为60°;如图,当两斜线PC,PD异向时,在PC上取点C,过C作CG⊥AB于G,在PD上取点D,使PD=CG,连结CD,∵二面角α-AB-β为直二面角,∴CG⊥β,则CG⊥GD.设CG=a,在Rt△CGP中,∵∠CPG=45°,∴PG=a,则PC=,PD=CG=,∵∠BPD=45°,∴∠DPG=135°.在△DPG中,GD2=PG2+PD2-2PG•PDcos135°==5a2.∴CD2=CG2+GD2=a2+5a2=6a2.在△DPC 中,.∴∠DPC=120°.∴PC 和PD 所成角为120°.所以∠CPD 的大小为60°或120°.故选D .12、如图,将边长为1的正方形ABCD ,沿对角线BD 折起来,使平面ABD ⊥平面C ′BD ,则AC ′=( )A .1B .C .D .答案:A解析:解:取BD 的中点O ,连接OA ,OC ′,则∵将边长为1的正方形ABCD 沿对角线BD 折起来,使平面ABD ⊥平面C ′BD , ∴AO ⊥CO ,AO=CO=,∴AC ′==1故选:A .13.一个正四棱锥的底面面积为Q ,则它的中截面(过各侧棱的中点的截面)的边长是( )C /AB C D OA .B .C .D .答案:A解析:解:由棱锥的几何特征可得棱锥的中截面与棱锥的底面是相似图形且相似比为则棱锥的中截面与棱锥的底面的面积之比为相似比的平方又∵棱锥的底面面积是Q ,∴棱锥的中截面面积是,则它的中截面的边长是故选A .14.某几何体的三视图如图实数,则当x+y 取最大值时,该几何体的体积为()A .B .C .D .答案:A解析: 正视图 侧视图 俯视图xyξ6 11解:该几何体是长方体一角,如图所示,可知AC=,BD=1,BC=y,AB=x.设CD=a,AD=b,则a2+b2=6,a2+1=y2,b2+1=x2,消去a2,b2得x2+y2=8≥,所以x+y≤4,当且仅当x=y=2时等号成立,此时a=b=,所以V==.故选A.15.空间三条直线a,b,c中,b和c是一对异面直线,取三条直线中某两条直线确定平面,那么可以确定平面个数是()A.0或1B.1或2C.0或2D.0或1或2答案:D解析:解:∵b和c是一对异面直线若a与b,c均相交,则可以确定两个平面;若a与b,c中一条平行与另一条相交,则可以确定两个平面;若a与b,c中一条平行与另一条异面,则可以确定一个平面;若a与b,c中一条相交与另一条异面,则可以确定一个平面;若a与b,c均异面,则可以确定零个平面;故选D16.已知二面角α-l-β的大小为60°,且m⊥α,n⊥β,则异面直线m,n所成的角为()A.30°B.120°C.90°D.60°答案:D解析:解:因为m,n为异面直线,且m⊥α,n⊥β,所以m,n所成的角就是二面角α-l-β的大小,因为二面角α-l-β的大小为60°,所以是60°故选D.17.设α、β表示平面,l表示不在α内也不在β内的直线,给出下列命题:①若l⊥α,l∥β,则α⊥β;②若l∥β,α⊥β,则l⊥α;③若l⊥α,α⊥β,则l∥β.其中正确的命题是()A.①③B.①②C.②③D.①②③答案:A解析:解:①,由l∥β,可以知道过l的平面与β相交,设交线为m,则l∥m,又l⊥α,所以m ⊥α,m⊂β,故α⊥β,正确;②,由l∥β,α⊥β,则l与α可以平行、相交垂直,故错误;③,l⊥α,α⊥β,则l与β平行或在β内,而条件是l表示不在α内也不在β内的直线,故只有l∥β,正确.故选A.18.三棱锥P-ABC中,PA=PB=PC=AC=1,△ABC是等腰直角三角形,∠ABC=90°.若E为PC 中点,则BE与平面PAC所成的角的大小等于()A.30°B.45°C.60°D.90°答案:B解析:解:作PO⊥平面ABC,垂足为O则∠POA=∠POB=∠POC=90°,而PA=PB=PC,PO是△POA、△POB、△POC的公共边∴△POA≌△POB≌△POC∴AO=BO=CO,则点O为三角形ABC的外心∵△ABC是等腰直角三角形,∠ABC=90°∴点O为AC的中点,则BO⊥AC而PO⊥BO,PO∩AC=O∴BO⊥平面PAC,连接OE∴∠BEO为BE与平面PAC所成的角∵点O为AC的中点,E为PC中点,PA=PB=PC=AC=1,ABC是等腰直角三角形,∠ABC=90°∴OE为中位线,且OE=,BO=又∵∠BOE=90°∴∠BEO=45°即BE与平面PAC所成的角的大小为45°故选B.19.在正方体A1C中,对角线A1C与平面B1BCC1所成的角是()A.∠A1CB1B.∠A1CC1C.∠A1CB D.∠A1B1C答案:A解析:解:∵正方体A1C中,A1B1⊥平面B1BCC1,∴直线B1C是直线A1C在平面B1BCC1内的射影因此∠A1CB1就是直线A1C与平面B1BCC1所成的角故选:A20.若m、n是两条不同的直线,α、β、γ是三个不同的平面,则下列命题中真命题是()A.若m⊥β,m∥α,则α⊥βB.若α∩γ=m,β∩γ=n,m∥n,则α∥βC.若m⊂β,α⊥β,则m⊥αD.若α⊥γ,α⊥β,则β⊥γ答案:A解析:解:对于A,m∥α,过m的平面与α交于n,则m∥n,∵m⊥β,∴n⊥β,∵n⊂α,∴α⊥β,故正确;对于B,不正确.如图,若平面ABCD∩平面ABFE=AB,平面ABFE∩平面CDEF=EF,AB∥EF,但平面ABCD与平面CDEF不平行.对于C,因为若α⊥β,m⊂β,则m与α的位置关系不确定,故m与α可能相交,可能平行,也可能是m⊂α,对于D,因为γ,β垂直于同一个平面α,故γ,β可能相交,可能平行.故选:A.二.填空题(共__小题)21.将边长为a的正方形ABCD沿对角线AC折起,使得BD=a,则三棱锥D-ABC的体积是______.答案:解析:解:如图,由题意知DE=BE=a,BD=a由勾股定理可证得∠BED=90°故三角形BDE面积是a2又正方形的对角线互相垂直,且翻折后,AC与DE,BE仍然垂直,故AE,CE分别是以面BDE 为底的两个三角形的高故三棱锥D-ABC的体积为×a ×a2=故答案为:.22.如图,图①、②、③是图④表示的几何体的三视图,其中图①是______,图②是______,图③是______(说出视图名称).答案:主视图左视图俯视图解析:解:根据三视图的定义,可得图①是主视图,图②是左视图,图③是俯视图.故答案为:主视图、左视图、俯视图.23.若空间四边形ABCD的两条对角线AC,BD的长分别为4,6,过AB的中点E且平行BD,AC的截面四边形的周长为______.答案:10解析:解:设截面四边形为EFGH,F、G、H分别是BC、CD、DA的中点,∴EF=GH=2,FG=HE=3,∴周长为2×(2+3)=10.故答案为:10.24、如图,以等腰直角三角形斜边BC上的高AD为折痕,把△ABD与△ACD折成互相垂直的两个平面后,某学生得出下列四个结论:①;②∠BAC=60°;③三棱锥D-ABC是正三棱锥;④平面ADC的法向量和平面ABC的法向量互相垂直.其中正确结论的序号是______.(请把正确结论的序号都填上)答案:②③解析:解:BD⊥平面ADC,⇒BD⊥AC,①错;AB=AC=BC,②对;DA=DB=DC,结合②,③对④错.故答案为:②③25.直角三角形ABC中,CA=CB=,M为AB的中点,将△ABC沿CM折叠,使A、B之间的距离为1,则三棱锥M-ABC外接球的体积为______.答案:解析:解:∵Rt△ABC中CA=CB=,∴AB=2,又∵M为AB的中点,∴MA=MB=MC=1,故对折后三棱锥M-ABC的底面为边长为1的等边三角形,如下图所示:其外接球可化为以MAB 为底面,以MC 为高的正三棱柱的外接球,设三棱锥M-ABC 外接球的球心为O ,则球心到MAB 的距离d=MC=,平面MAB 的外接圆半径r=,故三棱锥M-ABC 外接球的半径R===, 则外接球的体积为V=R 3== 故答案为:.三.简答题(共__小题)26、如图,多面体ABCDEFG 中,AB ,AC ,AD 两两垂直,平面ABC ∥平面DEFG ,平面BEF ∥平面ADGC ,AB=AD=DG=2,AC=EF=1.(1)证明四边形ABED 是正方形;(2)判断点B ,C ,F ,G 是否四点共面,并说明为什么?(3)连接CF,BG,BD,求证:CF⊥平面BDG.答案:证明:(1),同理AD∥BE,则四边形ABED是平行四边形.又AD⊥DE,AD=DE,∴四边形ABED是正方形(2)取DG中点P,连接PA,PF.在梯形EFGD中,FP∥DE且FP=DE.又AB∥DE且AB=DE,∴AB∥PF且AB=PF∴四边形ABFP为平行四边形,∴AP∥BF在梯形ACGD中,AP∥CG,∴BF∥CG,∴B,C,F,G四点共面(3)同(1)中证明方法知四边形BFGC为平行四边形.且有AC∥DG、EF∥DG,从而AC∥EF,∴EF⊥AD,BE∥AD又BE=AD=2、EF=1故,而,故四边形BFGC为菱形,CF⊥BG又由AC∥EF且AC=EF知CF∥AE.正方形ABED中,AE⊥BD,故CF⊥BD.27、如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD为梯形,AB平行于CD,,AD1⊥A1C,E是A1B1中点.(1)求证:CD⊥A1D1.(2)求二面角C-D1E-B1的大小.答案:解:(1)∵ABCD-A1B1C1D1是直四棱柱且AD=DD1;∴四边形AA1D1D是正方形,∴AD1⊥A1D,∵AD1⊥A1C,A1D∩A1C=A1;∴AD1⊥平面DA1C;∴AD1⊥DC∵DD1⊥DC,DD1∩AD1=D1;∴DC⊥平面AA1D1D;∴DC⊥A1D1(2)由(1)知以D1为坐标原点,建立空间直角坐标系;C(0,1,1);E(1,1,0);;由题意,平面D1EB1的法向量为=(0,0,1)设平面CD1E的法向量=(x,y,z),则,令y=-1,则=(1,-1,1)∴;由图形知,二面角C-D1E-B1为锐角,∴二面角C-D1E-B1的大小为.28、如图,直三棱柱ABC-A1B1C1中,AC=BC,AA1=AB,D为BB1的中点,E为AB1上的一点,AE=3EB1.(Ⅰ)证明:DE为异面直线AB1与CD的公垂线;(Ⅱ)设异面直线AB1与CD的夹角为45°,求二面角A1-AC1-B1的大小.答案:解:(1)连接A1B,记A1B与AB1的交点为F.因为面AA1BB1为正方形,故A1B⊥AB1,且AF=FB1,又AE=3EB1,所以FE=EB1,又D为BB1的中点,故DE∥BF,DE⊥AB1.作CG⊥AB,G为垂足,由AC=BC知,G为AB中点.又由底面ABC⊥面AA1B1B.连接DG,则DG∥AB1,故DE⊥DG,由三垂线定理,得DE⊥CD.所以DE为异面直线AB1与CD的公垂线.(2)因为DG∥AB1,故∠CDG为异面直线AB1与CD的夹角,∠CDG=45°设AB=2,则AB1=,DG=,CG=,AC=.作B1H⊥A1C1,H为垂足,因为底面A1B1C1⊥面AA1CC1,故B1H⊥面AA1C1C.又作HK⊥AC1,K为垂足,连接B1K,由三垂线定理,得B1K⊥AC1,因此∠B1KH为二面角A1-AC1-B1的平面角.B1H=,C1H=,AC1=,HK=tan∠B1KH=,∴二面角A1-AC1-B1的大小为arctan.29.按下列叙述画出图形(不必写作法):直线a,b相交于点M,点N不在直线a,b上,点N分别与直线a,b确定平面α,β.答案:解:满足直线a,b相交于点M,点N不在直线a,b上,点N分别与直线a,b确定平面α,β的图象如下图所示:30、如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,ABCD是直角梯形,AD∥BC,∠BAD=90°,BC=2AD.(1)求证:AB⊥PD;(2)在线段PB上是否存在一点E,使AE∥平面PCD,若存在,指出点E的位置并加以证明;若不存在,请说明理由.答案:解:(1)证明∵PA⊥平面ABCD,AB⊂平面ABCD,∴PA⊥AB.∵AB⊥AD,PA∩AD=A,∴AB⊥平面PAD,∵PD⊂平面PAD,∴AB⊥PD.(2)取线段PB的中点E,PC的中点F,连接AE,EF,DF,则EF是△PBC中位线.∴EF∥BC,,∵AD∥BC,,∴AD∥EF,AD=EF.∴四边形EFDA是平行四边形,∴AE∥DF.∵AE⊄平面PCD,DF⊂平面PCD,∴AE∥平面PCD.∴线段PB的中点E是符合题意要求的点.∴平面AEF∥平面PCD.∵AE⊂平面AEF,∴AE∥平面PCD.∴线段PB的中点E是符合题意要求的点.。
