构造法求数列通项解答题
高考数学构造法求数列通项的八种技巧(二)(解析版)
构造法求数列通项的八种技巧(二)【必备知识点】◆构造四:同型构造法所谓同型构造法,就是将找因式中的因子和数列项数相同或者相近的部分通过同除或同乘化归成结构相同的形式,形成新的数列,如常数列,等差数列或等比数列.下面让我们来看看有哪些模型结构吧.模型一：a n +1=nn +1⋅a n 左右同乘n +1 (n +1)a n +1=n ⋅a n ,构造b n =n ⋅a n ,则b n +1=b n ,b n 为常数数列.模型二：a n +1=n +1n ⋅a n 左右同除n +1 a n +1n +1=a n n ,构造b n =a n n,则b n +1=b n ,b n 为常数数列.模型三：a n +1=n +2n ⋅a n 左右同除n +2 n +1 a n +1(n +1)(n +2)=a n n (n +1),构造b n =a n n (n +1),则b n +1=b n,b n 为常数数列.模型四：na n +1=2(n +1)a n 左右同除n n +1a n +1n +1=2a n n ,构造b n =an n,则b n +1=2b n ,b n 为等比数列.模型五：a n +1=n +2n ⋅S n ⇒S n +1-S n =n +2n ⋅S n ⇒S n +1=2n +2n ⋅S n 左右同除n +1 S n +1n +1=2S n n,构造b n =S nn ,则b n +1=2b n ,b n 为等比数列.模型六：a n +1=n +1n ⋅a n +n +1左右同除n +1 a n +1n +1=a n n +1,构造b n =a n n,则b n +1=b n +1,b n 为等差数列.模型七：a n +1=2a n +2n +1左右同除2n +1a n +12n +1=a n 2n +1,构造b n =a n 2n,则b n +1=b n +1,b n 为等差数列.模型八：a n -a n +1=a n a n +1左右同除a n a n +11a n +1-1a n =1,构造b n =1an ,则b n +1-b n =1,b n 为等差数列.看了这么多模型,是不是觉得很多,很难记住呢,其实向大家展示这么多,只是想向大家展示,当看到这类式子,尽量将n +1和a n +1,n 和a n 等因子和数列项数相同的部分划归成结构相同的形式,构造成新数列.【经典例题1】已知数列a n 满足a 1=23,a n +1=nn +1⋅a n,求a n . 【解析】因为a n +1=nn +1a n,所以(n +1)a n +1=na n .令b n =na n ,则b n =b n +1,即b n 是常数数列,所以b n=b 1,即na n =1×a n =23,a n =23n.【经典例题2】已知数列a n 中,a n +1=nn +2a n且a 1=2,求数列a n 的通项公式.【解析】因为a n +1=nn +2a n,所以(n +2)a n +1=na n ,(n +1)(n +2)a n +1=n (n +1)a n .令b n =n (n +1)a n ,则b n +1=b n ,即b n 是常数数列,所以b n =b 1.因此n (n +1)a n =1×2×2,a n =4n (n +1).【经典例题3】已知数列a n 中,na n +1=2(n +1)a n +n (n +1)且a 1=1,求数列a n 的通项公式.【解析】na n +1=2(n +1)a n +n (n +1),等式两侧同除n (n +1),形成a n +1n +1=2a n n +1,令b n =an n,则b n +1=2b n +1,这又回到了构造一的形式,所以b n +1+1=2(b n +1),b n +1 是以2为首项,2为公比的等差数列,即b n +1=2×2n -1=2n , b n =2n -1,所以a nn=2n -1,a n =n (2n -1).【经典例题4】已知a 1=1,且na n +1=(n +2)a n +n ,求数列a n 的通项公式.【解析】等式两侧同除n (n +1)(n +2),得a n +1(n +1)(n +2)=a n n (n +1)+1(n +1)(n +2),即a n +1(n +1)(n +2)-a n n (n +1)=1(n +1)(n +2),a n +1(n +1)(n +2)-a n n (n +1)=1(n +1)-1(n +2),另b n =a n n (n +1)，所以b n +1-b n =1(n +1)-1(n +2),接下来就是叠加法发挥作用的时候了b 2-b 1=12-13b 3-b 2=13-14b 4-b 3=14-15⋯⋯b n -b n -1=1n -1(n +1)叠加得b n -b 1=12-1(n +1),b 1=a 12=12,所以b n =1-1(n +1)=n n +1，即a n n (n +1)=nn +1，a n =n 2.【练习1】已知数列a n 满足a 1=1,a n -a n +1=3a n a n +1,则a 10=()A.28B.128C.-28D.-128【答案】B【解析】数列a n 满足a 1=1,a n -a n +1=3a n a n +1,则:1a n +1-1a n=3(常数)则：数列1a n 是以1a 1=1为首项,3为公差的等差数列。
构造法求数列通项公式系列图表
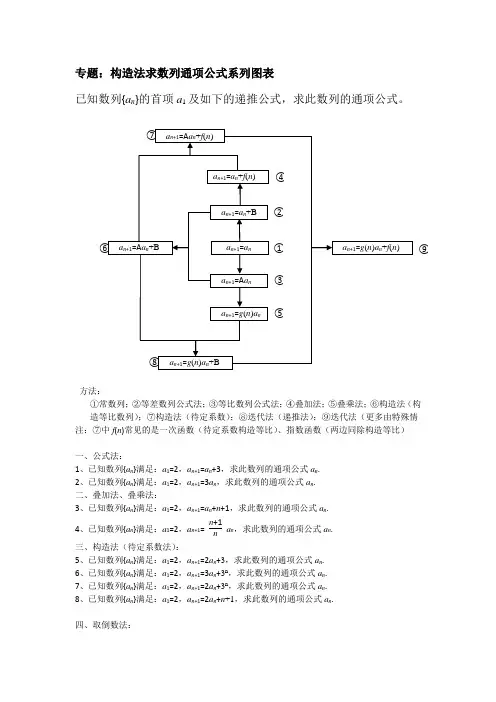
专题：构造法求数列通项公式系列图表已知数列{a n }的首项a 1及如下的递推公式，求此数列的通项公式。
方法：①常数列；②等差数列公式法；③等比数列公式法；④叠加法；⑤叠乘法；⑥构造法（构造等比数列）；⑦构造法（待定系数）；⑧迭代法（递推法）；⑨迭代法（更多由特殊情 注：⑦中f (n )常见的是一次函数（待定系数构造等比）、指数函数（两边同除构造等比）一、公式法：1、已知数列{a n }满足：a 1=2，a n +1=a n +3，求此数列的通项公式a n .2、已知数列{a n }满足：a 1=2，a n +1=3a n ，求此数列的通项公式a n .二、叠加法、叠乘法：3、已知数列{a n }满足：a 1=2，a n +1=a n +n +1，求此数列的通项公式a n .4、已知数列{a n }满足：a 1=2，a n +1= n +1n a n ，求此数列的通项公式a n .三、构造法（待定系数法）：5、已知数列{a n }满足：a 1=2，a n +1=2a n +3，求此数列的通项公式a n .6、已知数列{a n }满足：a 1=2，a n +1=3a n +3n ，求此数列的通项公式a n .7、已知数列{a n }满足：a 1=2，a n +1=2a n +3n ，求此数列的通项公式a n .8、已知数列{a n }满足：a 1=2，a n +1=2a n +n +1，求此数列的通项公式a n .四、取倒数法：⑨9、已知数列{a n }满足：a 1=2，a n +1= 3a n 3+a n，求此数列的通项公式a n . 10、已知数列{a n }满足：a 1=2，a n +1= 3a n 2+a n，求此数列的通项公式a n . 五、方程（或方程组）法：11、已知数列{a n }满足：a n ≥0，a n = 3na n+1 ，求此数列的通项公式a n . 12、已知正项数列{a n }中，a 1=2， (n+1)a n +12+a n a n -1－na n 2=0, 求此数列的通项公式a n .六、a n 与S n 的关系法：a n = ⎩⎨⎧S 1 (n=1)，S n -S n-1 (n ≥2)，13、已知S n 为数列{a n }的前n 项和，且S n =－n 2+3n ，求此数列的通项公式a n .14、已知S n 为数列{a n }的前n 项和，且S n =－n 2+3n +4，求此数列的通项公式a n .15、已知S n 为数列{a n }的前n 项和，且S n =2·3n -2求此数列的通项公式a n .16、已知S n 为数列{a n }的前n 项和，且a 1=2，a n +1 =2S n +n ，求此数列的通项公式a n .七、能力提升：17、（必修五课本第69页第6题：已知数列{a n }中，a 1=5，a 2=2，a n =2a n -1+3a n -2 ,(n ≥3)，对于这个数列的通项公式作一研究，能否写出它的通项公式？。
用构造法求数列通项公式
用构造法求数列的通项公式摘要:数列问题以其多变的形式和灵活的求解方法备受高考命题者的青睐,历年来都是高考命题的热点,求数列的通项公式更是高考重点考查的内容,作为常归的等差数列或等比数列可直接根据它们的通项公式求解,但也有一些数列要通过构造来形成等差数列或等比数列,之后再应用各自的通项公式求解。
关键词:归纳猜想构造例1.(2006年福建高考题)在数列{an｝中,a1=1,an+1=2an+1,则an等于()a.2nb.2n+1c.2n-1d.2n-1解:an+1=2an+1,所以an+1+1=2an+2=2(an+1),所以■=2,又a1+1=2,{an+1｝是首项为2公比为2的等比数列an+1=2·2n-1=2n,所以an=2n-1,所以选c.归纳小结若数列{an｝满足an+1=pan+q(p≠1,q为常数),则令an+1+?姿=p(an+?姿)来构造等比数列,并利用对应项相等求?姿的值,求通项公式.例2.在数列{an｝中,a1=1,a2=3,an+2=3an+1-2an,则an= . 解:an+2-an+1=2(an+1-an),因为a2-a1=2,所以{an-an-1｝为首项为2公比也为2的等比数列,an-an+1=2n-1,an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=2n-1+2n-2+…+2+1=■=2n-1.归纳小结:先构造{an-1-an｝等比数列,这是化归思想的具体应用,再用叠加法求出通项公式,当然本题也利用了等比数列求和公式。
例3.(必修5教材69页)已知数列{an｝中a1=5,a2=2,an=2an-1+3an-2(n≥3),求这个数列的通项公式.解:因为an=2an+3an-2,所以an+an-1=3(an-1+an-2),又a1+a2=7,{an+an-1｝形成首项为7,公比为3的等比数列,则an+an-1=7×3n-2,①又an-3an-1=-(an-1-3an-2),a2-3a1=-13,{an-3an-1｝形成了一个首项为-13,公比为-1的等比数列,则an-3an-1=(-13)·(-1)n-2,②①×3+②得4an=7×3n-1+13·(-1)n-1,所以an=■×3n-1+■(-1)n-1.归纳小结:本题是两次构造等比数列,属于构造方面比较级,最终用加减消元的方法确定出数列的通项公式。
数列通项的求法④构造法(已打)
通项的求法④构造法（待定系数法）以下所有题目默认：“数列{}n a 的前n 项和为n S ”(n ∈N *) 构造法目的：构造数列相邻两项①常数构造法：1n n a pa q +=+⇔1()n n a t p a t ++=+ ②一次构造法：1n n a pa qn r +=++⇔11212(1)[(()]n n a t n t p a t n t ++++=++③指数构造法：1n n n a pa rq +=+⇔11n n n n a a p rq q q q++=+⇔①常数构造法 ④递推构造法：11n n n a pa qa +-=+⇔11211()n n n n a t a t a t a +-+=+⑤倒数构造法：（两边取倒数）11(,,)0n n n n f a a a a --=或分式。
⑥对数构造法：（两边取对数）1r n n a pa +=⇔1lg lg()r n na a p +=⋅⇔1lg lg lg n n a r a p +=+⇔①常数构造法 例1． 111,21,n n n a a a a +==+=则注意：新数列首项是什么？例2．111,234,n n n a a a n a +==++=则 例3.111232,3++⋅+==n n n a a a ，则=n a例4．n n n a a a a a 23,3,11221-===++，则=n a 例5①.11,2a n =≥,112n n n n a a a a ---=, 则=n a 例5②.若21=a ，nnn a a a 311+=+，则=n a例6. a 1=2，21()n n a a n -=≥2，则=n a1①.32,111+==+n n a a a ，求{}n a1②.nn n a a a 32,111+==+，求{}n a1③.n n n a a a a a 23,2,11221-===++，求{}n a1④. 111(1)(1)n n a na n a n n +=-+=+，，求{}n a 2①.111,32n n a a a -==+，求n a 2②.111,32nn n a a a -==+，求n a 2③.1111,31n n n a a a a --==+，求n a2④.1a =1=n a3①{}n a 中，232,111-==+n n a a a ，求{}n a 3②{}n a 中，n a a a n n +==+2,111，求{}n a3③{}n a 中，nn n a a a 33,111+==+，求{}n a 3④*12211,5,()n n n a a a a a n N ++===-∈，则20a = 4①)(133,0*11N n a a a a n n n ∈+-==+，则20a =4②122120061,5,,n n n a a a a a a ++===-=则______ 4③11a =，22a =且212n n n a a a ++=-,则n a =4④若a 1=1，a 2=2，21(1)nn n a a +-=+-，则100S =_____5.(10广东) )3(3231,2,12121≥+===--n a a a a a n n n ，求数列{}n a 的通项公式.6.数列{}n a 满足2112,66n n n a a a a +==++ (Ⅰ)设5log (3)n n c a =+，求证{}n c 是等比数列； （Ⅱ）求数列{}n a 的通项公式。
构造法求数列通项7例
高二数学构造法求数列通项公式7题例1 数列{a n }的前n 项和记为S n ,已知a 1=1,a n+1=nn 2+S n (n=1,2,3……)，求a n .例2 已知数列{a n }的前n 项和为S n ,且满足a n +2S n S n-1=0(n ≥2);a 1=21,求通项a n .例3 已知函数f(x)=42-x (x ≤-2).(1)求f -1(x),(2)若a 1=1,a n =-f -1(a n-1),求数列{a n }的通项公式.例4 已知函数f(x)=(x +2)2(x>0),设正项数列{a n }的首项a 1=2,前n 项和S n 满足S n =f(S n-1)(n ≥2且n ∈N *),求通项a n .例5 已知数列{a n }中,a 1=1,且a n+1=3a n -1(n ∈N *),求a n .例6 已知正项数列{a n }的前项和S n 满足S n =21(a n +n a 1)，求通项a n .例7 已知数列{a n }中，a 1=2,a n =2211+--n n a a (n ≥2)，求通项a n .构造法求数列通项公式7题答案例1 解析：∵a n+1=S n+1-S n ,a n+1=nn 2+S n∴(n+2)S n=n(S n+1-S n )，整理得nS n+1=2(n+1)S n ,即11++n S n =2·nS n，故数列{nS n}是以11S =a 1=1为首项，2为公比的等比数列，即nS n=2n-1,S n =n ·2n-1，当n ≥2时，a n =S n -S n-1=n ·2n-1-(n-1)2n-2=(n+1)2n-2,当n=1时也适合，故a n =(n+1)·2n-2n ∈N *.例2 解析:当n ≥2时, a n =S n -S n-1=-2 S n S n-1,两边同除以S n S n-1得nS 1-11-n S =2,又11S =11a =2, ∴数列{nS 1}是以2为首项,2为公差的等差数列,则nS 1=2+2(n-1)=2n, S n =n 21,由a 1=21, n ≥2时,a n =S n -S n-1=n 21-)1(21-n =- )1(21-n n ,二式不能合并.例3 解析:(1)f -1(x)=-42+x (x ≥0),(2)由a n=-f-1(a n-1),∴a n =421+-n a ,两边平方得an 2-a n-12=4,∴数列{a n 2}是以a 12=1为首项,公差为4的等差数列,∴a n 2=1+(n-1)4=4n-3,又a n >0,∴a n =34-n .例4解析:∵a n >0,∴S n >0,由S n =f(S n-1)=(1-n S +2)2两边开方得nS =1-n S +2,∴数列{n S }是以1S =1a =2为首项,公差d=2的等差数列,即nS =2+(n-1)2=2n,则S n =2n 2,当n ≥2时,a n =S n -S n-1=4n-2,当n=1时,a 1=2也适合上式,故a n =4n-2(n ∈N *). 例5 解析:设a n+1+x=3(a n +x),则a n+1=3a n +2x,又a n+1=3a n -1,则2x=-1,即x=-21,故而a n+1-21=3(a n-21),则数列{a n-21}是以首项a 1-21=21,公比为3的等比数列,∴a n-21=21·3n-1,即a n=21·3n-1+21.例 6 解析：由S 1=a 1=21(a 1+11a )得a 1=1，又a n =S n -S n-1(n ≥2)∴S n =21(a n +na 1)=21(S n -S n-1+11--n n S S )可得S n +S n-1=11--n n S S ，即S n 2-S n-12=1,∴数列{S n 2}是首项为S 12=a 12=1,公差为1的等差数列.∴S n 2=1+(n-1)·1=n ，又S n >0，∴S n =n ,当n ≥2时，a n=S n-Sn-1=n -1-n ,当n=1时，a 1=1也适合，故通项a n=n -1-n .例7 解析：由题意知a n ≠0，在a n =2211+--n n a a 两边同时取倒数得，n a 1=1122--+n n a a =11-n a +21,即n a 1-11-n a =21,∴数列{na 1}是首项为11a ，公差为21的等差数列，∴n a 1=21+(n-1)21=2n , 则a n=n2.。
构造法求数列通项
构造法求数列通项
构造法就是在解决某些数学问题的过程中，通过对条件与结论的充分剖析，联想出一种适当的辅助模型，进行命题转换，产生新的解题方法，这种思维方法的特点就是“构造”。
若已知条件给的是数列的递推公式要求出该数列的通项公式。
运用乘、除、去分母、添项、去项、取对数、待定系数等方法，将递推公式变形成为f（n+1）=Af（n）（其中A为非零常数）形式，根据等比数列的定义知f（n）是等比数列，根据等比数列的通项公式，先求出f（n）的通项公式，再根据f（n）与an，从而求出an的通项公式。
构造法求递推数列的通项公式
巧用构造法求递推数列的通项公式蒋明权利用递推数列求通项公式，在理论上和实践中均有较高的价值，自从二十世纪八十年代以来，一直是全国高考和高中数学联赛的热点之一。
本文想介绍一下利用构造法求递推数列的通项公式的方法和策略，希望能抛砖引玉。
一、构造等差数列法例1.在数列{a n }中，a na n a n n n n n 1132212==+++++，()()()，求通项公式a n 。
解：对原递推式两边同除以n n n ()()++12可得：a n n a n nn n +++=++12112()()()① 令b a n nn n =+()1② 则①即为b b n n +=+12，则数列{b n }为首项是b a 1111132=+=()×，公差是b b n n +-=12的等差数列，因而b n n n =+-=-3221212()，代入②式中得a n n n n =+-12141()()。
故所求的通项公式是a n n n n =+-12141()() 二、构造等比数列法1.定义构造法 利用等比数列的定义q a a n n=+1，通过变换，构造等比数列的方法。
例2.设在数列{a n }中，a a a a n n n 112222==++，，求{a n }的通项公式。
解：将原递推式变形为a a a n n n++=+12222()① a a a n n n+-=-12222()② ①/②得：a a a a n n n n +++-=+-1122222[]， 即lg lg[]a a a a n n n n +++-=+-1122222③ 设b a a n n n =+-lg[]22④ ③式可化为a a n n +=12，则数列{b n }是以b 1＝lg[]lg lg()a a 11222222221+-=+-=+为首项，公比为2的等比数列，于是b n n n =+=+-22122211lg()lg()×，代入④式得：a a n n +-22＝()212+n ，解得a n n n=+++-221121122[()]()为所求。
(完整版)高中数学构造法求数列通
构造法求数列通项例题分析型如a n+1=pa n +f(n) (p 为常数且p ≠0， p ≠1)的数列(1)f(n)= q (q 为常数) 一般地，递推关系式a n+1=pa n +q (p 、q 为常数，且p ≠0，p ≠1)等价与)1(11pqa p p q a n n --=--+，则{p q a n --1}为等比数列，从而可求n a ．例1、已知数列{}n a 满足112a =，132n n a a --=（2n ≥），求通项n a ． 解：由132n n a a --=，得111(1)2n n a a --=--，又11210a -=≠， 所以数列{1}n a -是首项为12，公比为12-的等比数列， ∴11111(1)()1()22n n n a a -=---=+-．练习：已知数列}{n a 的递推关系为121+=+n n a a ，且11=a ，求通项n a ． 答案：12-=n n a ．(2) f(n)为等比数列，如f(n)= q n (q 为常数) ，两边同除以q n ，得111+=++nnn n q a p q a q， 令nnna b q =，则可转化为b n+1=pb n +q 的形式求解． 例1、已知数列{a n }中，a 1=65，1111()32n n n a a ++=+，求通项n a ． 解：由条件，得2 n+1a n+1=32(2 na n )+1，令b n =2 n a n ， 则b n+1=32b n +1，b n+1-3=32（b n -3） 易得 b n =3)32(341+--n ，即2 n a n =3)32(341+--n ， ∴ a n =nn 2332+-． 练习、已知数列{}n a 满足1232n n n a a +=+⨯，12a =，求通项n a ． 答案：31()222nn a n =-．(3) f(n)为等差数列，如1n n a Aa Bn C +=++型递推式，可构造等比数列．（选学，注重记忆方法）例1、已知数列{}n a 满足11=a ，11212n n a a n -=+-（2n ≥），求．解：令n n b a An B =++，则n n a b An B =--， ∴11(1)n n a b A n B --=---，代入已知条件，得11[(1)]212n n b An B b A n B n ---=---+-，即11111(2)(1)2222n n b b A n A B -=++++-，令202A +=，1022A B+-=，解得A =－4，B=6， 所以112n n b b -=，且46n n b a n =-+，∴{}n b 是以3为首项、以12为公比的等比数列，故132n n b -=，故13462nn a n -=+-． 点拨：通过引入一些尚待确定的系数，经过变形与比较，把问题转化成基本数列（等差或等比数列）求解．练习：在数列{}a n 中，132a =，1263n n a a n --=-，求通项a n ． 答案：a n n n-+=69912·()．解：由1263n n a a n --=-，得111(63)22n n a a n -=+-，令11[(1)]2n n a An B a A n B -++=+-+，比较系数可得：A =－6，B=9，令n n b a An B =++，则有112n n b b -=，又1192b a A B ==++，∴{}n b 是首项为92，公比为12的等比数列，所以b n n =-92121()，故a n n n -+=69912·()．(4) f(n)为非等差数列，非等比数列 法一、构造等差数列法例1、在数列{}n a 中，1112(2)2()n n n n a a a n λλλ+*+==++-∈N ，，其中0λ>，求数列{}n a 的通项公式．解：由条件可得111221n nn nn n a a λλλλ+++⎛⎫⎛⎫-=-+ ⎪⎪⎝⎭⎝⎭， ∴数列2nn n a λλ⎧⎫⎪⎪⎛⎫-⎨⎬ ⎪⎝⎭⎪⎪⎩⎭是首项为0，公差为1的等差数列，故21n n n a n λλ⎛⎫-=- ⎪⎝⎭，∴(1)2n n n a n λ=-+．练习：在数列{a n }中，a na n a n n n n n 1132212==+++++，()()()，求通项a n 。
2024年高考数学专项突破构造法求数列通项的八种技巧(一)(解析版)
构造法求数列通项的八种技巧(一)【必备知识点】◆构造一:待定系数之a n +1=Aa n +B 型构造等比数列求关于a n +1=Aa n +B (其中A ,B 均为常数,AB (A -1)≠0)类型的通项公式时,先把原递推公式转化为a n +1+M =A a n +M ,再利用待定系数法求出M 的值,再用换元法转化为等比数列求解.其实对于这类式子,我们只需要记住在等式两侧加上一个常数M ,构造成等比数列.常数M 的值并不需要背诵,我们可以通过待定系数法推导出来.【经典例题1】已知a n 满足a 1=3,a n +1=2a n +1求数列a n 的通项公式.【经典例题2】已知数列a n 中,a 1=1,a n +1=2a n +3,求数列a n 的通项公式.【经典例题3】已知数列a n 中,a 1=1,a n +1=3a n +4,求数列a n 的通项公式.【练习1】数列a n 中,a n +1=2a n -1,a 3=2,设其前n 项和为S n ,则S 6=()A.874 B.634 C.15 D.27【练习2】已知数列a n 的前n 项和为S n ,若3S n =2a n -3n ,则a 2018=()A.22018-1B.22018-6C.12 2018-72D.13 2018-103【练习3】在数列a n 中,a 1=2,a n +1=2a n +1,则a 5=_______.【练习4】已知数列a n 满足a 1=3,a n +1=2a n +1,则数列a n 的通项公式a n =______.【练习5】已知数列a n 的首项a 1=2,且a n +1=12a n +12n ∈N * ,则数列1a n -1 的前10项的和为______.【练习6】已知数列a n 中,a 1=1,a n +1=3a n +2,则a n =_______.◆构造二:待定系数之a n +1=Aa n +Bn +C 型构造等比数列求关于a n +1=Aa n +Bn +C (A ≠1,C ≠0,B ≠0)类型的通项公式时,与上面讲述的构造一的方法很相似,只不过等式中多了一项Bn ,在构造时我们也保持跟题干一样的结构,加一项pn 再构造等比数列就可以,即令a n +1+p (n +1)+q =A a n +pn +q ,然后与已知递推式各项的系数对应相等,解p ,q ,从而得到a n +pn +q 是公比为A 的等比数列.2024年高考数学专项突破构造法求数列通项的八种技巧（一）（解析版）【经典例题1】设数列a n满足a1=4,a n=3a n-1+2n-1(n≥2),求数列a n的通项公式.【经典例题2】已知:a1=1,n≥2时,a n=12a n-1+2n-1,求a n的通项公式.【练习1】已知数列a n是首项为a1=2,a n+1=13a n+2n+53.(1)求a n通项公式;(2)求数列a n的前n项和S n.【练习2】已知数列a n和b n,a n的前n项和S n,对于任意的n∈N*,a n,S n是二次方程x2-3n2x+b n=0的两根.(1)求a n和b n通项公式;(2)a n的前n项和S n.【练习3】设数列a n是首项为a1=1,满足a n+1=2a n-n2+3n(n=1,2,⋯).问是否存在λ,μ,使得数列a n+λn2+μn成等比数列?若存在,求出λ,μ的值,若不存在,说明理由;◆构造三:待定系数之a n+1=pa n+q n型构造数列求关于a n+1=pa n+q n(其中p,q均为常数,pq(p-1)≠0)类型的通项公式时,共有3种方法.方法一:先用待定系数法把原递推公式转化为a n+1+λq n+1=p a n+λq n,根据对应项系数相等求出λ的值,再利用换元法转化为等比数列求解.方法二:先在递推公式两边同除以q n+1,得a n+1q n+1=pq⋅a nq n+1q,引入辅助数列b n(其中b n=a nq n),得b n+1=pq⋅b n+1q,再利用待定系数法解决；方法二:也可以在原递推公式两边同除以p n+1,得a n+1p n+1=a np n+1p⋅qpn,引入辅助数列b n (其中b n=a n p n ),得b n+1-b n=1p⋅q.pn,再利用叠加法(逐差相加法)求解.【经典例题1】已知数列a n中a1=56,a n+1=13a n+12n+1,求an的通项公式.【经典例题2】已知数列a n满足a n+1=2a n+4⋅3n-1,a1=-1,求数列a n的通项公式.【练习1】已知数列a n满足a1=1,a n+1=3a n+2n n∈N*,b n=a n+1a n.设t∈Z,若对于∀n∈N*,都有b n>t恒成立,则t的最大值为()A.3B.4C.7D.9【练习2】已知数列a n满足a1=2,a n+1=a n+2n+2n∈N*.(1)判断数列a n-2n是否为等差数列,并说明理由;(2)记S n为数列a n的前n项和,求S n.【过关检测】一、单选题1.已知S n为数列a n的前n项和，若a n+1=2a n-2,S2=10，则a n的通项公式为( )A.a n=3n-4B.a n=2n+2C.a n=n2+nD.a n=3n2-12.已知数列a n中，a1=1，a n+1=2a n+1，则数列a n的通项公式为( )A.a n=nB.a n=n+1C.a n=2nD.a n=2n-13.已知数列a n满足a1=3，a n+1=5a n-8，则a2022的值为( )A.52021-2B.52021+2C.52022+2D.52022-24.设数列a n的前n项和为S n，若S n=2a n-2n+1，则S10=( )A.211-23B.210-19C.3×210-23D.3×29-195.在数列a n中，a1=1，且a n+1=2a n+1，则a n的通项为( )A.a n=2n-1B.a n=2nC.a n=2n+1D.a n=2n+16.数列a n中，a n+1=2a n+1，a1=1，则a100=( )A.2100+1B.2101C.2100-1D.21007.数列a n满足12a n=a n+1-12n+1，且a1=12，若a n<13，则n的最小值为( )A.3B.4C.5D.68.已知数列a n中，a1=1，a n=3a n-1+4(n∈N∗且n≥2)，则数列a n通项公式a n为( )A.3n-1B.3n+1-2C.3n-2D.3n9.数列a n满足a n=4a n-1+3n≥2且a1=0，则此数列第5项是( )A.15B.255C.16D.6310.在数列a n中，已知a1=1，a n+1=2a n+1，则a n=( )A.2n -1B.2n -1C.nD.2n -111.在数列a n 中，a 1=3，a n =2a n -1-n +2n ≥2,n ∈N + ，若a n >980，则n 的最小值是( )A.8B.9C.10D.1112.设数列{an }中，a 1=2，an +1=2an +3，则通项an 可能是()A.5-3nB.3·2n -1-1C.5-3n 2D.5·2n -1-313.在数列a n 中，若a 1=2，a n +1=3a n +2n +1，则a n =( )A.n ⋅2nB.52-12nC.2⋅3n -2n +1D.4⋅3n -1-2n +114.已知在数列a n 中，a 1=56，a n +1=13a n +12 n +1，则a n =( )A.32n -23n B.23n -32n C.12n -23n D.23n -12n 15.数列a n 满足a n +1=2a n +3,n ∈N *，若a 2017≥a 1，则a 1的取值范围为( )A.(-∞,-3]B.{-3}C.(-3,+∞)D.[-3,+∞)二、填空题16.设数列a n 满足a 1=1，且a n =3a n -1+4n ≥2 ，则数列a n 的通项公式为a n =___________.17.已知数列a n 中，a 1=1，a n +1=2a n +1，则a n 通项a n =______；18.数列{an }满足a 1=1，an +1=2an +1. (n ∈N *).数列{an }的通项公式为______．19.数列a n 满足a n =4a n -1+3，且a 1=0，则a 6=_________.20.已知数列a n 满足a n +1=2a n +12，且a n 前8项和为761，则a 1=______．三、解答题21.已知数列a n 满足a 1=1,a n +1=3a n +2.(1)证明1+a n 为等比数列，并求a n 的通项公式；(2)记数列11+a n 的前n 项和为S n ，证明S n <34.22.已知数列a n满足a1=3,a n+1=2a n-2.(1)求a n的通项公式；(2)求a n的前n项和S n.23.已知数列a n的首项a1=1，且1a n+1=2a n+1．(1)求数列a n的通项公式；(2)若数列b n满足a n⋅b n=n，求数列b n的前n项和S n．24.在数列a n中，a1=5，且a n+1=2a n-1n∈N*.(1)证明：a n-1为等比数列，并求a n的通项公式；(2)令b n=(-1)n⋅a n，求数列b n的前n项和S n.25.已知数列a n的前n项和为S n，a1=2，且a n+1=2a n+2．(1)求数列a n的通项公式；(2)令b n=2n+1a n+2，记数列b n的前n项和为T n，求证：T n<3．构造法求数列通项的八种技巧(一)【必备知识点】◆构造一:待定系数之a n +1=Aa n +B 型构造等比数列求关于a n +1=Aa n +B (其中A ,B 均为常数,AB (A -1)≠0)类型的通项公式时,先把原递推公式转化为a n +1+M =A a n +M ,再利用待定系数法求出M 的值,再用换元法转化为等比数列求解.其实对于这类式子,我们只需要记住在等式两侧加上一个常数M ,构造成等比数列.常数M 的值并不需要背诵,我们可以通过待定系数法推导出来.【经典例题1】已知a n 满足a 1=3,a n +1=2a n +1求数列a n 的通项公式.【解析】根据原式,设a n +1+m =2a n +m ,整理得a n +1=2a n +m ,题干中a n +1=2a n +1,根据对应项系数相等得m =1.∴a n +1+1=2a n +1 ,令b n =a n +1+1,b 1=a 1+1=3+1=4,所以a n +1 是4为首项,2为公比的等比数列.即a n +1=4⋅2n -1,a n =2n +1-1.【经典例题2】已知数列a n 中,a 1=1,a n +1=2a n +3,求数列a n 的通项公式.【解析】设a n +1+t =2a n +t ,整理得a n +1=2a n +t ,题干中a n +1=2a n +3,根据对应项系数相等,解得t =3,故a n +1+3=2a n +3 .令b n =a n +3,则b 1=a 1+3=4,且b n +1b n=a n +1+3a n +3=2.所以b n 是4为首项,2为公比的等比数列.所以b n =4×2n -1=2n +1,即a n =2n +1-3.【经典例题3】已知数列a n 中,a 1=1,a n +1=3a n +4,求数列a n 的通项公式.【解析】设a n +1+t =3(a n +t ),即a n +1=3a n +2t ,题干中a n +1=3a n +4,根据对应项系数相等,解得t =2,故a n +1+2=3a n +2 .令b n =a n +2,则b 1=a 1+2=3,且b n +1b n=a n +1+2a n +2=3.所以b n 是3为首项,3为公比的等比数列.所以b n =3×3n -1=3n ,即a n =3n -2.【练习1】数列a n 中,a n +1=2a n -1,a 3=2,设其前n 项和为S n ,则S 6=()A.874B.634C.15D.27【答案】A【解析】∵a n +1=2a n -1,a 3=2,可得2=2a 2-1,解得a 2=32,同理可得:a 1=54变形为a n +1-1=2a n -1 ,a 1-1=14. ∴数列a n -1 为等比数列,首项为14,公比为2.∴a n -1=14×2n -1,a n =2n -3+1.∴S 6=1426-1 2-1+6=874.故选:A .【练习2】已知数列a n 的前n 项和为S n ,若3S n =2a n -3n ,则a 2018=()A.22018-1B.22018-6C.12 2018-72D.13 2018-103【答案】A【解析】∵数列a n 的前n 项和为S n ,3S n =2a n -3n ,∴a 1=S 1=132a 1-3 ,解得a 1=-3,S n =132a n -3n ,(1),n ≥2,S n -1=132a n -1-3n +3 ,(2),(1)-(2),得a n =23a n -23a n -1-1,∴a n =-2a n -1-3,∴a n +1a n -1+1=-2,∵a 1+1=-2,∴a n +1 是以-2为首项,以-2为公比的等比数列,∴a n+1=(-2)n,∴a n=(-2)n-1,∴a2018=(-2)2018-1=22018-1.故选:A.【练习3】在数列a n中,a1=2,a n+1=2a n+1,则a5=_______.【答案】47【解析】数列 a n中, a1=2,a n+1=2a n+1,变形为:a n+1+1=2a n+1,a1+1=3,∴数列a n+1为等比数列,首项为3,公比为2,∴a n+1=3×2n-1,即a n=3×2n-1-1则a5=3×24-1=47.故答案为:47.【练习4】已知数列a n满足a1=3,a n+1=2a n+1,则数列a n的通项公式a n=______.【答案】a n=2n-1【解析】∵a n+1=2a n+1n∈N*,∴a n+1+1=2a n+1,∴a n+1是以a1+1=2为首项,2为公比的等比数列.∴a n+1=2n,故a n=2n-1.【练习5】已知数列a n的首项a1=2,且a n+1=12a n+12n∈N*,则数列1a n-1的前10项的和为______.【答案】1023【解析】数列a n的首项a1=2,且a n+1=12a n+12(n∈N*),则:a n+1-1=12a n-1 ,整理得:a n+1-1a n-1=12(常数) ,所以：数列a n-1是以a1-1=2-1=1为首项,12为公比的等比数列,所以:a n-1=1*12n-1,当n=1时,符合通项.故：1a n-1=2n-1,所以:S n=20+21+22+⋯+2n-1=2n-1所以：S10=210-1=1024-1=1023.【练习6】已知数列a n中,a1=1,a n+1=3a n+2,则a n=_______.【答案】a n=2×3n-1-1【解析】因为a n+1=3a n+2,所以a n+1+1=3a n+1,因为1+a1=2,所以数列1+a n是以2为首项,以3为公比的等比数列,所以1+a n=2×3n-1,故答案为:a n=2×3n-1-1.◆构造二:待定系数之a n+1=Aa n+Bn+C型构造等比数列求关于a n+1=Aa n+Bn+C(A≠1,C≠0,B≠0)类型的通项公式时,与上面讲述的构造一的方法很相似,只不过等式中多了一项Bn,在构造时我们也保持跟题干一样的结构,加一项pn再构造等比数列就可以,即令a n+1+p(n+1)+q=A a n+pn+q,然后与已知递推式各项的系数对应相等,解p,q,从而得到a n+pn+q是公比为A的等比数列.【经典例题1】设数列a n满足a1=4,a n=3a n-1+2n-1(n≥2),求数列a n的通项公式.【解析】将递推公式转化为a n+pn+q=3a n-1+p(n-1)+q,化简后得a n=3a n-1+2pn+2q-3p,与原递推式比较,对应项的系数相等,得2p=22q-3p=-1,解得p=1q=1,令bn=a n+n+1,则b n=3b n-1,又b1=6,故b n=6⋅3n-1=2⋅3n,b n=a n+n+1,得a n=2⋅3n-n-1.【经典例题2】已知:a 1=1,n ≥2时,a n =12a n -1+2n -1,求a n 的通项公式. 【解析】设a n +pn +q =12a n -1+p (n -1)+q ,a n =12a n -1-12pn -12p -12q .与题干原式比较,对应项系数相等得-12p =2-12p -12q =-1,解得p =-4q =6 ,首项a 1-4+6=3.所以a n -4n +6 是3为首项,12为公比的等比数列.所以a n -4n +6=3⋅12 n -1,即a n =32n -1+4n -6.【练习1】已知数列a n 是首项为a 1=2,a n +1=13a n +2n +53.(1)求a n 通项公式;(2)求数列a n 的前n 项和S n .【解析】因为a n +1-3(n +1)+2=13a n -3n + 2),且a 1-3+2=1,所以数列a n -3n +2 是以1为首项,13为公比的等比数列,则a n -3n +2=13n -1,即a n =13n -1+3n -2.【练习2】已知数列a n 和b n ,a n 的前n 项和S n ,对于任意的n ∈N *,a n ,S n 是二次方程x 2-3n 2x +b n =0的两根.(1)求a n 和b n 通项公式;(2)a n 的前n 项和S n .【解析】因为a n ,S n 是一元二次方程x 2-3n 2x +b n =0的两个根,所以a n +S n =3n 2a n S n =b n ,由 a n +S n =3n 2得a n +1+S n +1=3(n +1)2,两式相减得a n +1-a n +S n +1-S n =6n +3,所以a n +1=12a n +12(6n +3),令a n +1+A (n +1)+B =12a n +An +B ,则a n +1=12a n -12An -12B -A ,比较 以上两式的系数,得-12A =3-12B -A =32 ,解得A =-6B =9 .所以a n +1-6(n +1)+9=12a n -6n +9 .又 a 1+S 1=3,a 1=32,所以数列a n -6n +9 是以92为首项、12为公比的等比数列.所以 a n -6n +9=9212 n -1,a n =6n +92n +9,S n =3n 2-a n =3n 2-6n -92n +9,所以 b n =6n +92n -9 3n 2-6n -92n +9 【练习3】设数列a n 是首项为a 1=1,满足a n +1=2a n -n 2+3n (n =1,2,⋯).问是否存在λ,μ,使得数列a n +λn 2+μn 成等比数列?若存在,求出λ,μ的值,若不存在,说明理由;【解析】依题意,令a n +1+λ(n +1)2+μ(n +1)+γ=2a n +λn 2+μn +γ 所以a n +1=2a n +λn 2+μn -2λn +γ-λ-μ,即λ=-1μ-2λ=3γ-λ-μ=0, 解得λ=-1μ=1γ=0.所以数列a n -n 2+n 是以2为公比、a 1-1+1=1为首项等比数列.所以a n -n 2+n =2n -1,a n =n 2+2n -1-n ,即存在λ=-1,μ=1,使得数列a n -n 2+n 成等比数列.◆构造三:待定系数之a n+1=pa n+q n型构造数列求关于a n+1=pa n+q n(其中p,q均为常数,pq(p-1)≠0)类型的通项公式时,共有3种方法.方法一:先用待定系数法把原递推公式转化为a n+1+λq n+1=p a n+λq n,根据对应项系数相等求出λ的值,再利用换元法转化为等比数列求解.方法二:先在递推公式两边同除以q n+1,得a n+1q n+1=pq⋅a nq n+1q,引入辅助数列b n(其中b n=a nq n),得b n+1=pq⋅b n+1q,再利用待定系数法解决；方法二:也可以在原递推公式两边同除以p n+1,得a n+1p n+1=a np n+1p⋅qpn,引入辅助数列b n (其中b n=a n p n ),得b n+1-b n=1p⋅q.pn,再利用叠加法(逐差相加法)求解.【经典例题1】已知数列a n中a1=56,a n+1=13a n+12n+1,求an的通项公式.【解析】解法一:构造数列a n+1+λ12n+1=13a n+λ12n,化简成题干结构得a n+1=13a n-13λ12n+1,对应项系数相等得λ=-3,设b n=a n-312n,b1=a1-312 1=-23,所以数列b n 是以-23为首项,13为公比的等比数列,b n=-2313n-1,所以an=32n-23n.解法二:将a n+1=13a n+12n+1两边分别除12n+1,也就是乘2n+1,为方便计算,我们等式两边同乘2n+1,得2n+1⋅a n+1=232n⋅a n+1.令b n=2n⋅a n,则b n+1=23b n+1,这又回到了构造一的方法,根据待定系数法,得b n+1-3=23b n-3,所以数列b n-3是首项为b1-3=2×56-3=-43,公比为23的等比数列.所以b n-3=-43⋅23n-1即b n=3-2⋅23 n.所以a n=b n2n=32n-23n.解法三:将a n+1=13a n+12n+1两边分别除13n+1,也就是乘3n+1,得3n+1an+1=3n a n+32 n+1⋅令b n=3n⋅a n,则b n+1=b n+32 n+1,所以b n-b n-1=32 n,b n-1-b n-2=32 n-1，...，b2-b1=32 2⋅将以上各式叠加,得b n-b1=32 2+⋯+32 n-1+32 n,又b1=3a1=3×56=52=1+32,所以b n=1+32+32 2+⋯+32 n-1+32 n=1⋅1-32 n+11-32=2⋅32 n+1-2,即b n=2⋅32n+1-2.所以an=b n3n=32n-23n.【经典例题2】已知数列a n满足a n+1=2a n+4⋅3n-1,a1=-1,求数列a n的通项公式.【解析】解法一:设a n+1+λ⋅3n=2a n+λ⋅3n-1,待定系数法得λ=-4,则数列a n-4⋅3n-1是首项为a1-4⋅31-1 =-5,公比为2的等比数列,所以a n-4⋅3n-1=-5⋅2n-1,即a n=4⋅3n-1-5⋅2n-1.解法二:(两边同除以 q n+1) 两边同时除以3n+1得:a n+13n+1=23⋅a n3n+432,下面解法略.解法三:(两边同除以p n +1)两边同时除以2n +1得:a n +12n +1=a n 2n +32n -1,下面解法略.【练习1】已知数列a n 满足a 1=1,a n +1=3a n +2n n ∈N * ,b n =a n +1a n.设t ∈Z ,若对于∀n ∈N *,都有b n >t 恒成立,则t 的最大值为()A.3B.4C.7D.9【答案】A【解析】解法一：因为a n +1=3a n +2n ,所以a n +12n =3a n 2n +1,所以a n +12n +1=32⋅a n 2n +12,所以a n +12n +1+1=32a n 2n +1 ,因为a 1=1,所以a 121+1=32,所以数列a n 2n +1 是以32为首相以32为公比的等比数列,所以a n 2n+1=32 n ,所以a n =3n -2n,故选A .解法二:令a n +1+A ⋅2n +1=3a n +A ⋅2n ,因为a n +1=3a n +2n ,对比系数得:A =1,所以数列 a n +2n 是以3为首项,3为公比的等比数列,所以a n +2n =3n ,所以a n =3n -2n,所以 b n =a n +1a n =3n +1-2n +13n -2n=3⋅32 n-232 n -1n =3+132 n -1,因为∀n ∈N *,所以32 n -1≥12.所以0<132 n -1≤2,所以3<b n ≤5,对于∀n ∈N *,都有b n >t 恒成立,所以t ≥3,所以t 的最大值为3,故选 A .【练习2】已知数列a n 满足a 1=2,a n +1=a n +2n +2n ∈N * .(1)判断数列a n -2n 是否为等差数列,并说明理由;(2)记S n 为数列a n 的前n 项和,求S n .【解析】(1)数列a n 满足a 1=2,a n +1=a n +2n +2n ∈N * ,所以a n +1-2n +1 -a n -2n =2. a 1-2=0,所以数列a n -2n 为等差数列,首项为0，公差为2.(2)由(1)可得:a n -2n=0+2(n -1),可得:a n =2n+2(n -1),所以S n =22n -1 2-1+2×n (0+n -1)2=2n +1-2+n 2-n【过关检测】一、单选题1.已知S n 为数列a n 的前n 项和，若a n +1=2a n -2,S 2=10，则a n 的通项公式为( )A.a n =3n -4B.a n =2n +2C.a n =n 2+nD.a n =3n 2-1【答案】B 【解析】令n =1可得a 2=2a 1-2，又S 2=a 1+a 2=10，解得a 1=4，又a n +1-2=2a n -4=2(a n -2)，则a 1-2=2，a n +1-2a n -2=2，即a n -2 是以2为首项，2为公比的等比数列，则a n -2=2⋅2n -1，a n =2n +2.故选：B .2.已知数列a n 中，a 1=1，a n +1=2a n +1，则数列a n 的通项公式为( )A.a n =n B.a n =n +1C.a n =2nD.a n =2n -1【答案】D 【解析】∵a n +1=2a n +1，∴a n +1+1=2(a n +1),又a 1=1，a 1+1=2，所以数列a n +1 是首项为2，公比为2 的等比数列，所以a n +1=2×2n -1，∴a n =2n -1.故选：D .3.已知数列a n 满足a 1=3，a n +1=5a n -8，则a 2022的值为( )A.52021-2 B.52021+2C.52022+2D.52022-2【答案】B 【解析】因为a n +1=5a n -8，所以a n +1-2=5(a n -2)，又a 1-2=1，所以{a n -2}是等比数列，公比为5，首项是1，所以a n -2=5n -1，a n =5n -1+2，所以a 2022=52021+2．故选：B ．4.设数列a n 的前n 项和为S n ，若S n =2a n -2n +1，则S 10=( )A.211-23 B.210-19C.3×210-23D.3×29-19【答案】C 【解析】当n =1时，S 1=a 1=2a 1-2+1，解得a 1=1.当n ≥2时，S n -1=2a n -1-2n +3，所a n =S n -S n -1=2a n -2n +1-2a n -1-2n +3 ，即a n =2a n -1+2，所以a n +2=2a n -1+2 ，即a n +2a n -1+2=2，所以数列a n +2 是首项为3，公比为2的等比数列，则a n +2=3×2n -1，从而S n =3×2n -2n -3，故S 10=3×210-23.故选：C5.在数列a n 中，a 1=1，且a n +1=2a n +1，则a n 的通项为( )A.a n =2n -1 B.a n =2nC.a n =2n +1D.a n =2n +1【答案】A 【解析】解：∵a n +1=2a n +1，∴a n +1+1=2a n +1 ，由a 1=1，得a 1+1=2，∴数列a n +1 是以2为首项，2为公比的等比数列，∴a n +1=2⋅2n -1=2n ，即a n =2n -1．故选：A6.数列a n 中，a n +1=2a n +1，a 1=1，则a 100=( )A.2100+1B.2101C.2100-1D.2100【答案】C 【解析】数列a n 中，a n +1=2a n +1，故a n +1+1=2a n +1 ，故a n +1≠0，所以a n +1+1a n +1=2，因为a 1=1，所以a 1+1=2≠0，所以a n +1 是首项为2，公比为2的等比数列，所以a n +1=2n ，即a n =2n -1，故a 100=2100-1，故选：C .7.数列a n 满足12a n =a n +1-12n +1，且a 1=12，若a n <13，则n 的最小值为( )A.3B.4C.5D.6【答案】B【解析】因为12a n =a n +1-12 n +1，等式两边同时乘以2n +1可得2n a n =2n +1a n +1-1，所以，2n +1a n +1-2n a n =1且2a 1=1，所以，数列2n a n 是等差数列，且首项和公差都为1，则2n a n =1+n -1=n ，所以，a n =n2n，因为a n +1-a n =n +12n +1-n 2n =n +1-2n 2n +1=1-n2n +1.当n =1时，a 1=a 2=12；当n ≥2时，a n +1<a n ，即数列a n 从第二项开始单调递减，因为a 3=38>13，a 4=14<13，故当n ≤3时，a n >13；当n ≥4时，a n <13.所以，a n <13，则n 的最小值为4.故选：B .8.已知数列a n 中，a 1=1，a n =3a n -1+4(n ∈N ∗且n ≥2)，则数列a n 通项公式a n 为( )A.3n -1 B.3n +1-2C.3n -2D.3n【答案】C 【解析】由已知得a 2=7，a n +2a n -1+2=3进而确定数列{a n +2}的通项公式，即可求a n .由a 1=1，a n =3a n -1+4知：a 2=7且a n +2a n -1+2=3(n ≥2)，而a 1+2=3，a 2+2=9，∴{a n +2}是首项、公比都为3的等比数列，即a n =3n -2，故选：C 9.数列a n 满足a n =4a n -1+3n ≥2 且a 1=0，则此数列第5项是( )A.15 B.255C.16D.63【答案】B 【解析】∵a n=4a n-1+3n≥2，∴a n+1=4a n-1+1n≥2，∴a n+1是以1为首项，4为公比的等比数列，则a n+1=4n-1．∴a n=4n-1-1，∴a5=44-1=255．故选：B．10.在数列a n中，已知a1=1，a n+1=2a n+1，则a n=( )A.2n-1B.2n-1C.nD.2n-1【答案】B【解析】由a n+1=2a n+1，得a n+1+1=2a n+2=2a n+1，故数列a n+1为等比数列，首项为a1+1=2，公比为2，所以a n+1=2n，a n=2n-1，故选：B.11.在数列a n中，a1=3，a n=2a n-1-n+2n≥2,n∈N+，若a n>980，则n的最小值是( )A.8B.9C.10D.11【答案】C【解析】因为a n=2a n-1-n+2n≥2,n∈N+，所以a n-n=2a n-1-n-1.n≥2,n∈N+因为a1=3，所以a1-1=2，所以数列a n-n是首项和公比都是2的等比数列，则a n-n=2n，即a n=2n+n,因为a n-a n-1=2n-1+1>0，所以数列a n是递增数列,因为a9=521<980，a10=1034>980，所以满足a n>980的n的最小值是10,故选：C12.设数列{an}中，a1=2，an+1=2an+3，则通项an可能是()A.5-3nB.3·2n-1-1C.5-3n2D.5·2n-1-3【答案】D【解析】设a n+1+x=2a n+x，则a n+1=2a n+x，因为an+1=2an+3，所以x=3，所以a n+3是以a1+3为首项，2为公比的等比数列，a n+3=5×2n-1，所以a n=5⋅2n-1-3故选：D13.在数列a n中，若a1=2，a n+1=3a n+2n+1，则a n=( )A.n ⋅2nB.52-12n C.2⋅3n -2n +1 D.4⋅3n -1-2n +1【答案】C 【解析】令b n =a n 2n +2，则b n +1b n =a n +12n +1+2a n 2n +2=3a n +2n +12n +1+2a n 2n +2=32，又b 1=a 12+2=3，所以b n 是以3为首项，32为公比的等比数列，所以b n =a n 2n +2=3×32 n -1，得a n =2⋅3n -2n +1．故选：C ．14.已知在数列a n 中，a 1=56，a n +1=13a n +12n +1，则a n =( )A.32n -23n B.23n -32nC.12n -23n D.23n -12n 【答案】A【解析】解:因为a 1=56，a n +1=13a n +12n +1，所以2n +1⋅a n +1=23⋅2n a n +1，整理得2n +1⋅a n +1-3=23⋅2na n -3 ，所以数列2n a n -3 是以2a 1-3=-43为首项，23为公比的等比数列．所以2n a n -3=-4323 n -1，解得a n =32n -23n ．故选：A 15.数列a n 满足a n +1=2a n +3,n ∈N *，若a 2017≥a 1，则a 1的取值范围为( )A.(-∞,-3]B.{-3}C.(-3,+∞)D.[-3,+∞)【答案】D【解析】由a n +1=2a n +3可得a n +1+3=2a n +3 ，所以a n +3=a 1+3 ×2n -1所以a n =a 1+3 ×2n -1-3，所以a 2017=a 1+3 ×22016-3≥a 1所以a 1+3 ×22016≥a 1+3，所以a 1+3≥0，所以a 1≥-3故选：D二、填空题16.设数列a n 满足a 1=1，且a n =3a n -1+4n ≥2 ，则数列a n 的通项公式为a n =___________.【答案】3n -2##-2+3n 【解析】解：因为a n =3a n -1+4n ≥2 ，∴a n +2=3a n -1+2 ，∴a n +2a n -1+2=3，∵a 1=1，则a 1+2=3，∴数列a n +2 是以3为首项，3为公比的等比数列.∴a n +2=3⋅3n -1=3n ，所以a n =3n -2，故答案为：3n -217.已知数列a n 中，a 1=1，a n +1=2a n +1，则a n 通项a n =______；【答案】2n -1【解析】因为a n +1=2a n +1，所以a n +1+1=2(a n +1),∴a n +1+1a n +1=2，所以a n +1 是一个以a 1+1=2为首项，以2为公比的等比数列，所以a n +1=2×2n -1=2n ,∴a n =2n -1.故答案为：2n -118.数列{an }满足a 1=1，an +1=2an +1. (n ∈N *).数列{an }的通项公式为______．【答案】a n =2n -1n ∈N * ．【解析】∵a n +1=2a n +1(n ∈N *)，∴a n +1+1=2(a n +1)，又a 1+1=2∴a n +1 是以2为首项，2为公比的等比数列．∴a n +1=2n ．即a n =2n -1(n ∈N *)．故答案为：a n =2n -1n ∈N * ．19.数列a n 满足a n =4a n -1+3，且a 1=0，则a 6=_________.【答案】1023【解析】由题意知：a n +1=4a n -1+4=4(a n -1+1)，又a 1+1=1，故a n +1 是1为首项，4为公比的等比数列，故a 6+1=a 1+1 ×45=1024，故a 6=1023.故答案为：1023.20.已知数列a n 满足a n +1=2a n +12，且a n 前8项和为761，则a 1=______．【答案】52##2.5【解析】解：数列{a n }满足a n +1=2a n +12，整理得a n +1+12=2a n +12 ，若a 1=-12，则a n =-12，显然不符合题意，所以a n ≠-12，则a n +1+12a n +12=2(常数)；所以数列a n +12 是以a 1+12为首项，2为公比的等比数列；所以a n +12=a 1+12 ⋅2n -1，整理得a n =a 1+12 ⋅2n -1-12；由于前8项和为761，所以S 8=a 1+12 ⋅(1+2+...+27)-8×12=a 1+12 ×1-281-2-4=255a 1+12 -4=761，解得a 1=52．故答案为：52．三、解答题21.已知数列a n 满足a 1=1,a n +1=3a n +2.(1)证明1+a n 为等比数列，并求a n 的通项公式；(2)记数列11+a n 的前n 项和为S n ，证明S n <34.【答案】(1)证明见解析，a n =2⋅3n -1-1(2)见解析【解析】(1)证明：因为a n +1=3a n +2，所以a n +1+1=3a n +1 ，又a 1+1=2，所以数列1+a n 是以2为首项，3为公比的等比数列，则a n +1=2⋅3n -1，所以a n =2⋅3n -1-1；(2)证明：由(1)得1a n +1=12⋅3n -1，因为1a n +1+11a n +1=12⋅3n12⋅3n -1=13，1a 1+1=12，所以数列11+a n 是以12为首项，13为公比的等比数列，则S n =12×1-13n 1-13=341-13n ，因为1-13n <1，所以S n <34.22.已知数列a n 满足a 1=3,a n +1=2a n -2.(1)求a n 的通项公式；(2)求a n 的前n 项和S n .【答案】(1)a n =2n -1+2；(2)S n =2n +2n -1.【解析】(1)∵a n +1=2a n -2，∴a n +1-2=2a n -2 即∴a n +1-2a n -2=2∴数列a n -2 是以首相为1，公比为2的等比数列，∴a n -2=2n -1∴a n =2n -1+2(2)由(1)知a n =2n -1+2∴S n =a 1+a 2+a 3+⋯+a n=20+2 +21+2 +22+2 +⋯+2n -1+2 =20+21+22+⋯+2n -1 +2n =1×1-2n 1-2+2n=2n +2n -123.已知数列a n 的首项a 1=1，且1a n +1=2a n+1．(1)求数列a n 的通项公式；(2)若数列b n满足a n⋅b n=n，求数列b n的前n项和S n．【答案】(1)a n=12n-1(2)S n=n-12n+1+2-n n+12【解析】(1)∵1an+1=2an+1，等式两边同时加1整理得1an+1+1=21an+1又∵a1=1，∴1a1+1=2∴1an +1是首项为2，公比为2的等比数列．∴1an +1=2n， ∴a n=12n-1(2)∵a n⋅b n=n，∴b n=n an=n⋅2n-n.记n⋅2n的前n项和为T n则T n=1⋅21+2⋅22+3⋅23+⋅⋅⋅⋅⋅⋅+n-1⋅2n-1+n⋅2n所以2T n=1⋅22+2⋅23+3⋅24+⋅⋅⋅⋅⋅⋅+n-1⋅2n+n⋅2n+1相减得-T n=21+22+23+24+⋅⋅⋅⋅⋅⋅+2n-n⋅2n+1整理得T n=n-12n+1+2.所以S n=n-12n+1+2-n n+1224.在数列a n中，a1=5，且a n+1=2a n-1n∈N*.(1)证明：a n-1为等比数列，并求a n的通项公式；(2)令b n=(-1)n⋅a n，求数列b n的前n项和S n.【答案】(1)证明见解析，a n=2n+1+1(2)S n=432n-1,n=2k,k∈N*,-2n+2+73,n=2k-1,k∈N*.【解析】(1)解：因为a n+1=2a n-1，所以a n+1-1=2a n-1，又a1-1=4，所以a n+1-1a n-1=2，所以a n-1是以4为首项，2为公比的等比数列.故a n-1=4×2n-1，即a n=2n+1+1.(2)解：由(1)得b n=(-1)n⋅2n+1+1，则b n=2n+1+1,n=2k,k∈N*-2n+1+1,n=2k-1,k∈N* ，①当n=2k,k∈N*时，S n=-22-1+23+1-24+1+⋯+-2n-1+2n+1+1=-22+23-24+25+⋯-2n+2n+1=22+24+⋯+2n=432n-1;②当n=2k-1,k∈N*时，S n=S n+1-b n+1=432n+1-1-2n+2+1=-2n+2+73，综上所述，S n=432n-1,n=2k,k∈N*-2n+2+73,n=2k-1,k∈N*25.已知数列a n的前n项和为S n，a1=2，且a n+1=2a n+2．(1)求数列a n的通项公式；(2)令b n=2n+1a n+2，记数列b n的前n项和为T n，求证：T n<3．【答案】(1)a n=2n+1-2(2)证明见解析【解析】(1)解：因为a1=2，a n+1=2a n+2，所以a n+1+2=2a n+2，所以a n+2是以4为首项，2为公比的等比数列，所以a n+2=4×2n-1=2n+1，所以a n=2n+1-2；(2)解：由(1)可知b n=2n+1a n+2=2n+12n+1=n+12n，所以T n=221+322+423+⋯+n+12n①，所以12T n=2 22+323+424+⋯+n+12n+1②；①-②得12T n=1+122+123+⋯+12n-n+12n+1=1+1221-12n-11-12-n+12n+1=32-n+32n+1所以T n=3-n+32n<3；。
第四章 习题课 数列中的构造问题
2.下列说法错误的是 A.任意等差数列{an}和{bn}，数列{an＋bn}是等差数列 B.存在等差数列{an}和{bn}，数列{anbn}是等差数列
√C.任意等比数列{an}和{bn}，数列{an＋bn}是等比数列
D.存在等比数列{an}ຫໍສະໝຸດ {bn}，数列{anbn}是等比数列
1234
解析 A项，若{an}和{bn}都是等差数列，不妨设an＝k1n＋b1，bn＝k2n＋b2， 故可得an＋bn＝(k1＋k2)n＋b1＋b2，则an＋1＋bn＋1＝(k1＋k2)(n＋1)＋b1＋b2， 则an＋1＋bn＋1－(an＋bn)＝k1＋k2，故数列{an＋bn}是等差数列，则A正确； B项，设数列{an}是数列1,1,1；数列{bn}是数列2,2,2，故可得数列{anbn} 是数列2,2,2，是等差数列，故B正确. C 项，若{an}和{bn}是等比数列，设 an＝a1qn1，bn＝b1qn2，故可得 an＋bn＝ a1qn1＋b1qn2，an＋1＋bn＋1＝a1qn1＋1＋b1qn2＋1， 则ana＋n1＋＋bbnn＋1＝a1aqn11＋ q1n1＋ ＋bb11qq2n2n＋1，不是常数，故{an＋bn}不是等比数列，故 C 错误；
延伸探究 1.本例中“an＝2an－1＋2n”变为“an＝2an－1＋2n＋1”，其余不变，求 数列{an}的通项公式.
解 等式两边同时除以 2n，得a2nn＝a2nn－－11＋2，即a2nn－a2nn－－11＝2， 所以a2nn是以12为首项，以 2 为公差的等差数列， 所以a2nn＝12＋(n－1)×2，即 an＝2n－23×2n.
第四章 §4.3 等比数列
学习目标
1.掌握利用构造法求数列通项公式的方法. 2.会用构造法公式解决一些简单的问题.
高考数学-构造法求数列通项7例
高考数学-构造法求数列通项公式7题例1 数列{a n }的前n 项和记为S n ,已知a 1=1,a n+1=nn 2+S n (n=1,2,3……)，求a n .例2 已知数列{a n }的前n 项和为S n ,且满足a n +2S n S n-1=0(n ≥2);a 1=21,求通项a n .例3 已知函数f(x)=42-x (x ≤-2).(1)求f -1(x),(2)若a 1=1,a n =-f -1(a n-1),求数列{a n }的通项公式.例4 已知函数f(x)=(x +2)2(x>0),设正项数列{a n }的首项a 1=2,前n 项和S n 满足S n =f(S n-1)(n ≥2且n ∈N *),求通项a n .例5 已知数列{a n }中,a 1=1,且a n+1=3a n -1(n ∈N *),求a n .例6 已知正项数列{a n }的前项和S n 满足S n =21(a n +n a 1)，求通项a n .例7 已知数列{a n }中，a 1=2,a n =2211+--n n a a (n ≥2)，求通项a n .构造法求数列通项公式7题答案例1 解析：∵a n+1=S n+1-S n ,a n+1=nn 2+S n∴(n+2)S n=n(S n+1-S n )，整理得nS n+1=2(n+1)S n ,即11++n S n =2·nS n，故数列{nS n}是以11S =a 1=1为首项，2为公比的等比数列，即nS n=2n-1,S n =n ·2n-1，当n ≥2时，a n =S n -S n-1=n ·2n-1-(n-1)2n-2=(n+1)2n-2,当n=1时也适合，故a n =(n+1)·2n-2n ∈N *.例2 解析:当n ≥2时, a n =S n -S n-1=-2 S n S n-1,两边同除以S n S n-1得nS 1-11-n S =2,又11S =11a =2, ∴数列{nS 1}是以2为首项,2为公差的等差数列,则nS 1=2+2(n-1)=2n, S n =n 21,由a 1=21, n ≥2时,a n =S n -S n-1=n 21-)1(21-n =- )1(21-n n ,二式不能合并.例3 解析:(1)f -1(x)=-42+x (x ≥0),(2)由a n=-f-1(a n-1),∴a n =421+-n a ,两边平方得an 2-a n-12=4,∴数列{a n 2}是以a 12=1为首项,公差为4的等差数列,∴a n 2=1+(n-1)4=4n-3,又a n >0,∴a n =34-n .例4解析:∵a n >0,∴S n >0,由S n =f(S n-1)=(1-n S +2)2两边开方得nS =1-n S +2,∴数列{n S }是以1S =1a =2为首项,公差d=2的等差数列,即nS =2+(n-1)2=2n,则S n =2n 2,当n ≥2时,a n =S n -S n-1=4n-2,当n=1时,a 1=2也适合上式,故a n =4n-2(n ∈N *). 例5 解析:设a n+1+x=3(a n +x),则a n+1=3a n +2x,又a n+1=3a n -1,则2x=-1,即x=-21,故而a n+1-21=3(a n-21),则数列{a n-21}是以首项a 1-21=21,公比为3的等比数列,∴a n-21=21·3n-1,即a n=21·3n-1+21.例 6 解析：由S 1=a 1=21(a 1+11a )得a 1=1，又a n =S n -S n-1(n ≥2)∴S n =21(a n +na 1)=21(S n -S n-1+11--n n S S )可得S n +S n-1=11--n n S S ，即S n 2-S n-12=1,∴数列{S n 2}是首项为S 12=a 12=1,公差为1的等差数列.∴S n 2=1+(n-1)·1=n ，又S n >0，∴S n =n ,当n ≥2时，a n=S n-Sn-1=n -1-n ,当n=1时，a 1=1也适合，故通项a n=n -1-n .例7 解析：由题意知a n ≠0，在a n =2211+--n n a a 两边同时取倒数得，n a 1=1122--+n n a a =11-n a +21,即n a 1-11-n a =21,∴数列{na 1}是首项为11a ，公差为21的等差数列，∴n a 1=21+(n-1)21=2n , 则a n=n2.。
第六章数列中的构造问题
§6.4 数列中的构造问题题型一 形如a n ＋1＝pa n ＋f (n )型命题点1 a n ＋1＝pa n ＋q (p ≠0,1，q ≠0，其中a 1＝a )例1 (2022·九江模拟)在数列{a n }中，a 1＝5，a n ＋1＝3a n －4，求数列{a n }的通项公式． 解 由a n ＋1＝3a n －4，可得a n ＋1－2＝3(a n －2)，所以a n ＋1－2a n －2＝3. 又a 1＝5，所以{a n －2}是以a 1－2＝3为首项，3为公比的等比数列，所以a n －2＝3n ，所以a n ＝3n ＋2.命题点2 a n ＋1＝pa n ＋qn ＋c (p ≠0,1，q ≠0)例2 已知数列{a n }满足a n ＋1＝2a n －n ＋1(n ∈N *)，a 1＝3，求数列{a n }的通项公式． 解 ∵a n ＋1＝2a n －n ＋1，∴a n ＋1－(n ＋1)＝2(a n －n )，∴a n ＋1－(n ＋1)a n －n＝2， ∴数列{a n －n }是以a 1－1＝2为首项，2为公比的等比数列，∴a n －n ＝2·2n －1＝2n ，∴a n ＝2n ＋n .命题点3 a n ＋1＝pa n ＋q n (p ≠0,1，q ≠0,1)例3 在数列{a n }中，a 1＝－1，a n ＋1＝2a n ＋4·3n －1，求数列{a n }的通项公式． 解 方法一 原递推式可化为a n ＋1＋λ·3n ＝2(a n ＋λ·3n －1)．① 比较系数得λ＝－4，①式即是a n ＋1－4·3n ＝2(a n －4·3n －1)．则数列{a n －4·3n －1}是首项为a 1－4·31－1＝－5，公比为2的等比数列，∴a n －4·3n －1＝－5·2n －1，即a n ＝4·3n －1－5·2n －1.方法二 将a n ＋1＝2a n ＋4·3n －1的两边同除以3n ＋1，得a n ＋13n ＋1＝23·a n 3n ＋432， 令b n ＝a n 3n ， 则b n ＋1＝23b n ＋49， 设b n ＋1＋k ＝23(b n ＋k )，比较系数得k ＝－43， 则b n ＋1－43b n －43＝23， ∴⎩⎨⎧⎭⎬⎫b n －43是以－53为首项，23为公比的等比数列．∴b n －43＝⎝⎛⎭⎫－53·⎝⎛⎭⎫23n －1， 则b n ＝43－53·⎝⎛⎭⎫23n －1， ∴a n ＝3n ·b n ＝4·3n －1－5·2n －1.思维升华 (1)形如a n ＋1＝αa n ＋β(α≠0,1，β≠0)的递推式可用构造法求通项，构造法的基本原理是在递推关系的两边加上相同的数或相同性质的量，构造数列的每一项都加上相同的数或相同性质的量，使之成为等差数列或等比数列．(2)递推公式a n ＋1＝αa n ＋β的推广式a n ＋1＝αa n ＋β×γn (α≠0,1，β≠0，γ≠0,1)，两边同时除以γn ＋1后得到a n ＋1γn ＋1＝αγ·a n γn ＋βγ，转化为b n ＋1＝kb n ＋βγ(k ≠0,1)的形式，通过构造公比是k 的等比数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫b n －βγ(1－k )求解． 跟踪训练1 (1)(2022·武汉二中月考)已知正项数列{a n }中，a 1＝2，a n ＋1＝2a n ＋3×5n ，则数列{a n }的通项公式为( )A ．a n ＝－3×2n －1B ．a n ＝3×2n －1 C ．a n ＝5n ＋3×2n －1D ．a n ＝5n －3×2n －1 答案 D解析 方法一 将递推公式a n ＋1＝2a n ＋3×5n 的两边同时除以5n ＋1，得a n ＋15n ＋1＝25·a n 5n ＋35， ① 令a n 5n ＝b n ，则①式变为b n ＋1＝25b n ＋35， 即b n ＋1－1＝25(b n －1)， 所以数列{b n －1}是首项为b 1－1＝a 15－1＝－35， 公比为25的等比数列， 所以b n －1＝⎝⎛⎭⎫－35×⎝⎛⎭⎫25n －1， 即b n ＝1－35×⎝⎛⎭⎫25n －1＝1－3×2n －15n， 故a n ＝5n －3×2n －1.方法二 设a n ＋1＋k ×5n ＋1＝2(a n ＋k ×5n )，则a n ＋1＝2a n －3k ×5n ，与题中递推公式比较得k ＝－1，即a n ＋1－5n ＋1＝2(a n －5n )，所以数列{a n －5n }是首项为a 1－5＝－3，公比为2的等比数列，则a n －5n ＝－3×2n －1，故a n ＝5n －3×2n －1.(2)(2022·衡水质检)设数列{a n }的前n 项和为S n ，已知a 1＝1，S n ＋1－2S n ＝1，n ∈N *，则数列{a n }的通项公式为________．答案 a n ＝2n －1，n ∈N *解析 因为S n ＋1－2S n ＝1，所以S n ＋1＝2S n ＋1.因此S n ＋1＋1＝2(S n ＋1)，因为a 1＝S 1＝1，S 1＋1＝2，所以{S n ＋1}是首项为2，公比为2的等比数列．所以S n ＋1＝2n ，S n ＝2n －1.当n ≥2时，a n ＝S n －S n －1＝2n －1，a 1＝1也满足此式，所以a n ＝2n －1，n ∈N *.题型二 相邻项的差为特殊数列(形如a n ＋1＝pa n ＋qa n －1，其中a 1＝a ，a 2＝b 型) 例4 已知在数列{a n }中，a 1＝5，a 2＝2，a n ＝2a n －1＋3a n －2(n ≥3)，求这个数列的通项公式． 解 ∵a n ＝2a n －1＋3a n －2，∴a n ＋a n －1＝3(a n －1＋a n －2)，又a 1＋a 2＝7，∴{a n ＋a n －1}是首项为7，公比为3的等比数列，则a n ＋a n －1＝7×3n －2，① 又a n －3a n －1＝－(a n －1－3a n －2)，a 2－3a 1＝－13，∴{a n －3a n －1}是首项为－13，公比为－1的等比数列，则a n －3a n －1＝(－13)·(－1)n －2， ② ①×3＋②得，4a n ＝7×3n －1＋13·(－1)n －1，∴a n ＝74×3n －1＋134(－1)n －1. 思维升华 可以化为a n ＋1－x 1a n ＝x 2(a n －x 1a n －1)，其中x 1，x 2是方程x 2－px －q ＝0的两个根，若1是方程的根，则直接构造数列{a n －a n －1}，若1不是方程的根，则需要构造两个数列，采取消元的方法求数列{a n }．跟踪训练2 (1)数列{a n }中，a 1＝8，a 4＝2，且满足a n ＋2＝2a n ＋1－a n (n ∈N *)，则数列{a n }的通项公式为__________．答案 a n ＝10－2n (n ∈N *)解析 由题意知，a n ＋2－a n ＋1＝a n ＋1－a n ，所以{a n }为等差数列．设公差为d ，由题意得2＝8＋3d ⇒d ＝－2，得a n ＝8－2(n －1)＝10－2n .(2)在数列{a n }中，a 1＝1，a 2＝3，a n ＋2＝3a n ＋1－2a n ，则a n ＝________. 答案 2n －1解析 由题意知，a n ＋2－a n ＋1＝2(a n ＋1－a n )，∵a 2－a 1＝2，∴{a n －a n －1}是首项为2，公比为2的等比数列，a n －a n －1＝2n －1(n ≥2)， 当n ≥2时，a n ＝(a n －a n －1)＋(a n －1－a n －2)＋…＋(a 2－a 1)＋a 1 ＝2n －1＋2n －2＋…＋2＋1＝1－2n1－2＝2n －1. 显然n ＝1时满足上式，∴a n ＝2n －1.题型三 倒数为特殊数列⎝⎛⎭⎫形如a n ＋1＝pa n ra n＋s 型 例5 (1)已知数列{a n }中，a 1＝1，a n ＋1＝2a n a n ＋2，则a n ＝________. 答案 2n ＋1 解析 ∵a n ＋1＝2a n a n ＋2，a 1＝1， ∴a n ≠0，∴1a n ＋1＝1a n ＋12， 即1a n ＋1－1a n ＝12， 又a 1＝1，则1a 1＝1， ∴⎩⎨⎧⎭⎬⎫1a n 是以1为首项，12为公差的等差数列． ∴1a n ＝1＋(n －1)×12＝n 2＋12， ∴a n ＝2n ＋1(n ∈N *)．(2)已知在数列{a n }中，a 1＝2，a n ＋1＝a n a n ＋3(n ∈N *)，则a n ＝________. 答案 22×3n －1－1解析 ∵1a n ＋1＝3·1a n ＋1， ∴1a n ＋1＋12＝3⎝⎛⎭⎫1a n ＋12，1a 1＋12＝1， ∴⎩⎨⎧⎭⎬⎫1a n ＋12是以1为首项，3为公比的等比数列， ∴1a n ＋12＝3n －1， ∴1a n ＝3n －1－12， ∴a n ＝22×3n －1－1(n ∈N *)． 思维升华 两边同时取倒数转化为1a n ＋1＝s p ·1a n ＋r p 的形式，化归为b n ＋1＝pb n ＋q 型，求出1a n 的表达式，再求a n .跟踪训练3 (1)已知函数f (x )＝x 3x ＋1，数列{a n }满足a 1＝1，a n ＋1＝f (a n )(n ∈N *)，则数列{a n }的通项公式为____________．答案 a n ＝13n －2(n ∈N *) 解析 由已知得，a n ＋1＝a n 3a n ＋1， ∴1a n ＋1＝1a n ＋3，即1a n ＋1－1a n ＝3， ∴数列⎩⎨⎧⎭⎬⎫1a n 是首项为1a 1＝1，公差为d ＝3的等差数列， ∴1a n＝1＋(n －1)×3＝3n －2. 故a n ＝13n －2(n ∈N *)． (2)已知数列{a n }满足a 1＝1，a n ＋1＝a n 2na n ＋1，则a n ＝__________. 答案 1n 2－n ＋1解析 对递推关系两边取倒数，得1a n ＋1＝2na n ＋1a n ＝1a n＋2n .即1a n ＋1－1a n＝2n ，分别用1,2,3，…，n －1替换n ，有 1a 2－1a 1＝2×1，1a 3－1a 2＝2×2，1a 4－1a 3＝2×3，…，1a n －1a n －1＝2(n －1)，以上n －1个式子相加，得1a n －1a 1＝2[1＋2＋3＋…＋(n －1)]＝n (n －1)，所以1a n ＝n 2－n ＋1.所以a n ＝1n 2－n ＋1.课时精练1．数列{a n }满足a n ＝4a n －1＋3(n ≥2)且a 1＝0，则此数列第5项是() A ．15 B ．255C ．16D ．63 答案 B解析 ∵a n ＝4a n －1＋3(n ≥2)，∴a n ＋1＝4(a n －1＋1)(n ≥2)，∴{a n ＋1}是以1为首项，4为公比的等比数列， 则a n ＋1＝4n －1.∴a n ＝4n －1－1，∴a5＝44－1＝255.2．(2022·许昌模拟)数列{a n}的首项a1＝2，且a n＋1＝4a n＋6(n∈N*)，令b n＝log2(a n＋2)，则b1＋b2＋…＋b2 0222 022等于()A．2 020 B．2 021C．2 022 D．2 023答案 D解析∵a n＋1＝4a n＋6(n∈N*)，∴a n＋1＋2＝4a n＋6＋2＝4(a n＋2)>0，即a n＋1＋2a n＋2＝4且a1＝2，∴数列{a n＋2}是以4为首项，4为公比的等比数列，故a n＋2＝4n，由b n＝log2(a n＋2)得，b n＝log24n＝2n，设数列{b n}的前n项和为S n，则S2 022＝2(1＋2＋3＋…＋2 021＋2 022)＝2 022×2 023，∴b1＋b2＋…＋b2 0222 022＝2 022×2 0232 022＝2 023.3．(2022·绵阳模拟)已知数列{a n}满足：a1＝a2＝2，a n＝3a n－1＋4a n－2(n≥3)，则a9＋a10等于()A．47B．48C．49D．410答案 C解析由题意得a1＋a2＝4，由a n＝3a n－1＋4a n－2(n≥3)，得a n＋a n－1＝4(a n－1＋a n－2)，即a n ＋a n －1a n －1＋a n －2＝4(n ≥3)， 所以数列{a n ＋a n ＋1}是首项为4，公比为4的等比数列， 所以a 9＋a 10＝49.4．已知数列{a n }满足：a 1＝1，a n ＋1＝2a n ＋2n ，n ∈N *，则a 4等于( )A ．64B ．56C ．32D ．24答案 C解析 由a n ＋1＝2a n ＋2n 得a n ＋12n ＋1－a n 2n ＝12， 而a 12＝12， ∴数列⎩⎨⎧⎭⎬⎫a n 2n 是首项为12，公差为12的等差数列， ∴a n 2n ＝12＋(n －1)×12＝n 2， ∴a n ＝n ·2n －1，∴a 4＝4×24－1＝32.5．已知数列{a n }满足a 1＝1，a n ＋1＝a n a n ＋2(n ∈N *)．若b n ＝log 2⎝⎛⎭⎫1a n ＋1，则数列{b n }的通项公式b n 等于( )A.12n B ．n －1 C ．nD ．2n答案 C解析 由a n ＋1＝a n a n ＋2， 得1a n ＋1＝1＋2a n ， 所以1a n ＋1＋1＝2⎝⎛⎭⎫1a n ＋1， 又1a 1＋1＝2， 所以数列⎩⎨⎧⎭⎬⎫1a n ＋1是首项为2，公比为2的等比数列，所以1a n＋1＝2·2n －1＝2n ， 所以b n ＝log 2⎝⎛⎭⎫1a n＋1＝log 22n ＝n . 6．已知数列{a n }满足a 1＝1，a n ＋1＝a n 2＋3a n(n ∈N *)，则下列结论正确的是( ) A.⎩⎨⎧⎭⎬⎫1a n ＋3为等比数列 B ．{a n }的通项公式为a n ＝12n －1－3C ．{a n }为递增数列D.⎩⎨⎧⎭⎬⎫1a n 的前n 项和T n ＝2n ＋2－3n ＋4 答案 A解析 因为a n ＋1＝a n 2＋3a n， 所以1a n ＋1＝2＋3a n a n ＝2a n ＋3， 所以1a n ＋1＋3＝2⎝⎛⎭⎫1a n ＋3， 且1a 1＋3＝4≠0， 所以⎩⎨⎧⎭⎬⎫1a n ＋3是以4为首项，2为公比的等比数列，即1a n ＋3＝4×2n －1， 所以1a n＝2n ＋1－3， 可得a n ＝12n ＋1－3， 故选项A 正确，选项B 不正确；因为1a n＝2n ＋1－3单调递增， 所以a n ＝12n ＋1－3单调递减， 即{a n }为递减数列，故选项C 不正确； ⎩⎨⎧⎭⎬⎫1a n 的前n 项和T n ＝(22－3)＋(23－3)＋…＋(2n ＋1－3)＝(22＋23＋…＋2n ＋1)－3n＝22×1－2n1－2－3n ＝2n ＋2－3n －4. 故选项D 不正确．7．已知数列{a n }中，a 1＝1，a n ＋1＝3a n ＋3n ，则a 5等于( )A ．405B ．300C ．450D ．500 答案 A解析 ∵a n ＋1＝3a n ＋3n ，∴a n ＋13n ＋1－a n 3n ＝13， ∴数列⎩⎨⎧⎭⎬⎫a n 3n 是等差数列，公差为13， 又a 13＝13， ∴a n 3n ＝13＋(n －1)×13＝n 3， ∴a n ＝n ·3n －1，a 5＝5×34＝405.8．(2022·甘肃西北师大附中模拟)已知数列{a n }满足a 1＝110，a n －a n ＋1＝a n a n ＋1(n ∈N *)，则n ＋2na n的最小值为( )A.252 B ．12 C ．24 D.392答案 D解析 ∵a 1＝110，a n －a n ＋1＝a n a n ＋1(n ∈N *)， ∴1a 1＝10，1a n ＋1－1a n＝1， ∴数列⎩⎨⎧⎭⎬⎫1a n 是以10为首项，1为公差的等差数列， ∴1a n＝n ＋9， ∴n ＋2na n ＝(n ＋2)(n ＋9)n ＝n ＋18n＋11. ∵y ＝n ＋18n在(0,32)上单调递减，在(32，＋∞)上单调递增，∴当n ＝4时，n ＋2na n 取得最小值为392. 9．已知数列{a n }满足a 1＝1，a n －a n ＋1＝2a n a n ＋1，则a n ＝________. 答案 12n －1解析 因为a n －a n ＋1＝2a n a n ＋1，所以等式两边同除以a n a n ＋1得1a n ＋1－1a n＝2， 所以数列⎩⎨⎧⎭⎬⎫1a n 是以1a 1＝1为首项，2 为公差的等差数列， 所以1a n＝1＋2(n －1)＝2n －1， 所以a n ＝12n －1. 10．已知数列{a n }中，a 1＝56，a n ＋1＝13a n ＋⎝⎛⎭⎫12n ＋1，则a n ＝__________. 答案 3×⎝⎛⎭⎫12n －2×⎝⎛⎭⎫13n 解析 由a n ＋1＝13a n ＋⎝⎛⎭⎫12n ＋1， 两边同除以⎝⎛⎭⎫12n ＋1，即两边同乘以2n ＋1，得2n ＋1·a n ＋1＝23(2n ·a n )＋1， 令b n ＝2n ·a n ，则b n ＋1＝23b n ＋1， b n ＋1－3＝23(b n －3)， 所以{b n －3}是以b 1－3＝－43为首项，23为公比的等比数列， 即b n －3＝－43×⎝⎛⎭⎫23n －1， 所以b n ＝3－2×⎝⎛⎭⎫23n ，所以a n ＝b n 2n ＝3×⎝⎛⎭⎫12n －2×⎝⎛⎭⎫13n .11．已知首项为1的数列{a n }各项均为正数，且na 2n ＋1－(n ＋1)a 2n ＝a n a n ＋1，则a n ＝________.答案 n解析 因为na 2n ＋1－(n ＋1)a 2n ＝a n a n ＋1，所以n (a n ＋1＋a n )(a n ＋1－a n )＝a n (a n ＋1＋a n )， 因为数列{a n }各项均为正数，所以a n ＋1＋a n >0，所以n (a n ＋1－a n )＝a n ，所以a n ＋1n ＋1＝a n n， 所以⎩⎨⎧⎭⎬⎫a n n 为常数列， 由a 1＝1，所以a n n ＝a 11＝1， 所以a n ＝n .12．已知数列{a n }满足递推公式a n ＋1＝2a n ＋1，a 1＝1.设S n 为数列{a n }的前n 项和，则a n ＝______，4n ＋7－n －S n a n ＋1的最小值是________． 答案 2n －1 174解析 因为a n ＋1＝2a n ＋1，所以a n ＋1＋1＝2(a n ＋1)，所以数列{a n ＋1}是首项为a 1＋1＝2，公比为2的等比数列， 所以a n ＋1＝2n ，所以a n ＝2n －1；所以S n ＝2＋22＋23＋…＋2n －n ＝2(1－2n )1－2－n ＝2n ＋1－2－n ， 所以4n ＋7－n －S n a n ＋1＝4n ＋7－n －(2n ＋1－2－n )2n ＝2n ＋92n －2， 由对勾函数的性质可得，当n ＝1时，21＝2,21＋921－2＝2＋92－2＝92；当n ≥2时，2n ≥4，所以y ＝2n ＋92n －2单调递增， 当n ＝2时，22＋922－2＝4＋94－2＝174<92， 所以4n ＋7－n －S n a n ＋1的最小值是174.。
构造法求数列通项公式
构造法求数列通项公式求数列通项公式是高考考察的重点和热点,本文将通过构造等比数列或等差数列求数列通项公式作以简单介绍，供同学们学习时参考。
一、构造等差数列求数列通项公式运用乘、除、去分母、添项、去项、取对数、待定系数等方法，将递推公式变形成为(1)()f n f n +-=A （其中A 为常数）形式，根据等差数列的定义知)(n f 是等差数列，根据等差数列的通项公式,先求出)(n f 的通项公式，再根据)(n f 与n a ,从而求出n a 的通项公式。
例1 在数列{}n a 中，1a =12，1n a +=33n n a a +（n N +∈)，求数列{}n a 通项公式.解析:由a n+1=33+n na a 得，a n+1 a n =3 a n+1—3 a n =0，两边同除以a n+1 a n 得,=-+n n a a11131，设b n =n a 1,则b n+1— b n =31,根据等差数列的定义知， 数列{b n ｝是首相b 1=2，公差d=31的等差数列，根据等差数列的通项公式得b n =2＋31（n —1）=31n ＋35∴数列通项公式为a n =53+n评析：本例通过变形，将递推公式变形成为A a a nn =-+111形式，应用等差数列的通项公式，先求出na 1的通项公式，从而求出n a 的通项公式。
例2 在数列｛a n ｝中，S n 是其前n 项和,且S n ≠0，a 1=1，a n =1222-n n S S （n ≥2)，求S n 与a n 。
解析:当n ≥2时，a n =S n -S n-1 代入a n =1222-n n S S得，S n -S n-1=1222-n n S S ，变形整理得S n —S n —1= S n S n—1两边除以S n S n —1得，nS 1-11-n S =2,∴{nS 1｝是首相为1,公差为2的等差数列∴nS 1=1+2（n-1)=2n-1， ∴ S n =121-n （n ≥2),n=1也适合,∴S n =121-n (n ≥1)当n ≥2时,a n =S n —S n-1=121-n -321-n =-38422+-n n ，n=1不满足此式，∴a n =｛21138422≥=+--n n n n评析:本例将所给条件变形成A n f n f =-+)()1(，先求出)(n f 的通项公式,再求出原数列的通项公式，条件变形是难点。
高考数学题型全归纳：用构造法求数列的通项公式要点讲解(含答案)
用构造法求数列的通项公式求数列的通项公式是高考重点考查的内容，作为两类特殊数列----等差数列·等比数列可直接根据它们的通项公式求解，但也有一些数列要通过构造转化为等差数列或等比数列，之后再应用各自的通项公式求解，体现化归思想在数列中的具体应用。
例1:（06年福建高考题）数列{}=+==+n n n n a a a a a 则中12,1,11 ( ) A ．n2 B ．12+nC ．12-nD ．12+n解法1：121+=+n n a a)1(22211+=+=+∴+n n n a a a又211=+a2111=++∴+n n a a{}1+n a 是首项为2公比为2的等比数列12,22211-=∴=⋅=+-n n n n n a a ,所以选C解法2归纳总结：若数列{}n a 满足q p q pa a n n ,1(1≠+=+为常数），则令)(1λλ+=++n n a p a 来构造等比数列，并利用对应项相等求λ的值，求通项公式。
例2：数列{}n a 中，n n n a a a a a 23,3,11221-===++，则=n a 。
解：)(2112n n n n a a a a -=-+++212=-a a {}1--∴n n a a 为首项为2公比也为2的等比数列。
112--=-n n n a a ，（n>1） n>1时1221211222)()()(21112211-=--=++++=+-++-+-=-----n nn n n n n n n a a a a a a a a显然n=1时满足上式=n a 12-n小结：先构造{}n n a a --1等比数列，再用叠加法,等比数列求和求出通项公式，例3：已知数列{}n a 中)3(,32,2,52121≥+===--n a a a a a n n n 求这个数列的通项公式。
解： 2132--+=n n n a a a)(3211---+=+∴n n n n a a a a又{}121,7-+=+n n a a a a 形成首项为7，公比为3的等比数列，则2137--⨯=+n n n a a ………………………① 又)3(3211-----=-n n n n a a a a ，13312-=-a a ，{}13--n n a a 形成了一个首项为—13，公比为—1的等比数列则21)1()13(3---⋅-=-n n n a a ………………………② ①+⨯3② 11)1(13374---⋅+⨯=n n n a 11)1(413347---+⨯=∴n n n a 小结：本题是两次构造等比数列，属于构造方面比较级，最终用加减消元的方法确定出数列的通项公式。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1.设数列{}n a 满足11a =，121n n a a +=+． (1)求{}n a 的通项公式；(2)记()2log 1n n b a =+，求数列{}n n b a ⋅的前n 项和nS．答案：(1) 21nn a =- ；(2)()()111222n n n n ++-+-⋅ .解答： (1)11111211211201021n n n n n n n a a a a a a a a ++++=+∴+=++=≠∴+≠∴=+，（）（）,，，，∴{1}n a +是以2为公比、2为首项的等比数列，12n n a ∴+＝， ∴21nn a -＝；(2)22211221()(2)n n n n n n n n n a b log a log n b a n n n -∴+⋅∴⋅-⋅-＝，＝＝＝，＝＝，记122112222212122n n n A n A n n +=⨯+⨯++⋅∴=⨯++-⋅+⋅，（）， ()211121222222212212n n n n n A A A n n n +++-∴-=-=+++-⋅=-⋅=-⋅--（），1122n A n +∴=-⋅+（），()()()11121222n n n n S A n n ++=-+++-+-⋅＝．2. 已知数列{}n a ，0n a >，其前n 项和n S 满足122n n n S a +=-,其中*n ∈N ．(1){}n b 是等差数列； (2)设2nn n c b -=⋅，n T 为数列{}n c 的前n 项和，求证：3n T ；(3)设14(1)2n bn n n d λ-=+-⋅（λ为非零整数，*n ∈N ），试确定λ的值，使得对任意*n ∈N ，都有n n d d >+1成立． 答案： (1)1n b n =+；(2)略； (3)-1 解答：(1)当1n =时，1124S a =-，∴14a =，当2n ≥时，1112222n nn n n n n a S S a a +--=-=--+，∴122nn n a a --=，∴11n n b b --=（常数）， 又1122a b ==，∴{}n b 是首项为2，公差为1的等差数列，1n b n =+． (2)12(1)2n n n n c b n -=⋅=+⋅， 所以2231222n n n T +=+++，231123122222n n n n n T ++=++++， 相减得23111111122222n n n n T ++=++++- 211111(1)13112211222212n n n n n n -++-++=+-=---，∴213333222n n n n n n T ++=--=-<，(3) 由n n d d >+1得10n n d d +-> ，1211()441120()2n n n n n n λλ++-+-+---> ，111134312012n n n n n λλ-+-->∴⨯--∴-<（），（），(i)当n 为奇数时，即12n λ-<恒成立，当且仅当n=1时，12n -有最小值为1，1λ∴<；(ii)当n 为偶数时，即12n λ->-恒成立，当且仅当n=2时，12n --有最大值-2，2λ∴>-．21λ∴-<<，又λ为非零整数，则λ=-1．综上所述：存在λ=-1，使得对任意*n ∈N ，都有n n d d >+1成立．3. 已知数列{}n a 的首项11a =，23a =，前n 项和为n S ，且*1121(2,)n n n n n nS S a n n N S S a +--+=≥∈-，设11b =，*12log (1)()n n n b a b n N +=++∈(1)设11114n b n n n n c a a +-++=，记1nn k k G c ==∑，试比较n G 与1的大小，并说明理由；(2)若数列{}n l 满足*2log (1)(n n l a n N =+∈），在每两个k l 与1k l +之间都插入12(1,2,k k -=3,,*)k N ∈个2，使得数列{}n l 变成了一个新的数列{}p t ，试问：是否存在正整数m ，使得数列{}p t 的前m 项的和2015m T =？如果存在，求出m 的值；如果不存在，说明理由． 答案： (1) n G 小于1；(2) 存在990m =使得2015m T = 解答： (1)由题意得1121n n n n n nS S a S S a +--+=-，有121n n a a +=+*(2,)n n N ≥∈得112(1)n n a a ++=+*(2,)n n N ≥∈， 又2112(1)a a +=+，从而112(1)n n a a ++=+*()n N ∈ 又1+1=20a ≠，有10n a +≠，从而1121n n a a ++=+，故数列{}1n a +是以2为首项，2为公比的等比数列.从而12n n a +=，即21nn a =-，从而12log (1)n n n b a b +=++得1n n b b n +-=当2n ≥时，211b b -=，322b b -=，…，11n n b b n --=- 以上式子相加得(1)12n n n b -=+(2)n ≥，又11b =也适合，从而(1)12n n n b -=+， 则1111114211(21)(21)2121n b n n n n n n n n n c a a +-++++===-----， 2231111111111()()()1121212121212121nn k n n n k G c ++===-+-++-=-<-------∑(2)由(1)知22log (1)log 2nn n l a n=+==，数列{}p t 中，k l （含k l 项）前的所有项的和是0122(123)(2222)2k k -+++++++++⨯=(1)222k k k ++-， 当10k =时，其和为10552210772015+-=<， 当11k =时，其和为11662221122015+-=>， 又因为201510779384692-==⨯， 所以2810(1222)469990m =++++++=时，2015m T =所以存在990m =使得2015m T =.4. 已知数列{}n a 中，113,21(1)n n a a a n +==-≥，(1)设1(1,2,3)n n b a n L =-=，求证：数列{}n b 是等比数列； (2)求数列{}n a 的通项公式；(3)设12n n n n c a a +=，求证：数列{}n c 的前n 项和13n S <．答案： (1)略；(2) 21nn a =+；(3)略 解答：(1)由121n n a a +=-得112(1)n n a a +-=-即1121n n a a +-=-，又1n n b a =-，故12n nb b +=所以数列{}n b 是等比数列． (2)由(1)知{}n b 是1312b =-=，2q =的等比数列，故1112221n n n n n b b q a --====-，∴21nn a =+．(3)1111122(21)(21)11(21)(21)(21)(21)2121n n n n n n n n n n n n n c a a ++++++-+====-++++++，∴122311111111111()()()2121212121213213n n n n S ++=-+-++-=-<+++++++． 5. 设数列{}{},n n ab 均为正项数列，其中1122,1,3a b b ===，且满足： ,11,n n n a b a ++成等比数列，,1,n n n b a b +成等差数列.(1)(1)证明数列是等差数列；(2)求通项公式na ，nb ；(2)设1(2)n n x n a =+，数列{}n x 的前n 项和记为n S，证明：12n S <.答案： (1)略； (2)略 解答：(1)由题意可知：211n n n b a a ++=，12n n n a b b +=+，所以1n b +=2n ≥时，n b=，当2n ≥时，2n a ==所以数列是等差数列；因为1122,1,3a b b ===，所以222192b a a ====，故等差数列，)12n =-=)1n +，所以()2112n a n =+，()112n b n n =+，(2)由(I)可知()()212(2)12n n x n a n n ==+++，()111(1)(2)n n n n =-+++，所以121n n n S x x x x -=++++2112(1)(2)nnk k k x k k ====+⋅+∑∑12(1)(2)nk k k k =<⋅+⋅+∑111(1)(1)(2)nk k k k k =⎛⎫=- ⎪+++⎝⎭∑()()11112122n n =-<⨯++ .6. 已知数列{}n a 的相邻两项1,n n a a +是关于x 的方程2*20()n n x x b n N -+=∈的两实根，且1 1.a =(1)求234,,a a a 的值； (2)求证：数列1{2}3nn a -⨯是等比数列，并求数列{}n a 的通项公式． 答案：(1)2341,3,5a a a ===； (2)1[2(1)]3nn n a =-- 解答： (1)解：1,n n a a +是关于x 的方程2*20()n n x x b n N -⋅+=∈的两实根，112nn n n n n a a b a a ++⎧+=⎪∴⎨=⋅⎪⎩ ， 因为11a =，所以2341,3,5a a a ===．(2)111111222(2)333 1.111222333n n n n n n n n n nn n n a a a a a a +++-⨯--⨯--⨯===--⨯-⨯-⨯分 故数列1{2}3n n a -⨯是首项为12133a -=，公比为1-的等比数列．所以1112(1)33n n n a --⨯=⨯-，即1[2(1)]3n n n a =--．7. 已知数列{}n a 中，*1112,2(2,)n n a a n n N a -==-≥∈，设n S 是数列{}n b 的前n 项和，lg n n b a =，求99S .答案： 2 解答：111111111112,1,1,111111n n n n n n n n n n n a a a a a a a a a a a ------=-∴-=∴==+∴-=-----, ()1111(1),11n n n n a n N a n-∴=+-=∴=+∈*- ,()1lg lg 1lg 1lg ,n n b a n n n ⎛⎫∴==+=+- ⎪⎝⎭99lg100lg99lg99lg98lg 2lg12S ∴=-+-++-=.8. 设数列{}n a 的前n 项和为n S ，且首项113,3()n n n a a S n N *+≠=+∈.(1)求证：{}3n n S -是等比数列； (2)若{}n a 为递增数列，求1a 的取值范围. 答案： (1)略；(2) (9,3)(3,)-⋃+∞ 解答：（1）因为11n n n a S S ++=-，所以123nn n S S +=+ ，,所以11323n n nn S S ++-=-，分 且130a -≠，所以{3}nn S -是以13a -为首项，以2为公比的等比数列；（2）由（1）得，113(3)2n n n S a --=-⨯，所以11(3)23n nn S a -=-⨯+ 当2n ≥时，2111(3)223n n n n n a S S a ---=-=-⨯+⨯，若{}n a 为递增数列，则1n n a a +>对*n N ∈恒成立 当2n ≥时，11(3)223n n a --⨯+⨯>211(3)223n n a ---⨯+⨯即22132[12()3]02n n a --⨯+->对2n ≥，*n N ∈恒成立 则19a >-， 又2113a a a =+>所以1a 的取值范围是(9,3)(3,)-⋃+∞. 9. 已知数列{n a }满足：411=a ，1231=-+n n a a （n N *∈）； 数列{nb }满足：n n n a a b -=+1（n N *∈）.(1)求数列{n a }的通项公式及其前n 项和n S ； (2)证明：数列{n b }中的任意三项不可能成等差数列. 答案：(1) 1)32(431-⋅-=n n a （n N *∈）, 221()3293()243413n n n S n n --=-⨯=+--（n N *∈）. (2)略. 解答：(1)由1231=-+n n a a ，得)1(3211-=-+n n a a . 因为411=a ，所以4311-=-a . 因此数列{1-n a }是以43-为首项，32为公比的等比数列.所以1)32(431-⨯-=-n n a ，即1)32(431-⋅-=n n a （n N *∈）.所以])32()32(1[431121-+++-=+++=n n n n a a a S49)32(321)32(1432-+=--⨯-=-n n n n （n N *∈）. (2)由(1)，得111)32(41])32(431[])32(431[--+⋅=⋅--⋅-=-=n n n n n n a a b .下面用反证法证明：数列{n b }中的任意三项不可能成等差数列.假设数列{n b }中存在三项t s r b b b ,,（t s r <<）按某种顺序成等差数列，由于数列{n b }是首项为41，公比为32的等比数列，于是有t s r b b b >>，则只能有t r s b b b +=2成立. 所以111)32(41)32(41)32(412---⋅+⋅=⋅⋅t r s ，两边同乘r t --1123，化简得r t r t s t r s ----+=⋅⋅23322.因为t s r <<，所以上式左边为偶数，右边为奇数，故上式不可能成立，导致矛盾. 故数列{n b }中的任意三项不可能成等差数列.10. 已知数列{}n a 的前n 项和为n S ，对任意N n +∈，1(1)32n n n n S a n =-++-且 1()()0n n t a t a +--<恒成立，则实数t 的取值范围是 ．答案：311,44⎛⎫- ⎪⎝⎭解答：因为1(1)32n n n nS a n =-++- ①， 当1n =时，1111122a S a ==-⨯+-，即134a =-， 当2n ≥时，11111(1)42n n n n S a n ----=-++- ②， ①-②得11111111(1)(1)1(1)(1)1222n n n n n n n n n n n n a a a a a -----=---+-+=----+， 当n 为偶数时，解得1112n na -=-+；当n 为奇数时，解得111111111212(1)32222n n n n n n a a -++-=-+-=-+--+=-， 综上，111,213,2n n nn a n +⎧-+⎪⎪=⎨⎪-⎪⎩为奇数为偶数，所以，当n 为偶数时，2111133234n n a a =-≤=-=， 当n 为奇数时，1113124n n a a +=-+≤=-， 又1()()0n n t a t a +--<等价于介于相邻两项之间，所以31144t -<<. 11. 数列{}n a 满足1=1a ，()()1=11n n na n a n n ++++，且2=cos 3n n n b a π，记n S 为数列{}n b 的前n 项和，求120S . 答案：7280解答：由()()1=11n n na n a n n ++++得，111n n a a n n +=++，所以数列n a n ⎧⎫⎨⎬⎩⎭是以1为公差的等差数列，且111a =，所以n a n n =，2n a n =，22cos3n n b n π=，所以 222222212011111234561202222S =-⨯-⨯+-⨯-⨯+-+22222221(1223456120)2=-+-⨯++-+-222222221[(123120)3(369120)]2=-++++-⨯++++22222221139(1240)(123120)22=⨯⨯⨯++-⨯++++140418111201212413972802626⨯⨯⨯⨯=⨯⨯⨯-⨯=；12. 已知数列{}n a 的前n 项和为n S *()n N ∈，且满足21n n a S n +=+．(1)求数列{}n a 的通项公式； (2)求证：21223111112223n n n a a a a a a ++++<．答案： 解答：(1)∵21n n a S n +=+，令1n =，得123a =，∵21n n a S n +=+，∵112(1)1n n a S n --+=-+，*(2,)n n N ≥∈，分 ， 12n n n a a ++3111((2122n ++-++--． 13. 已知数列{}n a 中，311=a ，)(21*+∈-=N n a a a n n n . (1)求证：数列⎭⎬⎫⎩⎨⎧-11n a 是等比数列，并求{}n a 通项公式n a ；(2)设n nn a na b -=1，求证：21<∑=ni i b .答案：(1)证明见解答，121+=n n a ； (2)见解答． 解答：(1)由已知得：1211-=+nn a a ；∴)11(2111-=-+n n a a ，∴211111=--+nn a a ，所以⎭⎬⎫⎩⎨⎧-11n a 是首项为2111=-a ，公比为2的等比数列，∴n n n a 222111=⋅=--，∴121+=n n a . (2)n n n n na nab 21=-=， 令n n n S 222212+⋅⋅⋅++=，∴1322222121++⋅⋅⋅++=n n nS ， 相减得113222122121212121+++-=-+⋅⋅⋅+++=n n n n n n S ，∴2222<+-=n n n S .14. 已知函数()21f x x =+，数列{},{}n n a b 分别满足1(),()n n n a f n b f b -==，且11b =. 定义[]()x x x =+，[]x 为实数x 的整数部分，()x 为小数部分，且0()1x ≤<.(1)分别求{},{}n n a b 的通项公式； (2)记n c =()1nn a b +，求数列{}n c 的前项n 和. 答案：(1)12,12-=+=nn n b n a ；(2)1,12253,22n nn S n n ⎧=⎪⎪=⎨+⎪-≥⎪⎩.(1)已知可得()21n a f n n ==+,即21na n =+;()1121n n n b f b b --==+,()1121n n b b -∴+=+,1121n n b b -+∴=+,所以数列{}1n b +为首相为112b +=,公比为2的等比数列.11222n n n b -∴+=⋅=,21n n b ∴=-.(2)依题意，11131,2 2a c b ==；22251,44a cb ==； 当3n ≥时，可以证明0212n n <+<，即21012nn +<<， 所以2121c ()3)22n n n n n n ++==≥（， 则112S =，2113244S =+=，117921...(3)248162n n n S n +=+++++≥． 令7921...(3)8162n n W n +=+++≥，117921...(3)216322n n W n ++=+++≥， 两式相减得291219253)42242n n n n n W n -++=---≥=（． ∴2533)2n n n S n +=-≥（，检验知，1n =不合，2n =适合， ∴1,12253,22n nn S n n ⎧=⎪⎪=⎨+⎪-≥⎪⎩．15. 数列{}n a 满足*196(,2)n n a n N n a -=-∈≥. (1)求证：数列13n a ⎧⎫⎨⎬-⎩⎭是等差数列； (2)若16a =，求数列{}lg n a 的前999项的和.(1)见解答；(2) 3999 3.S lg =+ 解答：(1)证明：11111131111=33393393n n n n n n n a a a a a a a --------=-=-----(n ≥2). ∴数列13n a ⎧⎫⎨⎬-⎩⎭是等差数列； (2)∵1a =6，由(1)知1111=+(-1)=.3333n nn a a -- 31*),N n a n n n+∴=∈（）,(lg lg(1)lg lg3*).N a n n n n ∴=+-+∈,(∴数列{}lg n a 的前999项和99932132100099()9S lg lg lg lg lg lg lg =+-+-+⋯+-999 3 10003999 3.lg lg lg =+=+16. 数列{}n a 满足11a =,132nn n a a +=+．(1)求证数列{}2n n a +是等比数列； (2)证明：对一切正整数n ，有1211132n a a a +++<…． 答案：(1)证明见解答； (2)证明见解答.解答：(1)由132+=+n n n a a 有,)2(3211n n n n a a +=+++,又321=+a , 所以{}nn a 2+是以3位首项,3为公比的等比数列； (2)由(1)知nn n a 23-=,又)2(223≥>-n nn n ,故221211111113232n nn a a a +++=+++--231113131222222nn ⎛⎫<++++=-< ⎪⎝⎭. 17. 已知数列{}n a 满足1a =1，131n n a a +=+. (1)证明{}12n a +是等比数列，并求{}n a 的通项公式；(2)证明：1231112na a a ++<…+.答案：(1)n a =312n -；(2)见解答解答：(1)证明：由131n n a a +=+得1113()22n n a a ++=+，所以112312n n a a ++=+， 所以12n a ⎧⎫+⎨⎬⎩⎭是等比数列，首项为11322a +=，公比为3， 所以12n a +=1332n -⋅，解得n a =312n -.(2)由(1)知：n a =312n -，所以1231n n a =-， 因为当1n ≥时，13123n n --≥⋅，所以1113123n n -≤-⋅， 于是11a +21a +1n a 111133n -≤+++=31(1)23n -32<， 所以11a +21a +1n a 32<. 18. 设111,(*)n a a b n N +==∈(1)若1b =，求23,a a 及数列{}n a 的通项公式；(2)若1b =-，问：是否存在实数c 使得221n n a c a +<<对所有*n N ∈成立？证明你的结论. 答案：(1)1n a ()*n N ∈； (2)存在，14c = 解答：(1)解法一：232,1a a == 再由题设条件知()()221111n n a a +-=-+ 从而(){}21n a-是首项为0公差为1的等差数列，故()21n a -=1n -，即()*1,n a n N =∈解法二：232,1a a ==可写为1231,1,1,a a a ==.因此猜想1n a =. 下用数学归纳法证明上式： 当1n =时结论显然成立.假设n k =时结论成立，即1k a =.则1111k a +===这就是说，当1n k =+时结论成立.所以()*1,n a n N =∈(2)解法一：设()1f x =，则()1n n a f a +=.令()c f c =，即1c =，解得14c =. 下用数学归纳法证明加强命：2211n n a c a +<<<当1n =时，()()2310,01a f a f ====，所以23114a a <<<，结论成立. 假设n k =时结论成立，即2211k k a c a +<<<易知()f x 在(],1-∞上为减函数，从而()()()2121k c f c f a f a +=>>=即2221k c a a +>>>再由()f x 在(],1-∞上为减函数得()()()22231k c f c f a f a a +=<<=<. 故231k c a +<<，因此2(1)2(1)11k k a c a +++<<<，这就是说，当1n k =+时结论成立. 综上，符合条件的c 存在，其中一个值为14c =.解法二：设()1f x =，则()1n n a f a +=先证：01n a ≤≤()*n N ∈…………………………① 当1n =时，结论明显成立.假设n k =时结论成立，即01k a ≤≤ 易知()f x 在(],1-∞上为减函数，从而()()()01011k f f a f =≤≤<即101k a +≤≤这就是说，当1n k =+时结论成立，故①成立. 再证：221n n a a +<()*n N ∈………………………………②当1n =时，()()2310,01a f a f ====，有23a a <，即当1n =时结论②成立 假设n k =时，结论成立，即221k k a a +< 由①及()f x 在(],1-∞上为减函数，得()()2122122k k k k a f a f a a +++=>= ()()()()212221211k k k k a f a f a a +++++=<=这就是说，当1n k =+时②成立，所以②对一切*n N ∈成立.由②得21k a <即()22222122k k k a a a +<-+因此214k a <又由①、②及()f x 在(],1-∞上为减函数得()()221n n f a f a +> 即2122n n a a ++>所以211,n a +>解得2114n a +>. 综上，由②③④知存在14c =使2211n n a c a +<<<对一切*n N ∈成立.19. 数列{}n a 满足111,(1)(1),n n a na n a n n n N ++==+++∈(1)证明：数列{}na n是等差数列；(2)设3nn b ={}n b 的前n 项和n S 答案： (1)数列{}na n是等差数列； (2)1(21)334n n n S +-⋅+=.解答：(1)证明：由已知可得，111n n a a n n +=++，即111n n a an n+-=+， 所以{}n a n 是以111a=为首项，1为公差的等差数列. (2)由(1)得1(1)1na n n n=+-⋅=，所以2n a n =，从而3n n b n =⋅. 1231323333n n S n =⋅+⋅+⋅++⋅ ① 234131323333n n S n +=⋅+⋅+⋅++⋅ ②①－②得12123333n n n S n +-=+++-⋅113(13)(12)333132n n n n n ++⋅--⋅-=-⋅=-.所以1(21)334n n n S +-⋅+=.20. 设数列{}n a 的前n 项和为n S ，n *∈N ．已知11a =，232a =，354a =，且当2n ≥ 时，211458n n n n S S S S ++-+=+． (1)求4a 的值； (2)证明：112n n a a +⎧⎫-⎨⎬⎩⎭为等比数列； (3)求数列{}n a 的通项公式． 答案： (1)78； (2)证明见解答；(3)()11212n n a n -⎛⎫=-⨯ ⎪⎝⎭．解答：(1)当2n =时，4231458S S S S +=+， 即435335415181124224a ⎛⎫⎛⎫⎛⎫+++++=+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， 解得：478a =(2)因为211458n n n n S S S S ++-+=+（2n ≥），所以21114444n n n n n n S S S S S S ++-+-+-=-（2n ≥）， 即2144n n n a a a +++=（2n ≥），因为3125441644a a a +=⨯+==， 所以2144n n n a a a +++=，因为()2121111111114242212142422222n n n n n n n n n n n n n n n n n a a a a a a a a a a a a a a a a a +++++++++++-----====----，所以数列112n n a a +⎧⎫-⎨⎬⎩⎭是以21112a a -=为首项，公比为12的等比数列(3)由(2)知：数列112n n a a +⎧⎫-⎨⎬⎩⎭是以21112a a -=为首项，公比为12的等比数列， 所以111122n n n a a -+⎛⎫-= ⎪⎝⎭,即1141122n n n na a ++-=⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭，所以数列12n n a ⎧⎫⎪⎪⎪⎪⎨⎬⎛⎫⎪⎪⎪⎪⎪⎝⎭⎩⎭是以1212a =为首项，公差为4的等差数列， 所以()2144212nna n n =+-⨯=-⎛⎫⎪⎝⎭，即()()111422122n n n a n n -⎛⎫⎛⎫=-⨯=-⨯ ⎪ ⎪⎝⎭⎝⎭，所以数列{}n a 的通项公式是()11212n n a n -⎛⎫=-⨯ ⎪⎝⎭.答案：(1)56-=n a n ； (2)详见解答； (3))0,41(-. 解答：(1)因为)(211n n n n b b a a -=-++，53+=n b n ， 所以()1122(3835)6n n n n a a b b n n ++-=-=+--=，所以是等差数列，首项为11=a ，公差为6，即56-=n a n .}{n a(2)由)(211n n n n b b a a -=-++，得n n n n b a b a 2211-=-++，所以}2{n n b a -为常数列，1122b a b a n n -=-，即1122b a b a n n -+=， 因为n n a a ≥0，*∈N n ，所以111122220b a b b a b n n -+≥-+，即n n b b ≥0， 所以}{n b 的第0n 项是最大项.(3)因为n n b λ=，所以)(211nn n n a a λλ-=-++，当2≥n 时，112211)()()(a a a a a a a a n n n n n +-+⋅⋅⋅+-+-=---λλλλλλλ3)(2(2)(22211+-+⋅⋅⋅+-+-=---n n n n λλ+=n 2，当1=n 时，λ31=a ，符合上式， 所以λλ+=n n a 2，因为031<=λa ，且对任意*∈N n ，)6,61(1∈n a a ， 故0<n a ，特别地0222<+=λλa ，于是)0,21(-∈λ， 此时对任意*∈N n ，0≠n a ，当021<<-λ时，λλλ>+=n n a 22||2，λλλ<+-=--1212||2n n a ， 由指数函数的单调性知，}{n a 的最大值为0222<+=λλa ，最小值为λ31=a ，由题意，n ma a 的最大值及最小值分别是12321+=λa a 及31212+=λa a ，由61312>+λ及6123<+λ，解得041<<-λ， 综上所述，λ的取值范围是)0,41(-.22. 设数列{}n a 的前n 项和为n S .已知11a =,2121233n n S a n n n +=---,*n ∈N .(1) 求2a 的值;(2) 求数列{}n a 的通项公式; (3)) 证明:对一切正整数n ,有1211174n a a a +++<. 答案： (1)4；(2)2*,n a n n N =∈； (3)见解答.解答：(1) 解:2121233n n S a n n n +=---,n N *∈. ∴ 当1n =时,112212221233a S a a ==---=-又11a =,24a ∴= (2)解:2121233n n S a n n n +=---,n N *∈. ∴ ()()321112122333n n n n n n S na n n n na ++++=---=- ①∴当2n ≥时,()()()111213n n n n n S n a =-+=--，②由① — ②,得 ()()112211n n n n S S na n a n n -+-=---+ ,1222n n n a S S -=- ,()()1211n n n a na n a n n +∴=---+ ,111n n a a n n +∴-=+,数列n a n ⎧⎫⎨⎬⎩⎭是以首项为111a =,公差为1的等差数列. ()()2111,2nn a n n a n n n∴=+⨯-=∴=≥ ， 当1n =时,上式显然成立.2*,n a n n N ∴=∈；(3)证明:由(2)知,2*,n a n n N =∈①当1n =时,11714a =<,∴原不等式成立.②当2n =时,121117144a a +=+<,∴原不等式亦成立. ③当3n ≥时,()()()()221111,11n n n n n n >-⋅+∴<-⋅+ ()()()2221211111111111121324211n a a a n n n n n ∴+++=+++<+++++⨯⨯-⋅-⋅+111111111111111121322423522211n n n n ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=+-+-+-++-+- ⎪ ⎪ ⎪ ⎪ ⎪--+⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭1111111111112132435211n n n n ⎛⎫=+-+-+-++-+- ⎪--+⎝⎭1111171117121214214n n n n ⎛⎫⎛⎫=++--=+--< ⎪ ⎪++⎝⎭⎝⎭∴当3n ≥时,,∴原不等式亦成立.综上,对一切正整数n ,有1211174n a a a +++<. 23. 已知数列{}n a 满足11a =，11n n a aλ-=+，(1λ≠，2n ≥且*)n ∈N ． (1)求证：当0λ≠时，数列1{}1n a λ+-为等比数列； (2)如果2λ=，求数列{}n na 的前n 项和n S ； (3)如果[]n a 表示不超过n a 的最大整数，当1λ=时，求数列{[(1)]}n a λ-的通项公式．答案： (1)证明略； (2) 2222)1(21nn n n --+⨯-+；(3) []()()2)1(231212nnn n c ---+-++=．解答：(1)当0λ≠时，设11n n b a λ=+-，则 当2n ≥时，111111n n n n a b b a λλ--+-=+-． 因为 11n n a a λ-=+，所以 11111111n n n n a b b a λλλ---++-=+-11111()111111n n n n a a a a λλλλλλλλ----++--===++--为常数． 因为 11011a λλλ+=≠--，所以 数列1{}1n a λ+-是首项为1λλ-，公比为λ的等比数列． (2)由(1)知 2λ=时{1}n a +为首项为1λλ-，公比为λ的是等比数列，所以12nn a +=． 2n n na n n =-． 设212222n n A n =⨯+⨯++⨯， 则231212222n n A n +=⨯+⨯++⨯．相减得212222n n n A n +=----+⨯1(1)22n n +=-⨯+．设21222n n n B n =+++=+，n S =n n A B -=21(1)2222n n nn +-⨯+--．即n S =21(1)2222n n n n +-⨯+--．(3)由(1)可知111111n n n a λλλλλλ--=-=---． 设(1)11)1n n n n c a λλ=-=-=-， 由二项式定理可知1)(1)n n +为整数，所以1)(1)2,2,[]1)(1)1,2 1.n nn n nn k c n k ⎧+-=⎪=⎨+-=-⎪⎩*()k ∈N ． 所以3(1)[]1)(1)22nnnn c -=+--.24. 已知数列{}n a 的前n 项和n S 满足1n n n S a λλ=-+，(1λ≠±，*)n ∈N ． (1)如果0λ=，求数列{}n a 的通项公式；(2)如果2λ=，求证：数列1{}3n a +为等比数列，并求n S ； (3)如果数列{}n a 为递增数列，求λ的取值范围． 答案： (1)1n a =-；(2)1222333n n n n n S a ++=-=-；(3)1λ>或1λ<-． 解答：(1)0λ=时，n S n =-，当1n =时，111a S ==-， 当2n ≥时，11n n n a S S -=-=-， 所以1n a =-．(2)证明：当2λ=时，23n n nS a =-， 11123n n n S a +++=-， 相减得1123n n a a +=+．所以1112()33n n a a ++=+，又因为113a =，112033a +=≠，所以数列1{}3n a +为等比数列，所以1233n n a +=，1222333n n n n n S a ++=-=-．(3)由(1)可知，显然0λ≠当1n =时，则1111S a λλ=-+，得1211a λ=-． 当2n ≥时，1n n nS a λλ=-+，1111n n n S a λλ---=-+， 相减得12111n n a a λλλ-=+--， 即111()111n n a a λλλλ-+=++-+．因为1λ≠±，所以121011a λλλ+=≠+-．所以1{}1n a λ++为等比数列．所以12111()()111111n n n a λλλλλλλλλ-=-=---++-+． 因为数列{}n a 为递增数列，所以 10111λλλ⎧>⎪⎪+⎨⎪>⎪-⎩或 101011λλλ⎧<⎪⎪+⎨⎪<<⎪-⎩，所以λ的取值范围是1λ>或1λ<-．25. 已知数列{}n a 满足1112431n n n a a a -+=+⋅=，，求数列{}n a 的通项公式. 答案：114352n n n a --=⋅-⋅解答：解法一（待定系数法）：设11123(3n n n n a a λλλ-++=+⋅)，比较系数得124,2λλ=-=，则数列{}143n n a --⋅是首项为111435a --⋅=-，公比为2的等比数列，所以114352n n n a ---⋅=-⋅，即114352n n n a --=⋅-⋅解法二（两边同除以1+n q）： 两边同时除以13n +得：112243333n n n n a a ++=⋅+，下面解法略 解法三（两边同除以1+n p）： 两边同时除以12+n 得：nn n n n a a )23(342211⋅+=++，下面解法略 26. 在数列}{n a 中，,23,111n a a a n n +==+求通项n a .（逐项相减法） 解： ，,231n a a n n +=+ ①∴2≥n 时，)1(231-+=-n a a n n ，两式相减得 2)(311+-=--+n n n n a a a a .令n n n a a b -=+1,则231+=-n n b b ，所以2351+⋅=-n n b ，即 13511-⋅=--+n n n a a ②再由累加法可得213251--⋅=-n a n n . 亦可联立①②解出213251--⋅=-n a n n .27. 在数列{}n a 中，362,2311-=-=-n a a a n n ,求通项n a .答案：96)21(9-+⋅=n a nn解答：原递推式可化为y n x a y xn a n n ++-+=++-)1()(21 比较系数可得：x=-6,y=9,上式即为12-=n n b b 所以{}n b 是一个等比数列，首项299611=+-=n a b ,公比为21.1)21(29-=∴n n b 即：nn n a )21(996⋅=+- 故96)21(9-+⋅=n a nn .28. 已知数列{}n a 满足21123451n n a a n n a +=+++=，，求数列{}n a 的通项公式.答案：42231018n n a n n +=---解答：设221(1)(1)2()n n a x n y n z a xn yn z ++++++=+++ ，比较系数得3,10,18x y z ===，所以2213(1)10(1)182(31018)n n a n n a n n ++++++=+++ 由213110118131320a +⨯+⨯+=+=≠，得2310180n a n n +++≠则2123(1)10(1)18231018n n a n n a n n ++++++=+++， 故数列2{31018}n a n n +++为以21311011813132a +⨯+⨯+=+=为首项，以2为公比的等比数列，因此2131018322n n a n n -+++=⨯，则42231018n n a n n +=---。