钢筋混凝土梁正截面抗弯承载力
第三章 钢筋混凝土受弯构件正截面承载力计算
第三章钢筋混凝土受弯构件正截面承载力计算受弯构件（bendingmember）是指截面上通常有弯矩和剪力共同作用而轴力可以忽视不计的构件。
钢筋混凝土受弯构件的主要形式是板（Slab）和梁（beam）,它们是组成工程结构的基本构件，在桥梁工程中应用很广。
在荷载作用下，受弯构件的截面将承受弯矩M和V的作用。
因此设计受弯构件时，一般应满意下列两方面的要求：（1）由于弯矩M的作用，构件可能沿弯矩最大的截面发生破坏，当受弯构件沿弯矩最大的截面发生破坏时，破坏截面与构件轴线垂直，称为正截面破坏。
故需进行正截面承载力计算。
（2）由于弯矩M和剪力V的共同作用，构件可能沿剪力最大或弯矩和努力都较大的截面破坏，破坏截面与构件的轴线斜交，称为沿斜截面破坏，故需进行斜截面承载力计算。
为了保证梁正截面具有足够的承载力，在设计时除了适当的选用材料和截面尺寸外，必需在梁的受拉区配置足够数量的纵向钢筋，以承受因弯矩作用而产生的拉力；为了防止梁的斜截面破坏，必需在梁中设置肯定数量的箍筋和弯起钢筋，以承受由于剪力作用而产生的拉力。
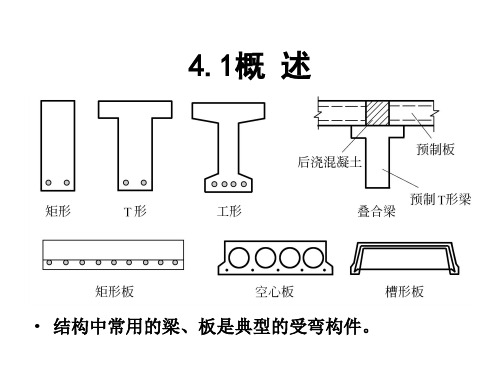
第一节受弯构件的截面形式与构造一、钢筋混凝土板的构造板是在两个方向上（长、宽）尺度很大，而在另一方向上（厚度）尺寸相对较小的构件。
钢筋混凝土板可分为整体现浇板和预制板。
在施工场地现场搭支架、立模板、配置钢筋，然后就地浇筑混凝土的板称为整体现浇板。
通常这种板的截面宽度较大，在计算中常取单位宽度的矩形截面进行计算。
预制板是在预制厂和施工场地现场预先制好的板，板宽度一般掌握在Inl左右，由于施工条件好，预制板不仅能采纳矩形实心板，还能采纳矩形空心板，以减轻板的自重。
板的厚度h由截面上的最大弯矩和板的刚度要求打算，但是为了保证施工质量及耐久性的要求，《大路桥规》规定了各种板的最小厚度；行车道板厚度不小于IOOmm人行道板厚度，就地浇注的混凝土板不宜小于80mm,预制不宜小于60mm。
空心板桥的顶板和底板厚度，均不宜小于80mm。
混凝土受弯构件正截面承载力计算
r As f y As a1 fcbx x a1 fc
bh0 bh0 f y bh0 f y h0 f y
令
x
h0
则
r
a1 fc
fy
令b为 = r max时的相对受压区高度，即
rmax
b
a1
f
fc
y
= r max时的破坏形态为受压区边缘混凝土达到极限压
c fc e0 e ecu
n
2
1 60
(
fcu,k
50)
2.0
各系数查表4-3
e0 0.002 0.5( fcu,k 50)105 0.002
ecu 0.0033 0.5( fcu,k 50)105 0.0033
4.钢筋应力—应变关系的假定（本构关系）
Ese e e y fy e ey
4.3钢筋混凝土受弯构件正截面试验研究
一、受弯构件正截面破坏过程
受弯构件正截面破坏分为三个阶段 • 第一阶段：裂缝开裂前 • 第二阶段：从开裂到钢筋屈服 • 第三阶段：从钢筋屈服到梁破坏
（1）第I阶段
当荷载比较小时，混凝土基本处 于弹性阶段，截面上应力分布为三 角形，荷载-挠度曲线或弯矩-曲率 曲线基本接近直线。截面抗弯刚度 较大，挠度和截面曲率很小，钢筋 的应力也很小，且都于弯矩近似成 正比。
My
Mu
Failure”，破坏前
可吸收较大的应变
能。
0
f
2．超筋梁(Over reinforced)破坏
钢筋配置过多，将发生这种破坏。 破坏特征：破坏时钢筋没有达到屈服强度，破坏是由 于压区混凝土被压碎引起，没有明显预兆，为脆性破 坏。
钢筋混凝土梁受弯构件 正截面承载力实验
有技术、技术秘密、软件、算法及各种新的产品、工程、技术、系统的应用示范等。
第三条本办法所称科技成果转化，是指为提高生产力水平而对科学研究与技术开发所产生的具有实用价值的科技成果所进行的后续试验、开发、应用、推广直至形成新技术、新工艺、新材料、新产品，发展新产业等活动。
第四条科技成果转化应遵守国家法律法规，尊重市场规律，遵循自愿、互利、公平、诚实信用的厚则，依照合同的约定，享受利益，承担风险，不得侵害学校合法权益。
第二章组织与实施第五条学校对科技成果转化实行统一管理。
合同的签订必须是学校或具有独立法人资格的校内研究机构，否则科技成果转化合同的签订均是侵权行为，由行为人承担相应的法律责任。
第六条各学院应高度重视和积极推动科技成果转化工作，并在领导班子中明确分管本单位科技成果转化工作的负责人。
第七条学校科学技术处是学校科技成果转化的归口管理部门，是科技成果的申报登记和认定的管理机构，负责确认成果的权属并报批科技成果转化合同。
第八条学校科技成果可以采用下列方式进行转化：（一）自行投资实施转化；（二）向他人转让；（三）有偿许可他人使用；（四）以该科技成果作为合作条件，与他人共同实施转化；（五）以该科技成果作价投资，折算股份或者出资比例；（六）其它协商确定的方式。
第九条不论以何种方式实施科技成果转化，都应依法签订合同，明确各方享有的权益和各自承担的责任，并在合同中约定在科技成果转化过程中产生的后续改进技术成果的权属。
第十条对重大科研项目所形成的成果，或拟转让的、作价入股企业的、金额达到100万元的科技成果，应先到科学技术处申请、登记备案，并报请学校校长办公会审核、批准、公示后才能进行。
第十一条科技成果转让的定价主要采取协议定价方式，实行协议定价的，学校对科技成果名称、简介、拟交易价格等内容进行公示，公示期15天。
第十二条对于公示期间实名提出的异议，学校科学技术处组织不少于3人的行业专家进行论证，并将论证结果反馈至科技成果完成人和异议提出者，如任何一方仍有异议，则应提交第三方评估机构进行评估，并以评估结论为准。
钢筋混凝土受弯构件正截面承载力计算
为保证钢筋混凝土结构的耐久性、防火性以及钢
筋与混凝土的粘结性能，钢筋的混凝土保护层厚
５度、一配般筋不率小于2A 5msm% ； ....4...2()
bh0
用下述公式表示
As bh0
%
公式中各符号含义：
As为受拉钢筋截面面积； b为梁宽；h0为梁的有效 高度，h0=h-as；as为所有受拉钢筋重心到梁底面 的距离，单排钢筋as= 35mm ，双排钢筋as= 55~60mm 。
M/ M u
Mu
1.0
0.8 My
0.6
II
0.4
III III a II a
M cr I a
I
0
f cr
fy
fu f
加载过程中弯矩－曲率关系
说明：
对于配筋合适的梁，在III
阶段，其承载力基本保持不 变而变形可以很大，在完全
M/ M u
Mu
1.0
破坏以前具有很好的变形能 力，破坏预兆明显，我们把
0.8 My
通常采用两点对称集中加荷，加载点位于梁跨度 的1/3处，如下图所示。这样，在两个对称集中荷载间 的区段(称“纯弯段”)上，不仅可以基本上排除剪力的 影响(忽略自重)，同时也有利于在这一较长的区段上(L ／3)布置仪表，以观察粱受荷后变形和裂缝出现与开 展的情况。在“纯弯段”内，沿梁高两侧布置多排测 点，用仪表量测梁的纵向变形。
梁破坏时的极限弯矩Mu小于在正常情况下的开
裂弯矩Mcr。梁配筋率越小， Mcr -Mu的差值越大； 越大(但仍在少筋梁范围内)， Mcr -Mu的差值越小。
当Mcr -Mu =0时，它就是少筋梁与适筋梁的界限。这
时的配筋率就是适筋梁最小配筋率的理论值min。
钢筋混凝土简支梁的正截面受弯承载力试验报告
5.随着试验的进行注意仪表及加荷装置的 粘贴好手持式应变仪的脚标，装好百分表
在标准荷载作用下持续时间不宜小于30min
在达到标准荷载以前，每级加载值不宜 大于标准荷载值的20％；超过标准荷载 值后，每级加载值不宜大于标准荷载值 的10％。
加载到达开裂荷载计算值的90％以后， 每级加载值不宜大于标准荷载值的5％。
加载到达破坏荷载计算值的90％以后， 每级加载值不宜大于标准荷载值的5％。
每级荷载的持续时间不应小于10min 在标准荷载作用下持续时间不宜小于
混凝土表面应变测点：纯弯段混凝土表面电阻 应变片测点为每侧四点（压区顶面一点，受拉 主筋处一点，中间两点），并在应变片测点处 对应地布置手持应变仪测点。
挠度测点布置：在跨中一点，支座各一点及分 配梁加载点各一点安装百分表。
进行1~3级预载，测读数据，观察试件、 装置和仪表工作是否正常并及时排除故 障。预加载值不宜超过试件开裂荷载计 算值的70％
将标准荷载下应变及挠度的计算值与实 测值进行比较
对梁的破坏形态和特征做出评定
六、虚拟演示
1、变形图（正视图） 2、变形图（轴测图） 3、位移图（正视图） 4、位移图（轴测图） 5、SZ应力图（正视图） 6、SZ应力图（轴测图） 7、MISE应力图（正视图） 8、 MISE应力图（轴测图）
试件材料的力学性能：钢筋和混凝土的 实测强度，钢筋和混凝土的弹性模量
根据实测截面尺寸和材料力学性能算出 梁的开裂荷载和破坏荷载，以及标准荷 载下的应变和挠度值
钢筋混凝土受弯构件正截面承载力计算—单筋矩形截面梁计算
受压混凝土的应力－应变关系
计算原则
2）等效矩形应力图
简化原则：受压区混凝土的合力大小不变；受压区混凝土的合力作用点不变。
等效矩形应力图形的混凝土受压区高度 x 1xn ，等效矩形应力图形的应力值 为 1 fc， 1、1 的值见下表。
表 1、1 值
混凝土强 度等级
≤C50
C55
C60
C65
C70
C75
（2）求跨中截面的最大弯矩设计值。
因仅有一个可变荷载，故弯矩设计值应有取下列两者中的较大值：
M 1 1.2g 1.4q l 2
8
1 1.2 5 1.4 10 5.02 62.5
8
M 1 1.35g 1.4 0.7q l 2
8
1 1.35 5 1.4 0.7 10 5.02 51.7
需要加固、补强
计算原则
1）基本假定
01 平截面假定。
02
钢筋的应力 s 等于钢筋应变 s 与其弹性模量 Es 的乘积，但不得大
于其强度设计值 fy，即
s sEs fv
03 不考虑截面受拉区混凝土的抗拉强度。
计算原则
04
受压混凝土采用理想化的应力－应变关系，当混凝土强度等级为
C50及以下时，混凝土极限压应变 cu=0.0033。
（1）受拉钢筋为4 25，As=1964 mm2； （2）受拉钢筋为3 18，As=763 mm²。
单筋矩形截面梁计算
解 查表得：
fc 9.6N/mm2
ft 1.10N/mm2
f y 300N/mm2 c 1.0
b 0.550
c 30mm
单筋矩形截面梁计算
（1）
d
25
h0 h c 2 450 30 2 408
钢筋混凝土梁正截面抗弯承载力计算表
C20 13.4 1.54 9.6 1.1 25500
HPB23 强度 类型 5 fyv N/mm2 210
HPB23
强度 类型 5
fy N/mm2 210
Es N/mm2 210000
直径
8~20
梁截面尺寸
b＝
300 (mm)
h＝
600 (mm)
c＝
35 (mm)
h0＝
565 (mm)
l0＝
3.000 (m)
300 )(N/mm2 纵筋抗拉压强度设计值 fy
200000 )
1.00
1.0<C50<内插<C80<0.94
0.80
0.8<C50<内插<C80<0.74
0.55
ξb＝β1/(1+fy/0.0033Es)
7.14
αE＝Es/Ec
混凝土强度及弹性模量
强度 类型 fck N/mm2 ftk N/mm2 fc N/mm2 ft N/mm2 Ec N/mm2
1.27 )(N/mm2 混凝土抗拉强度设计值 ft
28000 )
混凝土弹性模量 Ec
HPB fyv＝
235 (HNP/Bm(m2325,335,400) 箍筋强度等级
210 )
箍筋抗拉压强度设计值 fyv
HRB fy＝ Es＝ α1＝ β1＝ ξb＝ αE＝
335 (HNR/mB(m2325,335,400) 纵筋强度等级
Nj＝ φj＝
dj＝
2 6 (mm) 200 (mm)
ρj＝
0.283
跨中正筋直径 φz 跨中正筋面积 Asz 跨中正筋配筋率 ρz
箍筋肢数 Nj 箍筋直径 φj 箍筋间距 dj 配箍率 ρj
钢筋混凝土梁的正截面承载力计算全篇
第Ⅰ阶段前期是直线，后期是曲线； 3)受拉区边缘纤维的拉应变值到达混凝土的极限拉应变时，在最薄弱的某 截面受拉区出现第一条裂缝； 4)弯矩与截面曲率基本上是直线关系。
Ⅰa阶段可作为受弯构件抗裂度的计算依据。
（2）第Ⅱ阶段：混凝土开裂后至钢筋屈服前的裂缝阶段
4 单筋矩形截面受弯构件正截面设计
在正截面受弯承载力设计中，钢筋直径、数量和层数等 还不知道，因此纵向受拉钢筋合力点到截面受拉边缘的 距离as往往需要预先估计。 当环境类别为一类时（即室内环境），一般取
当采用单排钢筋时 当采用双排钢筋时
对钢筋混凝土板
h0 h 40(mm ) h0 h 65(mm ) h0 h 20(mm )
4. 计算钢筋截面面积As
As 1 fcbx f y =1.0×11.9×200×92.4/360=610.9mm2
二、受弯构件正截面的受弯性能
1 适筋梁正截面受弯的三个受力阶段
试验 梁
荷载分 配梁 P
外加荷 载
应变 计
位移
L/3
L/3 计
L
数据采集 系统
h0 h
As b
As
bh0
图2-1 适筋梁正截面受弯承载力试验装置
（1）第Ⅰ阶段：混凝土开裂前的未裂阶段
图2-2 适筋梁工作的第Ⅰ阶段混凝土应变、应力分布图
c c25mm
d
c
c
h h0
b
图1-2(b） 梁截面内纵向钢筋布置及截面有效高度h0
混凝土保护层厚度：从最外层钢筋（包括箍筋、构 造筋、分布筋等）的外表面到截面边缘的垂直距离。
混凝土保护层有三个作用： 1)防止纵向钢筋锈蚀； 2)在火灾等情况下，使钢筋的温度上升缓慢； 3)使纵向钢筋与混凝土有较好的粘结。
钢筋混凝土受弯构件正截面承载力计算
板厚度较大时如水闸，钢筋直径可用12~25mm，Ⅱ级钢筋； ◆ 受力钢筋间距一般在70~250mm之间；要便于混凝土浇捣。 ◆ 垂直于受力钢筋的方向应布置分布钢筋，以便将荷载均匀地传
递给受力钢筋，并便于在施工中固定受力钢筋的位置，同时也 可抵抗温度和收缩等产生的应力，每米不少于3根。
◆ 同时不应小于0.2%
◆ 对于现浇板和基础底板沿每个方向受拉钢筋的最小配筋 率不应小于0.15%。
板常用配筋率: 矩形截面 0.6 %～0.8 %
梁常用配筋率: 0.6%～1.5%
T形截面配筋率: 0.9%～1.8%
第三章 钢筋混凝土受弯构件正截面承载力计算
三、截面配筋计算步骤：
已知材料强度、截面尺寸，M 求 AS ?
结性能，钢筋的混凝土保护层厚度c一般不小于 25mm；
并符合附录四附表4—1的规定。 截面有效高度 h0 h as
Ý¡ 30mm
1.5d cݡ cmin
d
混凝土保护层计算厚度as:
h0
钢筋一层布置时 as=c+d/2 ，
钢筋二层布置时 as=c+d+e/2， a
其中e为钢筋之间净距。
Ý¡ cmin 1.5d
⑴ 等效前后混凝土压应力的合力C大小相等； ⑵ 等效前后两图形中受压区合力C的作用点不变。 见图3-10
第三章 钢筋混凝土受弯构件正截面承载力计算
㈢ 相对受压区高度
混凝土相对受压区高度
正截面混凝土受压区高度x与h0的比值为大小受压区高度
即
x
h0
当截面内纵向受力钢筋达到屈服时，混凝土受压区最
钢筋混凝土梁受弯构件正截面承载力实验
四、课程内容
第一章 计算机基础知识
一、教学目的与要求 本单元主要介绍计算机的基础知识，包括计算机的发展历史、计算机中的信息表示
和计算机组成等内容，使学生在具体任务的实践中了解计算机的基础知识。 二、讲授内容 1.计算机的基本软硬件、主要部件的性能参数； 2．进位制及数制间的转换方法； 3.计算机中的编码方式。 三、重点、难点 1.计算机的基本软硬件、主要部件的性能参数； 2．进位制及数制间的转换方法； 四、教学建议 在机房授课，理论结合实践操作，加强印象。
三、各教学环节学时分配：
章次
内容
第一章 计算机基础知识
第二章 WINDOWS XP 操作系统
第三章 文字处理软件 WORD 2003
第四章 电子表格处理软件 EXCEL 2003
第五章 演示文稿制作软件 POWERPOINT 2003
第六章 计算机网络基础
第七章 常用工具软件
合计
课内学时分配 4 6 10 10 10 4 4 48
第一阶段——弹性工作阶段 （从开始加荷到受拉边缘，混凝土达到极限拉应变） 第二阶段——带裂缝工作阶段（从开裂的临界状态到受拉钢筋达到屈服强度） 结论: 通过本次模拟实验掌握了正截面受弯的三个受力阶段，充分体验了钢筋混凝土受弯的 整个过程；同时还掌握了挠度和裂缝的计算。通过这次实验，我熟悉掌握其构件受力和 变形的三个阶段以及破坏特征、掌握了不同荷载强度下挠度和裂缝宽度的计算并且通过 计算三种情况下梁的屈服荷载和破坏荷载跟实验所得到的数值进行比较较，让我进一步 明白，在实际施工时应注意：一定要根据构件的安全等级计算好承载力和强度，以保证 施工安全和周边环境、构造物和人民财产的安全。到最后虽然梁被破环，但是梁仍然在 带裂缝工作。 适用专业： 全院
钢筋混凝土单筋矩形截而正截面受弯承载力计算基本公式的适用条件中,
钢筋混凝土单筋矩形截而正截面受弯承载力计算基本
公式的适用条件中,
钢筋混凝土单筋矩形截面正截面受弯承载力计算基本公式的适用条件主要包括以下几个方面：
1. 适用于一般承受静力荷载的简支梁或连续梁，其跨间挠度不得超过正常使用极限状态所规定的挠度值。
2. 适用于混凝土强度等级在C20~C50之间，钢筋采用HRB400级、HRB500级或HPB300级。
3. 适用于截面尺寸符合平截面假定，且受剪承载力满足要求的截面。
4. 适用于梁的跨高比在6~9的范围内，且梁的截面宽度不小于200mm。
5. 适用于梁的受拉区配有单层或双层钢筋，且受压区混凝土的抗压强度满足要求。
6. 适用于梁的受力钢筋直径不小于12mm，且梁的截面高度与宽度的比值不超过4。
7. 适用于梁的跨间挠度不超过正常使用极限状态所规定的挠度值。
综上所述，在使用钢筋混凝土单筋矩形截面正截面受弯承载力计算基本公式时，应确保满足上述条件，以确保计算结果的准确性和可靠性。
钢筋混凝土受弯构件正截面承载力计算
3 钢筋混凝土受弯构件正截面承载力计算3·1 概 述受弯构件是指主要承受弯矩和剪力为主的构件。
受弯构件是土木工程中应用数量最多，使用面最广的一类构件。
一般房屋中各种类型的楼盖和屋盖结构的梁、板以及楼梯和过梁；工业厂房中的屋面大梁、吊车粱、铁路、公路中的钢筋混凝土桥梁等都属于受弯构件。
此外，房屋结构中经常采用的钢筋混凝土框架的横梁虽然除承受弯矩和剪力外还承受轴向力(压力或拉力)，但由于轴向力值通常较小，其影响可以忽略不计，因此框架横粱也常按受弯构件进行设计。
按极限状态进行设计的基本要求，对受弯构件需要进行下列计算和验算：1．承载能力极限状态计算，即截面强度计算在荷载作用下，受弯构件截面一般同时产生弯矩和剪力。
设计时既要满足构件的抗弯承载力要求，也要满足构件的抗剪承载力要求。
因此，必须分别对构件进行抗弯和抗剪强度计算。
在进行截面强度计算时，荷载效应(弯矩M和剪力V)通常是按弹性假定用结构力学方法计算；在某些连续梁、板中，荷载效应也可以按塑性设计方法求得。
本章主要是介绍受弯构件抗弯强度的计算方法。
2．正常使用极限状态验算受弯构件一般还需要按正常使用极限状态的要求进行变形和裂缝宽度的验算。
这方面的有关问题将在第八章中介绍。
除进行上述两类计算和验算外，还必须采取一系列构造措施，方能保正构件具有足够的强度和刚度，并使构件具有必要的耐久性。
在本章的3·2中将讨论梁板结构的一般构造。
3.2 梁板结构的一般构造1、梁板截面的型式与尺寸梁和板均为受弯构件，梁的截面高度一般都大于其宽度，而板的截面高度则远小于其宽度。
钢筋混凝土梁、板可分为预制梁、板和现浇梁、板两大类。
钢筋混凝土预制板的截面形式很多，最常用的有平板、槽形板和多孔板三种(图3-1)。
钢筋混凝土预制梁最常用的截面形式为矩形和T形(图3-2)。
有时为了降低层高将梁做成十字梁、花篮梁，将板搁支在伸出的翼缘上，使板的顶面与梁的顶面齐平。
钢筋混凝土现浇梁、板的形式也很多。
钢筋混凝土受弯构件正截面承载力计算的依据
钢筋混凝土受弯构件正截面承载力计算的依据本文主要介绍了钢筋混凝土受弯构件正截面承载力计算的依据，包括受弯构件的受力情况、抗弯承载力的计算方法、受压区高度的确定、钢筋的计算以及计算公式的应用等方面。
文章旨在让读者了解钢筋混凝土受弯构件正截面承载力的计算方法及其理论基础，为工程设计提供参考。
关键词：钢筋混凝土、受弯构件、承载力、计算方法、理论基础一、引言钢筋混凝土结构是现代建筑中常见的一种结构形式，其具有承载能力强、耐久性好、施工方便等优点。
在钢筋混凝土结构中，受弯构件是常见的一种构件形式，其受力状态相对复杂，需要进行详细的分析和计算。
本文将介绍钢筋混凝土受弯构件正截面承载力计算的依据，以便工程设计人员能够更加准确地进行结构设计。
二、受弯构件的受力情况钢筋混凝土受弯构件是指在承受外力作用下，梁的截面产生弯曲形变的构件。
在受弯构件的截面上，由于外力的作用，截面上的混凝土产生了受压区和受拉区。
在受压区，混凝土会发生压缩变形，而在受拉区，混凝土会发生拉伸变形。
同时，在受拉区的底部，由于混凝土的拉伸变形导致纵向钢筋受拉，而在受压区的顶部，由于混凝土的压缩变形导致纵向钢筋受压。
因此，受弯构件的受力情况相对复杂，需要进行详细的分析和计算。
三、抗弯承载力的计算方法在钢筋混凝土受弯构件中，抗弯承载力是指截面在弯曲破坏前能够承受的最大弯矩。
抗弯承载力的计算方法主要有两种，分别是工作状态法和极限状态法。
工作状态法是指在结构使用过程中，按照一定的荷载组合来计算结构的承载能力。
在计算抗弯承载力时，需要考虑混凝土的强度、钢筋的强度以及受压区高度等因素。
具体计算方法如下：1. 根据混凝土的强度等级，计算混凝土的抗拉强度和抗压强度。
2. 根据受压区高度的不同，将截面分为若干个受压区。
3. 计算每个受压区的受压混凝土面积和受拉钢筋面积。
4. 根据钢筋的强度等级，计算钢筋的屈服强度和抗拉强度。
5. 计算受压区混凝土的抗弯承载力和受拉钢筋的抗弯承载力。
提高钢筋混凝土梁正截面承载力的有效方法
提高钢筋混凝土梁正截面的承载力可以采取以下有效方法：
1. 增加钢筋数量：通过增加梁截面内的钢筋数量可以提高梁的抗弯能力和承载力。
根据设计要求和结构计算，可以增加主筋、箍筋和横隔筋等的数量和直径。
2. 使用高强度钢筋：采用高强度钢筋可以提高梁的抗弯和抗拉能力。
常见的高强度钢筋包括HRB400和HRB500，根据设计要求选择合适的钢筋等级。
3. 使用高性能混凝土：高性能混凝土具有较高的强度和耐久性，可以提高梁的
整体承载能力。
在混凝土配合比设计中，选择合适的水灰比、胶凝材料和骨料，以确保混凝土的强度和耐久性。
4. 增加梁的截面尺寸：通过增加梁的截面尺寸可以增加梁的抗弯能力和承载力。
可以增加梁的高度或宽度，或者增加翼缘的厚度，以增加梁的截面积和抗弯矩。
5. 使用预应力或后张拉技术：预应力或后张拉技术可以通过施加预先或事后的
压力来改善梁的承载性能。
这种技术可以减小梁的挠度和裂缝，并提高梁的整体刚度和承载力。
6. 采用纤维增强复合材料：将纤维增强复合材料（如碳纤维、玻璃纤维等）与
钢筋混凝土梁结合使用可以提高梁的承载力和耐久性。
纤维增强复合材料具有较高的强度和刚度，并能有效抵抗裂缝扩展。
请注意，在进行任何结构设计和改进时，建议咨询专业的结构工程师，并遵循适用的建筑法规和标准。
钢筋混凝土受弯构件正截面承载力计算-混凝土结构设计原理
1 /171第四章 钢筋混凝土受弯构件正截面承载力计算本章学习要点:1、掌握单筋矩形截面、双筋矩形截面和T 形截面承载力的计算方法；2、了解配筋率对受弯构件破坏特征的影响和适筋受弯构件在各阶段的受力特点；3、熟悉受弯构件正截面的构造要求。
§4－1 概述一、受弯构件的定义同时受到弯矩M 和剪力V 共同作用，而轴力N 可以忽略的构件（图4—1)． 梁和板是土木工程中数量最多，使用面最广的受弯构件。
梁和板的区别：梁的截面高度一般大于其宽度，而板的截面高度则远小于其宽度。
受弯构件常用的截面形状如图4-2所示。
图4-1二、受弯构件的破坏特性正截面受弯破坏:沿弯矩最大的截面破坏,破坏截面与构件的轴线垂直。
斜截面破坏：沿剪力最大或弯矩和剪力都较大的截面破坏。
破坏截面与构件轴线斜交。
进行受弯构件设计时，要进行正截面承载力和斜截面承载力计算。
2 /172图4—3 受弯构件的破坏特性§4—2 受弯构件正截面的受力特性一、配筋率对正截面破坏性质的影响配筋率:为纵向受力钢筋截面面积A s 与截面有效面积的百分比.sA bh 式中 s A —-纵向受力钢筋截面面积。
b -—截面宽度，0h —－截面的有效高度（从受压边缘至纵向受力钢筋截面重心的距离)。
构件的破坏特征取决于配筋率、混凝土的强度等级、截面形式等诸多因素，但配筋率的影响最大。
受弯构件依配筋数量的多少通常发生如下三种破坏形式: 1、 少筋破坏当构件的配筋率低于某一定值时,构件不但承载力很低,而且只要其一开裂，裂缝就急速开展，裂缝处的拉力全部由钢筋承担,钢筋由于突然增大的应力而屈服,构件立即发生破坏。
图4—4 受弯构件正截面破坏形态2、适筋破坏当构件的配筋率不是太低也不是太高时,构件的破坏首先是受拉区纵向钢筋屈服，然后压区砼压碎。
钢筋和混凝土的强度都得到充分利用.破坏前有明显的塑性变形和裂缝预兆。
3、超筋破坏当构件的配筋率超过一定值时,构件的破坏是由于混凝土被压碎而引起的。
钢筋混凝土受弯构件正截面承载力计算
根据钢筋混凝土受弯构件的正截面承载力计算公式， 计算出梁或板的承载力。
结果分析与讨论
结果分析
对比实际工程载荷和计算出的承载力，分析承载力的安全储备和可能存在的风险。
讨论
针对不同工程实例，讨论影响钢筋混凝土受弯构件正截面承载力的因素，如截面尺寸、 配筋、混凝土强度等。
07 结论与展望
研究结论
钢筋混凝土受弯构件正 截面承载力计算
目录
Contents
• 引言 • 钢筋混凝土受弯构件的基本理论 • 钢筋混凝土受弯构件正截面承载力
的计算公式 • 钢筋混凝土受弯构件正截面承载力
的影响因素
目录
Contents
• 钢筋混凝土受弯构件正截面承载力 的试验研究
• 工程实例分析 • 结论与展望
01 引言
采用现有的钢筋混凝土受弯构件 正截面承载力的计算公式或软件 ，如SAP2000、Midas等。
对比分析
将试验结果与理论计算结果进行 对比，分析两者的差异和原因， 验证理论模型的准确性和适用性 。
结论与建议
根据对比结果，得出结论并提出 相应的建议，为实际工程中的钢 筋混凝土受弯构件设计提供参考 。
06 工程实例分析
试验表明，当构件达到承载力极限状 态时，其破坏形态与理想化的脆性破 坏形态相符，因此可以基于这种破坏 形态推导出承载力计算公式。
承载力计算公式的应用
承载力计算公式可用于各种类型的钢筋混凝土受弯构件，如 梁、板、拱等。
根据构件的截面尺寸、配筋率、混凝土强度等级等参数，使 用承载力计算公式可以快速准确地计算出构件的正截面承载 力。
工程概况
要点一
某桥梁工程
主梁采用钢筋混凝土结构，跨度为30米，宽度为10米，设 计载荷为20吨。
[工学]钢筋混凝土受弯构件正截面承载力计算
![[工学]钢筋混凝土受弯构件正截面承载力计算](https://img.taocdn.com/s3/m/d8a70b6b657d27284b73f242336c1eb91a37333e.png)
发生条件： ρmin.h/h0≤ρ≤ρb
c
c
c
c
MI
Mcr
MII
My
(Mu) MIII
t<ft
sAs
sAs t=ft(t =tu)
s<y
sAs
s= fyAs
y
(c=cu) c
fyAs s>y
1.适筋梁特点：
min.h/h0 max
• 一开裂, 砼应力由裂缝截面处的钢筋承担, 荷 载继续增加, 裂缝不断加宽。受拉钢筋屈服, 压区砼压碎
主页 目录 上一章 下一章 帮助
ห้องสมุดไป่ตู้
混凝土结构设计原理
第4章
§4.1 概 述
4.1.1几个基本概念
1.受弯构件:主要指各种类型的梁和板。 内力特点:截面上通常有弯矩和剪力共同作用。
２. 正截面：与构件计算轴线相垂直的截面。
３. 承载力计算公式： M ≤Mu
M —— 受弯构件正截面弯矩设计值； Mu——受弯构件正截面受弯承载力设计值。
宽度 ：b = 120、150、（180）、200、（220）、 250、300、350、…(mm)
高度：h=250、300、350、400、……、750、800、 900、…(mm)。
二、 截面尺寸和配筋构造
2. 板
c15mm d
分布钢筋
h0
h
d 6 ~ 12mm
h0 h 20
板厚的模数为10mm
主页 目录 上一章 下一章 帮助
混凝土结构设计原理
第4章
§4.3 正截面受弯承载力计算原则
4.3.1 基本假设
截面应变保持平面； 不考虑混凝土抗拉强度； 钢筋的应力-应变具有以下关系：
钢筋混凝土结构：正截面承载力计算基本假定
实测应力应变关系
规范采用的简化应力应变关系
正截面承载力计算基本假定
钢筋应力应变关系
D
B’
E
A
C
B
实测应力应变关系
s
fy
s=Ess
s
y
su
规范采用的简化应力应变关系
正截面承载力计算基本假定
压区混凝土等效矩形应力图形（全书核心概念） 目的：正截面承载力Mu与材料布置的关系，故必须计算破 坏时混凝土压应力合力及其作用位置。
《钢筋混凝土结构》
受弯构件正截面承载力计算
正截面承载力计算基本假定
正截面承载力计算基本假定
一、基本假定Basic Assumptions (1) 截面应变保持平面； (2) 不考虑混凝土的抗拉强度； (3) 混凝土的受压应力-应变关系； (4) 钢筋的应力-应变关系。
根据以上四个基本假定，从理论上来说钢筋混凝土构件的 正截面承载力（单向和双向受弯、受压弯、受拉弯）的计 算已不存在问题；
但直接用混凝土受压应力-应变关系进行计算，在实用上还 很不方便。
正截面承载力计算基本假定
P
（1）平截面假定----平均应变意
义上
L/3
L/3
L
As’
as’
ct
dy
c
s’ nh0
y
h0 h
As
s
(1-n)h0
变形协调
as
tb
b
正截面承载力计算基本假定
（2）不考虑混凝土的抗拉强度
P
当配筋适中时——适筋梁的破 坏过程
方法：简化。
相对受压区高度ξ
简化原则：合力的大小相等，合力作用点相同（即可查表得到，见表3-1，介于0.74～0.8之间。 至此，混凝土受弯正截面的压应力计算图式已明确。 计算正截面抗弯极限承载力已相当简单。
钢筋混凝土受弯构件正截面承载力简便计算
钢筋混凝土受弯构件正截面承载力简便计算正文：在钢筋混凝土结构设计中，受弯构件是一种常见的结构元素，其正截面承载力是设计中的关键参数之一。
正截面承载力的计算是评估构件的抗弯能力和安全性的基础，因此在设计中起着重要的作用。
本文将介绍钢筋混凝土受弯构件正截面承载力的简便计算方法，帮助读者更好地理解和应用。
1. 承载力计算的基本原理钢筋混凝土受弯构件的正截面承载力可以通过极限状态计算方法来评估。
其基本原理是根据构件的几何形状、材料性质和荷载作用下的应力分布，计算出构件的抗弯承载力。
在计算过程中，一般采用等效矩形应力分布假设来简化计算。
2. 等效矩形应力分布假设等效矩形应力分布假设是钢筋混凝土受弯构件计算的基础。
该假设认为在受弯构件的截面内，混凝土的应力分布可以近似为一个矩形。
在矩形应力分布中，混凝土的应力是一个线性递减的函数，而钢筋的应力则保持不变。
3. 正截面抗弯承载力计算公式根据等效矩形应力分布假设，可以得到钢筋混凝土受弯构件正截面的抗弯承载力计算公式。
常见的计算公式有多种，其中最常用的是弯矩-曲率法和应力-应变法。
- 弯矩-曲率法：根据截面的几何特性、材料特性和荷载情况，可以通过弯矩-曲率关系来计算截面的抗弯承载力。
具体计算公式如下：M = σs * As * d + σc * Ac * (d - x)其中，M为截面的弯矩，σs为钢筋应力，As为钢筋面积，d为截面的有效高度，σc为混凝土应力，Ac为混凝土面积，x为等效矩形应力分布中混凝土应力变为零的距离。
- 应力-应变法：根据混凝土和钢筋的应力-应变关系，可以分别计算出混凝土和钢筋的应力，然后将二者叠加得到截面的总应力。
具体计算公式如下：σ = σc + σs其中，σ为截面的总应力，σc和σs分别为混凝土和钢筋的应力。
4. 工程实例分析为了更好地理解和应用正截面承载力的简便计算方法，我们将通过一个具体的工程实例来进行分析。
假设有一根钢筋混凝土梁，截面尺寸为200mm×400mm，混凝土强度等级为C30，钢筋强度等级为HRB400。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
根据计算所得钢筋面积As选配钢筋，实际配筋面积应和计算 值接近，一般不宜少于计算值，但也不宜超过计算值得5%
3.3.2 复核
已知：材料，截面尺寸，配筋 As ， （荷载效应 M） 求 M u 或验算 M u≥? M
No
f y As
As ≤ min bh
Yes 少筋梁
M u =M cr
x
1 f c b
5.7.2 复核
As ?
1 f c b' f h ' f
fy
是 属于第一类T形截 面，计算方法同截 面尺寸为 b' f h 的单 筋矩形梁
否 属于第二类T形截面
1 f c b' f b h ' f
fy
As1 =
Hale Waihona Puke h' f M u1 1 f c b' f b h' f h0 2
As 2 As As1
M u 2 按受拉钢筋面积As 2 的单筋矩 形截面 b h 的抗弯承载力复核
M u M u1 M u 2
4.2.2 复核
已知：截面尺寸，材料， As ， A 's 求： M u
x f y As f ' y A 's
1 f c b
若 x 2 a 's
M u =f y As h0 a 's
若 2a 's ≤x≤b h0
若 x b h0
M u f ' y A 's h0 a 's s max1 f cbh02
As As1 As 2
Yes 适筋梁
As ≥ min bh
No 少筋梁，取
min
As min bh
对于双筋截面，其 最小配筋率一般均 能满足要求，可不 必检查
根据计算所得钢筋面积As选配钢筋，实际配筋面积应和计算 值接近，一般不宜少于计算值，但也不宜超过计算值得5%
1 1 2 s
≤ b
Yes
No 说明已知的As’太少，应 增加As’，重新计算，计 算方法同第一类问题
Yes 表明受压钢筋As’ 的应力达不到其抗 压强度的设计值
As M f y h0 a 's
x h0 2a 's
No
As 2 xb1 f c fy
P193，表 6-4，图 6-23
5.3 第一类 T 形截面的受弯承载力计算应力图形
P194，图 6-24
5.4 第二类 T 形截面的受弯承载力计算应力图形
P195，图 6-25
5.5 两种 T 形截面的鉴别
P196
5.6 最小配筋率验算 P194
As min bh
b ——腹板宽
5.7 抗弯承载力计算 5.7.1 设计
As As1 As 2
2、已知：荷载效应 M，截面尺寸，材料， A 's 求： As
为充分利用受压钢 筋，取 A f ' y A 's
s1
fy
M u1 =f ' y h0 a 's A 's
M u 2 M M u1
问题转化为已知M的 单筋矩形梁配筋设计
s
Mu2 1 f cbh02
No 超筋梁
M u s max1 f c bh02
x≤b h0
Yes 适筋梁
x M u f y As h0 2
No 不安全
M u ≥M
Yes 安全
四、双筋矩形梁
4.1 双筋矩形截面受弯承载力计算应力图形（P186） 4.2 双筋矩形梁抗弯承载力计算 4.2.1 设计
1、已知：荷载效应 M，截面尺寸，材料 求： As ， A 's
取 x b h0
一点说明
As 2
bbh01 f c
fy
M u 2 s max1 f cbh02
M u1 M M u 2
A 's
M u1 f ' y h0 a 's
As1
f ' y A 's fy
h' M u 2 M 1 f c b' f b h' f h0 f 2
对第二类 T 形截 面，其最小配筋率 一般均 能满 足要 求，可不必检查
按截面尺寸为b× h的单筋矩 形截面求得 As 2 ，注意必须 验算 ≤b 的条件
As As1 As 2
3.3.1 设计
已知：材料，截面尺寸，荷载效应 求：配筋 As
s
M 1 f cbh02
1 1 2 s
Yes
bh01 f c
fy
≤ b
No 超筋梁，说明截 面太小或者砼强 度太低
As
Yes 适筋梁
As ≥ min bh
No 少筋梁，取
min
As min bh
min max 0.2%, 0.45
的表达式
不一样
三、单筋矩形梁
3.1 等效矩形应力图形（P117）
cu
1 fc
1 fc
s
f y As
f y As
3.2 单筋矩形截面受弯承载力计算应力图形
3.3 单筋矩形混凝土梁抗弯承载力计算
单筋矩形 RC 梁抗弯承载力计算分为两类问题：设计截面和复核截面
x M u f ' y A 's h0 a 's 1 f cbx h0 2
超筋，截面有可能发生脆性破 坏。如有可能，应修改设计。
五、T 形梁
5.1 T 形截面梁受压翼缘应力分布及计算应力图形
P192，图 6-22
5.2 T 形及倒 L 形截受弯构件受压翼缘计算宽度
一、 s max ， b
当混凝土强度等级不超过 C50 时 钢筋级别
s max
b
HPB235 0.426 0.614
HRB335 0.399 0.550
HRB400 0.384 0.518
二、配筋率 ，最小配筋率 min
As bh0
ft fy
A 验算最小配筋率 s ≥min ，注意在验算最小配筋率时， bh
一般是已知弯矩设计值和截面尺寸，求受拉钢筋截面面积 As
h' M ?≤1 f cb' f h' f h0 f 2
是 属于第一类T形截 面，计算方法同截 面尺寸为 b' f h 的单 筋矩形梁
否 属于第二类T形截面
1 f c b' f b h' f
fy
As1