《计算机组成原理》第2章习题解答
《计算机组成原理》各章练习参考答案

《计算机组成原理》各章练习题参考答案第一章思考练习题一.填空1.电子数字计算机可以分为专用计算机和通用计算机两类。
2.硬件采用LSI或VLSI的电子计算机属于计算机发展过程中的第四代。
3.存储器中存放数据和程序。
4.一台计算机包括运算、存储、控制、输入及输出五个单元。
5.完成算术运算和逻辑运算的部件是运算器(或ALU);运算器的核心是加法器;控制、指挥程序和数据的输入、运行以及处理运算结果的部件是控制器。
6.CPU内部连接各寄存器及运算部件之间的总线是内部总线;CPU同存储器、通道等互相连接的总线是系统总线;中、低速I/O设备之间互相连接的总线是I/O总线。
7.在多总路线结构中,CPU总线、系统总线和高速总线相连通过桥实现。
8.计算机软件一般分为系统软件和应用软件。
9.完整的计算机系统由硬件系统和软件系统构成。
10.机器字长是指一台计算机一次所能够处理的二进制位数量。
11.数据分类、统计、分析属于计算机在数据处理方面的应用。
12.计算机是一种信息处理机,它最能准确地反映计算机的主要功能。
13.个人台式商用机属于微型机。
14.对计算机软硬件进行管理,是操作系统的功能。
15.用于科学技术的计算机中,标志系统性能的主要参数是MFLOPS。
16.通用计算机又可以分为超级机、大型机、服务器、工作站、微型机和单片机六类。
17.“存储程序控制”原理是冯.诺依曼提出的。
18.运算器和控制器构成CPU,CPU和主存构成主机。
19.取指令所用的时间叫取指周期,执行指令所用的时间叫执行周期。
20.每个存储单元都有一个编号,该编号称为地址。
21.现代计算机存储系统一般由高速缓存、主存和辅存构成。
22.计算机能够自动完成运算或处理过程的基础是存储程序和程序控制原理。
二.单选1.存储器用来存放( C )。
A.数据B.程序C.数据和程序D.正在被执行的数据和程序2.下面的描述中,正确的是( B )A.控制器能够理解、解释并执行所有的指令及存储结果。
计算机组成原理第2章课后题解

第 1 章
• 1.4 冯.诺伊曼机的主要设计思想?包括哪些组 成?
• 答:存储程序并按地址顺序执行。包括运 算器、控制器、存储器、输入和输出设备。
• 1.7 计算机如何区分内存中的指令和数据?
• 答:取指周期中,从内存读出的字是指令 字,该字送控制器(译码);执行周期中, 从内存读出或写入的字是数据字(操作数 或结果)。
要求变形补码,应包括两个符号位 • 5.(1)[x]补=0011011, [y]补=0000011。
• ∵结果符号位相同 ∴无溢出
• [x + y]补=0011110, x + y =+11110 • (2)[x]补=0011011, [y]补=1101011。 • ∵结果符号位相同 ∴无溢出 • [x + y]补=0000110,x + y =+00110 • (3)[x]补=1101010, [y]补=1111111。 • ∵结果符号位相同 ∴无溢出 • [x + y]补=1101001, x + y =-10111
+ + +
×2-2
[-|y|]补×2-3
[|y|]补×2-4 +
[|y|]补×2-5 +
0.1100000000 1.00001 1.1100100000 0.011111 0.0100010000 1.1100001 0.0000011000 1.11100001 1.1110011100 0.000011111 1.1111011010 0.0000011111 1.1111111001
按题目要求,写出x+y
0011011 + 0000011 0011110 0011011 + 1101011 0000110 1101010 + 1111111 1101001
计算机组成原理第2章答案

第2章综合应用题参考答案1. 在CRC校验中。
已知生成多项式是G(x)=x4+x3+1。
要求写出信息1011001的CRC 校验码。
解:生成多项式G(x)=11001,为5位,校验余数取4位,按模2除法计算过程如下:110101011001 1011001000011001111101100101111011001011100110011010余数R(x)= 1010CRC校验码=1011001 10102. 双方采用CRC循环校验码进行通信,已知生成多项式为x4+x3+x+1,接收到码字为10111010011。
判断该信息有无错误。
解:依题意,生成多项式G(x)=11011,如果信息正确,则模2除法余数应为0110010111011 1011101001111011110001101111100110111111111011100结果余数R(x)= 100不为零所以结果有错。
3. 简述算术移位与逻辑移位的区别算术移位,符号位保持不变,右移用符号位填充,左移用0填充逻辑移位,不考虑符号位,左右移位,空出位都用0填充4.已知机器字长n=8位,X=-44,Y=-53,按补码计算X-Y=?解:[X]补=11010100,[Y]补=11001011,[-Y]补=00110101[X]补11010100[-Y]补+) 00110101000010015. 设机器字长为8位(含1位符号位)设A=9/64, B=-13/32,计算[A±B]补,并还原成真值。
解:A=9/16=1001/26=0.0010010 B=-13/32=1101/25=-0.0110100[A]补=0.0010010 [B]补=1.1001100 [-B]补= 0.0110100[A]补 0.0010010[B]补 +) 1.10011001.1011110[A+B]补=1.1011110 真值A+B =-0.0100010=-17/64[A]补 0.0010010[-B]补 +)0.01101000.1000110[A-B]补=0.1000110 真值A-B =0.1000110=35/646. X=-0.1110,Y=-0.1101,采用原码一位乘法运算求[Z]原=[X×Y]原=?解:[X]原=1.1110 [Y]原=1.1101符号单独处理:积Z的符号位Zs=1 1=0被乘数、乘数都取绝对值:即[|X|] =00.1110 [|Y|]]原=0.1101部分积单元清000.0000 1101+X 00.111000.1110右移1位 00.0111 0110 1+0 00.000000.0111右移1位 00.0011 1011 0+X 00.111001.0001右移1位 00.1000 1101 1+X 00.111001.0110右移1位00.1011 0110 1积的绝对值 |Z|=0.10110110[Z]原=Zs.10110110=0.101101107. 若X=-0.1101, Y=-0.1011,用布斯算法求[X.Y]补=?解:对于Both补码乘法,符号参与运算,被乘数采用双符号位,乘数采用单符号,在乘数最末增加一个0,每次看最低两位(式中画底线的数字):相同(00,或11)则加0,若为10,则加[-X]补,若为01,则加[X]补[X]补=1.0011 [-X]补=0.1101 [Y]补=1.010100.0000 101010+[-X]补 00.110100.1101右移1位 00.0110 110101+[X]补 11.001111.1001右移1位 11.1100 111010+[-X]补 00.110100.1001右移1位 00.0100 111101+[X]补 11.001111.0111右移1位 11.1011 111110+[-X]补 00.110100.1000 1111最后一步不移位积的补码 [Z]补=0.10001111真值 Z= 0.100011118. 设X=-15,Y=-13, 用原码阵列乘法器求乘积Z=X×Y=? 并用十进制乘法验证。
计算机组成原理习题与解答第二章

1.把下列各数化成二进制数和八进制数(二进制取3位小数,八进制取一位小数): 7+3/4,±3/64,73.5,725.9375,25.34答:7+3/4=111.110B; 7+3/4=7.6O; ±3/64=±0.000B; ±3/64=±0.0O; 73.5=1001001.1 00B; 73.5=111.4O;725.9375=1011010101.111B; 725.9375=1325.7O; 25.34=11001.011B; 25.34=31.3O2.把下列各数化成十进制数:101.10011B ,22.2O,AD.4H答:101.10011B=5.59375; 22.2O=18.25; AD.4H=173.253.完成下列二进制数运算:101.111+11.011,1001.10-110.01,101.11*11.01,1011101 11/1101答:101.111+11.011=1001.01; 1001.10-110.01=11.01;101.11*11.01=10010.1011; 101110111/1101=11100.114.完成下列各十六进制数的运算:A39E+28DC,D5AB-7CE5,2BF*4C,C16E/3A答:A39E+28DC=CC7A; D5AB-7CE5=58C6; 2BF*4C=D014; C16E/3A=355.C25.先将15B*8E/2A中的十六进制数化成十进制数,再进行计算,最后再将结果化为十六进制数。
答:15BH*8EH/2AH=347*142/42=49274/42=1173.19=495.30AH6.试分别判断下列各组数据中哪个数据最大?哪个数据最小?(1) A=0.1001B,B=0.1001D,C=0.1001H(2) A=10111101B,B=1001D,C=111H答:(1) A最大, C最小; (2) B最大, A最小;1.写出下列各数的二进制原码和补码(最后两个用双字节): 0,96,-128,-38H,127,10 5,879H,-32768答:上述各数的原码依次为:00000000(10000000), 01100000, 无, 10111000, 011 11111, 01101001, 0000100001111001, 无;上述各数的补码依次为:00000000, 01100000, 10000000, 11001000, 01111 111, 01101001, 0000100001111001, 1000000000000000;2.分别列出下述10进制数的16进制数、非压缩的BCD数、压缩的BCD数、ASCII数字串(用16进制形式写出):10, 64, 78, 81, 92, 100, 125, 255答:上述各数的16进制数依次为:AH,40H,4EH,51H,5CH,64H,7DH,FFH;上述各数的非压缩的BCD数依次为:0100H,0604H,0708H,0801H,0902H,010000H, 010205H,020505H;上述各数的压缩的BCD数依次为:10H,64H,78H,81H,92H,0100H,0125H,0255H;上述各数的ASCII数字串依次为:3130H,3634H,3738H,3831H,3932H,313030H,313 235H, 323535H;3.用10进制数写出下列补码表示的机器数的真值:71H,1BH,80H,F8H,397DH,CF4 2H,9350H答:上述补码表示的各机器数的真值用10进制数分别表示为: +113,+27,-128,-8,+14717,-20670,-278284.若用一个字节来表示带符号数,判断下列各运算在机内进行时是否会产生溢出,写出判断过程。
计算机组成原理第二章课后习题答案

第二章运算方法和运算器练习一、填空题1. 补码加减法中,(符号位)作为数的一部分参加运算,(符号位产生的进位)要丢掉。
2. 为判断溢出,可采用双符号位补码,此时正数的符号用(00)表示,负数的符号用(11)表示。
3. 采用双符号位的方法进行溢出检测时,若运算结果中两个符号位(不相同),则表明发生了溢出。
若结果的符号位为(01),表示发生正溢出;若为(10),表示发生负溢出。
4. 采用单符号位进行溢出检测时,若加数与被加数符号相同,而运算结果的符号与操作数的符号(不一致),则表示溢出;当加数与被加数符号不同时,相加运算的结果(不会产生溢出)。
5. 利用数据的数值位最高位进位C和符号位进位Cf的状况来判断溢出,则其表达式为over=(C⊕Cf)。
6. 在减法运算中,正数减(负数)可能产生溢出,此时的溢出为(正)溢出;负数减(正数)可能产生溢出,此时的溢出为(负)溢出。
7. 补码一位乘法运算法则通过判断乘数最末位Yi和Yi-1的值决定下步操作,当YiYi-1=(10)时,执行部分积加【-x】补,再右移一位;当YiYi-1=(01)时,执行部分积加【x】补,再右移一位。
8. 浮点加减运算在(阶码运算溢出)情况下会发生溢出。
9. 原码一位乘法中,符号位与数值位(分开运算),运算结果的符号位等于(两操作数符号的异或值)。
10. 一个浮点数,当其补码尾数右移一位时,为使其值不变,阶码应该(加1)。
11. 左规的规则为:尾数(左移一位),阶码(减1)。
12. 右规的规则是:尾数(右移一位),阶码(加1)。
13. 影响进位加法器速度的关键因素是(进位信号的传递问题)。
14. 当运算结果的补码尾数部分不是(11.0×××××或00.1×××××)的形式时,则应进行规格化处理。
当尾数符号位为(01)或(10)时,需要右规。
计算机组成原理第二章参考答案

第2章 参考答案2写出下列十进制数的原码、反码、补码和移码表示(用8位二进制数)。
如果是小数,则用定点小数表示;若为整数,则用定点整数表示。
其中MSB 是最高位(符号位),LSB 是最低位。
(1)-1 (2) -38/64 解:(1)-1=(-0000001)2 原码: 10000001反码: 11111110 补码: 11111111 移码: 01111111(2)-38/64=-0.59375=(-0.1001100)2或-38/64=-(32+4+2)*2-6=-(100110)*2-6=(-0.1001100)2 原码: 1.1001100反码: 1.0110011补码: 1.0110100移码: 0.0110100注:-1如果看成小数,那么只有补码和移码能表示得到,定点小数-1的补码为:1.0000000此例类似于8位定点整数的最小值-128补码为100000003 有一字长为32位的浮点数,符号位1位;阶码8位,用移码表示;尾数23位,用补码表示;基数为2.请写出:(1)最大数的二进制表示,(2)最小数的二进制表示,(3)规格化数所能表示的数的范围。
解:(题目没有指定格式的情况下,用一般表示法做)(1)最大数的二进制表示:0 11111111 11111111111111111111111 (2)最小数的二进制表示:1 11111111 00000000000000000000000(1) 7232112*2---() (2) 7211*2--()(3)规格化最大正数:0 11111111 111111111111111111111117232112*2---()规格化最小正数:0 00000000 100000000000000000000007122*2--规格化最大负数:1 00000000 011111111111111111111117123222*2----+()规格化最小负数:1 11111111 000000000000000000000007211*2--()规格化数的表示的数的范围为:7777211232122321[1*2,22*2][2*2,12)*2]----------+- ()()(下面补充IEEE 754的规格化浮点数表示范围:IEEE 754的尾数采用1.M 的形式,原码表示;阶e=E-127 (相对于一般表示法的e=E-128,人为的加了1);并且最大的阶(11111111)和最小的阶(00000000)用去作为特殊用途。
第2章(计算机组成原理) 练习题、参考答案

第2章练习题参考答案一、判断题(正确Y,错误N)1. CPU在很大程度上决定了计算机的性能,CPU的运算速度又与CPU的工作频率密切相关。
因此,在其它配置相同时,使用主频为500MHz的Pentium4作为CPU 的PC机,比使用主频为1GHz Pentium4作为CPU的PC机速度快。
N2. 近年来,PC机中使用的1394接口比USB传输速度更快。
Y3. Cache存储器的存取速度比主存储器要快得多。
因此,为了提高程序的运行速度,在软件开发时,应尽可能多地使用Cache存储器。
N4. 主存储器在物理结构上由若干插在主板上的内存条组成。
目前,内存条上的芯片一般选用DRAM而不采用SRAM。
Y5. 在Pentium处理器中,整数ALU和浮点运算器可以分别对整数和实数同时进行运算处理。
Y6. RAM是随机存取存储器的缩写,其中“随机”的含义是:不论从(向)哪个地址读出或写入数据,所需时间都是相同的。
N7. 3.5英寸软盘的角上有一个小口,当滑动保护片将其盖住时,软盘就不能进行读写操作了。
N8. CPU工作时,它所执行的指令和处理的数据都是直接从磁盘或光盘中取出,处理结果也直接存入磁盘。
N9. 一般情况下,计算机加电后自动执行BIOS中的程序,将所需的操作系统软件装载到内存中,这个过程称为“自举”或“引导”。
Y10. 若某台PC机主板上的CMOS信息丢失,则该机器将不能正常运行,此时只要将其他计算机中的CMOS信息写入后,该机器便能正常运行。
N11. BIOS芯片和CMOS芯片实际上是一块芯片的两种叫法,是启动计算机工作的重要部件。
N12. 一个完整的计算机系统的两个基本组成部分是操作系统和数据库系统.N13. USB接口是一种高速的并行接口。
N14. 计算机中总线的重要指标之一是带宽,它指的是总线中数据线的宽度,用二进位数目来表示(如16位,32位总线)。
N15. 在BIOS中不包含扫描仪、打印机等设备的驱动程序。
(完整版)计算机组成原理第2章例题及参考答案
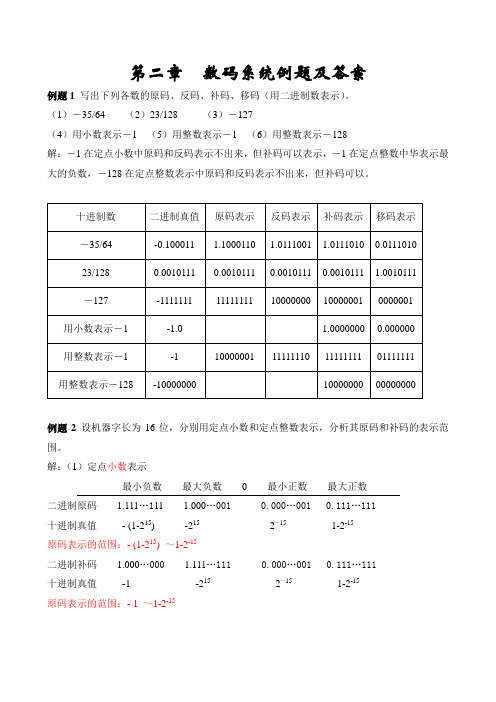
第二章数码系统例题及答案例题1写出下列各数的原码、反码、补码、移码(用二进制数表示)。
(1)-35/64 (2)23/128 (3)-127(4)用小数表示-1 (5)用整数表示-1 (6)用整数表示-128解:-1在定点小数中原码和反码表示不出来,但补码可以表示,-1在定点整数中华表示最大的负数,-128在定点整数表示中原码和反码表示不出来,但补码可以。
例题2设机器字长为16位,分别用定点小数和定点整数表示,分析其原码和补码的表示范围。
解:(1)定点小数表示最小负数最大负数0 最小正数最大正数二进制原码 1.111...111 1.000...001 0.000...001 0.111 (111)十进制真值- (1-215) -2152-151-2-15原码表示的范围:- (1-215) ~1-2-15二进制补码 1.000...000 1.111...111 0.000...001 0.111 (111)十进制真值-1 -2152-151-2-15原码表示的范围:- 1 ~1-2-15(2)定点整数表示最小负数最大负数0 最小正数最大正数二进制原码1111...111 1000...001 0000...001 0111 (111)十进制真值- (215-1) -1 +1 215-1原码表示的范围:- (215-1) ~215-1 [-32767 ~ +32767]二进制补码1000...0001111...111 0000...001 0111 (111)十进制真值-1 +1 215-1原码表示的范围:- 215~215-1 [-32768 ~ +32767]一、选择题1.下列数中最小的数为()。
A.(101001)2B.(52)8C.(101001)BCD D.(233)162.下列数中最大的数为()。
A.(10010101)2B.(227)8C.(96)16D.(143)53.在机器数中,()的零的表示形式是惟一的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章习题解答1.设机器数的字长8位(含1位符号位),分别写出下列各二进制数的原码、补码和反码:0,-0,0.1000,-0.1000,0.1111,-0.1111,1101,-1101。
解:2.写出下列各数的原码、补码和反码:7/16,4/16,1/16,±0,-7/16,-4/16,-1/16。
解:7/16=7*2-4=0.01114/16=4*2-4=0.01001/16=1*2-4=0.0001真值原码补码反码7/16 0.0111 0.0111 0.01114/16 0.0100 0.0100 0.01001/16 0.0001 0.0001 0.0001+0 O.0OOO O.0OOO O.0OOO-0 1.0OOO O.0OOO 1.1111-1/16 1.0OO1 1.1111 1.1110-4/16 1.0100 1.1100 1.1011-7/16 1.0111 1.1001 1.10003.已知下列数的原码表示,分别写出它们的补码表示:[X1]原=O.10100,[X2]原=l.10111。
解:[X1]补=0.10100,[X2]补=1.01001。
4.已知下列数的补码表示,分别写出它们的真值:[X1]补=O.10100,[X2]补=1.10111。
解: X1=O.10100, X2=-0.01001。
5.设一个二进制小数X≥0,表示成X=0.a1a2a3a4a5a6,其中a1~a6取“1”或“O”:(1)若要X>1/2,a1~a6要满足什么条件?(2)若要X≥1/8,a1~a6要满足什么条件?(3)若要1/4≥X>1/16,a1~a6要满足什么条件?解:(1) X>1/2的代码为:0.100001~0.111111。
a1=1,a2+a3+a4+a5+a6=1。
(2) X≥1/8的代码为:0.001001~0.111111(1/8~63/64)a1+a2=0,a3=1或a1=0,a2=1,或a2=1(3)1/4≥X>1/16的代码为:0.000101~0.01000(5/64~1/4)a1+a2+a3 =0, a4=1,a5+a6=1 或a1+a2=0,a3=1 或a2=1,a1+a3+a4+a5+a6=06.设[X]原=1.a1a2a3a4a5a6(1)若要X>-1/2,a1~a6要满足什么条件?(2)若要-1/8≥X≥-1/4,a1~a6要满足什么条件?解:(1) X>-1/2的代码为:1.000001~1.011111(-1/64~-31/64)。
a1=0,a2+a3+a4+a5+a6=1。
(2) -1/8≥X≥-1/4的代码为:1.001000~1.01000(-1/8~-1/4)a1+a2 =0, a3=1或a2=1,a1+a3+a4+a5+a6=07.若上题中[X]原改为[X]补,结果如何?解:(1) X>-1/2的代码为:1.100001~1.111111(-31/64~-1/64)。
a1=1,a2+a3+a4+a5+a6=1。
(2) -1/8≥X≥-1/4的代码为:1.110000~1.111000(-1/4~-1/8)a1*a2=1,a3=0或a1*a2*a3=1, a4+a5+a6=08.一个n位字长的二进制定点整数,其中1位为符号位,分别写出在补码和反码两种情况下:(1)模数;(2)最大的正数;(3)最负的数;(4)符号位的权;(5)-1的表示形式;(6)O的表示形式。
解:补码反码模数 Mod2n Mod(2n-1)最大的正数 2n-1-1 2n-1-1最负的数 -2n-1 -(2n-1-1)符号位的权 2n-1 2n-1-1的表示形式 11111111 11111110O的表示形式 00000000 00000000(11111111)9.某机字长16位,问在下列几种情况下所能表示数值的范围:(1)无符号整数(2)用原码表示定点小数;(3)用补码表示定点小数;(4)用原码表示定点整数(5) 用补码表示定点整数。
解:(1) 0≤X≤(216-1)(2) -(1-2-15)≤X≤(1-2-15)(3) -1≤X≤ (1-2-15)(4) -(215-1)≤X≤(215-1)(5) -215≤X≤(215-1)10.某机字长32位,试分别写出无符号整数和带符号整数(补码)的表示范围(用十进制数表示)。
解:无符号整数:O≤X≤(232-1)。
补码: -231≤X≤(231-1)。
11.某浮点数字长12位,其中阶符1位,阶码数值3位,数符1位,尾数数值7位,阶码以2为底,阶码和尾数均用补码表示。
它所能表示的最大正数是多少?最小规格化正数是多少?绝对值最大的负数是多少?解:最大正数=(1-2-7)×27=127最小规格化正数=2-1×2-8=2-9=1/512绝对值最大的负数-1×27=-128。
12.某浮点数字长16位,其中阶码部分6位(含1位阶符),移码表示,以2为底;尾数部分10位(含1位数符,位于尾数最高位),补码表示,规格化。
分别写出下列各题的二进制代码与十进制真值。
(1)非零最小正数;(2)最大正数;(3)绝对值最小负数;(4)绝对值最大负数。
解:(1)非零最小正数: 000000,0,100000000;2-1×2-32=2-33(2)最大正数: 111111,0,111111111;(1-2-9)×231(3)绝对值最小负数:000000,1,011111111;-(2-1+2-9)×2-32(4)绝对值最大负数:111111,1,000000000;-231。
13.一浮点数,其阶码部分为p位,尾数部分为q位,各包含1位符号位,均用补码表示;尾数基数r=2,该浮点数格式所能表示数的上限、下限及非零的最小正数是多少?写出表达式。
解:上限(最大正数)=(1-2-(q-1))×(2)22(p-1)-1下限(绝对值最大负数)-1×(2)22(p-1)-1最小正数=2-(q-1)×(2)2-(p-1)最小规格化正数=2-1×(2){-2 (p-1)}。
14.若上题尾数基数r=16,按上述要求写出表达式。
解:上限(最大正数)=(1-2-(q-1))×(16)22(p-1)-1下限(绝对值最大负数)-1×(16)22(p-1)-1最小正数=2-(q-1)×(16)2-(p-1)最小规格化正数=16-1×(16){-2 (p-1)}。
15.某浮点数字长32位,格式如下。
其中阶码部分8位,以2为底,补码表示, 尾数部分一共24位(含1位数符),补码表示。
现有一浮点代码为(8C5A3E00)16,试写出它所表示的十进制真值。
O 7 8 9 31解:(8C5A3EOO)16=1000 1100 0101 1010 0011 1110 0000 0000B符号位=0阶码=10001100-10000000=1100=(12)10尾数=10110100011111000000000O.10110100011111×212=(101101000111.11)2=(2887.75)1016.试将(-O.1101)。
用IEEE短浮点数格式表示出来。
解: -O.1101=-1.101×2-1符号位=1。
阶码:127-1=126。
1,01111110,10100000000000000000000。
结果=BF500000H。
17.将下列十进制数转换为IEEE短浮点数:,(1)28.75;(2)624;(3)-O.625;(4)+0.0;(5)-1000.5。
解:(1)(28.75)10=(11100.11)2=1.110011×24符号位=O阶码=127+4=1310,10000011,11001100000000000000000结果=41E60000H(2) (624)10=(1001110000)2=1.001110000×29符号位=O阶码=127+9=1360,10001000,00111000000000000000000。
结果=441C0000H。
(3) -(0.625)10=-(0.101)2=-1.01×2-1符号位=1阶码=127—1=126。
1,01111110,01000000000000000000000。
结果=BF200000H。
(4)+O.O。
结果=00000000H。
(5) -(1000.5)10=-(1111101000.1)2=-1.1111010001×29符号位=1阶码=127+9=136。
1,10001000,11110100010000000000000。
结果=C47A2000H。
18.将下列IEEE短浮点数转换为十进制数:(1)11000000 11110000 00000000 00000000:(2)00111111 00010000 00000000 00000000:(3)01000011 10011001 00000000 00000000;(4)01000000 00000000 00000000 00000000;(5)01000001 00100000 00000000 00000000;(6)00000000 00000000 00000000 00000000。
解:(1)1,10000001,11100000000000000000000:符号位=1阶码=129-127=21.111×22=11l1.1B=7.5所以结果=-7.5。
(2)O,01111110,00100000000000000000000符号位=0。
阶码=126-127=-11.001×2-1=0.1001B= O.5625所以结果=O.5625。
(3)O,10000111,00110010000000000000000符号位=0阶码=135-127=81.0011001×28=100110010B=306所以,结果=306。
(4)0,10000000,00000000000000000000000符号位=0。
阶码=128—127=1。
1.0×21=10B=2所以,结果=2。
(5)0,10000010,0100000 00000000 00000000符号位=O阶码=130-127=31.01×23=1010B=10。
所以,结果=10。
(6)0,00000000,00000000000000000000000阶码和尾数都等于全0,结果=O。
