江苏省南通市2020高考数学二轮冲刺小练(26)
江苏省南通市2020届高三数学下学期二模考前综合练习试题含解析

【答案】
【解析】
由图可知,当直线y=kx在直线OA与x轴(不含它们)之间时,y=kx与y=f(x)的图像有两个不同交点,即方程有两个不相同的实根.
8.已知关于x的不等式(ax﹣a2﹣4)(x﹣4)>0的解集为A,且A中共含有n个整数,则当n最小时实数a的值为_____.
【答案】
【解析】
【分析】
观察知各等式右边各项的系数和为1,最高次项的系数为该项次数的倒数,据此计算得到答案。
【详解】根据所给的已知等式得到:各等式右边各项的系数和为1,
最高次项的系数为该项次数的倒数,
∴A ,A 1,解得B ,所以A﹣B .
故答案为: .
【点睛】本题考查了归纳推理,意在考查学生的推理能力.
【详解】(1)因为角 为钝角, ,所以 ,
又 ,所以 ,
且 ,
所以
。
(2)因为 ,且 ,所以 ,
又 ,
则 ,
所以 .
16.如图,四棱锥V﹣ABCD中,底面ABCD是菱形,对角线AC与BD交于点O,VO⊥平面ABCD,E是棱VC的中点.
(1)求证:VA∥平面BDE;
(2)求证:平面VAC⊥平面BDE.
综上所述,a=﹣2.
故答案为:﹣2.
【点睛】本题考查了解不等式,均值不等式,意在考查学生的计算能力和综合应用能力.
9。已知双曲线 (a>0,b>0)的两个焦点为 、 ,点P是第一象限内双曲线上的点,且 ,tan∠PF2F1=﹣2,则双曲线的离心率为_____.
【答案】
【解析】
【分析】
根据正弦定理得 ,根据余弦定理得 2PF1•PF2cos∠F1PF2 3,联立方程得到 ,计算得到答案。
江苏南通2020 高考数学冲刺小练(2)
交 y 轴于 M , N ,且 ON 3OM ,则双曲线的离心率为
.
7.已知动圆 M 与圆 C1 : (x 1)2 y2 1 ,圆 C2 : (x 1)2 y2 25 均内切,则动圆圆心 M 的
轨迹方程是
.
8.设点 A1, 2 ,非零向量 a m, n ,若对于直线 3x y 4 0 上任意一点 P , AP a 恒为
P
(2) FG ∥平面 EBO .
E
F
A
G O
C
B
12. 数列{an}的前 n 项和为 Sn,若存在正整数 r,t,且 r<t,使得 Sr=t,St=r 同时成立,则称数 列{an}为“M(r,t)数列”. (1)若首项为 3,公差为 d 的等差数列{an}是“M(r,2r)数列”,求 d 的值; (2)已知数列{an}为等比数列,公比为 q.若数列{an}为“M(r,2r)数列”,r≤4,求 q 的值.
2
a2 a3,a3 a4,a4 a5 成等差数列,则 q 的值为
.
6.在平面直角坐标
xOy
中,双曲线 C
:
x2 a2
y2 b2
1(a
0,b
0)
的左右焦点分别为 F1, F2 , A, B
分别为
左,右顶点,点 P 为双曲线上一点,且满足 PF2 F1F2 ,点 Q 为 PF2 上一点,直线 QF1, BQ 分别
.
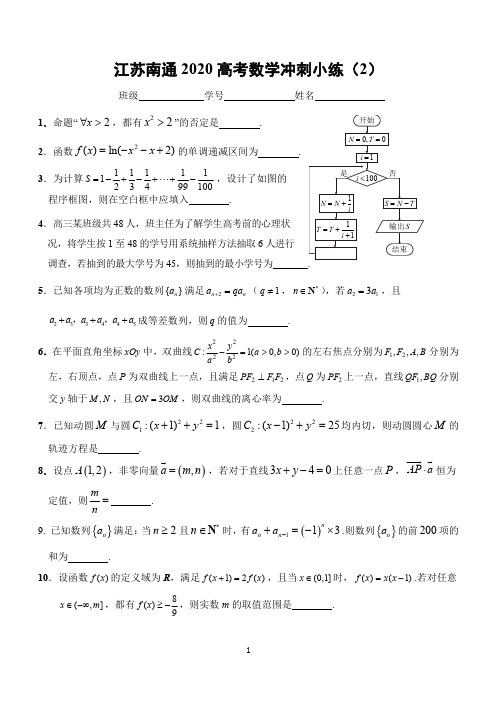
是 i 100 否
N N 1 i
S N T
4.高三某班级共 48 人,班主任为了解学生高考前的心理状 况,将学生按 1 至 48 的学号用系统抽样方法抽取 6 人进行
T
T
i
1 1
输出 S 结束
调查,若抽到的最大学号为 45,则抽到的最小学号为
江苏省南通市2020高考数学二轮冲刺小练(30)

江苏南通2020高考数学二轮冲刺小练(30) 班级 学号 姓名1.已知,a b 为实数,集合{,1},b M a =N={},0,:a f x x →表示把集合M 中的元素x 映射到集合N 中仍为x ,则a b += .2.若,i j 是互相垂直的两个单位向量,则2-i j 与2+i j 的夹角为 .3.点P (1,2,4)-关于点A (1,1,)a -的对称点是(,,2)Q b c -,则a b c ++= .4.设()f x 是定义在(0,)+∞上的增函数,且()()()xf f x f y y=-,若(2)1f =,则(4)f = .5.设全集22,{|4},{|1}1U M x y x N x x ===-=-R ≥ 都是U 的子集(如图所示),则阴影部分所示的集合是.6.已知G 是△ABC 的重心,过G 的一条直线交AB 、AC 两点分别于E 、 F ,且有,AE AB AF AC λμ==u u u r u u u r u u u r u u u r ,则11λμ+= . 7.已知函数)1lg(1)(222++++=x x x x x f ,且62.1)1(≈-f ,则≈)1(f . 8.设A ,B ,C ,D 是空间不共面的四点,且满足0,0,0,AB AC AC AD AB AD ⋅=⋅=⋅=u u u r u u u r u u u r u u u r u u u r u u u r 则△BCD 的形状是 三角形.(填“钝角”、“直角”、“锐角”之一)9.函数y=x 2(x>0)的图像在点(a k ,,a k 2)处的切线与x 轴交点的横坐标为a k+1,k 为正整数,a 1=16,则a 1+a 3+a 5=____ _.10.已知P 是直线3480x y ++=上的动点,PA 、PB 是圆222210x y x y +--+=的两条切线,A 、B 是切点,C 是圆心,那么四边形PACB 面积的最小值为 . 11.在△ABC 中,||2AB AC AB AC ⋅=-=u u u r u u u r u u u r u u u r . (1)求22||||AB AC +u u u r u u u r 的值; (2)当△ABC 的面积最大时,求∠A 的大小.12.如图,在四棱锥P-ABCD中PD⊥底面ABCD,底面为正方形,PD=DC,E、F分别是CD、PB的中点.(1)求证:EF//平面PAD;(2)求证:EF⊥AB;(3)在平面PAD内求一点G,使GF⊥平面PCB,并证明你的结论.。
江苏省南通市2020高考数学二轮冲刺小练(20)

江苏南通2020高考数学二轮冲刺小练(20)班级 学号 姓名1.对于命题p :x ∃∈R ,x 2+ x +1 < 0,则p ⌝为:_____ .2.复数13i z =+,21i z =-,则复数12z z 在复平面内对应的点位于第__ __象限. 3.一个靶子上有10个同心圆,半径依次为1,2,…,10,击中由内至外的区域的成绩依次为10,9,…,1环.不考虑技术因素,则射击一次,在有成绩的情况下成绩为10环的概率为 .4.△ABC 中,︒=∠==30,1,3B AC AB ,则△ABC 的面积等于__ _.5.给出下列命题中,正确命题的序号是__ .①“()x A B ∈I ”是“()x A B ∈U ”的充分不必要条件;②若0,0a b >>,则不等式3323a b ab +≥恒成立;③对于函数2()2f x x mx n =++,若()0,()0,f a f b >>则函数在(,)a b 内至多有一个零点; ④(2)y f x =-与(2)y f x =-的图象关于2x =对称.6.若△ABC 内切圆半径为r ,三边长为a 、b 、c ,则△ABC 的面积S =12 r (a +b +c ) ;若四面体内切球半径为R ,四个面的面积为S 1,S 2 ,S 3 ,S 4,则四面体的体积V = .7.已知数列{}n a 为等差数列,且17134a a a π++=,则212tan()a a +=_ _ _.8.已知(1,2),(3,4)A B ,直线1l :20,:0x l y ==和3:l x +3y 10-=.设i P 是i l (1,2,3)i =上与A 、B 两点距离平方和最小的点,则△P 1P 2P 3的面积是 .9.若21,0,()1,0,x x f x x ⎧+=⎨<⎩≥则满足不等式2(1)(2)f x f x ->的x 的范围是 . 10.已知点P 是抛物线24y x =上的动点,若点P 在y 轴上的射影是M ,点A 的坐标是(4,a ),则当||4a >时,||||PA PM +的最小值是11.某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分 成六段[40,50),[50,60),…,[90,100]后,画出如下部分频率分布直方图:(1)求第四小组的频率,并补全这个频率分布直方图;(2)观察频率分布直方图的信息,估计这0.01频率组距次考试的及格率(60分及以上为及格)和平均分.12.在△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,(2,cos ),(,cos )b c C a A =-=m n ,且//m n .(1)求角A 的大小; (2)求)23cos(sin 22B B y -+=π的值域.。
江苏南通2020 高考数学冲刺小练(3)

江苏南通2020高考数学冲刺小练(3)班级学号姓名1.设全集{|2,}U x x x =∈N ≥,集合2{|5,}A x x x =∈N ≥,则U C A =.2.复数z 满足()13i z i +=-,则z =.3.有3个不同的社团,甲、乙两名同学各自参加其中1个社团,每位同学参加各个社团的可能性相同,则这两位同学参加同一个社团的概率为.4.如图所示的程序框图中,若函)20()()(<<-=m m x f x F 总有四个零点,则a 的取值范围是.5.已知函数()0x xf x e =,设()1n f x +为()n f x 的导函数,()()'101x x f x f x e -⎡⎤==⎣⎦,()()'212x x f x f x e-⎡⎤==⎣⎦…,根据以上结果,推断()2019f x =.6.在公比为q 且各项均为正数的等比数列{}n a 中,n S 为{}n a 的前n 项和.若121a q=,且522S S =+,则q 的值为.7.已知△ABC 的三边长分别为a ,b ,c ,且43S △ABC =a 2+b 2+c 2,则A=.8.已知函数()f x 满足3()1f x a x -=+,且对任意实数x 都有()(2)2f x f x +-=,则(0)f 的值为.9.设O 为坐标原点,,M N 是圆224x y +=上的动点,且23MON π∠=,点P 在直线34120x y +-=上运动,则PM PN +的最小值为.10.已知实数a ,b ,c 满足2121a c b c e a b e +--+++≤(其中e 为自然对数的底数),则22a b +的最小值是.11.ABC △的内角A ,B ,C 的对边分别为a ,b ,c ,已知ABC △的面积为23sin a A.(1)求sin sin B C ;(2)若6cos cos 1B C =,3a =,求ABC △的周长.12.如图所示,椭圆2222:1(0)x y M a b a b+=>>的离心率为2,右准线方程为4x =,过点(0,4)P 作关于y 轴对称的两条直线12,l l ,且1l 与椭圆交于不同两点,A B ,2l 与椭圆交于不同两点,D C .(1)求椭圆M 的方程;(2)证明:直线AC 与直线BD 交于定点(0,1)Q .xy PAB DCl 1l 2O。
【附加15套高考模拟试卷】江苏省南通市2020届高三下学期第二次调研测试数学试题含答案

江苏省南通市2020届高三下学期第二次调研测试数学试题一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列关于命题的说法错误的是( )A .命题“若2320x x -+=,则2x =”的逆否命题为“若2x ≠,则2320x x -+≠”B .已知函数()f x 在区间[],a b 上的图象是连续不断的,则命题“若()()0f a f b <,则()f x 在区间(),a b 内至少有一个零点”的逆命题为假命题C .命题“x R ∃∈,使得210x x ++<”的否定是:“x R ∀∈,均有210x x ++≥”D .“若0x 为()y f x =的极值点,则()00f x '=”的逆命题为真命题2.高铁、扫码支付、共享单车、网购并称中国“新四大发明”,近日对全国100个城市的共享单车和扫码支付的使用人数进行大数据分析,其中共享单车使用的人数分别为123100,,,,x x x x L,它们的平均数为x ,方差为2s ;其中扫码支付使用的人数分别为132x +,232x +,332x +,L ,10032x +,它们的平均数为x ',方差为2s ',则x ',2s '分别为( )A .32x +,232s +B .3x ,23sC .32x +,29s D .32x +,292s +3.如图,在ABC △中,AD AB ⊥,3BC BD =u u u r u u u r ,||1AD =u u u r ,则AC AD ⋅=u u u r u u u r( )A .23B .32C .33 D .34..一个空间几何体的三视图如图所示,俯视图为正三角形,则它的外接球的表面积为( )A .4πB .1123πC .283πD .16π5.阅读如图的程序框图,当程序运行后,输出S 的值为( )A .57B .119C .120D .2476.已知是抛物线的焦点,,是该抛物线上两点,,则的中点到准线的距离为( ) A .B .2C .3D .47.程大位《算法统宗》里有诗云“九百九十六斤棉,赠分八子做盘缠.次第每人多十七,要将第八数来言.务要分明依次弟,孝和休惹外人传.”意为:996斤棉花,分别赠送给8个子女做旅费,从第一个开始,以后每人依次多17斤,直到第八个孩子为止.分配时一定要等级分明,使孝顺子女的美德外传,则第八个孩子分得斤数为( )A .65B .184C .183D .1768. “牟和方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体.它由完全相同的四个曲面构成,相对的两个曲面在同一个圆柱的侧面上(图1),好似两个扣合(牟合)在一起的方形伞(方盖).其直观图如(图2)所示,图中四边形是为体现其直观性所作的辅助线,当其正视图与侧视图完全相同时,它的正视图和俯视图分别可能是( )A .,a bB .,a cC .,c bD .,b d9.在三棱锥P ABC -中,2AB BC ==,22AC =PB ⊥面ABC ,M ,N ,Q 分别为AC ,PB ,AB 的中点,3MN =,则异面直线PQ 与MN 所成角的余弦值为( )A .105B.155C.35D.4510.已知数列{}n a和{}n b的前n项和分别为n S和n T,且0na>,2*634()n n nS a a n N=+-∈,()()1111nn nba a+=--,若对任意的n*∈N,nk T>恒成立,则的最小值为()A.13B.19C.112D.11511.设a b,为两条直线,αβ,为两个平面,下列四个命题中,正确的命题是()A.若a b,与α所成的角相等,则a b∥B.若aαβ∥,b∥,αβ∥,则a b∥C.若a b a bαβ⊂⊂P,,,则αβ∥D.若a bαβ⊥⊥,,αβ⊥,则a b⊥r r12.三世纪中期,魏晋时期的数学家刘徽首创割圆术,为计算圆周率建立了严密的理论和完善的算法.所谓割圆术,就是用圆内接正多边形的面积去无限逼近圆面积并以此求取圆周率的方法.按照这样的思路刘徽把圆内接正多边形的面积一直算到了正3072边形,如图所示是利用刘徽的割圆术设计的程序框图,若输出的24n=,则p的值可以是( )(参考数据: sin150.2588︒≈,sin7.50.1305︒≈,sin3.750.0654︒≈)A.2.6B.3C.3.1D.14二、填空题:本题共4小题,每小题5分,共20分。
江苏南通2020 高考数学冲刺小练(4)

江苏南通2020高考数学冲刺小练(4)班级学号姓名1.已知向量,,若,则实数.2.阅读右面的程序框图,运行相应的程序,若输入N 的值为24,则输出N 的值为.3.已知)(),(x g x f 分别是奇函数和偶函数,且32)()(2-+-=+x x x g x f ,则)()(x g x f -的表达式为.4.如图是甲、乙两名篮球运动员在五场比赛中所得分数的茎叶图,则在这五场比赛中得分较为稳定(方差较小)的那名运动员的得分的方差为.5.已知函数()[]()sin 0,f x x x π=∈和函数()1tan 2g x x =的图象交于A B C 、、三点,则ABC ∆的面积为.6.已知实数,x y 满足0043120x y x y ≥⎧⎪≥⎨⎪+-≤⎩,则231x y x +++的取值范围是.7.已知函数2()e (1)x f x x ax =++的单调减区间为()ln ln e e b a ,,则a b 的值为.8.设F 为双曲线C :22221x y a b-=(a >0,b >0)的右焦点,O 为坐标原点,以OF 为直径的圆与圆x 2+y 2=a 2交于P 、Q 两点.若|PQ |=|OF |,则C 的离心率为.9.若点P ,Q 分别是曲线4x y x+=与直线40x y +=上的动点,则线段PQ 长的最小值为.10.对任一实数序列),,,(321 a a a A =,定义新序列),,,(342312 a a a a a a A ---=∆,它的第n 项为n n a a -+1,假设序列)(A ∆∆的所有项都是1,且02212==a a ,则=n a .779089481035甲乙(第4题图)11.在三角形ABC 中,角C B A ,,的对边分别为c b a ,,,C b a cos 4=,10103sin =C .(1)求角B 的值;(2)若5=b ,求三角形ABC 的面积.12.某城市受雾霾影响严重,现欲在该城市中心P 的两侧建造A ,B 两个空气净化站(A ,P ,B三点共线),A ,B 两站对该城市的净化度分别为1a a -,,其中(01)a ∈,.已知对该城市总净化效果为A ,B 两站对该城市的净化效果之和,且每站净化效果与净化度成正比,与中心P 到净化站距离成反比.若1AB =,且当34AP =时,A 站对该城市的净化效果为3a ,B 站对该城市的净化效果为1a -.(1)设AP x =,(01)x ∈,,求A ,B 两站对该城市的总净化效果()f x ;(2)无论A ,B 两站建在何处,若要求A ,B 两站对该城市的总净化效果至少达到25,求a 的取值集合.。
2020年江苏南通高三下学期高考模拟数学试卷

,
.
,
,求函数 的单调增区间.
16. 如图,在四棱锥
锐角
所在平面
中,底面
底面
,
为梯形,
,
, 交 于,
,点 在侧棱 上,且
.
2
( 1 ) 求证: ( 2 ) 求证:
平面
.
.
17. 在平面直角坐标系 中,圆
,直线
点,弦 过点 ,过点 作 的垂线交 于点 .
(1) 若
,求
的面积.
( 2 ) 判断直线 与圆 的位置关系,并证明.
2 若对任意 ,
,必存在
使得
,求数列 的通项公式.
( , , 为常
,已知
,且
20. 若实数 满足 ( 1 ) 求函数
,则称
为函数
的不动点.
的不动点.
3
( 2 ) 设函数
1若
时,存在一个实数
,其中 , , 为实数.
,使得
既是
点(
是函数 的导函数),求实数 的取值范围.
2令
,若存在实数 ,使 ,
,
为正数的等比数列,求证:函数 存在不动点.
, ,
, ,
,所以直线
, 与圆 相切,得证.
时,体积最大.
设
,则
,
,
若以 为底、 为高,则圆柱底面半径
,
,
,
,
当
时,
,当
时,
,
所以
,
若以 为底, 为高,则圆柱底面半径
,
,
,
当 所以
时,
,令
,得
、
,
,当
时,
,
,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏南通2020高考数学二轮冲刺小练(26)
班级 学号 姓名
1.已知M={y |y =x 2},N={y |x 2+y 2=2},则M I N= .
2.已知{(,)|(3)34}{(,)|7(5)80}x y m x y m x y x m y ++=-+--==∅I ,则直线(3)34m x y m ++=+与坐标轴围成的三角形面积是 .
3.若点P (αcos ,αsin )在直线上x y 2-=上,则=+αα2cos 22sin .
4.已知函数12()log f x =1()x x
+,给出以下四个命题:
①()f x 的定义域为(0,)+∞; ②()f x 的值域为[)1,-+∞ ;
③()f x 是奇函数; ④()f x 在(0,1)上单调递增.
其中所有真命题的序号是 .
5.将直线0x =绕原点按顺时针方向旋转30︒,所得直线与圆22(2)3x y -+=的位置关系是 .
6.设][x 表示不超过x 的最大整数,则不等式2
[]3[]100x x --≤的解集是 .
7.已知函数22()1(,)f x x ax b b a b =-++-+∈∈R R ,对任意实数x 都有(1)(1)f x f x -=+ 成立,若当[1,1]x ∈-时,()0f x >恒成立,则b 的取值范围是 .
8.已知直线l 、m ,平面βα、,则下列命题中是真命题的序号是 . ①若βα//,α⊂l ,则β//l ;
②若βα//,α⊥l ,则β⊥l ;
③若α//l ,α⊂m ,则m l //;
④若βα⊥,l αβ=I ,α⊂m ,l m ⊥,则β⊥m .
9.实数,x y 满足(6)(6)0,14,
x y x y x -++-⎧⎨⎩≥≤≤ 则y x 的最大值是 . 10.已知函数①x x f ln 3)(=;②x e x f cos 3)(=;③x
e x
f 3)(=;④x x f cos 3)(=.其中对于
)(x f 定义域内的任意一个自变量1x 都存在唯一个自变量2x 3=成立的函
数序号是 .
11.已知函数)(x f y =是R 上的奇函数,且当0x ≤时,2
1193)(-+=x x x f , (1)判断并证明)(x f y =在)0,(-∞上的单调性; (2)求)(x f y =的值域.
12.已知圆O :222x y +=交x 轴于A ,B 两点,曲线C 是以AB
为长轴,离心率为2
的椭圆,其左焦点为F .若P 是圆O 上一点,连结PF ,过原点O 作直线PF 的垂线交椭圆C 的左准线于点Q .
(1)求椭圆C 的标准方程;
(2)若点P 的坐标为(1,1),求证:直线PQ 与圆O 相切;
(3)试探究:当点P 在圆O 上运动时(不与A 、B 重合),直线PQ 与圆O 是否保持相切
的位置关系?若是,请证明;若不是,请说明理由.。
