计数原理基本知识点.doc
计数原理知识点

计数原理知识点一、分类加法计数原理1. 原理内容- 完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法,那么完成这件事共有N = m + n种不同的方法。
- 推广:完成一件事有n类不同方案,在第1类方案中有m_1种不同的方法,在第2类方案中有m_2种不同的方法,……,在第n类方案中有m_n种不同的方法,那么完成这件事共有N=m_1 + m_2+·s+m_n种不同的方法。
2. 特点- 各类办法之间相互独立,都能独立地完成这件事,且各类方法中的每种方法也相互独立。
3. 示例- 从甲地到乙地,可以乘火车,也可以乘汽车。
一天中,火车有3班,汽车有2班。
那么一天中乘坐这些交通工具从甲地到乙地共有3 + 2=5种不同的走法。
二、分步乘法计数原理1. 原理内容- 完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法,那么完成这件事共有N = m× n种不同的方法。
- 推广:完成一件事需要n个步骤,做第1步有m_1种不同的方法,做第2步有m_2种不同的方法,……,做第n步有m_n种不同的方法,那么完成这件事共有N = m_1× m_2×·s× m_n种不同的方法。
2. 特点- 各个步骤相互依存,只有各个步骤都完成了,这件事才算完成。
3. 示例- 从甲地到丙地,要先从甲地到乙地,再从乙地到丙地。
从甲地到乙地有3条路可走,从乙地到丙地有2条路可走,那么从甲地到丙地共有3×2 = 6种不同的走法。
三、排列与组合的基本概念1. 排列- 定义:从n个不同元素中取出m(m≤ n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列。
- 排列数:从n个不同元素中取出m(m≤ n)个元素的所有排列的个数,叫做从n个不同元素中取出m个元素的排列数,记作A_{n}^m。
- 排列数公式:A_{n}^m=(n!)/((n - m)!)=n(n - 1)(n - 2)·s(n - m+1),其中n!=n×(n - 1)×(n - 2)×·s×2×1,规定0!=1。
计数原理必备知识点总结

计数原理必备知识点总结一、计数原理的基本概念1.1 事件和样本空间在概率论中,事件是指可能发生的结果,样本空间是指所有可能的结果的集合。
在计数原理中,我们通常需要计算在一定条件下事件发生的次数,因此需要对事件和样本空间进行分析和计算。
1.2 事件的互斥和独立在计数原理中,我们需要考虑事件之间的互斥和独立关系。
互斥事件是指两个事件不能同时发生,而独立事件是指两个事件之间没有相互影响。
1.3 条件概率和联合概率在计数原理中,我们需要考虑事件的条件概率和联合概率。
条件概率是指在给定某一事件发生的条件下,另一事件发生的概率;联合概率是指两个事件同时发生的概率。
1.4 达成事件的概率在计数原理中,我们需要计算事件发生的概率。
达成事件的概率是指在一定条件下事件发生的可能性,通常通过计数原理来进行计算。
二、排列组合2.1 排列在计数原理中,排列是指从给定的元素中选取一定数量的元素进行排列,排列中元素的顺序是重要的。
在计算排列时,通常使用阶乘的方法进行计算。
2.2 组合在计数原理中,组合是指从给定的元素中选取一定数量的元素进行组合,组合中元素的顺序是不重要的。
在计算组合时,通常使用二项式系数的方法进行计算。
2.3 组合公式在计数原理中,我们可以使用组合公式来计算组合的数量。
组合公式是指C(n,k)=n!/(k!(n-k)!),其中n表示元素的总数,k表示选取的元素的数量。
2.4 排列组合的应用在计数原理中,排列组合的方法具有广泛的应用。
在实际问题中,我们常常需要考虑元素的排列和组合,例如在排列组合中考虑位置的排列和顺序的组合等。
三、二项式系数3.1 二项式定理在计数原理中,二项式定理是指一个式子的平方等于两个式子相乘的和。
例如,(a+b)^2=a^2+2ab+b^2,这就是一个二项式定理的例子。
3.2 二项式系数的计算在计数原理中,我们可以使用二项式系数来计算二项式的展开式。
二项式系数是通过排列组合的方法进行计算的,通常使用组合公式来计算。
(精品计数原理基本知识点

(精品计数原理基本知识点计数原理是离散数学中的一个重要分支,用于研究计数和排列组合问题。
它在实际应用中有着广泛的应用,例如密码学、组合优化、统计学等领域。
以下是关于计数原理的基本知识点:1.乘法原理:乘法原理用于计算多个独立事件同时发生的总数。
根据乘法原理,若事件A发生的可能性为m种,事件B发生的可能性为n种,则事件A和B 同时发生的可能性为m×n种。
2.加法原理:加法原理用于计算两个或多个事件分别发生的总数。
根据加法原理,若事件A发生的可能性为m种,事件B发生的可能性为n种,则事件A或B发生的可能性为m+n种。
3.排列:排列是指从一组对象中选择一部分进行排列的方式。
如果有n个对象要排列,只选取其中的k个进行排列,那么排列的可能性总数可以表示为P(n,k)。
排列的计算公式为:P(n,k)=n!/(n-k)!4.组合:组合是指从一组对象中选择一部分对象,不考虑其顺序的方式。
如果有n个对象要选择,只选取其中的k个进行组合,那么组合的可能性总数可以表示为C(n,k)。
组合的计算公式为:C(n,k)=n!/(k!*(n-k)!)5.递推关系:递推关系是计数原理中常用的一种思维方法。
通过建立递推关系,可以从已知的计数问题推导出更复杂的计数问题的解。
例如,在排列和组合中可以使用递推关系快速计算出较大规模的情况。
6.容斥原理:容斥原理用于计算多个集合的交集和并集的大小。
根据容斥原理,若存在n个集合A_1、A_2、..、A_n,那么它们的并集的大小为:A_1∪A_2∪...∪A_n,=Σ,A_i,-Σ,A_i∩A_j,+Σ,A_i∩A_j∩A_k,-...+(-1)^(n-1),A_1∩A_2∩...∩A_n7.应用举例:计数原理的应用举例有很多,例如密码学中的密码破解问题,通过计算排列或组合的可能性来确定破解密码的策略。
另外,在组合优化问题中,例如旅行商问题(TSP)、集合覆盖问题等,也可以使用计数原理来计算问题的解。
专题42 计数原理(解析版)
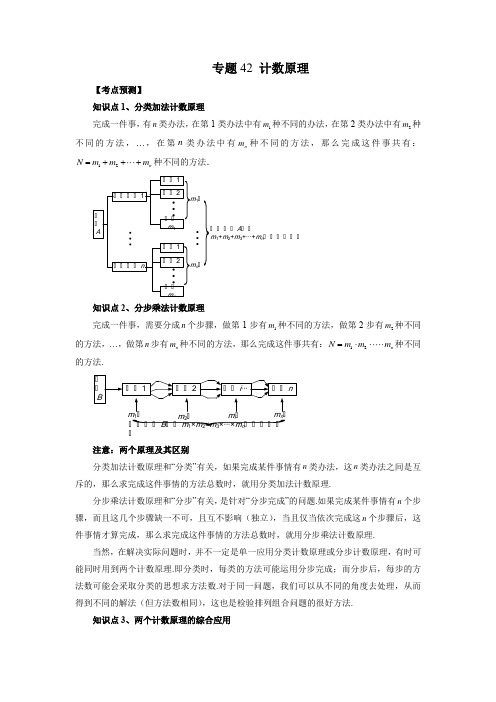
专题42 计数原理【考点预测】知识点1、分类加法计数原理完成一件事,有n 类办法,在第1类办法中有1m 种不同的办法,在第2类办法中有2m 种不同的方法,…,在第n 类办法中有n m 种不同的方法,那么完成这件事共有:12n N m m m =+++种不同的方法.事事A事事事事1事事1事事2事事m 1事事事事n事事1事事2事事m nm 1事m n 事事事事事A 事事m 1+m 2+m 3+···+m n 事事事事事事知识点2、分步乘法计数原理完成一件事,需要分成n 个步骤,做第1步有1m 种不同的方法,做第2步有2m 种不同的方法,…,做第n 步有n m 种不同的方法,那么完成这件事共有:12n N m m m =⋅⋅⋅种不同的方法.m 1事m n 事事事事事B 事事m 1×m 2×m 3×···×m n 事事事事事事m 2事m i 事注意:两个原理及其区别分类加法计数原理和“分类”有关,如果完成某件事情有n 类办法,这n 类办法之间是互斥的,那么求完成这件事情的方法总数时,就用分类加法计数原理.分步乘法计数原理和“分步”有关,是针对“分步完成”的问题.如果完成某件事情有n 个步骤,而且这几个步骤缺一不可,且互不影响(独立),当且仅当依次完成这n 个步骤后,这件事情才算完成,那么求完成这件事情的方法总数时,就用分步乘法计数原理.当然,在解决实际问题时,并不一定是单一应用分类计数原理或分步计数原理,有时可能同时用到两个计数原理.即分类时,每类的方法可能运用分步完成;而分步后,每步的方法数可能会采取分类的思想求方法数.对于同一问题,我们可以从不同的角度去处理,从而得到不同的解法(但方法数相同),这也是检验排列组合问题的很好方法.知识点3、两个计数原理的综合应用如果完成一件事的各种方法是相互独立的,那么计算完成这件事的方法数时,使用分类计数原理.如果完成一件事的各个步骤是相互联系的,即各个步骤都必须完成,这件事才告完成,那么计算完成这件事的方法数时,使用分步计数原理.【题型归纳目录】题型一:分类加法计数原理的应用 题型二:分步乘法计数原理的应用 题型三:两个计数原理的综合应用 【典例例题】题型一:分类加法计数原理的应用例1.(2022·上海崇明·二模)某学校每天安排4项课后服务供学生自愿选择参加.学校规定: (1)每位学生每天最多选择1项;(2)每位学生每项一周最多选择1次.学校提供的安排表如下:数值表示) 【答案】14【解析】由题知:周一、二、三、四均可选阅读,体育在周一、三、四, 编程在周一、二、四.①若周一选编程,则体育在周三或周四,故为2种, 阅读在剩下的两天中选为2种,共有224⨯=种方案. ②若周二选编程,则体育在周一,周三或周四,故为3种, 阅读在剩下的两天中选为2种,共有326⨯=种方案. ③若周四选编程,则体育在周一或周三,故为2种, 阅读在剩下的两天中选为2种,共有224⨯=种方案. 综上,共有46414++=种方案. 故答案为:14例2.(2022·全国·高三专题练习)已知集合{}1,2,3M =-,{}4,5,6,7N =--,若从这两个集合中各取一个元素作为点的横坐标或纵坐标,则可得平面直角坐标系中第一、二象限内不同点的个数是( ) A .18 B .16C .14D .10【答案】C【解析】分两类情况讨论:第一类,从M 中取的元素作为横坐标,从N 中取的元素作为纵坐标,则第一、二象限内的点共有326⨯=(个);第二类,从M 中取的元素作为纵坐标,从N 中取的元素作为横坐标,则第一、二象限内的点共有248⨯=(个),由分类加法计数原理,所以所求个数为6814+=. 故选:C例3.(2022·全国·高三专题练习)在某种信息传输过程中,用4个数字的一个排列(允许数字重复)表示一个信息,不同排列表示不同信息,若所用数字只有0和1,则与信息0110至多有两个对应位置上的数字相同的信息个数为( ) A .10 B .11 C .12 D .7【答案】B【解析】与信息0110至多有两个对应位置上的数字相同的信息包括三类:①与信息0110只有两个对应位置上的数字相同,有24C 6=(个); ②与信息0110只有一个对应位置上的数字相同,有14C 4=(个);③与信息0110对应位置上的数字均不相同,有1个.综上,与信息0110至多有两个对应位置上的数字相同的信息有64111++=(个). 故选:B例4.(2022·全国·高三专题练习)现有5幅不同的油画,2幅不同的国画,7幅不同的水彩画,从这些画中选一幅布置房间,则不同的选法共有( ) A .7种 B .9种C .14种D .70种【答案】C 【解析】分为三类:从国画中选,有2种不同的选法;从油画中选,有5种不同的选法;从水彩画中选,有7种不同的选法,根据分类加法计数原理,共有5+2+7= 14(种)不同的选法; 故选:C例5.(2022·全国·高三专题练习)从数字1,2,3,4中取出3个数字(允许重复),组成三位数,各位数字之和等于6,则这样的三位数的个数为( ) A .7 B .9C .10D .13【答案】C【解析】其中各位数字之和等于6的三位数可分为以下情形: ①由1,1,4三个数字组成的三位数:114,141,411共3个;②由1,2,3三个数字组成的三位数:123,132,213,231,312,321共6个;③由2,2,2三个数字可以组成1个三位数,即222. ∴共有36110++=个,故选:C .例6.(2022·湖南·株洲市南方中学高三阶段练习)用标有1克,5克,10克的砝码各一个,在一架无刻度的天平上称量重物,如果天平两端均可放置砝码,那么可以称出的不同克数(正整数的重物)有多少种?( ) A .10 B .11C .12D .13【答案】A【解析】①当天平的一端放1个砝码,另一端不放砝码时,可以成量重物的克数有1克,5克,10克;②当天平的一端放2个砝码,另一端不放砝码时,可以成量重物的克数有156+=克,11011+=克,51015+=克;③当天平的一端放3个砝码,另一端不放砝码时,可以成量重物的克数有151016++=克 ④当天平的一端放1个砝码,另一端也放1个砝码时,可以成量重物的克数有514-=克,1019-=克,1055-=克;⑤当天平的一端放1个砝码,另一端也放2个砝码时,可以成量重物的克数有105114+-=克,10156+-=克,()10514-+=克;去掉重复的克数后,可称重物的克数有10种, 故选:A例7.(2022·上海嘉定·高三阶段练习)正整数484有个不同的正约数___________. 【答案】9【解析】22484221111211=⨯⨯⨯=⨯设d 为484的正约数,则211i j d =⨯,(i =0,1,2,j =0,1,2) 例如:0i =,0j =时,00211=11=1d =⨯⨯是484的约数,1i =,2j =时,12211=2121=242d =⨯⨯是484的约数,2i =,2j =时,22211=4121=484d =⨯⨯是484的约数,因此,484的正约数个数,即d 的不同取值个数,第一步确定i 的值,有3种可能,第二步确定j 的值,有3种可能,因此d 的取值共有339⨯=种. 故答案为:9.题型二:分步乘法计数原理的应用例8.(2022·云南·高三阶段练习)图中的矩形的个数为( )D .120【答案】C【解析】由题意,矩形的两条邻边确定,矩形就确定,第一步先确定“横边”, 从5个点任选2个点可以组成一条“横边”,共有25C 种情况;第二步再确定“竖边”,共有24C 种情况,所以图中矩形共有2254C C 10660⨯=⨯=.故选:C.例9.(2022·四川·树德怀远中学高三开学考试(理))从0,2中选一个数字,从1,3,5中选两个数字,组成无重复数字的三位数,其中偶数的个数为( ) A .24 B .18 C .12 D .6【答案】C【解析】根据题意,要使组成无重复数字的三位数为偶数,则从0,2中选一个数字为个位数,有2种可能,从1,3,5中选两个数字为十位数和百位数,有23A 326=⨯=种可能,故这个无重复数字的三位数为偶数的个数为2612⨯=. 故选:C .例10.(2022·福建·高三阶段练习)为了丰富学生的课余生活,某学校开设了篮球、书法、美术、吉他、舞蹈、击剑共六门活动课程,甲、乙、丙3名同学从中各自任选一门活动课程参加,则这3名学生所选活动课程不全相同的选法有( ) A .120种 B .150种 C .210种 D .216种【答案】C【解析】依题意,每名同学都有6种选择方法,所以这3名学生所选活动课程不全相同的选法有366210-=种. 故选:C例11.(2022·全国·高三专题练习)核糖核酸RNA 是存在于生物细胞以及部分病毒、类病毒中的遗传信息载体.参与形成RNA 的碱基有4种,分别用A ,C ,G ,U 表示.在一个RNA 分子中,各种碱基能够以任意次序出现,假设某一RNA 分子由100个碱基组成,则不同的RNA 分子的种数为( ) A .4100 B .1004 C .1002 D .104【答案】B【解析】每个碱基有4种可能,根据分步乘法计数原理,可得不同的RNA 分子的种数为1004.故A ,C ,D 错误.故选:B.例12.(2022·全国·高三专题练习)某大学食堂备有6种荤菜、5种素菜、3种汤,现要配成一荤一素一汤的套餐,则可以配成不同套餐的种数为( ) A .30 B .14 C .33 D .90【答案】D【解析】因为备有6种素菜,5种荤菜,3种汤,所以素菜有6种选法,荤菜有5种选法,汤菜有3种选法,所以要配成一荤一素一汤的套餐,则可以配制出不同的套餐有65390⨯⨯=种 故选:D题型三:两个计数原理的综合应用例13.(2022·江苏·南京市第一中学高三阶段练习)为了进一步提高广大市民的生态文明建设意识,某市规定每年4月25日为“创建文明城生态志愿行”为主题的生态活动日,现有5名同学参加志愿活动,需要携带勾子、铁锹、夹子三种劳动工具,要求每人都要携带一个工具,并且要求:带一个勾子,铁锹至少带2把,夹子至少带一个,则不同的安排方案共有( ) A .50种 B .60种 C .70种 D .80种【答案】A【解析】携带工具方案有两类:第一类,1个勾子,1个夹子,3把铁锹,所以携带工具的方案数有3252C A 20=种; 第二类,1个勾子,2个夹子,2把铁锹,所以携带工具的方案数有2253C C 30=种;所以不同的安排方案共有50种, 故选:A例14.(2022·重庆·高三阶段练习)用1,2,3…,9这九个数字组成的无重复数字的四位偶数中,各位数字之和为奇数的共有( ) A .600个 B .540个 C .480个 D .420个【答案】A【解析】依题意要使各位数字之和为奇数则可能是3个奇数1个偶数,或3个偶数1个奇数,若为3个奇数1个偶数,则偶数一定排在个位,从4个偶数中选一个排在个位有14C 4=种, 再在5个奇数中选出3个排在其余三个数位,有35A 60=种排法,故有1345C A 240=个数字;若为3个偶数1个奇数,则奇数不排在个位,从5个奇数中选一个排在前三位有1153C A 15=种, 再在4个偶数中选出3个排在其余三个数位,有34A 24=种排法,故有113534C A A 360=个数字;综上可得一共有240360600+=个数字; 故选:A例15.(2022·全国·高三专题练习)用0,1,2,3,4可以组成没有重复数字的四位偶数的个数为( ) A .36 B .48 C .60 D .72【答案】C【解析】当个位数为0时,有3424A =个,当个位数为2或4时,有1233236A A =个,所以无重复数字的四位偶数有24+36=60个, 故选:C.例16.(2022·全国·模拟预测)将6盆不同的花卉摆放成一排,其中A 、B 两盆花卉均摆放在C 花卉的同一侧,则不同的摆放种数为( ) A .360 B .480 C .600 D .720【答案】B【解析】分类讨论的方法解决如图中的6个位置,① 当C 在位置1时,不同的摆法有55A 120=种;② 当C 在位置2时,不同的摆法有1434C A 72=种; ③ 当C 在位置3时,不同的摆法有23232333A A A A 48+=种;由对称性知C 在4、5、6位置时摆放的种数和C 在3、2、1时相同, 故摆放种数有()21207248480⨯++=. 故选:B.例17.(2022·全国·高三专题练习)用数字0,1,2,3,4,5组成没有重复数字的四位数,其中个位、十位和百位上的数字之和为偶数的四位数共有___________.个(用数字作答). 【答案】144【解析】当个位、十位和百位上的数字为3个偶数的有:3133A C 18=种;当个位、十位和百位上的数字为1个偶数2个奇数的有:11231333312322C C 6C A C A C 12+=种,根据分类计数原理得到共有18126144+=个. 故答案为:144.例18.(2022·全国·高三专题练习)有四张卡片,正面和背面依次分别印有数字“1,0,2,4”和“3,5,0,7”,一小朋友把这四张卡片排成四位整数,则他能排出的四位整数的个数为_________. 【答案】264【解析】当四位整数中无0出现时,则必有5和2,其中1和3二选一,4和7二选一,四个数再进行全排列,故共有114224C C A 96=种选择;当四位整数中出现一个0时,可能是从5和0种选取的,也可能是从2和0种选择的,有12C 种,0可能的位置在个位,十位或百位,从3个位置选择一个,有13C 种,另外1和3二选一,4和7二选一,有12C 12C 种,加上另一个非0数,三个数进行全排列,有33A 种,故共有1111323223C C C C A 144=种选择;当四位整数中出现两个0时,两个0的位置有23C 种选择,另外1和3二选一,4和7二选一,有12C 12C 种,这两个数再进行全排列,有22A 种,共有23C 12C 12C 22A =24种,综上:96+144+24=264种选择 故答案为:264例19.(2022·全国·高三专题练习)有0,1,2,3,4,5六个数字. (1)能组成多少个无重复数字的四位偶数?(2)能组成多少个无重复数字且为5的倍数的四位数? (3)能组成多少个无重复数字且比1230大的四位数? 【解析】(1)由题意组成无重复数字的四位偶数分为三类: 第一类:0在个位时,有35A 个;第二类:2在个位时,首位从1,3,4,5中选定1个,有14A 种,十位和百位从余下的数字中选,有24A 种,共有1244A A ⋅个;第三类:4在个位时,与第二类同理,也有1244A A ⋅个,由分类加法计数原理知,共有3121254444A A A A A 156+⋅+⋅=个无重复数字的四位偶数.(2)组成无重复数字且为5的倍数的四位数分为两类: 个位上的数字是0时,满足条件的四位数有35A 个;个位数上的数字是5时,满足条件的四位数有1244A A ⋅个, 故满足条件的四位数有312544A A A 108+⋅=(个).(3)组成无重复数字且比1230大的四位数分为四类: 第一类:形如2□□□,3□□□,4□□□,5□□□,共1345A A ⋅个; 第二类:形如13□□,14□□,15□□,共有1234A A ⋅个; 第三类:形如124□,125□,共有1123A A ⋅个; 第四类:形如123□,共有12A 个.由分类加法计数原理知,共有13121114534232A A A A A A A 284⋅+⋅+⋅+=(个).【方法技巧与总结】要明确完成一件事所包含的内容是如何进行的,若需分类按加法数原理,若需分步按乘法计数原理.分类时要做到“不重不漏”,分步时要做到“步骤完整”.有些计数问题既需要分类,又需要分步,此时要综合运用两个原理.【过关测试】一、单选题 1.(2022·全国·高三专题练习)7个不同型号的行李箱上分别对应贴有不同的标签以作标记,其中恰有3个行李箱标签贴错的种数为( ) A .49 B .70 C .265 D .1854【答案】B【解析】第一步,从7个行李箱中挑选3个,有37C 种方法; 第二步,3个行李箱标签贴错的方法有2种,所以恰有3个行李箱标签贴错的种数为372C 70=.故选:B2.(2022·全国·高三专题练习)在一次运动会上有四项比赛的冠军在甲、乙、丙三人中产生,那么不同的夺冠情况共有( )种 A .34A B .34C .43D .43⨯【答案】C【解析】由题意四项比赛的冠军依次在甲、乙、丙三人中选取,每项冠军都有3种选取方法,由乘法原理共有433333⨯⨯⨯=种.故A ,B ,D 错误. 故选:C .3.(2022·全国·高三专题练习)将6封信投入4个邮筒,且6封信全部投完,不同的投法有( ) A .64种 B .46种C .4种D .24科【答案】A【解析】将6封信投入4个邮筒,且6封信全部投完,根据乘法原理共有64444444⨯⨯⨯⨯⨯=种 故选:A4.(2022·全国·高三专题练习)某学校推出了《植物栽培》《手工编织》《实用木工》《实用电工》4门校本劳动选修课程,要求每个学生从中任选2门进行学习,则甲、乙两名同学的选课中恰有一门课程相同的选法为( ) A .16 B .24C .12D .36【答案】B【解析】甲先从4门课程选择1门,有4种选法,乙再从剩下的3门中选择1门,有3种选法,甲乙再从剩下的2门中共同选择1门,有2种选法,所以根据分步乘法计数原理可得甲、乙两名同学的选课中恰有一门课程相同的选法为43224⨯⨯=种. 故选:B.5.(2022·全国·高三专题练习)某医院从7名男医生(含一名主任医师),6名女医生(含一名主任医师)中选派4名男医生和3名女医生支援抗疫工作,若要求选派的医生中有主任医师,则不同的选派方案数为( ) A .350 B .500 C .550 D .700【答案】C【解析】所选医生中只有一名男主任医师的选法有3365C C 200,所选医生中只有一名女主任医师的选法有4265C C 150, 所选医生中有一名女主任医师和一名男主任医师的选法有3265C C 200,故所选医师中有主任医师的选派方法共有200150200550种, 故选:C6.(2022·全国·高三专题练习)用数字0,1,2,3,4组成没有重复数字且比1000大的四位奇数共有( ) A .36个 B .48个 C .66个 D .72个【答案】A【解析】先排末位数,有1和3在末位两种选法,再排千位有3种选法,十位和百位从剩余的3个元素中选两个进行排列有23A 6=种结果, 所以由分步乘法计数原理知共有四位奇数23636⨯⨯=个, 故选:A7.(2022·全国·高三专题练习)“回文联”是对联中的一种,既可顺读,也可倒读.比如,一副描绘厦门鼓浪屿景色的回文联:雾锁山头山锁雾,天连水尾水连天.由此定义“回文数”,n 为自然数,且n 的各位数字反向排列所得自然数n '与n 相等,这样的n 称为“回文数”,如:1221,2413142.则所有5位数中是“回文数”且各位数字不全相同的共有( ) A .648个 B .720个C .810个D .891个【答案】D【解析】根据“回文数”的特点,只需确定前3位即可,最高位即万位有9种排法,千位和百位各有10种排法,根据分步乘法计数原理,共有91010900⨯⨯=种排法,其中各位数字相同的共有9种,则所有5位数中是“回文数”且各位数字不全相同的共有9009891-=种. 故选:D.8.(2022·全国·高三专题练习)已知正整数有序数对(),,,a b c d 满足: ①12a b c d +++=;②225a b -=.则满足条件的正整数有序数对(),,,a b c d 共有( )组. A .24 B .12 C .9 D .6【答案】B【解析】由题意知,a b c d ,,,为正整数,故由225a b -=可得()()5a b a b +-=,因为||1a b -≥ ,故||5a b +≤,则满足225a b -=的数为3和2,则有序数对(,)a b 可能为(3,2),(2,3) , 再由12a b c d +++=可得7c d += ,则(,)c d 的可能有(1,6),(6,1),(2,5),(5,2),(3,4),(4,3)共6种情况, 故满足条件的正整数有序数对(),,,a b c d 共有2612⨯=组, 故选:B9.(2022·全国·高三专题练习)古希腊哲学家毕达哥拉斯曾说过:“美的线型和其他一切美的形体都必须有对称形式.”在中华传统文化里,建筑、器物、书法、诗歌、对联、绘画几乎无不讲究对称之美.如图所示的是清代诗人黄柏权的《茶壶回文诗》,其以连环诗的形式展现,20个字绕着茶壶成一圆环,无论顺着读还是逆着读,皆成佳作.数学与生活也有许多奇妙的联系,如2020年02月02日(20200202)被称为世界完全对称日(公历纪年日期中数字左右完全对称的日期).数学上把20200202这样的对称数叫回文数,若两位数的回文数共有9个(11,22,…,99),则所有四位数的回文数中能被3整除的个数是( )A .27B .28C .29D .30【答案】D【解析】要能被3整除,则四个数的和是3的偶数倍数.满足条件的回文数分为以下几类: 和为6的回文数:1221,2112,3003, 3个.和为12的回文数:3333,2442,4224,1551,5115,6006, 6个.和为18的回文数:1881,8118,2772,7227,3663,6336,4554,5445,9009,9个.和为24的回文数:3993,9339,4884,8448,5775,7557,6666,7个. 和为30的回文数:7887,8778,6996,9669,4个. 和为36的回文数:9999,1个. 故共有3+6+9+7+4+1=30个. 故选:D 二、多选题10.(2022·全国·高三专题练习)用数字0、1、2、3、4、5组成没有重复数字的四位数,则下列说法正确的是( ) A .可组成360个不重复的四位数 B .可组成156个不重复的四位偶数 C .可组成96个能被3整除的不重复四位数D .若将组成的不重复的四位数按从小到大的顺序排成一个数列,则第85个数字为2310 【答案】BC【解析】A 选项,有1355300C A =个,错,B 选项,分为两类:0在末位,则有3560A =种,0不在末位,则有11224496C C A =种, ∴共有6096156+=种,对,C 选项,先把四个相加能被3整除的四个数从小到大列举出来,即先选:(0123),,,,(0135),,,、(0234),,,、(0345),,,、(1245),,,, 它们排列出来的数一定可以被3整除,∴共有:134334496C A A ⋅+=种,对,D 选项,首位为1的有3560A =个,前两位为20的有2412A =个,前两位为21的有2412A =个,此时共有60121284++=个,因而第85个数字是前两位为23的最小数,即为2301,错, 故选:BC.11.(2022·全国·高三专题练习)如图,标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点 A 向结点 B 传递消息,信息可以分开沿不同的路线同时传递,小圆圈表示网络的结点,结点之间的连线表示他们有网线相连,则单位时间内传递的信息量可以为( )A.18B.19C.24D.26【答案】AB【解析】第一条线路单位时间内传递的最大信息量为3;第二条线路单位时间内传递的最大信息量为4;第三条线路单位时间内传递的最大信息量为6;第四条线路单位时间内传递的最大信息量为6.+++=,因此该段网线单位时间内可以通过的最大信息量为346619故选:AB12.(2022·全国·高三专题练习)某校实行选课走班制度,张毅同学选择的是地理、生物、政治这三科,且生物在B层,该校周一上午选课走班的课程安排如下表所示,张毅选择三个科目的课各上一节,另外一节上自习,则下列说法正确的是()C.自习不可能安排在第2节D.自习可安排在4节课中的任一节【答案】BD【解析】由于生物在B层,只有第2,3节有,故分两类:若生物选第2节,则地理可选第1节或第3节,有2种选法,其他两节政治、自习任意选,⨯=种(此种情况自习可安排在第1、3、4节中的某节);故有224若生物选第3节,则地理只能选第1节,政治只能选第4节,自习只能选第2节,故有1种.+=种.根据分类加法计数原理可得选课方式有415综上,自习可安排在4节课中的任一节.故选:BD.三、填空题13.(2022·江苏·睢宁县菁华高级中学有限公司高三阶段练习)为丰富学生的校园生活,拓宽学生的视野,某学校为学生安排了丰富多彩的选修课,每学期每名同学可任选2门进行学习. 甲同学计划从A ,B ,C ,D ,E ,F ,G 这7门选修课中任选2门,其中至少从课程B ,D ,E 中选一门,则甲同学的选择方法有______种.【答案】15【解析】根据题意,分2种情况讨论:①、当甲从B ,D ,E 中选1门时,另一门需要在A 、C 、F 、G 中选出,有1134C C 12=种选法,②、当甲从B ,D ,E 中选2门时,有23C 3=种选法,则甲的选择方法有12315+=种, 故答案为:15.14.(2022·全国·高三专题练习)国庆放假期间,4号到7号安排甲乙丙三人值班,其中,乙和丙各值班1天,甲连续值班2天,则所有的安排方法共有________种. 【答案】6【解析】甲的安排方法有3种,即4,5两天值班或5,6两天值班或6,7两天值班,再安排乙与丙两人有22A 2=种安排方法,所以所有的安排方法共有6种.故答案为:615.(2022·全国·高三专题练习)有红、蓝、黄、绿四种颜色的球各6个,每种颜色的6个球分别标有数字1、2、3、4、5、6,从中任取3个标号不同的球,这3个颜色互不相同且所标数字互不相邻的取法种数为______. 【答案】96【解析】从1、2、3、4、5、6中任取3个标号不同且3个标号数字互不相邻的取法有:135、136、146、246,共4种;3个颜色互不相同的取法有:3343C A 24=种;所以满足题意的取法共有:42496⨯=种.故答案为:96.16.(2022·全国·高三专题练习)如图,一条电路从A 处到B 处接通时,可以有_____________条不同的线路(每条线路仅含一条通路).【答案】9【解析】依题意按上、中、下三条线路可分为三类,上线路中有2种,中线路中只有1种,下线路中有236⨯=(种).++=(种).根据分类计数原理,共有2169故答案为:9.。
计数原理知识点

计数原理知识点计数原理是数字电路中的重要基础知识,它涉及计数器、时序电路等概念。
在数字系统和计算机中,计数和计时是必不可少的功能。
本文将介绍一些计数原理的基本知识点。
1. 二进制计数系统二进制是一种计数系统,它由0和1两个数字组成。
在二进制计数系统中,每个数字位置上的权重是2的幂次方。
例如,二进制数1101表示的是1 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = 13。
2. 计数器计数器是一种用于计数的电路。
它可以根据输入信号的触发来递增或递减其计数值。
计数器通常由触发器和逻辑门构成。
•触发器是用于存储和传输信息的元件。
常见的触发器有D触发器、JK触发器等。
•逻辑门用于控制触发器的工作状态。
常见的逻辑门有与门、或门、非门等。
计数器可以实现多种计数模式,如二进制计数、BCD码计数、循环计数等。
3. 摩尔斯电码计数器摩尔斯电码计数器是一种特殊的计数器,它可以将输入的二进制码转换为摩尔斯电码。
摩尔斯电码是一种用于通信的编码方式,由点(.)和划(-)组成。
摩尔斯电码计数器通常由三个触发器和逻辑门构成。
根据输入的二进制码,计数器可以输出摩尔斯电码。
例如,输入二进制码1011,计数器可以输出摩尔斯电码. …. .-.. .-..。
4. 时序电路时序电路是一种根据时钟信号来控制时序行为的电路。
它通常由时钟、触发器和逻辑门构成。
时序电路可以实现复杂的计时和控制功能。
时序电路可用于实现各种计数器、计时器和状态机等。
它在数字系统和计算机中的应用广泛。
5. 时钟信号时钟信号是时序电路中的重要信号之一。
它用来控制触发器和逻辑门的状态变化。
时钟信号通常是一个周期性方波信号,其频率和占空比决定了电路的工作频率和时序特性。
时钟信号的频率越高,电路的响应速度越快;而占空比的变化可以用来控制电路的工作时间和空闲时间。
时钟信号的设计和优化对于实现高性能的时序电路至关重要。
总结计数原理是数字电路中的重要知识,它涉及二进制计数系统、计数器、摩尔斯电码计数器、时序电路等概念。
1.1.1,2,3计数原理

方法1:3*2[2*2+(2+1)]=42
变式一: 在编号为1,2,3,4的四块土地上分别试种编号为 1,2,3,4的四个品种的小麦,但1号地不能种1号小麦,2 号地不能种2号小麦,3号地不能种3号小麦, 4号地不 能种4号小麦,那么有多少种不同的试种方案? N=9
抽卡问题方法1:3*3=9 方法2:4*3*2*1-4*2(1种相同)-6(2种相同)-1(4种相同)=9
方法2: 3*2*2*2*2-3*2*1*1*1=42
变式二: 5人写贺卡后,重新抽卡,自己不能拿自 己写的卡,那么有多少种不同的抽卡方案?
N=44
抽卡问题方法:4*(2+3*3)=44
涂
色
问
题
作业1(03全国):一个地区分为5个行政区域, 现给地图着色,要求相邻区域不得使用同一颜 色,现有4种颜色可供选择,则不同的着色方 法有多少种?(以数字回答)
火车1 汽车1
甲
火车2 火车3
乙
汽车2
丙
解:
从甲地经乙地去丙地有2步, 第一步, 由甲地去乙地有3种方法, 第二步, 由乙地去丙地有2种方法, 所以 从甲地经 乙地去丙地共 3 ×2 = 6 种不同的方法。
字母
A
Байду номын сангаас
数字 得到的号码 A1 问题2.2: 用前6个 1 大写英文字母和 A2 2 1~9九个阿拉伯数 A3 字,以A1,A2,· · · , 3 B1,B2,· · · 的方式 A 4 4 给教室里的座位编 A5 5 号,总共能编出多 少个不同的号码? A 6 6
2010年夏季在南非举行的第十
九届世界杯足球赛共有32支队伍参 决出16强,这16强按确定的程序进 行淘汰赛后,最后决出冠亚军,此外
计数原理知识点

计数原理知识点计数原理是概率论中非常重要的一部分,它主要用于解决各种计数问题。
在实际生活中,我们经常会遇到需要计数的情况,比如排列组合、概率统计等。
掌握计数原理的知识,对于解决这些问题至关重要。
本文将从基本概念、排列组合、二项式定理和应用实例等方面介绍计数原理的相关知识点。
一、基本概念。
1.1 排列。
排列是指从给定的n个元素中取出m(m≤n)个元素,按照一定的顺序排成一列的方式。
排列通常用P(n,m)表示,计算公式为P(n,m) = n!/(n-m)!。
1.2 组合。
组合是指从给定的n个元素中取出m(m≤n)个元素,不考虑元素的顺序。
组合通常用C(n,m)表示,计算公式为C(n,m) = n!/(m!(n-m)!).1.3 二项式定理。
二项式定理是代数中的一个重要定理,它用于展开任意幂的二项式。
二项式定理的公式为(a+b)^n = C(n,0)a^n + C(n,1)a^(n-1)b + ... + C(n,n)b^n。
二、排列组合。
排列和组合是计数原理中的两个重要概念,它们在实际问题中经常被使用。
2.1 排列的应用。
排列常常用于解决有关顺序的问题,比如从一堆书中选出几本书按照一定的顺序排列,或者从一组人中选出几个人按照一定的顺序站成一排等。
2.2 组合的应用。
组合常常用于解决不考虑顺序的问题,比如从一组人中选出几个人组成一个团队,或者从一组水果中选出几种水果组成一个水果篮等。
三、二项式定理。
二项式定理是代数中的一个重要定理,它在计数原理中也有着重要的应用。
3.1 二项式定理的计数应用。
二项式定理可以用于计算任意幂的展开式,这在一些计数问题中非常有用。
比如,我们可以利用二项式定理来计算某个事件发生k次的概率,或者计算某个排列组合的可能性等。
3.2 二项式定理的实际案例。
在实际生活中,二项式定理也有着广泛的应用。
比如在赌博游戏中,我们可以利用二项式定理来计算各种可能的情况,从而制定合理的策略。
又如在概率统计中,我们可以利用二项式定理来计算各种事件发生的概率,从而做出科学的决策。
基本计数原理知识点总结

基本计数原理知识点总结1. 基本计数原理的概念基本计数原理是指:如果一个任务可以分解成若干个独立的步骤,每个步骤有n个选择,那么整个任务有n1 * n2 * ... * nk种可能的选择。
简单来说,就是如果有n1种方式完成任务A,n2种方式完成任务B,那么完成A和B的方式一共有n1 * n2种。
2. 基本计数原理的应用基本计数原理通常用于解决排列和组合问题。
排列是指从一组元素中按照一定的顺序取出若干个元素,组成一种特定的排列方式。
组合是指从一组元素中不考虑顺序地取出若干个元素,组成一种特定的组合方式。
基本计数原理能够帮助我们快速计算出排列和组合的可能性。
3. 基本计数原理的例题解析举个例子来说明基本计数原理的应用。
假设有一个珠子摆放在环形的项链上,这个项链有6个位置可以放置这个珠子。
那么总共有多少种放置这个珠子的可能性呢?根据基本计数原理,可以得到答案:6种。
因为首先可以选择任意一个位置放置这个珠子,然后再考虑不同位置之间的相对顺序,最终得到总共6种可能的放置方式。
4. 基本计数原理的推广在实际问题中,基本计数原理也可以通过多次使用来计算复杂的排列和组合的可能性。
比如,如果有一个3位数由0到9的数字组成,那么总共有多少种可能的排列呢?根据基本计数原理,可以分别计算出第一位、第二位和第三位的选择可能性,然后将它们相乘,就可以得到总共的排列可能性。
即10 * 10 * 10 = 1000种可能性。
5. 基本计数原理的局限性虽然基本计数原理在计算排列和组合问题中非常有用,但是在某些情况下可能并不适用。
比如,在一些相互依赖的情况下,无法简单地将不同步骤的选择可能性相乘来计算整体的可能性。
这时就需要使用更多的数学工具和技巧来解决问题。
总的来说,基本计数原理是解决排列和组合问题的基础,通过它能够很方便地计算出各种可能的排列和组合的数量。
在实际问题中,只要善于分解任务并且正确地应用基本计数原理,就能够迅速解决各种复杂的排列和组合问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计数原理基本知识点
1.分类计数原理:做一件事情 ,完成它可以有n 类办法 ,在第一类办法中有1m 种不同的方法 ,在第二类办法中有2m 种不同的方法 ,…… ,在第n 类办法中有n m 种不同的方法那么完成这件事共有 12n N m m m =+++种不同的方法
2.分步计数原理:做一件事情 ,完成它需要分成n 个步骤 ,做第一步有1m 种不同的方法 ,做第二步有2m 种不同的方法 ,…… ,做第n 步有n m 种不同的方法 ,那么完成这件事有12n N m m m =⨯⨯⨯ 种不同的方法
3.排列的概念:从n 个不同元素中 ,任取m (m n ≤)个元素(这里的被取元素各不相同)按照一定的顺序.....排成一列 ,叫做从n 个不同元素中取出m 个元素的一个排列....4.排列数的定义:从n 个不同元素中 ,任取m (m n ≤)个元素的所有排列的个数叫
做从n 个元素中取出m 元素的排列数 ,用符号m n A 表示
5.排列数公式:(1)(2)(1)m n A n n n n m =---+(,,m n N m n *∈≤)
6 阶乘:!n 表示正整数1到n 的连乘积 ,叫做n 的阶乘规定0!1=.
7.排列数的另一个计算公式:m n A =!()!n n m - 8 组合的概念:一般地 ,从n 个不同元素中取出m ()m n ≤个元素并成一组 ,叫做从n 个不同元素中取出m 个元素的一个组合
9.组合数的概念:从n 个不同元素中取出m ()m n ≤个元素的所有组合的个数 ,叫做从
n 个不同元素中取出m 个元素的组合数...
.用符号m n C 表示. 10.组合数公式:(1)(2)(1)!m m
n n
m m A n n n n m C A m ---+== 或)!
(!!m n m n C m n -=,,(n m N m n ≤∈*且 11 组合数的性质1:m n n m n C C -=.规定:10=n C ;
12.组合数的性质2:m n C 1+=m n C +1-m n C
1.二项式定理及其特例:
(1)01()()n n n r n r r n n n n n n a b C a C a b C a b C b n N -*+=++
+++∈ , (2)1(1)1n r r n n n x C x C x x +=+++++. 2.二项展开式的通项公式:1r n r r r n T C a b -+=
3.求常数项、有理项和系数最大的项时 ,要根据通项公式讨论对r 的限制;求有理项时要注意到指数及项数的整数性 4 二项式系数表(杨辉三角)
()n a b +展开式的二项式系数 ,当n 依次取1,2,3…时 ,二项式系数表 ,表中每行两端都是1 ,除1以外的每一个数都等于它肩上两个数的和
5.二项式系数的性质:
(1)对称性.与首末两端“等距离”的两个二项式系数相等(∵m n m n n C C -=).直线2
n
r =是图象的对称轴.
(2)增减性与最大值:当n 是偶数时 ,中间一项2n
n
C 取得最大值;当n 是奇数时 ,中间两项1
2n n C - ,1
2n n
C +取得最大值. (3)各二项式系数和:
∵1(1)1n r r n n n x C x C x x +=+++++ ,
令1x = ,则0122n r n n n n n n C C C C C =+++
+++
[特别提醒]
1. 在运用二项式定理时一定要牢记通项公式1r n r r r n T C a b -+= ,注意()n a b +与()n
b a +虽然相同 ,但具体到它们展开式的某一面时却是不相同的 ,所以我们一定要注意顺序问题。
另外
二项展开式的二项式系数与该项的(字母)系数是两个不同的概念 ,前者只是指r n C ,而后者
是指字母外的部分。
2.在使用通项公式1r n r r r n T C a b -+=时 ,要注意:
(1)通项公式是表示第r +1项 ,而不是第r 项.
(2)展开式中第r +1项的二项式系数C r
n 与第r +1项的系数不同.
(3)通项公式中含有a ,b ,n ,r ,T 1+r 五个元素 ,只要知道其中的四个元素 ,就可以求出第五个元素.在有关二项式定理的问题中 ,常常遇到已知这五个元素中的若干个 ,求另外几个元素的问题 ,这类问题一般是利用通项公式 ,把问题归纳为解方程(或方程组).这里必须注意n 是正整数 ,r 是非负整数且r ≤n .。
