长整数的进制转换
关于二进制、十进制、八进制、十六进制数据转换计算方法详细总结
在我们接触编程知识时,总会接触有关进制转换的知识,最常见的就是10进制与二进制或十六进制之间的转换,很多时候我们总会遗忘,虽然现在也出现了很多可以直接使用的网络在线的进制转换工具,但考试中,我们就要靠自己通过公式进行运算了。
今天就跟大家分享一下有关进制转换的理论知识,大家可以通过对比从里面发现共同点,这样便于我们理解记忆。
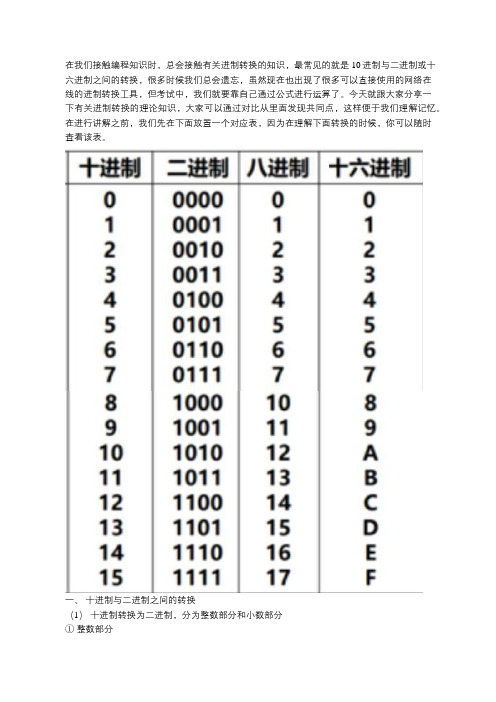
在进行讲解之前,我们先在下面放置一个对应表,因为在理解下面转换的时候,你可以随时查看该表。
一、十进制与二进制之间的转换(1)十进制转换为二进制,分为整数部分和小数部分①整数部分方法:除2取余法,即每次将整数部分除以2,余数为该位权上的数,而商继续除以2,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数读起,一直到最前面的一个余数。
下面举例:例:将十进制的168转换为二进制得出结果将十进制的168转换为二进制,(10101000)2分析:第一步,将168除以2商84余数为0。
第二步,将商84除以2,商42余数为0。
第三步,将商42除以2,商21余数为0。
第四步,将商21除以2,商10余数为1。
第五步,将商10除以2,商5余数为0。
第六步,将商5除以2,商2余数为1。
第七步,将商2除以2,商1余数为0。
第八步,将商1除以2,商0余数为1。
第九步,读数,因为最后一位是经过多次除以2才得到的,因此它是最高位,读数字从最后的余数向前读,即10101000②小数部分方法:乘2取整法,即将小数部分乘以2,然后取整数部分,剩下的小数部分继续乘以2,然后取整数部分,剩下的小数部分又乘以2,一直取到小数部分为零为止。
如果永远不能为零,就同十进制数的四舍五入一样,按照要求保留多少位小数时,就根据后面一位是0还是1,取舍,如果是零,舍掉,如果是1,向入一位。
换句话说就是0舍1入。
读数要从前面的整数读到后面的整数,下面举例:例1:将0.125换算为二进制得出结果:将0.125换算为二进制(0.001)2分析:第一步,将0.125乘以2,得0.25则整数部分为0小数部分为0.25;第二步将小数部分0.25乘以2得0.5则整数部分为0小数部分为0.5;第三步将小数部分0.5乘以2得1.0则整数部分为1小数部分为0.0;第四步读数从第一位读起读到最后一位即为0.001。
二进制八进制十进制十六进制之间的进制转换

二进制八进制十进制十六进制之间的进制转换详情可参考百度百科:进制转换这个词条【主要搞懂1和2两条,其他的进制之间的转化就迎刃而解,很好懂了】1. 十进制-> 二进制:将这个十进制数连续除以2的过程,第一步除以2,得到商和余数,将商再继续除以2,得到又一个商和余数,直到商为0。
最后将所有余数倒序排列,得到的数就是转换成二进制的结果。
2. 二进制-> 十进制:二进制数第1位的权值是2的0次方,第2位的权值是2的1次方,第3位的权值是2的2次方。
(例如1258这个十进制数,实际上代表的是:1x1000+2x100+5x10+8x1=1258)那么1011这个二进制数,实际上代表的是:1x8+0x4+1x2+1x1=11(十进制数11)。
(这里的8就是2的3次方,4就是2的2次方,2就是2的1次方,1就是2的0次方)3. 十进制-> 八进制:十进制数转换成八进制的方法,和转换为二进制的方法类似,唯一变化:除数由2变成8。
4. 八进制-> 十进制和转换为二进制的方法类似,唯一变化是,底数变成8,第1位表示8的0次方,第二位表示8的一次方,第三位表示8的2次方,第四位表示8的3次方。
例如1314这个八进制数,十进制数就是1x512+3x64+1x8+4x1=716(十进制)5. 十进制-> 十六进制10进制数转换成16进制的方法,和转换为2进制的方法类似,唯一变化:除数由2变成16。
十六进制是0123456789ABCDEF这十六个字符表示。
那么单独一个A就是10,单独一个B就是11,CDEF,就分表表示12,13,14,15。
而10这个十六进制数,实际就是十进制中的16。
6. 十六进制-> 十进制和转换为二进制的方法类似,唯一变化是,底数变成16,第1位表示16的0次方,第二位表示16的一次方,第三位表示16的2次方,第四位表示16的3次方。
7. 二进制<--->八进制,之间的相互转换,更简单一些,因为8本身是2的三次方。
整数的十进制、二进制、八进制、十六进制表示和转换方式

整数的十进制、二进制、八进制、十六进制表示和转换方式整数的不同进制表示方法是计算机科学中基本的知识之一。
在现代计算机中,二进制和十六进制是特别常用的进制,而八进制则进行很少的使用。
在本文中,我们将详细介绍整数的不同进制,以及如何在它们之间进行转换。
一、十进制表示十进制是我们常用的进制,它是使用十个数字 0 到 9 表示的。
以整数12345 为例,它在十进制下的表示方法为:12345(10)二、二进制表示在计算机中,二进制是计算机所使用的进制。
它仅使用 0 和 1 两个数字来表示。
以整数 12345 为例,它在二进制下的表示方法为:11000000111001(2)二进制转换为十进制时,将每个数位上的数乘以该数位所对应的 2 的幂次方,然后将乘积相加即可得到十进制结果。
二进制转换为十六进制时,将二进制数从右往左每 4 位分为一组,不足 4 位的高位补零,然后将每一组转换为一个十六进制数即可。
三、八进制表示八进制是由 0 到 7 这八个数字组成的一个进制。
在计算机科学中,它比较少被使用。
以整数 12345 为例,它在八进制下的表示方法为:30071(8)八进制转换为十进制时,将每个数位上的数乘以该数位所对应的 8 的幂次方,然后将乘积相加即可得到十进制结果。
八进制转换为十六进制时,将八进制数从右往左每 3 位分为一组,不足 3 位的高位补零,然后将每一组转换为一个十六进制数即可。
四、十六进制表示十六进制是由 0 到 9 这十个数字和 A 到 F 这六个字母共 16 个字符组成的进制。
在计算机科学中,它也是比较常用的进制之一。
以整数 12345 为例,它在十六进制下的表示方法为:3039(16)十六进制转换为十进制时,将每个数位上的数乘以该数位所对应的 16的幂次方,然后将乘积相加即可得到十进制结果。
十六进制转换为二进制时,将十六进制数每一位转换为 4 位的二进制数即可。
综上所述,整数的不同进制表示方法在计算机科学中是非常重要的。
进制的使用及转换

十六进制(英文名称:Hexadecimal),是计算机中数据的一种表示方法。
同我们日常生活中的表示法不一样。
它由0-9,A-F组成,字母不区分大小写。
与10进制的对应关系是:0-9对应0-9;A-F对应10-15;N进制的数可以用0~(N-1)的数表示,超过9的用字母A-F。
基本简介: 十六进制(英文名称:Hexadecimal),是计算机中数据的一种表示方法。
同我们日常生活中的表示法不一样。
它由0-9,A-F组成,字母不区分大小写。
与10进制的对应关系是:0-9对应0-9;A-F 对应10-15;N进制的数可以用0~(N-1)的数表示,超过9的用字母A-F。
表示方法: 十六进制照样采用位置计数法,位权是16为底的幂。
对于n位整数,m位小数的十六进制数用加权系数的形式表示如下:举例说明转换二进制转换十进制二进制数第0位的权值是2的0次方,第1位的权值是2的1次方……所以,设有一个二进制数:0,转换为10进制为:356用横式计算: 0×2+0×2+1×2+0×2+0×2+1×2+1×2+0×2+1×2=3560乘以多少都是0,所以我们也可以直接跳过值为0的位:1×2+1×2+1×2+1×2=3564+32+64+256 =356八进制转换十进制八进制就是逢8进1。
八进制数采用 0~7这八数来表达一个数。
八进制数第0位的权值为8的0次方,第1位权值为8的1次方,第2位权值为8的2次方……所以,设有一个八进制数:1507,转换为十进制为:839,具体方法如下:可以用横式直接计算: 7×8+0×8+5×8+1×8=839也可以用竖式表示: 第0位7×8^0=7第1位0×8^1=0第2位5×8^2=320第3位1×8^3=512十六进制转换十进制16进制就是逢16进1,但我们只有0~9这十个数字,所以我们用A,B,C,D,E,F这六个字母来分别表示10,11,12,13,14,15。
长整数的进制转换

*****大学信息与计算科学课程设计题目:长整数的进制转换成员:。
小组成员分工:(编程、调试程序)(编程、撰写报告)(编程、后期整理)一、实验目的1、熟练掌握C语言课程中所学的基本理论和基本方法;2、加强分析和解决问题的能力;3、加强同学们之间的团队合作经验;4、通过综合C语言的基本知识来解决实际问题。
二、题目要求题目:用一个整型数组表示一个长整数,数组的每个元素存储长整数的一位数字,则实际的长整数m表示为:m=a[k]×10k-1+a[k-1]×10k-2+….+a[2]×10+a[1]其中a[0]保存该长整数的位数。
要求:(1) 转换为16进制数输出;(2) 转换成8进制数输出。
三、算法设计1、长整数(1)由题目可知,用一个整型数组表示一个长整数,数组的每个元素存储长整数的一位数字,则实际的长整数m表示为:m=a[k]×10k-1+a[k-1]×10k-2+….+a[2]×10+a[1](2)长整数主程序:_int64 Num=0;for(i=1;i<=n;i++){Num+=a[n-i+1]* pow(10,i-1);}cout<<"输入的长整数为:";printf("%I64d",Num);cout<<endl;2、十进制转十六进制(1)十六进制:英文名称Hex number system,是计算机中数据的一种表示方法。
它由0-9,A-F组成,字母不区分大小写。
与10进制的对应关系是:0-9对应0-9;A-F对应10-15;N 进制的数可以用0---(N-1)的数表示超过9的用字母A-F。
采余数定理分解例:将十进制数487710 转成十六进制数487710÷16=30481....14(E)30481÷16=1905 (1)1905÷16=119 (1)119÷16=7 (7)7÷16=0 (7)结果:487710(10)=7711E(16)(2)十进制转换为十六进制主程序:void SixteenChange(_int64 num1){string aa[100];int y=0;while(num1!=0){int k=num1%16;num1/=16;if(k<10)aa[y]=k+48;else{switch(k){case 10:aa[y]='A';break;case 11:aa[y]='B';break;case 12:aa[y]='C';break;case 13:aa[y]='D';break;case 14:aa[y]='E';break;case 15:aa[y]='F';}}y++;}cout<<"十六进制数转化结果:";for(int z=y;z>=0;z--){cout<<aa[z];}cout<<endl;}(3)十进制转换为十六进制流程图:开始string aa[100];int y=0;num1!=0int k=num1%16; num1/=16;K是否大于10aa[y]=k+48 switch(k)case 10: case11: case 12: case 13: case 14: case 15: aa[y]='A'aa[y]='B’aa[y]='C'aa[y]='D'aa[y]='E'aa[y]='F'breaky++int z=yz-- z>=0 z输出结果aa[z]结束3、十进制化八进制(1)八进制:英文名称Octal,缩写OCT或O,是计算机中数据的一种表示方法。
无符号长整型常量

无符号长整型常量无符号长整型常量概述在C语言中,无符号长整型常量是一种特殊的数据类型,它表示一个没有符号位的长整数。
无符号长整型常量可以用十进制、八进制或十六进制表示。
定义无符号长整型常量的定义格式为:```U[unsigned]L[long][long] 常量值```其中,U表示无符号类型,L表示长整型类型。
如果需要更长的长度,则可以使用两个L。
例如:```123UL0xABCDEFUL0777ULL```上面三个例子分别表示十进制数123、十六进制数ABCDEF和八进制数777的无符号长整型常量。
注意事项1. 无符号长整型常量不带正负号,因此不能使用加减运算。
2. 如果一个有符号数和一个无符号数进行运算,则会将有符号数转换为无符号数进行计算。
3. 由于无符号长整型常量没有负数,因此它们的范围比有符号数据类型大一倍。
4. 在进行位运算时,需要注意位移操作可能会导致数据溢出。
示例代码下面是一些示例代码,演示了如何定义和使用无符号长整型常量:```c#include <stdio.h>int main(){unsigned long long num1 = 123456789ULL;unsigned long num2 = 123456789UL;unsigned int num3 = 0xABCDEFU;printf("%llu\n", num1);printf("%lu\n", num2);printf("%x\n", num3);return 0;}```输出结果为:```123456789123456789abcdef```结论无符号长整型常量是一种特殊的数据类型,它表示一个没有符号位的长整数。
它可以用十进制、八进制或十六进制表示。
在进行运算时需要注意数据类型转换和位移操作可能会导致数据溢出。
进制间的相互转化总结+例题

进制间的相互转化总结+例题进制转换:1. ⼗六进制与⼆进制相互转化 ⼗六进制的每⼀位占⼆进制中的四位,因此需要先定义⼗六进制从0~F的⼆进制值,即:string a[16] = {"0000", "0001", "0010", "0011", "0100", "0101", "0110","0111", "1000", "1001", "1010", "1011", "1100", "1101", "1110", "1111"};下标即⼗六进制数,再将每⼀个对应的⼆进制字符串拼起来就可以了。
如下例:2. ⼋进制与⼆进制相互转化 ⼆进制中的每三位对应⼋进制中的⼀位,因此也需要先对⼋进制中0~7定义其⼆进制值,即:string a[8] = {"000","001","010","011","100","101","110","111"};这样其下标就是⼋进制的值。
也可以⽤map定义,这样就可以直接根据字符串的值得到每⼀位⼋进制的值,再拼凑起来就可以了。
map<string,int> mp;mp["000"] = '0', mp["001"] = '1', mp["010"] = '2', mp["011"] = '3',mp["100"] = '4', mp["101"] = '5', mp["110"] = '6', mp["111"] = '7';3.⼆进制转⼗六进制 和⼆进制转⼋进制⼀样,只不过这⾥是每四位取⼀个⼗六进制,再拼起来就⾏了。
长整数的进制转换

长整数的进制转换在完成长整数的加减乘除运算时很麻烦,就是做通了也没拿满分。
才知道用重载的方法可以直接完成数组和整数间加减乘除运算。
结构体:用结构体内数组储存长整数,用结构体中的变量表示该整数的具体长度。
#include <iostream>/#include <cstring>/using namespace std;/struct hh{/结构体int n[200],l;/数组int n[200]储存长整形数}X;/整数l表示该长整数的确实位数加:这里考虑的是长整数+整数的情况。
当然了两个长整数也是可以解决的。
相对而言加是简单的,要考虑进位的事情,还有长整数长度的变化。
hh operator+(hh a,int y){/结构体和整数的加法a.n[1]+=y;/将该整数加到长整数的第一位int i=1;/从第一位开始while(a.n[i]>0||i<=a.l){/或者某位数大于0,或i小于等于长整数的长度都要循环a.n[i+1]+=a.n[i]/10;/将进位加到下一位a.n[i]%=10;/原位置留下个位i++;/准备算下一位}/a.l=i-1;/长整数的长度时i-1return a;/返回该长整数}/乘:加是只加到第一位就行,而乘是要乘到每一位上。
hh operator *(hh a,int y){/for(int i=1;i<=a.l;i++)a.n[i]*=y;/对每一位完成乘运算for(int i=1;i<=a.l;i++){/a.n[i+1]+=a.n[i]/10;/每一位大于10的部分加给下一位if(i==a.l&&a.n[i+1])a.l++;/如果是最后一位,而且下一位有内容,长度就得增加a.n[i]%=10;}/原位子留下个位数if(y==0)a.l=1;/如果和0乘的话,长整数位数变成1return a;/}/除:除得从最后一位算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
长整数的进制转换
发表时间:2018-08-22T13:44:33.280Z 来源:《教育学》2018年8月总第151期作者:贺小龙[导读] 在完成长整数的加减乘除运算时很麻烦,就是做通了也没拿满分。
才知道用重载的方法可以直接完成数组和整数间加减乘除运算。
新疆乌鲁木齐兵团一中830002 在完成长整数的加减乘除运算时很麻烦,就是做通了也没拿满分。
才知道用重载的方法可以直接完成数组和整数间加减乘除运算。
结构体:用结构体内数组储存长整数,用结构体中的变量表示该整数的具体长度。
#include <iostream>/
#include <cstring>/ using namespace std;/ struct hh{/结构体
int n[200],l;/数组int n[200]储存长整形数}X;/整数l表示该长整数的确实位数加:这里考虑的是长整数+整数的情况。
当然了两个长整数也是可以解决的。
相对而言加是简单的,要考虑进位的事情,还有长整数长度的变化。
hh operator+(hh a,int y){/结构体和整数的加法a.n[1]+=y;/将该整数加到长整数的第一位int i=1;/从第一位开始while(a.n[i]>0||i<=a.l){/或者某位数大于0,或i小于等于长整数的长度都要循环a.n[i+1]+=a.n[i]/10;/将进位加到下一位a.n[i]%=10;/原位置留下个位i++;/准备算下一位
}/
a.l=i-1;/长整数的长度时i-1 return a;/返回该长整数
}/
乘:加是只加到第一位就行,而乘是要乘到每一位上。
hh operator *(hh a,int y){/ for(int i=1;i<=a.l;i++)a.n[i]*=y;/对每一位完成乘运算for(int i=1;i<=a.l;i++){/ a.n[i+1]+=a.n[i]/10;/每一位大于10的部分加给下一位if(i==a.l&&a.n[i+1])a.l++;/如果是最后一位,而且下一位有内容,长度就得增加a.n[i]%=10;}/原位子留下个位数if(y==0)a.l=1;/如果和0乘的话,长整数位数变成1 return a;/
}/
除:除得从最后一位算。
如果数大于除数,就直接除,商是要得到的结果,余数乘10加到下一位;如果小,商就补零。
hh operator/(hh a,int y){/ int d=0,x;/
for(int i=a.l;i>=1;i--){/从最后一位遍历长整数x=d*10+a.n[i];/除数是余数乘以10加上该位if(x>=y){a.n[i]=x/y;d=x%y;x=0;}/如果被除数大于除数,该位留下商,余数要留着下次除时用。
else{d=x;a.n[i]=0;}/否则,该位留下零}/
while(a.n[a.l]==0&&a.l>1)a.l--;/如果最后一位是零,就要一直缩减。
很精妙return a;/
}/
求余数:求余数跟找商基本是一样的,只是要返回的是余数。
int operator %(hh a,int y){/ int d=0,x;/
for(int i=a.l;i>=1;i--){/也是从最后一位(也就是最左边的数字,高位)往前遍历x=d*10+a.n[i];/被除数是余数*10+当前位数if(x>=y){d=x%y;x=0;}/只有被除数大于除数,才可以除。
当然这里只需要余数,此时被除数要变成0。
else {d=x;a.n[i]=0;}/否则余数变成被除数}/
return d;/
}/
主程序:按照题意是要用逗号分开原进制,要转换进制的数和转换成的进制。
这里用文本记住所有信息,再分割开。
main(){/
int m;cin>>m;/共几组数据
for(int z=0;z<m;z++){/ string s;cin>>s;/将所有信息输入到字符串里int p=0,q=0,i;/P,q,记录原进制和变成的进制。
i记住位置for(i=0;s[i]!=’,’;i++)p=p*10+s[i]-’0’;/P原值乘10+下一位置的数字长整数变成十进制数当然内容是在逗号之间。
题意中说有0-9和A-Z,所以需要转换。
这里isdigit(char)用的好。
X=X*p+x,简直就精妙了。
这里当然是用上重载了,乘法和加法。
关键是这个算法,结果乘以进制+当前数就得到了。
for(++i;s[i]!=’,’;i++){/ int x;/ if(isdigit(s[i]))x=s[i]-’0’;/如果是数字就s[i]-’0’ else x=s[i]-’A’+10;/否则就是s[i]-’A’+10 X=X*p+x;/转换成十进制}/ 如果十进制是0就直接输出0,不用算了for(++i;s[i];i++)q=q*10+s[i]-’0’;/得到转换成的进制if(X.l==1 && X.n[1] == 0)/如果确定是0 { cout<<”0”<<endl; continue;}/就输出0。
考虑下一个。
Continue有意思,是放弃此次运算,直接进入下次循环。
for(int i=0;i<10;i++){/ if(i==5)continue;/当等于5时,就直接下个循环cout<<i<<endl;}/ 转换成q进制数string y;int j=0;/Y里放新数while(X.l!=1||X.n[1]!=0){/只要被除数没变成0就要循环char c;int x=X%q;/X是余数if(x>=0&&x<10)c=x+’0’;/转换成字符放进c里else c=x-10+’A’;/ y+=c;j++;/字符c再放进字符串y里X=X/q;/X本身要被q整除,逐渐变小}/ for(j=j-1;j>=0;j--)cout<<y[j];/从最后一位往前调cout<<endl;/ }/ }/。
