10 割补法巧算面积 练习(五上-同步)
割补法巧算面积
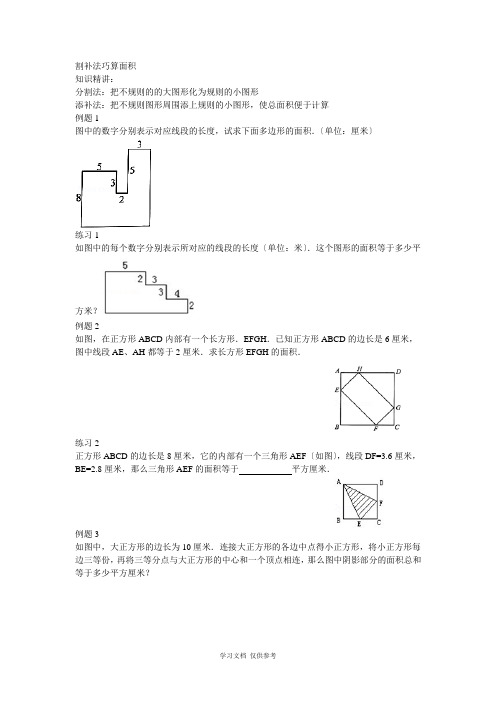
割补法巧算面积知识精讲:分割法:把不规则的的大图形化为规则的小图形添补法:把不规则图形周围添上规则的小图形,使总面积便于计算例题1图中的数字分别表示对应线段的长度,试求下面多边形的面积.〔单位:厘米〕练习1如图中的每个数字分别表示所对应的线段的长度〔单位:米〕.这个图形的面积等于多少平方米?例题2如图,在正方形ABCD内部有一个长方形.EFGH.已知正方形ABCD的边长是6厘米,图中线段AE、AH都等于2厘米.求长方形EFGH的面积.练习2正方形ABCD的边长是8厘米,它的内部有一个三角形AEF〔如图〕,线段DF=3.6厘米,BE=2.8厘米,那么三角形AEF的面积等于平方厘米.例题3如图中,大正方形的边长为10厘米.连接大正方形的各边中点得小正方形,将小正方形每边三等份,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影部分的面积总和等于多少平方厘米?练习3.1.如下图,正方形ABCD的边长acm,则图中阴影部分的面积为cm2.例题4. 如图1和图2,把两个相同的正三角形的各边分别五等分和七等分,并连接这些分点.已知图1中阴影部分的面积是294平方分米.请问:图2中的阴影部分的面积是多少平方分米?练习47.如下图,将三个相同的长方形从上到下排列,依次进行两等分、三等分、四等分,各取出其中的一份画上阴影,则阴影部分的面积占全部面积的几分之几?选做题例5 如图,在两个相同的等腰直角三角形中各作一个正方形,如果正方形A的面积是36平方厘米,那么正方形B的面积是多少平方厘米?例6.已知一个四边形ABCD的两条边的长度和三个角〔如下列图所示〕,求四边形ABCD的面积是多少?作业:1.如下图,平行四边形的面积是12,把一条对角线四等分,将四等分点与平行四边形另外两个顶点相连. 图中阴影部分的面积总和是多少?2. .〔2013秋•诸暨市校级期中〕如图,已知一个四边形的四条边AB,BC,CD和DA的长分别是3,4,13和12,其中∠B=90°,求这个四边形的面积3. 求阴影部分面积.4.求阴影部分面积.5. 求阴影部分面积:6.求阴影部分面积.7. 求阴影部分面积.8.〔2011秋•宁波期中〕求阴影部分的面积.9. 求阴影部分的面积.10. 求阴影部分的面积.11.求阴影部分的面积.12.求阴影部分的面积.。
小学奥数 几何 割补法求面积、等差法 知识点+例题+练习 (分类全面)

巩固.在直角三角形ABC中,四边形DECF为正方形,若AD=7,DB=8,则ΔADE与ΔBDF的面积之和是多少?AD EB CF巩固、如图所示,用一张斜边长为29厘米的红色直角三角形纸片、一张斜边长为50厘米的蓝色直角三角形纸片、一张黄色的正方形纸片,拼成一个直角三角形.红、蓝两张三角形纸片面积之和是多少?例2、五边形的三条边的长和四个角的度数,如下图所示,那么它的面积是多少?巩固.求下图(单位:厘米)中四边形ABCD的面积。
例3、如左下图所示,在一个等腰直角三角形中,削去一个三角形后,剩下一个上底长5厘米、下底长9厘米的等腰梯形(阴影部分)。
求这个梯形的面积。
巩固.在左下图所示的等腰直角三角形中,剪去一个三角形后,剩下的部分是一个直角梯形(阴影部分)。
已知梯形的面积为24平方厘米,上底为4厘米,求下底和高。
例4、在一个等边三角形中,两条与底边平行的线段将三角形的两条边等分成三段(见右图),求图中阴影部分的面积占整个图形面积的几分之几?巩固、如图,三个正方形的边长分别为8厘米、10厘米、6厘米拼在一起,求阴影部分的面积?巩固、下图是两块长方形草地,长方形的长是16,宽是10.中间有两条道路,一条是长方形,一条是平行四边形,那么有草部分的面积(阴影部分)分别有多大?等差法解题关键:找出组合图形的公共部分解题技巧:利用差不变原理进行等量代换:例1、如图ABCG是的长方形,AB=7,AG=4,DEFG是的长方形,GF=2,FE=10。
那么,三角形BCM的面积与三角形DEM面积之差是多少?巩固、如图ABCG是的长方形,AB=5,AG=3,DEFG是的长方形,GF=1,FE=9。
那么,三角形BCM的面积与三角形DEM面积之差是多少?例2、如图所示,平行四边形ABCD的边长BC长为8,直角三角形BCE的直角边CE长为6。
已知两块阴影部分的面积和比三角形EFG的面积大8,求CF的长度?巩固、如图,四边形BCEF是平行四边形,三角形ACB是直角三角形,BC的长是8厘米,AC长是7厘米。
小学巧求面积13题(辅助线法,割补法,代换法)
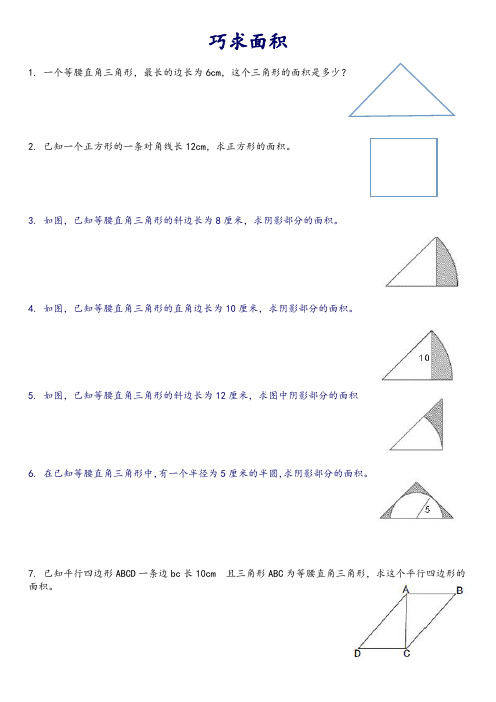
巧求面积
1. 一个等腰直角三角形,最长的边长为6cm,这个三角形的面积是多少?
2. 已知一个正方形的一条对角线长12cm,求正方形的面积。
3. 如图,已知等腰直角三角形的斜边长为8厘米,求阴影部分的面积。
4. 如图,已知等腰直角三角形的直角边长为10厘米,求阴影部分的面积。
5. 如图,已知等腰直角三角形的斜边长为12厘米,求图中阴影部分的面积
6. 在已知等腰直角三角形中,有一个半径为5厘米的半圆,求阴影部分的面积。
7. 已知平行四边形ABCD一条边bc长10cm 且三角形ABC为等腰直角三角形,求这个平行四边形的面积。
8. 求下列各图中阴影部分的面积:
9. 在一个等腰三角形中,两条与底边平行的线段将三角形的两条边等分成三段(见右图),求图中阴影部分的面积占整个图形面积的几分之几。
10. 下图中,甲、乙两个正方形的边长的和是20厘米,甲正方形比乙正方形
的面积大40厘米2。
求乙正方形的面积。
11. 正方形的面积是18.75平方厘米,在正方形内有两条与对角线平行的线段恰好
把正方形的面积分成3等份,求线段AB、CD的长。
12. 在四边形ABCD中,AC和BD互相垂直,AC=25厘米,BD=20厘米,求四边形的面积。
13. ABCD为等腰梯形,对角线AC和BD互相垂直,已知梯形有面积是40.5平方厘米,求梯形对角线的长度。
人教版五年级上册数学 割补法巧算面积专项训练

人教版五年级上册数学割补法巧算面积专项训练一.先割后补1:如图所示的四边形的面积等于多少?(单位:厘米)2:如图所示的四边形的面积等于多少?(单位:厘米)二.网格法1:如图由2个同样大小的等边三角形组合而成,每个大三角形的面积为6平方厘米,外围的6个小三角形均为形状大小相同的等边三角形,那么中间阴影部分的面积是多少平方厘米?2:两个正方形拼成如图所示的平面图形,已知大正方形的面积为64平方厘米。
请问:小正方形的面积是多少平方厘米?3:如图所示,三角形ABC是面积为20平方厘米的等腰直角三角形,D、E、F是三边的中点,请问:空白部分的面积是多少平方厘米?4:在一个等腰三角形中,两条与底边平行的线段将三角形的两条边等分成三段,如果这个等腰三角形的面积为9平方厘米,请问:图中阴影部分的面积是多少平方厘米?5:如图,把两个相同的正三角形的各边分别二等分和四等分,并连接这些等分点,已知左图中阴影部分的面积是100平方厘米,请问:右图中阴影部分的面积是多少平方厘米?6:把两个同样大小的正方形分别分成6×6和3×3的方格表,左图阴影部分的面积是400平方厘米,请问:右图中阴影部分的面积是多少平方厘米?7:两个正方形拼成如图所示的平面图形,已知大正方形的面积为36平方厘米,那么小正方形的面积是多少平方厘米?8. 如图,大正方形面积为10平方厘米,连接大正方形的各边中点得到一个小正方形,将小正方形每边三等分,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影部分的面积总和等于多少平方厘米?9. 把正三角形的每条边三等分,以各边的中间一段为边向外作小正三角形,得到一个六角形,再将这个六角形的六个“角”(即小正三角形)的两边三等分,又以它的中间段为边向外作更小的小正三角形,这样得到如图所示的图形。
如果所作的最小正三角形的面积为1平方厘米,请问:整个图形的面积是多少平方厘米?10.如图所示,大三角形的面积为20平方厘米,连接大正方形的各边中点得到小正三角形,将小正三角形如图三等分,那么图中阴影部分的面积总和等于多少平方厘米?11.把两个相同的正三角形的各边分别4等分和5等分,并连接这些等分点。
割补法巧算面积

割补法巧算面积割补法巧算面积知识精讲:分割法:把不规则的的大图形化为规则的小图形添补法:把不规则图形周围添上规则的小图形,使总面积便于计算例题1图中的数字分别表示对应线段的长度,试求下面多边形的面积.(单位:厘米)练习1如图中的每个数字分别表示所对应的线段的长度(单位:米).这个图形的面积等于多少平方米?例题2如图,在正方形ABCD内部有一个长方形.EFGH.已知正方形ABCD的边长是6厘米,图中线段AE、AH都等于2厘米.求长方形EFGH 的面积.例题4. 如图1和图2,把两个相同的正三角形的各边分别五等分和七等分,并连接这些分点.已知图1中阴影部分的面积是294平方分米.请问:图2中的阴影部分的面积是多少平方分米?练习47.如图所示,将三个相同的长方形从上到下排列,依次进行两等分、三等分、四等分,各取出其中的一份画上阴影,则阴影部分的面积占全部面积的几分之几?选做题例5 如图,在两个相同的等腰直角三角形中各作一个正方形,如果正方形A的面积是36平方厘米,那么正方形B的面积是多少平方厘米?例6.已知一个四边形ABCD的两条边的长度和三个角(如下图所示),求四边形ABCD的面积是多少?作业:1.如图所示,平行四边形的面积是12,把一条对角线四等分,将四等分点与平行四边形另外两个顶点相连. 图中阴影部分的面积总和是多少?2. .(2013秋•诸暨市校级期中)如图,已知一个四边形的四条边AB,BC,CD和DA的长分别是3,4,13和12,其中∠B=90°,求这个四边形的面积3. 求阴影部分面积.4.求阴影部分面积.5. 求阴影部分面积:6.求阴影部分面积.7. 求阴影部分面积.8.(2011秋•宁波期中)求阴影部分的面积.9. 求阴影部分的面积.10. 求阴影部分的面积.11.求阴影部分的面积.12.求阴影部分的面积.。
五年级奥数专题二十二:用割补法求面积

五年级奥数专题二十二:用割补法求面积关键词:三角正方图中面积题图奥数正方形三角形阴影图形在组合图形中,除了多边形外,还有由圆、扇形、弓形与三角形、矩形、平行四边形、梯形等图形组合而成的不规则图形,为了计算它们的面积,常常需要变动图形的位置或对图形进行分割、旋转、拼补,使它变成可以计算出面积的规则图形。
就是在多边形的组合图形中,为了计算面积,有时也要用到割补的方法。
例1求下列各图中阴影部分的面积:分析与解:(1)如左下图所示,将左下角的阴影部分分为两部分,然后按照右下图所示,将这两部分分别拼补在阴影位置。
可以看出,原题图的阴影部分等于右下图中AB 弧所形成的弓形,其面积等于扇形OAB与三角形OAB的面积之差。
π×4×4÷4-4×4÷2=4.56。
(2)在题图虚线分割的两个正方形中,右边正方形的阴影部分是半径为5的四分之一个圆,在左边正方形中空白部分是半径为5的四分之一个圆。
如下图所示,将右边的阴影部分平移到左边正方形中。
可以看出,原题图的阴影部分正好等于一个正方形的面积,为5×5=25。
例2在一个等腰三角形中,两条与底边平行的线段将三角形的两条边等分成三段(见右图),求图中阴影部分的面积占整个图形面积的几分之几。
分析与解:阴影部分是一个梯形。
我们用三种方法解答。
(1)割补法从顶点作底边上的高,得到两个相同的直角三角形。
将这两个直角三角(2)拼补法将两个这样的三角形拼成一个平行四边形(下页左上图)。
积和平行四边行面积同时除以2,商不变。
所以原题阴影部分占整个图形面(3)等分法将原图等分成9个小三角形(见右上图),阴影部分占3个小三角形,注意,后两种方法对任意三角形都适用。
也就是说,将例题中的等腰三角形换成任意三角形,其它条件不变,结论仍然成立。
例3如左下图所示,在一个等腰直角三角形中,削去一个三角形后,剩下一个上底长5厘米、下底长9厘米的等腰梯形(阴影部分)。
五年级割补求面积问题

五年级奥数用割补法求面积在组合图形中,除了多边形外,还有由圆、扇形、弓形与三角形、矩形、平行四边形、梯形等图形组合而成的不规则图形,为了计算它们的面积,常常需要变动图形的位置或对图形进行分割、旋转、拼补,使它变成可以计算出面积的规则图形。
就是在多边形的组合图形中,为了计算面积,有时也要用到割补的方法。
例1求下列各图中阴影部分的面积:分析与解:(1)如左下图所示,将左下角的阴影部分分为两部分,然后按照右下图所示,将这两部分分别拼补在阴影位置。
可以看出,原题图的阴影部分等于右下图中AB弧所形成的弓形,其面积等于扇形OAB与三角形OAB的面积之差。
π×4×4÷4-4×4÷2=4.56。
(2)在题图虚线分割的两个正方形中,右边正方形的阴影部分是半径为5的四分之一个圆,在左边正方形中空白部分是半径为5的四分之一个圆。
如下图所示,将右边的阴影部分平移到左边正方形中。
可以看出,原题图的阴影部分正好等于一个正方形的面积,为5×5=25。
例2在一个等腰三角形中,两条与底边平行的线段将三角形的两条边等分成三段(见右图),求图中阴影部分的面积占整个图形面积的几分之几。
分析与解:阴影部分是一个梯形。
我们用三种方法解答。
(1)割补法从顶点作底边上的高,得到两个相同的直角三角形。
将这两个直角三角(2)拼补法将两个这样的三角形拼成一个平行四边形(下页左上图)。
积和平行四边行面积同时除以2,商不变。
所以原题阴影部分占整个图形面(3)等分法将原图等分成9个小三角形(见右上图),阴影部分占3个小三角形,注意,后两种方法对任意三角形都适用。
也就是说,将例题中的等腰三角形换成任意三角形,其它条件不变,结论仍然成立。
例3如左下图所示,在一个等腰直角三角形中,削去一个三角形后,剩下一个上底长5厘米、下底长9厘米的等腰梯形(阴影部分)。
求这个梯形的面积。
分析与解:因为不知道梯形的高,所以不能直接求出梯形的面积。
五年级数学上册拓展. 出入相补法-割补法求图形面积

平行四边形的面积= 底
×高=== Nhomakorabea梯形的面积(= 上底+下底) ×(高÷2)
=
=
=
长方形的面积= 长 × 宽
梯形的面积(= 上底+下底) ×(高÷2)
梯形的面积=(上底+下底)×高➗2
出入相补原理
出入相补原理就 是把一个图形分割、移 补,而面积保持不变, 来计算它的面积。
世界十大数学家之 一、被称作“中国 数学史上的牛顿” 的山东人刘徽
割补法 倍拼法 倍拼法
用割补法把三角形转化成长方形或平行四边形,试一试。
= =
=
= = =
长方形的面积 = 长 × 宽 平行四边形的面积 = 底 × 高
三角形的面积 = 底 ×(高÷2) 三角形的 面积 = 底 ×(高÷2)
倍拼法
割补法
三角形的面积=底×高÷2
三角形的面积=底×(高÷2)
三角形的面积=底×高÷2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
割补法巧算面积
主讲:红豆
【练习1】如图,在两个相同的等腰直角三角形中各作一个正方形,如果三角形A的面积是16平方厘米,那么三角形B的面积是多少平方厘米?
A B
【练习2】如图所示,正六边形ABCDEF的面积是36平方厘米,M、N、P、Q、R、S分别是AB、BC、CD、DE、EF、FA的中点。
请问:阴影正六边形的MNPQRS的面积是多少平方厘米?
【练习3】如图所示,大正方形的边长为10厘米。
连接大正方形的各边中点得到一个小正方形,再连接大正方形的两条对角线。
请问:图中阴影部分的面积总和等于多少平方厘米?
【练习4】如图所示,正六边形ABCDEF的面积是36。
请问:阴影正六边形的面积是多少?
【练习5】如图所示,平行四边形的面积是12,把一条对角线四等分,将四等分点与平行四边形另外两个顶点相连。
请问:图中阴影部分的面积总和是多少?。
