初二数学-反比例函数难题拓展(学生版)
初二数学-反比例函数难题拓展(学生版).doc
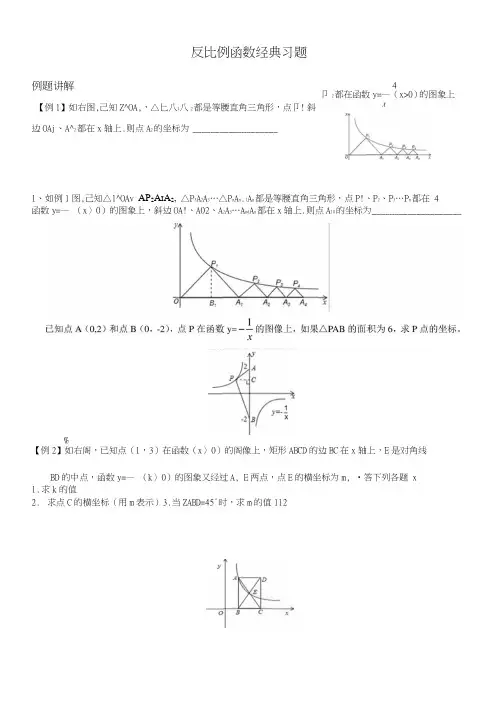
反比例函数经典习题例题讲解【例1】如右图,己知Z^OA,，△匕八|八2都是等腰直角三角形，点卩! 斜边OAj 、A^2都在x 轴上.则点A 2的坐标为 ___________________ 1、如例1图,己知△l^OAv AP 2A I A 2, △P 3A 2A 3…△P n A n .1A n 都是等腰直角三角形，点P!、P 2、P 3…P n 都在 4 函数y=— （x 〉0）的图象上，斜边OA!、A02、A 2A 3…A nd A n 都在x 轴上.则点A 10的坐标为 ____________________%【例2】如右阁，已知点（1，3）在函数（x 〉0）的阁像上，矩形ABCD 的边BC 在x 轴上，E 是对角线BD 的中点，函数y=— （k 〉0）的图象又经过A, E 两点，点E 的横坐标为m, •答下列各题 x1. 求k 的值2. 求点C 的横坐标（用m 表示）3.当ZABD=45°时，求m 的值1124 卩2都在函数y=— （x>0）的图象上， x21、已知：如图，矩形ABCD的边BC在x轴上，E是对角线AC、BD的交点，反比例函数y= —（x〉0）的图 x 象经过A, E两点，点E的纵坐标为m.（1）求点A坐标（用m表示）2、如图1,矩形ABCD的边BC在x轴的正半轴上，点E （m, 1）是对角线BD的中点,点A、E在反比例函数的阉象上.（1）求AB的长；b k（2）当矩形ABCD是正方形时，将反比例函数—的图象沿y轴翻折，得到反比例函数y= 2的图象（如图2），求卜的值；（3）直线y=-x上有一长为^动线段MN,作MH、NP都平行y轴交在条件（2）下，第一象限A的双曲线ky=—于点H、P,问四边形MHPN能否为平行四边形（如阁3） ?若能，请求出点M的坐标；若不能，请说明 x理由.【例3】在平面直角坐标系中，已知A（1，0），B（0，1）,矩形OMPN的相邻两边OM, ON分别在x, y轴的正半轴上，O为原点，线段AB与矩形OMPN的两边MRNP的交点分别为E,F,AAOF^ ABOE （顶点依次对应）（1）求ZFOE;（2）求证：矩形OPMN的顶点P必在某个反比例函数图像上，并写出该函数的解析式。
反比例函数经典拓展难题
反比例函数难题拓展填空题1. （2011浙江金华，16，4分）如图，将一块直角三角板OAB 放在平面直角坐标系中，B （2，0），∠AOC ＝60°，点A 在第一象限，过点A 的双曲线为y= kx ，在x 轴上取一点P ，过点P作直线OA 的垂线l ，以直线l 为对称轴，线段OB 经轴对称变换后的像是O ′B ′. （1）当点O ′与点A 重合时，点P 的坐标是.（2）设P （t ，0）当O ′B ′与双曲线有交点时，t 的取值范围是 .2. （2011广东东莞，6，4分）已知反比例函数ky x=的图象经过（1，－2）．则k = ． 3. （2011山东滨州，18，4分）若点A(m ，－2)在反比例函数4y x=的图像上，则当函数值y ≥－2时，自变量x 的取值范围是___________. 4. （2011四川南充市，14，3分）过反比例函数y=xk(k ≠0)图象上一点A ，分别作x 轴，y 轴的垂线，垂足分别为B,C ，如果⊿ABC 的面积为3.则k 的值为 .5. （2011宁波市，18，3分）如图，正方形A 1B 1P 1P 2的顶点P 1、P 2在反比例函数y ＝2x （x ＞0）的图像上，顶点A 1、B 1分别在x 轴和y 轴的正半轴上，再在其右侧作正方形P 2P 3A 2B 2，顶点P 3在反比例函数y ＝2x（x ＞0）的图象上，顶点A 3在x 轴的正半轴上，则点P 3的坐标为6. （2011浙江衢州,5,4分）在直角坐标系中，有如图所示的t ,R ABO AB x ∆⊥轴于点B ，斜35=(0)ky xx=>的图像经过AO的中点C，且与AB交于的坐标为 .7. (2011浙江绍兴，13，5分) 若点12(1,),(2,)A yB y是双曲线3yx=上的点，则1y2y（填“>”,“<”“=”）.8. （2011浙江丽水，16，4分）如图，将一块直角三角板OAB放在平面直角坐标系中，B(2，0)，∠AOC＝60°，点A在第一象限，过点A的双曲线为y=kx，在x轴上取一点P，过点P 作直线OA的垂线l，以直线l为对称轴，线段OB经轴对称变换后的像是O′B′.（1）当点O′与点A重合时，点P的坐标是.（2）设P(t，0)当O′B′与双曲线有交点时，t的取值范围是 .9. （2011湖南常德，5，3分）如图1所示的曲线是一个反比例函数图象的一支，点A在此曲线上，则该反比例函数的解析式为_______________.10．（2011江苏苏州，18,3分）如图，已知点A的坐标为（3，3），AB⊥x轴，垂足为B，（第15题）xyCDBOIy1OAx3图1连接OA ，反比例函数y=xk（k>0）的图象与线段OA 、AB 分别交于点C 、D.若AB=3BD ，以点C 为圆心，CA 的45倍的长为半径作圆，则该圆与x 轴的位置关系是___________（填“相离”、“相切”或“相交”）11. （2011山东济宁，11，3分）反比例函数1m y x-=的图象在第一、三象限，则m 的取值范围是 ．12. （2011四川成都，25,4分）在平面直角坐标系xOy 中，已知反比例函数2(0)ky k x=≠满足：当0x <时，y 随x 的增大而减小．若该反比例函数的图象与直线3y x k =-+都经过点P ，且7OP =，则实数k=_________.13. （2011安徽芜湖，15，5分）如图，在平面直角坐标系中有一正方形AOBC ，反比例函数ky x=经过正方形AOBC 对角线的交点，半径为（422-）的圆内切于△ABC ，则k 的值为 ．14. （2011广东省，6，4分）已知反比例函数ky x=的图象经过（1，－2）．则k = ． 15. (2011江苏南京，15，2分)设函数2y x =与1y x =-的图象的交战坐标为（a ，b ），则11a b-的值为__________．16. （2011上海，11，4分）如果反比例函数k yx=（k是常数，k≠0）的图像经过点(－1，2)，那么这个函数的解析式是__________．17. （2011湖北武汉市，16，3分）如图，□ABCD的顶点A，B的坐标分别是A（－1，0），B（0，－2），顶点C，D在双曲线y=xk上，边AD交y轴于点E，且四边形BCDE的面积是△ABE 面积的5倍，则k=_____．18. （2011湖北黄冈，4，3分）如图：点A在双曲线kyx=上，AB⊥x轴于B，且△AOB的面积S△AOB=2，则k=______．19. （2011湖北黄石，15，3分）若一次函数y=kx+1的图象与反比例函数y=x1的图象没有公共点，则实数k的取值范围是。
中考数学专题复习《反比例函数》拓展题(含答案)
《反比例函数》拓展题(含答案)知识点回顾由于反比例函数解析式及图象的特殊性，很多中考试题都将反比例函数与面积结合起来进行考察。
这种考察方式既能考查函数、反比例函数本身的基础知识内容，又能充分体现数形结合的思想方法，考查的题型广泛，考查方法灵活，可以较好地将知识与能力融合在一起。
下面就反比例函数中与面积有关的问题的四种类型归纳如下：一、利用反比例函数中|k|的几何意义求解与面积有关的问题设P为双曲线上任意一点，过点P作x轴、y轴的垂线PM、PN，垂足分别为M、N，则两垂线段与坐标轴所围成的的矩形PMON的面积为S=|PM|×|PN|=|y|×|x|=|xy|∴xy=k 故S=|k| 从而得结论1：过双曲线上任意一点作x轴、y轴的垂线，所得矩形的面积S为定值|k| 对于下列三个图形中的情形，利用三角形面积的计算方法和图形的对称性以及上述结论，可得出对应的面积的结论为：结论2：在直角三角形ABO中，面积S=结论3：在直角三角形ACB中，面积为S=2|k|结论4：在三角形AMB中，面积为S=|k|例题讲解【例1】如右图，已知△P10A1，△P2A1A2都是等腰直角三角形，点P1、P2都在函数y=4x（x＞0）的图象上，斜边OA1、A1A2都在x轴上．则点A2的坐标为 .1、如例1图，已知△P1OA1，△P2A1A2，△P3A2A3…△P n A n-1A n都是等腰直角三角形，点P1、P2、P3…P n都在函数y=4x（x＞0）的图象上，斜边OA1、A1A2、A2A3…A n-1A n都在x轴上．则点A10的坐标为2、已知点A（0,2）和点B（0，-2），点P在函数y=1x的图像上，如果△PAB的面积为6，求P点的坐标。
【例2】如右图，已知点（1,3）在函数y=kx（x＞0）的图像上，矩形ABCD的边BC在x轴上，E是对角线BD的中点，函数y=kx（k＞0）的图象又经过A,E两点，点E的横坐标为m，解答下列各题1.求k的值2.求点C的横坐标（用m表示）3.当∠ABD=45°时，求m的值1121、已知：如图，矩形ABCD的边BC在x轴上，E是对角线AC、BD的交点，反比例函数y=2 x（x＞0）的图象经过A，E两点，点E的纵坐标为m．（1）求点A坐标（用m表示）（2）是否存在实数m，使四边形ABCD为正方形，若存在，请求出m的值；若不存在，请说明理由2、如图1，矩形ABCD的边BC在x轴的正半轴上，点E（m，1）是对角线BD的中点，点A、E在反比例函数y=kx的图象上．（1）求AB的长；（2）当矩形ABCD是正方形时，将反比例函数y=kx的图象沿y轴翻折，得到反比例函数y=1kx的图象（如图2），求k1的值；（3）直线y=-x上有一长为2动线段MN，作MH、NP都平行y轴交在条件（2）下，第一象限内的双曲线y=kx于点H、P，问四边形MHPN能否为平行四边形（如图3）？若能，请求出点M的坐标；若不能，请说明理由．【例3】在平面直角坐标系中，已知A(1,0),B(0,1)，矩形OMPN的相邻两边OM，ON分别在x，y轴的正半轴上，O为原点，线段AB与矩形OMPN的两边MP,NP的交点分别为E,F,△AOF∽△BOE（顶点依次对应）（1）求∠FOE；（2）求证：矩形OPMN的顶点P必在某个反比例函数图像上，并写出该函数的解析式。
初二数学人教版(下册)反比例函数典型例题汇总(附答案)
例 下面函数中，哪些是反比例函数？ （1）3x y -=；（2）x y 8-=；（3）54-=x y ；（4）15-=x y ；（5）.81=xy 解：其中反比例函数有（2），（4），（5）．说明：判断函数是反比例函数，依据反比例函数定义，xky =)0(≠k ，它也可变形为1-=kx y 及k xy =的形式，（4），（5）就是这两种形式．反比例函数的典型例题二例 在以下各小题后面的括号里填写正确的记号．若这个小题成正比例关系，填(正)；若成反比例关系，填(反)；若既不成正比例关系又不成反比例关系，填(非)．(1)周长为定值的长方形的长与宽的关系 （ ）； (2)面积为定值时长方形的长与宽的关系 （ ）； (3)圆面积与半径的关系 （ ）； (4)圆面积与半径平方的关系 （ ）；(5)三角形底边一定时，面积与高的关系 （ ）； (6)三角形面积一定时，底边与高的关系 （ ）；(7)三角形面积一定且一条边长一定，另两边的关系 （ ）； (8)在圆中弦长与弦心距的关系 （ ）；(9)x 越来越大时，y 越来越小，y 与x 的关系 （ ）； (10)在圆中弧长与此弧所对的圆心角的关系 （ ）． 答：说明：本题考查了正比例函数和反比例函数的定义，关键是一定要弄清出二者的定义．例 已知反比例函数62)2(--=a xa y ，y 随x 增大而减小，求a 的值及解析式．分析 根据反比例函数的定义及性质来解此题． 解 因为62)2(--=ax a y 是反比例函数，且y 随x 的增大而减小，所以⎩⎨⎧>--=-.02,162a a 解得⎩⎨⎧>±=.2,5a a所以5=a ，解析式为xy 25-=．反比例函数的典型例题四例 （1）若函数22)1(--=mx m y 是反比例函数，则m 的值等于（ ）A ．±1B ．1C ．3D ．－1（2）如图所示正比例函数0(>=k kx y ）与反比例函数xy 1=的图像相交于A 、C 两点，过A 作x 轴的垂线交x 轴于B ，连结BC ．若ABC ∆的面积为S ，则：A ．1=SB ．2=SC ．3=SD ．S 的值不确定解：（1）依题意，得⎩⎨⎧-=-≠-,12,012m m 解得1-=m ．故应选D ． （2）由双曲线x y 1=关于O 点的中心对称性，可知：O BC O BA S S ∆∆=． ∴12122=⋅=⨯⨯==∆AB OB AB OB S S OBA ．故应选A ．例 已知21y y y +=，1y 与x 成正比例，2y 与x 成反比例，当1=x 时，4=y ；当3=x 时，5=y ，求1-=x 时，y 的值．分析 先求出y 与x 之间的关系式，再求1-=x 时，y 的值．解 因为1y 与x 成正比例，2y 与x 成反比例，所以)0(,212211≠==k k xk y x k y ． 所以xkx k y y y 2121+=+=．将1=x ，4=y ；3=x ，5=y 代入，得⎪⎩⎪⎨⎧=+=+.5313,42121k k k k 解得 ⎪⎪⎩⎪⎪⎨⎧==.821,81121k k 所以xx y 821811+=． 所以当1-=x 时，4821811-=--=y ． 说明 不可草率地将21k k 、都写成k 而导致错误，题中给出了两对数值，决定了21k k 、的值．反比例函数的典型例题六例 根据下列表格x 与y x …… 1 2 3 456 …y…6 3 2 1.5 1.2 1 …（1x 的取值范围． 解：（1）图像如右图所示． （2）根据图像，设)0(≠=k xky ，取6,1==y x 代入，得16k=． ∴6=k ．∴函数解析式为)0(6>=x xy ． 说明：本例考查了函数的三种表示法之间的变换能力，即先由列表法通过描点画图转化为图像法，再由图像法通过待定系数法转化为解析法，题目新颖别致，有较强的趣味性．反比例函数的典型例题七例（1）一次函数1+-=x y 与反比例函数xy 3=在同一坐标系中的图像大致是如图中的（ ）（2）一次函数12--=k kx y 与反比例函数xky =在同一直角坐标系内的图像的大致位置是图中的（ ）解：1+-=x y 的图像经过第一、二、四象限，故排除B 、C ；又xy 3=的图像两支在第一、三象限，故排除D ．∴答案应选A ．（2）若0>k ，则直线)1(2+-=k kx y 经过第一、三、四象限，双曲线xky =的图像两支在第一、三象限，而选择支A 、B 、C 、D 中没有一个相符；若0<k ，则直线)1(2+-=k kx y 经过第二、三、四象限，而双曲线的两支在第二、四象限，故只有C 正确．应选C ．例 已知函数24231-⎪⎭⎫ ⎝⎛+=mx m y 是反比例函数，且其函数图像在每一个象限内，y 随x 的增大而减小，求反比例函数的解析式．解：因为y 是x 的反比例函数，所以1242-=-m ，所以21=m 或.21-=m 因为此函数图像在每一象限内，y 随x 的增大而减小，所以031>+m ，所以31->m ，所以21=m ，所以反比例函数的解析式为.65xy = 说明：此题根据反比例函数的定义与性质来解反比例函数xky = )0(≠k ，当0>k 时，y 随x 增大而减小，当0<k 时，y 随x 增大而增大．例 一个长方体的体积是100立方厘米，它的长是y 厘米，宽是5厘米，高是x 厘米． （1）写出用高表示长的函数关系式； （2）写出自变量x 的取值范围； （3）当3=x 厘米时，求y 的值； （4）画出函数的图像．分析 本题依据长方体的体积公式列出方程，然后变形求出长关于高的函数关系式． 解 （1）因为长方体的长为y 厘米，宽为5厘米，高为x 厘米， 所以1005=xy ，所以xy 20=． （2）因为x 是长方体的高．所以0>x ．即自变量x 的取值范围是0>x ． （3）当3=x 时，326320==y （厘米） （4x … 0.525 1015…y … 40 10 4 2 311 …描点画图如图所示．例 已知力F 所作用的功是15焦，则力F 与物体在力的方向通过的距离S 的图象大致是（ ）．说明 本题涉及力学中作功问题，主要考查在力的作用下物体作功情况，由此，识别正、反比例函数，一次函数的图象位置关系．解 据S F W ⋅=，得15=S F ⋅，即SF 15=，所以F 与S 之间是反比例函数关系，故选（B ）．例 一个圆台形物体的上底面积是下底面积的.32如果如下图所示放在桌上，对桌面的压强是Pa 200，翻过来放，对桌面的压强是多少？解：由物理知识可知，压力F ，压强p 与受力面积S 之间的关系是.SFp =因为是同一物体，F 的数值不变，所以p 与S 成反比例． 设下底面是0S ，则由上底面积是032S ， 由SFp =，且0S S =时，200=p ， 有.20020000S S pS F =⨯==因为是同一物体，所以0200S F =是定值．所以当032S S =时，).Pa (3003220000===S S SF p因此，当圆台翻过来时，对桌面的压强是300帕．说明：本题与物理知识结合考查了反比例函数，关键是清楚对于同一个物体，它对桌面的压力是一定的．例 如图，P 是反比例函数xky =上一点，若图中阴影部分的矩形面积是2，求这个反比例函数的解析式．分析 求反比例函数的解析式，就是求k 的值．此题可根据矩形的面积公式及坐标与线段长度的转化来解．解 设P 点坐标为),(y x ．因为P 点在第二象限，所以0,0><y x ． 所以图中阴影部分矩形的长、宽分别为y x ,-．又2=-xy ，所以2-=xy ．因为xy k =，所以2-=k ． 所以这个反比例函数的解析式为xy 2-=． 说明 过反比例函数图像上的一点作两条坐标轴的垂线，可得到一个矩形，这个矩形的面积等于xk y =中的k ．例 当n 取什么值时，122)2(-++=n n x n n y 是反比例函数？它的图像在第几象限内？在每个象限内，y随x 增大而增大还是减小？分析 根据反比例函数的定义)0(≠=k x k y 可知，122)2(-++=n n x n n y 是反比例函数，必须且只需022≠+n n 且112-=-+n n ．解 122)2(-++=n n xn n y 是反比例函数，则⎪⎩⎪⎨⎧-=-+≠+,11,0222n n n n ∴⎩⎨⎧-==-≠≠.10,20n n n n 或且即 1-=n ．故当1-=n 时，122)2(-++=n nx n n y 表示反比例函数：xy 1-=． 01<-=k ，∴双曲线两支分别在二、四象限内，并且在每个象限内，y 随x 的增大而增大．11。
中考数学几何图形复习专题10 反比例函数的综合探究(数形结合)(学生版)
专题10 反比例函数的综合训练(数形结合)1．如图，一次函数4y x =-+的图象与反比例函数()0k y k x=≠在第一象限内的图象交于()1,A n 和()3,B m 两点．(1)求反比例函数的表达式．(2)在第一象限内，当一次函数4y x =-+的值大于反比例函数()0k y k x=≠的值时，写出自变量x 的取值范围(3)求△AOB 面积．2．如图，反比例函数2y x=的图象与一次函数y x b =+的图象交于(1, )A m ，(2, )B n -两点，一次函数图象与y 轴交于点C ，与x 轴交于点D ．（1）求一次函数的表达式；（2）观察图象，写出2kx b x>+时自变量x 的取值范围； （3）连接OA ，在第三象限的反比例函数图象上是否存在一点P ，使得2OCP OCA S S =△△？若存在，请求出点P 的坐标；若不存在，请说明理由.3．如图，在平面直角坐标系xOy 中，已知正比例函数y ＝12x 的图象与反比例函数y ＝k x的图象交于A （a ，﹣2），B 两点．（1）求反比例函数的表达式和点B 的坐标；（2）P 是第一象限内反比例函数图象上一点，过点P 作y 轴的平行线，交直线AB 于点C ，连接PO ，若△POC 的面积为3，求点P 的坐标．4．如图，等腰Rt ABO 的直角顶点O 与平面直角坐标系的原点重合，反比例函数()0m y x x=<的图象经过点A ，反比例函数()0n y x x =>的图象经过点B ．(1)试猜想m 与n 的数量关系，并说明理由；(2)若2n =，求当点B 的纵坐标分别为1和2时，等腰Rt ABO 的面积；(3)请直接写出当2n =时，等腰Rt ABO 的面积的最小值_________．5．如图，一次函数()=+0y mx n m ≠的图象与反比例函数()0k y k x =≠的图象相交于第二、四。
2023中考数学专项： 反比例函数与几何图形综合问题(重点突围)(学生版)
专题16反比例函数与几何图形综合问题【中考考向导航】目录【直击中考】 (1)【考向一反比例函数中K值的几何意义】 (1)【考向二反比例函数与三角形的综合问题】 (4)【考向三反比例函数与矩形的综合问题】 (6)【考向四反比例函数与菱形的综合问题】 (9)【考向五反比例函数与正方形的综合问题】 (11)【考向六反比例函数与圆的综合问题】 (15)【直击中考】【考向一反比例函数中K值的几何意义】【变式训练】1．（2023·安徽宿州·统考一模）如图，若反比例函数______在反比例函数3．（2022·黑龙江绥化·校考二模）如图，在过点A、C两点，点B在4．（2023秋·安徽池州·九年级统考期末）AC交y轴于点B，若点B是=【考向二反比例函数与三角形的综合问题】(1)求反比例函数的解析式；(2)过点A作AP垂直OA，交反比例函数的图象于点①求直线AC的解析式；②求点P的坐标．【变式训练】(1)求反比例函数的解析式；(2)坐标平面内有一点D，若以A(1)求反比例函数的表达式；(2)求等边△ACD的边长．【考向三反比例函数与矩形的综合问题】(1)直接写出B，C，D三点的坐标；(2)若将矩形向下平移，矩形的两个顶点值．【变式训练】上两点，的顶点【考向四反比例函数与菱形的综合问题】（1）求k的值及AB所在直线的函数表达式；（2）将这个菱形沿x轴正方向平移，当顶点【变式训练】是菱形，点(1)求一次函数与反比例函数的解析式；(2)设点P是直线AB上一动点，且ABCD(1)求双曲线y2的函数关系式及(2)判断点B是否在双曲线上，并说明理由；(3)若BA的延长线与双曲线【考向五反比例函数与正方形的综合问题】(1)求反比例函数的解析式；(2)若将正方形ABCD沿x轴向右平移得到正方形标，并判断点B′是否在该反比例函数的图象上，说明理由．【变式训练】在平面直角坐标系中，点(1)求反比例函数的解析式；(2)求四边形OAFM 的面积．2．（2022·山东济南·校考一模）如图，四边形35AE OE =．中点，以备用图4．（2022春·江苏苏州·八年级星海实验中学校考期中）如图，在平面直角坐标系中，四边形ABCD 为正方形，已知点()6,0A -、()7,3D -，点B 、C 在第二象限内．(1)点B 的坐标_________；(2)将正方形ABCD 以每秒2个单位的速度沿x 轴向右平移t 秒，若存在某一时刻t ，使在第一象限内点B 、D 两点的对应点B '、D ¢正好落在某反比例函数的图像上，请求出此时t 的值以及这个反比例函数的解析式；(3)在（2）的情况下，问是否存在y 轴上的点P 和反比例函数图像上的点Q ，使得以P 、Q 、B '、D ¢四个点为顶点的四边形是平行四边形？若存在，请直接写出符合题意的点Q 的坐标；若不存在，请说明理由．【考向六反比例函数与圆的综合问题】【变式训练】在反比例函数。
反比例函数压轴题经典培优好题难题(有答案)
B y A C
将y x 2
3 3 代入y 得， 2 x
D x
3 A(2, ) 2 3 C (2 , 0) 2 7 C ( , 0) 2
3 7 或C (2 , 0)即C ( , 0) 2 2 3 1 或C ( 2 , 0)即C ( , 0) 2 2
4 N 3 1 M 2
（2）若该反比例函数的图象与AB交于点Q，求直线PQ的 解析式．
∵AO=4 ∴A（-4，0） ∴Q的横坐标为-4 将x=-4代入y=-6/x得，y=3/2 ∴Q（-4，3/2） 设PQ：y=ax+b 将Q（-4，3/2）P（-2，3）代入得， -4a+b=3/2 -2a+b=3 a=3/4 解得 b=9/2 ∴PQ：y=3/4x+9/2
潮实：已知：如图，在直角坐标系xoy中，矩形OABC的边 OA在x轴的负半轴上，边OC在y轴的正半轴上，对角线AC 与OB相交于P，且BC=4，AB=6． （1）求过点P的反比例函数的解析式；
（1）如图，过P作PM⊥AO于M， PN⊥CO于N （ASA证明△BCP全等于△AOP， △OCP全等于△ABP） ∴AP=PO ∴∠1=∠2，∠3=∠4 ∴M是AO的中点，N是OC的中点 又∵OC=AB=6,AO=BC=4 ∴MO=1/2×4=2 ON=1/2×6=3 ∴P（-2，3） 设y=k/x 则k=xy=-2×3=-6 所以过P点的反比例函数解析式为 y=-6/x
6
Y
4
A
2
D E
-5
O B
-2
C
5
X
f x = 3 x
-4
【4】. 已知如图：点（1，3）在反比例函数y=
的图象上长方形ABCD的边BC在X轴上，E为对角线BD的中点， 反比例函数y= k (x > 0) 的图象又经过A，E两点，若E点的 x 横坐标为m. ①求反比例函数的解析式 ;
反比例函数经典拓展难题
1：（2007年浙江省初中数学竞赛）函数y ＝1x-图象的大致形状是（ ）A B C D3．已知y 与2x －3成反比例，且41=x 时，y ＝－2，求y 与x 的函数关系式．4．已知函数y ＝y 1－y 2，且y 1为x 的反比例函数，y 2为x 的正比例函数，且23-=x 和x ＝1时，y 的值都是1．求y 关于x 的函数关系式．5．作出反比例函数xy 12=的图象，并根据图象解答下列问题： (1)当x ＝4时，求y 的值；(2)当y ＝－2时，求x 的值；(3)当y ＞2时，求x 的范围．6．作出反比例函数xy 4-=的图象，结合图象回答： (1)当x ＝2时，y 的值；(2)当1＜x ≤4时，y 的取值范围；(3)当1≤y ＜4时，x 的取值范围．7．作出函数xy 12=的图象，并根据图象回答下列问题： (1)当x ＝－2时，求y 的值；(2)当2＜y ＜3时，求x 的取值范围； (3)当－3＜x ＜2时，求y 的取值范围．8．如图，A 、B 是函数xy 2=的图象上关于原点对称的任意两点，BC ∥x 轴，AC ∥y 轴， △ABC 的面积记为S ，则(s= )．9．如图，点A 、B 是函数y ＝x 与xy 1=的图象的两个交点，作AC ⊥x 轴于C ，作BD ⊥x 轴于D ，则四边形ACBD 的面积为( )．10．已知：如图，在平面直角坐标系xOy 中，Rt △OCD 的一边OC 在x 轴上，∠C ＝90°，点D 在第一象限，OC ＝3，DC ＝4，反比例函数的图象经过OD 的中点A ． (1)求该反比例函数的解析式；(2)若该反比例函数的图象与Rt △OCD 的另一边交于点B ，求过A 、B 两点的直线的解析式．11．如图，A 、B 两点在函数)0(>=x xmy 的图象上．(1)求m 的值及直线AB 的解析式；(2)如果一个点的横、纵坐标均为整数，那么我们称这个点是格点．请直接写出图中阴影部分(不包括边界)所含格点的个数．12．如图，已知点A 在反比例函数的图象上，AB ⊥x 轴于点B ，点C (0，1)，若△ABC 的面积是3，则反比例函数的解析式为____________．13．如图，直线y ＝mx 与双曲线xky =交于A ，B 两点，过点A 作AM ⊥x 轴，垂足为M ，连结BM ，若S △ABM ＝2，则k 的值是( )．14．如图，双曲线xky =(k ＞0)经过矩形OABC 的边BC 的中点E ，交AB 于点D 。
反比例函数提高训练题(难)
反比例函数提高训练题(难)一、选择题：1、反比例函数的解析式为y=k/x，因此选项D正确。
2、根据反比例函数的性质可知，x越大，y越小，因此选项B正确。
3、根据反比例函数的性质可知，y=k/x，当x越大，y越小，因此选项D正确。
4、反比例函数y=k/x的图象是一个双曲线，开口朝右上方，因此选项C正确。
5、根据题目条件可知，XXX(x1y2-y1x2)，因此选项B正确。
6、根据反比例函数的性质可知，y=k/x，当x越大，y越小，因此选项A正确。
二、填空题：1、反比例函数y=k/x的图象是一个双曲线，开口朝右上方，因此k>0.2、根据双曲线的性质可知，y=k/x的图象与x轴、y轴有渐近线，因此k≠0.3、根据反比例函数的性质可知，y=k/x，当x越大，y越小，因此m>0.4、根据双曲线的性质可知，y=k/x的图象与x轴、y轴有渐近线，因此k≠0.5、根据双曲线的性质可知，y=k/x的图象与x轴、y轴有渐近线，因此k≠0.6、根据反比例函数的性质可知，y=k/x，当x越大，y越小，因此m>0.7、根据双曲线的性质可知，y=k/x的图象与x轴、y轴有渐近线，因此k≠0.8、根据题目条件可知，点P关于y轴对称的点为(-a。
m/(a-1))，因此k=m/(a-1)。
9、根据反比例函数的性质可知，y=k/x，当x越大，y越小，因此m>0.10、根据题目条件可知，y2=8/(x-4)，因此选项C正确。
11、根据题目条件可知，A1、A2、A3在x轴上，因此选项B正确。
1.将文章中的格式错误和明显有问题的段落删除，改写每段话如下：1.在图中，点B1、B2、B3分别交于x轴平行线，过点xB3、C2、C3、B1、B3，分别与y轴交于点C1、OB2、OB3.阴影部分的面积之和为连接OB1、OB2、OB3的三角形面积加上连接OB1、OB3、C3、C2、OB2的梯形面积。
2.已知点A(-1.y1)、B(1.y2)、C(2.y3)在反比例函数y=k/x 的图象上，其中ky2>y3.3.如图所示，点P在y=k1/x和y=k2/x的图象上，PC⊥x 轴于点C，交y=k1/x的图象于点A，PD⊥y轴于点D，交y=k2/x的图象于点B。
反比例函数经典拓展难题
反比例函数难题拓展填空题1. （2011浙江金华，16,4分）如图，将一块直角三角板OAB放在平面直角坐标系中，B（2,k0）, Z AOC= 60°，点A在第一象限，过点A的双曲线为y -，在x轴上取一点P,过点PX作直线0A的垂线I，以直线I为对称轴，线段0B经轴对称变换后的像是0B.（1）当点0'与点A重合时，点P的坐标是___________ .2. （2011广东东莞，6, 4分）已知反比例函数y=k的图象经过（1,—2）.则k= ____________ .x6. （2011浙江衢州，5,4分）在直角坐标系中，有如图所示的 RHABO,AB_x 轴于点B ，斜3 k边AO =10, si n . AOB,反比例函数y 二―（x ■ 0）的图像经过AO 的中点C ，且与AB 交于 5 x点D ,则点D 的坐标为37. （2011浙江绍兴，13, 5分）若点A （1y ）,B （2, y 2）是双曲线y 上上的点，贝Uxy 1 ____________ y 2 （填 > ,<=）.8. （2011浙江丽水，16, 4分）如图，将一块直角三角板 OAB 放在平面直角坐标系中，B （2，k0），/AO G 60°，点A 在第一象限，过点A 的双曲线为y=-，在x 轴上取一点P,过点Px作直线0A 的垂线I ，以直线I 为对称轴，线段0B 经轴对称变换后的像是 0B. （1） 当点O'与点A 重合时，点P 的坐标是 __________ .（2） 设P （t ，0）当OB 与双曲线有交点时，t 的取值范围是 ——yICD Bx（第15题）9. （2011湖南常德，5，3分）如图1所示的曲线是一个反比例函数图象的一支，点A在此曲线上，则该反比例函数的解析式为 ____________________ .10. （2011江苏苏州，18,3分）如图，已知点 A 的坐标为（屈,3）, AB 丄x 轴，垂足为B ,k连接0A 反比例函数y=# （k>0）的图象与线段OA AB 分别交于点C D.若AB=3BD 以点xC 为圆心，CA 的5倍的长为半径作圆，则该圆与x 轴的位置关系是 _______________ （填“相离”、4“相切”或“相交”）m — 111. （ 2011山东济宁，11，3分）反比例函数y=—— 的图象在第一、三象限，则 m 的取值x 范围是 ____________ .12. （2011四川成都，25,4分）在平面直角坐标系xOy 中，已知反比例函数丫二仝你=0）满x足：当x ： 0时，y 随x 的增大而减小.若该反比例函数的图象与直线 y —X • Gk 都经过 点P ,且0P =万，则实数k= _____________ .13. （ 2011安徽芜湖，15，5分）如图，在平面直角坐标系中有一正方形 AOBC 反比例函数y=k 经过正方形AOBC 寸角线的交点，半径为（4-2血）的圆内切于△ ABC 则k 的值x 为 _________.14. （2011广东省，6, 4分）已知反比例函数y=^的图象经过（1,— 2）.则k=.x2 1 115. （2011江苏南京，15,2分）设函数y=—与y=x-1的图象的交战坐标为（a, b ）,则—-—x a b的值为 ___________ .k16. （2011上海，11, 4分）如果反比例函数y=k （ k 是常数，k 丸））的图像经过点（一1,x2），那么这个函数的解析式是 ____________ .17. （2011湖北武汉市，16, 3分）如图，□ ABCD 勺顶点A, B 的坐标分别是A （— 1, 0）, B（0,— 2）,顶点C, D 在双曲线y=-上，边AD 交y 轴于点E ,且四边形BCDE 勺面积是△ ABEx面积的5倍，则k= _____ .,, k18. （2011湖北黄冈，4, 3分）如图：点A 在双曲线y 二—上, AB 丄x 轴于B ,且SOB 的面x积S2AO=2，贝U k=_____ .x119.（2011湖北黄石，15, 3分）若一次函数y=kx+1的图象与反比例函数y=-的图象没有x 公共点，则实数k 的取值范围是 _____________ 。
初二数学反比例函数试题答案及解析
初二数学反比例函数试题答案及解析1.如图，在平面直角坐标系中，双曲线经过点B，连结OB．将OB绕点O按顺时针方向旋转90°并延长至A，使OA＝2OB，且点A的坐标为（4，2）．（1）求过点B的双曲线的函数关系式；（2）根据反比例函数的图像，指出当x＜－1时，y的取值范围；（3）连接AB，在该双曲线上是否存在一点P，使得S△ABP ＝S△ABO，若存在，求出点P坐标；若不存在，请说明理由．【答案】（1）双曲线的函数关系式为y=﹣；（2）当x＜﹣1时，0＜y＜2；（3）存在；点P坐标为（﹣，4）．【解析】（1）作AM⊥x轴于点M，BN⊥x轴于点N，由相似三角形的判定定理得出△AOM∽△OBN，OA=2OB，再根据OA=2OB，点A的坐标为（4，2）可得出B点坐标，进而得出反比例函数的关系式；（2）由函数图象可直接得出结论；（3）根据AB两点的坐标可知AB∥x轴，S△ABP =S△ABO=5，再分当点P在AB的下方与当点P在x轴上方两种情况即可得出结论．试题解析：（1）作AM⊥x轴于点M，BN⊥x轴于点N，∵OB⊥OA，∠AMO=∠BNO=90°，∴∠AOM=∠NBO，∴△AOM∽△OBN．∵OA=2OB，∴，∵点A的坐标为（4，2），∴BN=2，ON=1，∴B（﹣1，2）．∴双曲线的函数关系式为y=﹣；（2）由函数图象可知，当x＜﹣1时，0＜y＜2；（3）存在．∵yA =yB，∴AB∥x轴，∴S△ABP =S△ABO=5，∴当点P在AB的下方时，点P恰好在x轴上，不合题意舍去；当点P在x轴上方时，点P在第二象限，得AB•（yP ﹣2）=5，即×5×（yP﹣2）=5，解得yP=4，∴点P坐标为（﹣，4）．【考点】1、相似三角形的判定与性质；2、待定系数法；3、函数大小的比较；4、反比例函数2.已知点A（1，y1）、B（2，y2）、C（﹣3，y3）都在反比例函数的图象上，则y1、y2、y3的大小关系是____________________．【答案】y3＜y2＜y1．【解析】∵k=6＞0，∴图象在一、三象限，且在每一象限内y随x的增大而减小．∵x1＜x2，∴y1＞y2＞0，∵x3＜0，∴y3＜0，∴y3＜y2＜y1．故答案是y3＜y2＜y1．【考点】反比例函数图象上点的坐标特征．3.已知反比例函数y=的图象上有三个点（2，）,(3,),(,),则，，的大小关系是（）A．＞＞B．＞＞C．＞＞D．＞＞【答案】A.【解析】试题解析：∵-k2-1＜0∴反比例函数y=的图象在第二、四象限∴＞＞故选A.【考点】反比例函数图象上点的坐标特征．4.已知长方形的面积为10，则它的长y与宽x之间的关系用图象大致可表示为图中的（）A．B．C．D．【答案】A【解析】由长方形的面积公式得y=，且x＞0，y＞0，而B中有x＜0，y＜0的情况，C，D中有x=0或y=0的情况，据此即可得出结果．解：∵xy=10∴y=，（x＞0，y＞0）故选A．点评：现实生活中存在大量成反比例函数的两个变量，解答该类问题的关键是确定两个变量之间的函数关系，然后利用实际意义确定其所在的象限．5.已知反比列函数y=的图象在每一条曲线上，y都随x的增大而增大，（1）求k的取值范围；（2）在曲线上取一点A，分别向x轴、y轴作垂线段，垂足分别为B、C，坐标原点为O，若四边形ABOC面积为12，求此函数的解析式．【答案】（1）k＜0 （2）y=﹣【解析】（1）直接根据反比例函数的性质求解即可，k＜0；（2）直接根据k的几何意义可知：过双曲线上任意一点引x轴、y轴垂线，所得矩形面积为|k|，所以|k|=12，而k＜0，则k=﹣12．解：（1）∵反比列函数y=的图象在每一条曲线上，y都随x的增大而增大，∴k＜0；（2）设A（x，y），由已知得，|xy|=|k|=12，∵k＜0，∴k=﹣12，所以，反比例函数的解析式为y=﹣．点评：主要考查了反比例函数中k的几何意义，即过双曲线上任意一点引x轴、y轴垂线，所得矩形面积为|k|，是经常考查的一个知识点；这里体现了数形结合的思想，做此类题一定要正确理解k的几何意义．6.在同一平面直角坐标系中，正比例函数y=（m﹣1）x与反比例函数y=的图象的大体位置不可能是（）A．B．C．D．【答案】D【解析】根据题意，依次分析选项中的图象，根据图象，求出其参数的范围，并解看有无公共解，若有，则可能是它们的图象，若无解，则不可能是它们的图象；即可得答案．解：依次分析选项可得：A、4m＞0，m﹣1＞0；解可得m＞1；故可能是它们的图象．B、4m＞0，m﹣1＜0；解可得0＜m＜1；故可能是它们的图象．C、4m＜0，m﹣1＜0；解可得m＜1；故可能是它们的图象．D、4m＜0，m﹣1＞0；无解；故不可能是它们的图象．故选D．点评：本题考查正比例函数与反比例函数的图象性质，注意①正比例函数与反比例函数的图象与k的关系，②两个函数中参数的关系．7.若A（，b）、B（－1，c）是函数的图象上的两点，且＜0，则b与c的大小关系为（）A．b＜c B．b＞c C．b=c D．无法判断【答案】B【解析】反比例函数的性质：当时，图象在第一、三象限，在每一象限内，y随x的增大而减小；当时，图象在第二、四象限，在每一象限内，y随x的增大而增大.解：∵，∴故选B.【考点】反比例函数的性质点评：反比例函数的性质是初中数学的重点，是中考中比较常见的知识点，一般难度不大，需熟练掌握.8.如图，在直角坐标平面内，函数的图象经过A（1，4），B(a，b)，其中a>1，过点B作轴垂线，垂足为C，连接AC、AB.（1）m= ；（2）若△ABC的面积为4，则点B的坐标为【答案】（1）4；（2）【解析】（1）把A的坐标代入反比例函数的解析式，即可求出m和得出反比例函数的解析式；（2）设B的坐标是（a，b），根据B在反比例函数上得出ab的值，再根据△ABC的面积为4求解即可．（1）把A（1，4）代入得；（2）设B的坐标是（a，b），∵B在反比例函数上，∴ab=4∵△ABC的面积为4，∴×a×（4-b）=4，∴2a ab=4，∴2a-2=4，a=3，∵ab=4，∴b=．则点B的坐标为（3，）．【考点】反比例函数图象上点的坐标特征，用待定系数法求反比例函数的解析式，三角形的面积点评：待定系数法求函数的解析式是初中数学的重点，贯穿于整个初中数学的学习，是中考中比较常见的知识点，一般难度不大，需熟练掌握.9.如图，双曲线在第一象限内如图所示作一条平行y轴的直线分别交双曲线于A、B两点，连OA、OB，则S＝。
反比例函数压轴题精选(含答案)
中考反比例函数经典结论：如图,反比例函数k 的几何意义： (I) 12AOB AOC S S k ∆∆==; (II) OBAC S k =矩形. 下面两个结论是上述结论的拓展.(1) 如图①,OPA OCD S S ∆∆=,OPC PADC S S ∆=梯形.(2)如图②,OAPB OBCA S S =梯形梯形,BPE ACE S S ∆∆=.经典例题例 1.(1)(兰州)如图,已知双曲线(0)k y x x=>经由矩形OABC 边AB 的中点F 且交BC 于点E ,四边形OEBF 的面积为2,则k = 2 ;(2)如图,点A B 、为直线y x =上的两点,过A B 、两点分离作y 轴的平行线交双曲线1(0)y x x=>于C D 、两点,若2BD AC =,则224OC OD -= 6 例2．(陕西)假如一个正比例函数的图象与一个反比例函数xy 6=的图象交),(),,(2211y x B y x A ,那么))((1212y y x x --值为 24 .解析：因为A,B 在反比例函数xy 6=上,所以611=y x ,我们知道正比例函数与反比例函数的交点坐标关于原点成中间对称,是以),(),,(2211y x B y x A 中有1212,y y x x -=-=,所以24644))(())((1111111212=⨯==----=--y x y y x x y y x x例3．(山东威海)如图,一次函数b kx y +=的图象与反比例函数xm y =的图象交于点A ﹙－2,－5﹚,C ﹙5,n ﹚,交y 轴于点B,交x 轴于点D ．(1) 求反比例函数xm y =和一次函数b kx y +=(2) 衔接OA,OC ．求△AOC 的面积．解：(1)∵反比例函数xm y =的图象经由点A ﹙－2,－5﹚,∴m=(－2)×( －5)＝10．∴反比例函数的表达式为xy 10=．∵点C ﹙5,n ﹚在反比例函数的图象上,∴2510==n ．∴C 的坐标为﹙5,2﹚．∵一次函数的图象经由点A,C,将这两个点的坐标代入b kx y +=,得⎩⎨⎧+=+-=-.5225b k b k ，解得⎩⎨⎧-==.31b k ， ∴所求一次函数的表达式为y ＝x －3．(2) ∵一次函数y=x －3的图像交y 轴于点B,∴B 点坐标为﹙0,－3﹚．∴OB＝3．∵A 点的横坐标为－2,C 点的横坐标为5,∴S△AOC= S△AOB+ S△BOC=()22152215212-21=+⋅⋅=⋅⋅+⋅⋅OB OB OB ．例4．（福建福州）如图,已知直线12y x =与双曲线(0)k y k x=>交于A B ，两点,且点A 的横坐标为4． （1）求k 的值;（2）若双曲线(0)k y k x=>上一点C 的纵坐标为8,求AOC △的面积;（3）过原点O 的另一条直线l 交双曲线(0)k y k x=>于P Q ，两点（P 点在第一象面积为24,限）,若由点A B P Q ，，，为极点构成的四边形求点P 的坐标． 解：（1）点A 横坐标为4,∴当4x =时,2y =．∴点A 的坐标为(42)，． 点A 是直线12y x =与双曲线(0)k y k x=>的交点,428k ∴=⨯=．（2）解法一：如图1,点C 在双曲线上,当8y =时,1x =∴点C 的坐标为(18)，． 过点A C ，分离做x 轴,y 轴的垂线,垂足为M N ，,得矩形DMON ．32ONDM S =矩形,4ONC S =△,9CDA S =△,4OAM S =△．3249415AOC ONC CDA OAM ONDM S S S S S =---=---=△△△△矩形解法二：如图2,过点C A ，分离做x 轴的垂线,垂足为E F ，,点C 在双曲线8y x=上,当8y =时,1x =．∴点C 的坐标为(18)，．点C ,A 都在双曲线8y x=上,4COEAOF S S ∴==△△COE COA AOF CEFA S S S S ∴+=+△△△梯形．COA CEFA S S ∴=△梯形．1(28)3152CEFA S =⨯+⨯=梯形,15COA S ∴=△．（3）反比例函数图象是关于原点O OP OQ ∴=,OA OB =．∴四边形APBQ 是平行四边形． 1124644POA APBQ S S ∴==⨯=△平行四边形． 设点P 横坐标为(04)m m m >≠且,得8()P m m，．过点P A ，分离做x 轴的垂线,垂足为E F ，, 点P A ，在双曲线上,4PQE AOF S S ∴==△△． 若04m <<,如图3,POE POA AOF PEFA S S S S +=+△△△梯形,6POA PEFA S S ∴==△梯形．182(4)62m m ⎛⎫+-= ⎪⎝⎭∴·． 解得2m =,8m =-（舍去）．∴(24)P ，． 若4m >,如图4,AOF AOP POE AFEP S S S S +=+△△△梯形,图2图3图46POA PEFA S S ∴==△梯形．182(4)62m m ⎛⎫∴+-= ⎪⎝⎭,解得8m =,2m =-（舍去）．(81)P ∴，． ∴点P 的坐标是(24)P ，或(81)P ，． 例 5.(山东淄博) 如图,正方形AOCB 的边长为4,反比例函数的图象过点E （3,4）．（1）求反比例函数的解析式;（2）反比例函数的图象与线段BC 交于点D,直线1yx b 2过点D,与线段AB 订交于点F,求点F 的坐标;（3）衔接OF,OE,探讨∠AOF 与∠EOC 的数目关系,并证实． 【答案】解：（1）设反比例函数的解析式k yx , ∵反比例函数的图象过点E （3,4）,∴k 43,即k=12.∴反比例函数的解析式12yx. （2）∵正方形AOCB 的边长为4,∴点D 的横坐标为4,点F 的纵坐标为4.∵点D 在反比例函数的图象上,∴点D 的纵坐标为3,即D （4,3）. ∵点D 在直线1y x b 2上,∴134b 2,解得b=5.∴直线DF 为1yx 52.将y4代入1yx 52,得14x 52,解得x 2.∴点F 的坐标为（2,4）.（3）∠AOF＝12∠EOC.证实如下：在CD 上取CG=CF=2,衔接OG,衔接EG 并延伸交ｘ轴于点H.∵AO=CO=4,∠OAF=∠OCG=900,AF=CG=2, ∴△OAF≌△OCG（SAS ）.∴∠AOF=∠COG. ∵∠EGB=∠HGC,∠B=∠GCH=900,BG=CG=2,∴△EGB≌△HGC（AAS ）.∴EG=HG. 设直线EG ：ymxn ,∵E（3,4）,G （4,2）,∴43m n 24m n =+⎧⎨=+⎩,解得,m 2n=10=⎧⎨⎩－. ∴直线EG ：y 2x10.令y2x10=0,得x 5.∴H（5,0）,OH=5.在R ｔ△AOF 中,AO=4,AE=3,依据勾股定理,得OE=5.∴OH=OE.∴OG 是等腰三角形底边EH 上的中线.∴OG 是等腰三角形顶角的等分线. ∴∠EOG=∠GOH.∴∠EOG=∠GOC=∠AOF,即∠AOF＝12∠EOC.例 6.(山东威海)一次函数y ax b =+的图象分离与x 轴.y 轴交于点,M N ,与反比例函数ky x=的图象订交于点,A B ．过点A 分离作AC x ⊥轴,AE y ⊥轴,垂足分离为,C E ;过点B 分离作BF x ⊥轴,BD y ⊥轴,垂足分离为F D ，，AC 与BD 交于点K ,衔接CD ． （1）若点A B ，在反比例函数k y x=的图象的统一分支上,如图1,试证实： ①AEDK CFBK S S =四边形四边形; ②AN BM =．（2）若点A B ，分离在反比例函数k y=的图象的不合分支上,如图2,则AN 与BM还相等吗？试证实你的结论．解：（1）①AC x ⊥轴,AE y ⊥BF x ⊥轴,BD y ⊥轴,∴四边形AC x ⊥轴,BD y ⊥轴,∴四边形1111OC x AC y x y k ===，，,∴11AEOC S OC AC x y k ===矩形 2222OF x FB y x y k ===，，,∴22BDOF S OF FB x y k ===矩形．∴AEOC BDOF S S =矩形矩形．AEDK AEOC DOCK S S S =-矩形矩形矩形,CFBK BDOF DOCK S S S =-矩形矩形矩形,∴AEDK CFBK S S =矩形矩形)②由（1）知AEDK CFBK S S =矩形矩形．∴AK DK BK CK =．∴AK BKCK DK= 90AKB CKD ∠=∠=°,∴AKB CKD △∽△．∴CDK ABK ∠=∠．∴AB CD∥AC y ∥轴,∴四边形ACDN 是平行四边形．∴AN CD =．同理BM CD =．AN BM ∴=．（2）AN 与BM 仍然相等．AEDK AEOC ODKC S S S =+矩形矩形矩形,BKCF BDOF ODKC S S S =+矩形矩形矩形,又AEOC BDOF S S k ==矩形矩形,∴AEDK BKCF S S =矩形矩形∴AK DK BK CK =．∴CK DKAK BK=．K K ∠=∠,∴CDK ABK △∽△．∴CDK ABK ∠=∠．∴AB CD ∥．AC y ∥轴,∴四边形ANDC 是平行四边形．∴AN CD =．同理BM CD =．∴AN BM =．第一部分演习一.选择题1.(鄂州)如图,直线y=mx 与双曲线y=xk 交于A.B 两点,过点A 作AM⊥x 轴,垂足为M,贯穿连接BM,若ABM S ∆=2,则k 的值是2.(兰州) 如图,若正方形OABC 的极点B 和正方形ADEF 的极点E 都在函数1y x=（0x >）的图象上,则点E 的坐标是（,）.3.(泰安）如图,双曲线)0(＞k xk y =经由矩形OABC 的边BC 的中点E, 交AB 于点D.若梯形ODBC 的面积为3,则双曲线的解析式为A ．xy 1=B ．xy 2= C ．x y 3=D ．xy 6=OAB4.（仙桃）如图,已知双曲线)0k (xk y ＞=经由直角三角形斜边OB 的中点D,与直角边AB 订交于点C ．若△OBC 的面积为3,则k ＝____________．OC D KF E N yxABM图2xyABO1S2Sy xO P 1P 2P 3P 4 P 5A 1 A 2 A 3 A 4 A 52x 5.(牡丹江市)如图,点A .B 是双曲线3y x=上的点,分离经由A .B 两点向x 轴.y 轴作垂线段,若1S =阴影，则12S S +=．6.（莆田）如图,在x 轴的正半轴上依次截取112233445OA A A A A A A A A ====,过点12345A A A A A 、、、、分离作x 轴的垂线与反比例函数()20y x x=≠的图象订交于点12345P P P P P 、、、、,得直角三角形1112233344455OPA A P A A P A A P A A P A 2、、、、，并设其面积分离为12345S S S S S 、、、、，则5S 的值为．． 第4题图 第5题图 第6题图7.（包头）已知一次函数1y x =+与反比例函数ky x =的图象在第一象限订交于点A ,与x 轴订交于点C AB x ，⊥轴于点B ,AOB △的面积为1,则AC 的长为8.（ 嵊州市）如图,直线)0(<=k kx y 与双曲线xy 2-=交于),(),,(2211y x B y x A 两点,则122183y x y x -的值为A.－5 B.－10 C.5 D.10【答案】B9.（江苏无锡）如图,已知梯形ABCO 的底边AO 在x 轴上,BC∥AO,AB⊥AO,过点C 的双曲线ky x=交OB 于D,且OD ：DB=1:2,若△OBC 的面积等于3,则k 的值A ．等于2 B ．等于34C ．等于245D ．无法肯定【答案】B第7题图 第8题图 第9题图10.（江苏盐城）如图,A.B 是双曲线y= kx(k>0) 上的点,A.B 两点的横坐标分离是a.2a,线段AB 的延伸线交x 轴于点C,若S△AOC=6．则k=．【答案】4 11.（安徽蚌埠二中）已知点（1,3）在函数)0(>=x xk y 的图像上.正方形ABCD 的边BC 在x 轴上,点E 是对角线BD 的中点,函数)0(>=x x k y 的图像又经由A .E 两点,则点E 的横坐标为__________.612.（四川内江）如图,反比例函数y ＝kx(x ＞0)的图象经由矩形OABC 对角线的交点M,分离与AB.BC 订交于点D.E ．若四边形ODBE 的面积为6,则k 的值为y O AC B yBAoO ABCDxy图6yx O BC AAB C D E yxOMA ．1B ．2C ．3D ．4【答案】B第10题图 第11题图 第12题图13.（山东东营）如图,直线l 和双曲线(0)k y k x=>交于A.B 亮点,P 是线段AB 上的点（不与A.B 重合）,过点A.B.P 分离向x 轴作垂线,垂足分离是C.D.E,衔接OA.OB.OP,设△AOC 面积是S1.△BOD 面积是S2.△POE 面积是S3.则 A. S1＜S2＜S3B. S1>S2>S3C. S1=S2>S3D. S1=S2<S3 【答案】D①x＜0时,x2y =,②△OPQ 的面积为定值, ③x＞0时,y 随x 的增大而增大 ④MQ=2PM⑤∠POQ 可以等于90°个中准确的结论是A ．①②④B②④⑤C．③④⑤D．②③⑤ 【答案】B15.（甘肃兰州,15,4分）如图,矩形ABCD 的对角线BD 经由坐标原点,矩形的边分离平行于坐标轴,点C 在反比例函数221k k y x++=的图象上.若点A 的坐标为（－2,－2）,则k 的值为A ．1B ．－3C ．4D ．1或－3【答案】D轴于A.B 16.（四川乐山）如图,直线6y x =-交x 轴.y 直线下两点,P 是反比例函数4(0)y x x=>图象上位于xyOABCD方的一点,过点P 作x 轴的垂线,垂足为点M,交AB 于点E,过点P 作y 轴的垂线,垂足为点N,交AB 于点F.则AF BE ⋅= A ．8 B ．6 C ．4 D ．62 【答案】A17.（•德州）如图,两个反比例函数和的图象分离是l1和l2．设点P在l1上,PC⊥x 轴,垂足为C,交l2于点A,PD⊥y 轴,垂足为D,交l2于点B,则三角形PAB 的面积为A ． 3B ． 4C ．D ．5 解解：∵点P 在y=上,∴设P 的坐标是（a,）, ∵PA ⊥x 轴,∴A 的横坐标是a,∵A 在y=﹣上,∴A 的坐标是（a,﹣）, ∵PB ⊥y 轴,∴B 的纵坐标是, ∵B 在y=﹣上,∴代入得：﹣, 解得：x=﹣2a,∴B 的坐标是（﹣2a,）, ∴PA=﹣（﹣）=,PB=a ﹣（﹣2a ）=3a, ∵PA ⊥x 轴,PB ⊥y 轴,x 轴⊥y 轴,∴PA ⊥PB,∴△PAB 的面积是：PA ×PB=××3a=．故选C ．18.（福州）如图,过点C(1,2)分离作x 轴.y 轴的平行线,交直线y ＝－x ＋6于A. B 两点,若反比例函数y ＝kx (x ＞0)的图像与△ABC 有公共点,则k 的取值规模是A ．2≤k≤9 B．2≤k≤8C ．2≤k≤5D ．5≤k≤8 解答：解：∵点C(1,2),BC∥y 轴,AC∥x 轴,ABCOxy∴当x ＝1时,y ＝－1＋6＝5,当y ＝2时,－x ＋6＝2,解得x ＝4, ∴点A.B 的坐标分离为A(4,2),B(1,5),依据反比例函数系数的几何意义,当反比例函数与点C 订交时,k ＝1×2＝2最小,设与线段AB 订交于点(x,－x ＋6)时k 值最大,则k ＝x(－x ＋6)＝－x2＋6x ＝－(x －3)2＋9,∵ 1≤x≤4,∴当x ＝3时,k 值最大,此时交点坐标为(3,3), 是以,k 的取值规模是2≤k≤9．故选A ．19.（临沂）如图,若点M 是x 轴正半轴上随意率性一点,过点M 作PQ∥y 轴,分离交函数1(0)k y x x =>和2(0)ky x x=>的图象于点P 和Q,衔接OP 和OQ ．则下列结论准确的是A ．∠POQ 不成能等于90°B．12k PM QM k = C ．这两个函数的图象必定关于x 轴对称; D ．△POQ 的面积是()1212k k + 故选：D ．20.（湖北黄石）如图所示,已知11(,)2A y ,2(2,)B y 为反比例函数1y x=图像上的两点,动点(,0)P x 在x 正半轴上活动,当线段AP 与线段BP 之差达到最大时,点P 的坐标是DA. 1(,0)2B. (1,0)C. 3(,0)2D. 5(,0)2【解答】解：∵把A （1/2 ,y1）,B （2,y2）代入反比例函数y=1/ x 得：y1=2,y2=1/2 ,yxOABP∴A（1/2 ,2）,B （2,1/2 ）,∵在△ABP 中,由三角形的三边关系定理得：|AP－BP|＜AB,∴延伸AB 交x 轴于P′,当P 在P′点时,PA－PB=AB,即此时线段AP 与线段BP 之差达到最大,设直线AB 的解析式是y=kx+b,把 A.B 的坐标代入得： 2=1/2k+b ,1/2=2k+b,解得：k=－1,b=5/2 ,∴直线AB 的解析式是y=－x+5/2 ,当y=0时,x=5/2 ,即P （5/2 ,0）,故选D ．21.(湖北随州)如图,直线l 与反比例函数x y 2=的图象在第一象限内交于A.B 两点,交x 轴的正半轴于C 点,若AB ：BC=(m 一l)：1(m>l)则△OAB 的面积(用m 暗示)为A.m m 212-B.mm 12- C. m m )1(32- D.m m 2)1(32- 答案：B22.（江苏姑苏）如图,菱形OABC 的极点C 的坐标为(3,4),极点A 在x 轴的正半轴上．反比例函数y ＝k x(x ＞0)的图象经由极点B,则k 的值为A ．12B ．20C ．24D ．32【答案】D ．解：过C 点作CD⊥x 轴,垂足为D ．B AoxylO xyB A C∵点C 的坐标为（3,4）,∴OD=3,CD=4．∴OC= OD2+CD2=32+42=5．∴OC=BC=5．∴点B 坐标为（8,4）, ∵反比例函数y=k x（x ＞0）的图象经由极点B,∴k=32．23.（山东临沂）如图,等边三角形OAB 的一边OA 在x 轴上,双曲线y ＝3x在第一象限内的图象经由OB 边的中点C,则点B 的坐标是 A ．（1,3）B ．（3,1）C ．（2,23）D ．（23,2）【答案】：C ．24.(湖北孝感）如图,函数y=﹣x 与函数的图象订交于A,B 两点,过A,B 两点分离作y 轴的垂线,垂足分离为点C,D ．则四边形ACBD 的面积为A ．2 B ．4 C ． 6 D ．8 解答：解：∵过函数的图象上A,B 两点分离作y 轴的垂线,垂足分离为点C,D,∴S △AOC=S △ODB=|k|=2, 又∵OC=OD,AC=BD,∴S △AOC=S △ODA=S △ODB=S △OBC=2, ∴四边形ABCD 的面积为：S △AOC+S △ODA+S △ODB+S △OBC=4×2=8． 故选D ．25.（四川内江）如图,反比例函数（x ＞0）的图象经由矩形OABC 对角线的交点M,分离于AB.BC 交于点D.E,若四边形ODBE 的面积为9,则k 的值为A ． 1B ．2 C ．3 D ．4 解答：解：由题意得：E.M.D 位于反比例函数图象上,则S △OCE=,S △OAD=,过点M 作MG ⊥y 轴于点G,作MN ⊥x 轴于点N,则S □ONMG=|k|,又∵M 为矩形ABCO 对角线的交点, ∴S 矩形ABCO=4S □ONMG=4|k|, 因为函数图象在第一象限,k ＞0,则++9=4k, 解得：k=3．故选C ．26.(四川乐山)如图,已知第一象限内的点A 在反比例函数y = 2x 的图象上,第二象限内的点B 在反比例函数y = k x 的图象上,且OA⊥0B,cotA= 33,则k 的值为A ．－3 B.－6 C.－ 3 D.－2 3 在第一象27.（黔东南州）如图,直线y=2x 与双曲线y=限的交点为A,过点A 作AB⊥x 轴于B,将△ABO 绕点O 扭转90°,得到△A′B′O,则点A′的坐标为A.()1,0B. ()1,0或()1,0-C. ()2,0或()0,2-D. ()2,1-或()2,1-解答：解：联立直线与反比例解析式得：,消去y 得到：x2=1,解得：x=1或﹣1,∴y=2或﹣2, ∴A （1,2）,即AB=2,OB=1,依据题意画出响应的图形,如图所示,可得A ′B ′=A ′′B ′′=AB=2,OB ′=OB ′′=OB=1,依据图形得：点A ′的坐标为（﹣2,1）或（2,﹣1）． 故选D ．Ox y ABC28. （•威海）如图,在平面直角坐标系中,∠AOB=90°,∠OAB=30°,反比例函数的图象经由点A,反比例函数的图象经由点B,则下列关于m,n 的关系准确的是（ ）A ． m =﹣3nB ． m =﹣nC ．m=﹣nD ．m=n解答： 解：过点B 作BE ⊥x 轴于点E,过点A 作AF ⊥x 轴于点F,设点B 坐标为（a,）,点A 的坐标为（b,）,∵∠OAB=30°,∴OA=OB,设点B 坐标为（a,）,点A 的坐标为（b,）,则OE=﹣a,BE=,OF=b,AF=,∵∠BOE+∠OBE=90°,∠AOF+∠BOE=90°, ∴∠OBE=∠AOF,又∵∠BEO=∠OFA=90°, ∴△BOE ∽△OAF,∴==,即==,解得：m=﹣ab,n=,故可得：m=﹣3n ．故选A ．二.填空题1.（湖北武汉）如图,直线y ＝33x b -+与y 轴交于点A,与双4,则k曲线y ＝k x在第一象限交于点B,C 两点,且AB ⋅AC ＝＝． 答案：3（0x >）交2.（ 福建德化）如图,直线43y x =与双曲线ky x =于点A ．将直线43y x =向下平移个6单位后,与双曲线k y x=（0x >）交于点B ,与x 轴交于点C,则C 点的坐标为___________;若2AO BC=,则k =．【答案】（)0,29,123.（湖南衡阳）如图,已知双曲线)0k (xk y ＞=经由直角三角形OAB 斜边OB 的中点D,与直角边AB 订交于点C ．若△OBC 的面积为3, 则k ＝____________．【答案】24.（宁波市）如图,正方形A1B1P1P2的极点P1.P2在反比例函数y ＝2x （x ＞0）的图像上,极点A1.B1分离在x 轴和y 轴的正半轴上,再在其右侧作正方形P2P3A2B2,极点P3在反比例函数y ＝2x （x ＞0）的图象上,极点A3在x 轴的正半轴上,则点P3的坐标为 【答案】（3＋1,3－1）5.（安徽芜湖）如图,在平面直角坐标系中有一正方形AOBC,半径为反比例函数k y x=经由正方形AOBC 对角线的交点,（422）的圆内切于△ABC,则k 的值为． 【答案】46.（湖北武汉市）如图,ABCD 的极点A,B 的坐标分离是A AD 交（－1,0）,B （0,－2）,极点C,D 在双曲线y=xk 上,边y 轴于点E,且四边形BCDE 的面积是△ABE 面积的5倍,则k=_____． 【答案】12在双曲7.（湖北孝感）如图,点A 在双曲线1y x上,点B ABCD 的线3yx上,且AB∥x 轴,C.D 在x 轴上,若四边形面积为矩形,则它的面积为. 【答案】2xy第16题图BCEDoQ PA xy第16题图HF BCEDoQ PA 8.（湖北荆州,16,4分）如图,双曲线2(0)yx x经由四边形OABC 的极点A.C,∠ABC＝90°,OC等分OA 与x 轴正半轴的夹角,AB∥x 轴,将△ABC 沿AC 翻折后得到△AB＇C,B ＇点落在OA 上,则四边形OABC 的面积是.【答案】29.（浙江温州）如图,已知动点A 在函数点C,延4=y x(x>o)的图象上,AB⊥x 轴于点B,AC⊥y 轴于伸CA 至点D,使AD=AB,延伸BA 至点Ｅ,使AE=AC.直线DE 分离交x 轴,y 轴于点P,Q.当QE ：DP=4:9时,图中的暗影部分的面积等于____________. 如图,作EF⊥y 轴,DH⊥x 轴,由题意得：△QEF∽△DHP,∵QE：DP=4:9设AC= a,则AB=4a,49EF HP ,HP=94a ,∵△AED∽△DHP,∴424648==,==49934EA AD a a a a a DH HP a 得到：得：得：S暗影=2218+2a a=413+3=33） 10.（•聊城）如图,在直角坐标系中,正方形的中间在原点O,且正方形的一组对边与x 轴平行,点P （3a,a ）是反比例函数y=（k ＞0）的图象上与正方形的一个交点．若图中暗影部分的面积等于9,则这个反比例函数的解析式为．解答： 解答：解：∵反比例函数的图象关于原点对称,∴暗影部分的面积和正好为正方形面积的,设正方形的边长为b ,则b 2=9,解得b =6,∵正方形的中间在原点O , ∴直线AB 的解析式为：x =3, ∵点P （3a ,a ）在直线AB 上, ∴3a =3,解得a =1,∴P （3,1）, ∵点P 在反比例函数y =（k ＞0）的图象上,∴k=3, ∴此反比例函数的解析式为：y=．故答案为：y=的图象交11.（•衢州）如图,已知函数y=2x和函数于A.B两点,过点A作AE⊥x轴于点E,若△AOE的面积为4,P是坐标平面上的点,且以点B.O.E.P为极点的四边形是平行四边形,则知足前提的P点坐标是P1（0,﹣4）P2（﹣4,﹣4）P3（4,4）解答：解：如图∵△AOE的面积为4,函数的图象过一.三象限,∴k=8,∵函数y=2x和函数的图象交于A.B两点,∴A.B两点的坐标是：（2,4）（﹣2,﹣4）,∵以点B.O.E.P为极点的平行四边形共有3个,∴知足前提的P点有3个,分离为：P1（0,﹣4）,P2（﹣4,﹣4）,P3（4,4）．故答案为：P1（0,﹣4）,P2（﹣4,﹣4）,P3（4,4）．12.(甘肃兰州)如图,M为双曲线y＝3x上的一点,过点M作x轴.y轴的垂线,分离交直线y＝－x＋m于点D.C两点,若直线y＝－x＋m与y轴交于点A,与x 轴订交于点B,则AD•BC的值为．解答：解：作CE⊥x轴于E,DF⊥y轴于F,如图,对于y＝－x＋m,令x＝0,则y＝m;令y＝0,－x＋m＝0,解得x＝m,∴A(0,m),B(m,0),∴△OAB等腰直角三角形,∴△ADF和△CEB都是等腰直角三角形,设M的坐标为(a,b),则ab＝,CE＝b,DF＝a,∴AD＝DF＝a,BC＝CE＝b,∴AD•BC＝a•b＝2ab＝2．故答案为2．13.（.深圳）如图,双曲线ky(k0)x=>与⊙O在第一象限内交于P.Q两点,分离过P.Q 两点向x 轴和y 轴作垂线,已知点P 坐标为(1,3),则图中暗影部分的面积为．【答案】4.【剖析】∵⊙O 在第一象限关于y=x 对称,k y (k 0)x=>也关于y=x 对称,P 点坐标是（1,3）,∴Q 点的坐标是（3,1）,∴S 暗影=1×3+1×3－2×1×1=4.14.(•扬州)如图,双曲线y ＝经由Rt△OMN 斜边上的点A,与直角边MN 订交于点B,已知OA ＝2AN,△OAB 的面积为5,则k 的值是 12 ．解答： 过A 点作AC ⊥x 轴于点C,如图,则AC ∥NM,∴△OAC ∽△ONM,∴OC ：OM ＝AC ：NM ＝OA ：ON,而OA ＝2AN,即OA ：ON ＝2：3,设A 点坐标为(a,b),则OC ＝a,AC ＝b, ∴OM ＝a,NM ＝b,∴N 点坐标为(a,b), ∴点B 的横坐标为a,设B 点的纵坐标为y, ∵点A 与点B 都在y ＝图象上,∴k ＝ab ＝a •y, ∴y ＝b,即B 点坐标为(a,b),∵OA ＝2AN,△OAB 的面积为5,∴△NAB 的面积为, ∴△ONB 的面积＝5＋＝,∴NB •OM ＝,即×(b －b)×a ＝,∴ab ＝12,∴k ＝12．故答案为12．15.（武汉）如图,点A 在双曲线y=的第一象限的那一支上,AB 垂直于x 轴与点B,点C 在x 轴正半轴上,且OC=2AB,点E 在线段AC 上,且AE=3EC,点D 为OB 的中点,若△ADE 的面积为3,则k 的值为． 解答：解：连DC,如图,C∵AE=3EC,△ADE 的面积为3,∴△CDE 的面积为1, ∴△ADC 的面积为4,设A 点坐标为（a,b ）,则AB=a,OC=2AB=2a,而点D 为OB 的中点,∴BD=OD=b,∵S 梯形OBAC=S△ABO+S△ADC+S△ODC,∴（a+2a ）×b=a×b+4+×2a×b,∴ab=, 把A （a,b ）代入双曲线y=,∴k=ab=．16.(成都)如图,在平面直角坐标系xOy 中,直线AB 与x 轴.y 轴分离交于点A,B, 与反比例函数k y x=(k 为常数,且0k >)在第一象限的图象交于点E,F ．过点E 作EM⊥y 轴于M,过点F 作FN⊥x 轴于N,直线EM 与FN 交于点C ．若BE 1BF m=(m 为大于l的常数)．记△CEF 的面积为1S ,△OEF 的面积为2S ,则12S S=________． (用含m 的代数式暗示) 答案：11m m （k 的几何意义,线段比的转化,面积的几种求法）17.（湖北黄冈）已知反比例函数y ＝6x在第一象限的图象如图所示,点A 在其图象上,点B 为x 轴正半轴上一点,衔接AO.AB,且AO ＝AB,则S△AOB＝．【答案】6．【解析】如下图,过点A 作AC⊥OB 于点C,∵AO＝AB,∴OC＝BC ．而AC ＝AC,AO ＝AB,∴△AOC≌△ABC．∴S△AOC＝S△ABC．设点A 的坐标为(x,y)(x ＞0,y ＞0),则xy ＝6,AC ＝y,OC ＝x,∴S△AOB＝2S△AOC＝2×12×OC·AC＝xy ＝6．18.（四川宜宾）如图,直线x y 34=与双曲线)0(>=x x k y 交于点A,将直线x y 34=向右平移29个单位后,与双曲线)0(>=x x k y 交于点B,与x 轴交于点C,若2=BCAO,则k=．【答案】12．【解析】起首求出平移后直线的解析式,然后直线x y 34=与双曲线)0(>=x xk y 两解析式联立方程组求出点A 的纵坐标,平移后的直线解析式x y 34=－6与双曲线)0(>=x xky 两解析式联立方程组,求出点B 的纵坐标,依据类似三角形对应边成比例的性质可得A.B 的纵坐标的比等于AO ：BC,然后列出方程求解即可．19.（四川泸州）如图,()111P ,x y ,()222P ,x y ,……()P ,n n n x y 在函数()10y x x=>的图像上,11P OA ∆,212P A A ∆,323P A A ∆,……1P A A n n n -∆都是等腰直角三角形,斜边1OA .12A A .23A A ,……1A A n n -都在x 轴上（n是大于或等于2的正整数）,则点3P 的坐标是;点n P 的坐标是（用含n 的式子暗示）． 【答案】;【解析】过点P1作P1E⊥x 轴于点E,过点P2作P2F⊥x 轴于点F,过点P3作P3G⊥x 轴于点G,依据△P1OA1,△P2A1A2,△P3A2A3都是等腰直角三角形,可求出P1,P2,P3的坐标,从而总结出一般纪律得出点Pn 的坐标．21.（山东日照）如右图,直线AB 交双曲线xk y =于Ａ.B,交x 轴于点C,B 为线段AC 的中点,过点B 作BM⊥x 轴于M,贯穿连接OA.若OM=2MC,S⊿OAC=12.则k 的值为___________. 【答案】8【解析】过点A 作AD⊥x 轴于点D,则△ADO 的面积为21k,∵BM⊥x 轴,∴AD∥BM, ∵B 为线段AC 的中点,∴BM 为△ADC 的中位线,∴DM=MC, ∵OM=2MC, ∴OD=DM=MC.∴S⊿OAC=3S⊿OAD,=12=k 23,∴k=8.22.（•宁波）如图,等腰直角三角形ABC极点A在x轴上,∠BCA=90°,AC=BC=2,反比例函数y=（x＞0）的图象分离与AB,BC交于点D,E．贯穿连接DE,当△BDE∽△BCA时,点E的坐标为．【答案】．（,）．【解析】如图,∵∠BCA=90°,AC=BC=2,反比例函数y=（x＞0）的图象分离与AB,BC交于点D,E,∴∠BAC=∠ABC=45°,且可设E（a,）,D（b,）,∴C（a,0）,B（a,2）,A（2﹣a,0）,∴易求直线AB的解析式是：y=x+2﹣a．又∵△BDE∽△BCA,∴∠BDE=∠BCA=90°,∴直线y=x与直线DE垂直,=,即ab=3．∴点D.E关于直线y=x对称,则又∵点D在直线AB上,∴=b+2﹣a,即2a2﹣2a﹣3=0,解得,a=,∴点E的坐标是（,）．23.（•自贡）如图,在函数的图象上有点P1.P2.P3….Pn.Pn+1,点P1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1.P2.P3….Pn.Pn+1分离作x轴.y轴的垂线段,构成若干个矩形,如图所示,将图中暗影部分的面积从左至右依次记为S1.S2.S3….Sn,则S1=4 ,Sn=．（用含n的代数式暗示）解答： 解：当x=2时,P1的纵坐标为4,当x=4时,P2的纵坐标为2,当x=6时,P3的纵坐标为, 当x=8时,P4的纵坐标为1, 当x=10时,P5的纵坐标为：, 则S1=2×（4﹣2）=4=2[﹣]; S2=2×（2﹣）=2×=2[﹣]; S3=2×（﹣1）=2×=2[﹣];Sn=2[﹣]=;故答案为：4,．24.（•遵义）如图,已知直线y=x 与双曲线y=（k ＞0）交于A.B 两点,点B 的坐标为（﹣4,﹣2）,C 为双曲线y=（k ＞0）上一点,且在第一象限内,若△AOC 的面积为6,则点C 的坐标为（2,4）．解答：解：∵点B （﹣4,﹣2）在双曲线y=上,∴=﹣2,∴k=8, 依据中间对称性,点A.B 关于原点对称,所以,A （4,2）, 如图,过点A 作AE ⊥x 轴于E,过点C 作CF ⊥x 轴于F,设点C 的坐标为（a,）,则S △AOC=S △COF+S 梯形ACFE ﹣S △AOE=×8+×（2+）（4﹣a ）﹣×8,=4+﹣4,=,∵△AOC 的面积为6,∴=6,整顿得,a2+6a ﹣16=0,解得a1=2,a2=﹣8（舍去）,∴==4,∴点C 的坐标为（2,4）．故答案为：（2,4）．25.(武汉)如图,已知四边形ABCD 是平行四边形,BC ＝2AB,A,B 两点的坐标分离是（－1,0）,（0,2）,C,D 两点在反比例函数)0(<=x xk y 的图象上,则k 的值等于．答案：－12解析：如图,过C.D 两点作x 轴的垂线,垂足为F.G,CG 交AD于M 点,过D 点作DH⊥CG,垂足为H,∵CD∥AB,CD=AB,∴△CDH≌△ABO（AAS ）,∴DH=AO=1,CH=OB=2,设C （m,n ）,D （m －1,n －2）, 则mn ＝（m －1）（n －2）=k,解得n=2－2m, 设直线BC 解析式为y=ax+b,将B.C 两点坐标代入得2b n am b=⎧⎨=+⎩,又n=2－2m, BC ＝22(2)m n +-＝25m ,AB ＝5,因为BC ＝2AB,解得：m ＝－2,n ＝6,所以,k ＝mn ＝－12轴交于26.(咸宁)如图,一次函数y ax b =+的图像与x 轴.y两点,A B 、两点,与反比例函数k y x=的图象订交于C D、衔接分离过C D 、两点作y 轴.x 轴的垂线,垂足为E F 、,CF DE、.有以下四个结论：①CEF DEF S S ∆∆=;②AOB FOE ∆∆∽;③DCE CDF ∆∆≌;④AC BD =.个中准确的结论是 . 三.解答题1.(兰州) 如图,P1是反比例函数)0(＞k x ky =在第一象限图像上的一点,点A1的坐标为(2,0)． （1）当点P1的横坐标逐渐增大时,△P1OA1的面积将若何变更？（2）若△P1OA1与△P2A1A2均为等边三角形,求此反比例函数的解析式及A2点的坐标．FE D CB A o xyyx第15题图DCBAO2.（内蒙呼和浩特）在平面直角坐标系中,函数y＝mx（x＞0,m是常数）的图像经过点A（1,4）.点B（a,b）,个中a＞1.过点A作x中的垂线,垂足为C,过点B 作y轴的垂线,垂足为D,AC与BD订交于点M,贯穿连接AD.DC.CB与AB.（1）求m的值;（2）求证：DC∥AB;（3）当AD＝BC时,求直线AB的函数解析式.【答案】解：（1）∵点A（1,4）在函数y＝mx的图像上,∴4＝1m,得m＝4.……………………………2分（2）∵点B（a,b）在函数y＝mx的图像上,∴ab＝4.又∵AC⊥x轴于C,BD⊥y轴于D交AC于M,∴AC⊥BD于M∴M（1,b）,D（0,b）,C（1,0）∴tan∠BAC＝BMAM ＝14ab--＝1aab b--＝1b,tan∠DCM＝DMMC＝1b……………4分∴tan∠BAC＝tan∠DCM,所以锐角∠BAC＝∠DCM,DC∥AB………………………………………………6分（3）设直线AB的解析式为y＝kx＋b∵AB∥CD,AD＝BC,∴四边形ABCD是平行四边形或等腰梯形.①四边形ABCD是平行四边形时,AC与BD互相等分,又∵AC⊥BD,∴B（2,2）∴422k b k b +=⎧⎨+=⎩,解得26k b =-⎧⎨=⎩∴直线AB 的解析式为：y ＝－2x ＋6.………………8分 ②当四边形ABCD 是等腰梯形时, BD 与AC 相等且垂直,∵AC＝BD ＝4, ∴B（4,1）∴同理可求直线AB 的解析式为y ＝－x ＋5.…………………10分可以应用这一结论解决问题.如图,在统一向角坐标系中,正比例函数的图象可以看作是：将x 轴地点的直线绕着原点O xy 3=的图象分离交于第一.三象限的点B .D ,已知点)0,(m A -.)0,(mC .（1）直接断定并填写：不管α取何值,四边形ABCD 的外形必定是; （2）①当点B 为)1,(p 时,四边形ABCD 是矩形,试求p .α.和m 有值;②不雅察猜测：对①中的m 值,能使四边形ABCD 为矩形的点B 共有几个？(不必说理)（3）试探讨：四边形ABCD 能不克不及是菱形？若能, 直接写出B 点的坐标, 若不克不及, 解释来由. 【答案】解：（1）平行四边形 …………（3分）（2）①∵点)1,(p B 在xy 3=的图象上,∴p31=∴3=p ………………………………（4分） 过B 作E x BE 轴于⊥,则13==，BE OE 在BOE Rt ∆中,3331tan ===OE BE α α=30°∴2=OB又∵点B.D 是正比例函数与反比例函数图象的交点,∴点B.D 关于原点O 成中间对称∴OB=OD=2 ∵四边形ABCD 为矩形,且)0,(m A -)0,(m C ∴2====OD OC OB OA ∴2=m ;②能使四边形ABCD 为矩形的点B 共有2个; （3）四边形ABCD 不克不及是菱形. 法一：∵点A .C 的坐标分离为)0,(m -.)0,(m ∴四边形ABCD 的对角线AC 在x 轴上.又∵点B .D 分离是正比例函数与反比例函数在第一.三象限的交点. ∴对角线AC 与BD 不成能垂直. ∴四边形ABCD 不克不及是菱形法二：若四边形ABCD 为菱形,则对角线AC⊥BD,且AC 与BD 互相等分, 因为点A.C 的坐标分离为（－m,0）.（m,0）所以点A.C 关于原点O 对称,且AC 在x 轴上. 所以BD 应在y 轴上,这与“点B.D 分离在第一.三象限”抵触,所以四边形ABCD 不成能为菱形.4.（广西柳州）如图,过点P(－4,3)作x 轴.y 轴的垂线,分离交x 轴.y 轴于A.B 两点,交双曲线xk y =（k≥2）于E.F 两点．（1）点E 的坐标是________,点F 的坐标是________;（均用含k 的式子暗示）（2）断定EF 与AB 的地位关系,并证实你的结论; 如有,（3）记OEF PEF S S S ∆∆-=,S 是否有最小值？求出其最小值;若没有,请解释来由．解：（1）E （－4,－4k ）,F （3k ,3） ……3分（2）（证法一）结论：EF∥AB证实：∵P（－4,3）∴E（－4,－4k ）,F （3k ,3）,即得：PE=3+4k ,PF=3k +4 …∵1212433+=+=k k PEPA ,1212344+=+=k k PFPB ∠APB=∠EPF ∴△PAB∽△PEF∴∠PAB=∠PEF∴EF∥AB （证法二）结论：EF∥AB证实：∵P（－4,3）∴E（－4,－4k ）,F （3k ,3）,即得：PE=3+4k ,PF=3k +4 …在Rt△PAB 中,tan∠PAB=34=PAPB在Rt △PEF中,tan∠PEF=344343=++=k k PEPF ∴tan∠PAB= tan∠PEF∴∠PAB=∠PEF ∴ EF∥AB （3）（办法一）S 有最小值 ∵k S S S S FBO EAO PAOB PEDF +=++=∆∆12矩形四边形∴k S S S S PEF PEF PEDF EOF+-=-=∆∆∆12四边形由（2）知,)43)(43(2121++=⋅⋅=∆k k PF PE S PEF∴S=k S S S PEF OEFPEF --=-∆∆∆122=3)6(1211222-+=+k k k 又∵k≥2,此时S 的值随k 值增大而增大,∴当k=2时,37=最小S ∴S 的最小值是37（办法二）S 有最小值．分离过点E.F 作PF.PE 的平行线,交点为P′．由（2）知,P′⎪⎭⎫⎝⎛-43k k ，∵四边形PEP′为矩形,∴S△P′EF= S△PEF∴S=S△PEF－ S△OEF = S△P′EF－ S△OEF = S△OME +S 矩形OMP′N+ S△ONF=21222k k k ++=22k +k =3)6(1212-+k 又∵k≥2,此时S 的值随k 值增大而增大, ∴当k=2时,S 最小=37∴S 的最小值是37．5.（ 四川绵阳）如图,已知正比例函数y = ax （a≠0）的图象与反比例函致另—个交xk y =（k≠0）的图象的一个交点为A （－1,2－k2）,点为B,且A.B 关于原点O 对称,D 为OB 的中点,过点D 的线段OB 的垂直等分线与x 轴.y 轴分离交于C.E ．（1）写出反比例函数和正比例函数的解析式; （2）试盘算△COE 的面积是△ODE 面积的若干倍．【答案】（1）由图知k ＞0,a ＞0．∵点A （－1,2－k2）在xk y =图象上,∴ 2－k2 =－k,即k2－k －2 = 0,解得k = 2（k =－1舍去）,得反比例函数为xy 2=．此时A （－1,－2）,代人y = ax,解得a = 2,∴正比例函数为y = 2x ． （2）过点B 作BF⊥x 轴于F ．∵A（－1,－2）与B 关于原点对称, ∴B（1,2）,即OF = 1,BF = 2,得OB =5．由图,易知Rt△OBF∽Rt△OCD,∴OB : OC = OF : OD,而OD = OB∕2 =5∕2,∴OC = OB · OD∕OF = 2.5．由Rt△COE∽Rt△ODE 得5)5225()(22=⨯==∆∆OD OC S S ODE COE , 所以△COE 的面积是△ODE 面积的5倍． 7.（湖北荆州）已知：关于x 的一元二次方程()01222=+-+k x k x 的两根21,x x 知足02221=-x x ,双曲线xky 4=(x ＞0)经由Rt△OAB 斜边OB 的中点D,与直角边AB 交于C （如图）,求OBC △S ．【答案】解：()01222=+-+k x k x 有两根 ∴()041222≥--=∆k k 即41≤k 由02221=-x x 得：()()02121=+-x x x x当021=+x x 时,()012=--k 解得21=k ,不合题意,舍去 当021=-x x 时,21x x =,()041222=--=∆k k 解得：41=k 相符题意 ∴双曲线的解析式为：xy 1=过D 作DE⊥OA 于E,则21121S S OCA ODE =⨯==∆∆ ∵DE⊥OA,BA⊥OA∴DE∥AB∴△ODE∽△OBA∴42=⎪⎭⎫ ⎝⎛=∆∆OD OB S S ODE OBA ∴2214=⨯=∆OBA S∴23212=-=-=∆∆∆OCA OBA OBC S S S 8．（北京）已知反比例函数y= k x的图像经由点A （—3,1）（1）试肯定此反比例函数的解析式．（2）点O 是坐标原点,将线段OA 绕点O 顺时针扭转30°得到线段OB,断定点B 是否在反比例函数的图像上,并解释来由．（3）已知点P （）也在此反比例函数的图像上（个中m ＜0）,过p点作x 轴的的垂线,交x 轴于点M,若线段PM 上消失一点Q,使得△OQM 的面积是12,设Q 点的纵坐标为n,求n2－的值．【答案】解：（1）由题意德k=∴反比例函数的解析式为y= （2）过点A 作x 轴的垂线交x 轴于点C,在Rt△AOC 中可得 由题意,∠AOC=30°,OB=OA=2,∴∠BOC=60°过点B 做x 轴的垂线交x 轴于点D,在Rt△BOD 中,可得∴点B 坐标（－x=－1代入y= ,得∴点B （－y= x-的图像上．（3）由y=得xy=∵点P （）在反比例函数的y= 的图像上,m ＜0）=210m ++= ∵PQ⊥x 轴∴Q 点的坐标（m,n ） ∵△OQM 的面积为12∴12OM.QM=12∵m＜0 ∴m .n=－1 ∴22220m n n ++=∴21n -=-∴298n ++=．9.（广东广州市）已知Rt△ABC 的斜边AB 在平面直角坐标系的x 轴上,点C（1,3）在反比例函数y = k x 的图象上,且sin∠BAC= 35．（1）求k 的值和边AC 的长; （2）求点B 的坐标．【答案】（1）把C （1,3）代入y = kx 得k=3设斜边AB 上的高为CD,则sin∠BAC=CD AC =35∵C（1,3）∴CD=3,∴AC=5（2）分两种情形,当点B 在点A 右侧时,如图1有： AD=52－32=4,AO=4－1=3∵△ACD∽ABC∴AC2=AD·AB∴AB=AC2AD =254∴OB=AB－AO=254－3=134此时B 点坐标为（134,0）图1 图2当点B 在点A 左侧时,如图2此时AO=4＋1=5OB= AB －AO=254－5=54此时B 点坐标为（－54,0）所以点B 的坐标为（134,0）或（－54,0）．10.（山东聊城）如图,已知一次函数y ＝kx ＋b 的图象交反比例函数42my x-=（x>0）图象于点A.B,交x 轴于点C ．x yB A CD O O xyB A CD（1）求m 的取值规模;（2）若点A 的坐标是（2,－4）,且13BC AB =,求m 的值和一次函数的解析式;【答案】（1）因反比例函数的图象在第四象限,所以4－2m ＜0,解得m ＞2;（2）因点A(2,－4)在反比例函数图象上,所以－4＝224m-,解得m ＝6,过点A.B分离作AM⊥OC 于点M,BN⊥OC 于点N,所以∠BNC＝∠AMC ＝90°,又因为∠BCN ＝∠AMC,所以△BCN∽△ACM,所以ACBCAM BN =,因为31=AB BC ,所以41=AC BC ,即41=AM BN ,因为AM ＝4,所以BN ＝1,所以点B 的纵坐标为－1,因为点B 在反比例函数的图象上,所以当y ＝－1时,x ＝8,所以点B 的坐标为（8,－1）,因为一次函数y ＝kx ＋b 的图象过点A(2,－4),B(8,－1),所以⎩⎨⎧-=+-=+1842b k b k ,解得⎪⎩⎪⎨⎧-==521b k ,所以一次函数的解析式为y ＝21x －511.（江苏南通）如图,直线l 经由点A(1,0),且与双曲线y ＝m x（x ＞0）交于点B(2,1),过点P(p,p －1)（p ＞1）作x 轴的平行线分离交曲线y ＝m x（x ＞0）和y＝－m x（x ＜0）于M,N 两点.（1）求m 的值及直线l 的解析式;（2）若点P 在直线y ＝2上,求证：△PMB∽△PNA;（3）是否消失实数p,使得S△AMN＝4S△APM？若消失,要求出所有知足前提的p 的值;若不消失,请解释来由.【答案】（1）∵点B(2,1)在双曲线y ＝m x上,∴12m =,得m ＝2.设直线l 的解析式为y ＝kx ＋b∵直线l 过A(1,0)和B(2,1) ∴021k b k b +=⎧⎨+=⎩,解得11k b =⎧⎨=-⎩∴直线l 的解析式为y ＝x －1.(2) 证实：当x ＝p 时,y ＝p －1,点P(p,p －1)（p ＞。
反比例函数经典拓展难题
反比例函数难题拓展填空题1. （2011浙江金华，16，4分）如图，将一块直角三角板OAB 放在平面直角坐标系中，B （2，0），∠AOC ＝60°，点A 在第一象限，过点A 的双曲线为y= kx ，在x 轴上取一点P ，过点P作直线OA 的垂线l ，以直线l 为对称轴，线段OB 经轴对称变换后的像是O ′B ′. （1）当点O ′与点A 重合时，点P 的坐标是.（2）设P （t ，0）当O ′B ′与双曲线有交点时，t 的取值范围是 .2. （2011广东东莞，6，4分）已知反比例函数ky x=的图象经过（1，－2）．则k = ． 3. （2011山东滨州，18，4分）若点A(m ，－2)在反比例函数4y x=的图像上，则当函数值y ≥－2时，自变量x 的取值范围是___________. 4. （2011四川南充市，14，3分）过反比例函数y=xk(k≠0)图象上一点A ，分别作x 轴，y 轴的垂线，垂足分别为B,C ，如果⊿ABC 的面积为3.则k 的值为 .5. （2011宁波市，18，3分）如图，正方形A 1B 1P 1P 2的顶点P 1、P 2在反比例函数y ＝2x （x ＞0）的图像上，顶点A 1、B 1分别在x 轴和y 轴的正半轴上，再在其右侧作正方形P 2P 3A 2B 2，顶点P 3在反比例函数y ＝2x（x ＞0）的图象上，顶点A 3在x 轴的正半轴上，则点P 3的坐标为6. （2011浙江衢州,5,4分）在直角坐标系中，有如图所示的t ,R ABO AB x ∆⊥轴于点B ，斜(0)ky xx=>的图像经过AO的中点C，且与AB交于7. (2011浙江绍兴，13，5分) 若点12(1,),(2,)A yB y是双曲线3yx=上的点，则1y2y（填“>”,“<”“=”）.8. （2011浙江丽水，16，4分）如图，将一块直角三角板OAB放在平面直角坐标系中，B(2，0)，∠AOC＝60°，点A在第一象限，过点A的双曲线为y=kx，在x轴上取一点P，过点P 作直线OA的垂线l，以直线l为对称轴，线段OB经轴对称变换后的像是O′B′.（1）当点O′与点A重合时，点P的坐标是.（2）设P(t，0)当O′B′与双曲线有交点时，t的取值范围是 .9. （2011湖南常德，5，3分）如图1所示的曲线是一个反比例函数图象的一支，点A在此曲线上，则该反比例函数的解析式为_______________.10．（2011江苏苏州，18,3分）如图，已知点A的坐标为（3，3），AB⊥x轴，垂足为B，连接OA ，反比例函数y=xk（k>0）的图象与线段OA 、AB 分别交于点C 、D.若AB=3BD ，以点C 为圆心，CA 的45倍的长为半径作圆，则该圆与x 轴的位置关系是___________（填“相离”、“相切”或“相交”）11. （2011山东济宁，11，3分）反比例函数1m y x-=的图象在第一、三象限，则m 的取值范围是 ．12. （2011四川成都，25,4分）在平面直角坐标系xOy 中，已知反比例函数2(0)ky k x=≠满足：当0x <时，y 随x 的增大而减小．若该反比例函数的图象与直线y x =-+都经过点P ，且OP =k=_________.13. （2011安徽芜湖，15，5分）如图，在平面直角坐标系中有一正方形AOBC ，反比例函数ky x=经过正方形AOBC 对角线的交点，半径为（4-ABC ，则k 的值为 ．14. （2011广东省，6，4分）已知反比例函数ky x=的图象经过（1，－2）．则k = ． 15. (2011江苏南京，15，2分)设函数2y x =与1y x =-的图象的交战坐标为（a ，b ），则11a b-的值为__________．16. （2011上海，11，4分）如果反比例函数ky x=（k 是常数，k ≠0）的图像经过点(－1，2)，那么这个函数的解析式是__________．17. （2011湖北武汉市，16，3分）如图，□ABCD 的顶点A ，B 的坐标分别是A （－1，0），B （0，－2），顶点C ，D 在双曲线y=xk上，边AD 交y 轴于点E ，且四边形BCDE 的面积是△ABE 面积的5倍，则k=_____．18. （2011湖北黄冈，4，3分）如图：点A 在双曲线ky x=上，AB ⊥x 轴于B ，且△AOB 的面积S △AOB =2，则k=______．19. （2011湖北黄石，15，3分）若一次函数y=kx+1的图象与反比例函数y=x1的图象没有公共点，则实数k 的取值范围是 。
反比例函数经典拓展难的题目
1：〔2007年某某省初中数学竞赛〕函数y ＝1x-图象的大致形状是〔 〕A B C D2．(2009年某某市)如图，点A 、B 是双曲线3y x=上的点，分别经过A 、B 两点向x 轴、y 轴作垂线段，假如1S =阴影，如此12S S +=．3．y 与2x －3成反比例，且41=x 时，y ＝－2，求y 与x 的函数关系式．4．函数y ＝y 1－y 2，且y 1为x 的反比例函数，y 2为x 的正比例函数，且23-=x 和x ＝1时，y 的值都是1．求y 关于x 的函数关系式．5．作出反比例函数xy 12=的图象，并根据图象解答如下问题： (1)当x ＝4时，求y 的值；(2)当y ＝－2时，求x 的值；(3)当y ＞2时，求x 的X 围．6．作出反比例函数xy 4-=的图象，结合图象回答： (1)当x ＝2时，y 的值；(2)当1＜x ≤4时，y 的取值X 围；(3)当1≤y ＜4时，x 的取值X 围．7．作出函数xy 12=的图象，并根据图象回答如下问题： (1)当x ＝－2时，求y 的值；(2)当2＜y ＜3时，求x 的取值X 围； (3)当－3＜x ＜2时，求y 的取值X 围．xyABO1S2S8题图8．如图，A 、B 是函数xy 2=的图象上关于原点对称的任意两点，BC ∥x 轴，AC ∥y 轴， △ABC 的面积记为S ，如此(s= )．9．如图，点A 、B 是函数y ＝x 与xy 1=的图象的两个交点，作AC ⊥x 轴于C ，作BD ⊥x 轴于D ，如此四边形ACBD 的面积为( )．10．：如图，在平面直角坐标系xOy 中，Rt △OCD 的一边OC 在x 轴上，∠C ＝90°，点D 在第一象限，OC ＝3，DC ＝4，反比例函数的图象经过OD 的中点A ．(1)求该反比例函数的解析式；(2)假如该反比例函数的图象与Rt △OCD 的另一边交于点B ，求过A 、B 两点的直线的解析式．11．如图，A 、B 两点在函数)0(>=x xmy 的图象上．(1)求m 的值与直线AB 的解析式；(2)如果一个点的横、纵坐标均为整数，那么我们称这个点是格点．请直接写出图影局部(不包括边界)所含格点的个数．12．如图，点A 在反比例函数的图象上，AB ⊥x 轴于点B ，点C (0，1)，假如△ABC 的面积是3，如此反比例函数的解析式为____________．13．如图，直线y ＝mx 与双曲线xky =交于A ，B 两点，过点A 作AM ⊥x 轴，垂足为M ，连结BM ，假如S △ABM ＝2，如此k 的值是( )．14．如图，双曲线xky =(k ＞0)经过矩形OABC 的边BC 的中点E ，交AB 于点D 。
反比例函数经典拓展难题
反比例函数难题拓展填空题1. （2011浙江金华，16，4分）如图，将一块直角三角板OAB 放在平面直角坐标系中，B （2，0），∠AOC ＝60°，点A 在第一象限，过点A 的双曲线为y= kx ，在x 轴上取一点P ，过点P作直线OA 的垂线l ，以直线l 为对称轴，线段OB 经轴对称变换后的像是O ′B ′. （1）当点O ′与点A 重合时，点P 的坐标是.（2）设P （t ，0）当O ′B ′与双曲线有交点时，t 的取值范围是 .2. （2011广东东莞，6，4分）已知反比例函数ky x=的图象经过（1，－2）．则k = ． 3. （2011山东滨州，18，4分）若点A(m ，－2)在反比例函数4y x=的图像上，则当函数值y ≥－2时，自变量x 的取值范围是___________. 4. （2011四川南充市，14，3分）过反比例函数y=xk(k≠0)图象上一点A ，分别作x 轴，y 轴的垂线，垂足分别为B,C ，如果⊿ABC 的面积为3.则k 的值为 .5. （2011宁波市，18，3分）如图，正方形A 1B 1P 1P 2的顶点P 1、P 2在反比例函数y ＝2x （x ＞0）的图像上，顶点A 1、B 1分别在x 轴和y 轴的正半轴上，再在其右侧作正方形P 2P 3A 2B 2，顶点P 3在反比例函数y＝2x（x ＞0）的图象上，顶点A 3在x 轴的正半轴上，则点P 3的坐标为6. （2011浙江衢州,5,4分）在直角坐标系中，有如图所示的t ,R ABO AB x ∆⊥轴于点B ，斜35=(0)ky x x =>的图像经过AO 的中点C ，且与AB 交于的坐标为 .7. (2011浙江绍兴，13，5分) 若点12(1,),(2,)A y B y 是双曲线3y x=上的点，则 1y 2y （填“>”,“<”“=”）.8. （2011浙江丽水，16，4分）如图，将一块直角三角板OAB 放在平面直角坐标系中，B(2，0)，∠AOC ＝60°，点A 在第一象限，过点A 的双曲线为y= kx ，在x 轴上取一点P ，过点P作直线OA 的垂线l ，以直线l 为对称轴，线段OB 经轴对称变换后的像是O ′B ′. （1）当点O ′与点A 重合时，点P 的坐标是.（2）设P(t ，0)当O ′B ′与双曲线有交点时，t 的取值范围是 .（第15题）xyCDBOI9. （2011湖南常德，5，3分）如图1所示的曲线是一个反比例函数图象的一支，点A 在此曲线上，则该反比例函数的解析式为_______________.10．（2011江苏苏州，18,3分）如图，已知点A 的坐标为（3，3），AB ⊥x 轴，垂足为B ，连接OA ，反比例函数y=xk（k>0）的图象与线段OA 、AB 分别交于点C 、D.若AB=3BD ，以点C 为圆心，CA 的45倍的长为半径作圆，则该圆与x 轴的位置关系是___________（填“相离”、“相切”或“相交”）11. （2011山东济宁，11，3分）反比例函数1m y x-=的图象在第一、三象限，则m 的取值范围是 ．y1OAx3图112. （2011四川成都，25,4分）在平面直角坐标系xOy 中，已知反比例函数2(0)ky k x=≠满足：当0x <时，y 随x 的增大而减小．若该反比例函数的图象与直线3y x k =-+都经过点P ，且7OP =，则实数k=_________.13. （2011安徽芜湖，15，5分）如图，在平面直角坐标系中有一正方形AOBC ，反比例函数ky x=经过正方形AOBC 对角线的交点，半径为（422-）的圆内切于△ABC ，则k 的值为 ．14. （2011广东省，6，4分）已知反比例函数ky x=的图象经过（1，－2）．则k = ． 15. (2011江苏南京，15，2分)设函数2y x =与1y x =-的图象的交战坐标为（a ，b ），则11a b-的值为__________．16. （2011上海，11，4分）如果反比例函数ky x=（k 是常数，k ≠0）的图像经过点(－1，2)，那么这个函数的解析式是__________．17. （2011湖北武汉市，16，3分）如图，□ABCD 的顶点A ，B 的坐标分别是A （－1，0），B （0，－2），顶点C ，D 在双曲线y=xk上，边AD 交y 轴于点E ，且四边形BCDE 的面积是△ABE 面积的5倍，则k=_____．18. （2011湖北黄冈，4，3分）如图：点A 在双曲线ky x=上，AB ⊥x 轴于B ，且△AOB 的面积S △AOB =2，则k=______．19. （2011湖北黄石，15，3分）若一次函数y=kx+1的图象与反比例函数y=x1的图象没有公共点，则实数k 的取值范围是 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（x＞0）的图象上，斜边OA
1
、A
1
A
2
、A
2
A
3
…A
n-1
A
n
都在x轴上．则点A
10
的坐标为
反比例函数经典习题
例题讲解
【例△1】如右图，已知P10A1，△P2A1A2都是等腰直角三角形，点P1、P2都在函数y=
4
x（x＞0）的图象上，
斜边OA
1
、A
1
A
2
都在x轴上．则点A
2
的坐标为.
1、如例1图，已知△P
1
OA
△1
，P
2
A
1
A
△2
，P
3
A
2
A
△3
…P
n
A
n-1
A
n
都是等腰直角三角形，点P
1
、P
2
、P
3
…P
n
都在4
函数y=
x
2、已知点A（0,2）和点B（0，-2），点P在函数y=
1
x的图像上，如果△PAB的面积为6，求P点的坐标。
【例2】如右图，已知点（1,3）在函数y=
k
x（x＞0）的图像上，矩形ABCD的边BC在x轴上，E是对角线BD的中点，函数y=
k
x（k＞0）的图象又经过A,E两点，点E的横坐标为m，解答下列各题
1.求k的值
2.求点C的横坐标（用m表示）
3.当∠ABD=45°时，求m的值112
1、已知：如图，矩形ABCD的边BC在x轴上，E是对角线AC、BD的交点，反比例函数y=
2
x（x＞0）的图象经过A，E两点，点E的纵坐标为m．
（1）求点A坐标（用m表示）
（2）是否存在实数m，使四边形ABCD为正方形，若存在，请求出m的值；若不存在，请说明理由
2、如图1，矩形ABCD的边BC在x轴的正半轴上，点E（m，1）是对角线BD的中点，点A、E在反比例函数y=
k
x的图象上．
（1）求AB的长；
（2）当矩形ABCD是正方形时，将反比例函数y=
k
x
k
的图象沿y轴翻折，得到反比例函数y=1的图象（如
x
图2），求k1的值；
（3）直线y=-x上有一长为2动线段MN，作MH、NP都平行y轴交在条件（2）下，第一象限内的双曲线y=
k
x于点H、P，问四边形MHPN能否为平行四边形（如图3）？若能，请求出点M的坐标；若不能，请说明理由．
【例3】在平面直角坐标系中，已知A(1,0),B(0,1)，矩形OMPN的相邻两边OM，ON分别在x，y轴的正半轴上，O为原点，线段AB与矩形OMPN的两边MP,NP的交点分别为E,F,△AOF∽△BOE（顶点依次对应）
（1）求∠FOE；
（2）求证：矩形OPMN的顶点P必在某个反比例函数图像上，并写出该函数的解析式。
b（
b
如图，在平面直角坐标系中，直线y=-x+1分别交x轴、y轴于A，B两点，点P（a，b）是反比例函数y=
1
2x 在第一象限内的任意一点，过点P分别作PM⊥x轴于点M，PN⊥y轴于点N，PM，PN分别交直线AB于E，
F，有下列结论：①AF=BE；②图中的等腰直角三角形有4个；③△S
OEF
=
结论正确的序号是
1
2（a+b-1）；④∠EOF=45°．其中【例4】已知：如右图，已知反比例函数y=
k
2x和一次函数y=2x-1，其中一次函数的图像经过（a，），a+1，
b+k）.
（1）求反比例函数的解析式；
（2）如图，已知点A在第一象限，且同时在上述两个函数的图象上，求点A的坐标；
（3）利用（2）的结果，请问：在x轴上是否存在点P，使△AOP为等腰三角形？若存在，把符合条件的P
点坐标都求出来；若不存在，请说明理由．
已知反比例函数y=
k
2x和一次函数y=2x-1，其中一次函数的图象经过（a，），（a+k，b+k+2）
两点．
（1）求反比例函数的解析式；
（2）求反比例函数与一次函数两个交点A、B的坐标：
（3）根据函数图象，求不等式
k
2x＞2x-1的解集；
（4）在（2）的条件下，x轴上是否存在点P，使△AOP为等腰三角形？若存在，把符合条件
的P点坐标都求出来；若不存在，请说明理由。
x
（1）反比例函数的解析式为y=-6
一、巩固练习：解答题
1、已知反比例函数y=k
x图象过第二象限内的点A（-2，m），作AB⊥x轴于B，△R t AOB面积为3；若直
k
线y=ax+b经过点A，并且经过反比例函数y=的图象上另一点C（n，-1）．
x，m=3，n=6；
（2）求直线y=ax+b的解析式；
（3）设直线y=ax+b与x轴交于M，求AM的长；
（4）根据图象写出使反比例函数y=k
x值大于一次函数y=ax+b的值的x的取值范围。
2、已知如图：矩形ABCD的边BC在x轴上，E为对角线BD的中点，点B、D的坐标分别为B（1，0），D（3，3），反比例函
数y=k
x的图象经过A点，
（1）写出点A和点E的坐标；（2）求反比例函数的解析式；
3、如右图已知反比例函数y=k
x（k＜0）的图像经过点A（-3，m），过A点作AB⊥x轴于点△B且AOB
的面积为3。
123
(1)求k和m的值
(2)若一次函数y=ax+1的图像经过点A，并且与x轴相交于点M,求∠AMO和|AO|:|AM|的值
2交x轴于C，交y轴于D，点P为反比例函数y=
k
拓展训练
4、已知反比例函数y=
k
2x和一次函数y=2x-1，其中一次函数的图象经过（a，b）、（a+1，b+k）两点．
（1）求反比例函数的解析式；
（2）若两个函数图象在第一象限内的交点为A（1，m），请问：在x轴上是否存在点B，使△AOB为直角三角形？若存在，
求出所有符合条件的点B的坐标；
（3）若直线y=-x+
1
2x
线CD于E，过P作x轴的平行线交直线CD于F，求证：DE•CF为定值．
（x＞0）的图象上一点，过P作y轴的平行线交直
过手练习
1、已知：如右图已知反比例函数y=
12
x的图像与一次函数y=kx-7的图像都经过P（m，2）
（1）求这个一次函数的解析式；
（2）如果等腰梯形ABCD的顶点A、B在这个一次函数的图象上，顶点C、D在这个反比例函数的图象上，两底AD、BC与y轴平行，且A和B的横坐标分别为a和a+2，求a的值．。