2019最新重点高中提前招生数学试卷
2019年省重点高中提前招生选拔考试数学试卷

2019年省重点高中提前招生选拔考试数学试卷注意事项: 本卷全卷满分为120分,考试时间为100分钟.一、 填空题(本大题共有7小题,每题5分,共35分).1.同时抛掷两枚正方体骰子,所得点数之和为7的概率是 . 2.设a >b >0, a 2+b 2=4ab ,则a +b a -b的值等于 .3.如图,在△ABC 中,AB =AC ,∠BAD =20︒,且AE =AD ,则∠CDE = . 4.已知实数x 、y 满足x 2-2x +4y =5,则x +2y 的最大值为 . 5.将正偶数按下表排列: 第1列 第2列 第3列 第4列第1行 2第2行 4 6第3行 8 10 12 第1行 2第2行 4 6第3行 8 10 12第4行 14 16 18 20 ……根据上面的规律,则2006所在行、列分别是 .6.某学生为了描点作出函数y =ax 2+bx +c (a ≠0)的图象,取自变量的7个值,x 1<x 2<……<x 7,且x 2-x 1=x 3-x 2=……=x 7-x 6,分别算出对应的y 值,列表如下:但由于粗心算错了其中一个y 值,请指出算错的是___________.(从上述数据中选一个填入) 7.已知四边形ABCD 中,AD+DB+BC=16,则四边形ABCD 的面积的最大值为 .二、选择题(本大题共9小题,每小题5分,共45分.在每题所给出的四个选项中,只有一个是符合题意的,请把正确选项前的字母代号填在题后的括号内)8.方程1)1(32=-++x x x 的所有整数解的个数是( )A .2个B .3个C .4个D .5个AE D CB20°第3题 学校 姓名 试场号 座位号密 封 线 内 不 要 答 题9. 方程x1x x 2=-的解的情况是( )A .仅有一正根B .仅有一负根C .有一正根一负根D .无实根 10.甲、乙、丙、丁四名运动员参加4×100米接力赛,甲必须为第一接力棒或第四接力棒的运动员,那么这四名运动员在比赛过程中的接棒顺序有 ( )A .3种B .4种C .6种D .12种11. 如图,圆柱形开口杯底部固定在长方体水池底,向水池匀速注入水(倒在杯外),水池中水面高度是h ,注水时间为t ,则h 与t 之间的关系大致为下图中的 ( )A .B .C .D . 12.关于x 的不等式组⎩⎨⎧x +152>x -32x +23<x +a只有4个整数解,则a 的取值范围是( )A .-5≤a ≤-143B .-5≤a <-143C .-5<a ≤-143D .-5<a <-14313. 在3×3方格上做填字游戏,要求每行每列及对角线上三个方格中的数字和都等于S ,又填在图中三格中的数字如图,若要 能填成,则( )A . S =24B . S =30C . S =31D . S =3914.如图,已知⊙O 的半径是R ,C 、D 是直径AB 同侧圆周上的两点,弧AC 的度数为960,弧BD 的度数为360,动点P 在AB 上,则PC+PD 的最小值为( )A .2R BCD .R 15.观察图形,寻找规律,在“?”填上数字A .128B .136C .162D .18816. 一个三角形的边长分别为a,a,b ,另一个三角形的边长分别为b,b,a ,其中a>b ,若两个三角形的最小内角相等,则ab的值等于( ) 8 1013DCABOP?884826148422A C 三、解答题(本大题共3小题,满分40分,第17题10分,第18、19题15分,共40分).17.18.课间休息时,同学们到饮水机旁依次每人接水0.25升,他们先打开了一个饮水管,后来又打开了第二个饮水管.假设接水的过程中每根饮水管出水的速度是匀速的,在不关闭饮水管的情况下,饮水机水桶内的存水量)()(分与接水时间升x y 的函数关系图像如图所示.请结合图像回答下列问题:⑴ 存水量)()(分与接水时间升x y 的函数关系式;⑵ 如果接水的同学有28名,那么他们都接完水需要几分钟?⑶ 如果有若干名同学按上述方法接水,他们接水所用时间要比只开第一个饮水管接水的时间少用2分钟,那么有多少名学生接完水?19.已知抛物线y=ax2+bx+c经过点(1,2).(1)若a=1,抛物线顶点为A,它与x轴交于两点B、C,且△ABC为等边三角形,求b的值.(2)若abc=4,且a≥b≥c,求|a|+|b|+|c|的最小值.。
2019年省重点高中提前招生选拔考试数学试卷及答案

省重点高中提前招生选拔数学试卷注意事项:1.全卷满分150分,考试时间120分钟;2.考生在答题过程中,不能使用计数器。
一、填空题:(每小题3分,共30分)1、23-的绝对值是 。
2、方程x x 22=的解是 。
3、函数x y 21-=的自变量x 的取值笵围是 。
4、抛物线3)2(2-+-=x y 的对称轴为直线 。
5、写出一条经过第一、二、四象限,且过点(-1,3)的直线解析式 。
6、已知32=b a ,则=+bb a 。
7、一顶简易的圆锥形帐蓬,帐篷收起来时伞面的长度有4米,撑开后帐篷高2米,则帐篷撑好后的底面直径是 米。
8、在Rt △ABC 中,∠C=90°,AC=6,BC=8,则其外接圆的半径为 。
9、圆心在x 轴上的两圆相交于A 、B 两点,已知A 点的坐标为(-3,2),则B 点的坐标是 。
10、用长4㎝,宽3㎝的邮票300枚不重不漏摆成一个正方形,这个正方形的边长等于 ㎝。
二、选择题:(每小题3分,共30分.在每小题给出的四个选项中,只有一个是正确的)11、用科学记数法表示0.0625,应记作 ( )(A)0.625×101- (B)6.25210-⨯ (C)62.5310-⨯ (D)625410-⨯ 12、如果a >b,且c 为实数,那么下列不等式一定成立的是 ( )(A)ac >bc (B)ac <bc (C)ac 2>bc 2 (D)ac 2≥bc 213、元月份某一天,北京市的最低气温为-6℃,长泰县的最低气温为15℃,那么这一天长泰县的最低气温比北京市的最低气温高 ( )(A)15℃ (B)20℃ (C)-21℃ (D)21℃14、在下列图形中,既是中心对称图形又是轴对称图形的是 ( )(A)等腰三角形 (B)圆 (C)梯形 (D)平行四边形15、抛物线y=2x 2是由抛物线y=2(x+1)22+经过平移得到的,则正确的平移是( )(A)先向右平移1个单位,再向下平移2个单位(B)先向左平移1个单位,再向上平移2个单位(C)先向右平移2个单位,再向下平移1个单位(D)先向左平移2个单位,再向上平移1个单位数学试题第一页(共8页)16、在平面内有线段AB 和直线l,点A 、B 到直线l 的距离分别是4㎝、6㎝.则线段AB 的中点C 到直线l 的距离是 ( )(A)1 或 5 (B)3 或 5 (C)4 (D)517、在Rt △ABC 的直角边AC 边上有一动点P(点P 与点A 、C 不重合),过点P 作直线截得的三角形与△ABC 相似,满足条件的直线最多有 ( )(A)1条 (B)2条 (C)3条 (D)4条18、在1000个数据中,用适当的方法抽取50个作为样本进行统计,频数分布表中,54.5~57.5这一组的频率是0.12,那么,估计总体数据落在54.5~57.5之间的约有 ( )(A)6个 (B)12个 (C)60个 (D)120个19、若不等式组{148-<+>x x mx 的解集是x >3,则m 的取值范围是 ( )(A)m >3 (B)m ≥3 (C)m ≤3 (D)m <320、如图,一个等边三角形的边长与它的一边相外切的圆的周长相等,当这个圆按箭头方向从 某一位置沿等边三角形的三边做无滑动旋转,直至回到原出发位置时,则这个圆共转了( )(A)4圈 (B)3圈 (C)5圈 (D)3.5圈三、解答题:(共90分)21、(本题10分)计算:927)31()3(20-++--πtan30°数学试题第二页(共8页)22、(本题10分)解方程:113162=---x x23、(本题10分)将分别标有数字0,1,2,3的四张卡片洗匀后,背面朝上放在桌面上.抽取一张作为百位上的数字,再抽取一张作为十位上的数字, 再抽取一张作为个位上的数字,每次抽取都不放回.(1)能组成几个三位数?请写出个位数是“0”的三位数.(2)这些三位数中末两位数字恰好是“01”的概率为多少.数学试题第三页(共8页)24、(本题10分)已知:关于x 的方程022=-+k x x 有两个不相等的实数根.(1)求k 的取值范围;(2)若α、β是这个方程的两个实数根,求:ββαα+++11的值. (3)根据(2)的结果你能得出什么结论?数学试题第四页(共8页)25、(本题12分)如图,Rt △ABC 中,∠ABC=90°,OA=OB=1,与x 轴的正方向夹角为30°.求直线AB 的解析式. yBAO x数学试题第五页(共8页)26、(本题12分)已知:如图,AB是⊙O的直径,点C是⊙O上一点,CD⊥AB,垂足为D,点P在BA的延长线上,且PC是圆O的切线. C(1)求证:∠PCD=∠POC(2)若OD:DA=1:2,PA=8,求的半径的长.D OP A D B B数学试题第六页(共8页)27、(本题12分)已知:如图,⊙O1和⊙O2相交于A、B两点,动点P在⊙O2上,且在⊙O1外,直线PA、PB分别交⊙O1于C、D,问: ⊙O1的弦CD的长是否随点P的运动而发生变化?如果发生变化,请你确定CD最长和最短时P的位置;如果不发生变化,请你给出证明.C AO21OPBD数学试题第七页(共8页)28、(本题14分)已知抛物线y=-x2+bx+c与x轴的两个交点分别为A(x1,0)、B(x2,0)(A在B的左边),且x1+ x2=4.(1)求b的值及c的取值范围;(2)如果AB=2,求抛物线的解析式;(3)设此抛物线与y轴的交点为C,顶点为D,对称轴与x轴的交点为E,问是否存在这样的抛物线,使△AOC和△BED全等,如果存在,求出抛物线的解析式;如果不存在,请说明理由.+数学试题第八页(共8页)参考答案及评分标准一.1.2-3; 2。
2019年浙江省温州市重点中学提前招生数学试卷及答案

2019年浙江省温州市重点中学提前招生数学试卷一.仔细选一选(本题有10个小题,每小题3分,共30分)(下面每小题给出的四个选项中,只有一个是正确的。
) 1.下列计算正确的是().A.32a a a -=B.22(2)4a a -= C.326x x x --⋅= D.623x x x ÷= 2.如图,M ,N 两点在数轴上表示的数分别是m ,n ,则下列 式子中成立的是( ).A .-m <-nB . |m |-|n |>0C .m -1<n -1D .m +n <03. 用反证法证明命题“三角形中最多有一个角是直角或钝角”时,下列假设正确..的是( ). A .三角形中最少有一个角是直角或钝角 B .三角形中没有一个角是直角或钝角 C .三角形中三个角全是直角或钝角 D .三角形中有两个或三个角是直角或钝角4. 若函数mx x y ++=212的自变量x 的取值范围为一切实数,则m 的取值范围是( ).A .m<lB .m=1C . m>lD .m ≤15. 已知一个函数图象经过(1,-4),(2,-2)两点,在自变量x 的某个取值范围内,都有函数值y 随x 的增大而减小,则符合上述条件的函数可能是().A. 正比例函数B. 一次函数C. 反比例函数D. 二次函数6.已知四边形ABCD 的两条对角线AC 与BD 相等,则下列结论正确的个数是(). ①.当AC ⊥BD 时,四边形ABCD 一定是菱形②.当AB=AD ,CB=CD 时,四边形ABCD 一定是正方形 ③.当AB=AD=BC 时,四边形ABCD 一定是正方形④.当AC ⊥BD ,AD=AB 时,四边形ABCD 有可能是正方形 A. 1个 B. 2个 C. 3个 D. 4个 7.对于反比例函数ky x =,如果当2-≤x ≤1-时有最大值4=y ,则当x ≥8时,有(). A .最小值y =21- B .最小值1-=y C .最大值y =21- D .最大值1-=y8.七个正整数的中位数是4, 唯一众数是6, 则这七个正整数的和最小值为().A .32 B. 31 C.29 D.269. 如图,在平面直角坐标系中,以原点O 为圆心的圆过点A(13,0),直线y =kx -3k+4与⊙O 交于B 、C两点,则弦BC 长的最小值为( ). A.22B.105C.24D.123(第9题图) (第10题图)10.如图,正方形ABCD 的边长为4,点E 是AB 上的一点,将△BCE 沿CE 折叠至△FCE ,若CF 、CE 恰好与以正方形ABCD 的中心为圆心的圆O 相切,则圆O 的半径为( ).A. 1B.21- C. 31- D.312+ 二.认真填一填(本题有6个小题,每小题4分,共24分) 11. 计算:()222)4(160sin 4-+---πo =____________.12.如图,在⊙O 的内接五边形ABCDE 中,∠CAD=35°,则∠B+∠E=.(第12题图) (第13题图) (第16题图)13. 如图,在5×5的正方形网格中,△ABC 为格点三角形(顶点都在格点上),则图中与△ABC 相似(但不全等)的最小的三角形与最大的三角形的面积比值为__________.14.已知函数()31()y k x x k =+-,下列说法:①方程()31()3k x x k+-=-必有实数根;②若移动函数图象使其经过原点,则只能将图象向右移动1个单位;③当k >3时,抛物线顶点在第三象限;④若k <0,则当x<-1时,y 随着x 的增大而增大.其中正确的序号是.15.用18根火柴棒搭一个三角形,火柴棒不允许剩余、折断,则搭出的所有三角形中,属于锐角三角形的概率是________.16.如图,在四边形ABDC 中,AD=4,CD=32,∠ABC=∠ACB=∠ADC=045,则BD 的长是_________.三.全面答一答(本题有6个小题,共66分)解答应写出文字说明,证明过程或推演步骤.如果觉得有的题目有点困难,那么把自己能写出的解答写出一部分也可以.如图,在边长为4的正方形ABCD 中,请画出以A 为一个顶点,另外两个顶点在正方形ABCD 的边上,且含边长为3的所有大小不同的等腰三角形.(要求:以下为备用图,只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)18.(本小题满分10分)对x ,y 定义一种新运算▲,规定:x ▲y =by ax +(其中a ,b 均为非零常数), 例如:1▲0=a .已知1▲1=3,1-▲1=1-. (1)求a ,b 的值;(2)若关于m 的不等式组⎩⎨⎧>≤-p m m m m ▲▲24)21(3恰有3个整数解,求实数p 的取值范围.19. (本小题满分10分)记3(3)(43)(3)z x y x x y x y =---+.(1)若,x y 均为整数,求证:当x 是3的倍数时,z 能被9整除; (2)若1y x =+,求z 的最小值.小杰到学校食堂买饭,看到A ,B 两个窗口前排队的人一样多(设为a 人,8>a ),就站到A 窗口队伍的后面,观察了2分钟,他发现A 窗口每分钟有4人买了饭离开队伍,B 窗口每分钟有6人买了饭离开队伍,且B 窗口队伍后面每分钟增加5人。
2019年重点高中提前招生选拔考试数学试卷及答案

2019年重点高中提前招生选拔考试数学试卷(本卷满分120分,考试时间100分钟)一、选择题:(每小题4分,共40分) 1、已知y=12x -P (x ,y )所在的象限为( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 2、如图,△ABC 中,D 、E 分别是BC 、AC 的中点,BF 平分∠ABC ,交DE 于点F ,若BC=6,则DF 的长是( )A .2B .3C .52D .43、现规定一种新的运算:“*”:*()m n m n m n -=+,那么51*22=( )A.54B.5C.3D.9 4、已知⊙O 1和⊙O 2的半径分别为1和4,如果两圆的位置关系为相交,那么圆心距O 1O 2的取值范围在数轴上表示正确的是( )5、在学习掷硬币的概率时,老师说:“掷一枚质地均匀的硬币,正面朝上的概率是12”,小明做了下列三个模拟实验来验证。
①取一枚新硬币,在桌面上进行抛掷,计算正面朝上的次数与总次数的比值。
②把一个质地均匀的圆形转盘平均分成偶数份,并依次标上奇数和偶数,转动转盘,计算指针落在奇数区域的次数与总次数的比值。
③将一个圆形纸板放在水平的桌面上,纸板正中间放一个圆锥(如右图),从圆锥的正上方往下撒米粒,计算其中一半纸板上的米粒数与纸板上总米粒数的比值。
上面的实验中,不.科学的有( ) A .0个 B .1个 C .2个 D .3个6、抛物线2x y =上有三点P 1、P 2、P 3,其横坐标分别为m,m+1,m+3,则△P 1P 2P 3的面积为( )A .1B .2C .3D .47、矩形ABCD 中,8cm 6cm AD AB ==,.动点E 从点C 开始沿边CB 向点B 以2cm/sB .3 1 0 24 5D .3 1 0 24 5A .3 1 0 24 5C .3 1 0 24 5的速度运动至点B 停止,动点F 从点C 同时出发沿边CD 向点D 以1cm/s 的速度运动至点D 停止。
【重点高中】江西九江一中2019中考提前自主招生数学模拟试卷(6套)附解析

为 Q1( x'1, y'1)、 Q2(x'2, y'2)、 …、Q2015(x'2015, y'2015),则 P2015Q2015 的长度是
.
20.将连续正整数按以下规律排列,则位于第 7 行第 7 列的数 x 是
.
试卷第 4 页,总 7 页
三.解答题(共 6 小题,共 70 分)
21.若关于 x 的不等式组
)
A. B. C. D.
4.已知 x+y= ,| x|+| y| =5 ,则 x﹣y 的值为( )
A.
B.
C.
D.
5.二次函数 y=ax2+bx+c 的图象如图所示( a、b、 c 为常数),则函数 y=(4ac﹣b2) x+abc 和
y= 在同一平面直角坐标系中的图象,可能是(
)
试卷第 1 页,总 7 页
1.下列等式中,不一定成立的是(
)
A. =2
B.
C.a =﹣
D.
2.中国人民银行授权中国外汇交易中心公布, 2014 年 1 月 14 日银行间外汇市场人民币汇率
中间价为: 1 美元对人民币 6.0930 元,某上市公司持有美元资产为 980 万美元,用科学记数
法表示其美元资产折合成人民币为(
)元(保留两位有效数字)
A.
B.
6.关于 x 的一元二次方程 mx2+
()
A. m 且 m≠0 B.﹣
C.
D.
x+1=0 有两个不相等的同号实数根,则 m 的取值范围是
C.﹣
ቤተ መጻሕፍቲ ባይዱ
且 m≠0 D.0
7.由于货源紧缺,小王、小李两名商贩连续两次以不同的价格在同一公司购进了
2019年重点高中提前招生第一次选拔数学试卷及答案

MQNP重点高中提前招生第一次选拔试卷――数学一、选择题:(本大题共6小题,每小题5分,满分30分)1、若y <1是不等式a -3(a -y ) <y -4的解集,则a 的取值为( ) A .a >3 B 、a =3 C 、a <3 D 、a =42、在平面直角坐标系xOy 中,满足不等式2222x y x y +≤+的整数点坐标()x y ,的个数为( ) A 、10 B 、9 C 、7 D 、53、在平面直角坐标系中,点A 的坐标是(1,0),点B 的坐标是(3,3)--,点C 是y 轴上一动点,要使△ABC 为等腰三角形,则符合要求的点C 的位置共有( ) A 、2个 B 、3个 C 、4个 D 、5个4、如图,直角梯形MNPQ ,∠MNP =90°,PM ⊥NQ ,若 22PM NQ =,则=NPMQ( ) A 、21 B 、22 C 、4 D 、325、如图,三个半径为3的圆两两外切,且△ABC 的每一边都与其中的两个圆相切,则△ABC 的周长是( )A 、12+63B 、18+63C 、18+123D 、12+123 6、如图,四边形ABCD 中,AC ,BD 是对角线,△ABC 是等边三角形.30ADC ∠=︒,AD = 3,BD = 5,则CD 的长为( ) A 、23 B 、4 C 、52 D 、4.5 二、填空题(本大题共5小题,每小题5分,满分25分) 7、如果关于x 的方程22393042x kx k k ++-+=的两个实数根分别为1x ,2x ,那么2012220111x x 的值为 .8、如图,直角三角形AOB 中,O 为坐标原点,∠AOB =90°,∠B =30°,若点A 在反比例函数y =x1(x >0)图像上运动,那么点B 必在函数_________________的图像上运动。
(填写该函数表达式) 9、如图,半径为r 的圆O 沿折线ABCDE 作无滑动的滚动,如果2AB BC CD DE r π====,150,120ABC CDE BCD ∠=∠=∠=,那么,圆O 自点A至点E 转动了__________周.10、依次将正整数1,2,3,……的平方数排成一串:149162536496481100121144……,排在第1个位置的数字是1,排在第5个位置的数字是6,排在第10个位置的数字是4,排在第2008个位置的数字是_________________ 11、如果正数x ,y ,z 可以是一个三角形的三边长,那么称x y z (,,)是三角形数.若a b c (,,)和111a b c (,,)均为三角形数,且a ≤b ≤c ,则ac 的取值范围是 .三、解答题(本大题共2小题,共25分) 12、(12分)如图,⊙O 的内接四边形ABCD 中,AC ,BD 是它的对角线,AC 的中点I 是△ABD的内心. 求证:(1)OI 是△IBD 的外接圆的切线;(2)AB +AD =2BD .13、(13分)如图,在平面直角坐标系中,直角梯形OABC 的顶点A 、B 的坐标分别是(5,0)、(3,2),点D 在线段OA 上,BD =BA , 点Q 是线段BD 上一个动点,点P 的坐标是(0,3),设直线PQ 的解析式为y kx b =+.(1)求k 的取值范围;(2)当k 为取值范围内的最大整数时,若抛物线25y ax ax =-的顶点在直线PQ 、OA 、AB 、BC 围成的四边形内部,求a 的取值范围.QP xy DCBAO数学答案1.B2.B3.D4.A5.B6.B7、32-8、3y x-=9、 143 10、1 11、 1253≤<-c a12、解:(1)如图,根据三角形内心的性质和同弧上圆周角的性质知CID IAD IDA ∠=∠+∠,CDI CDB BDI BAC IDA IAD IDA ∠=∠+∠=∠+∠=∠+∠. 所以CID CDI ∠=∠, CI = CD .同理,CI = CB .故点C 是△IBD 的外心.连接OA ,OC ,因为I 是AC 的中点,且OA = OC ,所以OI ⊥AC ,即OI ⊥CI .故OI 是△IBD 外接圆的切线. (2)如图,过点I 作IE ⊥AD 于点E ,设OC 与BD 交于点F . 由BC CD =,知OC ⊥BD .因为∠CBF =∠IAE ,BC = CI = AI ,所以Rt BCF Rt AIE △≌△.所以BF = AE . 又因为I 是△ABD 的内心,所以22AB AD BD AE BD BD BF BD +-=+-==. 故2AB AD BD +=.13、解:(1)直线y kx b =+经过P (0,3),∴ 3b =. ∵B (3,2),A (5,0),BD =BA ,∴ 点D 的坐标是(1,0), ∴ BD 的解析式是1y x =-, 1 3.x ≤≤依题意,得 1,3.y x y kx =-⎧⎨=+⎩,∴4,1x k =-∴ 41 3.1k -≤≤解得13.3k --≤≤………………………………………… (2) 13,3k --≤≤且k 为最大整数,∴1k =-.则直线PQ 的解析式为3y x =-+.……………………………………………又因为抛物线25y ax ax =-的顶点坐标是525,24a ⎛⎫-⎪⎝⎭,对称轴为52x =.解方程组⎪⎩⎪⎨⎧=+-=.25,3x x y 得⎪⎪⎩⎪⎪⎨⎧==.21,25y x 即直线PQ 与对称轴为52x =的交点坐标为51(,)22,∴125224a <-<.解得 822525a -<<-.…………………………………… QPxy DC BAO。
重点高中提前招生考试语数英科试卷及答案

2019年重点高中高一分班考试考试数学试题满分:120分 时间:90分钟一、选择题(本题有10个小题,每小题3分,共30分)1.当1<a <2时,代数式︱a -2︱+︱1-a ︱的值是 ( ▲ ) A .-1 B .-3 C . 1 D .3 2.已知b a ,为实数,且1=ab ,设11+++=b b a a M ,1111+++=b a N ,则N M ,的大小关系是 ( ▲ )A .N M >B .N M =C .N M <D .无法确定3. 化简yx y x y x -+-22的结果是 ( ▲ ) A . y x + B .x y - C . y x - D . y x -- 4.已知()0332=++++m y x x 中,y 为负数,则m 的取值范围是 ( ▲ )A . m >9B . m <9C . m >9-D . m <9-5. 如图是一张简易活动餐桌,现测得OA=OB=30cm , OC=OD=50cm ,现要求桌面离地面的高度为40cm ,那么两条桌腿的张角∠COD 的大小应为 ( ▲ ) A .100° B .120° C .135° D .150° 6. 某市按以下标准收取水费:用水不超过20吨,按每吨1.2元收费,超 过20 吨则超过部分按每吨1.5元收费.某家庭五月份的水费是平均每吨1.25元, 那么这个家庭五月份应交水费 ( ▲ ) A .20元 B .24元 C .30元 D .36元 7.如图,一张半径为1的圆形纸片在边长为4的正方形内任意移动,则 在该正方形内,这张圆形纸片“能接触到的部分”的面积是 ( ▲ ) A .π-4 B . π C . π+12 D . 415π+8.已知一元二次方程x 2+bx -3=0的一根为-3,在二次函数y =x 2+bx -3的图象上有三点⎝⎛⎭⎫-45,y 1、⎝⎛⎭⎫-54,y 2、⎝⎛⎭⎫16,y 3,则y 1、y 2、y 3的大小关系是 ( ▲ ) A . y 1<y 2<y 3 B .y 2<y 1<y 3 C . y 3<y 1<y 2 D .y 1<y 3<y 29.已知20112012)322()223(-+=a ,则与a 最接近的整数是 ( ▲ ) A .6- B .5- C . 5 D . 610. 若不等式组⎪⎩⎪⎨⎧>>-a x x 1312的解为2>x ,则函数81)26(2+--=x x a y 图象与x 轴的交点情况是( ▲ )A .相交于两点B .没有交点C .相交于一点D .没有交点或相交于一点二、填空(本题有6个小题,每小题4分,共24分)11.分解因式 a a 64163+-= ▲ . 12.已知4个数据:4-,2,a ,b ,其中a ,b 是方程2220x x k +-=的两个根,则这4个数据的平均数是 ▲ . . 13. 已知31=-x x ,则代数式221xx += ▲ .14. 已知直角三角形的周长为14,斜边上的中线长为3,则直角三角形的面积为 ▲ .15. 已知a 、b 是一元二次方程012=-+x x 的两个根,则b a b a +++2222=___▲ .16.如图所示的二次函数y =ax 2+bx +c 的图象中,刘星同学观察得出了下面四条信息:(1)b 2-4ac >0; (2)0<+-c b a ; (3)2a -b <0; (4)a +b +c <0.你认为其中正确的有 ▲ (写出你认为正确的所有 信息的序号).三、解答题(本题有7小题,共66分) 17.(本题满分6分)如图,在梯形ABCD 中,AB ∥CD , °90D ∠=, 4CD =,ACB D ∠=∠,32tan =∠B , 求梯形ABCD 的面积.18. (本题满分10分)已知一次函数131+-=x y 和二次函数22+-=x x y (1)在同一坐标系中作出两个函数的图象;(2)写出二次函数的顶点坐标及与其x 轴的交点坐标;(3)根据图象写出满足>++-322x x 131+-x 的x19. (本题满分8分)(1)已知正数y x ,满足212342222=+-+yxy x y x ,且x ya =,求a 的值. (2)化简代数式()()3112131122+++-⨯-+-+a a a a a a a ,再根据(1)中求得的a 代入求值.20.(本题满分8分)如图,一次函数y =k 1x +b 的图象经过A (0,-2),B (1,0)两点,与反比例函数xk y 2= 的图象在第一象限内的交点为M ,若△OBM 的面积为2. (1)求一次函数和反比例函数的表达式;(2)在x 轴上找出点P 的坐标,使AM ⊥MP .A OBCD21.(本题满分10分)如图,C 为以AB 为直径的⊙O 上一点,AD 和过点C 的切线互相垂直,垂足为点D . (1)求证:AC 平分∠BAD ;(2)过点O 作线段AC 的垂线OE ,垂足为点E (尺规作图,保留作图痕迹,不写作法); (3)若CD =4,AC =45,求垂线段OE 的长.22.(本题满分12分)已知二次函数)0(2222≠--=m m mx x y 的图像与x 轴交于A 、B 两点,它的顶点在以AB 为直径的圆上. (1)证明:A 、B 是x 轴上两个不同的交点; (2)求二次函数的解析式;(3)设以AB 为直径的圆与y 轴交于C ,D ,求弦CD 的长.23.(本小题满分12分)矩形OABC 在直角坐标系中的位置如图所示,A 、C 两点的坐标分别为(6,0)A 、(0,3)C ,直线34y x =与BC 边相交于点D .(1) 若抛物线2(0)y ax bx a =+≠经过D 、A 两点,试确定此抛物线的表达式;(2) 若以点A 为圆心的⊙A 与直线OD 相切,试求⊙A 的半径;(3) 设(1)中抛物线的对称轴与直线OD 交于点M ,在对称轴上是否存在点Q ,以Q 、O 、 M 为顶点的三角形与OCD ∆相似,若存在,试求出符合条件的Q 点的坐标;若不存在,试说明理由.2018年重点高中分班考试语文试题(满分:120分考试时间:90分钟)一、下面短文中有10处文字差错,请找出并订正。
2019年省重点高中提前招生选拔考试数学试卷
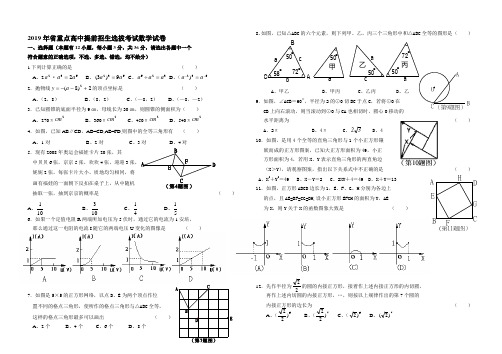
ac 乙︒50甲a︒507250︒︒︒58c a CB A(第9题图)B(第11题图) HGFED CBA (第4题图)DCBFEA E2019年省重点高中提前招生选拔考试数学试卷一、选择题(本题有12小题,每小题3分,共36分,请选出各题中一个 符合题意的正确选项,不选、多选、错选,均不给分)1.下列计算正确的是 ( ) A 、22a ·632a a = B 、6329)3(a a = C 、326a a a =÷ D 、(632)--=a a 2.抛物线2)8(2+--=a y 的顶点坐标是 ( ) A 、(2,8) B 、(8,2) C 、(—8,2) D 、(—8,—2) 3.已知圆锥的底面半径为9㎝,母线长为30㎝,则圆锥的侧面积为( ) A 、270π2cm B 、360π2cm C 、450π2cm D 、540π2cm 4.如图,已知AB ∥CD ,AB=CD,AE=FD,则图中的全等三角形有 ( ) A 、1对 B 、2对 C 、3对 D 、4对 5.现有2008年奥运会福娃卡片20张,其中贝贝6张,京京5张,欢欢4张,迎迎3张, 妮妮2张,每张卡片大小、质地均匀相同,将 画有福娃的一面朝下反扣在桌子上,从中随机抽取一张,抽到京京的概率是 ( ) A 、101 B 、103 C 、41 D 、516.如果一个定值电阻R 两端所加电压为5伏时,通过它的电流为1安培, 那么通过这一电阻的电流I 随它的两端电压U 变化的图像是 ( )7.如图是5×5的正方形网络,以点D 、E 为两个顶点作位 置不同的格点三角形,使所作的格点三角形与△ABC 全等, 这样的格点三角形最多可以画出 ( ) A 、2个 B 、4个 C 、6个 D 、8个8.如图,已知△ABC 的六个元素,则下列甲、乙、丙三个三角形中和△ABC 全等的图形是( )A 、甲乙B 、甲丙C 、乙丙9.如图,∠ACB =60○,半径为2的⊙0切BC 于点C CB 上向右滚动,则当滚动到⊙O 与CA 也相切时,圆心O 移动的水平距离为 ( ) A 、2π B 、4π C 、32 D 、4 10.如图,是用4个全等的直角三角形与1个小正方形镶 嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用X 、Y 表示直角三角形的两直角边(X >Y ),请观察图案,指出以下关系式中不正确的是 ( ) A 、X 2+Y 2=49 B 、X -Y =2 C 、2XY +4=49 D 、X +Y =13 11.如图,正方形ABCD 边长为1,E 、F 、G 、H 分别为各边上 的点,且AE=BF=CG=DH,设小正方形EFGH 的面积为Y ,AE为X ,则Y 关于X 的函数图象大致是 ( )12.先作半径为22的圆的内接正方形,接着作上述内接正方形的内切圆, 再作上述内切圆的内接正方形,…,则按以上规律作出的第7个圆的内接正方形的边长为 ( ) A 、(6)22 B 、(7)22 C 、(6)2 D 、7)2((第14题图)X二、填空题(第小题4分,共24分)13.我们知道,1纳米=10—9米,一种花粉直径为35000记为米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019年三位一体学科素养测试
数学试题卷
本试卷分试题卷和答题卷两部分,满分150分。
考试时间共90分钟。
一、选择题(本大题共8小题,每小题6分,共48分.在每小题给出的四个选项中) 1.不等式组10
20
x x +≥⎧⎨-<⎩的解在数轴上表示正确的是( ▲ )
2.已知实数,a b 满足2
2
17
404
a b a b +-++
=,那么ab -的平方根是 ( ▲ ) A . ±1 B .1 C .±21 D .2
1
3.下面哪个图形不是..正方体的展开图( ▲ )
4.若2
10x x --=,则3
2
25x x -+的值为( ▲ )
A .0
B .2
C .4
D .5
5.某大型超市从生产基地购进一批水果,运输过程中质量损失10%,假设不计超市其他费用,如果超市要想至少获得20%的利润,那么这种水果的售价在进价的基础上应至少提高( ▲ ) A . 40% B .
13 C .1
2
D . 30% 6.方程组2
23
x y x y ⎧+=⎪⎨+=⎪⎩的实数解的个数为( ▲ )
A .4
B .3
C .2
D .1
7.对于每个自变量x ,y 是2
1211y x y x =+=-,两个值中的最小值,则当32x -≤≤时,
函数y 的最小值与最大值的和是( ▲ )
A .
B .
C .
D .
A .
B .
C .
D .
第10题
第12题
A .2-
B .1
C .2
D .3
8.如图,在□ABCD 中,AB =2BC ,BE ⊥AD 于E ,F 为CD 中点, 设DEF α∠=,EFC β∠=,则下面结论成立的是( ▲ )
A .3βα<
B .4βα>
C .3βα=
D .4βα=
二、填空题 (本题有7个小题,每小题6分,共42分) 9.在2,2-,0三个整数中,任取一个,恰好使分式
x
x
-+22有意义...的概率是 ▲ . 10.已知一个几何体由一些大小相同的小正方体组成,它的主视图和俯视图如图所示,那么组成该几何体所需小正方体的个数最多为 ▲ . 11.求()
2
2
(sin 20)sin 70
tan 28tan 62++= ▲ .
12.如图,△ABC 是直角三角形,∠ABC=90︒,BC=6,BA=8,现以AC 为边在AC 的右侧作正方形ACDE ,则BE 的长为 ▲ . 13.已知△ABC 的两条高线的长分别为5和20, 若第三条高线的长也是整数,则第三条高线长的最大值为 ▲ .
14.抛物线2
21236y x tx t =-+-与x 轴有两个交点A 、B ,线段AB (含
端点)上有若干个横坐标为整数的点,且这些点的横坐标之和为21,则t 的取值范围是 ▲ . 15.设12211=112S +
+,22211=123S ++,32211=134S ++,…, 22
11
=1(1)n S n n +++,…, 1210S S S += ▲ .
第8题
A
B
C
D E F
三、解答题(本大题共4题,共60分.解答应写出文字说明、证明过程或演算步骤) 16.(本题满分12分) (Ⅰ)已知,,a b c 均不为0,且
232757
a b b c c a +--==
,求223c b
b a -+的值; (Ⅱ)已知:0x >,且
70x y -=,求x
y
的值.
17.(本题满分12分) 如图,点A 是函数1
11(0,0)k y k x x
=
>>图象上的任意一点,过点A 作AB ⊥x 轴,交另一个函数222(0,0)k y k x x =<>的图象于点B ,在y 轴上取点C ,使四边形ABCO 是平行四边形.
(Ⅰ)求证:平行四边形ABCO 的面积为定值;
(Ⅱ)设直线CB 与函数222(0,0)k y k x x =<>的图象相交于另一点D ,若不论点A 在何处,都
有CB BD =,试求12k k 与的关系式.
18.(本题满分18分)
已知矩形ABCD 中,AB =2,AD =5,点E 是AD 边上一动点,连接BE 、CE ,以BE 为直径作⊙O ,交BC 于点F ,过点F 作FH ⊥CE 于H . (Ⅰ)当直线FH 与⊙O 相切时,求AE 的长; (Ⅱ)若直线FH 交⊙O 于点G ,
(ⅰ)当FH ∥BE 时,求AE 的长;
(ⅱ)在点E 运动过程中,△OFG 能否成为等腰直角三角形?如果能,求出此时AE 的长;如果不能,说明理由. 19.(本题满分18分)
如图,Rt △ABC 的斜边AB 在x 轴上,AB =4,点B 的坐标为(-1,0),点C 在y 轴的正半轴.若抛物线2
(0)y ax bx c a =++≠的图象经过点A ,B ,C . (Ⅰ)求y 关于x 的函数解析式;
(Ⅱ)设对称轴与抛物线交于点E ,与AC 交于点D 。
在对称轴上,是否存在点P ,使以点P 、C 、D 为顶点的三角形与ΔADE 相似?若存在,请求出点P 的坐标;若不存在,请说明理由。
(Ⅲ)若在对称轴上有两个动点P 和Q (点P 在点Q 的上方),且PQ=3
3
,请求出使四边形BCPQ 周长最小的点P 的坐标.
H
F O B
C
A
E。
