时域分析法习题与解答
(自动控制原理)最近几年考试时域分析法的题总汇

自动控制原理时域分析考试试题总汇3-1设二阶控制系统的单位阶跃响应曲线如图所示,若该系统为单位反馈控制系统, 试确定其单位传递函数。
解:由图知,该系统为欠阻尼二阶系统,从图中直接得出%30%=σ s t p 1.0=根据公式3.0%21==--ζπζσe1.012=-=ζωπn p t,解得358.0)(ln )(ln 222=+=σπσζ1265.331-=-=s t p n ζπω于是开环传递函数为)1.24(3.1132)2()(2+=+=s s s s s G n ζωω 3-2单位反馈控制系统的微分方程为)(200)(200)(10)(t r t c t c t c =++•••(1) — (2) 求系统的传递函数C(s)/R(s)(3) 求系统的阻尼比和自然振荡频率 (4) 求系统的开环传递函数 (5) 若r(t)=1+2t,求稳态误差(6) 若r(t)=2sin(10t+5),求稳态输出3-4设电子心率起搏器系统如图所示,其中模仿心脏的传递函数相当于一纯积分器。
要求: (1) 若5.0=ζ对于最佳响应,问起搏器的增益K 应为多大(2) 若期望心速为60次/min ,并突然接通起搏器,问1s 后实际心速为多少瞬时最大心速为多大解:(1)系统的开环传递函数为:)105.0()(+=s s Ks G:所以闭环传递函数 Ks s KK s s K s 202020)105.0()(2++=++=φ5.0,202,202===ζζωωn n K解之得:K=20 20=n ω (2) 闭环传递函数写为40020400)(2++=s s s φ 闭环极点 j s 310102,1±-= 所以系统单位脉冲响应为)310sin 310(cos )(10t j t et h t+=- 所以阶跃响应 ⎰=τ)(60)(dt t h t c =)1(6010τ-+ec(1)=次/min 峰值时间181.025.0120141.312=-⨯=-=ζωπn p t s{%5.16%75.05.012===⨯---πζπζσee最大心率为m in /9.69%)5.161(60次=+⨯3-5已知控制系统结构如图所示,(1) 当b=0时,试确定单位阶跃输入时系统的阻尼系数、自然频率、最大超调量以及单位斜坡输入所引起的稳态误差。
第三章控制系统的时域分析例题

(3.3-1)若在图3-5(a)(b)的输入端 3.3若在图3 )(b 同时加阶跃信号, 同时加阶跃信号,它的输出信号变化相同 如果( 的输出随t线性增长, 吗?如果(a)的输出随t线性增长,说明 出现了什么问题? 出现了什么问题? (3.3-2)系统的方框图如图所示,试求系 3.3系统的方框图如图所示, 统的单位阶跃响应和调整时间。 统的单位阶跃响应和调整时间。
T / °C
85
83 82 81 80 78
81.81 80.19 6 20
24
t / min
• 答:由温度变量过程曲线可知: 由温度变量过程曲线可知:
最大偏差:A = 85 − 80 = 5°C 余差:C = 81 − 80 = 1°C 衰减比:第一个波峰值B = 85 − 81 = 4°C 第二个波峰值B′ = 83 − 81 = 2°C n = B / B′ = 4 : 1 过渡时间:由题要求,被控量进入新稳态的 ± 1%, 就可以认为过渡过程已经结束,那么限制范围应是 81 × (± 1% ) = ±0.81°C 由图可以看出,过渡时间为24min。 振荡周期:T = 20 − 6 = 14min
σ p = 73%
t s = 8s(∆ = 0.02)
解:
(2)ς
= 0.1,ω n = 1;
− 0.1×5t
2 e 1 × 1 − 0.12 t + arctan 1 − 0.1 x (t ) = 1 − sin 0.1 1 − 0.12 = 1 − 1.005e −0.1×5t sin (0.995t + 1.47 )
模 = 虚部 + 实部 = ω n
2 2
(3.4 − 9)对于欠阻尼的二阶系统
信号与系统第5章离散信号与系统的时域分析习题答案
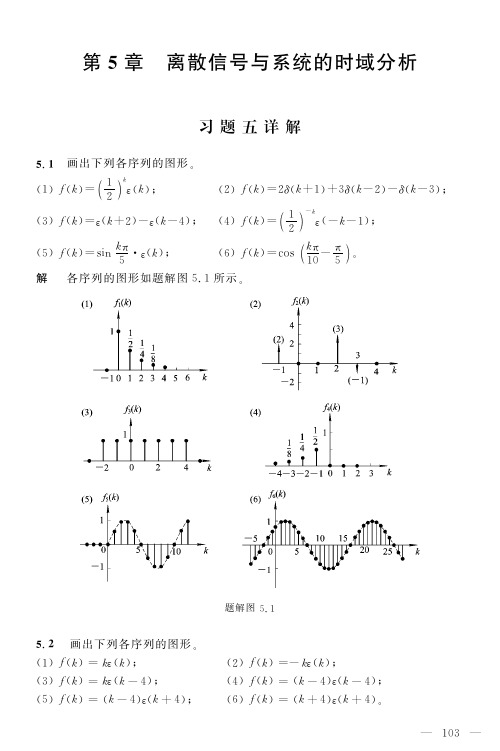
#*
!&! # * +" #%%%%%%% ) ’ # !&! 不 是 周 期 序 列 ’故 0 , ! !由 于 式中!&! # + $# , + 不 是 整 数’ ) * +" !’即 + $ ’ # ’ !&!
# $% !! (! 各序列图形如题图 (! # 所示 ’试求 + " #若 "" ’则 "" # / #和 "" #各是多少 0 ! ##$ " ## ## / # !" #" &" %# "" " #若 1" ’则 1" # / #和 1" #各是多少 0 # ##$ " ## ## / # #" %" &" %# 1" 解 ! 根据卷积和的图解机理 ’求得 " # #$ ’’!"" #$ ,’!"" #$ 5$ ! / # %# "" " # #$ !’! #$ ,’! #$ ,! # / # (! %# 1" 1" 1" !! )! 已知两序列 . ’ . ##$ , /’ !’ !’ !’ / ##$ , /’ !’ #’ %’ / !" !" #" " ! 试计算 " ! ## ## &" !" #" 解 ! 因为 "# + #! %!! !! !! ! " # # " # / "# + ! ! ! " ! # ! ! & ! !
《电路分析》西南交大 习题解答 第4章 一阶电路的时域分析

第4章 一阶电路的时域分析基础与提高题P4-1 uF 2电容器的端电压是V 10时,存储电荷是多少? 解:uC 20101026=⨯⨯==-CU qP4-2 充电到V 150的uF 20电容器,通过一个M Ω3电阻器放电,需要多长时间?何时的放电电流最大?最大值多少?解:s RC 60102010366=⨯⨯⨯==-τ,放电完毕约等于s 3005=τ 刚开始放电时电流最大,最大电流为uA 501031506=⨯ P4-3 当uF 2电容器电压如图P4-3所示时,画出流过此电容器的电流波形图。
假设电压与电流为关联参考方向。
图P4-3 图1解:关联参考方向,则电容电流dtt du C t i c c )()(=,分段求解如下: (1)A t i V t u ust c c 0)(,0)(,0=∴=≤(2)()A t i Vt t u us t c c 401020102)(,1020)(,10666=⨯⨯⨯=∴⨯=≤≤-(3)A t i V t u us t c c 0)(,20)(,41=∴=≤≤(4)()A t i V t t u us t c c 40)1020(102)(,1001020)(,64666-=⨯-⨯⨯=∴+⨯-=≤≤-(5)()A t i Vt t u us t c c 201010102)(,801010)(,86666=⨯⨯⨯=∴-⨯=≤≤-(6)A t i V t u ust c c 0)(,0)(,8=∴=≥ 电容的电流如图1所示。
P4-4 0.32tA 电流流过150mH 电感器,求s t 4=时,电感器存储的能量。
解:电感器存储的能量()23232.0101502121t Li W ⨯⨯⨯==- 当s t 4=时,电感器存储的能量为P4-5 由20V 电源与Ω2电阻、H 6.3电感组成的串联电路,合上开关后经过多长时间电流达到其最大值,最大值多少?设合上开关前电感无初始储能。
第三章 线性系统的时域分析与校正 习题及答案

第三章 线性系统的时域分析与校正习题及答案3-1 已知系统脉冲响应t e t k 25.10125.0)(-=试求系统闭环传递函数)(s Φ。
解 Φ()()./(.)s L k t s ==+00125125 3-2 设某高阶系统可用下列一阶微分方程T c t c t r t r t ∙∙+=+()()()()τ近似描述,其中,1)(0<-<τT 。
试证系统的动态性能指标为 T T T t d ⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛-+=τln 693.0t T r =22. T T T t s ⎥⎦⎤⎢⎣⎡-+=)ln(3τ 解 设单位阶跃输入ss R 1)(=当初始条件为0时有:11)()(++=Ts s s R s C τ 11111)(+--=⋅++=∴Ts T s s Ts s s C ττC t h t T Te t T()()/==---1τ 1) 当 t t d = 时h t T Te t td ()./==---051τ12=--T T e t T d τ/ ; T t T T d -⎪⎭⎫ ⎝⎛-=-τln 2ln ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+=∴T T T t d τln 2ln2) 求t r (即)(t c 从1.0到9.0所需时间)当 Tt e TT t h /219.0)(---==τ; t T T T 201=--[ln()ln .]τ 当 Tt e TT t h /111.0)(---==τ; t T T T 109=--[ln()ln .]τ 则 t t t T T r =-==21090122ln ... 3) 求 t sTt s s e TT t h /195.0)(---==τ ]ln 3[]20ln [ln ]05.0ln [ln TT T T T T T T T t s τττ-+=+-=--=∴3-3 一阶系统结构图如图3-45所示。
要求系统闭环增益2=ΦK ,调节时间4.0≤s t s ,试确定参数21,K K 的值。
信号与系统王明泉版本~第二章习题解答
第2章 线性时不变连续系统的时域分析2.1 学习要求(1)会建立描述系统激励与响应关系的微分方程;(2)深刻理解系统的完全响应可分解为:零输入响应与零状态响应,自由响应与强迫响应,瞬态响应与稳态响应;(3)深刻理解系统的零输入线性与零状态线性,并根据关系求解相关的响应; (4)会根据系统微分方程和初始条件求解上述几种响应; (5)深刻理解单位冲激响应的意义,并会求解;(6)深刻理解系统起始状态与初始状态的区别,会根据系统微分方程和输入判断0时刻的跳变情况; (7)理解卷积运算在信号与系统中的物理意义和运算规律,会计算信号的卷积。
; 2.2 本章重点(1)系统(电子、机械)数学模型(微分方程)的建立; (2)用时域经典法求系统的响应; (3)系统的单位冲激响应及其求解;(4)卷积的定义、性质及运算,特别是()t δ函数形式与其它信号的卷积; (5)利用零输入线性与零状态线性,求解系统的响应。
2.3 本章的知识结构2.4 本章的内容摘要2.4.1系统微分方程的建立电阻:)(1)(t v Rt i R R =电感:dtt di L t v L L )()(= )(d )(1)(0t i v Lt i L tL L +=⎰∞-ττ 电容:dtt dv C t i C C )()(= ⎰+=tt L C C t i i Ct v 0)(d )(1)(0ττ 2.4.2 系统微分方程的求解 齐次解和特解。
齐次解为满足齐次方程t n t t h e c e c e c t y 32121)(λλλ+⋅⋅⋅++=当特征根有重根时,如1λ有k 重根,则响应于1λ的重根部分将有k 项,形如t k t k t k t k h e c te c e t c e t c t y 111112211)(λλλλ++⋅⋅⋅++=--- 当特征根有一对单复根,即bi a +=2,1λ,则微分方程的齐次解bt e c bt e c t y at at h sin cos )(21+= 当特征根有一对m 重复根,即共有m 重ib a ±=2,1λ的复根,则微分方程的齐次解bt e t c bt te c bt c t y at m m at h cos cos cos )(121-+⋅⋅⋅++= bt e t d bt te d bt e d at m m at at sin sin sin 121-+⋅⋅⋅+++ 特解的函数形式与激励函数的形式有关。
控制系统的时域分析例题和习题

2
1
T0
10 K
TK0
0.2 2.5
因此有
ts 4.75T0 0.95 1
红河学院自动化系
自动控制原理
3-9 电子心脏起博器心律控制系统结构图如题3-49图所示,其中模仿心脏的传递函
数相当于一纯积分环节。
1.若 0.5 对应最佳响应,问起博器增益 K 应取多大?
2、若期望心速为60次/min,并突然接通起博器,问1s钟后实际心速为多
2.2T
阶跃响应到达并保持 在终值 5%误差带内
3) 求 ts
h(
ts
)
0.95
1
T
T
ets
/T
所需的最短时间
T
T
T
ts T [ln T
ln0.05 ] T [ln T
ln 20 ] T [ 3 ln T
]
红河学院自动化系
自动控制原理
3-5 一种测定直流电机传递函数的方法是给电枢加一定的
+
A4 s+3
按不相等实数极点确定A1 ,A3 ,A4 得:
A1=
-1 2
A3=
2 3
A4=112
A2=
-3 4
A2将=(各2-11待)!定( d系2-1[数Fd(代ss)2(入-1s-上p1 式)2]得) s=:p1 f(t)= =2-tde[-st(-d(sss+43+23e))-]t+s=32-1=+-41312 e-3t
K 应取何值,调节时间 ts 是多少?
解 依题意应取 1,这时可设闭环极点为
s1,2 1 T0 写出系统闭环传递函数
( s )
10 K
_第二章连续系统的时域分析习题解答

— P2-1 —第二章 连续系统的时域分析习题解答2-1 图题2-1所示各电路中,激励为f (t ),响应为i 0(t )和u 0(t )。
试列写各响应关于激励微分算子方程。
解:.1)p ( ; )1(1)p ( , 111 , 1111)( )b (;105.7)625(3 102 ;)(375)()6253(4)()()61002.041( )a (0202200204006000f i p f p u p f p p p u i f p p p ppft u pf i p pu i t f t u p t f t u p =+++=++⇒++=+=+++=++=⨯=+⇒⨯==+⇒=++-- 2-2 求图题2-1各电路中响应i 0(t )和u 0(t )对激励f (t )的传输算子H (p )。
解:.1)()()( ; 11)()()( )b (;6253105.7)()()( ; 6253375)()()( )a (220 20 40 0 +++==+++==+⨯==+==-p p p p t f t i p H p p p t f t u p H p p t f t i p H p t f t u p H f i f u f i fu2-3 给定如下传输算子H (p ),试写出它们对应的微分方程。
.)2)(1()3()( )4( ; 323)( )3(; 33)( )2( ; 3)( )1( +++=++=++=+=p p p p p H p p p H p p p H p p p H解:; 3d d 3d d )2( ; d d 3d d)1( f tf y t y t f y t y +=+=+ . d d 3d d 2d d 3d d )4( ; 3d d 3d d 2 )3( 2222t f tf y t y t y f t f y t y +=+++=+ 2-4 已知连续系统的输入输出算子方程及0– 初始条件为:.4)(0y ,0)(0y )y(0 ),()2(13)( )3(; 0)(0y ,1)(0y ,0)y(0 ),()84()12()( )2(;1)(0y ,2)y(0 ),()3)(1(42)( )1(---2---2--=''='=++==''='=+++-=='=+++=t f p p p t y t f p p p p t y t f p p p t yf (u 0(t ) (b) u 0(t ) (a)图题2-1— 2 —试求系统的零输入响应y x (t )(t /0)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章 时域分析法习题3-1设温度计需要在一分钟内指示出响应值的98%,并且假定温度计为一阶系统,试求时间常数T 。
如果将温度计放在澡盆内,澡盆的温度以min /C 10︒的速度线性变化,求温度计的误差。
解:min 25.0min 14=⇒=T T 传递函数125.01)(+=Φs stt r 10)(=425.025.01)125.0(10)()()(22++-=+=⋅Φ=s sss s s R s s C tet t c 45.25.210)(-+-=C t c t r t e e s s ss ︒=-==∞→∞→5.2)()(lim )(lim3-4 单位负反馈系统的开环传递函数为)1(1)(+=s s s G ,求该系统的上升时间r t 、峰值时间p t 、超调量%σ和调整时间s t 。
解:11)(2++=Φs s s12=n ξω,12=n ω.3arccos ,5.0,1πξβξω====⇒n 。
%16%100%,63.31,42.2121/22=⨯==-==--=--ξπξσξωπξωβπe t t n p n r%)2(84%),5(63=∆===∆==ns ns t t ξωξω3-6 系统的单位阶跃响应为tteet c 10602.12.01)(---+=,试求:(1) 系统的闭环传递函数;(2) 系统的阻尼比ξ和无阻尼自然振荡频率n ω。
解:(1)ss R s s ss C 1)(,102.1602.01)(=+-++=60070600)(2++=Φs s s(2) 702=n ξω,6002=n ω.43.1,5.24==⇒ξωn3-7 设单位负反馈二阶系统的单位阶跃响应曲线如图所示, 试确定其开环传递函数。
解:%30%100)13.1(%100%21/=⨯-=⨯=--ξπξσe6.33,356.01.012==⇒=-=n n p t ωξξωπ)9.23(1.1129)2()(2+=+=s s s s s G n nξωω3-8 单位负反馈系统的开环传递函数)1()(+=Ts s K s G 。
当)()(t t r ε=时,系统的动态性能指标%30%≤σ,%)5(3.0=∆≤s t s ,试选择参数K 及T 值。
解:TK s Ts TKKs TsK s ++=++=Φ1)(22TKTK TK Tn n n 21,,122==⇒==ξωωξω3.06,356.021%30%≤=≥⇒≤T t TKs σ5.39,05.0≤≤⇒K T3-11 闭环系统的特征方程如下,试用劳斯判据判断系统的稳定性。
(1)010092023=+++s s s (2)020092023=+++s s s (3)0516188234=++++s s s s (4)012362345=+++++s s s s s(1) Routh :s 3 1 9 s 220 100 s 1 4 s 0100 第一列同号,所以系统稳定。
(2) Routh :s 3 1 9 s 220 200s 1 -1s 0 200 第一列变号,所以系统不稳定。
(3) Routh :s4 1 18 5s 3 8 16s 2 16 5s 1 216s 0 5 第一列同号,所以系统稳定。
(4) Routh :s51 3 1s 4 6 2 1s 3 16 5 s 2 2 1s 1 -6s 0 1 第一列变号,所以系统不稳定。
3-12 单位负反馈系统的开环传递函数解:(1)系统特征方程:0401423=+++K s s sRouth : s 3 1 40 s 2 14 K s 1 560-Ks 0K系统稳定,560-K>0,K>0所以:0<K<560)10)(4()(++=s s s Ks G(1) 试确定系统稳定时的K 值范围;(2) 确定使闭环极点的实部不大于-1的K 值范围。
(2)将11-=s s 代入特征方程,得:027151112131=-+++K s s sRouth : s 31 15 s 211 K-27 s 1 192-Ks 0K-27 192-K>0,K-27>0所以:27<K<1923-13 系统结构如图所示,确定系统稳定时τ的取值范围。
解:开环传递函数:)101()1(10)(2τ+++=s s s s G特征方程:01010)101(23=++++s s s τRouth : s 3 1 10s 2τ101+ 10 s 1τ10s 0 10 系统稳定,010>τ,即0>τ3-16 单位反馈控制系统的开环传递函数如下。
试求各系统的静态位置误差系数p K 、速度误差系数v K 和加速度误差系数a K ,并确定当输入信号分别为2,2 ),()(t t t t r ε=和221t t ++时系统的稳态误差ss e 。
(1) )12.0)(11.0(20)(++=s s s G (2) )10)(2(200)(++=s s s s G解:(1)0)(lim ,0)(lim ,20)(lim 2======→→→s G s K s s G K s G Ks a s v s p∞====+==ss pss e t t r t t r Ke t t r 时,型系统,2)(,2)(;21111),()(0ε∞=++=ss e t t t r 时,221)((2)0)(lim ,10)(lim ,)(lim 2====∞==→→→s G s K s s G K s G K s a s v s pI 型系统 ∞======+==ss vss pss e t t r K V e t t r Ke t t r 时,2)(,2.0,2)(;011),()(ε∞=++=ss e t t t r 时,221)((3) )104()12(10)(22+++=s s s s s G (4) )2)(12()13(5)(2+++=s s s s s G(3)1)(lim ,)(lim ,)(lim 2==∞==∞==→→→s G s K s s G K s G Ks a s v s pII 型系统 2)(,0,2)(;011),()(2=======+==ass vss pss K A e t t r K V e t t r Ke t t r 时,ε221)(2=++=ss e t t t r 时,(4)由劳斯判据知系统不稳定,故不存在稳态误差。
3-17 闭环系统的结构如图所示。
(1) 当ss R 1)(=,超调量%20%=σ,调整时间%)5(8.1=∆=s t s 时,试确定参数1K 和τ的值;(2) 当输入信号分别为 ,)( ),()(t t r t t r =ε=221)(t t r =时,求系统的稳态误差。
解:(1)系统开环传递函数)()(11τK s s K s G +=闭环传递函数1121)(K s K s K s ++=Φτ65.38.13,456.0%20%100%21/=⇒===⇒=⨯=--n ns t eωξωξσξπξ25.04.13,33.32211=⇒====τωξωτn n K K(2)系统为I 型系统,)29.3(7.13)(+=s s s G开环增益为16.429.37.13==K∞=======ss e t t r t t r t t r ,21)(,24.016.41e ,)(,0e ,)()(2ss ss 时时时ε3-18 系统结构如图所示,试确定使阻尼比7.0=ξ和单位斜坡函数 输入时稳态误差25.0=ss e 的参数K 和τ的取值。
解: )K 2(K )(τ++=s s s G25.02212)(=+=+=+=KK KK e KK t t r ss τττ,时,开环增益为:K K n n τξωω+==22,186.0,36.31==⇒τK3-19 系统结构如图所示,其中)()()()(21t t d t d t r ε===。
试求:(1) 在)(t r 作用下系统的稳态误差;(2) 在)(1t d 和)(2t d 同时作用下系统的稳态误差; (3) 在)(1t d 作用下,且sK K s G p+=)(1和Jss F 1)(=时,系统的稳态误差。
解:(1)r(t)作用时,令0)()(21==t d t d )()(11)(s F s G s er +=Φ,ss R 1)(=,则))()(1(1)()()(s F s G s s R s s E er +=Φ=)0()0(11)(lim 0F G s sE e s ss +==→(2) )(),(21t d t d 作用时,令0)(=t r )()(1)()(1s F s G s F s ed +-=Φ,)()(11)(1s F s G s ed +-=Φ))()(1()(1))()()()(()(2211s F s G s s F s D s s D s s E ed ed +--=Φ+Φ=)0()0(1)0(1)(lim 0F G F s sE e s ss ++-==→(3)01)(11lim)()(lim )(lim 0110=++-=Φ==→→→Jss K KJs s D s s s sE e ps ed s s ss3-20 图示复合控制系统中bs as s G c +=2)(,)102.0)(11.0(10)(++=s s s s G ,试选择a 和b 的值,使系统由I 型系统的无差度提高为III 型系统的无差度。
解: 10)102.0)(11.0(1010)102.0)(11.0()(1)()(1)(2+++--++=+-=Φs s s bsass s s s G s G s G s c er要想系统误差度为III 型系统无差度,则需要当31)(ss R =时,稳态误差零。
10)102.0)(11.0(101012.0002.01lim)()(lim 2232+++--++⋅=Φ=→→s s s bsass s s ss s sR e s er s ss令0101,01012.0=-=-b a 得1.0,012.0==b a3-21 系统结构如图(a)所示,(1) 若)(,1)()(,0)(,1)(3212s G s G s G s D ss R ====为一阶环节,输出响应曲线如图(b)所示,求)(3s G ; (2) 若ss G s s G s K s G t t d t t r 25.0)(,18)(,12.0)(),(2)(,)(321=+=+=ε-==,试求当1=K 和5=K 时系统的稳态误差。
(a)(b)解:(1)设系统闭环传递函数为1)(+=ΦTs K s ,由输出响应曲线知,。
