实验三 数字PID控制
pid控制实验报告

pid控制实验报告实验报告:PID控制一、实验目的通过本实验,我们的目的是深入了解PID(比例、积分、微分)控制算法,理解其在实际控制中的应用,掌握PID参数的调整方法。
二、实验原理PID控制是依据被控对象的误差(偏差)与时间的积分、微分关系来确定控制器输出的控制方式。
具体来说,PID控制器输出的控制量=Kp*(当前误差+上次误差*dt+所有误差的积分),其中Kp、Ki和Kd分别为比例系数、积分系数和微分系数。
它通过对偏差的补偿,使得被控对象能够在振荡绕过设定值、稳定达到设定值的过程中快速、准确定位设定值。
三、实验设备本实验采用的设备为PID控制器、液晶显示屏、电压控制电机和传感器。
四、实验步骤1. 首先,我们需要将系统设为手动调节状态,关闭控制器。
2. 然后,我们将传感器和记录仪建立起连接。
3. 将系统调整为自动控制状态,让控制器自行计算控制量、作出相应控制。
4. 调整PID控制器的Kp系数,以调整控制精度。
5. 调整PID控制器的Ki系数,以调整控制的灵敏度。
6. 调整PID控制器的Kd系数,以调整控制器的稳定性。
7. 最终完成调整后,我们可以用振荡器数据展示出来实验结果。
五、实验结果在完成调整后,我们得出的控制器输出的控制量稳定在理论值附近,在控制精度与控制的灵敏度达到较好平衡的情况下,控制器的稳定性得到了保证。
实验结果具有较好指导意义。
六、结论本实验通过掌握PID控制算法的实际应用方法,以及对参数的合理设置为基础,完成了对PID控制器各参数调整技巧的掌握,极大地丰富了实验基础技能。
同时,实验结果为之后的实际应用提供了参考,有着极其重要的现实意义。
数字pid控制算法的研究实验报告

数字pid控制算法的研究实验报告数字PID控制算法是一种常用的控制系统算法,能够通过对比例、积分和微分三个参数进行调整来控制系统的稳定性和精度。
本文将对数字PID控制算法的研究实验进行详细的描述。
实验设计本次实验采用一个控制器,其输出为闭环信号,被用于控制一个加速变量,以实现一个平稳的控制过程。
实验的具体步骤如下:1. 确定控制器的输出参数根据控制系统的实际需求,确定控制器的比例参数、积分参数和微分参数。
2. 建立实验模型将实验系统建模为阻尼比为1,反馈系数为0.8的系统。
其中,加速变量的幅值为0.1,根据实验结果,调整PID参数后可以使系统达到稳定的输出状态。
3. 进行实验将实验模型连接到控制器上,通过输入信号控制加速变量的幅值,实现控制系统的平稳输出。
通过仿真软件对实验过程进行模拟,记录实验的增益、响应时间和精度等指标。
4. 分析实验结果根据实验结果,对PID控制器的输出参数进行调整,以获得更好的控制效果。
同时,对不同参数组合的增益、响应时间和精度等指标进行分析,探究不同参数组合对控制效果的影响规律。
实验结果通过本次实验,得到以下实验结果:- 比例参数对控制效果的影响规律为:当比例参数增大时,控制增益增大,但响应时间变慢;当比例参数减小时,控制增益减小,但响应时间变快。
- 积分参数对控制效果的影响规律为:当积分参数增大时,控制增益减小,但控制稳定性好;当积分参数减小时,控制增益增大,但控制稳定性差。
- 微分参数对控制效果的影响规律为:当微分参数增大时,控制增益增大,但控制稳定性好;当微分参数减小时,控制增益减小,但控制稳定性差。
结论通过本次实验,可知数字PID控制算法在平稳控制过程中具有较好的效果,不同的参数组合可以影响控制效果的稳定性和精度,可以根据实际应用的需要调整PID控制器的参数,以实现更好的控制效果。
PID控制实验报告

实验二 数字PID 控制计算机控制是一种采样控制,它只能根据采样时刻的偏差值计算控制量。
因此连续PID 控制算法不能直接使用,需要采用离散化方法。
在计算机PID 控制中,使用的是数字PID 控制器。
一、位置式PID 控制算法按模拟PID 控制算法,以一系列的采样时刻点kT 代表连续时间t ,以矩形法数值积分近似代替积分,以一阶后向差分近似代替微分,可得离散PID 位置式表达式:∑∑==--++=⎪⎪⎭⎫ ⎝⎛--++=k j di p k j D I p T k e k e k T j e k k e k k e k e T T j e T T k e k k u 00)1()()()())1()(()()()( 式中,D p d I pi T k k T k k ==,,e 为误差信号(即PID 控制器的输入),u 为控制信号(即控制器的输出)。
在仿真过程中,可根据实际情况,对控制器的输出进行限幅。
二、连续系统的数字PID 控制仿真连续系统的数字PID 控制可实现D/A 及A/D 的功能,符合数字实时控制的真实情况,计算机及DSP 的实时PID 控制都属于这种情况。
1.Ex3 设被控对象为一个电机模型传递函数BsJs s G +=21)(,式中J=0.0067,B=0.1。
输入信号为)2sin(5.0t π,采用PD 控制,其中5.0,20==d p k k 。
采用ODE45方法求解连续被控对象方程。
因为Bs Js s U s Y s G +==21)()()(,所以u dt dy B dty d J =+22,另y y y y ==2,1,则⎪⎩⎪⎨⎧+-==/J)*u ((B/J)y y y y 12221 ,因此连续对象微分方程函数ex3f.m 如下 function dy = ex3f(t,y,flag,para)u=para;J=0.0067;B=0.1;dy=zeros(2,1);dy(1) = y(2);dy(2) = -(B/J)*y(2) + (1/J)*u;控制主程序ex3.mclear all;close all;ts=0.001; %采样周期xk=zeros(2,1);%被控对象经A/D转换器的输出信号y的初值e_1=0;%误差e(k-1)初值u_1=0;%控制信号u(k-1)初值for k=1:1:2000 %k为采样步数time(k) = k*ts; %time中存放着各采样时刻rin(k)=0.50*sin(1*2*pi*k*ts); %计算输入信号的采样值para=u_1; % D/AtSpan=[0 ts];[tt,xx]=ode45('ex3f',tSpan,xk,[],para); %ode45解系统微分方程%xx有两列,第一列为tt时刻对应的y,第二列为tt时刻对应的y导数xk = xx(end,:); % A/D,提取xx中最后一行的值,即当前y和y导数yout(k)=xk(1); %xk(1)即为当前系统输出采样值y(k)e(k)=rin(k)-yout(k);%计算当前误差de(k)=(e(k)-e_1)/ts; %计算u(k)中微分项输出u(k)=20.0*e(k)+0.50*de(k);%计算当前u(k)的输出%控制信号限幅if u(k)>10.0u(k)=10.0;endif u(k)<-10.0u(k)=-10.0;end%更新u(k-1)和e(k-1)u_1=u(k);e_1=e(k); endfigure(1);plot(time,rin,'r',time,yout,'b');%输入输出信号图xlabel('time(s)'),ylabel('rin,yout');figure(2);plot(time,rin-yout,'r');xlabel('time(s)'),ylabel('error');%误差图程序运行结果显示表1所示。
实验三 数字式PID调节器控制算法仿真

实验三 数字式PID 调节器控制算法仿真一、实验目的1、了解并掌握基本的数字PID 控制算法和常用的PID 控制改进算法。
2、掌握用Matlab 进行仿真的方法。
3、了解PID 参数整定的方法及参数整定在整个系统中的重要性。
二、实验设备PC 机(Matlab 软件)三、实验原理1、基本的PID 控制算法:基本的数字P0控制有三种算法:位置式、增量式和速率式,其中应用最为广泛的是增量式,因为增量式算法只与最近几次采样值有关,不需要累加;计算机输出增量,误差动作时影响小。
因此这里采用增量式PID 算法:)]1()1(2)([)()]1()([)(-+--++--=∆k e k e k e k k e k k e k e k k u d i p其中设)]1()([)(--=k e k e k k u p p)()(k e k k u i i =)]2()1(2)([)(-+--=k e k e k e k k u d d则)()()()(k u k u k u k u d i p ++=∆2、数字PID 调节器参数的整定:为使系统性能满足一定的要求,必须确定算法中各参数的具体值,这就是参数整定。
参数整定是十分重要的,调节系统参数整定的好坏直接影响调节品质。
要想快速、灵活的将参数整定好,首先应透彻理解这些参数对系统性能的影响:增大比例系数,一般将加快系统的响应,这在有静差系统中有利于减小静差,但过大会使系统有较大超调,并产生振荡,使稳定性变坏。
增大积分时间(积分作用减弱)有利于减小超调,减小振荡,使系统更加稳定,但系统静差消除的过程将随之减慢。
增大微分时间(微分作用增强)有利于加快系统响应,使超调减小,稳定性增加,但系统对扰动有较敏感的响应。
四、实验要求1、在Matlab 环境中,按照给定对象,构建仿真PID 控制系统。
2、调整PID 参数,观察各参数对系统响应的影响。
3、采用增量式PID 算法进行控制系统仿真,对各参数进行整定,观察系统响应曲线,直到获得满意的响应曲线。
实验3 液位数字PID计算机控制系统实验

实验3 液位数字PID控制及参数整定提示:希望大家在做实验之前仔细阅读实验指导书,并且编写三个程序(P、PI、PID)争取能够到实验室就进行调节,观察效果,进行整定参数。
一、实验目的1、通过实验进一步学习单回路反馈控制系统的组成和工作原理。
2、掌握P、PI和PID调节器原理,并编写比例控制算法,比例积分控制算法,比例、积分、微分控制算法,并进行参数整定,使得液位控制在20cm处,超调量不超过10%,稳态误差5%。
3、定性地研究P、PI和PID调节器的参数对系统性能的影响。
二、实验设备过程控制实验装置、万用表、计算机控制教学实验开发平台CC-1型、ADS1.2软件开发环境,实验连接线数根。
三、实验原理图1 闭环控制系统原理图图1为单回路水箱液位控制系统。
单回路调节系统一般指在一个调节对象上用一个调节器来保持一个参数的恒定,而调节器只接受一个测量信号,其输出也只控制一个执行机构。
本系统所要保持的参数是液位的给定高度,即控制的任务是控制水箱液位等于给定值所要求的高度。
根据控制框图,这是一个闭环反馈单回路液位控制。
当调节方案确定之后,接下来就是整定调节器的参数,一个单回路系统设计安装就绪之后,控制质量的好坏与控制器参数选择有着很大的关系。
合适的控制参数,可以带来满意的控制效果。
反之,控制器参数选择得不合适,则会使控制质量变坏,达不到预期效果。
一个控制系统设计好以后,系统的投运和参数整定是十分重要的工作。
一般言之,用比例(P)调节器的系统是一个有差系统,比例度δ的大小不仅会影响到余差的大小,而且也与系统的动态性能密切相关。
比例积分(PI)调节器,由于积分的作用,不仅能实现系统无余差,而且只要参数δ,Ti调节合理,也能使系统具有良好的动态性能。
比例积分微分(PID)调节器是在PI调节器的基础上再引入微分D的作用,从而使系统既无余差存在,又能改善系统的动态性能(快速性、稳定性等)。
但是,并不是所有单回路控制系统在加入微分作用后都能改善系统品质,对于容量滞后不大,微分作用的效果并不明显,而对噪声敏感的流量系统,加入微分作用后,反而使流量品质变坏。
数字PID控制实验

计算机控制技术(实验课程名称)课程编码:H61010502实验指导书:《爱迪克教学实验系统》面向专业:自动化验证性实验项目名称:数字PID控制实验实验项目学时:4 实验要求:■必修□选修一、实验要求搭建如图所示系统,实现数字PID控制。
二、实验基本原理1.运算原理PID控制规律为:UE(t)为控制器输入;U(t)为控制器输出。
用矩阵法算积分,用向后差分代替微分,采样周期为T,算法为:2.PID系数不可过小,因为这会使计算机控制输出也较小,从而使系统量化误差变大,甚至有时控制器根本无输出而形成死区。
这时可将模拟电路开环增益适当减小,而使PID系数变大。
三、主要仪器设备及实验耗材爱迪克教学实验系统一套四、实验步骤1.接线:如图所示,①信号发生器模块B4的输出OUT作为系统输入R。
S2置0.2–6S档,S1置阶跃档,用短路块将S与ST,G和G1短路,观察B4单元的OUT端波形,调节调幅使其电压为3.5V,调节调频使其周期约为5S。
②从左至右依次使用运放模块A2,A3,A7,A4及电位器模块A5搭建图中模拟部分,第四级反馈电阻300K的接法(将A5中的330K电位器调到300K,再将两端分别与A4中的IN和OUT相连),最后的10K 电阻用A4中F和OUT之间的10K电阻构建(将F和OUT用短路套套好即可)。
其他连接见电路图。
③图中E点接A/D转换模块B5的IN7。
④B1数模转换单元的输出OUT2接至图中第三级运放的输入。
2.示例程序:见Cp5源文件。
3.运行虚拟示波器(方法参见实验1中的运行虚拟示波器方法)。
4.现象:根据临界比例算法计算PID三参数。
运行程序,用示波器观察输出C,如果现象不明显则可以调节最后一个330K电位器和B4中的调频调幅,记录M P,ts,PID参数,在下表中填入给此次的各参数与结果。
以下图形即仅供参考。
五、思考题1、如果P系数过小,会产生什么结果?六、主要参考书1、计算机控制系统分析与设计何克忠郝忠恕清华大学出版社2、过程控制系统及工程翁维勤周床海化学工业出版社3、微型计算机控制新技术曹承志机械工业出版社4、微型计算机控制技术于海生清华大学出版社5、数据采集与处理马明建周长城西安交通大学出版社。
实验三 PID 控制器参数对系统性能的影响
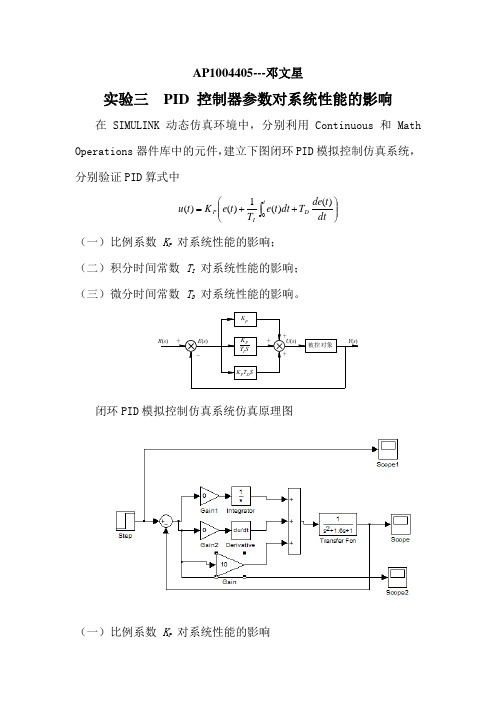
AP1004405---邓文星实验三 PID 控制器参数对系统性能的影响在SIMULINK 动态仿真环境中,分别利用Continuous 和Math Operations 器件库中的元件,建立下图闭环PID 模拟控制仿真系统,分别验证PID 算式中⎪⎪⎭⎫⎝⎛++=⎰dt t de T dt t e T t e K t u DtI P )()(1)()(0(一)比例系数 K P 对系统性能的影响; (二)积分时间常数 T I 对系统性能的影响; (三)微分时间常数 T D 对系统性能的影响。
闭环PID 模拟控制仿真系统仿真原理图(一)比例系数 K P 对系统性能的影响1.对动态特性的影响Kp=10;输入波形:输出波形:静态误差波形:Kp=100;偏大输入波形:输出波形静态误差波形:Kp=500;太大输入波形:输出波形:静态误差波形:✓比例系数加K P大,使系统的动作灵敏,速度加快。
✓K P偏大,则振荡次数增加,调节时间加长。
✓K P太大,系统会趋于不稳定。
✓K P太小,又会使系统动作缓慢。
2.对稳态误差的影响Kp=5;稳态误差图形Kp=100稳态误差波形✓加大比例系数K P,在系统稳定的情况下,可以减少稳态误差e ss,提高控制精度。
✓但加大K P只是能够减少稳态误差e ss,不能完全消除稳态误差e ss。
(二)积分时间常数T I对系统性能的影响1.对动态特性的影响Kp=20;Ti=0.5时输入波形:输出波形:静态误差波形:T i=1时输入波形:输出波形:静态误差波形:TI=200时输出波形:没有积分波形图:✓T I太小时,系统将不稳定。
✓T I偏小,则系统振荡次数较多。
✓T I太大时,对系统性能的影响减少。
✓当T I合适时,过渡过程的特性则比较理想。
3.对稳态误差的影响稳态误差波形图T I=4;I=200时✓积分控制能消除系统的稳态误差e ss,提高控制系统的控制精度。
✓但若T I太大时,积分作用太弱,以至不能减少稳态误差e ss。
pid控制实验报告

pid控制实验报告PID控制实验报告引言PID控制是一种常用的控制算法,广泛应用于工业自动化系统中。
本实验旨在通过实际的PID控制实验,验证PID控制算法的效果和优势,并对PID控制的原理、参数调节方法等进行探讨和分析。
一、实验目的本次实验的目的是通过一个简单的温度控制系统,使用PID控制算法来实现温度的稳定控制。
通过实验,验证PID控制算法的有效性和优越性,掌握PID控制的基本原理和参数调节方法。
二、实验设备和原理本实验所用的设备为一个温度控制系统,包括一个温度传感器、一个加热器和一个控制器。
温度传感器用于实时检测环境温度,加热器用于调节环境温度,控制器用于实现PID控制算法。
PID控制算法是基于误差的反馈控制算法,其主要原理是通过不断地调整控制器的输出信号,使得系统的实际输出与期望输出之间的误差最小化。
PID控制算法由比例控制、积分控制和微分控制三部分组成。
比例控制通过比例系数调整控制器的输出信号与误差的线性关系;积分控制通过积分系数调整控制器的输出信号与误差的积分关系;微分控制通过微分系数调整控制器的输出信号与误差的微分关系。
通过合理调节这三个系数,可以实现对系统的精确控制。
三、实验步骤1. 搭建温度控制系统:将温度传感器、加热器和控制器连接在一起,确保信号传输的正常。
2. 设置期望温度:根据实验要求,设置一个期望的温度作为控制目标。
3. 调节PID参数:根据实验的具体要求和系统的特性,调节PID控制器的比例系数、积分系数和微分系数,使得系统的响应速度和稳定性达到最佳状态。
4. 开始实验:启动温度控制系统,观察实际温度与期望温度的变化情况,记录实验数据。
5. 数据分析:根据实验数据,分析PID控制算法的效果和优势,总结实验结果。
四、实验结果与讨论通过实验,我们得到了一系列的实验数据。
根据这些数据,我们可以进行进一步的分析和讨论。
首先,我们观察到在PID控制下,温度的稳定性得到了显著的提高。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验三数字PID控制一、实验目的1.研究PID控制器的参数对系统稳定性及过渡过程的影响。
2.研究采样周期T对系统特性的影响。
3.研究I型系统及系统的稳定误差。
二、实验仪器1.EL-AT-III型计算机控制系统实验箱一台2.PC计算机一台三、实验内容1.系统结构图如3-1图。
图3-1 系统结构图图中 Gc(s)=Kp(1+Ki/s+Kds)Gh(s)=(1-e-TS)/sGp1(s)=5/((0.5s+1)(0.1s+1))Gp2(s)=1/(s(0.1s+1))2.开环系统(被控制对象)的模拟电路图如图3-2和图3-3,其中图3-2对应GP1(s),图3-3对应Gp2(s)。
图3-2 开环系统结构图1 图3-3开环系统结构图2 3.被控对象GP1(s)为“0型”系统,采用PI控制或PID控制,可系统变为“I型”系统,被控对象Gp2(s)为“I型”系统,采用PI控制或PID控制可使系统变成“II型”系统。
4.当r(t)=1(t)时(实际是方波),研究其过渡过程。
5.PI调节器及PID调节器的增益Gc(s)=Kp(1+K1/s)=KpK1((1/k1)s+1) /s=K(Tis+1)/s式中 K=KpKi , Ti=(1/K1)不难看出PI调节器的增益K=KpKi,因此在改变Ki时,同时改变了闭环增益K,如果不想改变K,则应相应改变Kp。
采用PID调节器相同。
6.“II型”系统要注意稳定性。
对于Gp2(s),若采用PI调节器控制,其开环传递函数为G(s)=Gc(s)·Gp2(s)=K(Tis+1)/s·1/s(0.1s+1)为使用环系统稳定,应满足Ti>0.1,即K1<107.PID递推算法如果PID调节器输入信号为e(t),其输送信号为u(t),则离散的递推算法如下:u(k)=u(k-1)+q0e(k)+q1e(k-1)+q2e(k-2)其中 q0=Kp(1+KiT+(Kd/T))q1=-Kp(1+(2Kd/T))q2=Kp(Kd/T)T--采样周期四、实验步骤1.连接被测量典型环节的模拟电路(图3-2)。
电路的输入U1接A/D、D/A卡的DA1输出,电路的输出U2接A/D、D/A卡的AD1输入。
检查无误后接通电源。
2.启动计算机,双击桌面“计算机控制实验”快捷方式,运行软件。
3.测试计算机与实验箱的通信是否正常,通信正常继续。
如通信不正常查找原因使通信正常后才可以继续进行实验。
4.在实验项目的下拉列表中选择实验三[数字PID控制], 鼠标单击鼠标单击按钮,弹出实验课题参数设置窗口。
5.输入参数Kp, Ki, Kd(参考值Kp=1, Ki=0.02, kd=1)。
6.参数设置完成点击确认后观察响应曲线。
若不满意,改变Kp, Ki, Kd的数值和与其相对应的性能指标σp、ts的数值。
7.取满意的Kp,Ki,Kd值,观查有无稳态误差。
8.断开电源,连接被测量典型环节的模拟电路(图3-3)。
电路的输入U1接A/D、D/A卡的DA1输出,电路的输出U2接A/D、D/A卡的AD1输入,将纯积分电容的两端连在模拟开关上。
检查无误后接通电源。
9.重复4-7步骤。
10.计算Kp,Ki,Kd取不同的数值时对应的σp、ts的数值,测量系统的阶跃响应曲线及时域性能指标,记入表中:实验结果参数δ% Ts 阶跃响应曲线Kp Ki Kd1 0.02 1 43.8% 1.2991 0.01 1 25.9% 1.1121 0.012 31.2% 1.1681 0.02 2 40.3% 1.9542 0.02 4 36.7% 0.9141 0.02 1 1 0.01 11 0.012 1 0.02 22 0.02 4五、实验报告1.画出所做实验的模拟电路图。
2.当被控对象为Gp1(s时)取过渡过程为最满意时的Kp, Ki, Kd,画出校正后的Bode 图,查出相稳定裕量γ和穿越频率ωc。
3.总结一种有效的选择Kp, Ki, Kd方法,以最快的速度获得满意的参数。
先通过改变Kp的值,使Kp满足要求,再改变Ki,最后是Kd,通过这样一次改变参数的方法可以很快的达到满意的效果。
参数整定(试凑法)增大比例系数Kp,一般加快系统响应,在有静差的情况下有利于减小静差,但过大的比例系数会使系统有较大超调,并产生震荡,使稳定性变坏;增大积分时间Ti,有利于减小超调,减小震荡,使系统更加稳定,但系统静差的消除将随之减慢;增大微分时间Td,亦有利于加快系统响应,使超调亮减小,稳定性增加,但对系统的扰动抑制能力减弱,对扰动有较敏感的响应;另外,过大的微分系数也将使得系统的稳定性变坏。
实验六大林算法一、实验目的1.掌握大林算法的特点及适用范围。
2.了解大林算法中时间常数T对系统的影响。
二、实验仪器1.EL-AT-III型计算机控制系统实验箱一台2.PC计算机一台三、实验内容1.实验被控对象的构成:(1)惯性环节的仿真电路及传递函数G(S)=-2/(T1+1)T1=0.2 (2)纯延时环节的构成与传递函数G(s)=e-Nττ=采样周期 N为正整数的纯延时个数由于纯延时环节不易用电路实现,在软件中由计算机实现。
图6-1 被控对象电路图(3)被控对象的开环传函为:G(S)=-2e-Nτ/(T1+1)2.大林算法的闭环传递函数:Go(s)=e-Nτ/(Ts+1) T=大林时间常数3.大林算法的数字控制器:D(Z)=(1-eτ/T)(1-e-τ/T1Z-1)/[k(1-e-τ/T1)[1-e-τ/TZ-1-(1-e-τ/T)Z-N-1] ]设k1=e-τ/T K2=e-τ/T1 T1=0.2 T=大林常数 K=2(K-Kk2)Uk=(1-k1)ek-(1-k1)k2ek-1+(k-kk2)k1Uk-1+(k-kk2)(1-k1)Uk-N-1四、实验步骤1.启动计算机,双击桌面“计算机控制实验”快捷方式,运行软件。
2.测试计算机与实验箱的通信是否正常,通信正常继续。
如通信不正常查找原因使通信正常后才可以继续进行实验。
3.量对象的模拟电路(图6-1)。
电路的输入U1接A/D、D/A卡的DA1输出,电路的输出U2接A/D、D/A卡的AD1输入。
检查无误后接通电源。
4.在实验项目的下拉列表中选择实验六[六、大林算法], 鼠标单击按钮,弹出实验课题参数设置对话框,在参数设置窗口设置延迟时间和大林常数,点击确认在观察窗口观测系统响应曲线。
测量系统响应时间Ts和超调量 p。
5.复步骤4,改变参数设置,将所测的波形进行比较。
并将测量结果记入下表中:性能指标参数设置阶跃响应曲线δ% Ts(秒) Tp(秒)延迟时间大林常数2 0.5 0 1.342 2.3151 0.5 0 1.443 2.5344 0.5 0 1.023 1.9341 0.8 0 1.923 3.2642 0.5 1 0.54 0.5 2 0.8五、实验报告1.分析开环系统下的阶跃响应曲线。
答:开环系统下的阶跃响应曲线会有较大的超调量和持续的震荡,使得系统的稳定性降低,对控制系统的控制性能极为不利。
2.分析大林时间常数对系统稳定性的影响。
答:随着大林常数的增大,系统响应的调节时间Ts和达到峰值的时间Tp都增大了,但是对超调量影响不大,所以使得系统的稳定性减弱。
六、大林算法软件流程图初始化控制步数、采样点数Point求K1、K2、K3初始化ek ,ek1,ek2,uk初始化系统输出希望值start画希望值曲线图中ek为误差,ek1为上一次的误差,uk是控制量,uk1是上一次的控制量ukn1是上N+1次的控制量实验七炉温控制实验一、实验目的1.了解温度控制系统的特点。
2.研究采样周期T对系统特性的影响。
3.研究大时间常数系统PID控制器的参数的整定方法。
二、实验仪器1.EL-AT-III型计算机控制系统实验箱一台2.PC计算机一台3.炉温控制实验对象一台三、炉温控制的基本原理1.系统结构图示于图7-1。
图7-1 系统结构图图中 Gc(s)=Kp(1+Ki/s+Kds)Gh(s)=(1-e-TS)/sGp(s)=1/(Ts+1)2.系统的基本工作原理整个炉温控制系统由两大部分组成,第一部分由计算机和A/D&D/A卡组成,主要完成温度采集、PID运算、产生控制可控硅的触发脉冲,第二部分由传感器信号放大,同步脉冲形成,以及触发脉冲放大等组成。
炉温控制的基本原理是:改变可控硅的导通角即改变电热炉加热丝两端的有效电压,有效电压的可在0~140V内变化。
可控硅的导通角为0~5CH。
温度传感是通过一只热敏电阻及其放大电路组成的,温度越高其输出电压越小。
外部LED灯的亮灭表示可控硅的导通与闭合的占空比时间,如果炉温温度低于设定值则可控硅导通,系统加热,否则系统停止加热,炉温自然冷却到设定值。
第二部分电路原理图见附录一。
3.PID递推算法:如果PID调节器输入信号为e(t),其输送信号为u(t),则离散的递推算法如下:Uk=Kpek+Kiek2+Kd(ek-ek-1),其中ek2是误差累积和。
四、实验内容:1.设定炉子的温度在一恒定值。
2.调整P、I、D各参数观察对其有何影响。
五、实验步骤1.启动计算机,双击桌面“计算机控制实验”快捷方式,运行软件。
2.测试计算机与实验箱的通信是否正常,通信正常继续。
如通信不正常查找原因使通信正常后才可以继续进行实验。
3. 20芯的扁平电缆连接实验箱和炉温控制对象,检查无误后,接通实验箱和炉温控制的电源。
闭环控制6. 在实验项目的下拉列表中选择实验七[七、炉温控制] 鼠标单击按钮,弹出实验课题参数设置对话框,选择PID,在参数设置窗口设置炉温控制对象的给定温度以及Ki、Kp、Kd值,点击确认在观察窗口观测系统响应曲线。
测量系统响应时间Ts和超调量 p。
性能指标参数阶跃响应曲线δ% Tp(秒)Ts(秒)Kp Ki Kd1 0.02 1 81% 81 5284 0.02 1 78% 79 3711 0.02 4 21% 78 180六、实验报告1.记录过渡过程为最满意时的Kp, Ki, Kd并画出其响应曲线。
Kp=1;Ki=0.02;Kd=42.分析此情况下的超调量、响应时间及稳态误差。
21%,78s,3.2%1 0.2 14 0.2 11 0.2 4 1 0.1 4七、温度控制软件流程图图中ek为误差,ek1为上一次的误差,ek2为误差的累积和,uk是控制量,可控硅导通角控制量α=0~5bH, α=0导通角最大,α=5b导通角为零。
实验九 步进电机控制实验一、实验目的1.了解步进电机的工作原理。
2.掌握步进电机的驱动及编程方法。
二、实验仪器1.EL-AT-III 型计算机控制系统实验箱一台 2.PC 计算机一台3.步进电机控制实验对象一台 三、步进电机的基本工作原理:步进电机多为永磁感应式,有两相、四相、六相等多种,实验所用电机为两相四拍式,通过对每相线圈中的电流的顺序切换来使电机作步进式旋转,驱动电路由脉冲信号来控制,所以调节脉冲信号的频率便可改变步进电机的转速: A 如图9-1所示,每相电流为0.2A,相电压为5V ,两相四拍 C 通电顺序如下:B D 反方向旋转正方向旋转四、实验原理:步进电机是一种电脉冲转化为角位移的执行机构。
