计算机控制实验三数字PID调节器算法的研究
数字PID

科 技
凑试法是通过模拟运行观察系统的响应曲线(如阶跃响应),然
大 学
后根据各调节参数对系统响应大致影响,反复凑试参数,以达到满意
网 络
的响应,从而确定PID的调节参数。
教 育
25
KP↑,系统响应加快,有利于减小静差,但KP过大,使系统有较大的 超调,产生振荡,使系统稳定性变坏; Ti↑,减小超调,使系统稳定,但静差的消除将减慢; Td↑,加快系统响应,减小超调量,稳定性增加,但对干扰的抑制 作用却减弱。 具体步骤:
技
大
学
网
络
教 育
6
图4.3 模拟PID调节器方框图
PID控制器把给定值W与实际输出值Y相减,得到控制偏差e,偏
西 南
差e经比例、积分、微分运算后,通过线性组合构成控制量u,然后
科 技
用u对对象进行控制。
大
学
网
络
教 育
7
1. 比例调节器
是一种简单的调节器,其控制 规律为:
u = KPe + u0
KP:比例系数, u0:控制常量, 即误差为零时的控制变量;如图所
数字PID控制算法是一种准连续控制过程,是建立在计算机对连 续PID控制进行数字仿真的基础上的控制。这种控制方式要求采样周 期与系统的时间常数比很小,采样周期越小,数字仿真越精确,控 制效果也就越接近连续控制,采样周期的选择是受多方面影响:
1. 根据香农采样定理,应满足:
其中:fmax为输入信号的上限频率。这样采样信号经过保持环节后, 仍可复原或近似复原为模拟信号,而不丢失任何信息。
西
2. 从执行机构的特性要求来看,需要输出信号保持一定的宽度;
南
科
3. 从控制系统的随动和抗干扰的性能要求采样周期短些;
《计算机控制技术》数字PID控制器设计与仿真实验报告
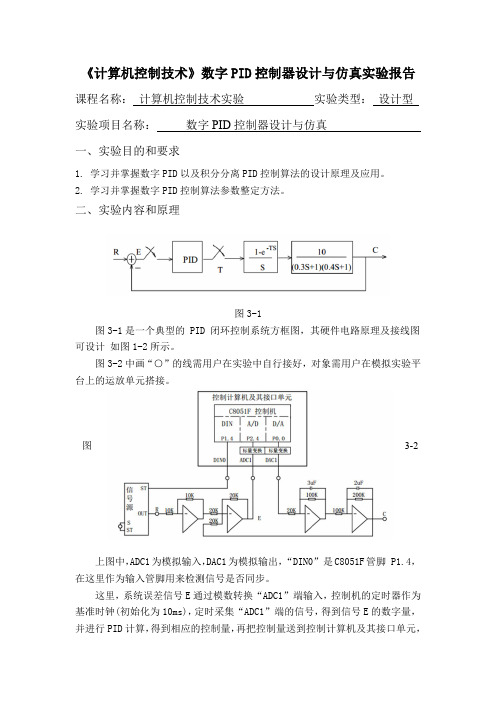
《计算机控制技术》数字PID控制器设计与仿真实验报告课程名称:计算机控制技术实验实验类型:设计型实验项目名称:数字PID控制器设计与仿真一、实验目的和要求1. 学习并掌握数字PID以及积分分离PID控制算法的设计原理及应用。
2. 学习并掌握数字PID控制算法参数整定方法。
二、实验内容和原理图3-1图3-1是一个典型的 PID 闭环控制系统方框图,其硬件电路原理及接线图可设计如图1-2所示。
图3-2中画“○”的线需用户在实验中自行接好,对象需用户在模拟实验平台上的运放单元搭接。
图3-2上图中,ADC1为模拟输入,DAC1为模拟输出,“DIN0”是C8051F管脚 P1.4,在这里作为输入管脚用来检测信号是否同步。
这里,系统误差信号E通过模数转换“ADC1”端输入,控制机的定时器作为基准时钟(初始化为10ms),定时采集“ADC1”端的信号,得到信号E的数字量,并进行PID计算,得到相应的控制量,再把控制量送到控制计算机及其接口单元,由“DAC1”端输出相应的模拟信号,来控制对象系统。
本实验中,采用位置式PID算式。
在一般的PID控制中,当有较大的扰动或大幅度改变给定值时,会有较大的误差,以及系统有惯性和滞后,因此在积分项的作用下,往往会使系统超调变大、过渡时间变长。
为此,可采用积分分离法PID控制算法,即:当误差e(k)较大时,取消积分作用;当误差e(k)较小时才将积分作用加入。
图3-3是积分分离法PID控制实验的参考程序流程图。
图3-3三、主要仪器设备计算机、模拟电气实验箱四、操作方法与实验步骤1.按照图3-2搭建实验仿真平台。
2.确定系统的采样周期以及积分分离值。
3.参考给出的流程图编写实验程序,将积分分离值设为最大值0x7F,编译、链接。
4.点击,使系统进入调试模式,点击,使系统开始运行,用示波器分别观测输入端R以及输出端C。
5.如果系统性能不满意,用凑试法修改PID参数,再重复步骤3和4,直到响应曲线满意,并记录响应曲线的超调量和过渡时间。
数字PID及其算法

printf("v1=%f",velocity_1); printf("v2=%f\n",velocity_2); u_1_i=K1*(error_1_i+T/Ti1*error_1_i2+Td1/T*(error_1_ierror_1_i1))+50.0; u_2_i=K2*(error_2_i+T/Ti2*error_2_i2+Td2/T*(error_2_ierror_2_i1))+50.0; /* u_1_i=K1*error_1_i+50.0; u_2_i=K2*error_2_i+50.0; */ /* u_1_i=K1*(error_1_i+T/Ti1*error_1_i2)+50.0; u_2_i=K2*(error_2_i+T/Ti2*error_2_i2)+50.0; */ motor(1,(int)u_1_i); motor(2,(int)u_2_i);
但是其中还存在不少问题,在电池电量不同的情 况下,能力风暴在相同设定值下的转速不同,这 样就会发生刚刚调的最好的PID 参数过一会就显 得没那么好了,所以我们要寻找鲁棒性最好的PID 参数。 并且需注意的是,以上的数据是基于某台能力风 暴,对于不同的能力风暴,机械特性不同,所以 可以参照我做实验的步骤,从测对象特性开始做 。我的实验数据的价值在于观察变化趋势,其绝 对值可能因为不同情况而不同。
/*用PID 控制算法实现的走直线控制,位置式算法 */ /*左右轮有相同的设定值,对误差进行调整;根 据左右轮的误差再对右轮进行调整, 使左右轮尽量保持一致,从而走直线。*/ float K1=0.05; float Ti1=15.0; float Td1=0.1; float K2=0.2; float Ti2=15.0; float Td2=0.1; float T=0.5; float velocity_1; float velocity_2; float u_1_i;/*控制量*/
PID自控原理实验报告范文pid调节实验报告范文

PID自控原理实验报告范文pid调节实验报告范文自动控制原理实验——第七次实验实验目的了解数字PID控制的特点,控制方式。
理解和掌握连续控制系统的PID控制算法表达式。
了解和掌握用试验箱进行数字PID控制过程。
观察和分析在标PID控制系统中,PID参数对系统性能的影响。
实验内容1、数字PID控制一个控制系统中采用比例积分和微分控制方式控制,称之为PID控制。
数字PID控制器原理简单,使用方便适应性强,可用于多种工业控制,鲁棒性强。
可以用硬件实现,也可以用软件实现,也可以用如见硬件结合的形式实现。
PID控制常见的是一种负反馈控制,在反馈控制系统中,自动调节器和被控对象构成一个闭合回路。
模拟PID控制框图如下:U(s)U(s)E(s)KpKiKd输出传递函数形式:其中Kp为调节器的比例系数,Ti为调节器的积分常数,Td是调节器的微分常数。
2、被控对象数学模型的建立1)建立模型结构在工程中遇到的实际对象大多可以表示为带时延的一阶或二价惯性环节,故PID整定的方法多从这样的系统入手,考虑有时延的单容被控过程,其传递函数为:这样的有时延的单容被控过程可以用两个惯性环节串联组成的自平衡双容被控过程来近似,本实验采用该方式作为实验被控对象,如图3-127所示。
2)被控对象参数的确认对于这种用两个惯性环节串联组成的自平衡双容被控过程的被控对象,在工程中普遍采用单位阶跃输入实验辨识的方法确认和τ,以达到转换成有时延的单容被控过程的目的。
单位阶跃输入实验辨识的原理方框如图3-127所示。
对于不同的T1、T2和K值,得到其单位阶跃输入响应曲线后,由和得到和,再利用拉氏反变换公式得到To=To=t2-t1Ln1-Yoτ=t2Ln1-Yot13、采样周期的选择采样周期选择0.05s。
4、数字PID调节器控制参数的工程整定方法虽然PID调节可全面、综合的考虑系统的各项性能,但在工程实际中,考虑到工程造价和调节器的易于实现,长采用PID三个参数来对系统进行校正。
计算机控制PID实验报告

实验报告实验名称:积分分离PID控制算法课程名称:计算机控制系统姓名:蓝娜学号:12062115班级:电气2班指导老师:陈雪亭日期:2014年11月11日实验背景:在数字控制系统中,积分控制分量的引入主要是为了消除静差,提高系统的精度。
但在过程启动、停车或大幅度改变设定值时,由于产生较大的偏差,加上系统本身的惯性和滞后,在积分作用下,计算得到的控制量将超出执行机构可能的最大动作范围对应的极限控制量,结果产生系统输出的较大超调,甚至引起系统长时间的振荡,这对大多数的生产过程是不允许的,由此引进积分分离PID 算法,既保持了积分作用,又可减少超调量,使系统的控制性能得到较大的改善。
实验基本思想:在偏差e(k)较大时,暂时取消积分作用;当偏差e(k)小于某个阈值时,才将积分作用投入。
1)根据实际需要,设定一个阈值ε>0。
2)当|e(k)|>ε,即偏差较大时,采用PD 控制,可避免大的超调,又使系统有较快的响应。
3)当|e(k)|<=ε,即偏差较小时,采用PID 控制或PI 控制,可保证系统的控制精度。
积分分离形式:u(k)=Kp{e(k)+)]1()([)(0--+∑=k e k e TTd j e Ti T k j β} 式中β=1(|e(k)<=ε|) 或β=0 (|e(k)|>ε)实验目的:利用Simulink 设计数字PID 控制器,加入模块Switch ,通过调整阈值实现积分分离,并通过Simulink 仿真与标准PID 控制进行比较。
实验线路图:普通PID 控制线路:上次实验得到较好系统性能的整定后的参数为Kp=600,Ki=450,Kd=26。
此次实验会在上次实验的基础上作进一步的改进,引入积分分离。
/s/blog_6a04c83201018gu9.html实验结果:(1)当Ki、Kd为0,Kp=1时得到的响应曲线如下:(2)当Kp逐渐增大,Ki、Kd=0时,得到图像如下:(2)由上图像得,只改变比例系数Kp,超调量变大,且稳定性能也不高。
数字PID调节器算法的研究实验报告

实验四数字PID 调节器算法的研究一、实验目的1.学习并熟悉常规的数字PID 控制算法的原理;2.学习并熟悉积分分离PID 控制算法的原理;3.掌握具有数字PID 调节器控制系统的实验和调节器参数的整定方法。
二、实验设备1.THTJ-1 型计算机控制技术实验箱2.THVLW-1 型USB 数据采集卡一块(含37 芯通信线、USB 电缆线各1 根)3.PC 机1 台(含上位机软件“THTJ-1”)三、实验内容1.利用本实验平台,设计并构成一个用于混合仿真实验的计算机闭环实时控制系统;2.采用常规的PI 和PID 调节器,构成计算机闭环系统,并对调节器的参数进行整定,使之具有满意的动态性能;3.对系统采用积分分离PID 控制,并整定调节器的参数。
四、实验原理在工业过程控制中,应用最广泛的控制器是 PID 控制器,它是按偏差的比例(P)、积分(I)、微分(D)组合而成的控制规律。
而数字PID 控制器则是由模拟PID 控制规律直接变换所得。
在 PID 控制规律中,引入积分的目的是为了消除静差,提高控制精度,但系统中引入了积分,往往使之产生过大的超调量,这对某些生产过程是不允许的。
因此在工业生产中常用改进的PID 算法,如积分分离PID 算法,其思想是当被控量与设定值偏差较大时取消积分控制;当控制量接近给定值时才将积分作用投入,以消除静差,提高控制精度。
这样,既保持了积分的作用,又减小了超调量。
五、实验步骤1、实验接线1.1 按图4-1 和图4-2 连接一个二阶被控对象闭环控制系统的电路;1.2 该电路的输出与数据采集卡的输入端AD1 相连,电路的输入与数据采集卡的输出端DA1 相连;1.3 待检查电路接线无误后,打开实验平台的电源总开关,并将锁零单元的锁零按钮处于“不锁零”状态。
2、脚本程序运行2.1 启动计算机,在桌面双击图标THTJ-1,运行实验软件;2.2 顺序点击虚拟示波器界面上的“开始采集”按钮和工具栏上的脚本编程器按钮;2.3 在脚本编辑器窗口的文件菜单下点击“打开”按钮,并在“计算机控制算法VBS\ 计算机控制技术基础算法\数字PID 调器算法”文件夹下选中“位置式PID”脚本程序并打开,阅读、理解该程序,然后点击脚本编辑器窗口的调试菜单下“步长设置”,将脚本算法的运行步长设为100ms;2.4 点击脚本编辑器窗口的调试菜单下“启动”;用虚拟示波器观察图4-2 输出端的响应曲线;2.5 点击脚本编辑器的调试菜单下“停止”,利用扩充响应曲线法(参考本实验附录4)整定PID控制器的P、I、D及系统采样时间Ts等参数,然后再运行。
(完整版)数字PID及其算法
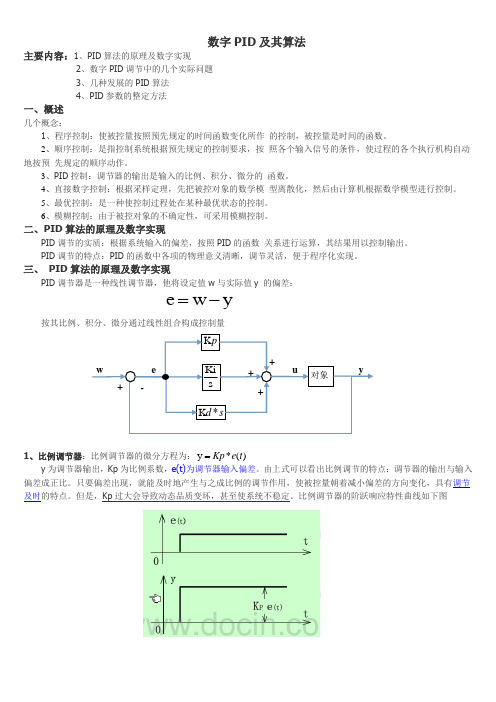
数字PID 及其算法主要内容:1、PID 算法的原理及数字实现2、数字PID 调节中的几个实际问题3、几种发展的PID 算法4、PID 参数的整定方法一、概述几个概念:1、程序控制:使被控量按照预先规定的时间函数变化所作 的控制,被控量是时间的函数。
2、顺序控制:是指控制系统根据预先规定的控制要求,按 照各个输入信号的条件,使过程的各个执行机构自动地按预 先规定的顺序动作。
3、PID 控制:调节器的输出是输入的比例、积分、微分的 函数。
4、直接数字控制:根据采样定理,先把被控对象的数学模 型离散化,然后由计算机根据数学模型进行控制。
5、最优控制:是一种使控制过程处在某种最优状态的控制。
6、模糊控制:由于被控对象的不确定性,可采用模糊控制。
二、PID 算法的原理及数字实现PID 调节的实质:根据系统输入的偏差,按照PID 的函数 关系进行运算,其结果用以控制输出。
PID 调节的特点:PID 的函数中各项的物理意义清晰,调节灵活,便于程序化实现。
三、 PID 算法的原理及数字实现PID 调节器是一种线性调节器,他将设定值w 与实际值y 的偏差:按其比例、积分、微分通过线性组合构成控制量1、比例调节器:比例调节器的微分方程为:)(*y t e Kp =y 为调节器输出,Kp 为比例系数,e(t)为调节器输入偏差。
由上式可以看出比例调节的特点:调节器的输出与输入偏差成正比。
只要偏差出现,就能及时地产生与之成比例的调节作用,使被控量朝着减小偏差的方向变化,具有调节及时的特点。
但是,Kp 过大会导致动态品质变坏,甚至使系统不稳定。
比例调节器的阶跃响应特性曲线如下图yw e -=sd *K s Ki pK 对象 we + - + + + u y2、积分调节器:积分作用是指调节器的输出与输入偏差的积分成比例的作用,其作用是消除静差。
积分方程为:TI 是积分时间常数,它表示积分速度的大小,TI 越大,积分速度越慢,积分作用越弱。
PID控制实验报告

实验二 数字PID 控制计算机控制是一种采样控制,它只能根据采样时刻的偏差值计算控制量。
因此连续PID 控制算法不能直接使用,需要采用离散化方法。
在计算机PID 控制中,使用的是数字PID 控制器。
一、位置式PID 控制算法按模拟PID 控制算法,以一系列的采样时刻点kT 代表连续时间t ,以矩形法数值积分近似代替积分,以一阶后向差分近似代替微分,可得离散PID 位置式表达式:∑∑==--++=⎪⎪⎭⎫ ⎝⎛--++=k j di p k j D I p T k e k e k T j e k k e k k e k e T T j e T T k e k k u 00)1()()()())1()(()()()( 式中,D p d I pi T k k T k k ==,,e 为误差信号(即PID 控制器的输入),u 为控制信号(即控制器的输出)。
在仿真过程中,可根据实际情况,对控制器的输出进行限幅。
二、连续系统的数字PID 控制仿真连续系统的数字PID 控制可实现D/A 及A/D 的功能,符合数字实时控制的真实情况,计算机及DSP 的实时PID 控制都属于这种情况。
1.Ex3 设被控对象为一个电机模型传递函数BsJs s G +=21)(,式中J=0.0067,B=0.1。
输入信号为)2sin(5.0t π,采用PD 控制,其中5.0,20==d p k k 。
采用ODE45方法求解连续被控对象方程。
因为Bs Js s U s Y s G +==21)()()(,所以u dt dy B dty d J =+22,另y y y y ==2,1,则⎪⎩⎪⎨⎧+-==/J)*u ((B/J)y y y y 12221 ,因此连续对象微分方程函数ex3f.m 如下 function dy = ex3f(t,y,flag,para)u=para;J=0.0067;B=0.1;dy=zeros(2,1);dy(1) = y(2);dy(2) = -(B/J)*y(2) + (1/J)*u;控制主程序ex3.mclear all;close all;ts=0.001; %采样周期xk=zeros(2,1);%被控对象经A/D转换器的输出信号y的初值e_1=0;%误差e(k-1)初值u_1=0;%控制信号u(k-1)初值for k=1:1:2000 %k为采样步数time(k) = k*ts; %time中存放着各采样时刻rin(k)=0.50*sin(1*2*pi*k*ts); %计算输入信号的采样值para=u_1; % D/AtSpan=[0 ts];[tt,xx]=ode45('ex3f',tSpan,xk,[],para); %ode45解系统微分方程%xx有两列,第一列为tt时刻对应的y,第二列为tt时刻对应的y导数xk = xx(end,:); % A/D,提取xx中最后一行的值,即当前y和y导数yout(k)=xk(1); %xk(1)即为当前系统输出采样值y(k)e(k)=rin(k)-yout(k);%计算当前误差de(k)=(e(k)-e_1)/ts; %计算u(k)中微分项输出u(k)=20.0*e(k)+0.50*de(k);%计算当前u(k)的输出%控制信号限幅if u(k)>10.0u(k)=10.0;endif u(k)<-10.0u(k)=-10.0;end%更新u(k-1)和e(k-1)u_1=u(k);e_1=e(k);endfigure(1);plot(time,rin,'r',time,yout,'b');%输入输出信号图xlabel('time(s)'),ylabel('rin,yout');figure(2);plot(time,rin-yout,'r');xlabel('time(s)'),ylabel('error');%误差图程序运行结果显示表1所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学院:********** 班级:********** 姓名:****** 学号:**********实验三数字PID调节器算法的研究实验项目名称:数字PID调节器算法的研究实验项目性质:普通所属课程名称:计算机控制技术实验计划学时:2学时一、实验目的1.学习并熟悉常规的数字PID控制算法的原理;2.学习并熟悉积分分离PID控制算法的原理;3.掌握具有数字PID调节器控制系统的实验和调节器参数的整定方法。
二、实验内容和要求1.利用本实验平台,设计并构成一个用于混合仿真实验的计算机闭环实时控制系统;2.采用常规的PI和PID调节器,构成计算机闭环系统,并对调节器的参数进行整定,使之具有满意的动态性能;3.对系统采用积分分离PID控制,并整定调节器的参数。
二、实验主要仪器和材料1.THTJ-1型计算机控制技术实验箱2.THVLW-1型USB数据采集卡一块(含37芯通信线、USB电缆线各1根)3.PC机1台(含上位机软件“THTJ-1”)四、实验方法、步骤及结果测试1、实验原理在工业过程控制中,应用最广泛的控制器是PID控制器,它是按偏差的比例(P)、积分(I)、微分(D)组合而成的控制规律。
而数字PID控制器则是由模拟PID控制规律直接变换所得。
在PID控制规律中,引入积分的目的是为了消除静差,提高控制精度,但系统中引入了积分,往往使之产生过大的超调量,这对某些生产过程是不允许的。
因此在工业生产中常用改进的PID算法,如积分分离PID算法,其思想是当被控量与设定值偏差较大时取消积分控制;当控制量接近给定值时才将积分作用投入,以消除静差,提高控制精度。
这样,既保持了积分的作用,又减小了超调量。
2、实验步骤1、实验接线1.1按图1和图2连接一个二阶被控对象闭环控制系统的电路;1.2该电路的输出与数据采集卡的输入端AD1相连,电路的输入与数据采集卡的输出端DA1相连;1.3待检查电路接线无误后,打开实验平台的电源总开关,并将锁零单元的锁零按钮处于“不锁零”状态。
2、脚本程序运行2.1启动计算机,在桌面双击图标THTJ-1,运行实验软件;2.2顺序点击虚拟示波器界面上的“”按钮和工具栏上的“”按钮(脚本编程器);2.3在脚本编辑器窗口的文件菜单下点击“打开”按钮,并在“计算机控制算法VBS\计算机控制技术基础算法\数字PID调器算法”文件夹下选中“位置式PID”脚本程序并打开,阅读、理解该程序,然后点击脚本编辑器窗口的调试菜单下“步长设置”,将脚本算法的运行步长设为100ms;2.4点击脚本编辑器窗口的调试菜单下“启动”;用虚拟示波器观察图4-2输出端的响应曲线;2.5点击脚本编辑器的调试菜单下“停止”,利用扩充响应曲线法(参考本实验七附录4)整定PID控制器的P、I、D及系统采样时间Ts等参数,然后再运行。
在整定过程中注意观察参数的变化对系统动态性能的影响;2.6 参考步骤2.4、2.4和2.5,用同样的方法分别运行增量式PID和积分分离PID脚本程序,并整定PID控制器的P、I、D及系统采样时间Ts等参数,然后观察参数的变化对系统动态性能的影响。
另外在积分分离PID程序运行过程中,注意不同的分离阈值tem对系统动态性能的影响;2.7 实验结束后,关闭脚本编辑器窗口,退出实验软件。
五、实验报告要求1.绘出实验中二阶被控对象在各种不同的PID控制下的响应曲线。
2.编写积分分离PID控制算法的脚本程序。
3.分析常规PID控制算法与积分分离PID控制算法在实验中的控制效果。
数据分析:(1):位置型PID响应曲线:(2):增量型PID响应曲线:超调量:7.293 峰值时间:0.235ms 达到稳态的时间:5.563ms 稳态值:2.0积分分离型PID响应曲线:超调量:6.514 峰值时间:0.277ms 达到稳态的时间:6.435ms 稳态值:2.0六、思考题1. 该实验中被控对象是什么?有什么特点?答:被控对象是一个积分放大电路的输出;其特点是刚上电的瞬间由于电容的充电作用,其输出电压值会有一个瞬时升高的过程,然后随着电容的充电,输出电压会逐渐稳定。
2. 试画出该实验中数字PID控制系统的方框图。
PID控制系统的方框图3. 试叙述带积分分离的PID 控制算法的特点和应用的场合。
答:带积分分离的PID 算法的特点是:偏差e(k)较大时,取消积分作用;当偏差e(k)较小时才将积分作用投入;其应用场合:当有较大的扰动或大幅度改变给定值采用积分分离措施。
4. 位置式PID 算式与增量式算式有何区别?各有什么优缺点?答:位置式算式提供了执行机构的位置u(k),增量式算式则反映了前后位置之差Δu(k);位置式算法的优点是简单明了,但较容易产生较大的累加误差;增量式算式的优点是误差较小,易于控制,但其算法相对复杂。
5. 数字PID 调节器的参数Kp 、Ti 、Td 和采样周期T 对系统响应有何影响?参数的整定使用什么方法?答:Kp 能控制误差,但其加大会造成系统不稳定;Ti 累积输出控制量以消除误差,但作用太强大会造成系统的超调量加大,甚至出到系统振荡;Td 可以减小超调量,提高稳定性,加快系统动态响应速度,减小调整时间,改善动态性能。
参数的整定用简易工程法中的扩充阶跃响应曲线法。
七、附录1.被控对象的模拟与计算机闭环控制系统的构成图1 数-模混合控制系统的方框图图中信号的离散化通过数据采集卡的采样开关来实现。
被控对象的传递函数为:)15.0)(1(5)2)(1(10)(++=++=s s s s S G它的模拟电路图如下图所示图2 被控二阶对象的模拟电路图2.常规PID 控制算法 1)常规PID 控制位置式算法为:})]1()([)()({)(1∑=--++=ki dip k e k e T T i e T Tk e k k u对应的Z 传递函数为:)1(11)()(D(Z)11---+-+==Z K z K K Z E z U d i P式中K p ---比例系数K i =i p T T K 积分系数,T 采样周期K d =TT K dp 微分系数其增量形式为:)]2()1(2)([)()]1()([)1()(-+--++--+-=k e k e k e K k e K k e k e K k u k u d i p3.积分分离PID 控制算法:系统中引入的积分分离算法时,积分分离PID 算法要设置分离阈E 0: 当 │e(kT)│≤│E 0│时,采用PID 控制,以保持系统的控制精度。
当 │e(kT)│>│E 0│时,采用PD 控制,可使δp 减小。
积分分离PID 控制算法为:∑=--++=kj d i e p k e k e K jT e K K k e K k u 0)1()([)()()(式中K e 称为逻辑系数: 当 │e(k)│≤│E0│时, Ke=1 当 │e(k)│>│E0│时, Ke=0对应的控制方框图为图4-3 上位机控制的方框图图中信号的离散化是由数据采集卡的采样开关来实现。
4.数字PID 控制器的参数整定在模拟控制系统中,参数整定的方法较多,常用的实验整定法有:临界比例度法、阶跃响应曲线法、试凑法等。
数字控制器参数的整定也可采用类似的方法,如扩充的临界比例度法、扩充的阶跃响应曲线法、试凑法等。
下面简要介绍扩充阶跃响应曲线法。
扩充阶跃响应曲线法只适合于含多个惯性环节的自平衡系统。
用扩充阶跃响应曲线法整定PID参数的步骤如下:①数字控制器不接入控制系统,让系统处于开环工作状态下,将被调量调节到给定值附近,并使之稳定下来。
②记录被调量在阶跃输入下的整个变化过程,如下图所示。
③在曲线最大斜率处作切线,求得滞后时间τ和被控对象时间常数Tx,以及它们的比值Tx/τ,然后查下表确定控制器的K P、K i、K d及采样周期T。
扩充阶跃响应曲线法通过测取响应曲线的τ、Tx参数获得一个初步的PID控制参数,然后在此基础上通过部分参数的调节(试凑)使系统获得满意的控制性能。
5.位置式PID数字控制器程序的编写与调试示例:5.1参考程序dim pv,sv,ei,K,Ti,Td,q0,q1,q2,mx,pvx,op ‘变量定义sub Initialize(arg) ‘初始化函数WriteData 0 ,1 '给通道一写0mx=0 '给mx赋初值pvx=0 '给pvx赋初值end sub '结束初始化子函数sub TakeOneStep (arg) ‘算法运行函数pv = ReadData(1) 'pv为当前测量值sv=2 ‘sv为给定值K=0.8 ‘比例系数PTi=5 ‘积分时间常数ITd=0 ‘微分时间常数DTs=0.1 ‘采样周期ei=sv-pv 'ei为当前偏差值q0=K*ei ‘比例项if Ti=0 thenmx=0q1=0elsemx=K*Ts*ei/Ti ‘当前积分项end ifq2=K*Td*(pvx-pv)/Ts ‘'微分项q1=q1+mx '当前积分项if q1>4.9 then ‘积分限幅,以防积分饱和q1=4.9end ifif q1<-4.9 thenq1=-4.9end ifpvx=pv '将当前输出值赋给pvx, 为下一时刻做准备op=q0+q1+q2 'op为控制器当前输出值if op<=-4.9 then '输出值限幅,op下限为-4.9op=-4.9end ifif op>=4.9 then 'op上限为4.9op=4.9end ifWriteData op ,1 '通道1写入op的值end sub '结束算法运行子函数sub Finalize (arg) ‘退出函数WriteData 0 ,1 '给通道一写0end sub '结束退出子函数5.2位置式PID (k=0.8,ti=5,td=0);运行步长100ms,超调量为27.5%。
(如图3)图36、积分分离PID控制算法的编程参考示例:6.1程序dim pv,sv,ei,K,Ti,Td,q0,q1,q2,mx,pvx,op,ke,tem '变量定义sub Initialize(arg) '初始化函数WriteData 0 ,1 '给通道一写0mx=0 '给mx赋初值pvx=0 '给pvx赋初值end sub '结束初始化子函数sub TakeOneStep (arg) '算法运行函数pv = ReadData(1) ' pv为当前测量值sv=2 'sv为给定值K=0.8 'K为比例系数Ti=5 'Ti为积分时间常数Td=0 'Td为微分时间常数Ts=0.1 ' Ts为采集周期ei=sv-pv 'ei为当前偏差值tem=abs(ei)if tem>=0.8 then '丨ei丨≥0.8时,ke=0;其中0.8为分离阈值ke=0elseke=1 '丨ei丨<0.8时,ke=1end ifq0=K*ei '比例项if Ti=0 thenmx=0q1=0elsemx=ke*K*Ts*ei/Ti '当前积分项end ifq2=K*Td*(pvx-pv)/Ts '微分项if mx>4.9 then '当前积分限幅,以防积分饱和mx=4.9end ifif mx<-4.9 thenmx=-4.9end ifq1=q1+mx '当前积分项pvx=pv '将当前输出值赋给pvx, 为下一时刻做准备op=q0+q1+q2 '当前输出值'op为控制器当前输出值if op<=-4.9 then '输出值限幅,op下限为-4.9op=-4.9end ifif op>=4.9 thenop=4.9 'op上限为4.9end ifWriteData op ,1 '通道1写入op的值end sub '结束算法运行子函数sub Finalize (arg) '退出函数WriteData 0 ,1 '给通道一写0end sub '结束退出子函数6.2积分分离PID (k=0.8,ti=5,td=0),超调量为15.6%7、增量式PID控制算法的编程参考示例:7.1参考程序dim pv,sv,ei,ex,ey,K,Ti,Td,q0,q1,q2,op '变量定义sub Initialize(arg) '初始化函数WriteData 0 ,1 '给通道一写0end sub '结束初始化子函数sub TakeOneStep (arg) '算法运行函数pv = ReadData(1) ' pv为当前测量值sv=2 'sv为给定值K=0.8 'K为比例系数Ti=5 'Ti为积分时间常数Td=0 'Td为积分时间常数Ts=0.1 ' Ts为采集周期ei=sv-pv 'ei为当前偏差值q0=k*(ei-ex) '比例项if Ti=0 thenq1=0elseq1=K*Ts*ei/Ti '当前积分项end ifq2=k*td*(ei-2*ex+ey) /Ts '微分项ey=ex '赋值,为下一时刻做准备ex=eiif q1>4.9 then '当前积分限幅,以防积分饱和q1=4.9end ifif q1<-4.9 thenq1=-4.9end ifop=op+q0+q1+q2 'op为控制器当前输出值if op<=-4.9 then '输出值限幅,op下限为-4.9 op=-4.9end ifif op>=4.9 then 'op上限为4.9op=4.9end ifWriteData op ,1 '通道1写入op的值end sub '结束算法运行子函数sub Finalize (arg) '退出函数WriteData 0 ,1 '给通道一写0end sub '结束退出子函数7.2增量式PID (k=0.8,ti=5,td=0),超调量为27.3%。
