第2章习题解a
教材第二章习题解答

第二章原子结构和元素周期律习题解答1.指出下列各原子轨道相应的主量子数n及角量子数l的数值是多少?轨道数分别是多少?2p 3d 4s 4f 5s【解答】 2p 主量子数2,角量子数1,轨道数33d 主量子数3,角量子数2,轨道数54s 主量子数4,角量子数0,轨道数14f 主量子数4,角量子数3,轨道数75s 主量子数5,角量子数0,轨道数1 2.当主量子数n=4时,可能有多少条原子轨道?分别用Ψn,l,m 表示出来。
电子可能处于多少种运动状态?(考虑自旋在内)【解答】当n=4时,可能有n2=16条原子轨道。
n l M4 01230,±10,±1,±20,±1,±2,±3Ψ4,0,0,Ψ4,1,0,Ψ4,1,1,Ψ4,1,-1,Ψ4,2,0,Ψ4,2,1,Ψ4,2,-1,Ψ4,2,2,Ψ4,2,-2,Ψ4,3,0,Ψ4,3,1,Ψ4,3,-1,Ψ4,3,2,Ψ4,3,-2,Ψ4,3,3,Ψ4,3,-3 每条轨道上可以容纳两个自旋相反的电子,16条原子轨道,电子可能处于32种运动状态。
3.将下列轨道上的电子填上允许的量子数。
(1)n=,l=2,m=0,ms=±1/2(2)n=2,l= ,m=0,ms=±1/2(3)n=4,l=2,m= ,ms=-1/2(4)n=3,l=2,m=2,m=s=-1/2(5)n=2,l= ,m=-1,ms=+1/2(6)n=5,l=0,m= ,ms【解答】(1) 3,4,5,……,正整数;(2) 0,1(3) 0,±1,±2(4) +1/2,-1/2(5) 1(6) 04.填上n、l、m、m s等相应的量子数:量子数确定多电子原子轨道能量E的大小;Ψ的函数式则是由量子数所确定;确定核外电子运动状态的量子数是;原子轨道或电子云的角度分布图的不同情况取决于量子数。
【解答】主量子数n和角量子数l;主量子数n、角量子数l和磁量子数m;主量子数n、角量子数l、磁量子数m和自旋量子数m;s 角量子数l和磁量子数m。
第二章习题解答

第二章2-3 设系统传递函数为342)(2++=s s s G 初始条件0/)0(,1)0(=-=dt dc c 。
求单位阶跃输入r (t)=1(t)时,系统的输出响应c (t)。
【解】系统传递函数与微分方程是一一对应的,故通过传递函数先求出微分方程,然后通过拉氏变换的方法求解微分方程。
系统对应的微分方程为 4()3()2()c c t c t r t ++= 在给定的非零初始条件下,进行拉氏变换22(43)()(0)(0)4(0)s s C s sc c c s++---=整理后2221()(43)(43)s C s s s s s s +=-++++部分分式展开后,拉氏反变换111223242/35/25/6()[()][][](43)(43)13255326t t s c t L C s L L s s s s s s s s e e -----+==-=-+++++++=-+2-4 在图2-48中,已知G (s) 和H (s)两方框对应的微分方程分别为()2()5()4()3()6()c t c t e t b t b t c t +=+=图2-48 习题2-4系统结构框图且初始条件为零,试求传递函数C (s)/R (s)。
【解】求出每个方框的传递函数,利用反馈等效的方法求C(s)/R(s)。
根据定义可得 5()2G s s =+,6()43H s s =+ 255()5()25(43)10075(2)56()1()()(2)(43)30411361(2)(43)C s G s s s s R s G s H s s s s s s s +++====+++++++++2-5 图2-49是由电阻、电容和运算法放大器组成的无源网络和有源网络,试列写以V in (t)为输入量,V out (t)为输出量的传递函数。
(a) (b )(c) (d)图2-49 习题2-5电路图【解】(a) 1211211,1RZ R Z C s RC s C s===+ 22112121211()1()11Z C s RC s G s R Z Z R C C s RC s C s +===+++++(b ) 21122211R Z R Z R Cs R Cs ===+ 2222111211()1R Z R Cs R G s Z R R R Cs +=-==-+ (c) 32321123232321()(1)1()1()1R R R R Cs Cs Z R Z R R Cs R R Cs R R Cs++==+==++++ 323232211132(1)()11()()1R R Cs R R Cs R Z R Cs G s Z R R R R Cs ++++=-=-=-++ (d)本题和(b)、(c)做法图通,因为反馈通路有接地的部分。
第二章习题解题过程和参考答案

第二章习题解题过程和参考答案第二章习题解题过程和参考答案2-1 试建立题2-1图所示各系统的微分方程 [其中外力)(t f ,位移)(t x 和电压)(t u r为输入量;位移)(t y 和电压)(t u c为输出量;k (弹性系数),μ(阻尼系数),R (电阻),C (电容)和m (质量)均为常数]。
解:2-1(a) 取质量m 为受力对象,如图,取向下为力和位移的正方向。
作用在质量块m 上的力有外力f(t),重力mg ,这两个力向下,为正。
有弹簧恢复力[]0)(y t y k +和阻尼力()dy t dtμ,这两个力向上,为负。
其中,0y 为0)(=t f 、物体处于静平衡位置时弹簧的预伸长量。
根据牛顿第二定理F ma ∑=,有[]22()()()()dy t d y t f t mg k y t y m dt dtμ+-+-= 其中:0ky mg =代入上式得22)()()()(dt t y d mdt t dy t ky t f =--μ整理成标准式:22()()()()d y t dy t m ky t f t dt dtμ++=μμ()f t[()k y t +()dy t dt或也可写成:22()()1()()d y t dy t k y t f t dt m dt m mμ++=它是一个二阶线性定常微分方程。
2-1(b) 如图,取A 点为辅助质点,设该点位移为()Ax t ,方向如图。
再取B 点也为辅助质点,则该点位移即为输出量()y t ,方向如图A 点力平衡方程:1()()[()()][]AAdx t dy t k x t x t dt dtμ-=- ① B 点力平衡方程:2()()()[]Adx t dy t k y t dt dtμ=- ②由①和②:12[()()]()A k x t x t k y t -= 得:21()()()Akx t x t y t k=-二边微分:21()()()Adx t k dx t dy t dt dt k dt=-③将③代入②:221()()()()[]k dx t dy t dy t k y t dt k dt dtμ=--整理成标准式:1221()()()k k k dy t dx t y t k dt dtμ++=或也可写成:()A t AB1211212()()()()k k k dy t dx t y t dt k k k k dtμ+=++它是一个一阶线性定常微分方程。
电力系统经济学原理习题解 第二章

电力系统经济学原理习题解第二章第2章经济学基础第2章经济学基础2.1 假设有一制造商,他生产某一产品的变动成本如下式所示:c q=25q____q[美元],其中c是总变动成本,q是生产数量。
(a) 推导出边际生产成本的表达式。
(b) 推导出按边际成本出售该产品时,制造商的收入与利润的表达式。
答:(a) 对于任意给定的生产水平,边际成本函数的数值等于生产单位增量商品的成本。
dc q dq=50q____2(b) 按边际成本出售该产品时,制造商的收入为P=q__215;其利润为profit=P c q=25q2dc q dq=50q2____q这里假定考虑的是长期过程,没有成本是固定的。
2.2 假定一群消费者对某类装饰品的反需求函数如下式所示:= 10q____[美元],其中q代表消费者需求,是该产品的单价。
(a) 计算消费者群体的最大消费需求。
(b) 计算消费者愿意支付的最高购买价格。
(c) 计算最大消费者剩余,并解释为什么消费者不可能实现这一数量的剩余。
(d) 当价格等于1000美元/单位产量时,计算消费量、总消费者剩余、生产者的收入以及净消费者剩余。
(e) 如果价格增加20%,计算此时的消费量与生产者收入变化值。
(f) 当价格=1000美元/单位产量时,消费者群体对该产品的需求价格弹性是多少?(g) 推导出以需求为变量的总消费者剩余函数与净消费者剩余函数,然后用(d)的结果对它进行检验。
(h) 推导出以价格为变量的总消费者剩余函数与净消费者剩余函数,然后用(d)的结果对它进行检验。
答:(a) 商品价格最低时,需求达到最大:2。
(完整版)计算机控制技术第二章习题答案整理及详解(.04.26修改版SK)

be i ng 第2章 习题参考答案1.什么是接口、接口技术和过程通道?答:接口是计算机与外设交换信息的桥梁,包括输入接口和输出接口。
接口技术是研究计算机与外部设备之间如何减缓信息的技术。
过程通道是计算机与生产过程之间的信息传送和转换的连接通道。
2.采用74LS244和74LS273与PC/ISA 总线工业控制机接口,设计8路数字量(开关量)输入接口和8路数字量(开关量)输出接口,请画出接口电路原理图,并分别编写数字量输入和数字量输出程序。
答:数字量输入接口设片选端口地址为port MOV DX,portMOV DPTR,PORTMOVX A,@DPTRINAL,DX74LS244PC 总线*IOR(*RD)_数字量输出接口MOV AL,DATA MOV A,DATAMOV DX ,port MOV DPTR,PORT OUTDX,ALMOVX @DPTR,A3.用8位A/D 转换器ADC0809与8051单片机实现8路模拟量采集。
请画出接口原理图,并设计出8路模拟量的数据采集程序。
输出信号PC 总线(*WR)程序:ORG 0000HMOV R0,#30H ;数据区起始地址存在R0MOV R6,#08H ;通道数送R6MOV IE,#84H ;开中断SETB IT1 ;外中断请求信号为下跳沿触发方式MOV R1,#0F0H ;送端口地址到R1NEXT:MOVX @R1,A ;启动A/D转换LOOP:SJMP LOOPINC R0INC R1DJNZ R6,NEXT ;8路采样未接受,则转NEXTCLR EX1 ;8路采样结束,关中断END中断服务程序:ORG 0003H ;外中断1的入口地址AJMP 1000H ;转中断服务程序入口地址ORG 1000HMOVX A,@R1 ;读入A/D转换数据MOV @R0,A ;将转换的数据存入数据区RETI ;中断返回ORG 0000HMOV R1,#30HMOV R2,#0F0HA1: MOV DPTR, R2MOVX @DPTR, ALOOP: JNB P3.2 , LOOPMOVX A, @DPTRMOV @R1,AINC R2INC R1CJNE R2, 0F7H, A1END4.用12位A/D 转换器AD574与PC/ISA 总线工业控制机接口,实现模拟量采集。
微积分第2版-朱文莉第2章极限与连续习题祥解

微积分第2版-朱文莉第2章极限与连续习题祥解第二章 极限与连续习题 2.1(A)1. 观察下列数列{}n x ,当n →∞时,极限是否存在,如存在,请写出其极限值.(1) {}(1)1n n x n ⎧⎫-=+⎨⎬⎩⎭; (2) {}1sin n x n ⎧⎫=⎨⎬⎩⎭;(3) {}1(1)2n n x ⎧⎫+-=⎨⎬⎩⎭; (4) {}11n n x n -⎧⎫=⎨⎬+⎩⎭;(5) {}{}(1)nn x n =-; (6) {}21n n x n ⎧⎫-=⎨⎬⎩⎭.解 (1) 当n →∞时,极限为1;(2) 当n →∞时,极限为0; (3) 当n →∞时,极限不存在; (4) 当n →∞时,极限为1; (5) 当n →∞时,极限不存在; (6) 当n →∞时,极限不存在. 2. 对于数列{}⎭⎬⎫⎩⎨⎧+=1n n x n ),2,1( =n ,给定 (1) 1.0=ε,(2) 01.0=ε, (3) 001.0=ε时,分别取怎样的N ,才能使当N n >时,不等式ε<-1n x 成立? 并利用极限的定义证明此数列的极限为1.解 (1) 要使1.011111=<+=-+=-εn n n x n ,只要101.011=>+n ,9n >,故取9=N 即可.(2) 要使01.011111=<+=-+=-εn n n x n ,只要10001.011=>+n ,99n >,故99=N 即可.(3) 要使001.011111=<+=-+=-εn n n x n ,只要1000001.011=>+n ,999n >,故取999=N 即可.对于任意给定的0>ε,要使ε<+=-+=-11111n n n x n ,即ε11>+n ,11->εn .取正整数⎥⎦⎤⎢⎣⎡-=11εN ,则当N n >时,恒有ε<-+=-111n nx n ,故lim 11n nn →∞=+. 习题 2.1 (B)1. 用数列极限的定义证明下列极限:(1) 1(1)lim 01nn n →∞+-=+; (2) 1lim313n n n →∞=+. 证明 (1) 对于任意给定的0ε>,要使不等式n x a -=1(1)22011n n n nε+--≤<<++成立,只需2n ε>成立. 取2N ε⎡⎤=⎢⎥⎣⎦,则当n N >时,恒有ε.所以 1(1)lim 01nn n →∞+-=+.(2) 对于任意给定的0ε>,要使不等式n x a -=1113133(31)9n n n nε--=<<++ 成立,只需19n ε>成立. 取19N ε⎡⎤=⎢⎥⎣⎦,则当n N >时,恒有 1313n n ε-<+. 所以 1lim313n n n →∞=+.2. 利用数列极限的定义证明:0n →∞=. 证明 对于任意给定的0ε>,要使不等式=-a xn 0ε-=<<成立,只需21n ε>成立. 取112+⎥⎦⎤⎢⎣⎡=εN ,则当n N >时,恒有0ε-<.所以 )0n →∞=.3. 若数列{}n x 有界,且lim 0n n y →∞=,证明lim 0n n n x y →∞=.证明 因为数列{}n x 有界,所以存在0M >,对所有的n x 都有n x M ≤,对于任意给定的0ε>,要使不等式0n n x y -=n n n x y M y ε≤<成立,只需n y M ε<,又因为lim 0n n y →∞=,所以对于给定的0Mεε'=>,存在N ,则当n N>时,恒有n y Mεε'<=. 取},max{N M K =,则当K n >时,恒有εε=<MMy x n n .所以lim 0n n n x y →∞=.4.对于数列}{n x ,若a x k →-12 )(∞→k ,a x k →2)(∞→k ,证明:a x n →)(∞→n .证明 因为a x k →-12 )(∞→k ,所以0>∀ε,1k ∃0>,当1k k >时,有ε<--a x k 12;又因为a x k →2)(∞→k ,所以对上述0>ε,2k ∃0>,当2k k >时,有ε<-a x k 2. 记},max{21k k K =,取K N 2=,则当N n >时,若12-=k n ,则121k K k >+>,得ε<-=--a x a x k n 12,若k n 2=,则2k K k ≥>,得ε<-=-a x a x k n 2. 从而只要N n >,就有ε<-a x n ,即lim n n x a →∞=.习题2.2(A)1. 对下图中所示函数)(x f ,求下列极限,如果极限不存在,说明理由.(1) 2lim ()x f x →-; (2) 1lim ()x f x →-; (3)0lim ()x f x →.解 (1) 2lim ()0x f x →-=;(2)1lim ()1x f x →-=-;(3)0lim ()x f x →不存在,因为)0()0(+-≠f f .2. 对下图中所示函数)(x f ,下列陈述中哪些是对的,哪些是错的?(1) 0lim ()x f x →不存在; (2) 0lim ()0x f x →=;(3) 0lim ()1x f x →=; (4)1lim ()0x f x →=;(5) 1lim ()x f x →不存在; (6) 对每个)1,1(0-∈x , 0lim ()x x f x →存在.解 (1) 错,因为0lim ()x f x →存在与否,与)0(f 的值无关.(2) 对,因为0)0()0(==+-f f .(3) 错,因为0lim ()x f x →的值与)0(f 的值无关.(4) 错,0)01(=+f ,1)01(-=-f ,故1lim ()x f x →不存在.(5) 对,因为)01()01(-≠+f f . (6) 对.3. 用极限定义证明:(1) 1lim(21)1x x →-=; (2) 224lim 42x x x →--=-+;(3) 23lim2x x x →∞+=; (4) lim 0x =.证明 (1)对于任意给定的0ε>,要使不等式()f x A -(21)121x x ε=--=-<成立,只需12x ε-<成立. 取2εδ=,则当01x δ<-<时,恒有(21)1x ε--<.所以 1lim(21)1x x →-=.(2)对于任意给定的0ε>,要使不等式()f x A -24(2)(2)(4)4222x x x x x x ε--+=--=+=+<++成立,只需取δε=即可. 则当0x δ<+<时,恒有24(2x x ε--+. 所以224lim 42x x x →--=-+.(3)对于任意给定的0ε>,要使不等式()f x A -2332x x xε+=-=< 成立,只需3x ε>成立. 取3M ε=,则当x M >时,恒有232x xε+-<. 所以 23lim2x x x →∞+=.(4)对于任意给定的0ε>,要使不等式()0f x A ε-=<< 成立,只需⎥⎦⎤⎢⎣⎡>21εx 成立. 取⎥⎦⎤⎢⎣⎡=21εM ,则当x M >时, 恒有0ε-<. 所以lim0x =.习题2.2 (B)1. 当2→x 时,4)(2→=x x f ,问δ等于多少,使当δ<-2x 时,001.04)(<-x f ?解 由于2→x ,02→-x ,不妨设12<-x ,即31<<x . 要使25)2)(2(42-<-+=-x x x x0002.02=-x , 取0002.0=δ,则当δ<-<20x 时,就有001.04)(<-x f .2. 当∞→x 时,2312)(22→++=x x x f ,问X 等于多少,使当X x >时,01.02)(<-x f ?解 因为222253523122)(x x x x x f <+=-++=-. 要使01.0231222<-++x x ,只要01.052<x,即510>x ,取510=X ,则当X x >时,就有01.02)(<-x f . 3. 讨论0x →时,下列函数的极限是否存在.(1) 1,0()0, 01,0x x f x x x x -<⎧⎪==⎨⎪+>⎩; (2) ⎩⎨⎧<<<<-=10 ,0,sin )(x x x x x f π. 解 (1)由于 0lim ()lim (1)1x x f x x --→→=-=-, 00lim ()lim (1)1x x f x x ++→→=+=,故 0lim ()lim ()x x f x f x -+→→≠. 所以 0lim ()x f x →不存在.(2)由于0lim ()lim sin 0x x f x x --→→==,0lim ()lim 0x x f x x ++→→==. 故0lim ()x f x -→0lim ()x f x +→=. 所以0lim ()0x f x →=. 4. 设函数3()53x x f x x x+=-,求:(1) lim ()x f x →+∞; (2) lim ()x f x →-∞;(3) 0lim ()x f x +→; (4) 0lim ()x f x -→.解 34(1)lim ()limlim2532x x x x x xf x x xx→+∞→+∞→+∞+===-.321(2)lim ()limlim5384x x x x x x f x x x x →-∞→-∞→-∞+===-.3(3)lim ()lim 253x x x x x f x x x ++→→→+==-. 0321(4)lim ()lim lim 5384x x x x x x f x x xx ---→→→+===-. 5. 设函数212()22x x f x x a x ⎧+≥=⎨+<⎩,问当a 取何值时,函数)(x f 在2→x 时的极限存在.解 因为 22lim ()lim (2)4x x f x x a a --→→=+=+, 222lim ()lim (1)5x x f x x ++→→=+=. 由极限存在的条件,有 2lim ()x f x -→2lim ()x f x +→=,得1a =.习题2.3(A)1. 下列变量在何种情况下为无穷小,又在何种情况下为无穷大? (1)11x -; (2) 211x x --; (3) ln(1)x -.解 (1)由于1lim 01x x →∞=-,故x →∞时,变量11x-为无穷小. 由于11lim 1x x →=∞-,故1x →时,变量11x-为无穷大. (2) 由于21lim01x x x →∞-=-,故x →∞时,变量211x x --为无穷小. 由于211lim 1x x x →--=∞-, 故1x →-时,变量211x x --为无穷大.(3) 由于2lim ln(1)0x x →-=,故2x →时,变量为ln(1)x -无穷小.由于lim ln(1)x x →+∞-=+∞,或 1lim ln(1)x x +→-=-∞,故x →+∞或1x +→时变量ln(1)x -为无穷大.2. 根据定义证明:(1) 1-=x y 为当1→x 时的无穷小; (2) xxy sin =为当∞→x 时的无穷小. 解 (1) 因为0)1(-=--x x ,所以0>∀ε,取εδ=,则当δ-<10x 时,就有ε<--0)1(x ,即1-=x y 为当1→x 时的无穷小.(2) 因为xx x 10cos ≤-,所以0>∀ε,取ε1=X ,则当X x >时,恒有ε<-0cos xx, xxy cos =为当∞→x 时的无穷小. 3. 求下列极限.(1) sin lim x x x→∞; (2) 221lim 56x x x x →+-+; (3) 224lim 2x x x →--.解 (1)因为sin x 是有界函数,x →∞时,1x为无穷小. 所以 sin lim0x xx→∞=.(2)当2x →时,1x +有界,256x x -+为无穷小. 所以221lim56x x x x →+=∞-+.(3) 22224(2)(2)lim lim lim(2)422x x x x x x x x x →→→-+-==+=--.习题2.3 (B)1. 举例说明,两个无穷小的商不一定是无穷小;无穷小与无穷大的积不一定是无穷小.解 (1) 例如 0)1(lim 1=-→x x ,0)1(lim 21=-→x x ,但2)1(lim 11lim 121=+=--→→x x x x x . 不是无穷小.(2) 例如 0)1(lim 1=-→x x ,∞=-→11lim21x x ,但是2111lim 11lim 11)1(lim 12121=+=--=--→→→x x x x x x x x 不是无穷小.2. 函数x x y cos =在),(+∞-∞内是否有界?这个函数是否为+∞→x 时的无穷大?解 因为0>∀M ,总有),(0+∞∈M x ,使得1cos 0=x ,从而M x x x y >==000cos ,所以,函数x x y cos =在),(+∞-∞内无界.又存在00>N ,0>∀X ,总有),(0+∞∈X x ,0cos 0=x ,从而0000cos N x x y <==, 所以,函数x x y cos =不是当+∞→x 时的无穷大.3. 根据定义证明:函数xxy 21+=为当0→x 时的无穷大. 问x 应满足什么条件,能使410>y ?证明 因为212121-≥+=+x x x x ,要使M x x >+21,只要M x>-21,即21+<M x . 所以0>∀M ,取21+=M δ,当δ<-<00x 时,就有M xx>+21,即函数xxy 21+=为当0→x 时的无穷大. 令410=M ,取21014+=δ,当2101004+<-<x 时,就能使41021>+xx. 习题2.4(A)1. 简要回答下列问题.(1) 若数列{}n x 收敛,而数列{}n y 发散,则数列{}n n x y ±及数列{}n n x y 是否收敛? (2) 若数列{}n x ,{}n y 均发散,则数列{}n n x y ±及数列{}n n x y 是否发散?解 (1) 数列{}n n x y ±发散. 如果{}n n x y ±收敛,那么()n n n n y x x y =--或()n n n n y x y x =+-也收敛.数列{}n n x y 不一定收敛. 例如:数列1n x n=收敛,(1)nn y =-发散, 1(1)n n n x y n =-收敛;又数列1n x n=收敛,2n y n =发散, n n x y n =发散. (2) {}n n x y ±及数列{}n n x y 不一定发散. 2. 求下列函数的极限.(1) 322042lim 32x x x x x x→-++; (2) 22132lim 43x x x x x →-+-+;(3) 4x →(4) )limx x →+∞;(5) 3131lim 11x x x →⎛⎫- ⎪--⎝⎭; (6) ()()()2030502332lim 21x x x x →∞-++;(7) 332lim 1x x x x →∞+-+ ; (8) 220()lim h x h x h→+-.解 (1) 322200424211limlim 32322x x x x x x x x x x →→-+-+==++. (2) 2211132(1)(2)(2)1lim lim lim 43(1)(3)(3)2x x x x x x x x x x x x x →→→-+---===-+---.(3) x x →→=4x x →→===322.(4) 1lim )limlim2x x x x →+∞===. (5) 3211312lim lim 1111x x x x x x x →→+⎛⎫-==⎪--++⎝⎭.(6) 203030203050503223(23)(32)3lim lim (21)212x x x x x x x x →∞→∞⎛⎫⎛⎫-+ ⎪ ⎪-+⎛⎫⎝⎭⎝⎭== ⎪+⎝⎭⎛⎫+ ⎪⎝⎭. (7) 3333232322lim 112lim lim 1111111lim 1x x x x x x x x x x x xx →∞→∞→∞→∞⎛⎫++ ⎪+⎝⎭===-+⎛⎫-+-+ ⎪⎝⎭.(8) 22222000()2limlim lim(2)2h h h x h x x xh h x x h x h h→→→+-++-==+=. 3. 求下列极限.(1) 1123lim 23n nn n n ++→∞++;(2)2n n(3) n →∞; (4) 1111242lim1111393n n n →∞++++++++; (5) 11lim 1335(21)(2n n →∞⎛+++⋅⋅-⎝.解 (1) 11212313lim lim 2332323nn nn n n n n ++→∞→∞⎛⎫+⎪+⎝⎭==+⎛⎫+ ⎪⎝⎭.(2) 2214n n n⎫⎪===. (3) lim n →∞0n ==.(4) 111121111112422lim lim 1111113933113n n n n n n ++→∞→∞⎛⎫- ⎪⎝⎭++++-==⎛⎫++++- ⎪⎝⎭-43. (5) 由于1111(21)(21)22121n n n n ⎛⎫=- ⎪-+-+⎝⎭,有1111323(21)(21)n n +++⋅⋅-+111111111123352121221n n n ⎛⎫⎛⎫=-+-++-=- ⎪ ⎪-++⎝⎭⎝⎭. 于是111111lim lim 11323(21)(21)2212n n n n n →∞→∞⎛⎫⎛⎫+++=-= ⎪ ⎪⋅⋅-++⎝⎭⎝⎭.习题2.4 (B)1. 设222lim 22x x ax bx x →++=--,求常数a ,b 的值.解 因为222lim 22x x ax bx x →++=--,推得b ax x ++2含有因式2x -,否则与已知矛盾.设2x ax b ++(2)()x x c =--,得2,(2)b c a c ==-+.又因为 22222(2)()2lim lim lim 22(2)(1)13x x x x ax b x x c x c cx x x x x →→→++----====---++,得4-=c ,从而得到2a =,8b =-.2. 设511lim 2-=⎪⎪⎭⎫⎝⎛+---∞→b ax x x x ,求常数a ,b 的值. 解 因为511)()1(lim 11lim 22-=⎪⎪⎭⎫⎝⎛---++-=⎪⎪⎭⎫ ⎝⎛+---∞→∞→x b x b a x a b ax x x x x ,推得105a ab -=⎧⎨+=-⎩, 得1a =,6b =-.3. 设⎪⎪⎩⎪⎪⎨⎧>≤<+≤+=,1,2,10,1,0,23)(2x xx x x x x f 分别讨论0→x 及1→x 的极限是否存在.解 (1) 由于 0lim ()lim (32)2x x f x x --→→=+=,200lim ()lim(1)1x x f x x ++→→=+=. 由于 0lim ()lim ()x x f x f x -+→→≠,所以 0lim ()x f x →不存在. (2) 由于 211lim ()lim(1)2x x f x x --→→=+=, 112lim ()lim 2x x f x x++→→==, 111lim ()lim ()lim ()2x x x f x f x f x -+→→→===, 所以 1lim ()x f x →存在.4. 设1lim ()x f x →存在,且21()2lim ()x f x x x f x →=+,求1lim ()x f x →和()f x .解 设1lim ()x f x A →=,则2()2f x x Ax =+,于是211lim ()lim(2)12x x A f x x Ax A →→==+=+,得1A =-,2()2f x x x =-.习题2.5(A)1. 求下列极限: (1) 0tan 2limsin 5x x x →;(2) 0lim x +→; (3) 02arcsin lim3x x x →; (4) lim 2sin (0)2nnn x x →∞≠;(5) 202lim sin 3x x x→; (6) 0tan sin limx x xx→-.解 (1) 00tan 22tan 222lim lim sin 5sin 5555x x xxx x x x xx→→==.(2) 00022lim limlim 2x x x x x+++→→→===(3) 令t x =arcsin ,则002arcsin 22limlim 33sin 3x t x t x t →→==.(4) sin 22lim 2sin lim sin lim 222nn n n n n n n nx x x x xx x x →∞→∞→∞===. (5) 22002293lim lim 9sin sin 33x x x x x x →→⎛⎫ ⎪⎝⎭==.(6) 0tan sin lim x x x x x →→-= 00sin (1lim lim cos x x x x x→→-=⋅2. 求下列极限:(1) 51lim 1n n n +→∞⎛⎫+ ⎪⎝⎭; (2) lim 1xx x x →∞⎛⎫⎪+⎝⎭; (3) 21lim 23xx x x →∞-⎛⎫⎪+⎝⎭; (4) 22lim 2xx x →-⎛⎫ ⎪⎝⎭; (5) ()1lim 12sin xx x →+; (6) ()3sec 2lim 1cos xx x π→+.解 (1) 55111lim 1lim 11n nn n e n n n +→∞→∞⎛⎫⎛⎫⎛⎫+=++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. (2) 11lim lim 111xx x x x x e x →∞→∞⎛⎫== ⎪+⎝⎭⎛⎫+ ⎪⎝⎭. (3) 令423t x -=+,则214lim lim 12323x xx x x x x →∞→∞--⎛⎫⎛⎫=+ ⎪ ⎪++⎝⎭⎝⎭2231322220lim(1)lim (1)lim(1)1t tt t t t t t e e ------→→→⎡⎤=+=++=⋅=⎢⎥⎣⎦. (4) 1221002lim lim 122xxx x x x e ---→→⎡⎤--⎛⎫⎛⎫⎢⎥=+= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦. (5) 012sin lim20lim(12sin )x xxx x ee →→+==.(6) 3cos 3sec 322lim(1cos )lim(1cos )x xx x x x e ππ→→+=+=.3. 设 21001lim 5xc x x e x →∞+⎛⎫= ⎪-⎝⎭,求c . 解 222012lim 2012510011006lim lim 155x xxxc x x x x e e e x x →∞-→∞→∞+⎛⎫⎛⎫=+=== ⎪ ⎪--⎝⎭⎝⎭,2012=c .习题2.5 (B)1. 利用极限存在准则,计算下列各题.(1) 222111lim (1)()n n n n n →∞⎡⎤+++⎢⎥++⎣⎦; (2) n →∞. 解 (1)由于222221111()(1)()n n n n n n n n n n<+++<=+++, 又因为 1lim0n n →∞=,2lim 0()n nn n →∞=+,由夹逼准则,有 222111lim 0(1)()n n n n n →∞⎡⎤+++=⎢⎥++⎣⎦. (2) 因为1sin 1n -<<,所以有223311n nn n -<<++,此时23lim 01nn n →∞-=+,23lim 01n n n →∞=+,由夹逼准则,有 0n →∞=. 2. 利用极限存在准则证明:数列2,22+,222++,…的极限存在,并求出该极限.解 归纳证明这个数列是严格单调增加的,并以2为上界.2<,假设1n n a a -<,那么1n n a a +=<=,可见数列是单调增加的. 2<,2n a <,可推出12n a +=<=,所以数列以2为上界. 由准则Ⅱ知,此数列是收敛数列,记极限为a .由在递推公式1n a +1lim n n a +→∞=即a =2a =.3. 某企业计划发行公司债券,规定以年利率6.5%的连续复利计算利息,10年后每份债券一次偿还本息1000元,问发行时每份债券的价格应定为多少元?解 设发行时每份债券的价格应定为0A 元,则65.0010%5.601000e A e A ==⨯,所以05.522100065.00≈⋅=-e A (元).4. 设本金为p 元,年利率为r . 若一年分n 期,存期t 年,若以复利方式结算,则本金与利息之和是多少?现某人将1000p =元存入某银行,年利率为0.06r =,2t =;请按单利、季度、月利及连续复利等结算方式计算本利和.解 按单利计算:本利和为=00.1120206.010001000=⨯⨯+(元). 由复利公式有ntn r p ⎪⎭⎫ ⎝⎛+1, 按季度结算方式计算:4n =,利和为49.1126406.011000124≈⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+⨯nt n r p (元),按月结算方式计算:12n =,本利和为.1511271206.0110001212≈⎪⎭⎫⎝⎛+=⎪⎭⎫ ⎝⎛+⨯nt n r p (元),连续复利结算方式计算:本利和为 1000rt rtpe e =1127.49≈(元).5. 根据函数极限的定义,证明极限存在的准则I '.证明 仅就0x x →的情形证明准则I ',∞→x 的情形类似证明.0>∀ε,因为A x g x x =→)(lim 0,01>∃δ,当100δ<-<x x ,有ε<-A x g )(,即εε+<<-A x g A )(, (3)又A x h x x =→)(lim 0,对于上面的0>ε,02>∃δ,当200δ<-<x x ,有ε<-A x h )(,即εε+<<-A x h A )(. (4)取},min{21δδδ=,则当δ<-<00x x ,假设(1)及式(3)、(4)同时成立,从而有εε+<≤≤<-A x h x f x g A )()()(,即ε<-A x f )(.因此,0lim ()x x f x →存在,且等于A .习题2.6(A)1. 当0→x 时,下列各函数都是无穷小,试确定哪些是x 的高阶无穷小?同阶无穷小?等价无穷小?(1) x x +2; (2) x x sin +;(3) x x sin -; (4) x 2cos 1-; (5) x arctan ; (6) x 2tan .解 (1) 因为200lim lim(1)1x x x xx x→→+=+=,所以x x +2是与x 等价的无穷小.(2) 因为00sin sin limlim 1112x x x x x x x →→+⎛⎫=+=+= ⎪⎝⎭,所以x x sin +是与x 同价的无穷小. (3) 因为00sin sin limlim 10x x x x x x x →→-⎛⎫=-= ⎪⎝⎭,所以x x sin -是比x 高价的无穷小. (4) 因为20001sin 1cos 2sin 2lim lim lim sin 02x x x xx x x x x x →→→-⎛⎫==⋅= ⎪⎝⎭,所以x 2cos 1-是比x 高价的无穷小.(5) 因为00arctan limlim 1x x x xx x →→==,所以x arctan 是与x 等价的无穷小.(6) 因为00tan 22limlim 2x x x xxx →→==,所以x 2tan 是与x 同价的无穷小. 2. 当1x →时,无穷小111xx-+是否为等价的无穷小?解1111x x x→→-=. 故11xx -+与1.3. 当1x →时,无穷小1x -与下列无穷小是否同阶,是否等价?(1) 1 (2)2(1.解 (1) 由于11113x x x →→→===故1x -与1.(2) 由于112(1lim11x x x →→==-,故1x -与2(1等价.4. 利用等价无穷小代换原理求下列极限.(1) 0arctan 3lim sin 2x x x →; (2) 0sin lim (,)(sin )mn x x m n x →正数;(3) 201lim 1cos x x e x→--; (4) 201lim 3x x e x x →-+;(5) 21arcsin(1)lim (1)ln(21)x x x x →---; (6) 30tan sin lim ln(1)x x xx →-+;(7) 0x →; (8) 2330235lim 42tan x x x x x x →+-+.解 (1) 00arctan 333limlim sin 222x x x x x x →→==.(2) 00sin lim lim (sin )mmn n x x x x x x→→==0,1,,m n m n m n >⎧⎪=⎨⎪∞<⎩. (3) 222001limlim 21cos 2x x x e x xx →→-==-. (4) 22000111lim lim lim 3333x x x x e x x x x x x →→→-===+++. (5) 2211arcsin(1)(1)1lim lim (1)ln(21)(1)(22)2x x x x x x x x →→--==----.(6) 2333000tan sin tan (1cos )12limlim lim ln(1)ln(1)2x x x x x x x x x x x x →→→⋅--===++.(7) 22lim42x x xx x →→==+.(8) 2330235lim 42tan x x x x x x →+-+2200220lim(235)2352lim 1tan tan 242lim 42x x x x x x x x x x x x x →→→+-+-====⎛⎫++ ⎪⎝⎭.习题2.6 (B)1. 证明当0→x 时,有如下结论:(1) x x ~arctan ; (2) 221~1sec x x -; (3)221~1sin 1x x x -+; (4) 222~11x x x --+. 证明 (1) 令x t arctan =,则t x tan =,当0→x 时,0→t . 于是000arctan cos limlim lim 1sin tan x t t x t tt x tt →→→===,故x x ~arctan .(2) 因为200002222111sec 11cos cos 2lim lim lim lim 11111cos cos 2222x x x x xx x x x x x x x x →→→→---====⋅⋅, 所以,221~1sec x x -.(3)因为0022sin lim 111)22x x x x x x x →→→===, 所以,221~1sin 1x x x -+. (4) 因为20001x x x →→→===,所以222~11x x x --+.2. 证明无穷小的等价关系具有下列性质:(1) αα~(自反性); (2) 若βα~,则αβ~(对称性); (3) 若βα~,γβ~,则γα~(传递性).证明 (1) 因为1lim=αα,所以αα~. (2) 因为βα~,即1lim=βα,所以1lim =αβ,即αβ~.(3) 因为βα~,γβ~,即1lim=βα,1lim =γβ,所以 1lim lim lim lim=⋅=⎪⎪⎭⎫ ⎝⎛⋅=γββαγββαγα,即γα~. 3. 当0x →时,变量122(1)1kx +-与变量cos 1x -为等价无穷小,求常数k 的值.解 2122200(1)12lim lim 1cos 12x x kx kx k x x →→+-==-=--. 即 1k =-.解其中x 习题2.7(A)1. 讨论下列函数的连续性.(1) ⎩⎨⎧>≤=0 ,0 ,sin )(2x x x x x f ; (2) ⎪⎩⎪⎨⎧>≤≤--<-=1 ,111 ,1,1)(2x x x x x f .解 (1) 因为,当0<x 时,x x f sin )(=是连续的;当0>x 时,2)(x x f =是连续的,由于lim sin 0x x -→=,20lim 0x x +→=,00sin )0(==f ,故()f x 在0x =处连续. 从而函数)(x f 在) ,(∞+-∞内连续.(2) 因为)(x f 为分函数,当1-<x ,11<<-x ,1>x 时,函数)(x f 均是连续的.在1-=x 处,由于1lim (1)1x -→--=-,21lim 1x x +→-=,所以1-=x 是跳跃间断点;在1=x 处,由于21lim 1x x -→=,1lim11x +→=,且1)1(=f ,所以,函数在1=x 处连续. 综上所述:函数)(x f 在区间) ,1()1 ,(∞+---∞ 内连续.2. 确定常数a ,b 使下列函数连续.(1) ⎩⎨⎧>+≤=0 ,0 ,)(x a x x e x f x ; (2) ⎪⎪⎩⎪⎪⎨⎧>=<-=0,sin 0 ,20 ,)31ln()(x x axx x bx x x f .解 (1) 当0<x 与0>x 时,函数)(x f 为初等函数,它是连续的. 要使函数)(x f 在) ,(∞+-∞内连续,只需要函数)(x f 在0=x 处连续即可.因为1)0(0==e f ,0lim 1x x e -→=,0lim ()x x a a +→+=,所以当1=a 时,即有 00lim ()lim ()(0)1x x f x f x f -+→→===, 即当1=a 时,函数)(x f 在0=x 处连续. 故当取1=a 时,函数)(x f 在) ,(∞+-∞内连续.(2) 当0<x 与0>x 时,函数)(x f 为初等函数,故它是连续的. 要使函数)(x f 在) ,(∞+-∞内连续,只需要函数)(x f 在0=x 处连续即可.因为00033lim ()lim lim x x x x f x bx b---→→→-==-,000sin lim ()x x x a axf x a x ax +→+→+→==.由函数)(x f 在0=x 处连续知,00lim ()lim ()(0)2x x f x f x f -+→→===,即得,23=-=ba . 故当2=a ,23-=b 时,函数)(x f 在0=x 处连续. 也即函数)(x f 在) ,(∞+-∞内连续.3. 考察下列函数在指定点的连续性. 如果是间断点,指出其属于哪一类;如果是可去间断点,则补充或改变函数的定义使其成为函数的连续点.(1) 23122+--=x x x y ,1=x ,2=x ;(2) xxy sin =, πk x =,),2 ,1 ,0( ±±=k ; (3) xy 1cos 2=,0=x ;(4) ⎩⎨⎧>-≤-=1,31,12x x x x y ,1=x .解 (1) 因为)2)(1()1)(1(23122--+-=+--=x x x x x x x y ,函数在1=x ,2=x 处无定义,所以都是间断点.又因为221lim )2)(1()1)(1(lim 231lim 11221-=-+=--+-=+--→→→x x x x x x x x x x x x , ∞=+--→231lim 222x x x x , 所以,1=x 为第一类间断点(可去间断点),重新定义,当1=x 时,令2-=y ,则函数在1=x 处连续.2=x 为第二类间断点(无穷间断点).(2) 函数xxy sin =在 πk x =,),2 ,1 ,0( ±±=k 处无定义,所以它们都是间断点. 因为1sin lim0=→xxx ,故0=x 是函数y 的第一类间断点(可去间断点).若令1)0(=y ,则函数在0=x 处连续;若0≠k ,则∞=→xxk x sin lim π,故 πk x =),2 ,1( ±±=k 为函数y 的第二类间断点(无穷间断点).(3) 对0=x ,因为21lim cos x x -→及201lim cos x x+→均不存在,所以0=x 为函数的第二类间断点.(4) 对1=x ,因为11lim ()lim(21)1x x f x x --→→=-=,11lim ()lim(3)2x x f x x ++→→=-=,所以 1=x 第一类间断点(跳跃间断点).4. 求函数32233()6x x x f x x x +--=+-的连续区间,并求0lim ()x f x →,3lim ()x f x →-,2lim ()x f x →.解 由于323223333()6(3)(2)x x x x x x f x x x x x +--+--==+-+-, 得()f x 的定义域为()()(),33,22,-∞--+∞. 由于初等函数在其定义区间内连续,故函数()f x 的连续区间为()()(),33,22,-∞--+∞.01lim ()(0)2x f x f →==,22333(3)(3)18lim ()lim lim (3)(2)25x x x x x x x f x x x x →-→-→-+-+-===-+--,由于0)3)(1()2)(3(lim )(1lim222=+--+=→→x x x x x f x x ,故 222(3)(3)lim ()lim (3)(2)x x x x x f x x x →→+-+==∞+-.5. 求下列极限(1) 52lim 20+-→x x x ; (2) 34)2(sin lim x x π→;(3) sin 0lim xx x e→;(4) 145lim1---→x xx x .解 (1) 5502052lim 220=+⨯-=+-→x x x .(2) 142sin )2(sin lim 334=⎪⎭⎫ ⎝⎛=→ππx x . (3) e e eex x xxx x ===→→1sin limsin 00lim .(4) )45)(1()1(4lim145lim11x x x x x x x x x +---=---→→21==→x .习题2.7 (B)1. 设2,01()2,1ln(1), 13ax b x f x x bx x ⎧+<<⎪==⎨⎪+<≤⎩, a ,b 为何值时,()f x 在1x =处连续?解 由于211lim ()lim()x x f x ax b a b --→→=+=+,11lim ()lim ln(1)ln(1)x x f x bx b ++→→=+=+. 要使()f x 在1x =处连续,须有ln(1)2,2b a b +=+=.解之得 23a e =-,21b e =-. 2. 讨论下列函数的连续性.(1) 1()lim(0)1n n f x x x →∞=≥+; (2) 221()lim 1nnn x f x x x →∞-=+.解 (1) 1, 0111()lim , 1120, 1nn x f x x x x →∞≤<⎧⎪⎪===⎨+⎪>⎪⎩, 由于 11lim ()lim11x x f x --→→==,11lim ()lim 00x x f x ++→→==,故1x =为间断点. (2) 22, ||11()lim 0, 11,||1n nn x x x f x x x x x x →∞<⎧-⎪===±⎨+⎪>⎩-, 由于 11lim ()lim 1x x f x x --→→==,11lim ()lim()1x x f x x ++→→=-=-. 故1x =为间断点. 同理1x =-也为间断点. 3. 求下列极限.(1) 21limcos ln 1x x x →∞⎡-⎤⎛⎫+ ⎪⎢⎥⎝⎭⎣⎦; (2) sin 0lim xxx e →;(3) 01limarctan x x e x →⎛⎫- ⎪⎝⎭; (4) ()110lim 2x x x x e -→+. 解 (1) 2121limcos ln(1)cos ln lim(1)cosln 3x x x x x x →∞→∞--⎡⎤⎡⎤+=+=⎢⎥⎢⎥⎣⎦⎣⎦.(2) 0sin sin limlim x x xxxx eee →→==.(3) 0011limarctan arctan lim arctan14x x x x e e x x π→→⎛⎫⎛⎫--=== ⎪ ⎪⎝⎭⎝⎭. (4) ()()11ln 2ln 2111lim 2lim 2x x e xx x x x x eee +---→→+===. 4. 下列陈述中,哪些是对的,哪些是错的?如果是对的,说明理由;如果是错的,试给出一个反例.(1) 如果函数)(x f 在点0x 连续,那么)(x f 也在点0x 连续; (2) 如果函数)(x f 在点0x 连续,那么函数)(x f 也在点0x 连续. 解 (1) 对. 因为0)()()()(00→-≤-x f x f x f x f )(0x x →,所以)(x f 也在点0x 连续. (2) 错. 例如⎩⎨⎧<-≥=0,10,1)(x x x f , 则)(x f 在点00=x 连续,但函数)(x f 在点00=x 不连续.习题2.8(A)1. 证明方程3310x x --=在区间(1,2)内至少有一个实根.证明 因为函数3()31f x x x =--在闭区间[1, 2]上连续,又(1)30f =-<,(2)10f =>,根据零点定理,在开区间(1, 2)内至少有一点ξ,使得()0f ξ=,即3310ξξ--=.故方程3310x x --=在区间(1,2)内至少有一个实根ξ.2. 设函数()f x 在闭区间[,]a b 上连续,且(),()f a a f b b <>,证明:至少有一个(,)a b ξ∈,使()f ξξ=.证明 构造辅助函数x x f x g -=)()(.因为函数()f x 在闭区间[, b]a 上连续,且(),()f a a f b b <>,所以x x f x g -=)()(在闭区间[, b]a 上也连续,且0)()(<-=a a f a g ,0)()(>-=b b f b g . 根据零点定理,x x f x g -=)()(在开区间(, b)a 内至少有一点ξ,使得()()0g f ξξξ=-=,即 ()f ξξ=.3. 设函数()f x 在闭区间[0,2]a 上连续,且(0)(2)f f a =,证明:在[0,]a 至少存在一点ξ,使()()f f a ξξ=+.证明 构造辅助函数:)()()(x f a x f x g -+=.因为函数()f x 在闭区间[0,2]a 上连续,且(0)(2)f f a =,所以)()()(x f a x f x g -+=在闭区间[0,]a 上也连续,且()()0)()2()2()()()0(≤--=a f a f a f a f a g g .根据零点定理,)()()(x f a x f x g -+=在开区间(0,)a 内至少有一点ξ,使得()()()0g f a f ξξξ=+-=,即()()f f a ξξ=+.4. 证明方程 sin x a x b =+(其中0,0a b >>)至少有一正根,并且不超过a b +. 证明 令()sin ,f x a x b x =+-[]0,x a b ∈+,()f x 在[]0,a b +上连续,又(0)0f b =>,()sin()()[sin()1]0f a b a a b b a b a a b +=++-+=+-≤。
结构力学第2章习题及参考答案
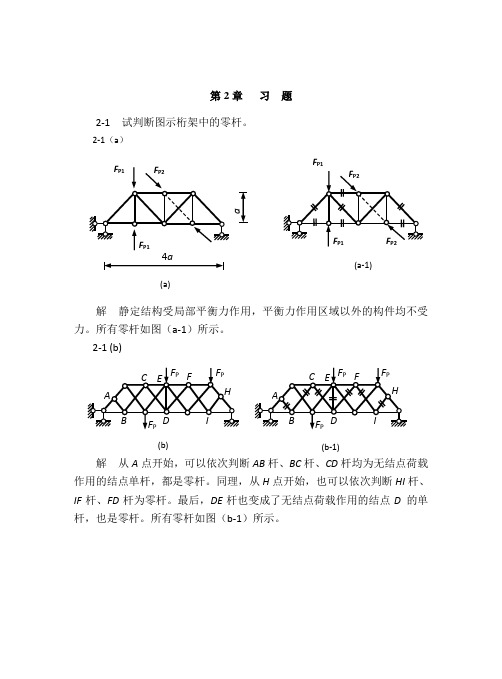
8 kN 20 kN
HI
J ⅠK
L
2 1
AC
D
E ⅠF
G
B
2.5m6 15m
2.5 m
(a)
K
LD
FNJK D
FN2
FNEF FD
G
B
FBy (b
)
解:(1)判断零杆。如图(a)所示。
(2)求支座反力
F x 0 , FAx 0
M A 0 , FB y 12.67 kN
F y 0 , FA y 15.33 kN
5 29
MK
M
0 K
FH yK
510 130 3 120
kN
m
FQK FQ0K cosK FH sinK 52
5 130 29
2 0 29
FNK FN0K sinK FH cosK 52
2 130 29
5 140 kN 29
2-12 图示圆弧三饺拱,求支座反力及截面 D 的 M 、FQ 、FN 值。 20kN/m
D
C
5m
5m
FH
30
A 5m
B 5m
FH
FAy
FBy
习题 2-12 图
解 (1)求支座反力。
FB y 100 kN , FA y 100 kN , FH 50 kN
(2)求等代梁 D 截面内力
M
0 D
FAy
2.5
1 2
20 2.52
187.5kNm
FQ0D FAy 20 2.5 50 kN
30 kN A 4 B 30 kN
3×2m
N 1
N
D
N
CN 2 E
N3
第2章 质点动力学 习题答案

2-8. 长为l的轻绳,一端固定,另一端系一质量为m的小 长为 的轻绳,一端固定,另一端系一质量为 的小 的轻绳 开始运动, 球,使小球从悬挂着的位置以水平初速度 v 0 开始运动, 求小球沿逆时针转过 解:法向方程 角度时的角速度和绳子张力。 角度时的角速度和绳子张力。 θ
T − mg cos θ = m ω 2 l m v + 2 gl (cos θ − 1) = l
r2
r
2
,求电子从 r1 运动到 r2 ( r1 > r2 )
r1
r r r2 k 1 1 f ⋅dr = − ∫ 2 dr = k − r r r1 r 2 1
2-14. 质量为 m = 2 × 10 −3 kg的子弹,在枪筒中前进时受到 的子弹, 的合力为 F = 400 − 300m/s,试计算枪筒的长度。 ,试计算枪筒的长度。 解:设枪筒的长度为
其速度是? 其速度是?
r 2-3. 一物体质量为 一物体质量为10kg,受方向不变的力 F = 30 + 40t ,
的作用,在开始的 内 此力的冲量大小为? 的作用,在开始的2s内,此力的冲量大小为?若物体的 方向与力同向,则在2s末物体 初速度大小为 10 m ⋅ s ,方向与力同向,则在 末物体 速度的大小等于? 速度的大小等于?
r r 2-2. 一质量为 一质量为10kg的物体在力 f = (120t + 40) i 作用 的物体在力 r r v0 = 6i m ⋅ s −1 ,则t=3时 轴运动, 时其速度 下,沿x轴运动,t=0时其速度 轴运动 时
r r r r f (120t + 40)i = = (12t + 4) i 解:a = m 10 r r r t r t r 2 v = ∫ adt = ∫ (12t + 4) i dt =(6t + 4t ) i + v0 0 0 r = ( 6t 2 + 4t + 6) i r r v ( 3) = 72i m ⋅ s −1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 动量守衡 质点动力学
2-1 一个原来静止的原子核,经放射性衰变,放出一个动量为9.22×10-16g ⋅cm/s 的电子,同
时该核在垂直方向上又放出一个动量为5.33×10-16g ⋅cm/s 的中微子,问蜕变后原子核的动量的大小和方向。
解: 衰变过程是: e v e B A ++→-,由动量守衡得 .0=++v e B P P P 大小:
e B P P =-==s cm g s cm g /1065.10/1033.522.9161622⋅⨯=⋅⨯+=--.
方向
: 3022
.933.51
1
===--tg tg
θ; 15030180=-=ϕ, 1203090=+=φ.
2-2 质量为M 的木块静止在光滑的水平桌面上。
质量为m ,速率为v 0的子弹水平地入射到
木块内(见本题图)并与它一起运动。
求 (1)子弹相对于木块静止后,木块的速率和动量,以及子弹的动量;(2)在此过程中子弹施于木块的冲量。
解:(1)设木块的速率为v , 由动量守衡: v m M mv )(0+=;
得0v m M m v +=, 木块的动量0v m M Mm mv p +==木,子弹的动量02
v m
M m mv p +==子.
(2)子弹施予木块的冲量为 00v m
M Mm
P I +=-=木木.
2-3 如本题图,已知绳的最大强度T 0 = 1.00 kg ,m = 500g , l = 30.0cm ,开始时m 静止。
水
平冲量I 等于多大才能把绳子打断?
解: 要求向心力mg T e v m F ->=02
,即要求l m mg T v ->0,l m
mg T m mv I ->-=00.
故 l mg T m I )(0-=
s m kg /86.0]
100.30)8.9105008.91(10500[2
1233⋅=⨯⨯⨯⨯-⨯⨯=---
2-4 一子弹水平地穿过两个前后并排在光滑水平桌面上的静止木块。
木块的质量分别为m 1
和m 2;设子弹透过两木块的时间间隔为t 1和t 2,子弹在木块中所受阻力为恒力f ,求子弹穿过时两木块各以多大的速度运动.
解: 当子弹穿出m 1时, m 1与 m 2一起运动, 故 1211)(v m m ft +=; 2
11
1m m ft v +=
.
当子弹穿出m 2时, 12222v m v m ft -=,解得 2
22112212m ft
m m ft m ft v v ++=+=.
2-5 质量70kg 的渔人站在小船上,设船和渔人的总质量为200kg .若渔人在船上向船头走
4.0m 后停止。
试问:以岸为参考系,渔人走了多远?
解: 设人向右走,对岸速度为v 人 , 相对船的速度为u 人 , 船向左行,对岸的速度为v 船 ;
则v 人 = -v 船+u 人 .
水平方向动量守恒 : m船v 船 - m人(-v 船 + u 人) = (m船 +m人)v 船-m人u 人 = 0.
两边积分得:人对船人船人船人人船人船S m S m m dt u m dt v m m t
t
=+⇒=+⎰
⎰
)()(0
.
由此可得 m S m m m S 4.14200
70
=⨯=+=人对船人船人船 (对岸)
m S S dt u dt v dt v S t
t
t
6.244.10
=+-=+-=+==
⎰
⎰⎰人对船船人船人人 (对岸).
2-6 两艘船依惯性在静止湖面上以匀速相向运动,它们的速率皆为6.0m/s .当两船擦肩相遇
时,将甲船上的货物都搬上乙船,甲船的速率未变,而乙船的速率变为4.0m/s .设甲船空载质量为50kg ,货物质量为60kg ,求乙船质量。
解: 已知 m 甲=500 kg , m 货= 60 kg , v 甲0= v 乙0= v 0 = 6.0 m/s , v 乙= 4.0 m/s ;待求:m 乙 。
忽略水中阻力,两船作为一个系统,其 动量守衡. 即: (m 甲+ m 货)v 0 - m 乙v 0 = m 甲v 0 - ( m 乙+m 货) v ;
kg m v v v v m 300604
64
600=⨯-+=-+=
∴货乙乙乙.
2-7 三只质量均为M 的小船鱼贯而行,速率均为v .由中间那只船上同时以水平速率M (相
对于船)把两质量均为m 的物体分别抛到前后两只船上。
求此后三只船的速率。
解: 设前v 、中v
、后v 分别为前、中、后三船的待求速度. u 与v 同向时为正, 反之为负. 由水平方向的动量守衡定律,有:
前: 前中v m M u v m v M
)()(+=++,
中: )中中中u v m u v m v m M v M ++-+-+()()2(,
后: 后中v m M u v m v M
)()(+=-+;
可推出: 前v = u m M m v ++
, 中v
= v , 后v = u m
M m v +-. ∵u 的正方向与v
同向,∴三船的速率分别为:
u m M m v v ++
=前, v v =中, u m
M m v v +-=后.
2-8 一质量为M 的有轨板车上有n 个人,各人质量均为m .开始时板车静止。
(1) 若所有人
一起跑到车的一端跳离车子,设离车前它们相对于车子的速度为u ,求跳离后车子的速度;(2) 若n 个人一个接一个地跳离车子,每人跳离前相对于车子的速度皆为u ,求车子最后速度的表达式;(3)在上述两种情况中,何者车子获得的速度较大? 解: (1) 人跳离后车子的速度为v ,由水平方向的动量守恒得:
0)(=++u v Nm Mv , 即 u Nm
M Nm v
+-
= (1)
(2) 第一人跳:0)(])1([11=++-+u v m v m N M ,得 u Nm
M m
v +-
=1 (2) 第二人跳: 122])1([)(])2([v m N M u v m v m N M
-+=++-+
得 ()u m
N M Nm M m u m N M m v v ])1(1
1[112-+++-=-+-
= (3)
最后一个人跳: 1)()(-+=++n n n v m M u v m v M
,由此可得 u m
M m m M m m N M Nm M m u m M m v v n n ]2)1(11[1+++++-+++-=+-=- (4)
这是车子最后速度的表达式.
(3) 比较(1)式和(4)式, 显然有v v n
>. 即一个接一个地跳(第二种情况)比集体跳,能使车子最后获得更大的动能.
2-9 一炮弹以速率v 0和仰角θ0发射,到达弹道的最高点时炸为质量相等的两块 (见本题图),
其中一块以速率v 1铅垂下落,求另一块的速率v 2及速度与水平方向的夹角 (忽略空气阻力)。
解: 炮弹在最高点时00cos θv v x =,0=y v .
在爆炸瞬间,内力>>重力,即外力可忽略不计,故此时动量守衡:
i mv j mv i mv v v m x y x =+=+))(2
1
(21.
即 ⎪⎪⎩
⎪⎪⎨⎧
-===1220021sin 210cos 21cos m v
m v m v m v m v x ααθ ,或 02
20212cos 4θv v v +=.
∴ 2
012110011cos 2cos
sin cos 2v v v v v v tg θθα---===。
2-10 求每分钟射出240发子弹的机枪平均反冲力,假定每粒子弹的质量为10g ,枪口速度
为900m/s 。
解: 设平均反冲力为 F = 射击时所需的平均力, 则机枪的动量变化为 =t F 子弹的动量变化 = 240 mv – 0 = 240 mv ,
N t mv F 3660
900
10102402403=⨯⨯⨯==∴-. 2-11 一起始质量为M 0的火箭以恒定率 |d M /d t | = u 排出燃烧过的燃料,排料相对于火箭的
速率为v 0.(a) 计算火箭从发射台竖直向上起动时的初始加速度;(b) 如果v 0=2000m/s ,则对于一个质量为100 t 的这种火箭,要给以等于0.5g 的向上初始加速度,每秒钟必须排出多少kg 的燃料?
解: (1) 仿照书上p.50的推导,可得火箭经过dt 时间后动量的改变为
dt F dM v v md P P
=+=-00 , 由此可得 F dM v dt
v d m =+0. 在发射台附近, M=M 0 , μ=dt
dM , F = M 0g , 方向向下与F v 0
; 0a dt dv =设, 则有: g M v a M 0000-=-μ, g M v
a -=μ0
00.
(2) 由上述式子可见 s kg g a v M /7358.9)15.0(2000
10100)(3
000=⨯+⨯=+=μ.。
