理论力学-刚体的基本运动
理论力学6—刚体的基本运动

§6-5 以矢量表示角速度和角加速度.以矢积表示点的速度和加速度
1、角速度矢量和角加速度矢量
角速度矢量
dj
ww
dt
大小
角速度矢沿轴线,弯向表示刚体转动的方向。
指向用右手螺旋法则。
w wk
角加速度矢量
dw dw
k k
dt
dt
§6-5 以矢量表示角速度和角加速度.以矢积表示点的速度和加速度
2
例6-6
某定轴转动刚体通过点M0(2,1,3),其角速度矢w 的方向
余弦为0.6,0.48,0.64,角速度 的大小ω=25rad/s 。求:刚体上点
M(10,7,11)的速度矢。
解:角速度矢量
w wn
其中 n (0.6,0.48,0.64)
M点相对于转轴上一点M0的矢径
r rM rM0 10,7,11 2,1,3 8,6,8
Z2=60,Z3=12,Z4=70。(a)求减速箱的总减速比i13 ;(b)如
果n1=3000r/min,求n3.
1
n1
2
n2
3
n3
4
解:求传动比:
n1 n1 n2 Z 2 Z 4
i13
34.8
n3 n2 n3 Z1 Z 3
则有:
n1 3000
n3
86r / min
i13
4 rad
dw dw d
dw
w
dt
d dt
d
dw
w
0.2
d
解:
w
w wdw
0
理论力学中的刚体运动与角速度的计算

理论力学中的刚体运动与角速度的计算刚体是指具有一定形状和大小,其内部各点间相对位置不会发生改变的物体。
在理论力学研究中,刚体运动是一个重要且常见的问题,其中角速度的计算是关键的一部分。
本文将介绍刚体运动的基本概念和相关计算方法。
一、刚体运动的基本概念刚体的运动可以分为平动和转动两种形式。
平动是指刚体整体沿直线运动,而转动则是刚体围绕某个轴旋转运动。
在刚体转动的过程中,角速度是一个重要的物理量。
角速度表示刚体某一点在单位时间内绕轴旋转的角度。
通常用符号ω表示,计量单位是弧度/秒。
二、角速度的计算方法1. 定义式计算:对于旋转角速度恒定的情况,可以通过定义式计算角速度。
角速度ω等于单位时间内转过的弧长与转动所需时间的比值。
ω = Δθ / Δt其中,Δθ是转过的弧长,Δt是转动所需时间。
2. 瞬时角速度计算:在某一时刻的瞬时角速度等于通过该点的切线所确定的线速度与该点到轴的距离之比。
即,ω = v / r其中,v表示质点在切线方向上的线速度,r表示质点到该轴的距离。
3. 利用转动惯量计算:转动惯量是刚体抵抗转动的特性参数。
利用转动惯量的计算公式,可以推导出角速度的表达式。
比如,对于圆盘形刚体绕垂直于其平面并通过质心的轴转动的情况,转动惯量I和角速度的关系公式为:Iω = L其中,I表示转动惯量,L表示刚体的角动量。
三、刚体运动与角速度的应用角速度的计算在刚体运动的分析和应用中发挥着重要作用。
下面以两个实例介绍其应用。
实例一:自转的地球地球自转是一个典型的刚体运动问题。
地球自转一周的周期是24小时。
将地球看作一个近似的刚体,其转动惯量与角速度的乘积等于地球的角动量。
通过计算地球的转动惯量和已知的角动量,可以求得地球的角速度。
实例二:陀螺稳定陀螺是另一个常见的刚体运动问题。
陀螺的稳定性与其角速度密切相关。
通过计算陀螺的角速度,可以分析陀螺的稳定性,并设计出能够保持平衡的陀螺。
总结:刚体运动与角速度的计算是理论力学中的重要内容。
理论力学--运动学总结
速度瞬心位置的确定总结
瞬时平动
几点注意 1、基点法是速度分析的基本方法;
2、速度投影法 应用起来简单,但必须知道待求速度 点的方位,致命的弱点—是不能求图形的角速度 2、当平面几何简单时,分析速度可采用瞬心法; 瞬心法既可以求某点的速度,也可以求刚体运动 的角速度; 4、确定速度瞬心的速度是该点的绝对运动速度; 5、具体分析时三种方法灵活运用;
(1)刚体的基本运动 平动
v A vB
aA aB
各点的轨迹相同;
可简化为一个点的运动。
定轴转动
v R
a R
an R 2
轮系的传动比:
1 n1 R1 Z 2 i12 2 n2 R2 Z1
各处不打滑时: 接触点有相同的线速度和相同的切向加速度。
(2)刚体的平面运动 1. 定义 任一点到某固定平面的距离保持不变。
B点的加速度分析
D
C
a a 2 a a 2 ae 2 ar 2
n
aa 2 ae 2
O1
30°
ar 2
B
aa 2cos60 aa2cos30 ae 2
n
aa 2
1
30° O2
n
A
a a2 O2 B 2
n 2 aa2 O2 B2
ae2 657mm/ s
2
三、刚体的运动
va=v
vCA
动点:滑块C 动系:固结于AE
u=vA
vr
vC' A
ωAE
分析三种运动
牵连运动:刚体的平面运动
牵连转动
va ( vA vCA ) vr
va cos vCA v A sin
刚体的简单运动—刚体绕定轴的转动(理论力学)

主轴转动两圈后停止 0
2 02 2
0 10π2 2 4π
负号表示 的转向与主轴转动方向相反,故为减速运动。
小结
1.刚体绕定轴转动 刚体运动时,有上或其扩展部分有两点保持不动,这种运动
为刚体的绕定轴转动。通过两点的直线称为转轴,不在转轴上 的各点都在垂直于转轴的平面内做圆周运动。
2.角速度
三、定轴转动的角速度和角加速度
1、角速度
lim
Δt 0
Δ Δt
d
dt
代数量 正负与转角相同
若已知转动方程 f (t)
f (t)
刚体转动的快慢和方向 单位为 rad/s
2、角加速度
设当t 时刻为 , t +△t 时刻为 +△
角加速度
lim
t 0
t
d
dt
d2
dt2
f (t)
表征角速度变化的快慢 单位:rad/s2 (代数量)
§6-2 刚体绕定轴的转动
一、刚体绕定轴转动
刚体运动时,其上或其扩展部分有两点保持不动, 这种运动为刚体的绕定轴转动。通过两点的直线称为 转轴,不在转轴上的各点都在垂直于转轴的平面内做 圆周运动。
二、转角和转动方程
____ 转角,单位弧度(rad)
=f(t)
转动方程
方向规定: 从Z轴正向看
逆时针为正
f (t) 刚体转动的快慢和方向 单位为 rad/s (代数量)
3.角加速度
f (t)
如果与同号,则转动是加速的;如果与异号,则转动是减
速的。
如果与同号,则转动是加速的; 如果与异号,则转动是减速的。
与同号,转动加速
与异号,转动减速
O
理论力学08刚体的基本运动

[例5] 图示仪表机构中,已知各齿轮齿数 z1 = 6、z2 = 24、z3 = 8、 z4 = 32,齿轮 5 的啮合圆半径 R = 4 cm。如齿条 AB 下移1 cm,试 求指针 OC 转过的角度。
解: 轮 5 转过的角度
5
1 4
轮 4 转过的角度
4
5
1 4
轮 3 转过的角度
3
4
i43
z4 z3
aMn
a
n A
π202l
16
cos
2
πt 4
aMt 0
aM
aMn
π202l
16
[例3] 如图,鼓轮绕轴 O 转动,已知鼓轮的半径 R = 0.2 m,转动方
程 = -t2+4t (t 以 s 计, 以 rad 计);不可伸长的绳索缠绕在鼓
轮上,绳索的另一端悬挂重物 A。试求当 t = 1 s 时,轮缘上的点 M 和重物 A 的速度和加速度。
[例1] 杆AO 套在套筒 B 中绕轴 O 转动,套筒 B 在竖直滑道中运动。 已知套筒 B 以匀速 v = 1 m/s 向上运动,滑道与轴 O 的水平距离 l =
400 mm,运动初始时 = 0°。试求 = 30°时,杆AO 的角速度和角
加速度。
解: 杆AO 的转动方程
arctan
BB0 OB0
第二节 刚体绕定轴转动
一、绕定轴转动刚体的转动方程
t
说明:1)转角 为代数量,正负号表示
转向,一般可按右手螺旋法则 确定。
2)转角 的单位:rad(弧度)
z
A A0
二、绕定轴转动刚体的角速度
d
dt 说明:1)绕定轴转动刚体的角速度 为代数
量,其正负号表示转向,角速度 的正 负号规定与转角 一致。 2)角速度 的单位:rad/s 3)角速度 与转速 n (r/min) 的换算关系
刚体的简单运动—转动刚体内各点的速度和加速度(理论力学)
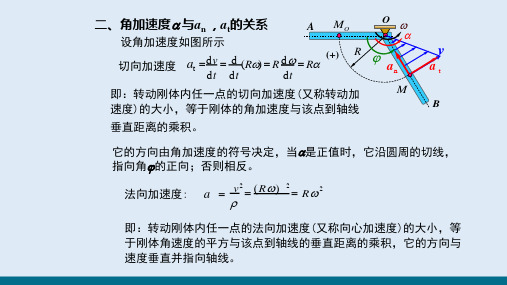
设角加速度如图所示
A MO
O
切向加速度 at dv d (R) R d R (+)
dt dt
dt
R
an
v
at
即:转动刚体内任一点的切向加速度(又称转动加 速度)的大小,等于刚体的角加速度与该点到轴线
M
B
垂直距离的乘积。
它的方向由角加速度的符号决定,当是正值时,它沿圆周的切线,
[例]半径R=0.2m的圆轮绕定轴O的转动方程 t 2 4t ,单位为弧度。 求t=1s时,轮缘上任一点M的速度和加速度。如在此轮缘上绕一柔软而不
可伸长的绳子并在绳端悬一物体A,求当t=1s时,物体A的速度和加速度。 解:圆轮在任一瞬时的角速度和角加速度为
d 2t 4
dt
d2 2
• ①滑轮3s内的转数; • ②重物B在3s内的行程;
• ③重物B在t=3s时的速度;
• ④滑轮边上C点在初瞬时的加速度;
• ⑤滑轮边上C点在t=3s时的加速度。
解:① 因为绳子不可以伸长,所以有
C aA 1m/s2
aCt 1 2 rad/s2
R 0.5
( )常数
vC
vA
1.5m /s, 0 vC
4.5m /s2
a (at )2 (an )2 12 4.52 4.61 m/s2
C
C
C
tan aCt 1 0.222, 12.5
aCn 4.5
⑤ t=3s 时,
at a
1m/s2,a n
R 2
2
0.5 9
40.5m/s2
a 12 40.52 40.51m/s2,tan 1 0.0247, 1.41 C
理论力学运动学知识点总结

运动学重要知识点一、刚体的简单运动知识点总结1.刚体运动的最简单形式为平行移动和绕定轴转动。
2.刚体平行移动。
·刚体内任一直线段在运动过程中,始终与它的最初位置平行,此种运动称为刚体平行移动,或平移。
·刚体作平移时,刚体内各点的轨迹形状完全相同,各点的轨迹可能是直线,也可能是曲线。
·刚体作平移时,在同一瞬时刚体内各点的速度和加速度大小、方向都相同。
3.刚体绕定轴转动。
•刚体运动时,其中有两点保持不动,此运动称为刚体绕定轴转动,或转动。
•刚体的转动方程φ=f(t)表示刚体的位置随时间的变化规律。
•角速度ω表示刚体转动快慢程度和转向,是代数量,。
角速度也可以用矢量表示,。
•角加速度表示角速度对时间的变化率,是代数量,,当α与ω同号时,刚体作匀加速转动;当α与ω异号时,刚体作匀减速转动。
角加速度也可以用矢量表示,。
•绕定轴转动刚体上点的速度、加速度与角速度、角加速度的关系:。
速度、加速度的代数值为。
•传动比。
一、点的运动合成知识点总结1.点的绝对运动为点的牵连运动和相对运动的合成结果。
•绝对运动:动点相对于定参考系的运动;•相对运动:动点相对于动参考系的运动;• 牵连运动:动参考系相对于定参考系的运动。
2.点的速度合成定理。
•绝对速度:动点相对于定参考系运动的速度;•相对速度:动点相对于动参考系运动的速度;•牵连速度:动参考系上与动点相重合的那一点相对于定参考系运动的速度。
3.点的加速度合成定理。
•绝对加速度:动点相对于定参考系运动的加速度;•相对加速度:动点相对于动参考系运动的加速度;•牵连加速度:动参考系上与动点相重合的那一点相对于定参考系运动的加速度;•科氏加速度:牵连运动为转动时,牵连运动和相对运动相互影响而出现的一项附加的加速度。
•当动参考系作平移或= 0 ,或与平行时, = 0 。
该部分知识点常见问题有问题一牵连速度和牵连加速度的意义。
问题二应用速度合成定理时要画速度矢量图。
理论力学6—刚体的基本运动分析

6.1 刚体的平行移动
平动的实例
夹 板 锤 的 锤 头
6.1 刚体的平行移动
2. 平动的特点
定理:当刚体作平动时,刚体内所有各点的轨迹形状完 全相同,而且在每一瞬时,刚体各点的速度相等,各点 的加速度也相等。 证明:
rA rB BA
◆速度 刚体平动时,刚体内任一线段AB 的长度和方向都保持不变。 因而 x
a a a R w
2 2 n 2
4
a tan 2 an w
( Rw ) 2 an Rw 2 R v2
即:转动刚体内任一点的法向加速度(又称向心加速度)的 大小,等于刚体角速度的平方与该点到轴线的垂直距离的 乘积,它的方向与速度垂直并指向轴线。
6.3 转动刚体内各点的速度和加速度
如果ω与同号,角速度的绝对 值增加,刚体作加速转动,这 时点的切向加速度 aτ 与速度 v 的指向相同。 如果ω与异号,刚体作减速转 动,aτ与v的指向相反。 点的全加速度为:
6.1 刚体的平行移动
刚体的两种最简单的运动是平行移动和定轴转动。以后可 以看到,刚体的更复杂的运动可以看成由这两种运动的合 成。因此,这两种运动也称为刚体的基本运动。
1. 刚体的平动
在运动过程中,刚 体上任意一条直线 都与其初始位置保 持平行。具有这种 特征的刚体运动, 称为刚体的平行移 动,简称为平动。
6.3 转动刚体内各点的速度和加速度
当刚体绕定轴转动时,刚体内任意一点都作圆周运动,圆心在 轴线上,圆周所在的平面与轴线垂直,圆周的半径 R 等于该点 到轴线的垂直距离。 由于点M绕点O作圆周运动,用自然法表示。点M的弧坐标为
s Rj
动点速度的大小为
ds dj v R Rw dt dt
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
的中点M的速度和加速度。
第二章 刚体的基本运动
例题 2-1
§2-1 刚体的平移
例题 2-1
O1 φl
A O
(+)
O2
解:
l
由于两条钢索O1A和O2B的长度相
等,并且相互平行,于是荡木AB在运
M
B
动中始终平行于直线O1O2,故荡木作
平移。
为求中点M 的速度和加速度,只需求出A点(或B点)的速度和加速
第二章 刚体的基本运动
§2-1 刚体的平移
思考题
思考题
在图示机构中,已知:O1A=O2B=l, O1O2=AB, AC=0.5BC。 O1A,O2B 与三角板铰接, O1A匀角速度ω 转动。
试问: (1). 三角板ABC作什么运动? 其角速度等于多少?
(2). 三角板BC边中点M的速度 和加速度各为多少?
静力学
刚体的基本运动
西北工业大学
第二章 刚体的基本运动
运动学
第 二
§2– 1 刚体的平移
章
§2–2 刚体的定轴转动
刚
体 的
§2–3 定轴转动刚体内各点的速度和 加速度
基
本
运
§2–4 用矢积表示刚体上点的速度和
动
加速度
第二章 刚体的基本运动
目录
刚体的基本运动
平动和定轴转动是刚体的两种最简单、最基本的 运动;以后可以看到,刚体的更复杂的运动可以看成 是由这两种运动的合成。因此,这两种运动称为刚体 的基本运动。
度即可。点A在圆弧上运动,圆弧的半径为l。如以最低点O为起点,规
定弧坐标s向右为正,则A点的运动方程为
s
0l sin
πt 4
将上式对时间求导,得A点的速度
v
ds dt
π 4
l0
cos
π 4
t
第二章 刚体的基本运动
§2-1 刚体的平移
例题 2-1
O1 φl
O2 l
再求一次导,得A点的切向加速度
§2-1 刚体的平移
平移的特点
应该注意,平移刚体内的点,不一定沿直线运动,也 不一定保持在平面内运动,它的轨迹可以是任意的空间曲 线。
如果平移刚体内各点的轨迹都是平面曲线或直线,则 这些特殊情形称为平面平移或直线平移。
由上述刚体平移的特点可见,当刚体作平移时,只须 给出刚体内任意一点的运动,就可以完全确定整个刚体的 运动。
O1 φl
ωA
C
O2 l B
M
第二章 刚体的基本运动
§2-1 刚体的平移
思考题
答: (1). 因为三角板ABC作平移运动,所以其角速度等于零。
(2). 三角板ABC作平移运动,点M与点B有相同的速度和加速 度。
vM=vB =rω aM=aB=rω2
第二章 刚体的基本运动
O1 φl l
ωA
O2
l
at
dv dt
π2 16
l
0
sin
πt 4
A
M
O
(+)
B
A点的法向加速度
an
v2 l
π2 16
l02
cos2
πt 4
代入t = 0和t = 2,就可求得这两瞬时A点的速度和加速度,亦即点M在 这两瞬时的速度和加速度。计算结果列表如下:
t (s) φ(rad) 00 2 φ0
v (m·s-1)
vB
B
vM
C
M
O1 φl
A O
(+)
§2-1 刚体的平移
例题 2-1
例2-1 荡木用两条等长的钢
O2
索平行吊起,如图所示。钢索长
l
为长l,长度单位为m。当荡木摆
动时钢索的摆动规律
M
B
为 间
0 sin
,单位为s;
π t ,其中 t 转4 角φ0的单
为时 位为
rad。试求当t=0和t=2 s时,荡木
vB
aB aA
rB
A2
即,在每一瞬时,平移刚体 内任意两点的速度和加速度 O
A rA
vA A1
y
分别相等。
x
第二章 刚体的基本运动
§2-1 刚体的平移
平移刚体上各点的速度
平移的特点
第二章 刚体的基本运动
§2-1 刚体的平移
平移刚体上各点的加速度
平移的特点
第二章 刚体的基本运动
这样,刚体平移问题就可看为点的运动问题来处理。
第二章 刚体的基本运动
§2-1 刚体的平移
平移的特点
综上所述,可以得出刚体平移的几个主要结论:
刚体上的各点具有形状相同的运动轨迹。
刚体上的各点在某一瞬时具有相同的速度 和 加速度。
刚体平移时的运动分析可以简化为其上任意 一点的运动分析。
第二章 刚体的基本运动
§2-1 刚体的平移
刚体的平移 平移的特点
第二章 刚体的基本运动
§2-1 刚体的平移
一、 刚体平移的定义
在运动过程中,刚体上任意一条直线的方位都保持不 变。具有这种特征的刚体运动,称为刚体的平行移动,简 称为平移。
第二章 刚体的基本运动
1. 刚体的平移
§2-1 刚体的平移
平移的实例
体的平移
第二章 刚体的基本运动
§2-1 刚体的平移
平移的实例
刚体的平移
第二章 刚体的基本运动
§2-1 刚体的平移
平移的实例
刚体的平移
第二章 刚体的基本运动
§2-1 刚体的平移
刚体的平移
刚体的平移
第二章 刚体的基本运动
§2-1 刚体的平移
刚体的平移
刚体的平移
第二章 刚体的基本运动
§2-1 刚体的平移
二、平移的特点
1.当刚体作平移时,刚体上所有各点的轨迹形状相同,
并且位置平行。
2.当刚体作平移时,同一瞬时,刚体上各点的速度相
等,各点的加速度也相等。
z
B2
证明: 刚体作平移时的特点1
B
B1
vB
可由图说明。
rB
A2
刚体作平移时的特点2 可证明如下:
始终保持不动,这种运动称为刚体的定轴转动。 该固定不动的直线称为转轴。
二、刚体定轴转动的特点 当刚体作定轴转动时,转动轴以外的各点都分别在垂
直于转轴的平面内作圆周运动,圆心在该平面与转轴之交 点上。
第二章 刚体的基本运动
§2-2 刚体的定轴转动
定轴转动实例
O
A rA
vA A1
y
x
第二章 刚体的基本运动
§2-1 刚体的平移
平移的特点
AB为刚体上任意一矢量,则有 rB rA AB
刚体平移时,刚体内任一线段AB的长度和方向都保持不变。
因而 d AB 0 dt
故
drB drA 或 dt dt
vB vA
z
B2
B
B1
上式再对时间t求导一次,即得
at (m·s-
2)
π 4
(0 水平向右)
0
0
π 16
0l
an (m·s-2)
π2 16
02(l 铅直向上)
0
第二章 刚体的基本运动
§2-2 刚体的定轴转动
刚体的定轴转动 转动规律 角速度 角加速度
第二章 刚体的基本运动
§2-2 刚体的定轴转动
一、 刚体的定轴转动 当刚体运动时,如其上(或其延展部分)有一条直线
