理论力学-刚体的基本运动
合集下载
理论力学6—刚体的基本运动
34.8
§6-5 以矢量表示角速度和角加速度.以矢积表示点的速度和加速度
1、角速度矢量和角加速度矢量
角速度矢量
dj
ww
dt
大小
角速度矢沿轴线，弯向表示刚体转动的方向。
指向用右手螺旋法则。
w wk
角加速度矢量
dw dw
k k
dt
dt
§6-5 以矢量表示角速度和角加速度.以矢积表示点的速度和加速度
2
例6-6
某定轴转动刚体通过点M0（2，1，3），其角速度矢w 的方向
余弦为0.6，0.48，0.64，角速度 的大小ω=25rad/s 。求：刚体上点
M（10，7，11）的速度矢。
解：角速度矢量
w wn
其中 n （0.6，0.48，0.64）
M点相对于转轴上一点M0的矢径
r rM rM0 10,7,11 2,1,3 8,6,8
Z2=60，Z3=12，Z4=70。(a)求减速箱的总减速比i13 ；(b)如
果n1=3000r/min，求n3.
1
n1
2
n2
3
n3
4
解：求传动比：
n1 n1 n2 Z 2 Z 4
i13
34.8
n3 n2 n3 Z1 Z 3
则有：
n1 3000
n3
86r / min
i13
4 rad
dw dw d
dw
w
dt
d dt
d
dw
w
0.2
d
解：
w
w wdw
0
§6-5 以矢量表示角速度和角加速度.以矢积表示点的速度和加速度
1、角速度矢量和角加速度矢量
角速度矢量
dj
ww
dt
大小
角速度矢沿轴线，弯向表示刚体转动的方向。
指向用右手螺旋法则。
w wk
角加速度矢量
dw dw
k k
dt
dt
§6-5 以矢量表示角速度和角加速度.以矢积表示点的速度和加速度
2
例6-6
某定轴转动刚体通过点M0（2，1，3），其角速度矢w 的方向
余弦为0.6，0.48，0.64，角速度 的大小ω=25rad/s 。求：刚体上点
M（10，7，11）的速度矢。
解：角速度矢量
w wn
其中 n （0.6，0.48，0.64）
M点相对于转轴上一点M0的矢径
r rM rM0 10,7,11 2,1,3 8,6,8
Z2=60，Z3=12，Z4=70。(a)求减速箱的总减速比i13 ；(b)如
果n1=3000r/min，求n3.
1
n1
2
n2
3
n3
4
解：求传动比：
n1 n1 n2 Z 2 Z 4
i13
34.8
n3 n2 n3 Z1 Z 3
则有：
n1 3000
n3
86r / min
i13
4 rad
dw dw d
dw
w
dt
d dt
d
dw
w
0.2
d
解：
w
w wdw
0
理论力学第三章刚体力学
d dt
线量和角量的对应
dr
dr v dt
d
d dt
dv a dt
d dt
6.欧勒角
1).欧勒角 章动 角 自转 角 Z轴位置由 θ，φ角决 定 进动 角
节线ON
0 0 2 0 2
2).欧勒运动学方程
在直角坐标系
x i y j z k
理 论 力 学
第三章 刚体运动
概述
1.刚体是一个理想模型，它可以看作是一种特
殊的质点组，这个质点组中任何两个质点之间
的距离不变.这使得问题大为简化，使我们能 更详细地研究它的运动性质，得到的结果对实 际问题很有用。 2.一般刚体的自由度为6.如果刚体运动受到约束, 自由度相应减少.
3.刚体的两种基本运动
刚体上任一点p的坐标分别为
v r ra a ra 而在系 a xy z r r ( r b a a b ra ) rb ra (rb ra )
得
r ra ra
2
drci (rci mi Jc ) dt i 1 n (e) (rci Fi ) Mc
n
i 1
简表为:
d Mc Jc dt
(6个方程正好确定刚体的6个独立变量)
刚体的动量矩 (角动量) n n ) 简表为: J J c J ci (ri mi vi ) rc mvc (rci mi vci
三.刚体的平衡
刚体平衡条件
(e) Fi 0
n i
n (e) Fi ) 0 (rci Mc i 1
线量和角量的对应
dr
dr v dt
d
d dt
dv a dt
d dt
6.欧勒角
1).欧勒角 章动 角 自转 角 Z轴位置由 θ，φ角决 定 进动 角
节线ON
0 0 2 0 2
2).欧勒运动学方程
在直角坐标系
x i y j z k
理 论 力 学
第三章 刚体运动
概述
1.刚体是一个理想模型，它可以看作是一种特
殊的质点组，这个质点组中任何两个质点之间
的距离不变.这使得问题大为简化，使我们能 更详细地研究它的运动性质，得到的结果对实 际问题很有用。 2.一般刚体的自由度为6.如果刚体运动受到约束, 自由度相应减少.
3.刚体的两种基本运动
刚体上任一点p的坐标分别为
v r ra a ra 而在系 a xy z r r ( r b a a b ra ) rb ra (rb ra )
得
r ra ra
2
drci (rci mi Jc ) dt i 1 n (e) (rci Fi ) Mc
n
i 1
简表为:
d Mc Jc dt
(6个方程正好确定刚体的6个独立变量)
刚体的动量矩 (角动量) n n ) 简表为: J J c J ci (ri mi vi ) rc mvc (rci mi vci
三.刚体的平衡
刚体平衡条件
(e) Fi 0
n i
n (e) Fi ) 0 (rci Mc i 1
理论力学课件—刚体的简单运动
解： 建立坐标系，
BCD平移，考察m点：
0
x r cos r cost
v d x r sin t
flash
dt
a d v r2 cost
dt
例：已知绳等长l，=0sinkt， 0，k为常数。
求任意时刻M点的速度和加速度。 O1
O2
解：AB平移，研究A点即可。
φ
A圆弧运动，以最低点处为弧坐标原点，A 向右为正，A的运动方程：
z2 z1
+ 为转向一致（内啮合） - 为转向相反（外啮合）
２.带轮传动
r11 vA vA vB vB r22
主要内容：
1.刚体的平移及其运动特征（尤其是作曲线平移的刚体）。
2.作定轴转动的刚体的转动方程、角速度、角加速度。
3.转动刚体内各点的速度、加速度。
难点：
1.曲线平移刚体上任一点的速度和加速度的确定。 2.作定轴转动的刚体内任一点的速度和加速度的矢积表示法 (初步了解)。
第六章 刚体的简单运动
刚体是由无数点组成的，在点的运动学
基础上可研究刚体的运动，研究刚体整体的
运动与其上各点运动之间的关系。 本章主要研究刚体的两种简单运动：
➢平移 ➢定轴转动
学习本章内容是为研究复杂运动（平面运动） 打基础。
§6-１ 刚体的平行移动
1.平行移动 刚体内任一直线在运动过程中始终平行于
初始位置。简称平移（平动）。
flash
flash
2.运动方程
k
角速度方程
d
dt
0 ch
kt
角加速度方程 d
dt
k0 sh
kt
例：边长为b的正方形绕定轴转动，
A aA
理论力学08刚体的基本运动
[例5] 图示仪表机构中，已知各齿轮齿数 z1 = 6、z2 = 24、z3 = 8、 z4 = 32，齿轮 5 的啮合圆半径 R = 4 cm。如齿条 AB 下移1 cm，试 求指针 OC 转过的角度。
解： 轮 5 转过的角度
5
1 4
轮 4 转过的角度
4
5
1 4
轮 3 转过的角度
3
4
i43
z4 z3
aMn
a
n A
π202l
16
cos
2
πt 4
aMt 0
aM
aMn
π202l
16
[例3] 如图，鼓轮绕轴 O 转动，已知鼓轮的半径 R = 0.2 m，转动方
程 = －t2＋4t （t 以 s 计， 以 rad 计）；不可伸长的绳索缠绕在鼓
轮上，绳索的另一端悬挂重物 A。试求当 t = 1 s 时，轮缘上的点 M 和重物 A 的速度和加速度。
[例1] 杆AO 套在套筒 B 中绕轴 O 转动，套筒 B 在竖直滑道中运动。 已知套筒 B 以匀速 v = 1 m/s 向上运动，滑道与轴 O 的水平距离 l =
400 mm，运动初始时 = 0°。试求 = 30°时，杆AO 的角速度和角
加速度。
解： 杆AO 的转动方程
arctan
BB0 OB0
第二节 刚体绕定轴转动
一、绕定轴转动刚体的转动方程
t
说明：1）转角 为代数量，正负号表示
转向，一般可按右手螺旋法则 确定。
2）转角 的单位：rad（弧度）
z
A A0
二、绕定轴转动刚体的角速度
d
dt 说明：1）绕定轴转动刚体的角速度 为代数
量，其正负号表示转向，角速度 的正 负号规定与转角 一致。 2）角速度 的单位：rad/s 3）角速度 与转速 n (r/min) 的换算关系
刚体的简单运动—转动刚体内各点的速度和加速度(理论力学)
二、角加速度 与an ，at的关系
设角加速度如图所示
A MO
O
切向加速度 at dv d (R) R d R (+)
dt dt
dt
R
an
v
at
即：转动刚体内任一点的切向加速度(又称转动加 速度)的大小，等于刚体的角加速度与该点到轴线
M
B
垂直距离的乘积。
它的方向由角加速度的符号决定，当是正值时，它沿圆周的切线，
[例]半径R=0.2m的圆轮绕定轴O的转动方程 t 2 4t ，单位为弧度。 求t=1s时，轮缘上任一点M的速度和加速度。如在此轮缘上绕一柔软而不
可伸长的绳子并在绳端悬一物体A，求当t=1s时，物体A的速度和加速度。 解：圆轮在任一瞬时的角速度和角加速度为
d 2t 4
dt
d2 2
• ①滑轮3s内的转数； • ②重物B在3s内的行程；
• ③重物B在ｔ＝3s时的速度；
• ④滑轮边上C点在初瞬时的加速度；
• ⑤滑轮边上C点在ｔ＝3s时的加速度。
解：① 因为绳子不可以伸长，所以有
C aA 1m/s2
aCt 1 2 rad/s2
R 0.5
（ ）常数
vC
vA
1.5m /s， 0 vC
4.5m /s2
a (at )2 (an )2 12 4.52 4.61 m/s2
C
C
C
tan aCt 1 0.222， 12.5
aCn 4.5
⑤ t=3s 时，
at a
1m/s2，a n
R 2
2
0.5 9
40.5m/s2
a 12 40.52 40.51m/s2，tan 1 0.0247， 1.41 C
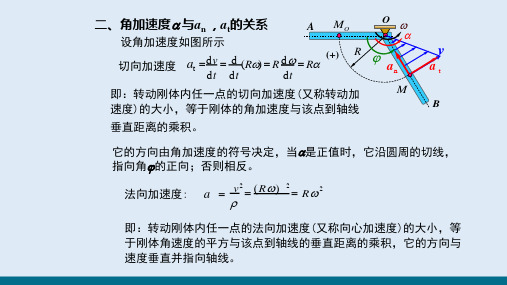
设角加速度如图所示
A MO
O
切向加速度 at dv d (R) R d R (+)
dt dt
dt
R
an
v
at
即：转动刚体内任一点的切向加速度(又称转动加 速度)的大小，等于刚体的角加速度与该点到轴线
M
B
垂直距离的乘积。
它的方向由角加速度的符号决定，当是正值时，它沿圆周的切线，
[例]半径R=0.2m的圆轮绕定轴O的转动方程 t 2 4t ，单位为弧度。 求t=1s时，轮缘上任一点M的速度和加速度。如在此轮缘上绕一柔软而不
可伸长的绳子并在绳端悬一物体A，求当t=1s时，物体A的速度和加速度。 解：圆轮在任一瞬时的角速度和角加速度为
d 2t 4
dt
d2 2
• ①滑轮3s内的转数； • ②重物B在3s内的行程；
• ③重物B在ｔ＝3s时的速度；
• ④滑轮边上C点在初瞬时的加速度；
• ⑤滑轮边上C点在ｔ＝3s时的加速度。
解：① 因为绳子不可以伸长，所以有
C aA 1m/s2
aCt 1 2 rad/s2
R 0.5
（ ）常数
vC
vA
1.5m /s， 0 vC
4.5m /s2
a (at )2 (an )2 12 4.52 4.61 m/s2
C
C
C
tan aCt 1 0.222， 12.5
aCn 4.5
⑤ t=3s 时，
at a
1m/s2，a n
R 2
2
0.5 9
40.5m/s2
a 12 40.52 40.51m/s2，tan 1 0.0247， 1.41 C
理论力学运动学知识点总结
运动学重要知识点一、刚体的简单运动知识点总结1.刚体运动的最简单形式为平行移动和绕定轴转动。
2.刚体平行移动。
·刚体内任一直线段在运动过程中，始终与它的最初位置平行，此种运动称为刚体平行移动，或平移。
·刚体作平移时，刚体内各点的轨迹形状完全相同，各点的轨迹可能是直线，也可能是曲线。
·刚体作平移时，在同一瞬时刚体内各点的速度和加速度大小、方向都相同。
3.刚体绕定轴转动。
•刚体运动时，其中有两点保持不动，此运动称为刚体绕定轴转动，或转动。
•刚体的转动方程φ=f(t)表示刚体的位置随时间的变化规律。
•角速度ω表示刚体转动快慢程度和转向，是代数量，。
角速度也可以用矢量表示，。
•角加速度表示角速度对时间的变化率，是代数量，，当α与ω同号时，刚体作匀加速转动；当α与ω异号时，刚体作匀减速转动。
角加速度也可以用矢量表示，。
•绕定轴转动刚体上点的速度、加速度与角速度、角加速度的关系：。
速度、加速度的代数值为。
•传动比。
一、点的运动合成知识点总结1.点的绝对运动为点的牵连运动和相对运动的合成结果。
•绝对运动：动点相对于定参考系的运动；•相对运动：动点相对于动参考系的运动；• 牵连运动：动参考系相对于定参考系的运动。
2.点的速度合成定理。
•绝对速度：动点相对于定参考系运动的速度；•相对速度：动点相对于动参考系运动的速度；•牵连速度：动参考系上与动点相重合的那一点相对于定参考系运动的速度。
3.点的加速度合成定理。
•绝对加速度：动点相对于定参考系运动的加速度；•相对加速度：动点相对于动参考系运动的加速度；•牵连加速度：动参考系上与动点相重合的那一点相对于定参考系运动的加速度；•科氏加速度：牵连运动为转动时，牵连运动和相对运动相互影响而出现的一项附加的加速度。
•当动参考系作平移或= 0 ，或与平行时， = 0 。
该部分知识点常见问题有问题一牵连速度和牵连加速度的意义。
问题二应用速度合成定理时要画速度矢量图。
理论力学6—刚体的基本运动分析
6.1 刚体的平行移动
平动的实例
夹 板 锤 的 锤 头
6.1 刚体的平行移动
2. 平动的特点
定理：当刚体作平动时，刚体内所有各点的轨迹形状完 全相同，而且在每一瞬时，刚体各点的速度相等，各点 的加速度也相等。 证明：
rA rB BA
◆速度 刚体平动时，刚体内任一线段AB 的长度和方向都保持不变。 因而 x
a a a R w
2 2 n 2
4
a tan 2 an w
( Rw ) 2 an Rw 2 R v2
即：转动刚体内任一点的法向加速度(又称向心加速度)的 大小，等于刚体角速度的平方与该点到轴线的垂直距离的 乘积，它的方向与速度垂直并指向轴线。
6.3 转动刚体内各点的速度和加速度
如果ω与同号，角速度的绝对 值增加，刚体作加速转动，这 时点的切向加速度 aτ 与速度 v 的指向相同。 如果ω与异号，刚体作减速转 动，aτ与v的指向相反。 点的全加速度为：
6.1 刚体的平行移动
刚体的两种最简单的运动是平行移动和定轴转动。以后可 以看到，刚体的更复杂的运动可以看成由这两种运动的合 成。因此，这两种运动也称为刚体的基本运动。
1. 刚体的平动
在运动过程中，刚 体上任意一条直线 都与其初始位置保 持平行。具有这种 特征的刚体运动， 称为刚体的平行移 动，简称为平动。
6.3 转动刚体内各点的速度和加速度
当刚体绕定轴转动时，刚体内任意一点都作圆周运动，圆心在 轴线上，圆周所在的平面与轴线垂直，圆周的半径 R 等于该点 到轴线的垂直距离。 由于点M绕点O作圆周运动，用自然法表示。点M的弧坐标为
s Rj
动点速度的大小为
ds dj v R Rw dt dt
第八章 刚体的基本运动
平移刚体在任一瞬时速度、加速度都一样， 平移刚体在任一瞬时速度、加速度都一样，各点的运动轨迹 形状相同。 平移刚体的运动可以简化为一个点的运动。 形状相同。即平移刚体的运动可以简化为一个点的运动。
理论力学电子教程
第八章 刚体的基本运动
荡木用两条等长的钢索平行吊起，如图所示。 例8-1 荡木用两条等长的钢索平行吊起，如图所示。钢索长 为 长 l， 长 度 单 位 为 m。 当 荡 木 摆 动 时 钢 索 的 摆 动 规 律 ， 。 π 为时间，单位为s；转角φ 为 ϕ =ϕ0 sin t ，其中 t 为时间，单位为 ；转角 0的单位为 4 rad，试求当 和t=2 s时，荡木的中点 的速度和加速度。 的速度和加速度。 ，试求当t=0和 时 荡木的中点M的速度和加速度
∴aτ =ε × r
∴a n =ω × v
a n =ω × v
理论力学电子教程
第八章 刚体的基本运动
三、定轴轮系的传动比 在实际工程中，不同机器的工作转速往往是不一样的， 在实际工程中，不同机器的工作转速往往是不一样的， 故需要利用轮系的传动来提高或降低机器转速。 故需要利用轮系的传动来提高或降低机器转速。常用的有 带传动和齿轮传动。一般将主动轮转速与从动轮转速之比， 带传动和齿轮传动。一般将主动轮转速与从动轮转速之比， 表示， 用i表示，即 表示 n主 ω主 i= = n从 ω 从 1．带传动 当主动轮Ⅰ转动时， 当主动轮Ⅰ转动时，利用胶带与带轮轮缘间的摩擦带动 从动轮Ⅱ转动。 从动轮Ⅱ转动。 不考虑胶带由于拉力引起的变形及胶带的厚度， 不考虑胶带由于拉力引起的变形及胶带的厚度，为此在 同一瞬时胶带上各点速度大小应相等， 同一瞬时胶带上各点速度大小应相等，即v1 = v = v2。若胶带 与带轮间没有滑动， 与带轮间没有滑动，则
理论力学电子教程
第八章 刚体的基本运动
荡木用两条等长的钢索平行吊起，如图所示。 例8-1 荡木用两条等长的钢索平行吊起，如图所示。钢索长 为 长 l， 长 度 单 位 为 m。 当 荡 木 摆 动 时 钢 索 的 摆 动 规 律 ， 。 π 为时间，单位为s；转角φ 为 ϕ =ϕ0 sin t ，其中 t 为时间，单位为 ；转角 0的单位为 4 rad，试求当 和t=2 s时，荡木的中点 的速度和加速度。 的速度和加速度。 ，试求当t=0和 时 荡木的中点M的速度和加速度
∴aτ =ε × r
∴a n =ω × v
a n =ω × v
理论力学电子教程
第八章 刚体的基本运动
三、定轴轮系的传动比 在实际工程中，不同机器的工作转速往往是不一样的， 在实际工程中，不同机器的工作转速往往是不一样的， 故需要利用轮系的传动来提高或降低机器转速。 故需要利用轮系的传动来提高或降低机器转速。常用的有 带传动和齿轮传动。一般将主动轮转速与从动轮转速之比， 带传动和齿轮传动。一般将主动轮转速与从动轮转速之比， 表示， 用i表示，即 表示 n主 ω主 i= = n从 ω 从 1．带传动 当主动轮Ⅰ转动时， 当主动轮Ⅰ转动时，利用胶带与带轮轮缘间的摩擦带动 从动轮Ⅱ转动。 从动轮Ⅱ转动。 不考虑胶带由于拉力引起的变形及胶带的厚度， 不考虑胶带由于拉力引起的变形及胶带的厚度，为此在 同一瞬时胶带上各点速度大小应相等， 同一瞬时胶带上各点速度大小应相等，即v1 = v = v2。若胶带 与带轮间没有滑动， 与带轮间没有滑动，则
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
〔例〕已知：重物A的
a A 1m/s2 （常数）初瞬时速度 v0 1.5m/s
方向如图示。 R 0.5m, r 0.3m
求：
①滑轮3s内的转数；
②重物B在3s内的行程； ③重物B在ｔ＝3s时的速度； ④滑轮边上C点在初瞬时的加速度； ⑤滑轮边上C点在ｔ＝3s时的加速度。
解：① 因为绳子不可以伸长，所以有 aC a A 1m/s2 , aC 1 ）常数 2 rad/s2 （ R 0.5 vC 1.5 vC v A 1.5m/s, w0 3rad/s （ ） R 0.5 1 2 1 2 w0t t 33 23 18rad,n 2.86(转） 2 2 2 ② ③
在 某瞬时测得 aM 40 m/s2 , 30 求： 转动方程;
t＝5s时，Ｍ点的速度和
向心加速度的大小。 解：
a R asin
M
a asin 40sin30 50 rad/s2 R R 0.4 w0 0, w0t 1t 2 1 50t 2 25t 2
2018/6/3
2.角加速度:
w dw d 2 角加速度 : lim 2 t 0 t dt dt
单位:rad/s2 (代数量)
与w方向一致为加速转动, 与w 方向相反为减速转动
3.匀速转动和匀变速转动 当w =常数,为匀速转动；当 =常数,为匀变速转动。
2018/6/3
2018/6/3
§7-2
刚体的定轴转动
一.刚体定轴转动的特征及其简化 特点:有一条不变的线称为转轴,其余各点都在垂直于转轴的平
面上做圆周运动。
二.转角和转动方程机构运动swf\swf0604.swf
z
定平面
---转角,单位弧度(rad) =f(t)---为转动方程
方向规定: 从z 轴正向看去,
v dS S lim dt t0 t
v lim
R wR t 0 t
v wR
2018/6/3
二.角加速度 与an ,a 的关系
a R,
an v2
Rw 2
|a全 ||an a | an 2 a 2 R 2 w 4
w w 0 t 1 2 与点的运动相类似。 w t t 常用公式 0 2 2 w 2 2 w 0
§7-3
转动刚体内各点的速度和加速度
(即角量与线量的关系)
一.线速度V和角速度w之间的关系
w , 对整个刚体而言(各点都一样)；
v, a 对刚体中某个点而言(各点不一样)。
刚体的基本运动
§7–1 刚体的平行移动 §7–2 刚体的定轴转动 §7–3 定轴转动刚体内各点的速题
2018/6/3
§7-1刚体的平行移动(平动)
2018/6/3
二.刚体平动的特点: 1、其上任一直线始终平行于它的初始位置； 2、任一点的轨迹可是直线也可是曲线； 3、 平动时各点轨迹形状相同； 4、在任一瞬时各点的运动轨迹形状,速度,加速度都一样。 即:平动刚体的运动可以简化为一个点的运动。
n
⑤ t=3s 时，
aC a A 1m/s 2 ,aC n R w 2 0.59 2 40.5m/s 2
aC 12 40.52 40.51m/s2 , tg
1 0.0247 , 1.41 40.51
[例] 已知：圆轮O由静止开始作等加速转动，OM＝0.4m，
a R t g 2 2 an w R w
2018/6/3
各点速度分布图
各点加速度分布图
2018/6/3
刚体定轴转动 转动方程:
f (t )
w
d dt
角速度:
角加速度: 匀速转动:
dw d 2 2 dt dt
0 wt 匀变速运动: w w 0 t 2 w 2 2 1 2 w 0 0 w 0 t t 2
2 2
转动方程 25t 2
w w0 t 50t, vM Rw 0.450t 20t
当ｔ＝5s时，
vM 205100m/s
M
2 v 1002 M n aM 25000 m/s2 R 0.4
x
O
逆时针为正
2018/6/3
顺时针为负
2018/6/3
三.定轴转动的角速度和加速度 1.角速度：
定义:
Δ d w lim Δ t 0 Δ t dt
(代数量)
工程中常用单位：
n = 转/分(r / min)
则n与w的关系为:
2n n n w (rad/s ) 60 30 10
s r 0.3185.4m
w w0 t 3239 rad/s
vB rw 0.392.7m/s
（
），
④
t = 0 时，
aC a A 1m/s2 , aC n Rw 0 2 0.532 4.5m/s2
aC (aC ) 2 (aC ) 2 12 4.52 4.61 m/s2 a 1 tg C n 0.222, 12.5 aC 4.5