第六章刚体的基本运动习题解答
理论力学

| a全 || an a | an a R 2 w 4
2 2
a R t g 2 2 an w R w
21
结论: ① v方向与w 相同时为正 , R ,与 R 成正比。
②各点的全加速度方向与各点转动半径夹角θ都一致,且 小于90o , 在同一瞬间的速度和加速度的分布图为:
习题课
35
匀 速 直 匀 a=C 线 变 运 动 变 dv a 速 dt 曲 线 运 动 匀 速 匀 变 变 速 0
a 0
点的运动(刚体平动) 加速度 v an a 0 0 v C 0 0 a =C
v v0 at
s
s f ( t ) vt
1 s v0 t at 2 2
1
第六章 刚体的基本运动
§6–1 刚体的平行移动
§6–2 刚体的定轴转动 §6–3 定轴转动刚体内各点的速度与加速度 §6–4 绕定轴转动刚体的传动问题 §6–5 角速度与角速度的矢量表示 点的速度与加速度的矢积表示 习题课
2
由于研究对象是刚体,所以运动中要考虑 其本身形状和尺寸大小,又由于刚体是几何形 状不变体,所以研究它在空间的位置就不必一 个点一个点地确定,只要根据刚体的各种运动 形式,确定刚体内某一个有代表性的直线或平 面的位置即可。
π 0l 16
v (m· s-1)
0
14
§6-2
刚体的定轴转动
一.刚体定轴转动的特征及其简化 当刚体运动时,如其上(或其延展部分)有一
条直线始终保持不动,这种运动称为刚体的定轴转
动。该固定不动的直线称为转轴。 特点:有一条不变的线称为转轴,其余各点都在垂
直于转轴的平面上做圆周运动,圆心在该平面与转
理论力学课后习题答案-第6章--刚体的平面运动分析
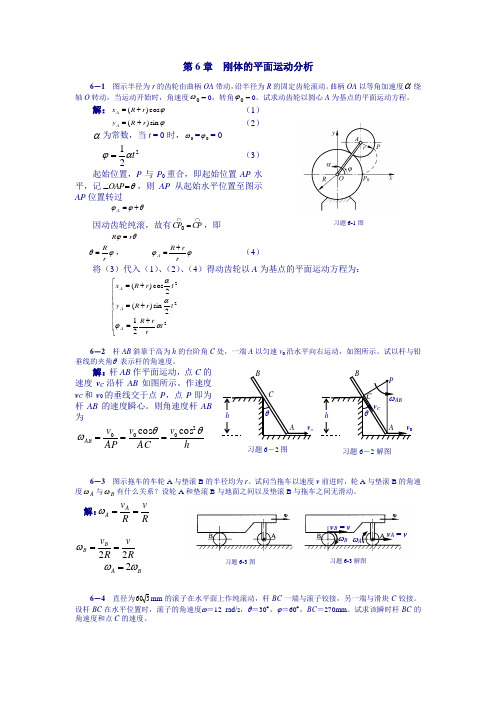
第6章 刚体的平面运动分析6-1 图示半径为r 的齿轮由曲柄OA 带动,沿半径为R 的固定齿轮滚动。
曲柄OA 以等角加速度α绕轴O 转动,当运动开始时,角速度0ω= 0,转角0ϕ= 0。
试求动齿轮以圆心A 为基点的平面运动方程。
解:ϕcos )(r R x A += (1) ϕsin )(r R y A +=(2)α为常数,当t = 0时,0ω=0ϕ= 0 221t αϕ=(3)起始位置,P 与P 0重合,即起始位置AP 水平,记θ=∠OAP ,则AP 从起始水平位置至图示AP 位置转过θϕϕ+=A因动齿轮纯滚,故有⋂⋂=CP CP 0,即 θϕr R = ϕθr R =, ϕϕrr R A += (4)将(3)代入(1)、(2)、(4)得动齿轮以A 为基点的平面运动方程为:⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=222212sin )(2cos )(t r r R t r R y t r R x A A A αϕαα6-2 杆AB 斜靠于高为h 的台阶角C 处,一端A 以匀速v 0沿水平向右运动,如图所示。
试以杆与铅垂线的夹角θ 表示杆的角速度。
解:杆AB 作平面运动,点C 的速度v C 沿杆AB 如图所示。
作速度v C 和v 0的垂线交于点P ,点P 即为杆AB 的速度瞬心。
则角速度杆AB 为6-3 图示拖车的车轮A 与垫滚B 的半径均为r 。
试问当拖车以速度v 前进时,轮A 与垫滚B 的角速度A ω与B ω有什么关系?设轮A 和垫滚B 与地面之间以及垫滚B 与拖车之间无滑动。
解:RvR v A A ==ωR v R v B B 22==ωB A ωω2=6-4 直径为360mm 的滚子在水平面上作纯滚动,杆BC 一端与滚子铰接,另一端与滑块C 铰接。
设杆BC 在水平位置时,滚子的角速度ω=12 rad/s ,θ=30︒,ϕ=60︒,BC =270mm 。
试求该瞬时杆BC 的角速度和点C 的速度。
hv AC v AP v ABθθω2000cos cos ===习题6-1图ABCv 0hθ习题6-2图PωABv CABCv ohθ习题6-2解图习题6-3解图习题6-3图v A = vv B = v ωAωB习题6-6图习题6-6解图解:杆BC 的瞬心在点P ,滚子O 的瞬心在点D BDv B ⋅=ωBPBD BP v B BC ⋅==ωω ︒︒⨯=30sin 27030cos 36012 rad/s 8=PC v BC C ⋅=ωm/s 87.130cos 27.08=︒⨯=6-5 在下列机构中,那些构件做平面运动,画出它们图示位置的速度瞬心。
大物第六七节习题册答案

由机械能守恒定律
E0 Ex
解出
k mg sin 2 Ek Ek 0 ( x ) 2 k
6 设想有两个自由质点,其质量分别为m1和m2,它们之间的相互作用符
合万有引力定律。开始时,两质点间的距离为l,它们都处于静止状态
试求当它们的距离变为1/2 l时,两质点的速度各为多少?
• 解:两自由质点组成的系统在自身的引力场中运动时,系 统的动量和机械能均守恒。 设两质点的间距变为L/2
2
1
1 2 Md ( J ) = 2
1 1 2 J 2 J 12 2 2
合外力矩对定轴转动刚体所做的功等于刚体转动动能的增量。
1)质点对固定点的角动量 L r mv
角动量是矢量,角动量L的方向垂直 于r和mv 所组成的平面,其指向可用 右手螺旋法则确定。
v v v
2 x
2 y
答案:B
2
1
1 1 2 2 F .d r mv2 mv1 2 2
• 2 一质点在几个外力同时作用下运动时, 下述哪种说法正确? ( ) (A)质点的动量改变时,质点的动能一定改 变。 (B)质点的动能不变时,质点的动量也一定 不变。 (C)外力的冲量是零,外力的功一定为零。 (D)外力的功为零,外力的冲量一定为零。 解析:结果为C
时,它们的速度分别为v1及v2则有
m1v1 m2v2 0
(1)
- Gm1m2 1 1 2Gm1m2 2 m1v12 m2v2 l 2 2 l 联立(1) (2)解得:
(2)
v1 m2
2G l (m1 m2 )
v2 m1
2G l (m1 m2 )
刚体习题和答案

作业5 刚体力学♫刚体:在力的作用下不发生形变的物体⎰=-⇒=210t t dt dtd ωθθθω角速度⎰=-⇒=210t t dt dtd βωωωβ角加速度1、根底训练〔8〕绕定轴转动的飞轮均匀地减速,t =0时角速度为05rad s ω=,t =20s 时角速度为00.8ωω=,那么飞轮的角加速度β= -0.05 rad/s 2 ,t =0到 t =100 s 时间飞轮所转过的角度θ= 250rad . 【解答】飞轮作匀变速转动,据0t ωωβ=+,可得出:200.05rad s tωωβ-==-据2012t t θωβ=+可得结果。
♫定轴转动的转动定律:定轴转动的角加速度与它所受的合外力矩成正比,与刚体的转动惯量成反比.βJ M =质点运动与刚体定轴转动对照[C ]1、根底训练〔2〕一轻绳跨过一具有水平光滑轴、质量为M 的定滑轮,绳的两端分别悬有质量为m 1和m 2的物体(m 1<m 2),如下图.绳与轮之间无相对滑动.假设某时刻滑轮沿逆时针方向转动,那么绳中的力 (A) 处处相等. (B) 左边大于右边. (C) 右边大于左边. (D) 哪边大无法判断. 【解答】逆时针转动时角速度方向垂直于纸面向外, 由于(m 1<m 2),实际上滑轮在作减速转动,角加速m 2m 1 O度方向垂直纸面向,所以,由转动定律21()T T R J β-=可得:21T T >[C ] 2、自测提高〔2〕将细绳绕在一个具有水平光滑轴的飞轮边缘上,现在在绳端挂一质量为m 的重物,飞轮的角加速度为.如果以拉力2mg 代替重物拉绳时,飞轮的角加速度将(A) 小于. (B) 大于,小于2. (C) 大于2. (D) 等于2. 【解答】设飞轮的半径为R ,质量为m ,根据刚体定轴转动定律M J β=,当挂质量为m 的重物是:mg T maTR J a R ββ-=== 所以2mgRJ mRβ=+,当以2F mg =的拉力代替重物拉绳时,有: '2mgR J β=,2'mgRJβ=,比拟二者可得出结论。
理论力学练习册及答案(南华版)

动系固连摇杆CB上,定系固连机架。
由速度合成定理 作速度平行四边形。
B点速度为:
由加速度合成定理 作加速度图。
取 方向投影,得:
B点加速度为:
7-4.半径为R的半圆形凸轮以匀速V0沿水平线向右平动,带动顶杆AB沿铅直方向运动,当OA与铅直线夹角为300时,求此时杆AB的速度和加速度。
解:动点取杆OA上A点,动系固连杆O1C上,定系固连机架。
由速度合成定理 作速度平行四边形。
由加速度合成定理 作加速度图。
取 方向投影,得:
再取动点杆O1C上C点,动系固连套筒B上,定系固连机架。
由速度合成定理 作速度平行四边形。
由加速度合成定理:
作加速度图。
取 方向投影,得:
取 方向投影,得:
第八章 刚体平面运动
分别取节点A、B为研究对象,受力如图
对于节点A: ,
(压)
对于节点B: , (压)
2-11.计算桁架中1、2、3杆的受力。
解:取I-I剖面右边部分为研究对象,受力如图。
,
(拉)
,
(压)
研究节点B: ,
(压)
第三章 空间力系
3-1.图示正立方体,各边长为a,四个力F1、F2、F3、F4大小皆等于F,如图所示,作用的相应的边上。求此力系简化的最终结果,并在图中画出。
8-7.四杆机构中,曲柄OA以匀角速度ω0=25 rad/s绕O轴转动,OA=50 cm,AB=100 cm,O1B= cm。求∠OAB=900时,B点的加速度,摇臂O1B的角速度和角加速度。
8-8.图示机构中,设当OA与水平线成450角的瞬时,曲柄OA有反时针方向的匀角速度ω=25 rad/s,连杆AB水平,扇形板BD铅垂。求扇形板绕定轴D转动的角加速度ε。
《刚体运动习题》课件

刚体的转动问题涉及到分析刚体的转动惯量、角速度、角加速度等物理量,以及力和扭矩对刚体转动的影响。通过解决刚体的转动问题,可以了解刚体在转动过程中的运动规律和特点。
刚体的复合运动问题涉及到刚体的平动和转动同时发生的情况。
总结词
刚体的复合运动问题需要综合考虑刚体的平动和转动,分析其相互影响和耦合作用。这类问题通常比较复杂,需要运用力学和运动学的知识进行求解。
总结词
在解答进阶习题时,学生需要具备较强的分析能力和计算能力,能够根据题目要求进行正确的分析和计算,并得出正确的结论。
详细描述
总结词:高难度习题是刚体运动中的高级题目类型,主要考察学生对刚体运动理论的深入理解和应用能力。
感谢您的观看
THANKS
详细描述
刚体的振动问题主要研究刚体在周期性外力作用下的振动现象。
总结词
刚体的振动问题涉及到分析刚体的振动频率、振幅、相位等物理量,以及周期性外力对刚体振动的影响。通过解决刚体的振动问题,可以了解刚体在振动过程中的运动规律和特点,对于工程实践中的振动控制和减振设计具有重要意义。
详细描述
刚体运动的解题方法
03
它基于力学的基本原理和数学工具,如微积分、线性代数和常微分方程等,来推导和求解刚体运动的数学模型。
解析法可以给出精确的解,但有时可能比较复杂,需要较高的数学水平。
解析法是一种通过数学公式和定理来求解刚体运动问题的方法。
几何法是通过图形和几何形状来描述和解决刚体运动问题的方法。
它通过绘制刚体的运动轨迹、速度和加速度等矢量图,以及分析刚体的转动和角速度等来解决问题。
04
建筑结构中的刚体运动是指建筑物在风、地震等外力作用下产生的运动,包括平动、扭转和复合运动等。
理论力学(机械工业出版社)第六章刚体的基本运动习题解答

习 题6-1 杆O 1A 与O 2B 长度相等且相互平行,在其上铰接一三角形板ABC ,尺寸如图6-16所示。
图示瞬时,曲柄O 1A 的角速度为rad/s 5=ω,角加速度为2rad/s 2=α,试求三角板上点C 和点D 在该瞬时的速度和加速度。
图6-16m/s 5.051.01=⨯===ωA O v v D C2221n n m/s 5.251.0=⨯===ωA O a a D C 21ττm/s 2.021.0=⨯===αA O a a D C6-2 如图6-17所示的曲柄滑杆机构中,滑杆BC 上有一圆弧形轨道,其半径R =100mm ,圆心O 1在导杆BC 上。
曲柄长OA =100mm ,以等角速度rad/s 4=ω绕O 轴转动。
设t =0时,0=ϕ,求导杆BC 的运动规律以及曲柄与水平线的夹角︒=30ϕ时,导杆BC 的速度和加速度。
图6-17m 4cos 2.04cos 1.02cos 2cos 21t t t R OA x O =⨯⨯===ωϕ m/s 4sin 8.01t xO -= ︒=30ϕ时 m/s 4.01-=O x 21m/s 4cos 2.3t x O -= 21m/s 36.1-=O xm /s 4.0=v 22m/s 771.2m/s 36.1==a6-3 一飞轮绕定轴转动,其角加速度为2ωαc b --=,式中b 、c 均是常数。
设运动开始时飞轮的角速度为0ω,问经过多长时间飞轮停止转动?2ωαc b --= t c b d d 2-=+ωω ⎰⎰-=+t t c b 002d d 0ωωωt bc bc-=00|)arctan(1ωω )arctan(10ωb cbct =6-4 物体绕定轴转动的转动方程为334t t -=ϕ。
试求物体内与转轴相距R =0.5m 的一点,在t =0及t =1s 时的速度和加速度度的大小,并问物体在什么时刻改变其转向。
234t t -=ϕ 294t -=ϕt 18-=ϕ t =0时4=ϕ0=ϕ m/s 245.0=⨯==ωR v 222n m /s 845.0=⨯==ωR a 0τ==αR a2n m/s 8==a a t =1s 时5-=ϕ18-=ϕ m/s 5.255.0=⨯==ωR v222n m /s 5.12)5(5.0=-⨯==ωR a 2τm/s 9)18(5.0-=-⨯==αR a2m/s 4.15=a什么时刻改变其转向0942=-=t ϕs 32=t6-5 电机转子的角加速度与时间t 成正比,当t =0时,初角速度等于零。
刚体的转动部分习题分析与解答

动轨迹为一个圆弧。
刚体的定轴转动和平面转动的比较
03
定轴转动和平面转动是刚体转动的两种基本形式,它们在运动
学和动力学上有一些不同之处,如角速度、角加速度等。
03
刚体的动能与势能
刚体的动能
总结词
刚体的动能是指刚体在转动过程中所 具有的能量,与刚体的转动速度和质 量分布有关。
详细描述
刚体的动能计算公式为$E_{k} = frac{1}{2}Iomega^{2}$,其中$I$为刚体的转 动惯量,$omega$为刚体的角速度。转动惯量 是描述刚体质量分布对其转动影响的物理量, 与刚体的质量分布、形状和大小有关。
解答过程
钢球下落过程中,其速度逐渐增大,故其动能在 不断增加。同时,钢球离地面的高度逐渐减小, 故其势能在不断减小。由于钢球下落过程中只有 重力做功,故其机械能守恒。
习题五:关于刚体的机械能守恒的题目
总结词
理解机械能守恒的概念,掌握机械能守恒的条件和机械能守恒的计算方法。
详细描述
机械能守恒是指系统内各种形式的能量在相互转化时总量保持不变。对于刚体系统,只有重力或弹力 做功时机械能守恒。机械能
刚体的势能
总结词
刚体的势能是指刚体在转动过程中相对于某一参考点所具有 的能量。
详细描述
刚体的势能计算公式为$U = -GMmcostheta$,其中$G$为万 有引力常数,$M$和$m$分别为两个质点的质量,$theta$为 两质点连线和垂直于势能参考平面的夹角。对于刚体,势能的 具体值取决于参考点的选择。
实际问题。
习题五解答与解析
要点一
总结词
刚体的角动量守恒
要点二
详细描述
这道题目考察了学生在刚体转动中如何应用角动量守恒的 知识。学生需要理解角动量的概念,知道角动量等于刚体 的转动惯量乘以角速度,并能够根据角动量守恒的条件判 断刚体的运动状态。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章刚体的基本运动习题解答习题6-1 杆O 1A 与O 2B 长度相等且相互平行,在其上铰接一三角形板ABC ,尺寸如图6-16所示。
图示瞬时,曲柄O 1A 的角速度为ω=5rad/s,角加速度为α=2rad/s2, 试求三角板上点C 和点D 在该瞬时的速度和加速度。
图6-16v C =v D =O 1A ω=0. 1⨯5=0. 5m/sa C =a D =O 1A ωττn n 2=0. 1⨯5=2. 5m/s222a C =a D =O 1A α=0. 1⨯2=0. 2m/s6-2 如图6-17所示的曲柄滑杆机构中,滑杆BC 上有一圆弧形轨道,其半径R=100mm,圆心O 1在导杆BC 上。
曲柄长OA =100mm,以等角速度ω=4rad/s绕O 轴转动。
设t =0时,求导杆BC 的运动规律以及曲柄与水平线的夹角ϕ=30︒时,导杆BC 的速度和加速度。
ϕ=0,图6-17x O 1=2OA cos ϕ=2R cos ωt =2⨯0. 1⨯cos 4t =0. 2cos 4t m O 1=-0. 8sin 4tm/s ϕ=30︒时 x O 1=-0. 4m / s xO 1=-3. 2cos 4t m/s2 O 1=-1. 63m /s 2 x xv =0. 4m /s a =1. 63m /s 2=2. 771m /s 26-3 一飞轮绕定轴转动,其角加速度为α=-b -c ω2, 式中b 、c 均是常数。
设运动开始时飞轮的角速度为ω0,问经过多长时间飞轮停止转动?α=-b -c ω2d ωb +c ω2=-d t ⎰d ωb +c ω2ω0=⎰t-d tarctan(1bcc bω) |ω=-tarctan(c bω0)6-4 物体绕定轴转动的转动方程为ϕ=4t -3t 3。
试求物体内与转轴相距R =0.5m的一点,在t =0及t =1s时的速度和加速度度的大小,并问物体在什么时刻改变其转向。
2=4-9t 2 ϕ =-18t ϕ=4t -3t ϕt =0时=4 ϕ =0 ϕv =R ω=0. 5⨯4=2m/s2=0. 5⨯4=8m/s222a τ=R α=0a =a n =8m /s t =1s时=-5 ϕ =-18 ϕv =R ω=0. 5⨯5=2. 5m/sa n =R ω2=0. 5⨯(-5) =12. 5m/s222a τ=R α=0. 5⨯(-18) =-9m/sa =15. 4m/s 什么时刻改变其转向 =4-9t 2=0 t = ϕ23s26-5 电机转子的角加速度与时间t 成正比,当t =0时,初角速度等于零。
经过3s 后,转子转过6圈。
试写出转子的转动方程,并求t =2s时转子的角速度。
α=ct d ω=ct d t d ϕ=1ct ϕ=2⎰ωd ω=⎰tct d t ω=12ct21d t 26t =3s时,ϕ=6⨯2π=12π 12π=ct312794π3ϕ=t =1. 396t 3916c =612π⨯c ⨯3 =4π3t =2s时ω=6-6 杆OA 可绕定轴O 转动。
一绳跨过定滑轮B ,其一端系于杆OA 上A 点,另一端以匀速u 向下拉动,如图6-18所示。
设OA=OB=l ,初始时ϕ=0,试求杆OA 的转动方程。
AB =2l -ut4π3t2=4π3⨯4=16π3=16. 76r a d /scos ∠OAB =即 cosAB /2OA =1-ut 2l=2l -ut 2l=1-ut 2lϕ2ϕ=2arccos(1-ut 2l)6-7 圆盘绕定轴O 转动。
在某一瞬时,轮缘上点A 的速度为v A =0. 8m/s,转动半径为盘上任一点B 的全加速度a B 与其转动半径OB 成θ角,且tan θ=0. 6,如图6-19r A =0. 1m ;所示。
试求该瞬时圆盘的角加速度。
v A r Av A =r A ω=0. 8m/s ω=tan θ=图6-190. 8==8r a d / s 0. 12αω2=0. 6 |α|=0. 6⨯ω=38. 4r a d /s26-8 如图6-20所示,电动机轴上的小齿轮A 驱动连接在提升铰盘上的齿轮B ,物块M 从其静止位置被提升,以匀加速度升高到1.2m 时获得速度0.9m/s。
试求当物块经过该位置时:(1)绳子上与鼓轮相接触的一点C 的加速度;(2)小齿轮A 的角速度的角加速度。
图6-20(1)0. 9-0=2a τ⨯1. 2 a τ=220. 492. 4=0. 3375ωB =a n =ωA ωB=0. 90. 6=1. 5 a n =0. 6⨯1. 52=1. 3520. 3375R B R A a τR C==+1. 352=1. 39m/s2450150=3 ωA =3ωB =4. 5r a d / s=0. 5625 αA =3αB =1. 6875r a d /s2αB =0. 33750. 66-9 杆OA 的长度为l , 可绕轴O 转动,杆的A 端靠在物块B 的侧面上,如图6-21所示。
若物块B 以匀速v 0向右平动,且x =v 0t , 试求杆OA 的角速度和角加速度以及杆端A 点的速度。
图6-21x =v 0t cos ϕ=x lv 0t lϕ=a r c c 0 lv tv 0=ωO =ϕl -(v 0t l )2=lv 0222-v tO =αO =ω v 0t (l23223-v t )v A =l ωO =lv 0l -v t22206-10 图6-22所示机构中,杆AB 以匀速v 向上滑动,通过滑块A 带动摇杆OC 绕O 轴作定轴转动。
开始时ϕ=0,试求当ϕ=π/4时,摇杆OC 的角速度和角加速度。
图6-22tan ϕ=vt lv l v对时间求导sec ϕ=ϕ2=v l2cos ϕ=ω=ϕl sec ϕ2= α=ωv l⨯(-s i n 2ϕ) ω=-v l222s i n 2ϕc o s ϕϕ=π/4时ω=v 2lα=-v 2l226-11 如图6-23所示,电动绞车由皮带轮Ⅰ和Ⅱ以及鼓轮组成,鼓轮Ⅲ和皮带轮Ⅱ刚性地固定在同一轴上。
各轮的半径分别为r 1=0. 3m ,r 2=0. 75m ,r 3=0. 4m ,轮Ⅰ的转速为n 1=100r/min。
设皮带轮与皮带之间无相对滑动,求重物M 上升的速度和皮带各段上点的加速度。
图6-23ω1=πn 130r 1=10π30. 3⨯10π3=4π3ω2=r 2ω1=0. 75v =r 3ω2=0. 4⨯a AB =a CD =04π3=1. 6755m/sa AD =r 1ω=0. 3⨯(2110π3) =210π32=32. 8987m/s2a BC =r 2ω=0. 75⨯(224π3) =24π322=13. 1595m/s6-12 两轮Ⅰ、Ⅱ铰接于杆AB 的两端,半径分别为r 1=150mm ,r 2=200mm ,可在半径为R =450mm的曲面上运动,在图6-24所示瞬时,点A 的加速度大小为a A=1200mm/s2,方向与OA 连线成60︒角。
试求该瞬时:(1)AB 杆的角速度和角加速度;(2)点B 的加速度。
图6-24a A =1200mm/sanA2=a A cos 60︒=600mm/s 2=v A R +r 122=(R +r 1) ωω=600450+150=1rad/sa A =a A sin 60︒=600τ3=(R +r 1) αα=6003R +r 1=23rad/sa B =(R +r 2) ωτn2=650mm/s2a B =(R +r 2) α=650a B =1300mm/s23mm/s26-13 如图6-25所示,机构中齿轮Ⅰ紧固在杆AC 上,AB=O1O 2,齿轮Ⅰ与半径为r 2的齿轮Ⅱ啮合,齿轮Ⅱ可绕O 2轴转动且与曲柄O 2B 没有联系。
设O 1A = O2B=l ,ϕ=b sin ωt ,试确定t=π(2ω) 时,轮Ⅱ的角速度的角加速度。
图6-25ωO 当t =π2B=b ωc o s =-b ω=ϕωt αO B =ϕ22s i n ωtωO2B2ω=0 v B =02=-b ω a B =l αO 2B =-bl ω a D =a B =-bl ω时v D =v B =0(齿轮Ⅰ与杆AC 平动,点D 为轮I 、II 接触点) ωII =0αOτ2ττ22BαII =a D r 2τ=-bl ωr 226-14 如图6-26所示,摩擦传动机构的主动轴Ⅰ的转速为n =600r/min。
轴Ⅰ的轮盘与轴Ⅱ的轮盘接触,接触点按箭头A 所示的方向移动。
距离d 的变化规律为d =100-5t ,其中d 以mm 计,t 以s 计。
已知r=50mm,R =150mm。
求:(1)以距离d 表示的轴Ⅱ的角加速度;(2)当d =r 时,轮B 边缘上一点的全加速度。
图6-26(1)ω=πn 301000πd =20πω2=1000π 1000π5000π2d =-⨯(-5) =rad/s 222d d d2=-α2=ω(2) d =r 时ω2=1000π504=20π2α2=2πrad/sa B =R ω2+α2=1502(20π)+4π42=300π40000π+1=592. 177⨯10mm/s232=592. 177m/s26-15 如图6-27所示,录音机磁带厚为δ,图示瞬时两轮半径分别为r 1和r 2,若驱动轮Ⅰ以不变的角速度ω1转动,试求轮Ⅱ在图示瞬时的角速度和角加速度。
图6-27r 1ω1=r 2ω2 ω2=r 1r 2ω1 1ω1-r 2ω2rr 22= 2 ω 1ω1=r 2ω2+r 2ωrδ2πd ϕ1轮Ⅰ转过一周(2π),半径增大δ,转过d ϕ1,则增大故 d r 1= d r 1d t 1=rδ2πd ϕ1=δ2π⨯d ϕ1d tδ2πω1r 1r 22=-δ,故r而在轮Ⅰ转过一周(2π)时,轮Ⅱ半径减小2=α2=ω1ω1-r 2ω2rr 2δ2π⨯r 1r 2⨯ω11ω1-r 2⨯r =r 1r 2ω1=1r 2-r 1r 2r r ⨯22ω1δ=2πω1⨯r 2+r 1⨯ 2δ2πr 1r 2ω1ω1r22r 2(1+r 1=r2) 2r 2⨯δ2πω2122=ω1δ2πr (1+ r 1)2r22。
