第6章刚体的平面运动习题解答080814
理论力学-刚体的平面运动

ω
O
vB
ψ
B
x
vB = vA+ vBA
其中vA的大小 vA=R ω 。
vBA
例题
刚体的平面运动
由速度合成矢量图可得
例 题 3
vA
y
A
vA
vA vBA vB π π sin( ) sin( ) sin( ) 2 2
ω
O
所以
vB vA
y
π 2 π 2
ω
O φ
A B
刚体的平面运动
作业 9-1
曲柄连杆机构如图所 示,OA= r , AB 3r 。如 曲柄 OA 以匀角速度 ω 转动, A ω
求当 60,0 和 90 时点 B的速度。 B
刚体的平面运动
vA
ω
作业 9-1
解:
A vA vB
基点法
连杆AB作平面运动,以A为基点,B点
sin( ) sin( ) R cos cos
例题
刚体的平面运动
例 题 4
在图中,杆 AB 长 l ,
B
滑倒时 B 端靠着铅垂墙
壁。已知 A点以速度u沿 水平轴线运动,试求图
ψ u
A
示位置杆端 B 点的速度 及杆的角速度。
O
例题
刚体的平面运动
解: 基点法
B ω A
60
C D
60
E
例题
刚体的平面运动
解 : 基点法
例 题 2
vDB
B ω A
60
C
vB
60
vD
60
理论力学课后习题答案第6章刚体的平面运动分析
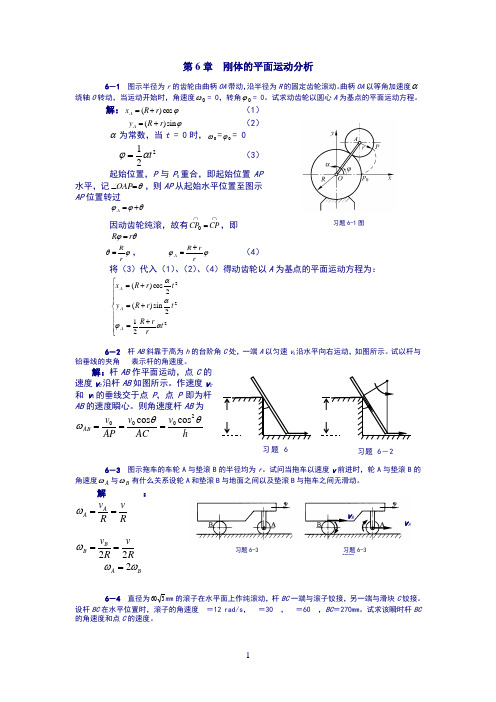
第6章 刚体的平面运动分析6-1 图示半径为r 的齿轮由曲柄OA 带动,沿半径为R 的固定齿轮滚动。
曲柄OA 以等角加速度α绕轴O 转动,当运动开始时,角速度0ω= 0,转角0ϕ= 0。
试求动齿轮以圆心A 为基点的平面运动方程。
解:ϕcos )(r R x A += (1) ϕsin )(r R y A += (2) α为常数,当t = 0时,0ω=0ϕ= 0 221t αϕ=(3)起始位置,P 与P 0重合,即起始位置AP 水平,记θ=∠OAP ,则AP 从起始水平位置至图示AP 位置转过θϕϕ+=A因动齿轮纯滚,故有⋂⋂=CP CP 0,即 θϕr R =ϕθr R =, ϕϕrr R A += (4)将(3)代入(1)、(2)、(4)得动齿轮以A 为基点的平面运动方程为:⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=222212sin )(2cos )(t r r R t r R y t r R x A A A αϕαα6-2 杆AB 斜靠于高为h 的台阶角C 处,一端A 以匀速v 0沿水平向右运动,如图所示。
试以杆与铅垂线的夹角 表示杆的角速度。
解:杆AB 作平面运动,点C 的速度v C 沿杆AB 如图所示。
作速度v C 和v 0的垂线交于点P ,点P 即为杆AB 的速度瞬心。
则角速度杆AB 为hv AC v AP v ABθθω2000cos cos ===6-3 图示拖车的车轮A 与垫滚B 的半径均为r 。
试问当拖车以速度v 前进时,轮A 与垫滚B 的角速度A ω与B ω有什么关系设轮A 和垫滚B 与地面之间以及垫滚B 与拖车之间无滑动。
解:R v R v A A ==ωR v R v B B 22==ω B A ωω2=6-4 直径为360mm 的滚子在水平面上作纯滚动,杆BC 一端与滚子铰接,另一端与滑块C 铰接。
设杆BC 在水平位置时,滚子的角速度=12 rad/s ,=30,=60,BC =270mm 。
合肥工业大学理论力学答案08刚体平面运动

八、刚体的平面运动8.1 如图所示,O 1A 的角速度为ω1,板ABC 和杆O 1A 铰接。
问图中O 1A 和AC 上各点的速度分布规律对不对?8.2如图所示,板车车轮半径为r ,以角速度ω 沿地面只滚动不滑动,另有半径同为r 的轮A 和B 在板车上只滚动不滑动,其转向如图,角速度的大小均为ω,试分别确定A 轮和B 轮的速度瞬心位置。
[解] 板车作平动,轮A 、B 与板车接触点 E 、F 的速度相同,且r v v v O F E ω=== 对A 轮由基点法求轮心A 的速度 A E AE =+v v v ,r v AE ω=∴ r v A ω2=,且A 轮的速度瞬心在E 点下方r 处。
同理可得B 轮的速度瞬心就在轮心B 处。
8.3直杆AB 的A 端以匀速度v 沿半径为R 的半圆弧轨道运动,而杆身保持与轨道右尖角接触。
问杆AB 作什么运动?你能用几种方法求出杆AB 的角速度?E FPOE v Av Fv Ov[解] AB 杆作平面运动。
(一) 瞬心法AB 杆作平面运动,速度瞬心为P 。
Rv AP v AAB2==ω (二)基点法D A DA =+v v v ,DA v v AB A DA ωθ==sin又 DA =2R cos(90o -θ)=2R sin θ ∴ Rv AB 2=ω(三)自然法: d d AB tϕω=,而R S ϕ2= ∴d d 2d d S R v t t ϕ==, d d 2vt R ϕ= ∴ Rv AB 2=ω 8.4如图所示四连杆机构OABO 1中,OA=O 1B=AB/2,曲柄OA 的角速度ω=3rad/s 。
当OA 转到与OO 1垂直时,O 1B 正好在OO 1的延长线上,求该瞬时AB 杆的角速度ωAB 和曲柄O 1B 的角速度ω1。
[解]取AB 为研究对象,AB 作平面运动。
以A 为基点,画B 点速度合成图 由B A BA =+v v v(rad/s)32230sin o==∴⋅=⋅==ωωωωAB OAAB OA v v AB AB ABABBBvvvDAv Dv Dv111cos3022(rad/s)B BAv v OA O Bωωω=︒=⋅=∴=8.5图示曲柄摇机构中,曲柄OA以角速度oω绕O轴转动,带动连杆AC在摇块B内滑动,摇块及与其固结的BD杆绕B铰转动,杆BD长l;求在图示位置时摇块的角速度及D点的速度。
刚体平面运动习题

第8章 刚体平面运动习题1.是非题(对画√,错画×)8-1.刚体平面运动为其上任意一点与某一固定平面的距离始终平行的运动。
( ) 8-2.平面图形的运动可以看成是随着基点的平移和绕基点的转动的合成.( ) 8-3.平面图形上任意两点的速度在某固定轴上投影相等。
( ) 8-4.平面图形随着基点平移的速度和加速度与基点的选择有关。
( ) 8-5.平面图形绕基点转动的角速度和角加速度与基点的选择有关。
( ) 8-6.速度瞬心点处的速度为零,加速度也为零。
( ) 8-7.刚体的平移也是平面运动。
( ) 2.填空题(把正确的答案写在横线上)8-8.在平直轨道作纯滚动的圆轮,与地面接触点的速度为 。
8-9.平面图形上任意两点的速度在 上投影相等。
8-10.某瞬时刚体作平移,其角速度为 ;刚体上各点速度 ;各点加速度 。
3.简答题8-11.确定图示平面运动物体的速度瞬心位置。
题8-11图(a) (b)(c)8-12.若刚体作平面运动,下面平面图形上A 、B 的速度方向正确吗? 题8-12图(a) (b) (c)8-13.下面图形中O 1A 和AC 的速度分布对吗?8-14.圆轮做曲线滚动,某瞬时轮心的速度o v 和加速度o a ,轮的半径为R ,则轮心的角加速度等于多少?速度瞬心点处的加速度大小和方向如何确定?题8-13图B8-15.用基点法求平面图形个点的加速度时,为什么没有科氏加速度? 4.计算题8-16.椭圆规尺AB 由曲柄OC 带动,曲柄以匀角速度o ω绕O 轴转动,如图所示,若取C 为基点,OC=BC=AC=r ,试求椭圆规尺AB 的平面运动方程。
8-17.半径为r 的齿轮由曲柄OA 带动,沿半径为R 的固定齿轮滚动,如图所示。
曲柄以匀角加速度α绕O轴转动,设初始时角速度0=ω、角加速度0=α、转角0=ϕ,若选动齿轮的轮心C 点为基点,试求动齿轮的平面运动方程。
题8-16图题8-17图8-18.曲柄连杆机构,已知OA =40cm ,连杆AB =1m ,曲柄OA 绕O 轴以转速180=n r/min 匀速转动,如图所示。
刚体的平面运动

BD
B
BD
206 60
3 . 43 rad / s
M MD BD 30 3 . 43 103 cm / s
O
D
O1 D
1D
0
p.12
例
题
例
题
例9.曲柄OO’=l,以匀角速度1绕定轴O转动,同时带动可绕曲 柄一端的轴销O’转动的轮II沿固定轮I滚动而不滑动。已知 轮II的半径为r,求在图示位置轮缘上A、B两点的加速度aA 及aB,A点在OO’的延长线上,而B点位于通过O’点并与 O’O垂直的半径上。 B a a A O’B O’ 解:(1)分析刚体的运动: aO’ O’ aO’A aB OO’作定轴转动 轮II作平面运动 vO’
2 1 / s
D
E E
D
v B AB 40 126 cm / s
BD刚体以B基点
vB sin 120
v D v BD vB sin 120
v D v B v BD
vD sin 30
3 3
v BD sin 30
vD
vB
vBD
方向
大小
1000
C1 vB
A1
v AB
200 cos
sin 45
2000 7 2
2 2
143 cm / s
AB
v AB l
7 200
0 . 714 rad / s
p.10
例
题
例
题
例7.(续) 解:(2)速度瞬心法:速度瞬心是C
刚体平面运动习题课

v 3r B BC2 3l
vC CC2 BC
3r 3
vC
8
例2 平面四连杆机构的尺寸和位置如图所示,如果杆AB以等角速 度 = 1 rad/s绕A轴转动,求C点的加速度。 解:AB和CD作定轴转动,BC 作平面运动,其B、C两点的运 动轨迹已知为圆周,由此可知 vB和vC的方向,分别作vB和vC两 个速度矢量的垂线得交点O即 为该瞬时BC的速度瞬心。由几 何关系知
8. 求平面图形上一点加速度的方法 n 基点法:aB a A aBA aBA ,A为基点, 是最常用的方法 此外,当 =0,瞬时平动时也可采用方法 a B AB a A AB 它是基点法在 =0时的特例。
5
二.解题步骤和要点 1. 根据题意和刚体各种运动的定义,判断机构中各刚体的运动 形式。注意每一次的研究对象只是一个刚体。 2. 对作平面运动的刚体,根据已知条件和待求量,选择求解速 度(图形角速度)问题的方法, 用基点法求加速度(图形角加速
刚体基本运动
1、 平动 刚体上的各点具有形状相同的运动轨迹;
刚体上的各点在某一瞬时具有相同的速度和加速度;
1
2、定轴转动
( t )
——转动方程
d ——瞬时角速度 dt d ——瞬时角加速度
dt
刚体作定轴转动,刚体上任意一点以该点到转轴的距离为半 径作圆周运动。 任意点速度、加速度 v=R
C
a
aB
t C
a +a a a
n C t C n B
n CB
a
t CB
n aCB
n
n aB AB 2 100 mm/s2
n aCB BC BC 2 25 2 mm/s 2
第6章刚体的平面运动习题解答080814

,(逆时针)、
,
杆OB得角速度为
,(逆时针)、
两齿轮啮合点M得速度为,则轮1得角速度为
,(逆时针)、
6-9如图所示,轮O在水平面上匀速滚动而不滑动,轮缘上固连销钉连接滑块B,此滑块在摇杆得槽内滑动,并带动摇杆绕轴转动。已知轮得半径m,在图示位置时,就是轮得切线,轮心得速度m/s,摇杆与水平面得夹角为。求摇杆得角速度与角加速度。
解:如图所示,对各构件进行速度分析、
1)杆作平面运动、因,所以杆为瞬时平移,得
、
2)杆作平面运动、由找得杆得速度瞬心为D点,所以,杆上得速度分布好像与三角板一起绕作定轴转动一样,得
,方向如图示、
3)杆作平面运动、由找得杆得速度瞬心为,故有
,(顺时针);
,(方向向上).
6—5图示四连杆机构中,连杆由一块三角板ABD构成。已知曲柄得角速度rad/s,mm,mm,mm。当mm铅直时,AB平行于,且、A、D在同一直线上,角。求三角板ABD得角速度与点D得速度.
解:1)速度分析、
动齿轮A在定齿轮O上作纯滚动,所以,动齿轮A上与定齿轮O接触得这点就就是动齿轮得A得速度瞬心,于就是有
,,(逆时针)、
、
选BE杆上得B点为动点,套筒C为动系,如图(a)。由速度合成定理
,
得
,
、
式中、从而杆BE得角速度为
,(顺时针)、
当选BE杆上得为动点时,牵连速度为零,又因为杆相对于套筒就是作平移,从而杆BE上得点得速度为
解出
,
,
于就是,杆得角速度为
,(逆时针);
杆得角速度为
,(顺时针)、
选取滑块上得销钉C为动点,摇杆为动系,则
刚体平面运动

6. 1 概述 6. 2 刚体平面运动的解析法 6. 3 刚体平面运动的分解 6. 4 速度分析 6. 5 加速度分析 合成法
1
6.1 概述 1、定义 刚体运动时,其上各点至某一固定平面距离不变。
A
O1 O2
B
车轮--平面运动 连杆AB --平动
2
2、 刚体平面运动的简化: 平面运动可简化为平面图形S 在其自身平面内的运动。
& = 0.359 rad/s 代入(4) ⇒ ω AB = θ & B = −0.167 m s 代入(3) ⇒ vB = x
7
【强调】 (1)用解析法时ϕ、θ 均为有向角,规定:由定线至动线的方向 为正,本题ϕ 逆时为正,θ 顺时为正,不必统一。
&、θ && &、ϕ &&;θ & B、& &B 都是代数量,其正向与ϕ、θ 、x一致。 (2) ϕ ;x x & > 0, 表示与ϕ、θ 同向, & 为逆 ϕ & > 0、θ & B < 0, 表示与x轴反向; ϕ 本题 x & 为顺时。 时, θ
C θ B
vC = v A + vCA
vcA
vCA = AC ⋅ ωCA = AC ⋅ ωBA
先分析B点求ω AB = 0.359 rad/s
θ = 10.18°
vCA = AC ⋅ ω AB = 0.0718 m s
x : vCx = −v A cos 45 − vCA sin θ=-0.154 m/s y : vCy = v A sin 45 − vCA cos θ = 0.07 m/s
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章 刚体的平面运动本章要点一、刚体平面运动的描述1 刚体的平面运动方程:)(t x x A A =,)(t y y A A =,)(t ϕϕ=.2 平面图形的运动可以看成是刚体平移和转动的合成运动:刚体的平面运动(绝对运动)便可分解为随动坐标系(基点)的平移(牵连运动)和相对动坐标系(基点)的转动(相对运动)。
其平移部分与基点的选取有关,而转动部分与基点的选取无关。
因此,以后凡涉及到平面图形相对转动的角速度和角加速度时,不必指明基点,而只说是平面图形的角速度和角加速度即可。
二、平面运动刚体上点的速度1 基点法:平面图形内任一点B 的速度,等于基点A 的速度与B 点绕基点转动速度的矢量和,即BA A B v v v +=,其中BA v 的大小为ωABv BA =,方向垂直于AB ,指向与图形的转动方向相一致。
2投影法速度投影定理:在任一瞬时,平面图形上任意两点的速度在这两点连线上的投影相等,即AB A AB B v v ][][=3瞬心法任意瞬时平面运动图形上都存在速度为零的点,称为该平面图形的瞬时速度中心,简称瞬心。
平面图形上各点速度在某瞬时绕瞬心的分布与绕定轴转动时的分布相同,但有本质区别。
绕定轴转动时,转动中心是一个固定不动的点,而速度瞬心的位置是随时间而变化的。
面图形内任意一点的速度,其大小等于该点到速度瞬心的距离乘以图形的角速度,即ωCM v M =,其方向与CM 相垂直并指向图形转动的一方。
若在某瞬时,0=ω,则称此时刚体作瞬时平移,瞬时平移刚体的角加速度不为零。
解题要领:1 建立平面运动刚体的运动方程时要注意选取合适的点为基点,以使问题简单,。
2 由于在基点建立的是平移坐标系,因此,相对基点的角速度就是相对惯性坐标系的角速度。
3 平面运动刚体上点的速度计算的3种方法各有所长:基点法包含刚体运动的速度信息,但过程繁杂;速度投影法能快捷地求出一点的速度,但失去角速度信息;瞬心法简单明了和直观是常用的方法。
4 当用基点法时,要注意基点的速度矢和相对基点的速度矢组成速度平行四边形的两边,对角向才是这一点的速度矢。
速度基点法能且只能解2个未知量,因此,在涉及的3个速度中至少有一个速度的大小和方向都是已知的,在画速度平行四边形时先画这个速度。
5 应用速度投影法时,要注意投影是有正负的,两点的速度必须协调,符合刚体的定义。
6 在找速度瞬心时,作速度矢量时要注意各速度的协调,同一刚体上的两点速度方向可以确定速度瞬心的位置。
三、平面运动刚体上点的加速度平面图形上任意一点的加速度,等于基点的加速度与该点绕基点转动的切向加速度和法向加速度的矢量和,即nt BA BA A B a a a a ++=,进一步,当基点A 和所求点B 都作曲线运动时,它们的加速度也应分解为切向加速度和法向加速度,上式写为nttnntBA BA A A B B a a a a a a +++=+, 其中 BBnBv a ρ2=,AAn Av a ρ2=,2ωAB a n BA =,αAB a tBA =,B A ρρ,分别为B A ,点的曲率半径。
特殊地,当刚体作瞬时平移时,0=nBA a ,有加速度投影定理 AB A AB B ][][a a =. 解题要领1 加速度基点法一般涉及6个加速度矢量,其中3个法向加速度是与速度或角速度有关,这可以通过速度分析求得,而tBA a 的方向与B A ,垂直为已知,剩下5个因素中只可以存在2个未知量。
2 一般选加速度的大小和方向都已知的一点为基点。
3 加速度基点法最多涉及6个矢量,应通过列投影式解代数方程求解。
投影式中等号一边是B 点加速度的投影,另一边是基点A 的加速度和相对于基点加速度投影的代数和,千万不能写成“平衡方程”的形式。
4 加速度投影定理只在刚体作瞬时平移时成立。
5 可以证明刚体作平面运动时也存在加速度瞬心,即加速度为零的点,但这必须在角速度和角加速度皆已知的情况下才能确定,因此无助于解题,所以没有“加速度瞬心法”。
第七章 刚体的平面运动 习题解答6-1 椭圆规尺AB 由曲柄OC 带动,曲柄以角速度Oω绕O 轴匀速转动,如图所示。
如r AC BC OC ===,并取C 为基点,求椭圆规尺AB 的平面运动方程。
解:AB 杆作平面运动,设0=t 时,0=ϕ,则t 0ωϕ=。
选AB 杆上的C 点位基点,建立平移坐标系y x C ''-,在图示坐标系中,AB 杆在固定坐标系xy O -的位置由坐标),,(ϑC C y x 确定,所以AB 杆的平面运动方程为:t r x C 0cos ω=,t r y C 0sin ω=,t 0ωϕθ==.6-2 杆AB 的A 端沿水平线以等速v 运动,在运动时杆恒与一半圆周相切,半圆周半径为R ,如图所示。
如杆与水平线的夹角为θ,试以角θ表示杆的角速度。
解: 解法一:杆AB 作平面运动。
选取A 为基点,由速度基点法CA A C v v v +=,作图示几何关系,图中v v A =,解得θθsin sin v v v A CA ==,A B 杆的角速度为 θθωcos sin 2R v AC v CA == (逆时针). 解法二:在直角三角形△ACO 中,xR=ϑsin ,对时间求导,得 x xR 2cos -=ϑϑ 其中,ϑ,R x v x== ,解得A B 杆的角速度为 Rv ϑϑϑcos sin 2-= ,(负号表示角速度转向与ϑ角增大的方向相反,即逆时针)题6-1图题 6-2图6-3 半径为r 的齿轮由曲柄OA 带动,沿半径为R 的固定齿轮转动,如图所示。
如曲柄OA 以等角加速度α绕O 轴转动,当运动开始时,角速度0=O ω,转角0=ϕ。
求动齿轮以中心A 为基点的平面运动方程。
解:动齿轮作平面运动。
建立与曲柄OA 固结的转动坐标系ξη-O ,和在动齿轮的A 点建立平移坐标系y x A ''-,如图所示,从图中可见,因动齿轮和固定齿轮间没有滑动,所以存在关系ϑϕr R =小轮半径AM 相对平移坐标系y x A ''-,也即固定坐标系得转角为)1(r R A +=+=ϕϑϕϕ, 而 221t αϕ=,可得小轮平面运动方程为)21cos()(2t r R x A α+=, )21sin()(2t r R y A α+=. 6-4 图示机构中,已知10.OA =m ,10.BD =m ,10.DE =m ,310.EF =m ;4=OA ωrad/s 。
在图示位置时,曲柄OA 与水平线OB 垂直;且B 、D 和F 在同一铅直线上,又EF DE ⊥。
求EF 的角速度和点F 的速度。
解:如图所示,对各构件进行速度分析. 1)AB 杆作平面运动. 因B A v v // ,所以AB 杆为瞬时平移,得s m OA v v OA A B /4.0=⋅==ω.2)BC 杆作平面运动. 由B C v v ,找得BC 杆的速度瞬心为D 点,所以,BC 杆上的速度分布好像与三角板DEC 一起绕D 作定轴转动一样,得m/s 4.0==⋅=⋅=B B C E v BDvDE DC v DE v ,方向如图示. 3)EF 杆作平面运动. 由F E v v ,找得EF 杆的速度瞬心为EF C ,故有题 6-4图题6-3图r a d /s 333.1==EFEEF EC v ω,(顺时针); m/s 462.0=⋅=EF EF F FC v ω,(方向向上)。
6-5 图示四连杆机构中,连杆由一块三角板ABD 构成。
已知曲柄的角速度21=A O ωrad/s ,1001=A O mm ,5021=O O mm ,50=AD mm 。
当A O 1mm 铅直时,AB 平行于21O O ,且1O 、A 、D 在同一直线上,角30=ϕ。
求三角板ABD 的角速度和点D 的速度。
解:1AO 杆和2BO 杆作定轴转动,三角板ABD 做平面运动, 由B A v v ,找得三角板ABD 的速度瞬心为ABD C 点,如图所示. 故m /s 2.011=⋅=A O A AO v ω, 三角板ABD 的角速度:rad/s 07.1==AC v ABD A ABD ω,(逆时针).D 点的速度:rad/s 254.0=⋅=ABD ABD D D C v ω.6-6 图示双曲柄连杆机构中,滑块B 和E 用杆BE 连接,主动曲柄OA 和从动曲柄OD 都绕O 轴转动。
OA 以匀角速度120=ωrad/s 转动。
已知100=OA mm ,120=OD mm ,260=AB mm ,120=BE mm ,3120=DE mm 。
求当曲柄OA 垂直于滑块的导轨方向时,曲柄OD 和连杆DE 的角速度。
解:如图机构中,主动曲柄OA 作定轴转动, m/s 2.1=⋅=ωOA v A ,AB 杆作平面运动,在图示瞬时,由B A v ,v 知,AB 杆作瞬时平移,有 m/s 2.1==A B v v .BE 作平移,B E v v =. 有E D v ,v 找得ED 杆速度瞬心为D 点.在图示位置上可得 OD EB OA AB OE =--=22,题 6-5图题 6-6图由此可知30=∠=∠OED ODE ,ED 杆角速度为 rad/s 77.53310===CEv E DE ω, D 点的速度为m/s 08.236.3==⋅=DE D CD v ω, 曲柄OD 的角速度为rad/s 32.17310===ODv DDO ω, (逆时针). 6-7 使砂轮高速转动的装置如图所示。
杆21O O 绕1O 轴转动,转速为9004=n r/min ,2O 处用铰链连接一半径为2r 的动齿轮2,杆21O O 转动时,轮2在半径为3r 的固定内齿轮3上滚动,并使半径1121/r r =的轮1绕1O 轴转动。
轮1上装有砂轮,随同轮1高速转动。
求砂轮的转速。
解:如图所示: 设轮1和杆21O O 的角速度分别为1ω和4ω,杆21O O 作定轴转动,故4212)(ωr r v O +=轮1和轮2啮合点M 的速度 22O M v v =,注意2132r r r +=,可得轮1的角速度441211112ωωω=+==r r r r v M ,(顺时针) 轮1的转速为mi n r/108001241==n n ,(顺时针).6-8 图示瓦特行星传动机构中,平衡杆A O 1绕1O 轴转动,并借连杆AB 带动曲柄OB ;而曲柄OB 活动地装在O 轴上;在O 轴上装有齿轮1,齿轮2的轴安装在连杆AB 的另一端。
已知:330021==r r mm ,mm 7501=A O ,mm 1500=AB ;又平衡杆的角速度61=O ωrad/s 。
求当 60=θ和 90=β时,曲柄OB 和齿轮1的角速度。
