刚体的平面运动例题
合集下载
刚体的自由度和平面平行运动
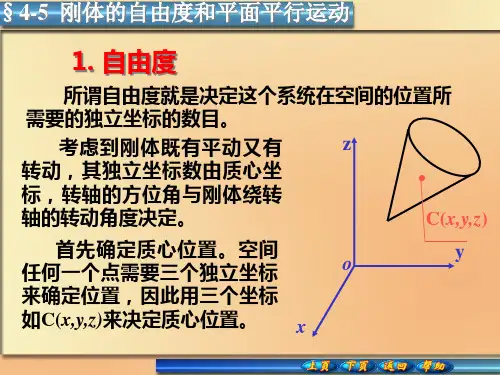
G点的速度 vG vC
r
0
B点的速度
vB vC R 2vC
A点的速度
vA vC2 (R)2
RA
A
2vC
B
RB
RB
v RA RG C
G
刚体的平面平行运动
刚体的动能
Ek
1 2
i
mi
(vi
)
2
1 2
i
mi
[vC2
2vC
(
ri )
(
ri
)
2
]
1 2
(
i
mi )vC2
vC
(
aCx g sin
刚体的平面平行运动
而圆柱体对质心的角加速度与角速度为
0 ， 0
如果圆柱体从静止沿斜面下滑的距离也是x ，则质心所获得的速度由
v2 2aCx x 2gxsin 2gh
求得
v 2gh
在上述纯粹滚动与纯粹滑动两种情况中， 我们看到，两者加速度之比是2/3，两者速度
之比是 2 3
刚体的平面平行运动
本题也可用机械能守恒定律讨论。圆柱体在斜面上
作纯粹滚动下落时，所受到的斜面的摩擦力和正压力
都不作功，满足机械能守恒的条件。圆柱体从静止滚
下，它没有初动能，只有重力势能mgh，当它滚动下
降这段高度时，全部动能是
Ek
1 2
mv
2
C
1 2
J
C
2
对纯粹滚动而言，vc=r，以此代入得
Ek
1 2
m1
JC mr 2
v
2
C
由机械能守恒定律得
刚体的平面平行运动
mgh
1 2
刚体的平面运动1答案
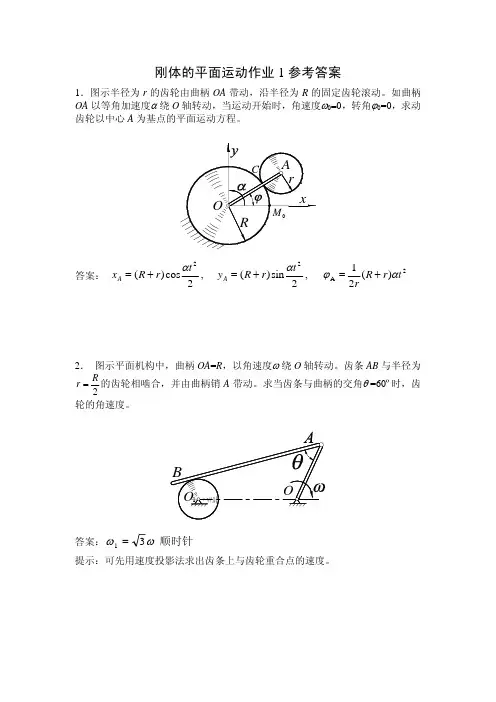
刚体的平面运动作业1参考答案1．图示半径为r 的齿轮由曲柄OA 带动，沿半径为R 的固定齿轮滚动。
如曲柄OA 以等角加速度α 绕O 轴转动，当运动开始时，角速度ω0=0，转角ϕ0=0，求动齿轮以中心A 为基点的平面运动方程。
答案： 2A 22)(21, 2sin)( , 2cos )(t r R rt r R y t r R x A A αϕαα+=+=+=2． 图示平面机构中，曲柄OA =R ，以角速度ω 绕O 轴转动。
齿条AB 与半径为2Rr =的齿轮相啮合，并由曲柄销A 带动。
求当齿条与曲柄的交角θ =60º时，齿轮的角速度。
答案：顺时针 31ωω=提示：可先用速度投影法求出齿条上与齿轮重合点的速度。
3．图中曲柄OA 长150mm ，连杆AB 长200mm ，BD 长300mm 。
设OA ⊥OO 1时，AB ⊥OA ，θ =60º，曲柄OA 的角速度为4rad/s ；求此时机构中点B 和D 的速度以及杆AB 、O 1B 和BD 的角速度。
答案：逆时针顺时针顺时针 rad/s 34 , rad/s 4, rad/s 3 , mm/s 800 , mm/s 34001O =====BD B AB D B v v ωωω提示：在图示瞬时，杆AB 的速度瞬心为点C ，杆BD 的速度瞬心为点E 。
4．图示平面机构中，曲柄长OA =r ，以角速度ω0绕O 轴转动。
某瞬时，摇杆O 1N 在水平位置，而连杆NK 和曲柄OA 在铅垂位置。
连杆上有一点D ，其位置为DK =31NK ，求D 点的速度。
答案：←=320ωr v D 提示：在图示瞬时，杆AB 瞬时平动，杆KN 的速度瞬心为点N 。
工程力学 第6章 刚体的基本运动
A
v M
M
刚体的基本运动
例 已知 O1A = O2B = l = 4cm， O1O2 = AB，曲柄 O1A 的转动规律：
工程力学
Engineering Mechanics
第6章 刚体的基本运动
刚体的基本运动
刚体运动的分类 工程中，刚体在运动过程中，会受到一定约束的限制， 根据约束条件不同，刚体的运动可以分为 平行移动、 基本刚体运动， 定轴转动、 复杂的运动可以看作这两种基本运动的合成。 平面运动、 定点运动、 以及最一般的运动。
刚体的基本运动
6.1 刚体的平移 刚体在运动过程中，其上任意一根直线始终与初始位置平行（或方位不变）， 刚体的这种运动称为平行移动，简称平移（或平动）。
浪木
直线行驶的汽车的车厢
发动机中的活塞
刚体的基本运动
6.1 刚体的平移
刚体平移时，具有如下特性： v
(1) 刚体上任意两点在同一时间间隔内的位移相等。 B
刚体的基本运动
6.2 刚体的定轴转动 定轴转动刚体上点 M 的运动之 运动方程： s 速度
大小： v s ω r sin ωr
方向： 圆的切线方向； ω, r
z
M0
s
M
r
O1
v ω
O
v ωr d r
dt
定轴转动刚体上任一点的速度等于刚体的角速度矢量与该点矢径的叉积。
刚体的基本运动
d
dt
为其大小，右手法则确定正负。
刚体的基本运动
6.2 刚体的定轴转动 刚体定轴转动的运动方程：
(t)
d d k ω k
dt dt
角速度矢量
α dω d k k
dt dt
刚体的自由度和平面平行运动
J
C
2
刚体的动能等于质心的平动动能与对质心的转动
动能之和。
刚体的平面平行运动
例题4-9 讨论一匀
y
N
质实心的圆柱体在斜
O
x
面上的运动。
fr r
解 圆柱体所受的力共有三个： 重力G ，斜面的支承力N 和
aCx
G=mg
摩擦力f r，如图所示。设圆柱体的质量为m，半径
为r，那么，它对其几何的转动惯量
JC
1 mR2 2
aC
F
联立以上四式，解得
刚体的平面平行运动
aC
2F(R l) 3mR
f R 2l F 3R
由此可见
l<r/2, f>0, 静摩擦力向后 l>r/2, f<0, 静摩擦力向前 l=r/2, f=0
刚体的平面平行运动
aC
2F(R l) 3mR
f R 2l F 3R
J 1 mr 2 2
刚体的平面平行运动
我们取和斜面平行而向下的方向为x轴的方向，和 斜面垂直而向上为y轴的方向
这样可得
maCx mg sin fr
maCy N mg cos J frr
以上三式中，aCx和aCy是圆柱体质心在x轴和y轴方
向的加速度，是圆柱体对其通过质心的几何轴转
车轮上任意一点的速度
v vC r
G点的速度
vG vC r 0
B点的速度
vB vC R 2vC
A点的速度
vA vC2 (R)2
RA
A
2vC
B
RB
RB
RA RG vC
7刚体的平面运动
7.2 求平面图形内各点速度的基点法 例题
例7-1 在图所示的曲柄连杆机构中，曲柄OA长r，连
杆AB长l，曲柄以匀角速度转动，当OA与铅垂线的 夹角 = 45时，OA正好与AB垂直，试求此瞬时AB杆
的角速度、AB杆中点C的速度及滑块B的速度。
返回首页
7.2 求平面图形内各点速度的基点法
选速度已知的点A为基点
而vDA ＝II·r2。
O
vDA
I
所以
II
vDA r2
0 (r1 r2 )
r2
以A为基点, 分析点B的速度。 vB vA vBA
II
vDA r2
0 (r1 r2 )
r2
vBA II BA 0 (r1 r2 ) vA
vBA与vA垂直且相等, 点B的速度
返回首页
7.3 求平面图形内各点速度的瞬心法 7.3.2 速度瞬心法
几点讨论
每瞬时平面图形上都存在唯一的速度瞬心。它可 位于平面图形之内，也可位于图形的延伸部分。 瞬心只是瞬时不动。在不同的瞬时，图形具有不 同的速度瞬心。即速度瞬心的速度等于零，加速度 并不等于零。 平面图形在其自身平面内的运动，也可以看成是 绕一系列的速度瞬心的转动。
返回首页
8.1 刚体平面运动的运动方程 绕基点转动的特点
基点不同转角相同
B
1 2
A
ω1 ω2
B
B
A
A
1 2
结论：任意瞬时，平面图形绕其平面内任意基 点转动的角速度与角加速度都相同。
返回首页
7.1 刚体平面运动的运动方程
讨论
选择不同的基点，平面图形随同基点平移的速度和 加速度不相同。 相对基点转动的角速度、角加速度与基点的选择无 关。于是可以直接称为平面运动的角速度和角加速度 今后标注平面图形的角速度和角加速度时，只需注 明它是哪个刚体的，不必注明它是相对于哪个基点。
点的合成运动刚体的平面运动
第一：传动机构中所有运动构件都作基本运动，且至少有两个运 动构件之间的接触点相对其中一个构件有相对运动时，采用点的 速度合成定理。 第二：传动机构中至少有一个运动构件作平面运动，且每两个运 动构件之间都是通过普通圆柱铰链连接的，采用平面运动的相关 方法。 第三：如果有运动构件作平面运动的，且存在运动构件之间接触 点相对一个运动构件的相对运动的，属于综合问题。
做出速度平行四边形, 如图示
ve va cos l cos 45
2 l()
2
小车的速度：v ve
vr
va
ve
[例] 曲柄肘杆压床机构 已知OA=0.15m , n=300r/min , AB=0.76m, BC=BD=0.53m。
图示位置时, AB水平求该位置时的 BD 、 AB 及 vD
解：轴O, 杆OC, 楔块M均作平动, 圆盘作平面运动，P为速度瞬心
vA v12 cm/s ,
vA/PA12/rcos 12/4cos302 3 rad/s
(） vo POrsin4sin302 34 3 m/s()
PB PO 2 OB 2 2 PO OB cos120 22 42 2 2 4 1 2 7m 2
解：OA,BC作定轴转动, AB,BD均作平面运动 根据题意：
n 300 10 rad/s
30 30 研究AB, P１为其速度瞬心
vA OA 0.15 10 1.5 m/s （ ）
AB
vA AP1
1.5
AB sin 60
1.5 2
0.76 3
7.16 rad/s
vB BP1 AB ABcos607.160.760.57.162.72 m/s
vB PB 2 72 34 2118.3 m/s ( PB)
做出速度平行四边形, 如图示
ve va cos l cos 45
2 l()
2
小车的速度：v ve
vr
va
ve
[例] 曲柄肘杆压床机构 已知OA=0.15m , n=300r/min , AB=0.76m, BC=BD=0.53m。
图示位置时, AB水平求该位置时的 BD 、 AB 及 vD
解：轴O, 杆OC, 楔块M均作平动, 圆盘作平面运动，P为速度瞬心
vA v12 cm/s ,
vA/PA12/rcos 12/4cos302 3 rad/s
(） vo POrsin4sin302 34 3 m/s()
PB PO 2 OB 2 2 PO OB cos120 22 42 2 2 4 1 2 7m 2
解：OA,BC作定轴转动, AB,BD均作平面运动 根据题意：
n 300 10 rad/s
30 30 研究AB, P１为其速度瞬心
vA OA 0.15 10 1.5 m/s （ ）
AB
vA AP1
1.5
AB sin 60
1.5 2
0.76 3
7.16 rad/s
vB BP1 AB ABcos607.160.760.57.162.72 m/s
vB PB 2 72 34 2118.3 m/s ( PB)
理论力学 第7章 刚体的平面运动
M4 ω
M2
C ωO
A
r
M1
M3
O R
解: OA绕O转动
v2
v4
M4
vA
ω A
r
M2 v3
C ωO
M1 Ⅱ M3
RO
Ⅰ
vA AC r OAO (R r) O
C点是齿轮II的速度瞬心
因此轮
II
的角速度
R r
r
O（逆时针）
所以轮 II 上 M1，M2 ，M3 和 M4 各点的速度分别为：
8
7.2 平面图形内各点速度的求法 1、基点法 通常把平面图形中速度为已知的点选为基点
平面图形内任一点的速度 =基点的速度与绕基点转动
速度的矢量和
9
y
例7.1 椭圆规尺的A端以速度vA沿x 轴的负向运动，
AB=l。
B
解：一、基点法
1、 AB 作平面运动
O
基点：A
2、 vB vA vBA
大小 ？ vA ?
vA AB ACv , vB AB BCv
得
vB
BCv ACv
vA
对三角形ABC应用正弦定理，可得
ACv
BCv
sin ( π ) sin ( )
2
注意到
，代入上式后得
B
x
vB
R0
sin ( ) cos
速度投影法
应用速度投影定理，有
vAcos vBcos
将v A = R ω ， α ＝90o -ψ - β ＝ψ
速度瞬心C必定在速度垂线上
速度垂线A N
速度瞬心C
vM vA vMA vM vA AM
v
v 0 AC A
第四章 刚体的平面运动
vB = vA cot ϕ
vA vBA = sin ϕ
vBA vA ωAB = = l l sin ϕ
例2 如图所示平面机构中，AB=BD= DE= l=300mm。在图示位置时，BD∥AE，杆AB的角速度为 ω=5rad/s。 求：此瞬时杆DE的角速度和杆BD中点C的速度。
解：1 、 BD作平面运动
2 2 vC = vB − vCB ≈1.299m s
方向沿BD杆向右
2、速度投影定理
由
r r r vB = vA + vBA
沿AB连线方向上投影
r r ( vB ) AB = ( vA ) AB
同一平面图形上任意两点的速度在这两点连线上 的投影相等。
例5 如图所示的平面机构中，曲柄OA长100mm， 以角速度ω=2rad/s转动。连杆AB带动摇杆CD，并拖 动轮E沿水平面纯滚动。已知：CD=3CB，图示位置 时A，B，E三点恰在一水平线上，且CD⊥ED。 求：此瞬时点E的速度。
由速度投影定理得
vB sin β = vC cos β
vC = vB tan β = rω0 tan β
圆轮瞬心在E 圆轮瞬心在E点
vA = vB = rω0
vC rω0 ωC = = tan β R R
§4-4 用基点法求平面图形内各点的加速度
A ：基点
Ax ' y '
：平移坐标系
r r rt rn aB = ae + ar + ar r r rt rn aB = aA + aBA + aBA
va= vB
ve= vA
vr= vAB
r r r v =v +v
B A
BA
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
?
? AB
? VBA ? l?
AB l
??
（）
例1
解二：速度投影法解 （1）以整体为研究对象 （2）做运动分析
OA杆做定轴转动 VA=ω*l 速度矢量图如图。
例1
（3）应用速度投影定理
vA ? vBcos?
解得：
vB ?
vA
cos?
?
l? ?
cos45?
2l?
(? )
? 速度投影法不能直接求出ωAB
刚体平面运动习题课
一、刚体平面运动问题解题思路 （1）取整体为研究对象 （2）作运动分析
各运动构件作什么运动? 画速度矢量图、作图求瞬心 （3）应用合成法、或速度投影法、或瞬心 法解
例1
已知：曲柄连杆机构OA=AB=l ，曲柄 OA以匀角速 ? 转动。 求：当? = 45o时, 滑块B的速度及AB 杆的角速度。
例3
解：（1）取整体为研究对象 （2）运动分析 AB 杆作刚体平面运动 圆柱也作刚体平面运动 C点为圆柱的瞬心 E点为AB杆的瞬心 速度及角速度如图所示。
例3
（3）速度瞬心法解
VA ? ? AB ? VD ? ? O
AE DE DC ΔADC 为等边三角形
DC ? DE ? 3R ? 3 ? 0.5 ? 0.866 m AE ? 3DC ? 3 ? 0.866 ? 1.5 m6 ? 4 rad / s 1.5
VD ? ? AB ?DE
?o
?
VD DC
?
?
AB ?DE DC
? ? AB ? 4 rad / s
答：杆的角速度为 4 rad/s （逆时针）。 圆柱的角速度为 4 rad/s （顺时针）。
R
VA ? 0
B
O
D
vO
ω
A
VB ? ? ?AB ? 2 V0
VC ? ? ?AC ? 2V0 VD ? ? ?AD ? 2 V0
例3
如图，杆AB靠在一半径为0.5m的圆柱上， 其一端A以匀速VA=6m/s 沿地面向右运动。 杆与圆柱间有足够的摩擦力带动圆柱向右滚 动，设圆柱与杆 及地面间均无滑动，求 图示位置时杆及圆柱的 角速度。
例1
解一：基点法解 （1）以B点为动点，
动系固结于A点 （2）做运动分析
OA杆做定轴转动， VA=ω*l，Va=VB，Ve=VA，Vr=VBA 速度矢量图如图
例1
（3）应用速度合成定理
VB ? VA ? VBA
VB
?
VA
cos?
?
l ??
cos 45?
? 2l? (? )
VBA ? VA ?tan? ? l ?? ?tan 45? ? l?
例1
解三：速度瞬心法解 （1）以整体为研究对象 （2）做运动分析
OA杆做定轴转动； 滑块B做直线运动； AB杆做平面运动， 其速度瞬心C如图所示。
例1
（3）应用瞬心法解
? ? vA ? ? AB ? vB
vA ? l? AC ? l BC ? 2l
? AB ?
vA ? AC
l ??
l
??
vB ? BC ?? AB ? 2l? (? )
例2
已知：半径为R的圆轮在直线轨道上滚而 不滑。轮心速度为V0 。求：轮缘上A、B、C、 D四点的速度。
C
B
O
D
vO
A
例2
解：
（1）以轮为研究对象
C
（2）做运动分析 圆轮做平面运动
B
O
D
vO
轮与地面接触点A为
ω
A
轮的速度瞬心。
例2
（3）应用瞬心法解
C
设轮的角速度为ω
由V0 ＝Rω 得到:
? ? V0 ,