理论力学课后习题答案 第6章 刚体的平面运动分析(2020年7月整理).pdf
理论力学简明教程第六章答案
第六章 分析力学滔滔长江东逝水，浪花淘尽英雄。
达朗贝尔，拉格朗日，哈密顿等许多前贤相聚于此“力学论剑”，其“冲击波”使非线性问题也不攻自破。
长江后浪推前浪，你或许在此能够加倍“忘乎因此‘。
微分方程将叱咤风云。
[要点分析与总结]1虚功原理：（平稳时）理想条件下，力学系的平稳条件是各质 点上的主动力所作的虚功之和为零：10ni i i W F r δδ==•=∑用广义坐标来表述：310n ii i x W F q q ααδδ=∂==∂∑ 2达朗贝尔原理（动力学下的虚功原理）： 1()0ni i i i i W F m r r δδ==-•=∑〈析〉r δ，W δ均是在时刻未转变（0dt =）时所假想的量，而广义坐标a q 能够是角度，长度或其它的独立的坐标变量。
3拉格朗日方程()d T TQ dt q q ααα∂∂-=∂∂ (1,2,3,,)a s =在保守力下，取拉氏数 L T V =-方程为：()0d L L dt q q αα∂∂-=∂∂ 假设拉氏数中L 不显含广义坐标q β，那么：0Lq β∂=∂ 即 循环积分： Lp const q ββ∂==∂ 4微振动非线性系统在小角度近似下，对拉氏方程的应用 5哈密顿函数与正那么方程 （1） 哈密顿函数1(,,)sH p q t L p q ααα==-+∑式中T Lp q q ααα∂∂==∂∂为广义坐标动量 （2） 正那么方程Hq P Hp q H Lt tαααα∂=∂∂=-∂∂∂=-∂∂ (1,2,3,,)a s =假设哈氏函数H 中不显含广义坐标q β，那么：0Hp q ββ∂=-=∂ 即：循环积分 Tp const q ββ∂==∂ 在稳固条件下（H 中不显含t ），12sp q T ααα==∑那么有能量积分：H T V =+6泊松括号1[,]()sG H G HG H q p p q ααααα=∂∂∂∂=-∂∂∂∂∑ 7哈密顿原理与正那么变换 （1）哈密顿原理保守力系下：210t t Ldt δ=⎰概念：21t t S Ldt =⎰为主函数（3） 正那么变换通过某种变数的变换，找到新的函数*H ，使正那么方程的形式不变（相当于坐标变换）。
理论力学课后习题答案-第6章--刚体的平面运动分析
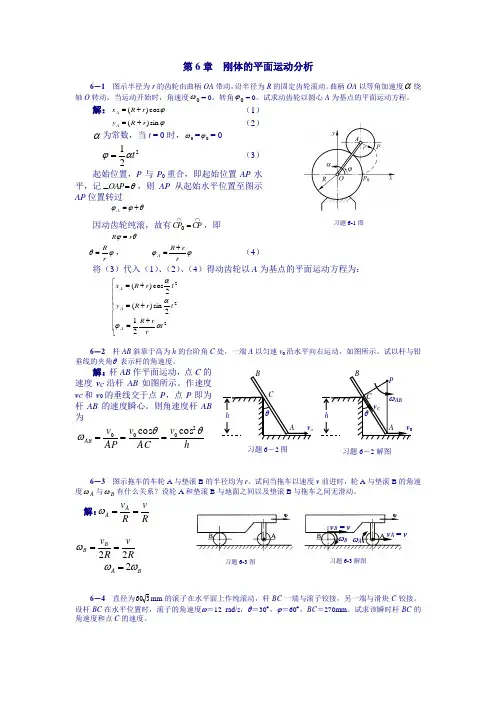
第6章 刚体的平面运动分析6－1 图示半径为r 的齿轮由曲柄OA 带动，沿半径为R 的固定齿轮滚动。
曲柄OA 以等角加速度α绕轴O 转动，当运动开始时，角速度0ω= 0，转角0ϕ= 0。
试求动齿轮以圆心A 为基点的平面运动方程。
解：ϕcos )(r R x A += （1） ϕsin )(r R y A +=（2）α为常数，当t = 0时，0ω=0ϕ= 0 221t αϕ=（3）起始位置，P 与P 0重合，即起始位置AP 水平，记θ=∠OAP ，则AP 从起始水平位置至图示AP 位置转过θϕϕ+=A因动齿轮纯滚，故有⋂⋂=CP CP 0，即 θϕr R = ϕθr R =， ϕϕrr R A += （4）将（3）代入（1）、（2）、（4）得动齿轮以A 为基点的平面运动方程为：⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=222212sin )(2cos )(t r r R t r R y t r R x A A A αϕαα6－2 杆AB 斜靠于高为h 的台阶角C 处，一端A 以匀速v 0沿水平向右运动，如图所示。
试以杆与铅垂线的夹角θ 表示杆的角速度。
解：杆AB 作平面运动，点C 的速度v C 沿杆AB 如图所示。
作速度v C 和v 0的垂线交于点P ，点P 即为杆AB 的速度瞬心。
则角速度杆AB 为6－3 图示拖车的车轮A 与垫滚B 的半径均为r 。
试问当拖车以速度v 前进时，轮A 与垫滚B 的角速度A ω与B ω有什么关系？设轮A 和垫滚B 与地面之间以及垫滚B 与拖车之间无滑动。
解：RvR v A A ==ωR v R v B B 22==ωB A ωω2=6－4 直径为360mm 的滚子在水平面上作纯滚动，杆BC 一端与滚子铰接，另一端与滑块C 铰接。
设杆BC 在水平位置时，滚子的角速度ω＝12 rad/s ，θ＝30︒，ϕ＝60︒，BC ＝270mm 。
试求该瞬时杆BC 的角速度和点C 的速度。
hv AC v AP v ABθθω2000cos cos ===习题6-1图ABCv 0hθ习题6－2图PωABv CABCv ohθ习题6－2解图习题6-3解图习题6-3图v A = vv B = v ωAωB习题6-6图习题6-6解图解：杆BC 的瞬心在点P ，滚子O 的瞬心在点D BDv B ⋅=ωBPBD BP v B BC ⋅==ωω ︒︒⨯=30sin 27030cos 36012 rad/s 8=PC v BC C ⋅=ωm/s 87.130cos 27.08=︒⨯=6－5 在下列机构中，那些构件做平面运动，画出它们图示位置的速度瞬心。
理论力学第6章 刚体的平面运动分析
于是，平面图形的平面运动分解为随同基点A的平移 （牵连运动）和绕基点A的转动（相对运动）。
刚体平面运动时 ，刚体上各点的轨迹 、速度与加速度各不 相同。 平移运动的轨迹
、速度和加速度随基
点选取的不同而不同 。
平面运动的转动角速度以及角加速度 都与基点的位置无关
＝ lim
1 2 lim t 0 t t 0 t
A
vA
AC ＝
0
vA
瞬时速度中心的概念－速度瞬心的特点
y´
vC A
P
S
0
C
1. 瞬时性－不同的瞬时， 有不同的速度瞬心； 2. 唯一性－某一瞬时只 有一个速度瞬心；
vA
x´
vA
A
3. 瞬时转动特性－平面图 形在某一瞬时的运动都可以视 为绕这一瞬时的速度瞬心作瞬 时转动.
应用瞬时速度中心确定刚体平面 运动的速度 —— 速度瞬心法
瞬时速度中心法
瞬时速度中心的概念 应用瞬时速度中心确定刚体平面 运动的速度 —— 速度瞬心法 几种特殊情形下瞬时速度中心位 置的确定
瞬时速度中心的概念
y´
P
vA
平面图形S上的基点A，基点 速度vA ,平面图形角速度 0 。 过A点作vA的垂直线PA，P A上各点的速度由两部分组成：
S
应用瞬时速度中心确定刚体平面 运动的速度 —— 速度瞬心法
刚体平面运动实例
刚体平面运动实例
刚体平面运动实例
刚体平面运动实例
刚体平面运动实例
刚体平面运动实例
刚体的平面运动—— 刚体上处于同一平面内 各点到某一固定平面的距离保持不变。
前面研究了点的复合运动。这里研究刚体 的平面运动。刚体的平面运动可以看做与点的 复合运动相对应。是两个典型代表对象的典型 复合运动。
理论力学第6章答案
环 量 为 Γ ， 则 根 据 多 连 通 域 的 斯 托 克 斯 定 理 有 ： Γ − Γ( 0 , 0 ) =
∫∫ Ω dA = 0 ， 即
z
Γ = Γ( 0, 0) = 2πC
6-8
Q圆r = a1 , r = a2是流线 ∴圆r = a1 , r = a2上的流体速度沿切向方向
即 r = a1时，υθ = υ0，υ r = 0；r = a2时，υθ = 0，υr = 0
Ω=
6-9
π (a − a )
2 2 2 1
Γa2 − Γa1
=
0 − 2πa1υ0 2a υ = 2 1 02 2 2 π (a2 − a1 ) a1 − a2
由单连通域的斯托克斯定理可知： Γ k3 = 0 ， Γ k4 = ΩA = 2π r
2 0
ω
k2 ，k4 所在为多连通域，由多连通域的斯托克斯定理可知： Γ k1 − Γ a = 0 ，所以
Γ k1 = Γ a = 2π a 2ω Γ k4 = ΩA = 2π r02ω
Γ k2 = Γ AB + Γ Bo + Γ oC + ΓCD + Γ DA = Γ AB + Γ Bo + Γ oC + ΓCD + Γ DA + Γ BC − Γ BC = Γ AB + Γ Bo + Γ oC + ΓCD + Γ DA + Γ BC + ΓCB = (Γ AB + Γ BC + ΓCD + Γ DA ) + (Γ Bo + Γ oC + ΓCB ) 1 2 π a 2ω = 0 + π a 2ω = 4 2
理论力学习题集
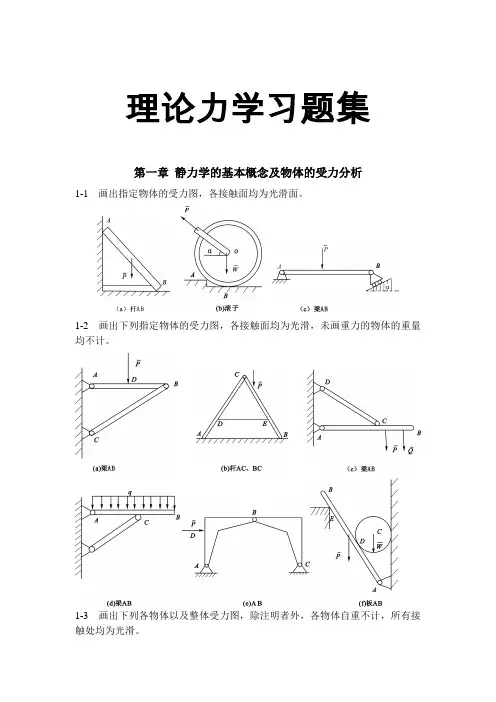
理论力学习题集第一章静力学的基本概念及物体的受力分析1-1 画出指定物体的受力图，各接触面均为光滑面。
1-2 画出下列指定物体的受力图，各接触面均为光滑，未画重力的物体的重量均不计。
1-3 画出下列各物体以及整体受力图，除注明者外，各物体自重不计，所有接触处均为光滑。
(a) (b)(c) (d)(e) (f)第二章平面一般力系2-1 物体重P=20kN，用绳子挂在支架的滑轮B上，绳子的另一端接在铰车D 上，如图所示。
转动铰车，物体便能升起，设滑轮的大小及滑轮转轴处的摩擦忽略不计，A、B、C三处均为铰链连接。
当物体处于平衡状态时，试求拉杆AB和支杆CB所受的力。
2-2 用一组绳悬挂重P=1kN的物体，求各绳的拉力。
2-3 某桥墩顶部受到两边桥梁传来的铅直力P1=1940kN，P2=800kN及制动力T=193kN，桥墩自重W=5280kN，风力Q=140kN。
各力作用线位置如图所示，求将这些力向基底截面中心O简化的结果，如能简化为一合力，试求出合力作用线的位置。
2-4 水平梁的支承和载荷如图所示，试求出图中A、B处的约束反力。
2-5 在图示结构计算简图中，已知q=15kN/m，求A、B、C处的约束力。
2-6 图示平面结构，自重不计，由AB、BD、DFE三杆铰接组成，已知：P=50kN，M=40kN·m，q=20kN/m，L=2m，试求固定端A的反力。
图2-6 图2-72-7 求图示多跨静定梁的支座反力。
2-8 图示结构中各杆自重不计，D、E处为铰链，B、C为链杆约束，A为固定端，已知：q G=1kN/m，q=1kN/m，M=2kN·m，L1=3m，L2=2m，试求A、B、C 处约束反力。
图2-8 图2-92-9 支架由两杆AO、CE和滑轮等组成，O、B处为铰链，A、E是固定铰支座，尺寸如图，已知：r=20cm，在滑轮上吊有重Q=1000N的物体，杆及轮重均不计，试求支座A和E以及AO杆上的O处约束反力。
理论力学练习册及答案(南华版)
动系固连摇杆CB上，定系固连机架。
由速度合成定理 作速度平行四边形。
B点速度为：
由加速度合成定理 作加速度图。
取 方向投影，得：
B点加速度为：
7-4.半径为R的半圆形凸轮以匀速V0沿水平线向右平动，带动顶杆AB沿铅直方向运动，当OA与铅直线夹角为300时，求此时杆AB的速度和加速度。
解：动点取杆OA上A点，动系固连杆O1C上，定系固连机架。
由速度合成定理 作速度平行四边形。
由加速度合成定理 作加速度图。
取 方向投影，得：
再取动点杆O1C上C点，动系固连套筒B上，定系固连机架。
由速度合成定理 作速度平行四边形。
由加速度合成定理:
作加速度图。
取 方向投影，得：
取 方向投影，得：
第八章 刚体平面运动
分别取节点A、B为研究对象，受力如图
对于节点A： ，
(压)
对于节点B： , (压)
2-11.计算桁架中1、2、3杆的受力。
解：取I-I剖面右边部分为研究对象，受力如图。
,
(拉)
,
(压)
研究节点B: ，
(压)
第三章 空间力系
3-1.图示正立方体，各边长为a，四个力F1、F2、F3、F4大小皆等于F，如图所示，作用的相应的边上。求此力系简化的最终结果，并在图中画出。
8-7.四杆机构中，曲柄OA以匀角速度ω0=25 rad/s绕O轴转动，OA=50 cm，AB=100 cm，O1B= cm。求∠OAB=900时，B点的加速度，摇臂O1B的角速度和角加速度。
8-8.图示机构中，设当OA与水平线成450角的瞬时，曲柄OA有反时针方向的匀角速度ω＝25 rad/s，连杆AB水平，扇形板BD铅垂。求扇形板绕定轴D转动的角加速度ε。
理论力学答案
三、b)c) CD 是二力杆，A 是固定绞支座d) DC 是二力杆，A 是固定绞支座e ) BC 是二力杆，A 处是固定绞支座f ) CD 是二力杆，A 处是固定绞支座特别需要强调的是：1) 无论是单个刚体还是整体，受力图都必须去掉约束。
根据定义，受力图是在分离体上画出全部外力的图形。
而分离体的定义则是：解除了约束的研究对象。
分离体必须用规、矩画，但不必完全如原图一样，只需画成相似的简图即可。
2) 有关作用力与反作用力的问题：AyF Ax F 'C F CDF AyF AxF DF CF BFAyF AxF CF 'AyF AxF BF CF 'AyF Ax F DF AyF AxF DF CF AF FCF 或AyF AxF C 'F AyF AxF DF DF CF AF B F TFa ) 习惯上，先找出二力杆，并标示一约束反力(如F D ，将其认为是作用力)。
在另一受力图上的相联点(如D 点)，然后根据作用力与反作用力定律确定的约束反力当作反作用力，标示为F'D 。
其中，符号 ' 是为了表示它是F D 的反作用力。
所以，它是有确切含义的。
标注符号时，要注意先后顺序，先确定的约束反力不标注 ' 符号，后确定的约束反力一定要标注符号 ' 。
两者必须成对、反向画。
b ) 为了明确地表示两者的作用力与反作用力关系，两个力的下脚标必须一致，如上述的D 。
不能随手写其它符号，以免产生误解。
下脚标通常用该点的符号表示，不宜象中学物理中那样，标示成数字。
3) 整体受力图一般最后画，整体受力图上的约束反力，应该与各单个刚体上已经画出的约束反力方向一致，以免产生岐义。
一、b ) k 点是光滑面约束，A 是光滑铰链，B 、O 是固定铰支座。
c ) 先确定斜杆(标注为DE )是二力杆，A 是固定绞支座，B 是可动绞支座。
BC 杆带铰，C 铰与AC 杆上C 孔铰接，力F 作用在铰上。
理论力学第六章习题答案
解 y x
a
A 动系圆环
a a = a rn + a en + a k
a ay = −rω 2 − 3rω 2 − 2rω 2 = −6rω 2 a ax = 0
B 动系圆环
a a = a rn + aen + a k
y x b y x
e a ay = −a n ( 2 / 5 ) = − 2 rω 2
o
曲柄长 OA = r
并以匀角速度 ω 绕 O 轴转动
o
装在水平
杆上的滑槽 DE 与水平线成 60 角 杆 BC 的速度
试求当曲柄与水平轴的交角分别为 ϕ = 0
30o 时
解
以 A 为动点
以 BC 杆为动系 有
va = ve + vr
在 ϕ = 0° 时 矢量右如图
υ BC = v e =
3 3 va = ωr 3 3
a a = a an + a at = a e + a rt + a rn + a c
式中各矢量如图 把各矢量分别向 x 方向和 y 方向投影得:
a an cos 60° + a at cos 30° = − a e cos 30° − a r cos 30° + a c cos 60° − a rn cos 60° a at sin 30° − a an sin 60° = − a e sin 30° + a rt sin 30° + a c sin 60° − a rn sin 60°
齿 条 又 带 动 半 径 为 0.1m 的 齿 轮 D 绕 固 定 轴 O1 转 动
ω = 5rad/s
理论力学课后习题部分答案
B
A FAC FBA
P
(l)
(l1)
(l2)
(l3)
图 1-1
1-2 画出下列每个标注字符的物体的受力图。题图中未画重力的各物体的自重不计，所 有接触处均为光滑接触。
(a)
B
FN1
C
FN 2
P2 P1
FAy
A
FAx
(a2)
(b)
FN1
A
P1
FN
(b2)
C
FN′
P2
(a1)
B
FN1
FN 2
FN
P1
F Ay
FCy
FAx (f2)
C FC′x
FC′y F2
FBy
FBx B (f3)
FAy A FAx
FB
C B
(g)
FAy
FAx A
D FT C FCx
(g2)
FB
B
F1
FB′ B
FAy
A
FAx
(h)
(h1)
P (g1)
FC′y
FT
C
FC′x
P (g3)
D
FCy
FB
F2
C FCx
B
(h2)
A FAx
FAy
FCy
D FAy
A
FAx
(k3)
6
FB
F1
FB′
B B
FD D
(l) FD′ D
A FA
(l1) F2
C
FC (l2)
F1
D
F2
B
A
E
FE
FA
(l3) 或
F1
FB′
2024年中科大理论力学课后习题答案
注意事项
在使用课后习题答案时，学生需要注意以下几点：一是不要完全依赖答案，要 注重自己的思考和总结；二是要注意答案的适用范围和条件，避免盲目套用； 三是要及时反馈和纠正答案中的错误或不足之处。
2024/2/29
6
02 质点与刚体运动 学
2024/2/29
7
质点运动学基本概念
质点的定义
质点是一个理想化的物理模型，忽略 物体的形状和大小，只考虑其质量。
2024/2/29
02
答案
根据牛顿第二定律，合外力$F_{ 合}=ma$，则合外力做的功 $W_{合}=F_{合}l=mal$，其中 $l=v_{0}t+frac{1}{2}at^{2}$为 物体在t时间内的位移。功率 $P_{合}=F_{合}v=mav$，其中 v为物体在t时刻的瞬时速度， $v=v_{0}+at$。
15
实际应用举例及拓展
2024/2/29
01
应用一
汽车行驶过程中的动力学分析。汽车行驶时受到发动机的动力、地面的
摩擦力和空气阻力等作用，通过动力学分析可以优化汽车的设计和行驶
性能。
02
应用二
航空航天领域的动力学问题。航空航天领域涉及大量的动力学问题，如
火箭发射、卫星轨道计算等，需要运用动力学原理进行精确分析和计算
03 题目2
一轻绳跨过定滑轮，两端分别系 有质量为m1和m2的物体，且 m1>m2，开始时两物体均静止 ，当剪断轻绳后，求两物体的加 速度和速度变化。
25
04
答案
剪断轻绳后，两物体均做自由落 体运动，加速度均为g。由于两 物体初始时刻均静止，因此速度 变化量相同，即$Delta v=gt$， 其中t为物体下落的时间。
理论力学课后习题及答案解析..
第一章习题4-1．求图示平面力系的合成结果，长度单位为m。
解：(1) 取O点为简化中心，求平面力系的主矢：求平面力系对O点的主矩：(2) 合成结果：平面力系的主矢为零，主矩不为零，力系的合成结果是一个合力偶，大小是260Nm，转向是逆时针。
习题4－3．求下列各图中平行分布力的合力和对于A点之矩。
解：(1) 平行力系对A点的矩是：取B点为简化中心，平行力系的主矢是：平行力系对B点的主矩是：向B点简化的结果是一个力R B和一个力偶M B，且：如图所示；将R B向下平移一段距离d，使满足：最后简化为一个力R，大小等于R B。
其几何意义是：R的大小等于载荷分布的矩形面积，作用点通过矩形的形心。
(2) 取A点为简化中心，平行力系的主矢是：平行力系对A点的主矩是：向A点简化的结果是一个力R A和一个力偶M A，且：如图所示；将R A向右平移一段距离d，使满足：最后简化为一个力R，大小等于R A。
其几何意义是：R的大小等于载荷分布的三角形面积，作用点通过三角形的形心。
习题4-4．求下列各梁和刚架的支座反力，长度单位为m。
解：(1) 研究AB杆，受力分析，画受力图：列平衡方程：解方程组：反力的实际方向如图示。
校核：结果正确。
(2) 研究AB杆，受力分析，将线性分布的载荷简化成一个集中力，画受力图：列平衡方程：解方程组：反力的实际方向如图示。
校核：结果正确。
(3) 研究ABC，受力分析，将均布的载荷简化成一个集中力，画受力图：列平衡方程：解方程组：反力的实际方向如图示。
校核：结果正确。
习题4-5．重物悬挂如图，已知G=1.8kN，其他重量不计；求铰链A的约束反力和杆BC所受的力。
解：(1) 研究整体，受力分析（BC是二力杆），画受力图：列平衡方程：解方程组：反力的实际方向如图示。
习题4-8．图示钻井架，G=177kN，铅垂荷载P=1350kN，风荷载q=1.5kN/m，水平力F=50kN；求支座A的约束反力和撑杆CD所受的力。
刚体的平面运动动力学课后答案
其中： 是从速度瞬心 引向M点的矢径， 为平面图形的角速度矢量。
4、平面图形上各点的加速度
基点法公式：
（7－9）
其中： 。基点法公式建立了平面图形上任意两点的加速度与平面图形的角速度和角加速度间的关系。只要平面图形的角速度和角加速度不同时为零，则其上必存在唯一的一点，其加速度在该瞬时为零，该点称为平面图形的加速度瞬心，用 表示。
(b)
再根据对固定点的冲量矩定理：
系统对固定点A（与铰链A重合且相对地面不动的点）的动量矩为滑块对A点的动量矩和AB杆对A点的动量矩，由于滑块的
动量过A点，因此滑块对A点无动量矩，AB杆对A点的动量矩（也是系统对A点的动量矩）为：
将其代入冲量矩定理有：
(c)
由（a,b,c）三式求解可得：
(滑块的真实方向与图示相反)
其中：aK表示科氏加速度；牵连加速度就是AB杆上C点的加速度，即：
将上述公式在垂直于AB杆的轴上投影有：
科氏加速度 ，由上式可求得：
3-14：取圆盘中心 为动点，半圆盘为动系，动点的绝对运动为直线运动；相对运动为圆周运动；牵连运动为直线平移。
由速度合成定理有：
速度图如图A所示。由于动系平移，所以 ，
根据点的复合运动速度合成定理有：
其中： ，根据几何关系可求得：
AB杆作平面运动，其A点加速度为零，
B点加速度铅垂，由加速度基点法公式可知
由该式可求得
由于A点的加速度为零，AB杆上各点加速度的分布如同定轴转动的加速度分布，AB杆中点的加速度为：
再取AB杆为动系，套筒C为动点，
根据复合运动加速度合成定理有：
3－25设板和圆盘中心O的加速度分别为
，圆盘的角加速度为 ，圆盘上与板
清华理论力学课后答案6
vE 10 = 3 = 5.77 rad/s ， CE 3
r3 = r1 + 2r2 ，可得轮 1 的角速度 v r +r （顺时针） ω1 = M = 1 2 ω4 = 12ω4 ， r1 r1
轮 1 的转速为 （顺时针）. n1 = 12n4 = 10800 r/ min ，
kh da
习题解答
作图示几何关系，图中 v A = v ，解得
解法二：在直角三角形△ACO 中，
sin ϑ =
̇ cosϑ = − R x ̇ ϑ x2 ̇ = v, x = R sin ϑ ，解得 AB 杆的角速度为 其中， x
2 ̇ = − sin ϑ v ， ϑ cos ϑ R （负号表示角速度转向与 ϑ 角增大的方向相反，即逆时针）
（d） (e) =
再选定销钉 B 为动点，摇杆为动系，如图（c） ，有
a B = aen + aet + ar + ac
由式（d）,(e)得 大小： 方向： 向 BO 轴上投影 解出 ae = aBO − ac ，于是摇杆的角加速度为
τ n
a
n BO
a
n e
+
a
t e
+
a r + ac
？
2 RωO
O1B ⋅ ω 2 O1
其中 ae = aC′ = a A + a 大小: 方向: ？ √
t c ′A
答
aB
=
aA
案
+
网
杆的角速度为 ω AB =
vA = 1 rad/s ，而 C 点的牵连速度为 C AB A
t a BA
+
《理论力学》课后习题解答(赫桐生版)
理论力学（郝桐生）第一章习题1-1．画出下列指定物体的受力图。
解：习题1-2．画出下列各物系中指定物体的受力图。
解：习题1-3．画出下列各物系中指定物体的受力图。
解：第二章习题2-1．铆接薄钢板在孔心A、B和C处受三力作用如图，已知P1=100N沿铅垂方向，P2=50N沿AB方向，P3=50N沿水平方向；求该力系的合成结果。
解：属平面汇交力系；合力大小和方向：习题2-2．图示简支梁受集中荷载P=20kN，求图示两种情况下支座A、B的约束反力。
解：(1)研究AB，受力分析：画力三角形：相似关系：几何关系：约束反力：(2) 研究AB，受力分析：画力三角形：相似关系：几何关系：约束反力：习题2-3．电机重P=5kN放在水平梁AB的中央，梁的A端以铰链固定，B端以撑杆BC支持。
求撑杆BC所受的力。
解：(1)研究整体，受力分析：(2) 画力三角形：(3) 求BC受力习题2-4．简易起重机用钢丝绳吊起重量G=2kN的重物，不计杆件自重、磨擦及滑轮大小，A、B、C三处简化为铰链连接；求杆AB和AC所受的力。
解：(1) 研究铰A，受力分析（AC、AB是二力杆，不计滑轮大小）：建立直角坐标Axy，列平衡方程：解平衡方程：AB杆受拉，BC杆受压。
(2) 研究铰A，受力分析（AC、AB是二力杆，不计滑轮大小）：建立直角坐标Axy，列平衡方程：解平衡方程：AB杆实际受力方向与假设相反，为受压；BC杆受压。
习题2-5．三铰门式刚架受集中荷载P作用，不计架重；求图示两种情况下支座A、B的约束反力。
解：(1) 研究整体，受力分析（AC是二力杆）；画力三角形：求约束反力：(2) 研究整体，受力分析（BC是二力杆）；画力三角形：几何关系：求约束反力：习题2-6．四根绳索AC、CB、CE、ED连接如图，其中B、D两端固定在支架上，A端系在重物上，人在E点向下施力P，若P=400N，α=4o，求所能吊起的重量G。
解：(1) 研究铰E，受力分析，画力三角形：由图知：(2) 研究铰C，受力分析，画力三角形：由图知：习题2-7．夹具中所用的两种连杆增力机构如图所示，书籍推力P作用于A点，夹紧平衡时杆AB与水平线的夹角为；求对于工件的夹紧力Q和当α=10o时的增力倍数Q/P。
(完整word版)刚体的平面运动作业习题参考答案1
8-1 图示四杆机构1OABO 中，AB B O OA 211==；曲柄OA 的角速度s rad /3=ω。
求当090=ϕ而曲柄B O 1重合于1OO 的延长线上时，杆AB 和曲柄B O 1的角速度。
参考答案：因OA 杆作定轴转动，故OA v A ⋅=ω。
AB 杆做平面运动其速度瞬心为O 点，s rad OAv AAB /3===ωω，而OA OB v AB B ⋅=⋅=ωω3， 所以s rad s rad BO OAB O v B B O /2.5/3333111≈==⋅==ωωω（逆时针）8-2 四连杆机构中，连杆AB 上固联一块三角板 ABD 。
机构由曲柄A O 1带动。
已知：曲柄的角速度s rad A O /21=ω；曲柄cm A O 101=，水平距离cm O O 521=；AD=5cm ,当A O 1铅垂时，AB 平行于21O O ，且AD 与1AO 在同一直线上；角030=ϕ。
求三角板ABD 的角速度和D 点的速度。
参考答案：三角板 ABD C ，由此可得：s rad ctg O O AO AO AC v A O A/07.121111=⋅+⋅==ϕωωs cm CD v D /35.25=⋅=ω8-7 如图所示，在振动机构中，筛子的摆动由曲柄连杆机构所带动。
已知曲柄OA 的转速cm OA r n 30min,/40==。
当筛子BC 运动到与点O 在同一水平线上时，090=∠BAO ，求此瞬时筛子BC 的速度。
解：由图示机构知BC 作平行移动，图示位置时，B v 与CBO 夹角为30°，与AB 夹角为60°。
Av Bv Dv Av CωAv Bv由题意知 m/s π40.030.03040π=⨯⨯=⋅=OA v A ω 由速度投影定理 AB B AB A v v )()(= 得 ︒=60cos B A v vm/s 2.51π8.060cos ==︒==AB BC v v v8-6 图示机构中，已知cm EF cm DE cm BD cm OA 310,10,10,10==== OA ωs rad /4=，在图示位置，曲柄OA 与水平线OB 垂直，且B 、D 和F 在同一铅直线上。
理论力学_第06章_刚体的平面运动分析_4 (NXPowerLite)
vB= vA+ vBA
x´ 其中， B点相对速度(定轴转动线速度)：
(B点绕A点 作定轴转动)
vBA = ω ×rB
任意点的速度 = 基点绝对速度 + B点相对速度 (矢量和)
速度分析： 速度投影法
速度投影定理法：
用速度投影定理分析平面 图形上点的速度的方法
vBA vB
B
rAB B vA A A vA
定轴转动
曲柄滑块机构
直线平移
刚体平面运动的模型简化
刚体平面运动： 刚体上处于同一平面内的各点到固定平面的
距离保持不变 运动轨迹在各平面内
S2面内：
S和A点到S1面的距离相同，S点相对A 点转动或静止（两点间距固定，不可
能相对平动；二者可同时平动）；
面内各点运动可由SA直线的运动代表
A1A2线上：
yP
r2 (l-l1) l
sin ωt
平面运动分解（平移+转动）
在t内，平面图形由位置I运动到Ⅱ， 线段从AB运动到A´B´
A点处地安放平移坐标系，其原点A称为基 点。
由平面运动方程可见: A点固定不动，刚体作定轴转动 线段AB方位不变（=常数），刚体作平移
平面运动分解为随基点A的平移（牵连运动）和绕基点A的转动（相对运动）
B 速度分析： 瞬时速度中心法
rAB B A A vA
vA
vB= vA+ vBA vBA = ω ×rB
瞬时速度中心的概念
只有vA和vBA共线时, 合速度才可能为0
y’ vCA
P
C
S
vA
0 A
vA
过A点作vA的垂直线PA，PA上各点的速度由两
理论力学习题解答(第六章)
6－1在图示四连杆机构中，已知：匀角速度O ω，OA =B O 1=r 。
试求在°=45ϕ且AB ⊥B O 1的图示瞬时，连杆AB 的角速度AB ω及B 点的速度。
解：连杆AB 作平面运动，由基点法得BA A B v v v +=由速度合成的矢量关系，知φcos v A BA =v杆AB 的角速度)(/AB /O BA AB 2122+==ωωv （逆时针）B 点的速度2245/r cos v O A B ω=°=v （方向沿AB ）6－2. 在图示四连杆机构中，已知：3.021===L B O OA m ，匀角速度2=ωrad/s 。
在图示瞬时，11==L OB m ，且杆OA 铅直、B O 1水平。
试求该瞬时杆B O 1的角速度和角加速度。
解：一．求1ω60230..OA v A =×=⋅=ω m/s取A 为基点，则有BA A B v v v += 得 23.0/6.0ctg v v A B ===ϕ m/sm09.2)3.01()3.0/6.0(sin /v v 2/122A BA =+×==ϕ杆B O 1的角速度67630211../BO /v B ===ω rad/s 顺时针 二．求1ε取点A 为基点，则有n BA A a a a a a ++=+ττBA nB B将上式向X 轴投影21222857s /m .B O /ctg v )sin AB /v (OA ctg a )sin /a (a a a sin a cos a sin a BBA n B n BA A B nBA A n B B +=⋅+⋅+⋅−=++−=−=+−ϕϕωϕϕϕϕϕττ杆B O 1的角加速度7.1923.0/8.57/11===B O a B τεrad/s 2逆时针6－3.图示机构中，已知：OA =0.1m ， DE =0.1m ，m 31.0=EF ，D 距OB 线为h=0.1m ；rad 4=OA ω。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
而曲柄 O1B 重合于 OO1 的延长线上时，杆 AB 和曲柄 O1B 的角速度。
解：杆 AB 的瞬心在 O
AB
=
vA OA
=
=
3 rad/s
vB = 3l
O1B
= vB l
=
3 = 5.2 rad/s
6－7 绕电话线的卷轴在水平地面上作纯滚习动题，6线-6 图上的点 A 有向右的速度 vA= 0.8m/s，试求卷轴中心 O 的速度与卷轴的角速度，并问此时卷轴是向左，还是向右方滚动？
解：杆 AB 作平面运动，点 C 的
B
速度 vC 沿杆 AB 如图所示。作速度
B P
vC 和 v0 的垂线交于点 P，点 P 即为
C
杆 AB 的速度瞬心。则角速度杆 AB
为
h
C
AB
vC
h
AB
=
v0 AP
=
v0 cos AC
=
v0 cos2 h
A vo 习题 6－2 图
A v0 习题 6－2 解图
6－3 图示拖车的车轮 A 与垫滚 B 的
vA
B vB C
vA = O 2r = 20 2 m/s
AB
=
vA AP
=
20 2 sin 45 1.5 cos
= 10 2 =14.1 rad/s
A v1
v2 = vO − Or
O
解得：
vO
=
v1
+ v2 2
O
=
v1 − v2 2r
B v2
习题 6－8 图
习题 6-7 图
一齿轮，其半径为
A v1
O
O
vO
B v2
习题 6－8 解图
6－9 曲柄－滑块机构中，如曲柄角速度 = 20rad/s，试求当曲柄 OA 在两铅垂位置和两水平位置时
配汽机构中气阀推杆 DE 的速度。已知 OA = 400mm，AC = CB = 200 37 mm。
O
vC E
A
C
vD
=
v DE D
(a)
B
=
0°时，图（b）， vC
=
1 2
vA
（↑）
此时 CD 杆瞬时平移
E
vDE
= vD
= vC
=
1 2
vA
=
4 m/（↑）
同理 = 180°时，vDE = 4m/s（↓）
(b) 习题 6－9 解图
6－10 杆 AB 长为 l = 1.5 m，一端铰接在半径为 r = 0.5 m 的轮缘上，
第 6 章 刚体的平面运动分析 6－1 图示半径为 r 的齿轮由曲柄 OA 带动，沿半径为 R 的固定齿轮滚动。曲柄 OA 以等角加速度 绕
轴 O 转动，当运动开始时，角速度 0 = 0，转角 0 = 0。试求动齿轮以圆心 A 为基点的平面运动方程。
解： xA = (R + r) cos
（1）
yA = (R + r) sin
（4）
将（3）代入（1）、（2）、（4）得动齿轮以 A 为基点的平面运动方程为：
x
A
=
(R
+ r) cos
2
t2
y
A
=
(R
+
r) sin
2
t2
A
=
1 2
R + r t 2 r
6－2 杆 AB 斜靠于高为 h 的台阶角 C 处，一端 A 以匀速 v0 沿水平向右运动，如图所示。试以杆与铅
垂线的夹角 表示杆的角速度。
设杆 BC 在水平位置时，滚子的角速度＝12 rad/s，＝30，＝60，BC＝270mm。试求该瞬时杆 BC 的
角速度和点 C 的速度。
解：杆 BC 的瞬 心在点 P，滚子 O 的瞬心在点 D
vB = BD
B
C
P
BC
vB
B
C
O
1
O
vC
习题 6-4 图
D
习题 6-4 解图
BC
=
vB BP
半径均为 r。试问当拖车以速度 v 前进时，轮 A 与垫滚 B 的角速度 A 与 B 有什么关系？设轮 A 和垫滚 B
与地面之间以及垫滚 B 与拖车之间无滑动。
解
：
A
=
vA R
=
v R
B
=
vB 2R
=
v 2R
习题 6-3 图
vB = v B A
习题 6-3 解图
vA = v
A = 2B
6－4 直径为 60 3 mm 的滚子在水平面上作纯滚动，杆 BC 一端与滚子铰接，另一端与滑块 C 铰接。
vA
A
C
B
解：OA 定轴 习题 6－9 图
90o vC
转动；AB、CD 平面运动O，DE 平移。 vB
1．当 = 90°，270°时，OA 处于铅垂位置，图
vA
D
（a）表示 = 90°情形，此时 AB 瞬时平移，vC 水平，
而 vD 只能沿铅垂， D 为 CD 之瞬心
vDE = 0 同理， = 270°时，vDE = 0 2． = 180°，0°时，杆 AB 的瞬心在 B
解：如图
O
=
vA 0.9 − 0.3
=
0.8 0.6
= 1.333 rad/s
vO
= 0.9O
= 0.9 8 6
= 1.2 m/s
2
卷轴向右滚动。
6－8 图示两齿条以速度 v1 和 v 2 作同方向运动，在两齿条间夹
r，求齿轮的角速度及其中心 O 的速度。
解：如图，以 O 为基点：
v1 = vO + Or
=
BD BP
= 12 60 3 cos30 270sin 30
= 8 rad/s
vC = BC PC
= 8 0.27cos30 = 1.87 m/s
6－5 在下列机构中，那些构件做平面运动，画出它们图示位置的速度瞬心。
D
A
B
A
AC
O1
C
A
O
O
BB
D
O
O1
习题 6-5 图
解：图（a）中平面运动的瞬心在点 O，杆 BC 的瞬O心在点 C。 O
图（b）中平面运动的杆 BC 的瞬心在点 P，杆 AD 做瞬时平移。
BC D
vA A
A
O1 O
O
vB
BB
vC C
D
习题 6-5 解图
1
vA A
A
O
2
vD vAB AB
D
vC
BC
C
AB
D
l
2l
B
O 5
O1 B
O1
B
O1
O
O 习题 6-6 解图
(a)
(b)
1
2
P
6－6 图示的四连杆机械 OABO1 中，OA = O1B = 1 AB，曲柄 OA 的角速度 = 3rad/s。试求当示。 = 90° 2
为常数，当 t = 0 时， 0 = 0 = 0
（2）
= 1 t2 2
（3）
起始位置，P 与 P0 重合，即起始位置 AP 水 平，记 OAP = ，则 AP 从起始水平位置至图示
AP 位置转过
A = +
因动齿轮纯滚，故有
CP0
=
CP
，即
习题 6-1 图
R = r
= R ，
r
A
=
R+r r
另一端放在
水平面上，如图所示。轮沿地面作纯滚动，已知轮心 O 速度的大小为 vO = 20 m/s。试求图示瞬时（OA 水
平）B 点的速度以及轮和杆的角速度。
解：轮 O 的速度瞬心
为点 C ，杆 AB 的速度瞬
心为点 P
O
=
vO r
=
20 0.5
= 40 rad/s
B
O vO A
O O vO A
A
A