理论力学 刚体平面运动速度分析
理论力学：刚体平面运动的运动学 (2)
2020/12/9
3
理论力学
§7-1 刚体平面运动的运动学
三、平面图形上各点的加速度
y 动 系：Ax’y’
y' aBt A
动 点：刚体上的B点 牵连运动：平移
B
A
aBnA x'
相对运动：圆周运动
o
aA x
aa ae arn art
ae aA,
an r
an BA
,
at r
at BA
aBt A AB ,
vA vB u AB 0
2、求加速度： 研究AB 杆
aB
aA
aBnA
aBt A
a
t BA
aBt
aBn
上式在铅垂轴上投影： aBt A cos
aBn
u2 L
u
上式在水平轴上投影： aBt A sin aBt
AB
aBt A AB
u2
L2 cos
2020/12/9
BC
aBt BC
u2 L2
2020/12/9
vrB vrO vrBO vaB veB vrB vaB ve vrO vrBO
12
理论力学
§7-1 刚体平面运动的运动学
A
B
an rBO
vr O
at rBO
ar
a
3、求圆盘最高点B的加速度
arB
arO
at rBO
an rBO
aaB aeB arB
aaB
A
aA
ωOA O
C
Ca
vC
aB
B
aC
ω
aB
α
vC 2R aC vC 2R 2R
平面运动刚体上各点的速度
vA
ωAB
C1
n v A OA OA 30 1.5 m/s
vB vC
ωBC
C2
点C1为杆AB的速度瞬心 vA AB 7.16rad/s AC1
vB BC1 AB 2.72 m/s vB 5.13rad/s 点C2为杆BC的速度瞬心 BC BC2
vB vBA vA
ω
A
B
取点A为动点，则点B的速度为
vB v A vBA
其中
vA
v BA AB
13
方向垂直AB。
7.2
平面运动刚体上各点的速度（基点法）
例：半径为R的车轮，沿直线轨道作无滑动的滚动。已知 轮轴以匀速v0前进。求轮缘上A、B、C、D各点的速度。
vA vO vAO vO vBO
取点A为基点，则点B速度
vB
vBA
vB v A vBA
v AB vA vB sin 45 sin(90 ) sin(45 )
l sin r sin 45
作速度图，得
vA vB sin( 45 ) 162 cm/s cos v AB 1 v A AB sin 45 0.714 rad/s l l cos
θ
vCB vB vC
再取点B为基点，则点C的速度
vC vB vCB
vBA vB
vA
ωABC
2 练习：7-3 vB rO 2 1 vCB BC ABC 2r O rO 2 2 2 vC vB vCB 2vB vCB cos 45
10 rO 2 vB sin 135 arcsin 18 26' vC 19
合肥工业大学理论力学答案08刚体平面运动
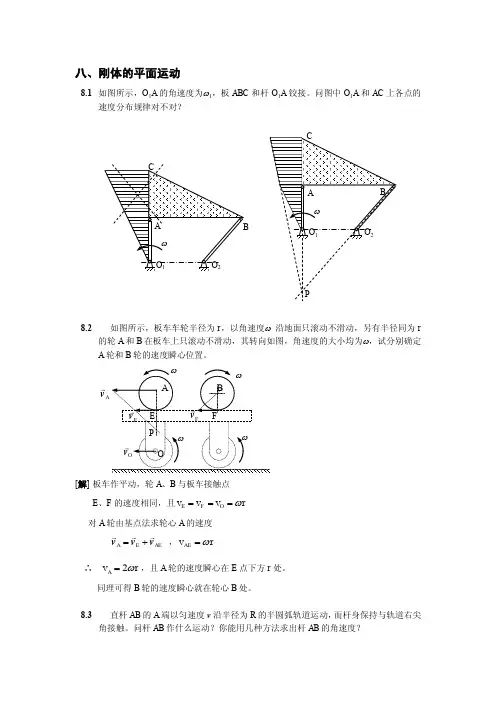
八、刚体的平面运动8.1 如图所示，O 1A 的角速度为ω1，板ABC 和杆O 1A 铰接。
问图中O 1A 和AC 上各点的速度分布规律对不对？8.2如图所示，板车车轮半径为r ，以角速度ω 沿地面只滚动不滑动，另有半径同为r 的轮A 和B 在板车上只滚动不滑动，其转向如图，角速度的大小均为ω，试分别确定A 轮和B 轮的速度瞬心位置。
[解] 板车作平动，轮A 、B 与板车接触点 E 、F 的速度相同，且r v v v O F E ω=== 对A 轮由基点法求轮心A 的速度 A E AE =+v v v ，r v AE ω=∴ r v A ω2=，且A 轮的速度瞬心在E 点下方r 处。
同理可得B 轮的速度瞬心就在轮心B 处。
8.3直杆AB 的A 端以匀速度v 沿半径为R 的半圆弧轨道运动，而杆身保持与轨道右尖角接触。
问杆AB 作什么运动？你能用几种方法求出杆AB 的角速度？E FPOE v Av Fv Ov[解] AB 杆作平面运动。
(一) 瞬心法AB 杆作平面运动，速度瞬心为P 。
Rv AP v AAB2==ω (二)基点法D A DA =+v v v ，DA v v AB A DA ωθ==sin又 DA ＝2R cos(90o －θ)＝2R sin θ ∴ Rv AB 2=ω(三)自然法： d d AB tϕω=，而R S ϕ2= ∴d d 2d d S R v t t ϕ==， d d 2vt R ϕ= ∴ Rv AB 2=ω 8.4如图所示四连杆机构OABO 1中，OA=O 1B=AB/2，曲柄OA 的角速度ω=3rad/s 。
当OA 转到与OO 1垂直时，O 1B 正好在OO 1的延长线上，求该瞬时AB 杆的角速度ωAB 和曲柄O 1B 的角速度ω1。
[解]取AB 为研究对象，AB 作平面运动。
以A 为基点，画B 点速度合成图 由B A BA =+v v v(rad/s)32230sin o==∴⋅=⋅==ωωωωAB OAAB OA v v AB AB ABABBBvvvDAv Dv Dv111cos3022(rad/s)B BAv v OA O Bωωω=︒=⋅=∴=8.5图示曲柄摇机构中，曲柄OA以角速度oω绕O轴转动，带动连杆AC在摇块B内滑动，摇块及与其固结的BD杆绕B铰转动，杆BD长l；求在图示位置时摇块的角速度及D点的速度。
理论力学(哈工大版)第九章：刚体的平面运动
第五章 刚体的平面运动5-1 刚体的平面运动方程一．平面运动的定义二．平面运动的简化刚体的平面运动可以简化为平面图形S 在其自身平面内的运动．三、平面运动分解为平动和转动1.平面运动方程为了确定代表平面运动刚体的平面图形的位置，我们只需确定平面图形内任意一条线段的位置．平面运动方程)(1t f x A = )(2t f y A = )(3t f =ϕ2．平面运动分解为平动和转动刚体平面运动可以看成是平动和转动的合成运动．刚体的平面运动可以分解为随基点的平动和绕基点的转动．3.刚体平面运动的角速度和角加速度平面运动随基点平动的运动规律与基点的选择有关，而绕基点转动的规律与基点选取无关(即在同一瞬间，图形绕任一基点转动的ε ,ω都是相同的）5-2 平面图形内各点的速度一．基点法（合成法）BA A B v v v +=平面图形上任一点的速度等于基点的速度与该点随图形绕基点转动的速度的矢量和二．速度投影法（自：就是基点法的变式） 速度投影定理：[][]AB A AB B v v =平面图形上任意两点的速度在该两点连线上的投影彼此相等三．瞬时速度中心法（速度瞬心法）1. 问题的提出2．速度瞬心的概念即在某一瞬时必唯一存在一点速度等于零，该点称为平面图形在该瞬时的瞬时速度中心，简称速度瞬心．３．几种确定速度瞬心位置的方法 ①已知图形上一点的速度A v 和图形角速度ω，可以确定速度瞬心的位置．（P 点）②已知一平面图形在固定面上作无滑动的滚动, 则图形与固定面的接触点P 为速度瞬心．③已知某瞬间平面图形上A ,B 两点速度B A v v ,的方向，且B A v v 不平行过A , B 两点分别作速度B A v v ,的垂线,交点P 即为该瞬间的速度瞬心.④ 已知某瞬时图形上A ,B 两点速度B A v v ,大小,且AB v AB v B A ⊥⊥ ,⑤已知某瞬时图形上A ,B 两点的速度方向相同，且不与AB 连线垂直．瞬时平动注意：瞬时平动与平动不同瞬时平动构件上各点的速度都相等，但各点的加速度并不相等。
4.2.2刚体平面运动-速度分析
刚体的平面运动-速度分析2面运动图形上速度分布规律？定理：只要 ，任一瞬时平面图形上都唯一存在一个速度等于零的点。
3、速度瞬心法≠ω证明:已知A 点的速度，任一点的速度MAA M v v v +=垂线AL 上点M 的速度大小可表示为MA A M v v v -=ω⋅-=AM v A 因此，在AL 上必存在一点P ，其速度为零。
A v v L 'SAAv MAMLP速度瞬心 某瞬时，平面图形上速度为零点。
ωAv AP =∴0=⋅-=ωAP v v A P唯一性：在某一瞬时，图形只有一个速度瞬心。
瞬时性：在不同瞬时，速度瞬心在平面图形上的位置不同。
注意：速度瞬心的加速度并不为零！S A AvAvMAv ML P特点：速度为零的点P在A点速度的垂线上。
5S 方向： ω⋅=BP v B P选取速度瞬心P 为基点，则平面图形上任一点B 的速度如图所示：BBv AC由此可见，只要已知在某一瞬时平面图形速度瞬心的位置和平面图形的角速度，就可求出该瞬时图形上各点的速度。
BP P B v v v +=大小： ⊥BP ，指向与ω 转向相一致。
Av Cv BPv =S P过速度瞬心P的任一直线上各点的速度分布就速度分布而言，平面图形的运动可视为绕该瞬时的速度瞬心作转动。
—与图形绕定轴转动时的速度分布类似。
有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）672. 已知某瞬间平面图形上A , B 两点速度v A 、v B 的方向几种确定速度瞬心位置的方法1. 已知一平面图形在固定面上作无滑动的滚动已知某瞬时图形上A , B 两点的速度大小相等，方向相同． 各点的加速度是否相等？此时, 图形的瞬心在无穷远处，图形的角速度 =0, 图形上各点速度相等, 这种情况称为 瞬时平动.ABOBv Av MMv例题. 沿直线轨道作纯滚动的车轮，其半径为R ，轮心的速度为v o ，求轮上A 、B 、C 、D 的速度。
理论力学课件 刚体平面运动的加速度分析
aBnA
=
AB
⋅
ω
2 AB
= 4m
s2
加速度矢量式投影到η轴上得
aB cos 45o = aBnA
aB = 5.66 m s2
αAB
an BA
at
y BA
aB aA B
加速度矢量式投影到y轴上得
0
= −a
aBt A
A cos
= 16
45° +
m s2
aBnA
cos
45°
+ aBt A
α AB
sin 45°
•结论：平面图 形角速度不为 零，任一瞬时， 速度瞬心必存在 且唯一。
6-2 刚体平面运动的速度分析
速度瞬心的特点
1、瞬时性：不同的瞬时，有不同的速度瞬心。 2、唯一性：某一瞬时只有一个速度瞬心。 速度瞬心不是一个固定点。理解成“角色”
思考题：杆做什么运动？
vB
ω
vA
定轴转动
车轮在地面上纯滚动
6-2 刚体平面运动的速度分析
6-2 刚体平面运动的速度分析
平移
vvA = vvB
ωAB = 0
avA = avB α AB = 0
瞬时平移
vvA = vvB avA ≠ avB
ωAB = 0 α AB ≠ 0
vA A
ω
O
vB B
牢记！
6-2 刚体平面运动的速度分析
2、确定速度瞬心位置的方法
已知A、B两点的速度方向，
试确定速度瞬心的位置。
例6-5 图示机构，已知曲柄OA的角速度为ω，OA＝AB＝BO1＝ O1C＝r，角α = β = 60º，求滑块C的速度。
解：AB和BC作平面运动，其瞬心分别为P1和P2点，则
理论力学课后知识题目解析第6章刚体的平面运动分析
第6章 刚体的平面运动分析6－1 图示半径为r 的齿轮由曲柄OA 带动，沿半径为R 的固定齿轮滚动。
曲柄OA 以等角加速度α绕轴O 转动，当运动开始时，角速度0ω= 0，转角0ϕ= 0。
试求动齿轮以圆心A 为基点的平面运动方程。
解：ϕcos )(r R x A += （1） ϕsin )(r R y A +=（2）α为常数，当t = 0时，0ω=0ϕ= 0 221t αϕ=（3）起始位置，P 与P 0重合，即起始位置AP 水平，记θ=∠OAP ，则AP 从起始水平位置至图示AP 位置转过θϕϕ+=A因动齿轮纯滚，故有⋂⋂=CP CP 0，即 θϕr R = ϕθr R =， ϕϕrr R A += （4）将（3）代入（1）、（2）、（4）得动齿轮以A 为基点的平面运动方程为：⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=222212sin )(2cos )(t r r R t r R y t r R x A A A αϕαα6－2 杆AB 斜靠于高为h 的台阶角C 处，一端A 以匀速v 0沿水平向右运动，如图所示。
试以杆与铅垂线的夹角θ 表示杆的角速度。
解：杆AB 作平面运动，点C 的速度v C 沿杆AB 如图所示。
作速度v C 和v 0的垂线交于点P ，点P 即为杆AB 的速度瞬心。
则角速度杆AB 为6－3 图示拖车的车轮A 与垫滚B 的半径均为r 。
试问当拖车以速度v 前进时，轮A 与垫滚B 的角速度A ω与B ω有什么关系？设轮A 和垫滚B 与地面之间以及垫滚B 与拖车之间无滑动。
解：RvR v A A ==ωhv AC v AP v ABθθω2000cos cos ===习题6-1图ABCv 0hθ习题6－2图PωABv CABCv ohθ习题6－2解图习题6-3解图习题6-3图v A = vv B = v ωAωBR vR v B B 22==ω B A ωω2=6－4 直径为360mm 的滚子在水平面上作纯滚动，杆BC 一端与滚子铰接，另一端与滑块C 铰接。
《理论力学》第八章 刚体平面运动
平面运动刚体绕基点转动的角速 度和角加速度与基点的选择无关！
HOHAI UNIVERSITY ENGINEERING MECHANICS
以蓝点为基点
以红点为基点
平移的速度与加速度与基点选择有关不同，而绕 基点转动的角速度与角加速度与基点的选择无关
例1: 已知曲柄－滑块机构中OA=r , AB=l;曲柄OA 以匀角速度绕O轴转动。求连杆AB的运动方程。 解： 建立图示参考坐标系，
已知图形上两点的速度平行，但两点 连线与速度方位不垂直 可以认为速度
0
瞬心在无穷远
平面 运动
平动图形上各点 的速度和加速度 是相同的，但瞬 时平动其上各点 的速度相同而各 点的加速度一般 不同
作平面运动的刚体上求各点速度的方法的适 用范围 1、基点法：已知基点速度和作平面运动刚体
的角速度。是基本方法，可求平面图形的速度 和角加速度，图形上一点的速度。
例2：曲柄滑块机构如图所示，曲柄OA以匀角速度 ω转动。已知曲柄OA长为R，连杆AB长为l。当曲柄 在任意位置 = ωt时，求滑块B的速度。
HOHAI UNIVERSITY ENGINEERING MECHANICS
解： 一、基点法
因为A点速度 vA已知，故选A为基点
vA
AB
v B v A v BA
平动方程 y
称O为基点
y
P
HOHAI UNIVERSITY ENGINEERING MECHANICS
f3 ( t )
讨论：
1. 为常数
刚体平 面运动 方程
y0 转动方程 O1 x 0
O
S x
x 刚体随基点平移 (随同动系平移)
2. (xO,yO)为常数
《理论力学》第八章刚体的平面运动
刚体的平面运动特点
刚体的平面运动具有 连续性，即刚体上任 意一点的运动轨迹都 是连续的。
刚体的平面运动具有 周期性，即刚体的运 动轨迹可以是周期性 的。
刚体的平面运动具有 对称性，即刚体的运 动轨迹可以是对称的。
02
刚体的平面运动分析
刚体的平动分析
平动定义
刚体在平面内沿着某一确定方向作等速直线运动。
详细描述
通过综合分析动能和势能的变化，可以深入理解刚体在平面运动中的能量转换过程。例 如，当刚体克服重力做功时，重力势能转化为动能；当刚体克服摩擦力做功时，机械能 转化为内能。这种能量转换过程遵循能量守恒定律，即系统总能量的变化等于外界对系
统所做的功与系统内能变化之和。
06
刚体的平面运动的实例分析
刚体的平面运动通常可以分为两种类型：纯滚动和滑动。在 纯滚动中，刚体只滚不滑，刚体上任意一点在任意时刻都位 于一个固定的圆周上。在滑动中，刚体既滚又滑，刚体上任 意一点在任意时刻都位于一个变化的圆周上。
刚体的平面运动分类
纯滚动
刚体只滚不滑，刚体上任意一点 在任意时刻都位于一个固定的圆 周上。
滑动
刚体既滚又滑，刚体上任意一点 在任意时刻都位于一个变化的圆 周上。
势能定理
总结词
势能定理描述了势能与其他形式的能量转换的关系。
详细描述
势能定理指出，在刚体的平面运动过程中，非保守力（如摩擦力、空气阻力等）对刚体所做的功等于系统势能的 减少量。非保守力做正功时，系统势能减少；非保守力做负功时，系统势能增加。
动能和势能的综合分析
总结词
在刚体的平面运动中，动能和势能的综合分析有助于理解运动过程中能量的转换和守恒。
做平动，这种运动也是复合运动。
理论力学运动学知识点总结
理论力学运动学知识点总结第一篇：理论力学运动学知识点总结运动学重要知识点一、刚体的简单运动知识点总结1.刚体运动的最简单形式为平行移动和绕定轴转动。
2.刚体平行移动。
·刚体内任一直线段在运动过程中，始终与它的最初位置平行，此种运动称为刚体平行移动，或平移。
·刚体作平移时，刚体内各点的轨迹形状完全相同，各点的轨迹可能是直线，也可能是曲线。
·刚体作平移时，在同一瞬时刚体内各点的速度和加速度大小、方向都相同。
3.刚体绕定轴转动。
• 刚体运动时，其中有两点保持不动，此运动称为刚体绕定轴转动，或转动。
• 刚体的转动方程φ=f(t)表示刚体的位置随时间的变化规律。
• 角速度ω表示刚体转动快慢程度和转向，是代数量，以用矢量表示。
，当α与ω。
角速度也可• 角加速度表示角速度对时间的变化率，是代数量，同号时，刚体作匀加速转动；当α 与ω异号时，刚体作匀减速转动。
角加速度也可以用矢量表示。
• 绕定轴转动刚体上点的速度、加速度与角速度、角加速度的关系：。
速度、加速度的代数值为。
• 传动比。
一、点的运动合成知识点总结1.点的绝对运动为点的牵连运动和相对运动的合成结果。
• 绝对运动：动点相对于定参考系的运动；• 相对运动：动点相对于动参考系的运动；• 牵连运动：动参考系相对于定参考系的运动。
2.点的速度合成定理。
• 绝对速度：动点相对于定参考系运动的速度；• 相对速度：动点相对于动参考系运动的速度；• 牵连速度：动参考系上与动点相重合的那一点相对于定参考系运动的速度。
3.点的加速度合成定理。
• 绝对加速度：动点相对于定参考系运动的加速度；• 相对加速度：动点相对于动参考系运动的加速度；• 牵连加速度：动参考系上与动点相重合的那一点相对于定参考系运动的加速度；• 科氏加速度：牵连运动为转动时，牵连运动和相对运动相互影响而出现的一项附加的加速度。
• 当动参考系作平移或 = 0，或与平行时，= 0。
刚体平面运动中的速度分析
龙源期刊网 刚体平面运动中的速度分析作者：刘战辉张雅男苏静徐飞来源：《科技资讯》2012年第27期摘要：在普通物理教学中，刚体平面运动的纯滚动问题是刚体章节中的重点和难点，对学生而言，也是较为难以掌握的内容。
本文从教学的角度从基本物理概念出发，利用简单的数学知识对刚体平面运动中的速度进行了深入浅出的分析，使学生对这部分知识有更好的理解和掌握。
关键词：刚体平面运动速度分析中图分类号：G64 文献标识码：A 文章编号：1672-3791（2012）09（c）-0249-01刚体平面运动的纯滚动问题中，存在质心C和瞬心P两个特殊点。
其中质心的速度与刚体转动角速度之间满足：vC=Rω。
而瞬心是指刚体任意时刻与接触水平面的接触点，对于刚体平面运动的纯滚动问题，刚体与接触面之间无相对滑动，因此任意时刻瞬心的速度为零，保持静止不动（注：瞬心在不同时刻在刚体上的位置不同，是刚体与水平面的接触点）。
对于解决刚体平面运动的纯滚动问题可以选择任意位置作为基点来讨论刚体的运动，取不同基点，速度形式不同，但是选质心和瞬心为基点最为方便。
综上所述，在刚体平面运动中，其运动可以看作是质心的平动和刚体绕质心的转动的组合，又可以看成绕瞬心作匀速圆周运动，而且选择质心C或瞬心P作为基点可以简单明了认识其运动，但是选择不同的基点运动形式不同。
选择质心C，运动形式比较复杂（圆周运动和直线运动的叠加），但是其物理现象简洁，容易理解。
而选择瞬心P，运动形式简单（圆周运动），但是其物理过程不易理解。
参考文献[1] 刘克哲，张承琚.物理学（上卷）[M].北京：高等教育出版社，2005，6.[2] 刘克哲，张承琚.物理学学习指导[M].北京：高等教育出版社，2006.1.。
刚体的平面运动-速度分析
φ
A
50
D
ωAB
100
0 CD － 1 v 272 mm s 故 B cos
曲柄AB的角速度 AB
vB 2.09 rad s－1 AB
2. 求E点的速度。
E B α α vE
50
由于构件BCE上C点的速度 vC 垂直于 CE ，根据速度投影定 理可知 E 点的速度 vE 也应垂直于 CE。 应 用 速 度 投 影 定 理 ,vB 与 vE 在 BE连线上的投影相等，即
15
G
例8-8
已知： AB 600mm, OE 100mm, 10 rad s , BG GD 500mm 。 求 : AB。
vE
已由杆GE得 vG=1.066m/s 2、杆BG作平面运动， 瞬心为C
ωAB
vB
B
75 15
A
O
E
ωGE C 1
ω
BG
BC vB BG BC vG GC vG cos
取基点A
v
B
v
A
v
BA
其中 只对同一个刚体成立，刚体之间则不一定成立！
2.速度投影定理
v B AB v A AB
同一平面图形上任意两点的速度 在这两点连线上的投影相等。
3、瞬心法
（1）速度瞬心—— 平面图形内某一瞬时绝对速度等于零的点 （2）平面图形的运动可看成为绕速度瞬心的转动。 （3）平面图形上任一点M的速度大小为
A
vB
B
vA
C
S
（3）已知 v A ∥ v B ，且 v A⊥连线 AB 速度瞬心C ：在连线 AB 与 v A v B 矢端连线的交点
理论力学第八章平面运动
r vM
r vMC
r
uuuur CM
• 速度瞬心的确定方法
已知 vA ,的vB方向， 且 v不A 平行于 v。B
vrA // vrB ,且不垂直于AB
vrB
vvrrBBvArAvr0AvrABvrMAB
0
瞬时平移(瞬心在无穷远处)
纯滚动(只滚不滑)约束
找出下列平面运动刚体的速度瞬心。 A
第八章 刚体平面运动
1、刚体平面运动的定义及运动方程 2、刚体平面运动分解为随基点平动和绕基点转动 3、平面运动图形上点的速度分析 4、平面运动图形上点的加速度分析
1、刚体平面运动的定义
若刚体在运动过程中，刚体上的任意一点与 某一固定平面始终保持相等的距离，这种运 动称为平面运动。
刚体平面运动特点
刚体上所有各点均在平行于某固 定平面的平面内运动。
刚体的平面运动，可以简化为平面 图形在其自身平面内的运动来研究。
平面图形 S 的位置可用其上任一 线段如AB 来确定，线段AB的位 置又可用A 点的坐标 xA 、yA 和 线段AB与 x 轴的夹角 φ 来确定。 点 A 称为基点。
刚体平面运动方程
当平面图形 S 运动时，坐标 xA 、
yA 和夹角 φ 一般都是随时间 t 而 变化的，分别为时间 t 的单值连
续函数，即
xA f1 (t)
y A f 2 (t)
f3 (t)
这就是平面图形S 的运动方程，也就是刚体平面运动的运动方程。
2、刚体平面运动分解为随基点平动和绕基点转动
xO f1 t
1.5rad
/
s
BC
vB BC
2.25rad
/s
vA
2）瞬心法
刚体平面运动中的速度分析
刚体平面运动中的速度分析
物体在静止状态下，无论它拥有任何形式的运动，它都可以分解为两个分量，即速度分量和加速度分量。
它们的定义如下：
● 速度：描述物体的实际移动，是物体空间位置的变化量。
● 加速度：速度的变化量。
也就是运动中物体空间位置变化量的变化量。
当物体在空间中运动时，它可以在任何方向上以任意速度移动。
它可以向任
何方向运动，也可以加速或减速。
此外，它的运动受外力的影响。
假定物体的运动是由物理定律所驱动的，那么这种运动就称为平面运动。
在平面运动中，物体速度的变化只受其空间位置的改变影响，并且不受外部力的影响。
因此，在刚体平面运动中，物体的速度由它的空间位置的变化来描述，我们
可以使用下面的方程式来计算：
速度 = 量/时间
加速度 = 速度/时间
例如，让我们考虑一个滑块在水平方向上以一定速度移动的情况。
速度可以
用大写字母V表示，而加速度可以用小写字母a来表示。
因此，这个滑块的速度
可以使用以下方程式来计算：
V = S/t
其中，S表示滑块空间位置的变化，而t表示这个位置变化发生的时间。
这个滑块的加速度可以使用以下方程式来计算：
a = V/t
这里，V表示滑块的速度，而t表示滑块速度发生变化的时间。
刚体的平面运动学分析
刚体的平面运动学分析刚体平面运动学分析是物理学中研究刚体在平面上运动规律的一门学科，它通过分析刚体的位置、速度和加速度等运动参数，揭示刚体的运动规律和运动轨迹。
本文将从三个方面对刚体平面运动学进行详细分析，分别是刚体的位移、速度和加速度。
1. 刚体的位移刚体的位移是指刚体从初始位置到最终位置之间的位移变化。
假设刚体在平面上做平动运动，其初始位置为P1，最终位置为P2。
刚体在平动过程中，可以沿着直线路径移动，也可以绕着某个固定点旋转。
对于直线平动，刚体的位移可以用矢量表示，位移矢量的大小等于两个位置之间的距离，方向沿着直线运动的方向。
对于绕固定点旋转的情况，刚体的位移可以由角位移表示，角位移的大小等于刚体绕固定点旋转的角度。
2. 刚体的速度刚体的速度是指刚体在平面上做运动时，单位时间内位移的变化率，即速度矢量的大小和方向。
刚体在平面上做平动运动时，其速度大小等于位移的变化率，方向沿着位移的方向。
刚体在旋转过程中，速度的大小等于刚体绕固定点旋转的角速度，方向垂直于位于刚体上某一点的矢径方向。
3. 刚体的加速度刚体的加速度是指刚体在平面上做运动时，单位时间内速度的变化率，即加速度矢量的大小和方向。
刚体的加速度可以分为线加速度和角加速度两种情况。
对于平动运动，刚体的线加速度大小等于速度的变化率，方向沿着速度的方向。
对于旋转运动，刚体的角加速度大小等于刚体绕固定点旋转的角度的变化率，方向垂直于位于刚体上某一点的矢径方向。
通过对刚体的位移、速度和加速度的分析，可以得到以下几个重要结论：1) 若刚体的速度和加速度均为零，则刚体处于静止状态；2) 若刚体的速度不为零但加速度为零，则刚体做匀速直线运动；3) 若刚体的速度和加速度均不为零，则刚体做变速直线运动或者曲线运动；4) 若刚体的速度为零但加速度不为零，则刚体处于转动状态。
总之，刚体的平面运动学分析是研究刚体在平面上运动规律的重要学科。
通过对刚体的位移、速度和加速度的分析，可以揭示刚体的运动规律和运动轨迹，为解决实际问题提供理论依据。
第九章刚体的平面运动_理论力学
刚体作平面运动时，任意瞬时，平面图形上存在 且仅存在一个点，在此瞬时该点的绝对速度为零，称该点为此瞬时刚体的瞬时速度中心， 或 称速度瞬心（简称瞬心） ，此瞬时刚体上其他各点的速度分布规律等效于此瞬时图形以刚体 的角速度 绕 瞬 心 作 定 轴 转 动 时 的 速 度 分 布 一 样 。 如 图 9-11 （ b ） 所 示 。
例 9-1 图 9-18 所示曲柄连杆机构。 已知
，
。 ① 求图示位置连杆 AB 之瞬心；
② 求 OA 在铅垂位置时连杆 AB 之运动特点。
解：① 分析各构件运动， OA 绕 O 作定轴转动， ，方向如图示；AB 杆作平面运动；B 点作直线运动。VB 沿 OB 方向，属于已知 两点速度方位，过 A、B 两点分别作 vA 和 vB 的垂线,其交点 C 即为图示瞬时之瞬心 C 。 ② 当 OA 位于铅垂位置时的情形。如图 9-19 所示。此时 vA∥vB ，但与 AB 不垂直，
由定义不难推出， 在刚体运动过程中， 由此推出以下结论。
的运动 （见§7-1.2） 。
结。
刚体平面运动方程式 现在来描述平面图形 在空间的位置。 （1）在图形上作直线 （2）运动方程式 ，只需确定 的位置就可以确定 的位置。见图 9-6
（9-1） §9-2 平面运动分解为平动和转动
因此式（9-2）改写成： (9-3) 其中：vM 为动点 的绝对速度
vA 为基点的速度（相对于定系） vMA 为动点 见图 9-9，则 (9-4) 2. 速 度 投 影 定 理 -- 速 度 分 析 的 第 二 种 方 法 （ 亦 称 " 基 点 法 的 推 论 " ） 相对于基点 的速度 （相对速度） ,若在平面运动刚体上另取一点 B ，
这样，平面运动分解成跟随基点的平动和相对于基点的转动。这种分解方法称为基点法。 2. 基点法的特点 （1）平动部分与基点选择有关。 （2）转动部分与基点选择无关。读者试用作图方法验证之。 （3）相对于动系转动的角速度 形的角速度，与基点选择无关。 §9-3 平面运动刚体上各点的速度分析 。由于是平动动系，所以 。称为图
理论力学 刚体平面运动速度分析
B
O
ϕ
vA A
x
6-2 刚体平面运动的速度分析
分析： 1、AB做平面运动。 2、用基点法求解，基点A y vB vA B vBA
作用线 大小
v v v v B = v A + v BA
√
？
√
√
？ ωl
vA
ω
O
ϕ
vA A
一个矢量方程在平面情况 下，可解2个未知。 x
6-2 刚体平面运动的速度分析
y vB vA B vBA 解：基点A
B C vA vA D vDA A II ωA
v A = (r1 + r2 )ωO
以A为基点，两轮接触点D的速度。
v v v v D = v A + v DA
ωO
O I
vD = 0
vDA (r1 + r2 )ωO ωA = = r2 r2
以A为基点，点B的速度。
v v v v B = v A + v BA
2、 已知平面图形上一点A的速度 vA
和图形角速度 ω
v 速度瞬心P：过点A作 v A 的垂线，
并取 PA =
vA
A
vA
vA
P ω
ω
。
S
ω
6-2 刚体平面运动的速度分析
3、平面运动刚体在固定平面上做纯滚动时，其接触点为速度瞬 心。
v
P
注意：只有在接触面是固定面时, 圆轮上接触点才是 速度瞬心.
6-2 刚体平面运动的速度分析
vB vBA
ω
B
v v v v B = v A + v BA
vA
v v BA
v v A 基点速度
刚体平面运动中的速度分析
刚体平面运动中的速度分析摘要:在普通物理教学中,刚体平面运动的纯滚动问题是刚体章节中的重点和难点,对学生而言,也是较为难以掌握的内容。
本文从教学的角度从基本物理概念出发,利用简单的数学知识对刚体平面运动中的速度进行了深入浅出的分析,使学生对这部分知识有更好的理解和掌握。
关键词:刚体平面运动速度分析刚体平面运动的纯滚动问题中,存在质心C和瞬心P两个特殊点。
其中质心的速度与刚体转动角速度之间满足:vC=Rω。
而瞬心是指刚体任意时刻与接触水平面的接触点,对于刚体平面运动的纯滚动问题,刚体与接触面之间无相对滑动,因此任意时刻瞬心的速度为零,保持静止不动(注:瞬心在不同时刻在刚体上的位置不同,是刚体与水平面的接触点)。
对于解决刚体平面运动的纯滚动问题可以选择任意位置作为基点来讨论刚体的运动,取不同基点,速度形式不同,但是选质心和瞬心为基点最为方便。
现选择半径为R的匀质圆盘在水平面上作纯滚动为例来研究其速度情况。
其中圆盘的质心与圆心重合,瞬心P点为圆盘与水平面的接触点,绕圆心转动的角速度为ω,选择如图1所示坐标系。
在纯滚动过程中,圆盘绕质心转动,而质心始终在作匀速直线运动。
因此对边缘各点的运动可看成绕质心C以角速度为ω,半径为R 作匀速圆周运动和与C以相同速度作匀速直线运动的叠加。
现从基本的物理概念出发对圆盘边缘上四个特殊位置(与坐标轴的交点)的速度进行分析。
对于瞬心P点,,与瞬心的定义任意时刻速度为零保持一致。
其它各点的速度可分别表示为:的方向垂直于PA,其大小可以表示为PA×ω。
因此可知A点的运动可以看成绕瞬心P作以PA长度为半径,角速度为ω作匀速圆周运动。
同理,B点和D点的运动也可以看成分别绕瞬心P作以PB、PD 长度为半径,角速度为ω作匀速圆周运动。
很多教师在教学过程中,推广开来,得到刚体边缘上所有点都可以看成绕瞬心P作匀速圆周运动。
但是,对于学生却很困惑,边缘上其它点的运动是不是这样的呢？下面我们分析边缘上任意点的情况。
平面运动刚体内各点的速度分析.
AB AC
vA
r 1
vB AB.BC 1.1551
摇杆O2B的角速度ω2
AB tan60
r 1
3r 3
Байду номын сангаас
0.1921
2
vB 0.385 1 B O2
瞬心法：应用瞬心来求平面图形内各点的速度的方法。
几种确定瞬心位置的方法： （1）平面图形沿某一固定面作纯滚动（无滑动地 滚动）时，它与固定面的接触点就是该瞬时平面图 形的速度瞬心。
（2）平面图形内任意丙点的速度已知（14.7a），通过这两点作其速度矢量的垂 线，两垂线的交点C即为瞬心。 （3）若平面图形内两点的速度方向平行，且垂直于两点的连线（图14.7b，c）， 则瞬心在这两点的连线或其延长线上，且各点的速度与它们到瞬心的距离成 正比。
（4）若平面图形内两点的速度方向平行，且大小相等（图14.8a，b），则瞬心 趋于无穷远。即平面图形为瞬时平动。所以，此时平面图形内各点的速度 相同。
例2：四连杆机构如图（14.9），O1A=r，AB=O2B=3r，曲柄O1A角速度ω1绕O1 轴转动。在图示位置时，O1A与AB垂直，θ=60º ，以求图示瞬心摇杆O2B的角速 度ω2。 解：连杆AB作平面运动，点A的速度已知，vA=rω1，方向和O1A垂直；点B速度方 向已知，vB与O2B垂直。过A、B两点分别作vA和vB的垂线，交点C即为瞬心。 设连杆的角速度ωAB，因平面运动可看成是绕瞬心的转动，故
（14.1）
平面图形上任意一点的速度等于基点的速度与该点绕基点转动的速度的矢量和， 这就是基点法（速度合成法）。
例1：发动机的曲柄连杆机构如图（图14.5），已知曲柄OA长r=200mm，以匀 角速度ω=2rad/s绕O点转动，连杆AB长L=990。试求当角θ=90º 时，滑块B的速 度及连杆AB的角速度。
4.2.1刚体平面运动-速度分析
观察一种现象
离车轮与地面的接触处近 的钢丝看得较清楚 而离得远的钢丝则模糊不 清，甚至看不见。 如何解释这种现象？
基点法
vB vA vBA (vBA AB )
特点：既能求速度，也能求 ，但不能明显反映速
度分布的规律。
速度投影法
vB AB
v
A
AB
特点：计算简便，但无法求出图形的角速
度 。也不能明显反映速度分布的规律。
vBA SA
vB
B
vA
vA
是否存在一种速度分析方法，可以 直接描述出运动刚体上速度分布规律？
A为基点
有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）
谢 谢！
= 2 rad/s
A
取A为基点C为动点. vC = vA + vCA (2)
vA
vA = 20 cm/s
vCA = (CA) = 20 cm/s
对(2)式应用余弦定理得:
vB
vBA
B vC
vA C
vA
vCA
A
vC
v
2 A
vC2A
2 vA
vCA cos1200
20 cm / s
有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）
B
Cபைடு நூலகம்
vA
A
解: (1)取A为基点，B为动点.
vB = vA + vBA
(1)
把(1)式向AB方向投影得:
vA
vB sin = vA cos
vB = vA ctg = 34.64 cm/s
把(1)式向 vA方向投影得:
0 = vA - vBA sin vBA = 40 cm/s
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
vA vB vBA B vA
vC vCA
vA
C
v v v v C = v A + v CA
O
A II ωA D
ωO
课后练习
I
6-2 刚体平面运动的速度分析
2、速度投影法
v v v v B = v A + v BA
投影于AB连线
vB vBA
B
vA
[vB ]AB = [v A ]AB
2、 已知平面图形上一点A的速度 vA
和图形角速度 ω
v 速度瞬心P：过点A作 v A 的垂线，
并取 PA =
vA
A
vA
vA
P ω
ω
。
S
ω
6-2 刚体平面运动的速度分析
3、平面运动刚体在固定平面上做纯滚动时，其接触点为速度瞬 心。
v
P
注意：只有在接触面是固定面时, 圆轮上接触点才是 速度瞬心.
6-2 刚体平面运动的速度分析
定轴转动
6-2 刚体平面运动的速度分析
瞬时平移的说明
vA
O
A
ω
vA
A
M
ω
B 该瞬时，连杆AB的速度瞬心在无穷远处 选A为基点，则连杆AB上任一点M的速度 该瞬时AB上各点的速度相等。
vB
O
vM vB
B
ω AB = 0
vM = v A
各点加速度是否相等?
6-2 刚体平面运动的速度分析
x A = f1 (t ) y A = f 2 (t ) ϕ = f 3 (t )
刚体平面运动的角速度和角加速度为
& ω =ϕ
& =ϕ && α =ω
刚体平面运动的角速度和角加速度为代数量且唯一
6-2 刚体平面运动的速度分析
1、基点法 运动分解：B点的速度=随基点Ａ的平动 速度+绕基点Ａ的转动速度
平面图形上任意两点的速度在 这两点连线上的投影相等。
ω
A
vA
6-2 刚体平面运动的速度分析
速度投影法说明
[vB ]AB = [v A ]AB
1、速度投影定理不能求平 面图形的角速度。 2、反映了刚体不变形的性 质,适用于任何形式的刚体 运动。
vB vBA
B
vA
ω
A
vA
6-2 刚体平面运动的速度分析
vA
O A
ω
vB
B
结论：平面运动刚体作 瞬时平移时，刚体上各 点的速度皆相同，刚体 角速度为零。但各点的 加速度不同，刚体角加 速度不为零。
牢记！
现在，你能解释 这种现象了吗？
P
离车轮与地面的接触处近的钢丝看得较清楚，而 离得远的钢丝则模糊不清，甚至看不见。
6-2 刚体平面运动的速度分析
例6-4 椭圆规尺的A端以速度vA沿 x 轴的负向运 动，如图所示，AB=l。试求B端的速度以及规尺AB的 角速度。和杆AB中点D的速度。 （速度瞬心法求解） y
v v v A = vB
vA
O A
ω
vB
B
6-2 刚体平面运动的速度分析
特例2 两垂线共线。则速度瞬心在两点速度矢端连线与AB延长 线的交点处。
A B P
vA vB
6-2 刚体平面运动的速度分析
特例2 两垂线共线。则速度瞬心在两点速度矢端连线与AB延长 线的交点处。
A P
vA
vB
B
6-2 刚体平面运动的速度分析
B C vA vA D vDA A II ωA
v A = (r1 + r2 )ωO
以A为基点，两轮接触点D的速度。
v v v v D = v A + v DA
ωO
O I
vD = 0
vDA (r1 + r2 )ωO ωA = = r2 r2
以A为基点，点B的速度。
v v v v B = v A + v BA
刚体ED应用速度投影定理
v E cos 30 o = v D
速度投影法只能在一个刚体上应用，不能求刚体角速度
如何解释 这种现象？
离车轮与地面的接触处近的钢丝看得较清楚，而 离得远的钢丝则模糊不清，甚至看不见。
6-2 刚体平面运动的速度分析
3、速度瞬心法 1）寻找平面图形S上速度为零的点
vPA
S
N P
vB vBA
ω
B
v v v v B = v A + v BA
vAΒιβλιοθήκη v v BAv v A 基点速度
Ｂ绕Ａ转动的速度 A
vA
v BA = AB ⋅ ω
平面图形上任意一点的速度等于基点的速度与该点绕基点转 动的速度的矢量和。
6-2 刚体平面运动的速度分析
例6-1 椭圆规尺的A端以速度vA沿 x 轴的负向运 动，如图所示，AB=l。试求B端的速度以及规尺AB的 角速度。 y
vA vD
D A
ω
P P
vB
ω
B
速度分布而言，平面图形的运动可视为绕该瞬时的速度瞬心作 瞬时转动。与定轴转动速度分布类似。
6-2 刚体平面运动的速度分析
速度瞬心位置的确定
1、已知任意两点 的速度方向，则两 速度垂线的交点为 速度瞬心P
P
ωAB
vA
ω
A
O
vB
B
6-2 刚体平面运动的速度分析
特例1：两垂线平行。则速度瞬心P在无穷远处。这种情况称 瞬时平移。ω=0
B
O
ϕ
vA A
x
6-2 刚体平面运动的速度分析
分析： 1、AB做平面运动。 2、用基点法求解，基点A y vB vA B vBA
作用线 大小
v v v v B = v A + v BA
√
？
√
√
？ ωl
vA
ω
O
ϕ
vA A
一个矢量方程在平面情况 下，可解2个未知。 x
6-2 刚体平面运动的速度分析
y vB vA B vBA 解：基点A
例6-3 图所示平面机构中，曲柄OA=100 mm，以角速度ω = 2 rad·s－1转动。连杆AB带动摇杆CD，并拖动轮E 沿水平 面滚动。已知CD = 3CB，图示位置时A，B，E 三点恰在 一水平线上，且CD⊥ED，试求此瞬时E点的速度。
D
30o
E
B
60o
A C O
ω
6-2 刚体平面运动的速度分析
B
ω
O
ϕ
vA A
x
6-2 刚体平面运动的速度分析
y vB B vD D O vA ϕ A x
解：
ω
AB的速度瞬心为P
P
vA vA = ω= AP l sin ϕ
v B = BP ⋅ ω = v A cot ϕ
l vA vA vD = DP ⋅ ω = ⋅ = 2 l sin ϕ 2 sin ϕ
速度瞬心的特点
1、瞬时性：不同的瞬时，有不同的速度瞬心，速度瞬心具有加 速度。如果加速度为零，变为定轴转动。 2、唯一性：某一瞬时只有一个速度瞬心，速度瞬心不一定在平 面图形内。一个刚体只有一个速度瞬心。
速度瞬心不是一 个固定点。理解 成“角色”
6-2 刚体平面运动的速度分析
思考题： 1、下图所示速度瞬心是否正确？ 2、杆做什么运动？
v v v vP = v A + vPA
可找到一点P，满足
vA
A
v PA = v A
vP = 0
（P为速度瞬心）
ω
vA
在某一瞬时，平面图形内速度等于0的点，称为速 度瞬心。
6-2 刚体平面运动的速度分析
2）若以Ｐ为基点，任一点速度
v v v v B = v P + v BP
v B = v BP = BP ⋅ ω
v v v v B = v A + v BA
ω
v B = v A cot ϕ
x
O
ϕ
vA A
v BA
vA = sin ϕ
v BA vA = ω = l l sin ϕ
6-2 刚体平面运动的速度分析
刚体平面运动的速度分析的解题步骤（基点法）
1、选基点（一般选择速度已知的点） 2、作速度平行四边形。本题B点速度必须在平行四 边形的对角线。速度方向不能假设。 3、解速度三角形。求解的速度和角速度需要图示。 用vBA的方向判断角速度的转向。 速度矢量式含有6个要素,必须知道4个要素,方能求解
解 vD
D
30o
v A = OA ⋅ ω = 0.2m/s
v B cos 30 o = v A
刚体AB应用速度投影定理
E
B
60o
vB
C O
A
vA
vE
vB =
ω
vA = 0 . 231 m/s o cos 30 v v D = B ⋅ CD = 0 .693 m/s CB
v E = 0 .8 m / s
6-2 刚体平面运动的速度分析
思考：本题可以以B为基点吗？ B
ω
O
vB
v v v v A = v B + v AB
ϕ
vA vAB
例6-2 行星轮系机构如图。大齿轮I固定，半径为r1；行星齿轮II 沿轮 I 只滚而不滑动，半径为 r2 。系杆 OA 角速度为 ωO 。求轮 II 的 角速度ωA及其上B，C两点的速度。 解 杆OA定轴