平面机构的运动分析答案
机械原理习题及答案
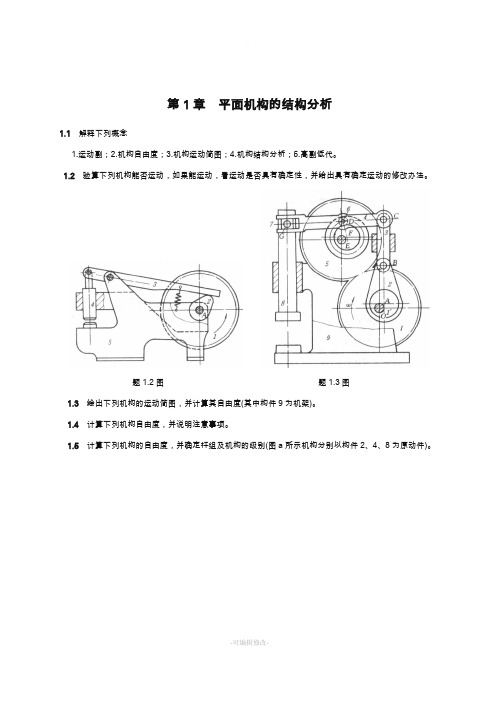
第1章平面机构的结构分析1.1解释下列概念1.运动副;2.机构自由度;3.机构运动简图;4.机构结构分析;5.高副低代。
1.2验算下列机构能否运动,如果能运动,看运动是否具有确定性,并给出具有确定运动的修改办法。
题1.2图题1.3图1.3 绘出下列机构的运动简图,并计算其自由度(其中构件9为机架)。
1.4 计算下列机构自由度,并说明注意事项。
1.5计算下列机构的自由度,并确定杆组及机构的级别(图a所示机构分别以构件2、4、8为原动件)。
题1.4图题1.5图第2章平面机构的运动分析2.1试求图示各机构在图示位置时全部瞬心。
题2.1图2.2在图示机构中,已知各构件尺寸为l AB=180mm , l BC=280mm , l BD=450mm ,l CD=250mm ,l AE =120mm ,φ=30º, 构件AB上点E的速度为v E=150 mm /s ,试求该位置时C、D两点的速度及连杆2的角速度ω2。
2.3 在图示的摆动导杆机构中,已知l AB=30mm , l AC=100mm , l BD=50mm ,l DE=40mm ,φ1=45º,曲柄1以等角速度ω1=10 rad/s沿逆时针方向回转。
求D点和E点的速度和加速度及构件3的角速度和角加速度(用相对运动图解法)。
题2.2图题2.3图2.4 在图示机构中,已知l AB =50mm , l BC =200mm , x D =120mm , 原动件的位置φ1=30º, 角速度ω1=10 rad/s ,角加速度α1=0,试求机构在该位置时构件5的速度和加速度,以及构件2的角速度和角加速度。
题2.4图2.5 图示为机构的运动简图及相应的速度图和加速度图。
(1)在图示的速度、加速度多边形中注明各矢量所表示的相应的速度、加速度矢量。
(2)以给出的速度和加速度矢量为已知条件,用相对运动矢量法写出求构件上D 点的速度和加速度矢量方程。
平面机构的结构分析机械原理习题集答案

2)求 、
3)求当 =0时
由渐开线函数表查得:
2、试问渐开线标准齿轮的齿根圆与基圆重合时,其齿数 应为多少,又当齿数大于以上求得的齿数时,基圆与齿根圆哪个大?
解
由 有
当齿根圆与基圆重合时,
当 时,根圆大于基圆。
3、一个标准直齿圆柱齿轮的模数 =5mm,压力角 =20º,齿数 =18。如图所示,设将直径相同的两圆棒分别放在该轮直径方向相对的齿槽中,圆棒与两侧齿廓正好切于分度圆上,试求1)圆棒的半径 ;2)两圆棒外顶点之间的距离(即棒跨距) 。
机构的基本杆组图为
此机构为Ⅱ级机构
3)取构件EG为原动件时
此机构的基本杆组图为
此机构为Ⅲ级机构
平面机构的运动分析
1、试求图示各机构在图示位置时全部瞬心的位置(用符号 直接标注在图上)。
2、在图a所示的四杆机构中, =60mm, =90mm, = =120mm, =10rad/s,试用瞬心法求:
1)当 = 时,点C的速度 ;
解
取坐标系xAy,并标出各杆矢量及方位角如图所示:
1)位置分析机构矢量封闭方程
分别用 和 点积上式两端,有
故得:
2)速度分析式a对时间一次求导,得
上式两端用 点积,求得:
式d)用 点积,消去 ,求得
3)加速度分析将式(d)对时间t求一次导,得:
用 点积上式的两端,求得:
用 点积(g),可求得:
351.063
平面连杆机构及其设计
1、在图示铰链四杆机构中,已知: =50mm, =35mm, =30mm, 为机架,
1)若此机构为曲柄摇杆机构,且 为曲柄,求 的最大值;
2)若此机构为双曲柄机构,求 的范围;
1 平面机构运动简图和自由度 习题答案
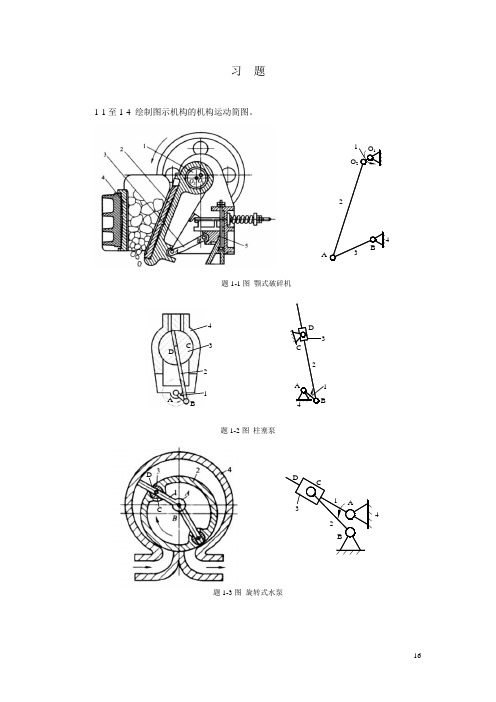
习 题1-1至1-4 绘制图示机构的机构运动简图。
题1-1图 颚式破碎机题1-2图 柱塞泵题1-3图 旋转式水泵O 1O 2AB1 234ABCD 1 2 3 4 A B CD1 234 AB CD1 2 34CD题1-4图 冲压机构1-5至1-10 指出机构运动简图中的复合铰链、局部自由度和虚约束,并计算各机构的自由度。
题1-6图解:构件3、4、5在D 处形成一个复合铰链,没有局部自由度和虚约束。
32352701L H F n P P =--=⨯-⨯-=解:没有复合铰链、局部自由度和虚约束。
323921301L H F n P P =--=⨯-⨯-= 题1-5图题1-5图56 ABCDEFO 1 O 2 D F1 2 345 6EGFEG题1-7图题1-8图题1-9图 题1-10图解:A 处为复合铰链,没有局部自由度和虚约束。
323721001L H F n P P =--=⨯-⨯-=解:A 处为复合铰链,没有局部自由度和虚约束。
323721001L H F n P P =--=⨯-⨯-=解:B 处为局部自由度,没有复合铰链和虚约束。
32352710L H F n P P =--=⨯-⨯-=解:C 处为复合铰链,E 处为局部自由度,没有虚约束。
32372912L H F n P P =--=⨯-⨯-=AB C DE IFG HADBECAEBCDGF1-11图示为一手动冲床机构,试绘制其机构运动简图,并计算自由度。
试分析该方案是否可行;如果不可行,给出修改方案。
题1-11图手动冲床答:此方案自由度为0,不可行。
改进方案如图所示:手动冲床运动简图手动冲床改进方案。
机械原理复习试题(附答案)

平面机构的运动分析选择题:仔细阅读每一题,并选择适合的答案。
1、机构中的构件是由一个或多个零件所组成,这些零件间_____产生相对运动。
可以不可以不一定能2、原动件的自由度应为_____。
123、在机构中原动件数目_____机构的自由度时,该机构具有确定的运动。
大于等于小于4、机构具有确定运动的条件是_____。
自由度大于零自由度等于原动件数自由度大于15、由K 个构件汇交而成的复合铰链应具有_____个转动副。
K-1KK+16、一个作平面运动的自由构件有_____个自由度。
1367、通过点、线接触构成的平面运动副称为_____。
转动副移动副高副8、通过面接触构成的平面运动副称为_____。
低副高副移动副9、平面运动副的最大约束数是_____。
12310、杆组是自由度等于_____的运动链。
1原动件数11、具有局部自由度的机构,在计算机构的自由度时,应当首先除去局部自由度。
是否12、具有虚约束的机构,在计算机构的自由度时,应当首先除去虚约束。
是否13、虚约束对运动不起作用,也不能增加构件的刚性。
是否14、若两个构件之间组成两个导路平行的移动副,在计算自由度时应算作两个移动副。
是否15、若两个构件之间组成两个轴线重合的转动副,在计算自由度时应算作两个转动副。
是否16、六个构件组成同一回转轴线的转动副,则该处共有三个转动副。
是否17、当机构的自由度F>0,且等于原动件数,则该机构具有确定的相对运动。
是否18、虚约束对机构的运动有限制作用。
是否19、瞬心是两构件上瞬时相对速度为零的重合点。
是否20、利用瞬心既可以求机构的速度,又可以求加速度。
是否平面连杆机构及其设计选择题:仔细阅读每一题,并选择适合的答案。
1、铰链四杆机构存在曲柄的必要条件是最短杆与最长杆长度之和_____其他两杆之和。
<=>=>2、铰链四杆机构存在曲柄的必要条件是最短杆与最长杆长度之和小于或等于其他两杆之和,而充分条件是取_____为机架。
机械原理答案

第二章 平面机构的结构分析题2-1 图a 所示为一简易冲床的初拟设计方案。
设计者的思路是:动力由齿轮1输入,使轴A 连续回转;而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构使冲头4上下运动,以达到冲压的目的。
试绘出其机构运动简图(各尺寸由图上量取),分析是否能实现设计意图,并提出修改方案。
解:1)取比例尺,绘制机构运动简图。
(图2-1a)2)要分析是否能实现设计意图,首先要计算机构的自由度。
尽管此机构有4个活动件,但齿轮1和凸轮2是固装在轴A 上,只能作为一个活动件,故 3=n 3=l p 1=h p原动件数不等于自由度数,此简易冲床不能运动,即不能实现设计意图。
分析:因构件3、4与机架5和运动副B 、C 、D 组成不能运动的刚性桁架。
故需增加构件的自由度。
3)提出修改方案:可以在机构的适当位置增加一个活动构件和一个低副,或用一个高副来代替一个低副。
(1) 在构件3、4之间加一连杆及一个转动副(图2-1b)。
(2) 在构件3、4之间加一滑块及一个移动副(图2-1c)。
(3) 在构件3、4之间加一滚子(局部自由度)及一个平面高副(图2-1d)。
在适当位置上添加一个构件(相当于增加3个自由度)和1个低副(相当于引入2个约束),如图2-1(b )(c )所示,这样就相当于给机构增加了一个自由度。
用一个高副代替一个低副也可以增加机构自由度,如图2-1(d )所示。
题2-2 图a 所示为一小型压力机。
图上,齿轮1与偏心轮1’为同一构件,绕固定轴心O 连续转动。
在齿轮5上开有凸轮轮凹槽,摆杆4上的滚子6嵌在凹槽中,从而使摆杆4绕C 轴上下摆动。
同时,又通过偏心轮1’、连杆2、滑杆3使C 轴上下移动。
最后通过在摆杆4的叉槽中的滑块7和铰链G 使冲头8实现冲压运动。
试绘制其机构运动简图,并计算自由度。
解:分析机构的组成:此机构由偏心轮1’(与齿轮1固结)、连杆2、滑杆3、摆杆4、齿轮5、滚子6、滑块7、冲头8和机架9组成。
机械原理习题及答案

机械原理习题及答案-CAL-FENGHAI.-(YICAI)-Company One1兰州2017年7月4日于家属院复习资料第2章平面机构的结构分析1.组成机构的要素是和;构件是机构中的单元体。
2.具有、、等三个特征的构件组合体称为机器。
3.从机构结构观点来看,任何机构是由三部分组成。
4.运动副元素是指。
5.构件的自由度是指;机构的自由度是指。
6.两构件之间以线接触所组成的平面运动副,称为副,它产生个约束,而保留个自由度。
7.机构具有确定的相对运动条件是原动件数机构的自由度。
8.在平面机构中若引入一个高副将引入______个约束,而引入一个低副将引入_____个约束,构件数、约束数与机构自由度的关系是。
9.平面运动副的最大约束数为,最小约束数为。
10.当两构件构成运动副后,仍需保证能产生一定的相对运动,故在平面机构中,每个运动副引入的约束至多为,至少为。
11.计算机机构自由度的目的是______。
12.在平面机构中,具有两个约束的运动副是副,具有一个约束的运动副是副。
13.计算平面机构自由度的公式为F=,应用此公式时应注意判断:(A)铰链,(B)自由度,(C)约束。
14.机构中的复合铰链是指;局部自由度是指;虚约束是指。
15.划分机构的杆组时应先按的杆组级别考虑,机构的级别按杆组中的级别确定。
16.图示为一机构的初拟设计方案。
试:(1〕计算其自由度,分析其设计是否合理如有复合铰链,局部自由度和虚约束需说明。
(2)如此初拟方案不合理,请修改并用简图表示。
23题16图 题17图17.在图示机构中,若以构件1为主动件,试:(1)计算自由度,说明是否有确定运动。
(2)如要使构件6有确定运动,并作连续转动,则可如何修改说明修改的要点,并用简图表示。
18.计算图示机构的自由度,将高副用低副代替,并选择原动件。
19.试画出图示机构的运动简图,并计算其自由度。
对图示机构作出仅含低副的替代机构,进行结构分析并确定机构的级别。
机械原理习题答案

pR12 M A
1ω O
ω 21
2
ω 23
3 pR32
B
P
4
2)确定ω21、ω23 的方向(如图)
pR12
A
ω 21
ω
M 1O
ω 23
2
3
B 4
P PR32
3)判断总反力应切于 A、B 处摩擦圆的上方还是下方(如图)
O
ω
1M
PR1
A
ω 21
2
ω 23
3 P
B 4 PR32
2.在图示曲柄滑块机构中 ,曲柄 1 在驱动力矩 M1 作用下等速转动。设已知各转动副的轴颈半径 r=10mm,当量摩擦系数 fv = 0.15 ,移动副中的滑块摩擦系数 f = 0.15 ,lAB = 100 mm,lBC = 350 mm。 各构件的质量和转动惯量忽略不计。当 M1 = 20 Nm 时,试求机构在图示位置所能克服的有效阻力 F3 及
uuur aBt 1 = 1× 55×102 = 5.5 m s2
uuuuur
ak B 2 B1
=
2
×10
×
0.55
=
11m
s2
uur a3
=
µα
.l p 'b2 '
=
0.2 ×
60
=
12
m
s2
4.已 知 图 所 示 的 机 构 的 尺 寸 及 ω 1=
1rad/s,试用图解法求ω3,a3,vD和 aD。
FR 21 Q
=
sin(π + ϕ ) 2
sin(π − α − 2ϕ )
2
FR 21
=
sin 98.53° sin 12.94°
平面机构的运动分析习题和答案
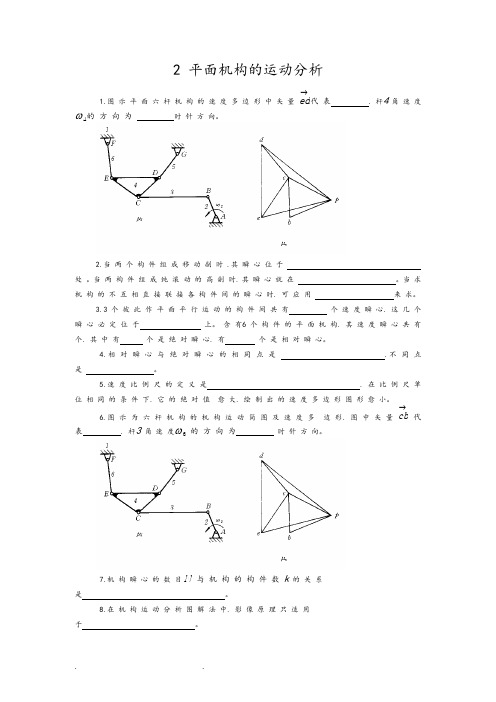
2 平面机构的运动分析1.图 示 平 面 六 杆 机 构 的 速 度 多 边 形 中 矢 量 ed →代 表 . 杆4 角 速 度ω4的 方 向 为时 针 方 向。
2.当 两 个 构 件 组 成 移 动 副 时 .其 瞬 心 位 于 处 。
当 两 构 件 组 成 纯 滚 动 的 高 副 时. 其 瞬 心 就 在 。
当 求 机 构 的 不 互 相 直 接 联 接 各 构 件 间 的 瞬 心 时. 可 应 用 来 求。
3.3 个 彼 此 作 平 面 平 行 运 动 的 构 件 间 共 有 个 速 度 瞬 心. 这 几 个瞬 心 必 定 位 于 上。
含 有6 个 构 件 的 平 面 机 构. 其 速 度 瞬 心 共 有 个. 其 中 有 个 是 绝 对 瞬 心. 有 个 是 相 对 瞬 心。
4.相 对 瞬 心 与 绝 对 瞬 心 的 相 同 点 是 .不 同 点 是 。
5.速 度 比 例 尺 的 定 义 是 . 在 比 例 尺 单 位 相 同 的 条 件 下. 它 的 绝 对 值 愈 大. 绘 制 出 的 速 度 多 边 形 图 形 愈 小。
6.图 示 为 六 杆 机 构 的 机 构 运 动 简 图 及 速 度 多 边 形. 图 中 矢 量 cb →代表 . 杆3 角 速 度ω3 的 方 向 为 时 针 方 向。
7.机 构 瞬 心 的 数 目N 与 机 构 的 构 件 数 k 的 关 系 是 。
8.在 机 构 运 动 分 析 图 解 法 中. 影 像 原 理 只 适 用 于 。
9.当 两 构 件 组 成 转 动 副 时. 其 速 度 瞬 心 在 处; 组 成 移 动 副 时. 其 速 度 瞬 心 在 处; 组 成 兼 有 相 对 滚 动 和 滑 动 的 平 面 高 副 时. 其 速 度 瞬 心 在 上。
10..速 度 瞬 心 是 两 刚 体 上 为 零 的 重 合 点。
11.铰 链 四 杆 机 构 共 有 个 速 度 瞬 心.其 中 个 是 绝 对 瞬 心. 个 是 相 对 瞬 心。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.速度瞬心是两刚体上瞬时速度相等的重合点。
2.若瞬心的绝对速度为零,则该瞬心称为绝对瞬心;
若瞬心的绝对速度不为零,则该瞬心称为相对瞬心。
3.当两个构件组成移动副时,其瞬心位于垂直于导路方向的无穷远处。
当两构件组成高副时,两个高副元素作纯滚动,则其瞬心就在接触点处;若两个高副元素间有相对滑动时,则其瞬心在过接触点两高副元素的公法线上。
4.当求机构的不互相直接联接各构件间的瞬心时,可应用三心定理来求。
5.3个彼此作平面平行运动的构件间共有 3 个速度瞬心,这几个瞬心必定位于一条直线上。
6.机构瞬心的数目K与机构的构件数N的关系是K=N(N-1)/2 。
7.铰链四杆机构共有 6 个速度瞬心,其中 3 个是绝对瞬心。
8.速度比例尺μ
ν
表示图上每单位长度所代表的速度大小,单位为: (m/s)/mm 。
加速度比例尺μa表示图上每单位长度所代表的加速度大小,单位为 (m/s2)/mm。
9.速度影像的相似原理只能应用于构件,而不能应用于整个机构。
10.在摆动导杆机构中,当导杆和滑块的相对运动为平动,牵连运动为转动时(以上两空格填转动或平动),两构件的重合点之间将有哥氏加速度。
哥氏加速度的大小为2×相对速度×牵连角速度;方向为相对速度沿牵连角速度的方向转过90°之后的方向。
二、试求出图示各机构在图示位置时全部瞬心的位置(用符号
ij
P直接标注在图上)。
P
24)
12
三、 在图a 所示的四杆机构中,
l AB =60mm,l CD =90mm ,l AD =l BC =120mm ,ω2=10rad/s ,试用瞬心法求:
1)当φ=165°时,点C 的速度v C ; 2)当φ=165°时,构件3的BC 线上速度最小的一点E 的位置及速度的大小;
3)当v C =0时,φ角之值(有两个解); 解:1)以选定的比例尺μl 作机构运动简图(图b )。
2)求v C ,定出瞬心P 13的位置(图b )
a )
(P 13)
P
P 23→∞
v C =ω33413P P μl =
34132313B
l l
v P P P P μμg g
g =1060583833
⨯⨯⨯⨯≈×174=418(mm/s)
3)定出构件3的BC 线上 速度最小的点E 的位置:
E 点位置如图所示。
v E =ω313EP μl ≈×52×3 =374(mm/s)
4)定出v C =0时机构的两个位置(作于图c ),量出:
φ1≈45° φ2≈27°
想一想:
1.要用瞬心法求解某构件(如构件3)上点的速度,首先需要定出该构件的何种瞬心
2.构件(如构件3)上某点的速度为零,则该点一定就是它的什么瞬心
四、 在图示摆动导杆机构中,∠BAC =90°,L AB =60mm ,L AC =120mm ,曲柄AB 以等角速度ω1=30rad/s 转动。
请按照尺寸按比例重新绘制机构运动简图,试用相对运动图解法求构件3的角速度和角加速度。
解:取长度比例尺mm m l /001.0=μ作机构运动简图 v B2=ω1•l AB =30•60=1800mm/s=1.8m/s
a B2=ω12
AB =3022 3232B B B B v v v =+v v v BC ⊥AB ∥BC
B 1
C 2(P 13)
13
大小: ω1l AB ω1≈6rad/s ,顺时针
3323232n t k r B B B B B B B a a a a a +=++v v v v v
方向:B →C ⊥BC B →A ⊥CB //CB
大小:ω32l BC ω12l AB 2ω2v B3B2 =V μmm s m //
32k B B a v
'p
α1≈210rad/s 2
,逆时针 (注:ω1和α1计算过程略)
五、 图示的各机构中,设已知各构件的尺寸,原动件1以等角速度ω1顺时针方向转动。
试用图解法求机构在图示位置时构件3上C 点的速度及加速度(列出相对运动图解法矢量公式,进行大小、方向分析,最后将下面的速度矢量图和加速度矢量图补充完整。
) 上图中,AB CD BC l l l 2==
C B CB v v v =+v v v n t n t
C C B CB CB a a a a a +=++v v v v v
方向:⊥CD ⊥AB ⊥BC 方向:C →D ⊥CD B →A C →B ⊥CB 大小: ω1l AB 大小:ωCD 2l CD ω12l AB ωCB 2l CB
有:v C
=0,ω3
=0,ω2
=ω
1
a C
= a C
t
= a B
=ω
1 2 l AB
b 3
b 2
b 3’
b
33232C B C B C C C v v v v v
=+=+v v v v v
方向: ⊥AB ⊥BC ∥BC 大小: ω1l AB 0
33323232n t k r C B C B C B C C C C C a a a a a a a =++=++v v v v v
方向: B →A C
→B ⊥CB ∥BC 大小: ω12l AB ω32l CB 0 2ω3v C3C2=0
有:v
C3
=ω1l AB a C3=0
六、已知:在图示机构中,l AB =l BC =l CD =l ,且构件1以ω1匀速转动。
AB 、BC 处于水平位置CD⊥BC,试用相对运动图解法求ω3,α3 (μv 和μa 可任意选择)。
解: 属于两构件间重合点的问题
思路:因已知B 2点的运动,故通过B 2点求B 3点的运动。
1)速度分析
3232B B B B v v v =+v v v
方向:⊥BD ⊥AB ∥CD 大小: ω12l
在速度多边形中,∵b 3与极点p 重合,∴v B3=0
且ω3=v B3/ l BD =0,由于构件2与构件3套在一起,∴ω2=ω3=0
2)加速度分析
33
323232n t n k r B B B B B B B B a a a a a a =+=++v v v v v v 方向: ⊥BD B →A ∥CD 大小: 0 ω12l 0
在加速度多边形中,矢量'
3b πuuu v 代表3t B a v
则有:223
31t
B BD a l αω=== 将矢量'
3b πuuu v
移至B 3点,可见为α3逆时针。
七、已知铰链四杆机构的位置、速度多边形和加速度多边形如下图所示。
试求: ①构件1、2和3上速度均为X v 的点X 1、X 2和X 3的位置; ②构件2上加速度为零的点Q 位置,并求出该点的速度Q v ; ③构件2上速度为零的点H 位置,并求出该点的加速度H a ;
(各速度矢量和加速度矢量的大小任意,但方向必须与此答案相同)
b ´
c。
