第3章-平面机构的运动分析答案
机械工程基础答案(第3章)

co m
50 2mm / mm 25
3-27.设计一滚子对心直动从动件盘形凸轮。已知凸轮顺时 针转动,rb=32mm,rT=8mm,从动件的运动规律为:
ww
w.
kh
匀加速匀 从动件 减速上升 运动 20mm
课
后
答
凸轮转 0°~120° 120°~150° 150°~330° 330°~360° 角
ww
w.
kh
da w.
案
课
后
答
网
co m
作图比例: ul
kh ww w.
da w.
案
AB1 33.1mm, DC1 55.6mm AD 48.3mm
课
后
答
网
l AB 33.1 2 66.2mm, lCD 55.6 2 111.2mm l AD 48.3 2 96.6mm
ww
w.
kh
1. 4 1 180 30 1. 4 1
课
后
答
比例:ul 2mm / mm
da w.
案
网
co m
ww
w.
AB2 17.7 mm, B2C2 46.2mm
l AB AB2 ul 17.7 2 35.4mm l BC B2C2 ul 46.2 2 92.4mm
3-1(C)
ww
w.
复合铰链
kh
da w.
案
网
解:无局部自由度和虚约束 n=8,PL=11,PH=1
后
答
F=3n-2PL–PH = 3×8-2×11-1=1
课
co m
3-1(d)
西工大教材-机械原理各章习题及答案
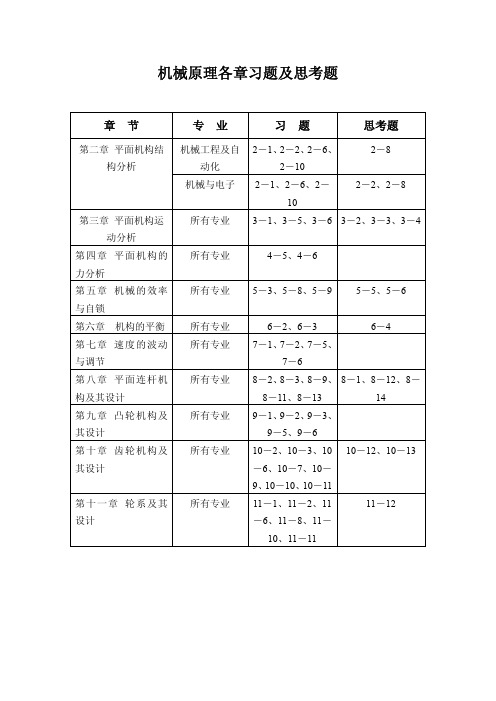
电动机所需的功率为
p = ρ • v /η = 5500 ×1.2 ×10−3 / 0.822 = 8.029(KW )
5-8 在图示斜面机构中,设已知摩擦面间的摩擦系数 f=0.2。求在 G 力作用下(反行程),此斜面 机构的临界自锁条件和在此条件下正行程(在 F 力作用下)的效率。 解 1)反行程的自锁条件 在外行程(图 a),根据滑块的平衡条件:
解 1 ) 取 比 例 尺 μ 1 = 1mm/mm 绘 制 机 构 运 动 简 图 ( 图 b )
(a)
2 )计算该机构的自由度
n=7
pι=9
ph=2(算齿轮副,因为凸轮与齿轮为一体) p’=
F’= F=3n-2pe-ph
=3x7-2x8-2 =1
G7
D 64 C
EF
3
9
B
2
8
A
ω1
b)
2-6 试计算如图所示各机构的自由度。图 a、d 为齿轮一连杆组合机构;图 b 为凸轮一连杆组合 机构(图中在 D 处为铰连在一起的两个滑块);图 c 为一精压机机构。并问在图 d 所示机构中, 齿轮 3 与 5 和齿条 7 与齿轮 5 的啮合高副所提供的约束数目是否相同?为什么?
C3 重合点继续求解。
解 1)速度分析(图 b)取重合点 B2 与 B3,有
方向 大小 ?
v vv vB3 = vB2 + vB3B2 ⊥ BD ⊥ AB // CD ω1lAB ?
D
C
3 d3
ω3
4
ω3 90°
2
B(B1、B2、B3)
ω1
A1 ϕ = 90°
机械原理习题及答案
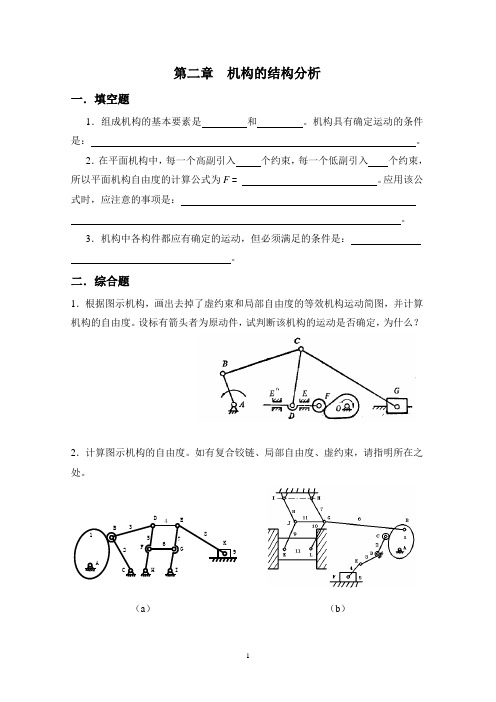
第二章 机构的结构分析一.填空题1.组成机构的基本要素是 和 。
机构具有确定运动的条件是: 。
2.在平面机构中,每一个高副引入 个约束,每一个低副引入 个约束,所以平面机构自由度的计算公式为F = 。
应用该公式时,应注意的事项是: 。
3.机构中各构件都应有确定的运动,但必须满足的条件是: 。
二.综合题1.根据图示机构,画出去掉了虚约束和局部自由度的等效机构运动简图,并计算机构的自由度。
设标有箭头者为原动件,试判断该机构的运动是否确定,为什么?2.计算图示机构的自由度。
如有复合铰链、局部自由度、虚约束,请指明所在之处。
(a ) (b )ADECHGF IBK1234567893.计算图示各机构的自由度。
(a)(b)(c)(d)(e)(f)4.计算机构的自由度,并进行机构的结构分析,将其基本杆组拆分出来,指出各个基本杆组的级别以及机构的级别。
(a)(b)(c)(d)5.计算机构的自由度,并分析组成此机构的基本杆组。
如果在该机构中改选FG 为原动件,试问组成此机构的基本杆组是否发生变化。
6.试验算图示机构的运动是否确定。
如机构运动不确定请提出其具有确定运动的修改方案。
(a)(b)第三章平面机构的运动分析一、综合题1、试求图示各机构在图示位置时全部瞬心的位置(用符号P直接在图上标出)。
ij2、已知图示机构的输入角速度ω1,试用瞬心法求机构的输出速度ω3。
要求画出相应的瞬心,写出ω3的表达式,并标明方向。
3、在图示的齿轮--连杆组合机构中,试用瞬心法求齿轮1与3的传动比ω1/ω2。
4、在图示的四杆机构中,AB l =60mm, CD l =90mm, AD l =BC l =120mm, 2ω=10rad/s ,试用瞬心法求:(1)当ϕ=165°时,点C 的速度c v ;(2)当ϕ=165°时,构件3的BC 线上速度最小的一点E 的位置及其速度的大小; (3)当0c v =u u u v时,ϕ角之值(有两个解)。
《机械原理》第八版课后习题答案

第2章 机构的结构分析(P29)2-12:图a 所示为一小型压力机。
图上,齿轮1与偏心轮1’为同一构件,绕固定轴心O 连续转动。
在齿轮5上开有凸轮轮凹槽,摆杆4上的滚子6嵌在凹槽中,从而使摆杆4绕C 轴上下摆动。
同时,又通过偏心轮1’、连杆2、滑杆3使C 轴上下移动。
最后通过在摆杆4的叉槽中的滑块7和铰链G 使冲头8实现冲压运动。
试绘制其机构运动简图,并计算自由度。
解:分析机构的组成:此机构由偏心轮1’(与齿轮1固结)、连杆2、滑杆3、摆杆4、齿轮5、滚子6、滑块7、冲头8和机架9组成。
偏心轮1’与机架9、连杆2与滑杆3、滑杆3与摆杆4、摆杆4与滚子6、齿轮5与机架9、滑块7与冲头8均组成转动副,滑杆3与机架9、摆杆4与滑块7、冲头8与机架9均组成移动副,齿轮1与齿轮5、凸轮(槽)5与滚子6组成高副。
故解法一:7=n 9=l p 2=h p12927323=-⨯-⨯=--=h l p p n F解法二:8=n 10=l p 2=h p 局部自由度1='F11210283)2(3=--⨯-⨯='-'-+-=F p p p n F h l(P30) 2-17:试计算如图所示各机构的自由度。
图a 、d 为齿轮-连杆组合机构;图b 为凸轮-连杆组合机构(图中在D 处为铰接在一起的两个滑块);图c 为一精压机机构。
并问在图d 所示机构中,齿轮3与5和齿条7与齿轮5的啮合高副所提供的约束数目是否相同?为什么?解: a) 4=n 5=l p 1=h p11524323=-⨯-⨯=--=h l p p n Fb) 5=n 6=l p 2=h p12625323=-⨯-⨯=--=h l p p n F12625323=-⨯-⨯=--=h l p p n Fc) 5=n 7=l p 0=h p10725323=-⨯-⨯=--=h l p p n Fd) 6=n 7=l p 3=h p13726323=-⨯-⨯=--=h l p p n F(C 可看做是转块和导块,有1个移动副和1个转动副)齿轮3与齿轮5的啮合为高副(因两齿轮中心距己被约束,故应为单侧接触)将提供1个约束。
机械原理习题提示(华东理工)

第2章机构的组成原理与结构分析第3章平面机构的运动分析一、填空题1、在平面机构中具有一个约束的运动副是副。
2、使两构件直接接触并能产生一定相对运动的联接称为。
3、平面机构中的低副有转动副和副两种。
4、平面机构中的低副有副和移动副两种。
5、机构中的构件可分为三类:固定构件(机架)、原动件(主动件)、件。
6、机构中的构件可分为三类:固定构件(机架)、从动件。
7、机构中的构件可分为三类:、原动件(主动件)、从动件。
8、在平面机构中若引入一个高副将引入个约束。
9、在平面机构中若引入一个低副将引入个约束。
10、在平面机构中具有两个约束的运动副是副。
11、速度瞬心是两刚体上为零的重合点。
12、当两构件组成回转副时,其相对速度瞬心在。
13、当两构件不直接组成运动副时,其瞬心位置用确定。
二、判断题1、具有局部自由度的机构,在计算机构的自由度时,应当首先除去局部自由度。
()2、具有虚约束的机构,在计算机构的自由度时,应当首先除去虚约束。
()3、虚约束对运动不起作用,也不能增加构件的刚性。
()4、若两个构件之间组成两个导路平行的移动副,在计算自由度时应算作两个移动()5、若两个构件之间组成两个轴线重合的转动副,在计算自由度时应算作两个转动副。
()6、六个构件组成同一回转轴线的转动副,则该处共有三个转动副。
()7、当机构的自由度F>0,且等于原动件数,则该机构具有确定的相对运动。
()8、虚约束对机构的运动有限制作用。
()9、瞬心是两构件上瞬时相对速度为零的重合点。
()10、利用瞬心既可以求机构的速度,又可以求加速度。
()三、选择题1、机构中的构件是由一个或多个零件所组成,这些零件间产生相对运动。
A、可以B、不能C、不一定能2、原动件的自由度应为。
A、0B、1C、23、在机构中原动件数目机构的自由度时,该机构具有确定的运动。
A、大于B、等于C、小于4、机构具有确定运动的条件是。
A、自由度大于零B、自由度等于原动件数C、自由度大于15、由K 个构件汇交而成的复合铰链应具有个转动副。
机械原理习题参考答案

习题参考答案第二章机构的结构分析2-2 图2-38所示为一简易冲床的初拟设计方案。
设计者的思路是:动力由齿轮1输入,使轴A连续回转;而固装在轴A上的凸轮2与杠杆3组成的凸轮机构将使冲头4上下运动以达到冲压的目的。
试绘出其机构运动简图,分析其运动是否确定,并提出修改措施。
4351 2解答:原机构自由度F=3⨯3- 2 ⨯4-1 = 0,结构均可:1为滚子;2为摆杆;3为滑块;4为滑杆;5为齿轮及凸轮;6为连杆;7为齿轮及偏心轮;8为机架;9为压头。
试绘制其机构运动简图,并计算其自由度。
O齿轮及偏心轮ωA齿轮及凸轮BEFDC压头机架连杆滑杆滑块摆杆滚子解答:n=7; P l =9; P h =2,F=3⨯7-2 ⨯9-2 = 12-6 试计算图2-42所示凸轮—连杆组合机构的自由度。
解答:a) n=7; P l =9; P h =2,F=3⨯7-2 ⨯9-2 =1 L 处存在局部自由度,D 处存在虚约束b) n=5; P l =6; P h =2,F=3⨯5-2 ⨯6-2 =1 E 、B 处存在局部自由度,F 、C 处存在虚约束b)a)A EMDFELKJIFBCCDBA2-7 试计算图2-43所示齿轮—连杆组合机构的自由度。
BDCA(a)CDBA(b)解答:a) n=4; P l =5; P h =1,F=3⨯4-2 ⨯5-1=1 A 处存在复合铰链b) n=6; P l =7; P h =3,F=3⨯6-2 ⨯7-3=1 B 、C 、D 处存在复合铰链2-8 试计算图2-44所示刹车机构的自由度。
并就刹车过程说明此机构自由度的变化情况。
解答:① 当未刹车时,F=3⨯6-2 ⨯8=2② 在刹车瞬时,F=3⨯5-2⨯7=1,此时构件EFG 和车轮接触成为一体,位置保持不变,可看作为机架。
③ 完全刹死以后,F=3⨯4-2⨯6=0,此时构件EFG 、HIJ 和车轮接触成为一体,位置保持不变,可看作为机架。
平面机构的运动分析习题和答案Word版
24.在同一构件上.任意两点的绝对加速度间的关系式中不包含哥氏加速度。- - - - ( )
25.当牵连运动为转动.相对运动是移动时.一定会产生哥氏加速度。- - - - - - - - ( )
26.在平面机构中.不与机架直接相连的构件上任一点的绝对速度均不为零。- - - ( )
27.两构件组成一般情况的高副即非纯滚动高副时.其瞬心就在高副接触点处。- - ( )
28.给定导杆机构在图示位置的速度多边形。该瞬时 和 的正确组合应是图。
29.给定图示六杆机构的加速度多边形.可得出
(A)矢量 代表 . 是顺时针方向;
(B)矢量 代表 . 是逆时针方向;
(C)矢量 代表 . 是顺时针方向;
(A)绝对速度等于零的重合点;
(B)绝对速度和相对速度都等于零的重合点;
(C)绝对速度不一定等于零但绝对速度相等或相对速度等于零的重合点。
40.下图是四种机构在某一瞬时的位置图。在图示位置哥氏加速度不为零的机构为。
41.利用相对运动图解法求图示机构中滑块2上 点的速度 的解题过程的恰当步骤和利用的矢量方程为:
9.当两构件组成转动副时.其速度瞬心在处;组成移动副时.其速度瞬心在处;组成兼有相对滚动和滑动的平面高副时.其速度瞬心在上。
10..速度瞬心是两刚体上为零的重合点。
11.铰链四杆机构共有个速度瞬心.其中个是绝对瞬心.个是相对瞬心。
12.速度影像的相似原理只能应用于的各点.而不能应用于机构的的各点。
13.作相对运动的3个构件的3个瞬心必。
14.当两构件组成转动副时.其瞬心就是。
15.在摆动导杆机构中.当导杆和滑块的相对运动为动.牵连运动为动时.两构件的重合点之间将有哥氏加速度。哥氏加速度的大小为;方向与的方向一致。
平面机构的运动分析习题和答案
2 平面机构的运动分析1.图 示 平 面 六 杆 机 构 的 速 度 多 边 形 中 矢 量 ed →代 表 . 杆4 角 速 度ω4的 方 向 为时 针 方 向。
2.当 两 个 构 件 组 成 移 动 副 时 .其 瞬 心 位 于 处 。
当 两 构 件 组 成 纯 滚 动 的 高 副 时. 其 瞬 心 就 在 。
当 求 机 构 的 不 互 相 直 接 联 接 各 构 件 间 的 瞬 心 时. 可 应 用 来 求。
3.3 个 彼 此 作 平 面 平 行 运 动 的 构 件 间 共 有 个 速 度 瞬 心. 这 几 个瞬 心 必 定 位 于 上。
含 有6 个 构 件 的 平 面 机 构. 其 速 度 瞬 心 共 有 个. 其 中 有 个 是 绝 对 瞬 心. 有 个 是 相 对 瞬 心。
4.相 对 瞬 心 与 绝 对 瞬 心 的 相 同 点 是 .不 同 点 是 。
5.速 度 比 例 尺 的 定 义 是 . 在 比 例 尺 单 位 相 同 的 条 件 下. 它 的 绝 对 值 愈 大. 绘 制 出 的 速 度 多 边 形 图 形 愈 小。
6.图 示 为 六 杆 机 构 的 机 构 运 动 简 图 及 速 度 多 边 形. 图 中 矢 量 cb →代表 . 杆3 角 速 度ω3 的 方 向 为 时 针 方 向。
7.机 构 瞬 心 的 数 目N 与 机 构 的 构 件 数 k 的 关 系 是 。
8.在 机 构 运 动 分 析 图 解 法 中. 影 像 原 理 只 适 用 于 。
9.当 两 构 件 组 成 转 动 副 时. 其 速 度 瞬 心 在 处; 组 成 移 动 副 时. 其 速 度 瞬 心 在 处; 组 成 兼 有 相 对 滚 动 和 滑 动 的 平 面 高 副 时. 其 速 度 瞬 心 在 上。
10..速 度 瞬 心 是 两 刚 体 上 为 零 的 重 合 点。
11.铰 链 四 杆 机 构 共 有 个 速 度 瞬 心.其 中 个 是 绝 对 瞬 心. 个 是 相 对 瞬 心。
机械原理第八版答案与解析
机械原理第八版答案与解析Prepared on 22 November 2020机械原理第八版 西北工业大学平面机构的结构分析1、如图a 所示为一简易冲床的初拟设计方案,设计者的思路是:动力由齿轮1输入,使轴A 连续回转;而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构将使冲头4上下运动以达到冲压的目的。
试绘出其机构运动简图(各尺寸由图上量取),分析其是否能实现设计意图并提出修改方案。
解 1)取比例尺l μ绘制其机构运动简图(图b )。
2)分析其是否能实现设计意图。
图 a )由图b 可知,3=n ,4=l p ,1=h p ,0='p ,0='F 故:00)0142(33)2(3=--+⨯-⨯='-'-+-=F p p p n F h l因此,此简单冲床根本不能运动(即由构件3、4与机架5和运动副B 、C 、D 组成不能运动的刚性桁架),故需要增加机构的自由度。
图 b )3)提出修改方案(图c )。
为了使此机构能运动,应增加机构的自由度(其方法是:可以在机构的适当位置增加一个活动构件和一个低副,或者用一个高副去代替一个低副,其修改方案很多,图c 给出了其中两种方案)。
图 c1) 图 c2)2、试画出图示平面机构的运动简图,并计算其自由度。
图a )解:3=n ,4=l p ,0=h p ,123=--=h l p p n F图 b )解:4=n ,5=l p ,1=h p ,123=--=h l p p n F3、计算图示平面机构的自由度。
将其中的高副化为低副。
机构中的原动件用圆弧箭头表示。
3-1解3-1:7=n ,10=l p ,0=h p ,123=--=h l p p n F ,C 、E 复合铰链。
3-2解3-2:8=n ,11=l p ,1=h p ,123=--=h l p p n F ,局部自由度 3-3解3-3:9=n ,12=l p ,2=h p ,123=--=h l p p n F 4、试计算图示精压机的自由度解:10=n ,15=l p ,0=h p 解:11=n ,17=l p ,0=h p (其中E 、D 及H 均为复合铰链) (其中C 、F 、K 均为复合铰链)5、图示为一内燃机的机构简图,试计算其自由度,并分析组成此机构的基本杆组。
机械原理第三章习题答案
第三章 平面机构的运动分析习题3-1图1.a 图1.b图1.c 图1.d习题3-2由于齿轮是纯滚动,因此1、2齿轮的瞬心为12P ,2、3的瞬心为23P ,根据三心定量,齿轮1、3的瞬心一定在直线2312P P 与直线3616P P 的交点上,即图示13P,在该点处的速度有 l l P P P P P v μωμω133631316113==故齿轮3的角速度为1336131613P P P ωω=。
传动比为1316133631P P P P =ωω。
习题3-3答:1)三个瞬心中,14P 、12P 为绝对瞬心,24P 为相对瞬心。
2)不利用其它的三个瞬心,因为它们全是相对瞬心。
3)构件2和4之间的转向关系可以根据瞬心24P 的瞬时绝对速度方向判断。
习题3-4 取比例尺为mmm l 003.0=μ,作图如下1) 由图上可知:l l P P P P P v μωμω241442412224==,根据量得的长度,得s rad P P P P /455.414.72/14.32102414241224=⨯==ωω 可计算出C 点的速度为:s m CD v l C /4.0003.030455.44=⨯⨯==μω2) 构件1、3的瞬心在点13P 处,且为绝对瞬心,因此构件3的角速度为 ()s rad C P v l c /53.2)67.52003.0/(4.0133=⨯==μω 显然构件3上速度最小点在E 点,则其速度为s m EP v l E /36.0003.04.4753.2133=⨯⨯==ω3) 要使0=C v ,需瞬心12P 、24P 重合(如图),两位置分别为0126'=∠=DAB ϕ,02227''=∠=DAB ϕ。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、填空题:
1.速度瞬心是两刚体上瞬时速度相等的重合点。
2.若瞬心的绝对速度为零,则该瞬心称为绝对瞬心;
若瞬心的绝对速度不为零,则该瞬心称为相对瞬心。
3.当两个构件组成移动副时,其瞬心位于垂直于导路方向的无穷远处。
当两构件组成高副时,两个高副元素作纯滚动,则其瞬心就在接触点处;若两个高副元素间有相对滑动时,则其瞬心在过接触点两高副元素的公法线上。
4.当求机构的不互相直接联接各构件间的瞬心时,可应用三心定理来求。
5.3个彼此作平面平行运动的构件间共有 3 个速度瞬心,这几个瞬心必定位于一条直线上。
6.机构瞬心的数目K与机构的构件数N的关系是K=N(N-1)/2 。
7.铰链四杆机构共有 6 个速度瞬心,其中 3 个是绝对瞬心。
表示图上每单位长度所代表的速度大小,单位为: (m/s)/mm 。
8.速度比例尺μ
ν
加速度比例尺μa表示图上每单位长度所代表的加速度大小,单位为 (m/s2)/mm。
9.速度影像的相似原理只能应用于构件,而不能应用于整个机构。
10.在摆动导杆机构中,当导杆和滑块的相对运动为平动,牵连运动为转动时(以上两空格填转动或平动),两构件的重合点之间将有哥氏加速度。
哥氏加速度的大小为2×相对速度×牵连角速度;方向为相对速度沿牵连角速度的方向转过90
°之后的方向 。
二、试求出图示各机构在图示位置时全部瞬心的位置(用符号ij P 直接标注在图上)。
12
三、 在图a
所示的四杆机构中,
24)
14(P 13)
P
24
P 23→∞
l AB =60mm,l CD =90mm ,l AD =l BC =120mm ,ω2=10rad/s ,试用瞬心法求:
1)当φ=165°时,点C 的速度v C ;
2)当φ=165°时,构件3的BC 线上速度最小的一点E 的位置及速度的大小; 3)当v C =0时,φ角之值(有两个解); 解:1)以选定的比例尺μl 作机构运动简图(图b )。
2)求v C ,定出瞬心P 13的位置(图b )
v C =ω33413P P μl =
34132313B
l
l
v P P P P μμ =1060583833
⨯⨯⨯⨯≈2.4×174=418(mm/s)
3)定出构件3的BC 线上 速度最小的点E 的位置:
E 点位置如图所示。
v E =ω313EP μl ≈2.4×52×3 =374(mm/s)
4)定出v C =0时机构的两个位置(作于图c ),量出:
φ1≈45° φ2≈27°
想一想:
1.要用瞬心法求解某构件(如构件3)上点的速度,首先需要定出该构件的何种瞬心?
2.构件(如构件3)上某点的速度为零,则该点一定就是它的什么瞬心?
四、 在图示摆动导杆机构中,∠BAC =90°,L AB =60mm ,L AC =120mm ,曲柄AB 以等角速度ω1=30rad/s 转动。
请按照尺寸按比例重新绘制机构运动简图,试用相对运动图解法求构件3的角速度和角加速度。
B 1
P 13
解:取长度比例尺mm m l /001.0=μ作机构运动简图 v B2=ω1•l AB =30•60=1800mm/s=1.8m/s
a B2=ω12•l AB =302•60=54m/s 2
3232B B B B v v v =+BC ⊥AB ∥BC
? ω1l AB ? 6rad/s ,顺时针
323232t k r B B B B B B a a a a +=++
⊥BC B →A ⊥CB //CB
? ω12l AB 2ω2v B3B2 ? =V μ0.1mm s m // 'p 11)
五、 图示的各机构中,设已知各构件的尺寸,原动件1以等角速度ω1顺时针方向转动。
试用图解法求机构在图示位置时构件3上C 点的速度及加速度(列出相对运动图解法矢量公式,进行大小、方向分析,最后将下面的速度矢量图和加速度矢量图补充完整。
b 3
b b 3’
’’
)
上图中,AB CD BC l l l 2==
C B CB v v v =+ n t n t
C
C B CB CB a a a a a +=++ 方向:⊥C
D ⊥AB ⊥BC 方向:C →D ⊥CD B →A C →B ⊥CB 大小: ? ω1l AB ? 大小:ωCD 2l CD ? ω12l AB ωCB 2l CB ?
有:v C
=0,ω3
=0,ω2
=0.5ω
1
a C
= a
C
t =1.5 a B =1.5ω1 2 l AB
3
3232C B C B C C C v v v v v =+=+
方向: ? ⊥AB ⊥BC ∥BC 大小: ? ω1l AB ? 0 ?
33323232n t k r C B C B C B C C C C C a a a a a a a =++=++
方向: ? B →A C →B ⊥CB ∥BC 大小: ? ω12l AB ω32l CB ? 0 2ω3v C3C2=0 ?
有:v
C3
=ω1l AB a C3=0
六、已知:在图示机构中,l AB =l BC =l CD =l ,且构件1以ω1匀速转动。
AB 、BC 处于水平位置CD⊥BC,试用相对运动图解法求ω3,α3 (μv 和μa 可任意选择)。
解: 属于两构件间重合点的问题
思路:因已知B 2点的运动,故通过B 2点求B 3点的运动。
1)速度分析
3232B B B B v v v =+
方向:⊥BD ⊥AB ∥CD 大小: ? ω12l ?
在速度多边形中,∵b 3与极点p 重合,∴v B3=0
且ω3=v B3/ l BD =0,由于构件2与构件3套在一起,∴ω2=ω3=0 2)加速度分析
333232
32
n
t n k r B B B B B B B B a a a a a
a
=+=++
方向: ⊥BD B →A ∥CD 大小: 0 ? ω12l 0 ? 在加速度多边形中,矢量'3b π代表3t
B a
则有:223
31t
B BD a l αω=== 将矢量'
3b π移至B 3点,可见为α3逆时针。
七、已知铰链四杆机构的位置、速度多边形和加速度多边形如下图所示。
试求:
32B B v
3t
B a
32r B B a
①构件1、2和3上速度均为
v的点X1、X2和X3的位置;
X
②构件2上加速度为零的点Q位置,并求出该点的速度
v;
Q
③构件2上速度为零的点H位置,并求出该点的加速度
a;
H
(各速度矢量和加速度矢量的大小任意,但方向必须与此答案相同)
b ´
c
(注:可编辑下载,若有不当之处,请指正,谢谢!)。
