第八章刚体的平面运动习题解答资料
合肥工业大学理论力学答案08刚体平面运动
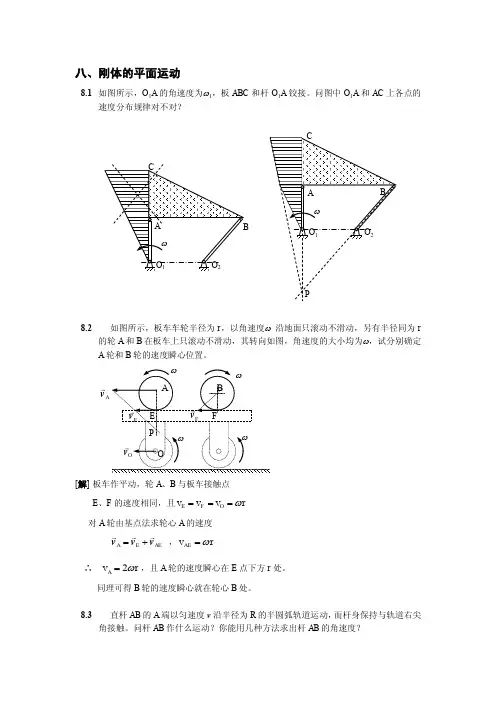
八、刚体的平面运动8.1 如图所示，O 1A 的角速度为ω1，板ABC 和杆O 1A 铰接。
问图中O 1A 和AC 上各点的速度分布规律对不对？8.2如图所示，板车车轮半径为r ，以角速度ω 沿地面只滚动不滑动，另有半径同为r 的轮A 和B 在板车上只滚动不滑动，其转向如图，角速度的大小均为ω，试分别确定A 轮和B 轮的速度瞬心位置。
[解] 板车作平动，轮A 、B 与板车接触点 E 、F 的速度相同，且r v v v O F E ω=== 对A 轮由基点法求轮心A 的速度 A E AE =+v v v ，r v AE ω=∴ r v A ω2=，且A 轮的速度瞬心在E 点下方r 处。
同理可得B 轮的速度瞬心就在轮心B 处。
8.3直杆AB 的A 端以匀速度v 沿半径为R 的半圆弧轨道运动，而杆身保持与轨道右尖角接触。
问杆AB 作什么运动？你能用几种方法求出杆AB 的角速度？E FPOE v Av Fv Ov[解] AB 杆作平面运动。
(一) 瞬心法AB 杆作平面运动，速度瞬心为P 。
Rv AP v AAB2==ω (二)基点法D A DA =+v v v ，DA v v AB A DA ωθ==sin又 DA ＝2R cos(90o －θ)＝2R sin θ ∴ Rv AB 2=ω(三)自然法： d d AB tϕω=，而R S ϕ2= ∴d d 2d d S R v t t ϕ==， d d 2vt R ϕ= ∴ Rv AB 2=ω 8.4如图所示四连杆机构OABO 1中，OA=O 1B=AB/2，曲柄OA 的角速度ω=3rad/s 。
当OA 转到与OO 1垂直时，O 1B 正好在OO 1的延长线上，求该瞬时AB 杆的角速度ωAB 和曲柄O 1B 的角速度ω1。
[解]取AB 为研究对象，AB 作平面运动。
以A 为基点，画B 点速度合成图 由B A BA =+v v v(rad/s)32230sin o==∴⋅=⋅==ωωωωAB OAAB OA v v AB AB ABABBBvvvDAv Dv Dv111cos3022(rad/s)B BAv v OA O Bωωω=︒=⋅=∴=8.5图示曲柄摇机构中，曲柄OA以角速度oω绕O轴转动，带动连杆AC在摇块B内滑动，摇块及与其固结的BD杆绕B铰转动，杆BD长l；求在图示位置时摇块的角速度及D点的速度。
理论力学-刚体的平面运动案例
大小 0
?
2 AB
AO
?
2evr
方向
沿aet方向投影
0
at e
aC
at e
aC
3v 2 4l
AB
aet AO
3 3v2 8l 2
另解： 1.取坐标系Oxy
2. A点的运动方程
xA l cot
3.速度、加速度
xA l sin 2 v
v sin 2
l
v l
sin
2
v2 l2
aB
aA
at BA
an BA
ar
aC
大小 aB
aA ?
2 AE
AB
?
2 AE vr
方向
沿
a
t B
方A 向投影
aB
cos 30o
aA
sin 30o
at BA
aC
沿 a方r 向投影
aB
sin 30
aA
cos 30
an BA
ar
ar 65 mm s2
AE
at BA
AB
3 rad s2 6
第八章 刚体的平面运动
例8-1 已知：椭圆规尺的A端以速度vA沿x 轴的负向运动， 如图所示，AB=l。
求：B端的速度以及尺AB的角速度。
解： 1. AB作平面运动 基点： A
2. vB vA vBA 大小 ？ vA ? 方向
vB vA cot
vBA
vA
sin
AB
vBA l
vA
l sin
DE
vD DE
vB l
5rad
s
BD
vDB BD
《理论力学》第八章_刚体的平面运动习题解
vE
vO
v0
1 (157.05 52.35) 52.35(mm / s) （方向：向上。） 2
vD
[习题8-6] 两刚体Ｍ，Ｎ用铰Ｃ连结，作平面平行运动。已知ＡＣ＝ＢＣ＝６００ｍｍ，在图 示位置，ｖＡ＝２００ｍｍ／ｓ， ｖＢ＝１００ｍｍ／ｓ，方向如图所示。试求Ｃ点的速度。 解：
y
x
'
O
'
B
vB
300
A
60
0
O
0 v A
解：
v A OA 0 200 3 600(rad / s)
v B v A v BA [v B ] AB [v A ] AB
v B cos 30 0 v A 600
vB 600 692.84(mm / s) 0.866
C3 0
A
Rr t 2 2r
故，动齿轮以中心Ａ为基点的平面运动方程为：
x A ( R r ) cos y A ( R r ) sin
t 2
2
t 2
2
A
Rr t 2 2r
[习题8-3] 试证明：作平面运动的平面图形内任意两点的连线中点的速度等于该两点速度的矢 量和之一半。 已知：如图所示， AC CB ， 求证： vC 证明：
300
v B v A v BA
ve
O
vBA AB 200 2 400(mm / s)
v B v A v BA 2v A v BA cos 150 0
2 2
5332 400 2 2 533 400 0.866
工程力学 第八章 刚体的平面运动
例8.1.曲柄连杆机构OA=AB=l，曲柄OA以匀 转动。 求： 当 =45º 时, 滑块B的速度及AB杆的角速度。 a.基点法; b.速度投影法 解：机构中,OA作定轴转动, AB作平面运动,滑块B作平移。
基点法
研究 AB，以 A为基点， 且 v A l , 方向如图示。 根据
vB vA vBA ,
va ve vr vB vA vBA
所以，任意A，B两点，若A为基点，则：
v
B
v
A
v
BA
v
B
v
A
v
BA
平面图形内任一点的速度等于基点的速度与该点随图形绕 基点转动速度的矢量和。这种求解速度的方法称为基点法．
其中
vBA
大小
vBA AB
方向垂直于 AB ，指向同
2 l ( )
在Ｂ点做速度平行四边形，如图示。
vB v A / sin l / sin 45 vBA v A /tg l / tg 45 l AB vBA / AB l / l
（
）
速度投影法
研究AB, vA l ,
方向OA, vB方向沿BO直线
因此，图形S 的位置决定于x A , y A , 三个独立的参变量．
平面运动方程
x A f1 (t ) yA f2 ( t ) f 3 (t )
1)当图形S上A点固定不动，则刚体将作定轴转动； 2)当图形S上角不变时（ =常数），则刚体将作平移。
故刚体平面的运动可以看成是平移和转动的合成运动。
根据速度投影定理 vB AB vA AB
vB sin vA
vB v A / sin l / sin 45 2l( )
第八章 刚体平面运动(陆)
B
N
vA = vB = ωr
而轮B作纯滚动，I点为瞬心，所以此刻轮B的角 速度为： v r B B
R R
最后
r v N B NI 2 R 2r R
方向如图
★理论力学电子教案
第8章 刚体平面运动
22
例题8-4
如图所示的行星系中，大齿轮Ⅰ固定，半径为r1；行 星齿轮Ⅱ沿轮Ⅰ只滚而不滑动，半径为r2 。系杆OA角速
即 v A AI v B BI vC CI
相当于定轴转动的计算.
v AI v BI
B
A
vCI
C I
但请注意：I点仅仅此时刻速度为零，一般 情况下，速度瞬心的加速度不等于零，下一瞬 时I的速度也就不再为零了。因此，速度瞬心 在图形本身上和在固定平面上的位置都是随时 间而变的，在不同的瞬时，图形具有不同的速 度瞬心。
△SE
4m
4m
★理论力学电子教案
第8章 刚体平面运动
26
§8-3 平面运动刚体上各点加速度
根据速度基点法的分析，由点的 合成运动方法可以导出平面运动刚 体上各点的加速度计算公式：
ω
a BA n a BA
A α
aB
B
n t a B a A a BA aBA
aA
讨论： 1.φ为常数 2.(xO,yO)为常数 3.O点位置和φ 均变化 刚体作平动
平面图形的位置
定轴转动
平面运动
由此看出，平面运动可以分解为“平动”和“定轴转动”
★理论力学电子教案
第8章 刚体平面运动
4
三、运动分解
平面运动 = “随基点的平动” + “绕基点的转动” 所谓基点，是在平面图形上任意取定的那点。
《理论力学》第八章刚体的平面运动
刚体的平面运动特点
刚体的平面运动具有 连续性，即刚体上任 意一点的运动轨迹都 是连续的。
刚体的平面运动具有 周期性，即刚体的运 动轨迹可以是周期性 的。
刚体的平面运动具有 对称性，即刚体的运 动轨迹可以是对称的。
02
刚体的平面运动分析
刚体的平动分析
平动定义
刚体在平面内沿着某一确定方向作等速直线运动。
详细描述
通过综合分析动能和势能的变化，可以深入理解刚体在平面运动中的能量转换过程。例 如，当刚体克服重力做功时，重力势能转化为动能；当刚体克服摩擦力做功时，机械能 转化为内能。这种能量转换过程遵循能量守恒定律，即系统总能量的变化等于外界对系
统所做的功与系统内能变化之和。
06
刚体的平面运动的实例分析
刚体的平面运动通常可以分为两种类型：纯滚动和滑动。在 纯滚动中，刚体只滚不滑，刚体上任意一点在任意时刻都位 于一个固定的圆周上。在滑动中，刚体既滚又滑，刚体上任 意一点在任意时刻都位于一个变化的圆周上。
刚体的平面运动分类
纯滚动
刚体只滚不滑，刚体上任意一点 在任意时刻都位于一个固定的圆 周上。
滑动
刚体既滚又滑，刚体上任意一点 在任意时刻都位于一个变化的圆 周上。
势能定理
总结词
势能定理描述了势能与其他形式的能量转换的关系。
详细描述
势能定理指出，在刚体的平面运动过程中，非保守力（如摩擦力、空气阻力等）对刚体所做的功等于系统势能的 减少量。非保守力做正功时，系统势能减少；非保守力做负功时，系统势能增加。
动能和势能的综合分析
总结词
在刚体的平面运动中，动能和势能的综合分析有助于理解运动过程中能量的转换和守恒。
做平动，这种运动也是复合运动。
第八章：刚体的平面运动
y
w
M
O
A
B
vA
x
y vMD vM
M
vD O A
D
w vD B
1、求vM
vD= vA= 2m/s vA 基点：D点 x
vMD MD w 2rw 2.12 m S
vM vVM VD O
w VD B
vMD 2.12 m S
vM vM2 x vM2 y 3.8 m
B
C
A II wII
D
wO
O
I
vA wO OA wO (r1 r2 )
分析两轮接触点D
vD＝0
vD vA vDA
0 vA vDA
vDA＝vA＝wO(r1+r2)
wII
vDA DA
wO (r1
r2
r2 )
B
C
vA A II wII
vA D
wO
vDA
O
I
以A为基点，分析点B的速度。
第八章 刚体的平面运动
§8–1 刚体平面运动的概述和运动分解 §8–2 求图形内各点速度的基点法 §8–3 求平面图形内各点速度的瞬心法 §8–4 用基点法求平面图形内各点的加速度 §8–5 运动学综合应用
注重学习分析问题的思想和方法
刚体的平面运动
• 重点 • 刚体平面运动的分解； • 熟练应用各种方法求平面图形上任一 点的速度。 • 求平面图形上任一点的加速度。
3、刚体绕基点转动的角速度ω和角加速度α是刚体自 身的运动量 与基点的选择无关。
注意：
虽然基点可任意选取
选取运动情况已知的点作为基点。
§8-2 求图形内各点速度的基点法
一．基点法
va ve vr
刚体平面运动习题
刚体平面运动习题第八章刚体平面运动的练习1.真或假(勾选正确和交叉错误)8-1。
刚体的平面运动是一种运动，在这种运动中，刚体上的任何一点与固定平面之间的距离总是平行的。
()8-2。
平面图形的运动可以看作基点的平移和围绕基点的旋转的组合。
()8-3。
平面图形上任意两点的速度都相等地投影在一个固定的轴上。
()()()8-6。
瞬时速度中心的速度为零，加速度为零。
()8-7。
刚体的平移也是一种平面运动。
()2。
填空(在横线上写出正确答案)8-8。
在直线轨道上纯滚动时，圆轮与地面接触点的速度为。
8-9。
平面图上任意两点的速度在上投影中相等。
8-10。
瞬时刚体平移时的角速度是:刚体上每个点的速度；每个点的加速度。
3.简短回答问题8-11。
确定图中所示平面运动物体的瞬时速度中心的位置。
AbabaccωOboaωOdbω(b)Co(a)(c)图8-11 (d)8-12。
如果一个刚体在一个平面上运动，下面平面图中A和B的速度方向是正确的吗？问题8-12图(c)8-13。
下图中O1A和AC的速度分布是否正确？8-14。
当圆形车轮在曲线上滚动时，某一瞬时车轮中心的速度vo和加速度ao，而车轮的半径是R，即车轮中心的角度加速度是多少？如何确定瞬时速度中心的加速度的大小和方向？蟹爪兰O1VβA01ωO2P 8-13图8-148-15。
为什么用基点法计算平面图中单个点的加速度时没有科里奥利加速度？4.计算问题8-16。
椭圆规AB由曲柄OC驱动，曲柄OC以均匀的角速度ω O绕O轴旋转。
如图所示，如果以C为基点，OC=BC=AC=r，试着找出椭圆规AB的平面运动方程。
8-17。
半径为R的齿轮由曲柄OA驱动，沿半径为R的固定齿轮滚动，如图所示。
曲柄以均匀的角加速度α绕O轴旋转，并设定初始角速度ω。
角加速度α？0.角落？？0.如果选择移动齿轮的中心C点作为基点，试着找出移动齿轮的平面运动方程。
yay rarαφBMMoxorBx 8-16图ωOO图8-178-18。
第八章刚体的平面运动习题解答
轮O
即
B处，选摇杆为动系，轮O上的B点为动点
向
故
8-23图8-50所示平面机构中，已知套筒A的速度大小 是一常量，当OA连线水平时，OA=AD=R， 。试求该瞬时杆AB的角速度和角加速度。
图8-50
加速度分析
杆AB
以导套C为动系，杆AB上C点为动点
杆BC
故
向
向 （求 ）
8-24图8-51所示机构中曲柄OA长为2l，以匀角速度 绕轴O转动。在图示瞬时，AB=BO，OAD= 。试求此时套筒D相对于杆BC的速度和加速度。
图8-33
瞬心法
基点法
8-7在如图8-34所示的筛动机构中，筛子BC的摆动是由曲柄连杆机构所带动。已知曲柄长OA=0.3m，转速为n=40r/min。当筛子运动到与点O在同一水平线上时， ，试求此时筛子BC的速度。
图8-34
速度投影定理
8-8长为l=1.2m的直杆AB作平面运动，某瞬时其中点C的速度大小为vC=3m/s，方向与AB的夹角为 ，如图8-35所示。试求此时点A可能有的最小速度以及该瞬时杆AB的角速度。
习题
8-1椭圆规尺AB由曲柄OC带动，曲柄以匀角速度 绕轴O转动，初始时OC水平，如图8-28所示。OC=BC=AC=r，取C为基点，试求椭圆规尺AB的平面运动方程。
图8-28
8-2半径为R的圆柱缠以细绳，绳的B端固定在天花板上，如图8-29所示。圆柱自静止下落，其轴心的速度为 ，其中g为常量，h为轴心A至初始位置的距离。试求圆柱的平面运动方程。
圆盘
故
向
即
8-21图8-48所示机构中，圆轮A的半径R=0.2m，圆轮B的半径r=0.1m，两轮均在水平轨道上作纯滚动。在图示瞬时，A轮上C点在最高位置，轮心速度vA=2m/s，加速度aA=2m/s2，试求轮B滚动的角速度和角加速度。
工程力学：第八章 刚体的平面运动
大小
at BA
AB
方向垂直于 AB，指向同
大小 aBnA 2 AB
aBnA 方向由 B指向 A
动力学
研究受力物体的运动与作用力之间的关系
➢质点动力学的基本方程 ➢动量定理 ➢动量矩定理 ➢动能定理
质点动力学
牛顿三定律：
第一定律（惯性定律）
第二定律（力与加速度之间的关系的定律）
第三定律（作用与反作用定律）
刚体绕定轴的转动微分方程
主动力: F1, F2 , , Fn
Jz
d
dt
M z (Fi )
或 J z M z (F )
或
Jz
d2
dt 2
Mz(F)
转动微分方程
简单形状物体的转动惯量计算
(1)均质细直杆对一端的转动惯量
Jz
1 3
ml 2
均质细直杆对中心轴 ml 2
的转动惯量
12
（2）均质薄圆环对中心轴的转动惯量
质点和质点系的动量矩
质点Q对点 O 的动量矩
MO (mv) r mv
对 z 轴的动量矩 M z (mv) MO (mv)xy
z
MO(mv) Mz(mv)
q
O
r
A mv
Q y
A
x
Q
[M O (mv )]z M z (mv )
质点系的动量矩
z
vi
m2
O ri
mi m1
y
x m3 mn
二者关系
求平面图形内各点速度
基点法
已知平面图形内A 点的速度和图形 的角速度，则另一点B 点的速度:
vB vA vBA
其中 vBA AB
速度投影定理
工程力学A 参考习题之刚体的平面运动习题及解答
刚体的平面运动习题及解答已知：OA 的转速n=40r/min,OA=r=0.3 m求：图示瞬时，筛子BC 的速度。
解: A ，B 两点速度如图所示,图中ππω3460n 2==rad/s由速度投影定理得： 0B A cos60.v v = 解出筛子BC 平动的速度为：m/s513.2r 2 v 2v A B ===ω 254.0.==ωCD v D m/s已知：1m.0DE BD OA===,,m 31.0EF =s /rad 4OA =ω;求 EF 杆的角速度ω和滑块F 的速度F v 。
解: 各点速度分析如图所示, AB 杆为瞬时平动,故4.0.OA OA A B ===ωv v m/sBC 杆的速度瞬心为点D ，三角形DEC 绕D 点作定轴转动，得BB CE v B Dv .DE DC.DE v ===v由 FEE Fv v v +=解出462.0cos30v 0E F ==v m/s ，333.1EF FEEF ==v ω rad/s已知：滚子纯滚动，m12r R AB OA====,s /rad 2=ω求 图示瞬时点B 和点C 的速度与加速度。
解: 先作速度分析如图（a ）所示, C2.R A B ===ωv vm/s42rB B ===ωωv rad/s2.828.r 22.C ===ωωB PC v m/s取A 为基点，对B 点作加速度分析如图（a ）所示 有BAn BA A B n B a a a a a ++=+ττ大小：？r vB22R ω ？ 0R BA 2=ω 方向： 如图所示向AB 轴投影得 0a B =τ，故B 点加速度为8rvaa B2Bn B === 2s /m最后取B 为基点，对C 点作加速度分析如图（b ）所示，即CBCB n B C a a a a τ++=大小：？r vB2r B 2ωr rar BB ==τα方向： 如图所示 故C 点加速度为11.31aaa CB2n B2C =+=2s/m已知：r OA =,r 32AB = ，轨道半径2r B O 1=，OA 杆的角速度和角加速度为O ω和O α； 求： 图示瞬时滑块B 的加速度。
东北大学理论力学第八章 刚体的平面运动(作业解析)
⑶ 由速度合成定理求解
va ve vr
? √ √ √
aBA
n aBA v r
C D
大小 方向
? √
aB
va
ve
E
AB
AB
A
va vr ve
3 3 15求解 n aB aA aBA aBA
ω1 ve O1D 6.19 rad/s
Northeastern University
8-23
已知OA=50mm,ω=10 rad/s,θ=β=60°,O1D＝70mm,求摇杆 O1C的角速度和角加速度。 y A vA n aBA a A 60 aBA B ⑶ 取A点为基点, 60 O1 O 由基点法求B vr vB aB 点加速度 D aA v v a D 1 n ve aB aA aBA aBA
绝对运动：直线运动 相对运动：直线运动 牵连运动：平面运动
vA 1 rad/s CA
B
vr
C D
AB
ve
E
A
va
vA
AB杆瞬心为C AB
ve CD AB 0.2 m/s
Northeastern University
8-27
已知AB = 0.4m,vA＝0.2m/s。图示位置,θ= 30°,AD=DB,求此 瞬时DE杆的速度和加速度。
大小 方向 ？ √ √ √ ? √ √ √
a A OA 2
C
n 2 aBA BA AD 0
将此方程沿y方向投影得 0 aA a BA cos30
τ 2a A aBA ω2 aBA AD BA 3 3
《理论力学》第八章-刚体平面运动试题及答案
理论力学8章作业题解8-2 半径为r 的齿轮由曲柄OA 带动，沿半径为R 的固定齿轮滚动。
如曲柄OA 以匀角加速度a 绕O 轴转动，且当运动开始时，角速度00=w ，转角0=j 。
求动齿轮以中心Ａ为基点的平面运动方程。
解：图示，A 轮平面运动的转角为=A j ∠C 3AC 2=j +∠CAC 2由于弧长CC 1=CC 2，故有 ∠CAC 2=r R /j ，所以22/t rr R r r R r R A a j j j j +=+=+=A 轮平面运动方程为ïïîïïíì+=+=+=+=+=22212212)sin()()sin()()cos()(cos )(tr r R t r R r R y t r R r R x A A A a j a j a j8-6两刚体M ，N 用铰C 连结，作平面平行运动。
已知AC=BC=600mm ，在题附图所示位置s mm v s mm v B A /100,/200==，方向如图所示。
试求C 点的速度。
解：由速度投影定理得()()0==BC C BC B v v 。
则v C 必垂直于BC 连线，v C 与AC 连线的夹角为30°。
由()()AC A AC C v v = 即得：s mm v v A C /200== ，方向如题4-6附图示。
解毕。
8-9 图所示为一曲柄机构，曲柄OA 可绕O 轴转动，带动杆AC 在套管B 内滑动，套管B 及与其刚连的BD 杆又可绕通过B 铰而与图示平面垂直的水平轴运动。
已知：OA ＝BD ＝300mm ，OB ＝400mm ，当OA 转至铅直位置时，其角速度ωo ＝2rad/s ，试求D 点的速度。
C 12Aj C解 (1)平面运动方法： 由题可知：BD AC w w =确定AC 杆平面运动的速度瞬心。
套筒中AC 杆上一点速度沿套筒(为什么？)s rad IAOA IA v A AC /72.00=´==w w , s mm BD BD v AC BD D /216=´=´=w w D 点加速度如何分析？关键求AC 杆角加速度(=BD 杆角速度) 基点法，分析AC 杆上在套筒内的点(B’)：(1) tA B n A B A B a a a a ¢¢¢++=r r r r大小：× ∠ ∠ × 方位：× ∠ ∠ ∠ 再利用合成运动方法：动点：套筒内AC 杆上的点B’，动系：套筒。
第8章刚体的平面运动习题
第8章 刚体平面运动习题1.是非题（对画√，错画×）8-1.刚体平面运动为其上任意一点与某一固定平面的距离始终平行的运动。
（ ） 8-2.平面图形的运动可以看成是随着基点的平移和绕基点的转动的合成.( ) 8-3.平面图形上任意两点的速度在某固定轴上投影相等。
（ ） 8-4.平面图形随着基点平移的速度和加速度与基点的选择有关。
（ ） 8-5.平面图形绕基点转动的角速度和角加速度与基点的选择有关。
（ ） 8-6.速度瞬心点处的速度为零，加速度也为零。
（ ） 8-7.刚体的平移也是平面运动。
（ ） 2.填空题（把正确的答案写在横线上）8-8.在平直轨道作纯滚动的圆轮，与地面接触点的速度为 。
8-9.平面图形上任意两点的速度在 上投影相等。
8-10.某瞬时刚体作平移，其角速度为 ；刚体上各点速度 ；各点加速度 。
3.简答题8-11.确定图示平面运动物体的速度瞬心位置。
题8-11图(a) (b)(c)8-12.若刚体作平面运动，下面平面图形上A 、B 的速度方向正确吗？ 题8-12图(a) (b) (c)8-13.下面图形中O 1A 和AC 的速度分布对吗？8-14.圆轮做曲线滚动，某瞬时轮心的速度o v 和加速度o a ，轮的半径为R ，则轮心的角加速度等于多少？速度瞬心点处的加速度大小和方向如何确定？题8-13图B8-15.用基点法求平面图形个点的加速度时，为什么没有科氏加速度？ 4.计算题8-16.椭圆规尺AB 由曲柄OC 带动，曲柄以匀角速度o ω绕O 轴转动，如图所示，若取C 为基点，OC=BC=AC=r ，试求椭圆规尺AB 的平面运动方程。
8-17.半径为r 的齿轮由曲柄OA 带动，沿半径为R 的固定齿轮滚动，如图所示。
曲柄以匀角加速度α绕O轴转动，设初始时角速度0=ω、角加速度0=α、转角0=ϕ，若选动齿轮的轮心C 点为基点，试求动齿轮的平面运动方程。
题8-16图题8-17图8-18.曲柄连杆机构，已知OA =40cm ，连杆AB =1m ，曲柄OA 绕O 轴以转速180=n r/min 匀速转动，如图所示。
刚体平面运动习题课
大小 方向
？ ？
√
BC BC
？ BC
BC
2
√
√
√
A
aA
a CB
a CB
n
t
BC
B
BC
2
aB
1
O1
O2
a A a CA a CA a B a CB a CB
t n t n
两式相等：
大小
方向
√ √
AC
AC
？ AC
AC
2
√ √
BC BC
？ BC
BC
2
√
√
√
√
解出αAC 或 αBC 即可求解 a C
A
aA
AC
AC
a
a CA
t CA
a CB n
n a CB BC
t
BC
B
aB
2
O2
1
O1
图示机构，已知vA为常矢量，匀质圆盘在水平面上做纯滚动， AB杆长l，圆盘半径为R。试求图示位置时圆盘中心O的速度 和加速度。
B
D
60° M A
vA
解：求角速度。 分析：齿轮、齿条AB都做平面一般运动，齿轮纯滚动，M点为齿 轮的速度瞬心，于是D点的速度方向已知，AB的速度瞬心p已知。 几何关系MAD为等边三角形
MD 2 r sin 60 MA
Ap MA tan 60
2r
sin
2
60
cos 60
a CA
t
C
an CA
加速度分析
aC
大小
《理论力学》刚体平面运动习题
[例4] 导槽滑块机构
请看动画
13
[例4] 导槽滑块机构
已知： 曲柄OA= r , 匀角速度 转动, 连杆AB的中点C处连接一 滑在块同C一可水沿平导线槽上O, 1ODA滑动AB,,ABA=Ol,图1C示= 瞬=3时0。O,A,O1三点
求：该瞬时O1D的角速度． 解：OA, O1D均作定轴转动,
根据 va ve vr ，作速度平行四边形
ve vC cos rcos30
3 r
2
又ve O1CO1D
O1D
ve O1C
3 2r l /sin
3r
2l
(
）
2
这是一个需要联合应用点的合成运动和刚体平面运动理论
求解的综合性问题．注意这类题的解法，再看下例．
15
[例5] 平面机构
请 看 动 画
16
4. 基点
可以选择平面图形内任意一点,通常是运动状态已知的点．
1
5. 瞬心（速度瞬心）
任一瞬时,平面图形或扩大部分都唯一存在一个速度为零的
点
瞬心位置随时间改变．
每一瞬时平面图形的运动可视为绕该瞬时瞬心的转
动．这
种瞬时绕瞬心的转动与定轴转动不同．
=0, 瞬心位于无穷远处, 各点速度相同, 刚体作瞬时平
合成运动方法常用来确定两个相接触的物体在接触点处有
相对滑动时的运动关系的传递．
3
二．解题步骤和要点
1. 根据题意和刚体各种运动的定义，判断机构中各刚体的运动 形式．注意每一次的研究对象只是一个刚体．
2. 对作平面运动的刚体，根据已知条件和待求量，选择求解速 度(图形角速度)问题的方法, 用基点法求加速度(图形角加速 度)
8
理论力学(8.4)--刚体的平面运动习题解答
第八章作业答案
1、解 取C 为基点。
将规尺的平面运动分解为随基点的平移和绕基点的转动。
故规尺AB 的平面运动方程为
2、解 筛子BC 作平移，如图b 所示。
3、解 杆AB 作瞬时平移。
杆BC 的速度瞬心在点D，故
由速度投影定理得
杆EF 的速度瞬心在点P
4、解
5、解 （1）杆AB 作曲线平移
以C 为基点，则
（2）ω 为常数，ωC 为常数， 0
=α
6、解 速度分析，如图7b 所示，杆AB 瞬心在点P
加速度分析，如图c 所示。
以A 为基点
7、解 轮A 的瞬心在点P，如图b 所示。
以套筒上点C 为动点，动系固结于杆BE
由速度投影定理得
加速度分析，如图c、d 所示。
以套筒上点C 为动点，BE 为动系。
以B 为基点
8、解 速度分析，如图b 所示。
加速度分析，如图c 所示。
第八章刚体的平面运动习题解答
基点法
瞬心法
8-10在瓦特行星机构中，杆O1A绕轴O1转动，并借连杆AB带动曲柄OB绕轴O转动（曲柄OB活动地装在O轴上），如图8-37所示。齿轮Ⅱ与连杆AB固连于一体，在轴O上还装有齿轮Ⅰ。已知 ；又杆O1A的角速度 。试求当 且 时，曲柄OB和齿轮Ⅰ的角速度。
图8-37
瞬心法
基点法
8-11图8-38所示的双曲柄连杆机构中，滑块B和E用杆BE连接，主动曲柄OA和从动曲柄OD都绕O轴转动。主动曲柄OA作匀速转动，角速度的大小为 。已知各部件的尺寸为： 。试求当曲柄OA垂直于滑块的导轨方向时，从动曲柄OD和连杆DE的角速度。
图8-59
以O为动点，杆AB为动系
(1)速度分析
(2)加速度分析
圆轮O
以O为基点，分析C点
向y
8-33图8-60所示机构中，已知曲柄OA以匀角速度 绕定轴O转动，OA=100mm，l=500mm。在图示位置， ，试确定杆BD的角速度和角加速度。
图8-60
以A为动点，杆AB为动系
(1)速度分析
(2)加速度分析
图8-43
速度分析
加速度分析
8-17边长l=400mm的等边三角板ABC在其所在平面内运动，如图8-44所示。已知某瞬时点A的速度 ，加速度 ，方向均沿AC；点B的速度大小为 ，加速度大小为 。试求该瞬时点C的速度和加速度。
图8-44
即
(1)
向图示x、y方向投影
(2)
向图示x、y方向投影
8-18图8-45所示机构中，曲柄OA长为 ，以匀角速度 绕轴O转动；滑块B可在水平滑槽内滑动。已知AB=AC=2l，在图示瞬时，OA铅直，试求此时点C的速度及加速度。
图8-62
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
习 题8-1 椭圆规尺AB 由曲柄OC 带动，曲柄以匀角速度O ω绕轴O 转动，初始时OC 水平，如图8-28所示。
OC = BC = AC =r ，取C 为基点，试求椭圆规尺AB 的平面运动方程。
图8-28t t r y t r x O O C O C ωϕωω===sin cos8-2 半径为R 的圆柱缠以细绳，绳的B 端固定在天花板上，如图8-29所示。
圆柱自静止下落，其轴心的速度为3/32gh v A =，其中g 为常量，h 为轴心A 至初始位置的距离。
试求圆柱的平面运动方程。
图8-293/32gh v A = 3/22gh v A= 3/g a A = 3/2gt x A = 0=A y )3/(2r gt A =ϕ8-3 杆AB 的A 端以等速v 沿水平面向右滑动，运动时杆恒与一半径为R 的固定半圆柱面相切，如图8-30所示。
设杆与水平面间的夹角为θ，试以角θ表示杆的角速度。
图8-30瞬心法θθθθωcos sin cot sin 2R v Rv AI v A === 基点法θsin v v CA =θθθθωcos sin cot sin 2R v R v CA v CA ===8-4 图8-31所示两平行齿条同向运动，速度分别为v 1和v 2，齿条之间夹一半径为r 的齿轮，试求齿轮的角速度及其中心O 的速度。
图8-31AB B A v v v += ωr v v 221+= rv v 221-=ω OB B O v v v += 2212v v r v v O +=+=ω8-5 两直杆AC 、BC 铰接于点C ，杆长均为l ，其两端A 、B 分别沿两直线运动，如图8-32所示。
当ADBC 成一平行四边形时，m/s 4.0m/s,2.0==B A v v ，试求此时点C 的速度。
图8-32CB B CA A C v v v v v +=+=向x︒=︒+-60cos 30cos B CA A v v v 38.02/3214.02.030cos 60cos =⨯+=︒︒+=B A CA v v v 向ξ︒-=︒-30cos 60cos CB B A v v v3130cos 60cos =︒︒+=A B CB v v v m/s 306.038.023314.02314.030cos 2222==⨯⨯⨯-+=︒-+=CB B CB B C v v v v v8-6 图8-33所示机构中，OA =200mm ，AB =400mm ，BD =150mm ，曲柄OA 以匀角速度rad/s 4=ω绕轴O 转动。
当︒=45θ时，连杆AB 恰好水平、BD 铅直，试求该瞬时连杆AB 及构件BD 的角速度。
图8-33瞬心法800==ωOA v Arad/s 414.122400800====AB A AB AI v ω24002400=⨯==AB AB B BI v ωrad/s 711.32381502400====BD v B BD ω 基点法8-7 在如图8-34所示的筛动机构中，筛子BC 的摆动是由曲柄连杆机构所带动。
已知曲柄长OA =0.3m ，转速为n =40r/min 。
当筛子运动到与点O 在同一水平线上时，∠︒=90OAB ，试求此时筛子BC 的速度。
图8-34π4.04030π3.0=⨯⨯==ωOA v A 速度投影定理 A B v v =︒60cosm/s 2512.0π8.0260cos ===︒=A AB v v v8-8 长为l =1.2m 的直杆AB 作平面运动，某瞬时其中点C 的速度大小为v C =3m/s ，方向与AB 的夹角为︒60，如图8-35所示。
试求此时点A 可能有的最小速度以及该瞬时杆AB 的角速度。
图8-35︒-+=30cos 222AC C AC C A v v v v v对AC v 求导，并令其等于0，得︒=30cos C AC v v 即AC A v v ⊥时m/s 5.130sin =︒=C A v v ︒=30cos C AC v vrad/s 33.435.26.0233==⨯==AC v AC ABω8-9 如图8-36所示的四连杆机构中，连杆AB 上固连一块直角三角板ABC ，曲柄O 1A 的角速度恒为rad/s 21=ω，已知O 1A =0.1m ，O 1 O 2=AC ＝0.05m ，当O 1A 铅直时，AB 平行于O 1 O 2，且AC 与O 1A 在同一直线上，︒=30ϕ 。
试求此时直角三角板ABC 的角速度和点C 的速度。
图8-36基点法m/s 2.021.01=⨯==ωA O v Am/s 32.030tan =︒=A BA v vrad/s 0718.1135.021.0305.02.031.005.032.0=+=+=+==AB v BA ABC ωm/s 2536.00718.105.02.0=⨯+=+=+=ABC A CA A C AC v v v v ω瞬心法305.01.030cot 05.01.011+=︒+=+=I O A O AI m/s 2.021.01=⨯==ωA O v Arad/s 0718.1305.01.02.0=+==AI v A ABC ωm/s 2536.00718.1)305.01.005.0(=⨯++==ABC C CI v ω8-10 在瓦特行星机构中，杆O 1A 绕轴O 1转动，并借连杆AB 带动曲柄OB 绕轴O 转动（曲柄OB 活动地装在O 轴上），如图8-37所示。
齿轮Ⅱ与连杆AB 固连于一体，在轴O 上还装有齿轮Ⅰ。
已知m 5.1m,75.0m,33.0121====AB A O r r ；又杆O 1A 的角速度rad/s 61=O ω 。
试求当︒=60γ 且︒=90β 时，曲柄OB 和齿轮Ⅰ的角速度。
图8-37瞬心法360cos =︒=ABAI 35.160tan =︒=AB BIm/s 5.4675.011=⨯==O A A O v ωrad/s 5.135.4===AI v A AB ωm/s 325.25.135.1=⨯==AB B BI v ω rad/s 75.336.0325.2===OB v B OB ω m/s 38.15.1)33.035.1(=⨯-==AB C CI v ω rad/s 633.038.1I ===OC v C ω 基点法m/s 5.4675.011=⨯==O A A O v ωm/s 325.2235.430cos =⨯=︒=A B v v rad/s 75.336.0325.2===OB v B OB ω m/s 25.230sin =︒=A BA v vrad/s 5.15.155.2===AB v BA AB ωm/s 38.15.133.0325.2=⨯-=-=CB B C v v v r a d /s633.038.1I ===OC v C ω8-11 图8-38所示的双曲柄连杆机构中，滑块B 和E 用杆BE 连接，主动曲柄OA 和从动曲柄OD 都绕O 轴转动。
主动曲柄OA 作匀速转动，角速度的大小为rad/s 12=O ω。
已知各部件的尺寸为：m 312.0m,12.0m,26.0m,12.0m,1.0=====DE BE AB OD OA 。
试求当曲柄OA 垂直于滑块的导轨方向时，从动曲柄OD 和连杆DE 的角速度。
图8-38m 24.01.026.02222=-=-=OA AB OB m 12.012.024.0=-=-=EB OB OE 杆AB 瞬时平动m/s 2.1121.0=⨯==O A OA v ωm/s 2.1==A B v v杆EB 平动m/s 2.1==B E v v杆DE 平面运动(瞬心法)︒=∠=∠=∠30EIO DEO EDO312.0==DE EI 36.0=DIrad/s 3310310312.02.1====EI v E DE ω m/s 32.1331036.0=⨯==DE D DI v ω rad/s 31012.032.1===OD v D OD ω加速度分析(讨论) 杆AB 瞬时平动222m/s 4.14121.0=⨯==O A OA a ω2m/s 624.01.04.144.14tan =⨯=⨯==OB OA a a A B ϕ (向右)杆EB 平动2m/s 6==B E a a杆DE 平面运动(基点法)以E 为基点，分析D 点nτn τD ED E E D D a a a a a ++=+ 36)310(12.022n =⨯==O D D OD a ω 34)3310(312.022n =⨯==DE DE DE a ω向ξnτn 30cos 30sin 30cos DEE D D a a a a +︒=︒-︒ ︒-︒-=︒-︒-︒=30sin 30cot )(30sin 30cos 30cos nnn n τDE E D DE E D Da a a a a a a 3222343)636(=⨯--= 2τr a d /s 5.3173355063110012.0322=====OD a D ODα (逆时针)8-12 图8-39所示机构中，已知：m;31.0m,1.0m,1.0m,1.0====EF DE BD OA 曲柄OA 的角速度为rad/s 4=O ω。
在图示位置时，OA 垂直于水平线OB ；B 、D 和F 位于同一铅直线上；又DE 垂直于EF 。
试求此时杆EF 的角速度和点F 的速度。
图8-39杆AB 瞬时平动m/s 4.041.0=⨯==O A OA v ω m/s 4.0==A B v v杆BC 平面运动(瞬心法)，瞬心在D 点rad/s 41.04.0===BD v B BC ωCDE C CDv ω== 杆EF 平面运动(瞬心法)3.0=EI 32.0=FIm/s 4.041.0=⨯==CDE E DE v ωrad/s 3333.1343.04.0====EI v E EF ωm/s 4619.0338.03432.0==⨯==EF F FI v ω8-13 半径为r 的圆柱形滚子沿半径为R 的固定圆弧面作纯滚。
在图8-40所示瞬时，滚子中心C 的速度为C v 、切向加速度为τC a 。
试求此时滚子与圆弧面的接触点A 以及同一直径上最高点B 的加速度。
图8-40r v C =ω r a C τ=α r R v a C nC -=2nACτAC n C τC A a a a a a +++= rv r a C nAC22==ω ττCAC a r a ==α rr R Rv r v r R v a a a C C C nAC n C A )(222-=+-=+= nBC τBC n C τC B a a a a a +++= τCBC a r a ==ατrv r aCn BC22==ωττ2CBC C B a a a a =+=ττ r r R v r R r R v r v a aa CC C nCn BCnB)()2(222--=--===8-14 绕线轮沿水平面滚动而不滑动，轮的半径为R 。