理论力学第8章(刚体的平面运动)
合肥工业大学理论力学答案08刚体平面运动

八、刚体的平面运动8.1 如图所示,O 1A 的角速度为ω1,板ABC 和杆O 1A 铰接。
问图中O 1A 和AC 上各点的速度分布规律对不对?8.2如图所示,板车车轮半径为r ,以角速度ω 沿地面只滚动不滑动,另有半径同为r 的轮A 和B 在板车上只滚动不滑动,其转向如图,角速度的大小均为ω,试分别确定A 轮和B 轮的速度瞬心位置。
[解] 板车作平动,轮A 、B 与板车接触点 E 、F 的速度相同,且r v v v O F E ω=== 对A 轮由基点法求轮心A 的速度 A E AE =+v v v ,r v AE ω=∴ r v A ω2=,且A 轮的速度瞬心在E 点下方r 处。
同理可得B 轮的速度瞬心就在轮心B 处。
8.3直杆AB 的A 端以匀速度v 沿半径为R 的半圆弧轨道运动,而杆身保持与轨道右尖角接触。
问杆AB 作什么运动?你能用几种方法求出杆AB 的角速度?E FPOE v Av Fv Ov[解] AB 杆作平面运动。
(一) 瞬心法AB 杆作平面运动,速度瞬心为P 。
Rv AP v AAB2==ω (二)基点法D A DA =+v v v ,DA v v AB A DA ωθ==sin又 DA =2R cos(90o -θ)=2R sin θ ∴ Rv AB 2=ω(三)自然法: d d AB tϕω=,而R S ϕ2= ∴d d 2d d S R v t t ϕ==, d d 2vt R ϕ= ∴ Rv AB 2=ω 8.4如图所示四连杆机构OABO 1中,OA=O 1B=AB/2,曲柄OA 的角速度ω=3rad/s 。
当OA 转到与OO 1垂直时,O 1B 正好在OO 1的延长线上,求该瞬时AB 杆的角速度ωAB 和曲柄O 1B 的角速度ω1。
[解]取AB 为研究对象,AB 作平面运动。
以A 为基点,画B 点速度合成图 由B A BA =+v v v(rad/s)32230sin o==∴⋅=⋅==ωωωωAB OAAB OA v v AB AB ABABBBvvvDAv Dv Dv111cos3022(rad/s)B BAv v OA O Bωωω=︒=⋅=∴=8.5图示曲柄摇机构中,曲柄OA以角速度oω绕O轴转动,带动连杆AC在摇块B内滑动,摇块及与其固结的BD杆绕B铰转动,杆BD长l;求在图示位置时摇块的角速度及D点的速度。
08-理论力学-第二部分运动学第八章刚体的平面运动

形S在该瞬时的位置也就确定了。
88
运动学/刚体的平面运动
四、平面运动的分解 ——平移和转动
当图形S上A点不动时,则
刚体作定轴转动 。
当图形S上 角不变时,
则刚体作平移。
故刚体平面运动可以看成是 平移和转动的合成运动。
例如:车轮的平面运动可以看成: 车轮随同车厢的平移 和相对车厢的转动的合成。
99
2121
如图示平面图形,某瞬时速度瞬心为P点, 该瞬时平面图形内任一点B速度大小
vB vP vBP vBP
B
大小:vB BP
方向:BP,指向与 转向相一致。
vB
S
vA
C
vC
同理:vA=ω·AP, vC=ω·CP
由此可见,只要已知图形在某一瞬时的速度瞬心 位置和角速度 ,就可求出该瞬时图形上各点的速度。
的平面Ⅱ内的运动。
66
运动学/刚体的平面运动
二、平面运动的简化 刚体的平面运动可以简化为
平面图形S在其自身平面内的运动。 即在研究平面运动时,不需考虑 刚体的形状和尺寸,只需研究平 面图形的运动,确定平面图形上 各点的速度和加速度。
三、平面运动方程 为了确定代表平面运动刚体的
平面图形的位置,我们只需确定平 面图形内任意一条线段的位置。
vBA
s
B
vB vA
A
vA
方向: AB, 指向与 转向一致。
即:平面图形上任一点的速度等于基点的速度与该点随
平面图形绕基点转动的速度的矢量和。 ——基点法
基点法是求解平面图形内一点速度的基本方法。 1414
运动学/刚体的平面运动
二、速度投影法
由于A, B点是任意的,因此
《理论力学》第八章 刚体平面运动

平面运动刚体绕基点转动的角速 度和角加速度与基点的选择无关!
HOHAI UNIVERSITY ENGINEERING MECHANICS
以蓝点为基点
以红点为基点
平移的速度与加速度与基点选择有关不同,而绕 基点转动的角速度与角加速度与基点的选择无关
例1: 已知曲柄-滑块机构中OA=r , AB=l;曲柄OA 以匀角速度绕O轴转动。求连杆AB的运动方程。 解: 建立图示参考坐标系,
已知图形上两点的速度平行,但两点 连线与速度方位不垂直 可以认为速度
0
瞬心在无穷远
平面 运动
平动图形上各点 的速度和加速度 是相同的,但瞬 时平动其上各点 的速度相同而各 点的加速度一般 不同
作平面运动的刚体上求各点速度的方法的适 用范围 1、基点法:已知基点速度和作平面运动刚体
的角速度。是基本方法,可求平面图形的速度 和角加速度,图形上一点的速度。
例2:曲柄滑块机构如图所示,曲柄OA以匀角速度 ω转动。已知曲柄OA长为R,连杆AB长为l。当曲柄 在任意位置 = ωt时,求滑块B的速度。
HOHAI UNIVERSITY ENGINEERING MECHANICS
解: 一、基点法
因为A点速度 vA已知,故选A为基点
vA
AB
v B v A v BA
平动方程 y
称O为基点
y
P
HOHAI UNIVERSITY ENGINEERING MECHANICS
f3 ( t )
讨论:
1. 为常数
刚体平 面运动 方程
y0 转动方程 O1 x 0
O
S x
x 刚体随基点平移 (随同动系平移)
2. (xO,yO)为常数
《理论力学》第八章刚体的平面运动

刚体的平面运动特点
刚体的平面运动具有 连续性,即刚体上任 意一点的运动轨迹都 是连续的。
刚体的平面运动具有 周期性,即刚体的运 动轨迹可以是周期性 的。
刚体的平面运动具有 对称性,即刚体的运 动轨迹可以是对称的。
02
刚体的平面运动分析
刚体的平动分析
平动定义
刚体在平面内沿着某一确定方向作等速直线运动。
详细描述
通过综合分析动能和势能的变化,可以深入理解刚体在平面运动中的能量转换过程。例 如,当刚体克服重力做功时,重力势能转化为动能;当刚体克服摩擦力做功时,机械能 转化为内能。这种能量转换过程遵循能量守恒定律,即系统总能量的变化等于外界对系
统所做的功与系统内能变化之和。
06
刚体的平面运动的实例分析
刚体的平面运动通常可以分为两种类型:纯滚动和滑动。在 纯滚动中,刚体只滚不滑,刚体上任意一点在任意时刻都位 于一个固定的圆周上。在滑动中,刚体既滚又滑,刚体上任 意一点在任意时刻都位于一个变化的圆周上。
刚体的平面运动分类
纯滚动
刚体只滚不滑,刚体上任意一点 在任意时刻都位于一个固定的圆 周上。
滑动
刚体既滚又滑,刚体上任意一点 在任意时刻都位于一个变化的圆 周上。
势能定理
总结词
势能定理描述了势能与其他形式的能量转换的关系。
详细描述
势能定理指出,在刚体的平面运动过程中,非保守力(如摩擦力、空气阻力等)对刚体所做的功等于系统势能的 减少量。非保守力做正功时,系统势能减少;非保守力做负功时,系统势能增加。
动能和势能的综合分析
总结词
在刚体的平面运动中,动能和势能的综合分析有助于理解运动过程中能量的转换和守恒。
做平动,这种运动也是复合运动。
理论力学8章分析解析

2018/10/20
理论力学第8章
22
补充例题。圆轮纯滚动的运动特点。 1. 圆轮在水平面上作纯滚动。轮心A作水平直 线运动。 无滑动条件:轮心A的 水平位移OC等于轮缘 滚动过的弧长,即 OC=MC。设OC长度为x, MC的圆心角为φ,则
x r
2018/10/20 理论力学第8章 23
OA sin AB sin r sin sin l
2018/10/20 理论力学第8章 13
2018/10/20
理论力学第8章
14
用基点法建立A和B的 速度关系。
v B v A v BA vB v A sin vBA sin 0 v A cos vBA cos r cos vBA AB l cos cos sin( ) vB r sin r sin r cos cos cos r , cos
2018/10/20
理论力学第8章
34
轮A的速度和加速度分析:
vA v A r A, A 10rad / s R vC 2 R A 4m / s aA aA r A , A 10rad / s 2 R t n aC a A aCA aCA
v B v A v BA vB cos30 v A cos30 vB sin 30 v A sin 30 vBA v B v A r vBA 0,
2018/10/20
BA 0
理论力学第8章
19
对于轮B: C为瞬心。
vC v B vCB 0 vB vCB vCB vB r vCB B r
理论力学(8.6)--刚体的平面运动-思考题
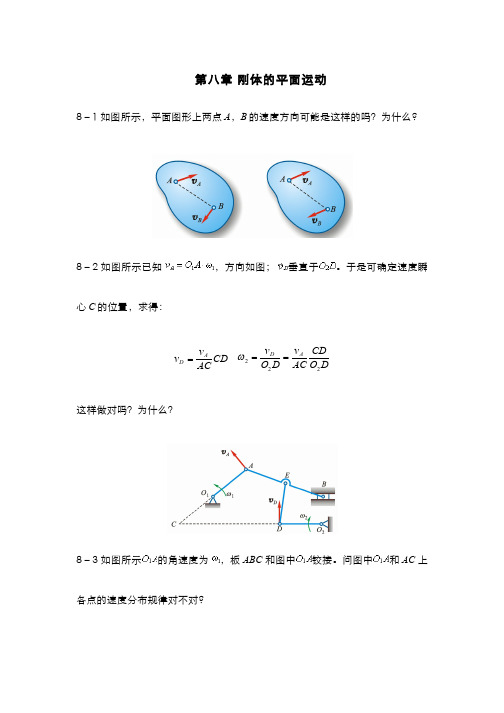
第八章 刚体的平面运动8-1 如图所示,平面图形上两点A ,B 的速度方向可能是这样的吗?为什么?8-2 如图所示已知 ,方向如图; 垂直于。
于是可确定速度瞬心C 的位置,求得:CD ACv v A D = D O CD AC v D O v A D 222==ω这样做对吗?为什么?8-3 如图所示的角速度为 ,板 ABC 和图中铰接。
问图中和 AC 上各点的速度分布规律对不对?8-4 平面图形在其平面内运动,某瞬时其上有两点的加速度矢相同。
试判断下述说法是否正确:(1)其上各点速度在该瞬时一定都相等。
(2)其上各点加速度在该瞬时一定都相等。
8-5 如图所示瞬时,已知 和平行,且=,问与 、与 是否相等?车轮的角加速度是否等于 ?速度瞬心C的加速度大小和方向如何确定?8-7试证:当 ω=0时,平面图形上两点的加速度在此两点连线上的投影相等。
8-8 如图所示各平面图形均作平面运动,问图示各种运动状态是否可能?图a中,和平行,且=-。
图b中,和都与A,B连线垂直,且和反向。
图c中,沿A,B连线,与A,B连线垂直。
图d中,和都沿A,B连线,且> 。
图e中,和都沿A,B 连线,且< 。
图f中,沿A,B连线。
图g中,和都与AC连线垂直,且> 。
图h中, AB 垂直于AC,沿A,B连线,在AB连线上的投影与相等。
图i中,与平行且相等,即=。
图j中,和都与 AB 垂直,且,在A,B连线上的投影相等。
图k中,,在AB连线上的投影相等。
图l中,矢量与在AB线上的投影相等,在AB线上。
8-9 如图所示平面机构中,各部分尺寸及图示瞬时的位置已知。
凡图上标出的角速度或速度皆为已知,且皆为常量。
欲求出各图中点C的速度和加速度,你将采用什么方法?说出解题步骤及所用公式。
8-10 杆AB作平面运动,图示瞬时A,B两点速度,的大小、方向均为已知,C,D两点分别是, 的矢端,如图所示。
试问(l)AB杆上各点速度矢的端点是否都在直线 CD上?(2)对AB杆上任意一点E,设其速度矢端为H,那么点H在什么位置?(3)设杆AB为无限长,它与CD的延长线交于点P。
理论力学第八章平面运动
r vM
r vMC
r
uuuur CM
• 速度瞬心的确定方法
已知 vA ,的vB方向, 且 v不A 平行于 v。B
vrA // vrB ,且不垂直于AB
vrB
vvrrBBvArAvr0AvrABvrMAB
0
瞬时平移(瞬心在无穷远处)
纯滚动(只滚不滑)约束
找出下列平面运动刚体的速度瞬心。 A
第八章 刚体平面运动
1、刚体平面运动的定义及运动方程 2、刚体平面运动分解为随基点平动和绕基点转动 3、平面运动图形上点的速度分析 4、平面运动图形上点的加速度分析
1、刚体平面运动的定义
若刚体在运动过程中,刚体上的任意一点与 某一固定平面始终保持相等的距离,这种运 动称为平面运动。
刚体平面运动特点
刚体上所有各点均在平行于某固 定平面的平面内运动。
刚体的平面运动,可以简化为平面 图形在其自身平面内的运动来研究。
平面图形 S 的位置可用其上任一 线段如AB 来确定,线段AB的位 置又可用A 点的坐标 xA 、yA 和 线段AB与 x 轴的夹角 φ 来确定。 点 A 称为基点。
刚体平面运动方程
当平面图形 S 运动时,坐标 xA 、
yA 和夹角 φ 一般都是随时间 t 而 变化的,分别为时间 t 的单值连
续函数,即
xA f1 (t)
y A f 2 (t)
f3 (t)
这就是平面图形S 的运动方程,也就是刚体平面运动的运动方程。
2、刚体平面运动分解为随基点平动和绕基点转动
xO f1 t
1.5rad
/
s
BC
vB BC
2.25rad
/s
vA
2)瞬心法
理论力学08_4刚体平面运动微分方程
6 刚体平面运动微分方程刚体的平面运动可简化成刚体的平面图形S 在某一固定平面内的运动,用3个独立坐标描述。
作用在刚体上的外力可简化为S 平面内的一平面力系F i (=1, 2,…,n )。
设坐标系Oxy 为固定的惯性参考系,Cx ′ y ′为质心平移坐标系,如图8-6所示。
平面图形的运动可用质心坐标x C , y C 和绕质心的转动角ϕ描述。
刚体的绝对运动可分解成跟随质心的平移和相对质心平移坐标系的转动。
由动量定理所述,刚体跟随质心的平移仅与外力系的主矢有关,由质点系相对质心的动量矩定理可知,刚体相对质心平移坐标系的运动仅与外力系对质心的主矩有关。
于是,由式(8.1.11)可写出y C x C F ym F x m R R ,==&&&& (8.1.55) 式中m 为刚体的质量,F R x , F R y 分别是外力系的主矢在y x ,方向上的分量。
由式(8.1.54)在垂直于平面图形S 方向上的投影,可得Cz CzM tL =d d (8.1.56) 其中M Cz 是外力系对通过质心且垂直于平面图形S 的轴之矩的代数和。
而ϕ&C Cz J L =,J C 是刚体对于通过质心且垂直于平面图形S 的轴的转动惯量。
应用质心运动定理和相对质心的动量矩定理,得到了三个动力学方程,给出了三个广义坐标x C , y C 和ϕ的封闭方程组,用以解决刚体的平面运动问题。
动力学方程组m (8.1.57)Cz C ni iy C n i ix C M J F ym F x ===∑∑==ϕ&&&&&&,,11称为刚体平面运动微分方程组。
给出相应的初始条件,例如,t =0时,刚体质心的位置分别为x C 0和y C 0,质心在初始时的速度分别为和,平面图形S 在初始时的角位移和角速度分别为ϕ0C x &0C y&0和0ϕ&。
东北大学理论力学第八章 刚体的平面运动(作业解析)
⑶ 由速度合成定理求解
va ve vr
? √ √ √
aBA
n aBA v r
C D
大小 方向
? √
aB
va
ve
E
AB
AB
A
va vr ve
3 3 15求解 n aB aA aBA aBA
ω1 ve O1D 6.19 rad/s
Northeastern University
8-23
已知OA=50mm,ω=10 rad/s,θ=β=60°,O1D=70mm,求摇杆 O1C的角速度和角加速度。 y A vA n aBA a A 60 aBA B ⑶ 取A点为基点, 60 O1 O 由基点法求B vr vB aB 点加速度 D aA v v a D 1 n ve aB aA aBA aBA
绝对运动:直线运动 相对运动:直线运动 牵连运动:平面运动
vA 1 rad/s CA
B
vr
C D
AB
ve
E
A
va
vA
AB杆瞬心为C AB
ve CD AB 0.2 m/s
Northeastern University
8-27
已知AB = 0.4m,vA=0.2m/s。图示位置,θ= 30°,AD=DB,求此 瞬时DE杆的速度和加速度。
大小 方向 ? √ √ √ ? √ √ √
a A OA 2
C
n 2 aBA BA AD 0
将此方程沿y方向投影得 0 aA a BA cos30
τ 2a A aBA ω2 aBA AD BA 3 3
理论力学第八章复习
1.刚体平面运动定义 刚体作平面运动的充要条件是:刚体在运动过程中,其上任何一点到 某固定平面的距离始终保持不变。 2.平面运动方程 刚体的平面运动可以简化成平面图形在平面上的运动。运动方程:
习题8-1
其中A为基点。如果以 A 为原点建立平动动系,则平面运动分解为跟随基点(动系) 的平动和相对于基点(动系)的转动。
注意:(1)平动部分与基点选择有关。 (2)转动部分与基点选择无关。
刚体平面运动
3.研究平面运动的基本方法
(1)基点法--本章重点 (2)绕两平行轴转动的合成--常用于研究行星轮系统的传速比。 4.平面运动刚体上各点的速度分析 三种方法: (1)基点法--应用速度合成定理 (2)速度投影定理(由基点法推论) (3)瞬心法(由基点法推论) 5.加速度分析 只推荐用基点法分析平面运动刚体上各点的加在自身平面内运动,若其顶点 A、B、C、D 的加速度大小 相等,方向由图(a)、(b)表示,则------。
① (a)、(b)两种运动都可能 ③ (a)运动可能,(b)运动不可能
② (a)、(b)两种运动都不可能 ④ (a)运动不可能,(b)运动可能
2.曲柄连杆机构中,曲柄 OA 以匀角速度 连杆AB 的角加速度为------。其大小为?
① ② ③ ④ =r
,
_________,加速度的大小为_________。
半径为 r 的车轮沿固定圆弧面作纯滚动,若某瞬时轮子的角速度为ω,
角加速度为ε,则轮心 O 的切向加速度和法向加速度的大小分别为------。
① ② ③ ④ =r
3.半径为 r 的车轮沿固定圆弧面作纯滚动,若某瞬时轮子的角速度为ω,
角加速度为ε,则轮心 O 的切向加速度和法向加速度的大小分别为------。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、平面运动方程 为了确定代表平面运动刚体的平面图形的位置,
我们只需确定平面图形内任意点的坐标和AB与x轴夹
角表示。因此图形S 的位
置决定于 x A , y A , 三个 独立的参变量。所以
平面运动方程
对于每一瞬时 t ,都可以求出对应的 x A , y A , , 图形S 在该瞬时的位置也就确定了。 四、平面运动分面解为平动和转动
vB AB vA AB
—速度投影定理
平面图形上任意两点的速度在该两点连线上的投影相等。这种
求解速度的方法称为 速度投影法。(对任意一个刚体均成立)
例3 图示的平面机构中,曲柄 OA=100mm 以角速度ω=2rad/s 转动。连杆AB带动摇杆CD,并拖动轮E沿水平面滚动。已知 CD=3CB,图示位置时A、B、E三点恰在一水平线上, 且CD⊥ ED 。试求此瞬时点E的速度。 D
(绝对运动)
三种运动都 是刚体运动
动系Ax y 相对静系的平动 (牵连运动)
车轮相对动系Ax y 的转动 (相对运动)
我们称动系上的原点A为基点,于是 刚体的平面运动可以分 解为随基点的平动(牵 连运动)和绕基点的转 动(相对运动)。 车轮的平面运动
随基点A的平动
绕基点A'的转动
再例如: 平面图形S在t 时间内从位置I运动到位置II
①以A为基点: 随基点A平移到A'B''后, 绕基点转 1角到A'B';
② 以B为基点: 随基点B平移到A''B'后, 绕基点转
2角到A'B'。
图中看出:AB A'B'' A''B' , 1 2 ;于是有 1 2 d 1 d 2 lim lim 1 2 ; ,1 2 t 0 t t 0 t dt dt 结论: 平面运动可取任意基点而分解为平动和转动; 其中平动的速度和加速度与基点的选择有关; 平面图形绕基点转动的角速度和角加速度与基点选择无关。
例: 曲柄连杆机构中连杆AB的运动, A点作圆周运动,B点作直线运动,因此, AB 杆的运动既不是平动也不是定轴转动, 而是平面运动。
行星齿轮机构
行星轮
一、平面运动的定义 在运动过程中,刚体上任 一点到某一固定平面的距离始 终保持不变。也就是说,刚体 上任一点都在与该固定平面平 行的某一平面内运动。具有这 种特点的运动称为刚体的平面
3. 选定基点(设为A),而另一点(设为B)可应用公式, 作速度平行四边形。作图时要使vB 成为平行四边形的对角线。
vB v A vBA
4. 利用几何关系,求解平行四边形中的未知量。 5. 研究另一个作平面运动的物体,可按上述步骤继续进行。
例2 图示平面机构中,AB=BD=DE=l=300mm。在图示位置, BD//AE,杆AB的角速度为ω=5rad/s。求此瞬时杆DE的角速度和 v DB 杆BD中点C的速度。 解:1) 杆AB, DE定轴转动, BD作平面运动; 2)B,D,C各点速度分析 3)取B点为基点 D的速度。 D v
60 0
DE
E
vB
vCB BD
大小
l 0.75 m / s 2
方向
2 2 2 vC v B vCB cos( ) 2v C v B
2 2 vC v B vCB 2v B vCB cos120 0
1.5 2 0.75 2 2 1.5 0.75 (0.5)
[例1] 已知轮子在地面上作纯滚动,轮心的速度为v,半径 为r。求轮子上A1、A2、A3和A4点的速度。 解:很显然速度瞬心在轮子与地 面的接触点即A1 A3
vO r v
x A f1 (t ) y A f 2 (t ) f 3 (t )
当图形S 上A点不动时,
则刚体作定轴转动; 当图形 S上角不变时,
则刚体作平动。
故刚体平面运动可以看成是 平动和转动的合成运动。
例如
车轮的运动
车轮的平面运动可以看 成是车轮随同车厢的平动和
相对车厢的转动的合成。
车轮对于静系的平面运动
刚体的平面运动 分 解 绕基点的转动
随基点的平动
合成
基 点
运动规律与基 点的选择有关
、 与
基点无关
运动规律与基 点的选择无关
任意选取,通常选取运动情况已知的点作为基点
§8-2
平面图形内点的速度分析
一、基点法(速度合成法) 已知:图形S内一点A的速度 v A , 图形角速度 。求 v B 。 取A为基点, 将动系固结于A点, 动系随基点作平动。 取B为动点,则B点的运动可视为牵连运动为平动和相对 运动为圆周运动的合成, va vB ; ve v A ; vr vBA , 其中vBA大小:vBA=BA· ;垂直BA并指向与 转向一致。 根据速度合成定理 va ve vr , 则B点速度为:
4)轮E沿水平面滚动,轮心 E的速度方向为水平。
vD
D
5)ED 作平面运动 由速度投影定理, D、E 两点的速度关系为:
CD
B
60 0
30 0
vB
E
30
0
A
vA
vE
O
C
v E cos30 0 v D
解出
vD 3v A 0.6 vE 0.8 m / s 0 2 0 0.75 cos30 cos 30
vA
O
A
vB
B
例如: 曲柄连杆机构在图示位置时,连杆AB作瞬时平动。
此时连杆AB的图形角速度AB 0 ,
此瞬时AB 杆上各点的速度都相等。 但各点的加速度并不
n 2 相等。设为匀角速,则 a A a A OA ()
vA
O
A
vB
B
而 a A 的方向沿AO的,aB
a A 瞬时平动与平 动不同
解题步骤如下:
1)分析题中各物体的运动,平动,转动,平面运动 2)研究作平面运动的物体, 分析点的速度大小和方向 。 分析已知要素 3)根据己知条件,求出图形的速度瞬心的位置和平面图
形转动的角速度,最后求出速度。
4)研究由几个图形组成的平面机构,则可依次对每一图 形按上述步骤进行,直到求出所需的全部未知量为止。
B
BD
C vB
D
60 0 60 0
vD
60
0
vB
v B v DBA v B l 1.5 m / s
60
0
DE
E
v D v DB v B 1.5 m / s
此时杆DE的角速度: DE
vDB 为点D绕B的转动速度:
得瞬时杆BD角速度:
v DB DB BD
vB v A vBA
即平面图形上任一点的速度等于基点的速度与该点随图形绕基 点转动速度的矢量和。这种求解速度的方法称为基点法,也称 为速度合成法。它是求解平面图形内一点速度的基本方法。
例1:椭圆规尺的A点速度为vA, 沿 x轴的负向运动,AB=l,求B点速度 和AB的角速度。 解:1)曲柄定轴转动,滑块平动, 尺AB作平面运动。 2)尺AB的各点速度 3)选A点为基点,B点的速度
运动。
二、平面运动的简化 刚体的平面运动 简 化 到固定平面 Ⅰ的距离不变
平面图形S在与Ⅰ 平行的平面Ⅱ内运动
所有与平面图形S垂直的直线段, 例如A1A2,都作平动,所以刚体的 平面运动,可以简化为平面图形S 在其自身平面内的运动
研究平面运动
不需考虑刚体的形状和尺寸,只 需研究平面图形的运动,确定平 面图形上各点的速度和加速度。
v DB 5 rad / s l
vD 5 rad / s l
BD
4)分析杆BD 取B点为基点,分析C点速度.
vC v B vCB
√
√
B
BD
vCB
v DB
vC
D
60 0 60 0
vD
大小 ×
方向 ×
√
√
A
60 0
C v B vB
0.75 3 1.299 m / s
(0.75 3 ) 2 1.5 2 0.75 2 2 0.75 3 1.5
3 2
30 0
二、速度投影法(对任意一个刚体均成立) 由于A, B点是任意的,因此 vB v A vBA 表示了图形上任 意两点速度间的关系。由于恒有 vBA AB ,因此将上式在 AB上投影,有
确定瞬心的一般方法:
P
vB P B vA A
A B
P
vA vB
A
vA
B A
vB vA
A B
vA vB
P
B vB
4.速度瞬心法 利用速度瞬心求解平面图形上点的速度的方法,称为速度瞬心法。 平面图形在任一瞬时的运动可以视为绕速度瞬心的瞬时 转动,速度瞬心又称为平面图形的瞬时转动中心。 若P点为速度瞬心,则任意一点A的速度 大小 v A AP ;方向AP,指向与 一致。 5.注意的问题 ①速度瞬心在平面图形上的位置不是固定的,而是随时间不 断变化的。在任一瞬时是唯一存在的。 ② 速度瞬心的速度为零, 其加速度一定不为零,不同于定轴转动。 ③刚体作瞬时平动时,虽然各点的速度相同,但各点的加速 度是一定不相同的,不同于刚体作平动。
vB
y
v BA
vA
B
C AB M
vA
x
A
vB v A vBA
