点和直线PPT课件
合集下载
《点到直线的距离》ppt课件

2.当A=0或B=0(直线与坐标轴垂直)时,仍 然可用公式,这说明了特殊与一般的关系
3..例2的变式练习,用图形解释运算结果,又 一次让我们体会了数学与形式结合的思想.
作业:书97页5、6、7 数学之友相应练习
X
教学目标
1. 进一步巩固点到直线的距离公式 2. 理解两条平行直线间的距离公式的推导 3. 掌握两条平行直线间的距离公式并会运用 4. 渗透数形结合思想,对学生进行对立统一
2
由题意得
-1
∴k2+8k+7=0
∴所求直线的方程为x+y-1=0 或7x+y+5=0.
例2的变式练习
求过点A(-1,2)且与原点的距离等于
(1).距离改为1;
(2).距离改为 ; (3).距离改为3(大于 ). 想一想?在练习本上画图形做.
例2的变式练习
(1).距离改为1, 则用上述方法得4(y-2)=3(x+1) 或x=-1(易漏掉)
怎么能够得到线段PQ的长?
利用两点间的距离公式求出|PQ|.
步骤
L1
P(x0,y0)
L
Q
(1)求直线L1的斜率; (2)用点斜式写出L1 的方程;
L:Ax+By+C=0
(3)求出Q点的坐标;
(4)由两点间距离公式d=|PQ|.
一般情况 A≠0 ,B≠0时
解:设A≠0,B≠0,过点P作L的垂 线L1,垂足为Q,
X
教学目标:
1. 会直接运用点到直线的距离公式进行计算 2. 会根据已知的 若干点到直线的距离大小
求点的坐标或直线的方程,渗透方程 思 想 3. 渗透由特殊到一般的思想 4. 理解点到直线的距离公式的推导
3..例2的变式练习,用图形解释运算结果,又 一次让我们体会了数学与形式结合的思想.
作业:书97页5、6、7 数学之友相应练习
X
教学目标
1. 进一步巩固点到直线的距离公式 2. 理解两条平行直线间的距离公式的推导 3. 掌握两条平行直线间的距离公式并会运用 4. 渗透数形结合思想,对学生进行对立统一
2
由题意得
-1
∴k2+8k+7=0
∴所求直线的方程为x+y-1=0 或7x+y+5=0.
例2的变式练习
求过点A(-1,2)且与原点的距离等于
(1).距离改为1;
(2).距离改为 ; (3).距离改为3(大于 ). 想一想?在练习本上画图形做.
例2的变式练习
(1).距离改为1, 则用上述方法得4(y-2)=3(x+1) 或x=-1(易漏掉)
怎么能够得到线段PQ的长?
利用两点间的距离公式求出|PQ|.
步骤
L1
P(x0,y0)
L
Q
(1)求直线L1的斜率; (2)用点斜式写出L1 的方程;
L:Ax+By+C=0
(3)求出Q点的坐标;
(4)由两点间距离公式d=|PQ|.
一般情况 A≠0 ,B≠0时
解:设A≠0,B≠0,过点P作L的垂 线L1,垂足为Q,
X
教学目标:
1. 会直接运用点到直线的距离公式进行计算 2. 会根据已知的 若干点到直线的距离大小
求点的坐标或直线的方程,渗透方程 思 想 3. 渗透由特殊到一般的思想 4. 理解点到直线的距离公式的推导
点到直线的距离PPT教学课件

用于暗反应
水的光解:
2H2O
光 色素
O2+4H++4e-
酶
NADPH的形成: NADP++2e+H+
NADPH
ATP的形成: ADP+Pi + 电能 酶(A活T跃P化学能)
碳反应
二氧化碳还原为糖的一系列反应成为碳 循环,又称卡尔文循环。
(二)碳反应阶段
碳反应总结
场所: 叶绿体的基质中
条件:
多种酶、 [H] 、ATP
)
2ab a 2 b2
A到BC的距离h=( a 2 b2 )
因为|PE|+|PF|=h,所以原命题得证。
点到直线的距离
d Ax0 By0 C A2 B2
1.此公式的作用是求点到直线的距离; 2.此公式是在A、B≠0的前提下推导的; 3.如果A=0或B=0,此公式恰好也成立; 4.如果A=0或B=0,一般不用此公式; 5.用此公式时直线要先化成一般式。
②图中C是[H——] ,它被传递到叶绿体的基——质部位,用于—C—3的。还原
③图中DA是T—P—,在叶绿体中合成D所需的能量来自色—的素—光吸能收 ④图光中反的应H表示——,NAHD为PIH提和供A—T—P
4. 光合作用过程中,产生ADP和消耗ADP的
部位在叶绿体中依次为
(B )
①外膜
②内膜
③基质
能用无机 物制造有
机物
举例 绿色植物 光合细菌
硫细菌 铁细菌 硝化细菌
异养型
摄取的有 机物中储 存的能量
摄取现成 的有机物
人、动物和 营寄生、腐
生的菌类
相同点
都是从外界 摄取物质, 经过极其复 杂的变化, 转变成自身 组成成分, 并且储存能
高中数学必修二《 点到直线的距离》ppt课件

.
新课探究
一、点到直线的距离
过点 P 作直线 l 的
垂线,垂足为 Q 点,线 段 P Q 的长度叫做点 P
到直线 l 的距离.
.
y
Q·
·P
O
x
问题1 当A=0或B=0时,直线为y=y1或 x=x1的形式.如何求点到直线的距离?
y y=y1
o
P (x0,y0)
Q(x0,y1) x
y (x1,y0)
4 (2)点P(-1,2)到直线3y=2的距离是___3 ___.
.
练习2 求原点到下列直线的距离:
(1) 3x+2y-26=0 2 13 (2) y=x 0 练习3 (1)A(-2,3)到直线 9 3x+4y+3=0的距离为_____. 5
(2)B(-3,5)到直线 2y+8=0的距离为
______. 9
=0
所以l1:
Byx-Ay-Bx0+Ay0=0
P0(x0, y0)
B x1-Ay1-Bx0+Ay0=0
太麻烦!
x1
B2x0
AB0yAC A2B2
换y1个A角BA 0度2xBB 思02y考BC !
|P| Q (x 0x 1)2 (y0y 1)2
Q
O
x
l:AxByC0
.
Ax1+By1+C=0
B x1-Ay1-Bx0+Ay0=0
.
[思路二] 构造直角三角形求其高。
y
S Q
O
P(x0,y0)
R
x
L:Ax+By+C=0
.
y
S P(x0,y0)
Q
新课探究
一、点到直线的距离
过点 P 作直线 l 的
垂线,垂足为 Q 点,线 段 P Q 的长度叫做点 P
到直线 l 的距离.
.
y
Q·
·P
O
x
问题1 当A=0或B=0时,直线为y=y1或 x=x1的形式.如何求点到直线的距离?
y y=y1
o
P (x0,y0)
Q(x0,y1) x
y (x1,y0)
4 (2)点P(-1,2)到直线3y=2的距离是___3 ___.
.
练习2 求原点到下列直线的距离:
(1) 3x+2y-26=0 2 13 (2) y=x 0 练习3 (1)A(-2,3)到直线 9 3x+4y+3=0的距离为_____. 5
(2)B(-3,5)到直线 2y+8=0的距离为
______. 9
=0
所以l1:
Byx-Ay-Bx0+Ay0=0
P0(x0, y0)
B x1-Ay1-Bx0+Ay0=0
太麻烦!
x1
B2x0
AB0yAC A2B2
换y1个A角BA 0度2xBB 思02y考BC !
|P| Q (x 0x 1)2 (y0y 1)2
Q
O
x
l:AxByC0
.
Ax1+By1+C=0
B x1-Ay1-Bx0+Ay0=0
.
[思路二] 构造直角三角形求其高。
y
S Q
O
P(x0,y0)
R
x
L:Ax+By+C=0
.
y
S P(x0,y0)
Q
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PPT)

人教版 数学 四年级 上册
5 平行四边形和梯形
点到直线的距离
课前导入
探究新知
课堂练习
课堂小结
课后作业
点到直线的距离
课前导入
过直线外一点怎样画垂线呢?
1.边线重合。 2.平移到点。 3.画线标号。
返回
点到直线的距离
探究新知
从直线外一点A,到这条直线画几条线段。
A
量一量这些线段的长
度,你有什么发现?
返回
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PP T)
点到直线的距离
下图中,游泳运动员如果从南岸游到北岸,怎样 游路线最短?为什么?把最短的路线画出来。
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PP T)
从A点向北岸引垂线, 这就是最短路线。
返回
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PP T)
点到直线的距离
请用在例3中发现的规律,检验下面各组直线a、b是否平行。
平行线间的垂直线段的长度都相等,直线a、b平行。
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PP T)
返回
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PP T)
点到直线的距离
判断题。(正确的画“√”,错误的画“✕”) (1)同一平面内,如果两条直线都与同一条直线垂直,那
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PP T)
返回
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PP T)
点到直线的距离
课后作业
1.从教材课后习题中选取; 2.从课时练中选取。
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PP T)
5 平行四边形和梯形
点到直线的距离
课前导入
探究新知
课堂练习
课堂小结
课后作业
点到直线的距离
课前导入
过直线外一点怎样画垂线呢?
1.边线重合。 2.平移到点。 3.画线标号。
返回
点到直线的距离
探究新知
从直线外一点A,到这条直线画几条线段。
A
量一量这些线段的长
度,你有什么发现?
返回
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PP T)
点到直线的距离
下图中,游泳运动员如果从南岸游到北岸,怎样 游路线最短?为什么?把最短的路线画出来。
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PP T)
从A点向北岸引垂线, 这就是最短路线。
返回
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PP T)
点到直线的距离
请用在例3中发现的规律,检验下面各组直线a、b是否平行。
平行线间的垂直线段的长度都相等,直线a、b平行。
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PP T)
返回
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PP T)
点到直线的距离
判断题。(正确的画“√”,错误的画“✕”) (1)同一平面内,如果两条直线都与同一条直线垂直,那
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PP T)
返回
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PP T)
点到直线的距离
课后作业
1.从教材课后习题中选取; 2.从课时练中选取。
四年级上册数学优秀课件- 点到直线的距离(人教版)(共17张PP T)
东华大学画法几何及工程制图-第1章-点和直线

判断两直线的相对位置 方法二
c
d b a k c d
方法一
X
a’s’ s’b’ b0 s0
b a s b
c d
X
a k b c
d
a s : s b= as : sb 结论:AB平行CD
11:14:59 东华大学机械工程学院
AB、CD同面
36
§1.5 点、直线的相对位置-两直线的相对位置-相交 C K B Z b b c A D c k k d d a a c a b k O H X c b
Y
X
O a
B
b
b
东华大学机械工程学院
11:14:59
17
§1.3 直线的投影-各类直线的投影特性-特殊位置直线-正平线
b
Z
B
Z b b
a
a
b
a
X
O
a
YW
A
X
a
O
b
a
b YH
投影特性: 1. ab OX ; a b OZ 2. a b=AB 3. 反映、的真实大小
东华大学机械工程学院
10
第1章 点和直线
§1.1 点的投影
§1.2 两点的相对位置
§1.3 直线的投影
§1.4 直线段的实长和对投影面的倾角
§1.5 点、直线与直线的相对位置
机械工程学院
§1.2 两点的相对位置-相对位置的确定
b
a
A
B
b a
前后-左右-上下
XA > XB , B点在A点右 YA < YB , B点在A点前 ZA < ZB , B点在A点上
最基本的图形-点和线PPT课件

11
22
33
44
CHENLI
55
66
77
88
16
数学理论
第二种方法是:叠合法先把两条线段的一端
重合,另一端落在同侧,根据另一端落下的
位置,来比较。
C
D
E
F
M
N
①A
B AB>CD
②A
B AB=EF
③A
CHENLI
B AB<MN
17
数学运用
观察下列三组图形,分别比较线段a、
b的长短 a b (1)
(3)
图①
例2、如图②,下列说法不能判断点C是线段AB
的中点的是( C )
( A)AC=CB
( B)AB=2AC
(C)AC+CB=AB
( D)2CB=AB
图② A
C
B
CHENLI
25
数学运用
例3、AB=6cm,点C是线段AB的中点,点D是线段 CB的中点,求线段AD的长。
A
C
D
B
解: AC=BC= 1 AB=3cm
结论: 两点间线段最短
生活中运用 “两点间线段
最短”的事例,你能列举吗?
CHENLI
8
数学理论
A
B
线段公理:两点之间,线段最短
连结两点所得线段的长度叫做这两点间的距离 。
CHENLI
9
问题情境、学生活动
画一画
1.过一点A画一条直线, 请问可以画几条?
2.过两点A、B可以画几条直线? 请动手试一试。
概念辨析:
“若AC=BC,则点C是线段AB的中点”这种 说
法对吗?
A
C
B
点关于直线对称ppt课件

2
点关于直线对称
点A (x0 , y0 ) 关于直线l:Ax+By+C=0的对称点为
B(x,y)
A(x0,y0)
l
kAB kl 1 AB中点在l上
P
B(x,y)
3
点关于直线对称
点A (x0 , y0 ) 关于直线l:Ax+By+C=0的对称点为
B(x,y)
A(x0,y0)
l
8
课堂小结
点A (x0 , y0 ) 关于直线l:Ax+By+C=0的对称点为 B(x,y)
垂直 平分
y x
y0 x0
(
A) B
1
A(x0,y0)
A
x
x0 2
B
y
y0 2
C
0
P
l
B(x,y)
9
10
y x
y0 x0
(
A) B
1 ຫໍສະໝຸດ Ax x0 2
B
y
y0 2
C
0
P
B(x,y)
4
例:求点A(2,1)关于直线l: x+y+1=0的对称点B的坐标.
5
练习1:求点A(2,-1)关于直线l: x-y+1=0的对称点B的坐标.
6
练习2:课本P144 A组第七题.
7
规律总结
例:点A(2,1)关于直线l:x+y+1=0的对称 点B的坐标为(-2,-3).
练习1:点A(2,-1)关于直线l:x-y+1=0的对 称点B的坐标为(-2,3).
点关于直线对称
点A (x0 , y0 ) 关于直线l:Ax+By+C=0的对称点为
B(x,y)
A(x0,y0)
l
kAB kl 1 AB中点在l上
P
B(x,y)
3
点关于直线对称
点A (x0 , y0 ) 关于直线l:Ax+By+C=0的对称点为
B(x,y)
A(x0,y0)
l
8
课堂小结
点A (x0 , y0 ) 关于直线l:Ax+By+C=0的对称点为 B(x,y)
垂直 平分
y x
y0 x0
(
A) B
1
A(x0,y0)
A
x
x0 2
B
y
y0 2
C
0
P
l
B(x,y)
9
10
y x
y0 x0
(
A) B
1 ຫໍສະໝຸດ Ax x0 2
B
y
y0 2
C
0
P
B(x,y)
4
例:求点A(2,1)关于直线l: x+y+1=0的对称点B的坐标.
5
练习1:求点A(2,-1)关于直线l: x-y+1=0的对称点B的坐标.
6
练习2:课本P144 A组第七题.
7
规律总结
例:点A(2,1)关于直线l:x+y+1=0的对称 点B的坐标为(-2,-3).
练习1:点A(2,-1)关于直线l:x-y+1=0的对 称点B的坐标为(-2,3).
教学课件PPT 点、直线、平面的投影
其投影特性取决于直线与三个投影 面间的相对位置
平行于某一投影面而 与其余两投影面倾斜
正平线(平行于V面)
投影面平行线 侧平线(平行于W面)
水平线(平行于H面)
统称特殊位置直线
正垂线(垂直于V面)
垂直于某一投影面 投影面垂直线 侧垂线(垂直于W面)
铅垂线(垂直于H面)
与三个投影面都倾斜的直线
一般位置直线
② 另外两个投影,反映线段实长,且垂直 于相应的投影轴。
⑶ 一般位置直线
V
b
B b
a
βγ
W
a
X
Ab
a
aH
a
投影特性
b Z b
a
O
Y
b
Y
三个投影都倾斜于投影轴,其与投影轴的夹角 并不反映空间线段与三个投影面夹角的大小。三个 投影的长度均比空间线段短,即都不反映空间线段 的实长。
二、直线与点的相对位置
a
a
三个投影都类似。
b
a
c
例:正垂面ABC与H面的夹角为45°,已知其水平投影 及顶点B的正面投影,求△ABC的正面投影及侧面 投影。
c
c
a
a
b ● 45°
b
a
c b
思考:此题有几个解?
三、平面上的直线和点
⒈ 平面上取任意直线
位于平面上的直线应满足的条件:
若一直线过平面上 的两点,则此直线 必在该平面内。
度量性较差。
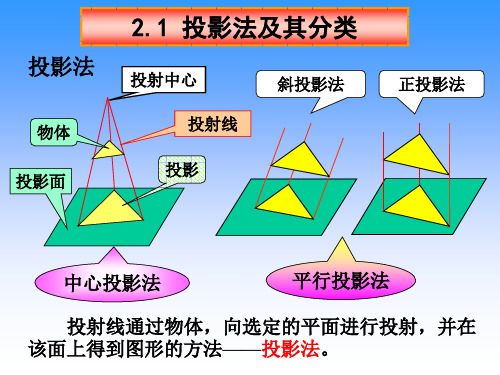
平行投影法
投影特性 投影大小与物体和投影面之间的距离无关。 度量性较好。 工程图样多数采用正投影法绘制。
画透视图
中心投影法
画斜轴测图
投影法
斜投影法
平行投影法
平行于某一投影面而 与其余两投影面倾斜
正平线(平行于V面)
投影面平行线 侧平线(平行于W面)
水平线(平行于H面)
统称特殊位置直线
正垂线(垂直于V面)
垂直于某一投影面 投影面垂直线 侧垂线(垂直于W面)
铅垂线(垂直于H面)
与三个投影面都倾斜的直线
一般位置直线
② 另外两个投影,反映线段实长,且垂直 于相应的投影轴。
⑶ 一般位置直线
V
b
B b
a
βγ
W
a
X
Ab
a
aH
a
投影特性
b Z b
a
O
Y
b
Y
三个投影都倾斜于投影轴,其与投影轴的夹角 并不反映空间线段与三个投影面夹角的大小。三个 投影的长度均比空间线段短,即都不反映空间线段 的实长。
二、直线与点的相对位置
a
a
三个投影都类似。
b
a
c
例:正垂面ABC与H面的夹角为45°,已知其水平投影 及顶点B的正面投影,求△ABC的正面投影及侧面 投影。
c
c
a
a
b ● 45°
b
a
c b
思考:此题有几个解?
三、平面上的直线和点
⒈ 平面上取任意直线
位于平面上的直线应满足的条件:
若一直线过平面上 的两点,则此直线 必在该平面内。
度量性较差。
平行投影法
投影特性 投影大小与物体和投影面之间的距离无关。 度量性较好。 工程图样多数采用正投影法绘制。
画透视图
中心投影法
画斜轴测图
投影法
斜投影法
平行投影法
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一条直线.(简称为:两点确定一条直线)
2020年10月2日
4
●
A
2020年10月2日
●
B
5
1.要在墙上钉一根木条,至少要钉 几颗钉子?为什么? 2.你还能举出一些应用直线公理的 例子吗?
2020年10月2日
6
从A地到B地有三条道路可以走, 你会选择哪一条?为什么?
A
B
线段公理:两点之间,线段最短.
表示方法:射线OA
4.线段:
﹒A ﹒B
a
直线上两点和它们之间的部分叫做线段.
表示方法:(1).线段AB.(或线段BA)
(2).线段a.
2020年10月2日
3
已知:平面上有两点A和B.
﹒ ﹒B A 画一画:1.过点A画直线.能画几条?
2.过点A和点B画直线.能画几条?
直线公理: 经过两点有一条直线,并且只有
站A使供电站A到C,D两村所用电线之
和最短,问供电站A的位置应该如何 确
定?为什么?
.C
2020年10月2日
A
. D
L
12
演讲完毕,谢谢观看!
Thank you for reading! In order to facilitate learning and use, the content of this document can be modified, adjusted and printed at will after downloading. Welcome to download!
两点间的距离:两点间线段的长, 叫做两点间
的距离.例如:点A与点B的距离为30cm.
应用:有时需要把弯曲的河道改直,根据什么?
2020年10月2日
7
练习:1.填表:
表示方法 端点个数 向几个方 向延伸
直线 1.直线AB
2.直线L
0 两方
射线 射线OA
1
一方
线段 1.线段AB 2.线段a
2020年10月2日
2.直线AB与直线BA是同一条直线.(√ )
3.射线AB与射线BA是同一条射线.(× )
4.线段AB与线段BA是同一条线段.(√ )
5.射线比线段长也可能线段比射线长.(× )
6.在两个点之间,一定是线段最短.( )
﹒﹒﹒ 7.线段上只有两个点.( )
A√ B C
8.射线AB和射线AC是×同一条射线.( )
汇报人:XXX 汇报日期:2线 公理
线段 公理
8
练习2.按照图形(1)填空.
①.点O在直线__.
②.点B在射线AB___.
③.点A是线段AB的一个___.
按照图(2)填空.
④.以O为端点的射线有__条C.
B
.. . A O
A O
B
(1) 2020年10月2日
(2)
9
判断题:
1.拉紧的细绳子不是射线而是线段.(√ )
一年数学组
2020年10月2日
1
1.点:通常表示一个物体的位置.
. A
.B
2.直线:向两方无限延伸着的. _______A_._____B_. ____ a
表示方法:(1)可以用两个大写字母来表示.
(2)可以用一个小写字母来表示.
2020年10月2日
2
3.射线:
﹒A
直线上一点和它一旁的部分叫做射线.
2020年10月2日
√
10
画一画
﹒ (一):已知,平面上有三点A,B,C. A
1.画直线AB.
C
2.画射线AC. 3.连结BC.
﹒B
(二):平面上有三点﹒A,B,C,不在同一条直线上, 过其中每两个点画直线,可以画出几条?
2020年10月2日
11
在一条笔直的公路L两侧,分别有C,D
两个村庄,现在要在公路上建一个供电
