金属的结构和性质体心立方堆积中八面体空隙与四面体空隙半径计算
高中化学选修二第三章《晶体结构与性质》测试(包含答案解析)(13)

一、选择题1.(0分)[ID :139815]有关晶体的结构如图所示,下列说法中不正确的是( )A .在NaCl 晶体中,距Na 最近的Cl 形成正八面体B .在2CaF 晶体中,每个晶胞平均占有4 个Ca 2+C .在金刚石晶体中,碳原子与碳碳键个数的比为1:2D .该气态团簇分子的分子式为EF 或FE2.(0分)[ID :139897]图a 、b 、c 分别为氯化钠在不同状态下的导电实验的微观示意图(X Y 、均表示石墨电极,且与直流电源连接方式相同,表示水分子).下列说法正确的是A .Y 电极与电源负极相连B .能导电的装置中,Y 电极产物相同C .NaCl 是电解质,三种状态下都能导电D .图b 说明通电后发生了:NaCl Na Cl +-=+ 3.(0分)[ID :139888]下列关于晶体的说法正确的是 A .能导电的固体一定是金属晶体B .判断某固体是否是晶体的直接方法是X-射线衍射实验C .分子晶体中分子间作用力越强,分子越稳定D .石墨晶体中没有大π键4.(0分)[ID :139878]将少量硫酸铜溶液滴入氨基乙酸钠溶液(22H N CH COONa --)中即可得到结构如图所示的产物。
下列叙述错误的是A .氨基乙酸钠中的氮原子采取3sp 杂化B .221mol H N CH COONa --中含有A 8N 个σ键C .产物中Cu 、N 原子均为四面体形结构D .向该反应后的混合溶液中滴加NaOH 溶液,会产生蓝色沉淀 5.(0分)[ID :139873]下列关于Na 2O 2的说法中,正确的是 A .Na 2O 2属于碱性氧化物B .Na 2O 2固体中既有离子键又有共价键C .Na 2O 2在反应中只能作氧化剂D .Na 2O 2固体中阴离子和阳离子的个数比为1:1 6.(0分)[ID :139872]关于晶体的叙述中,正确的是 A .分子晶体中,共价键的键能越大,熔、沸点越高 B .分子晶体中,分子间作用力越大,该分子越稳定 C .共价晶体中,共价键的键能越大,熔、沸点越高D .某晶体溶于水后,可电离出自由移动的离子,该晶体一定是离子晶体 7.(0分)[ID :139856]下列说法不正确的是 A .某些胶态金属氧化物分散于玻璃中可制成有色玻璃 B .以NaCl 为原料,工业上可制备纯碱和烧碱C .牺牲阳极的阴极保护法是利用原电池原理保护金属的一种方法D .通常,只有那些分子较小、分子形状呈长形或碟形的物质,才易形成液晶态 8.(0分)[ID :139848]下列描述正确的是 A .2CS 为V 形的极性分子 B .3NO -与23SO -的中心原子均为3sp 杂化C .3NF 的键角大于3NCl 的键角D .金属键无方向性和饱和性9.(0分)[ID :139836]下列说法正确的是A .2C O 、2SO 均是非极性分子 B .羊毛织品水洗后会变形、DNA 双螺旋结构均与氢键有关 C .金属的导热性和导电性都是通过自由电子的定向运动实现的D .2SiO 晶体中,原子未排列成紧密堆积结构的原因是共价键具有饱和性 10.(0分)[ID :139835]邻二氮菲(phen)与Fe 2+生成稳定的橙红色邻二氮菲亚铁离子()23Fe phen +⎡⎤⎣⎦,可用于2Fe +浓度的测定,邻二氮菲的结构简式如图所示。
四面体间隙和八面体间隙 铁素体 奥氏体

四面体间隙和八面体间隙是固体物质中晶格间隙的一种特殊排列结构,它们在固体材料中起着非常重要的作用。
铁素体和奥氏体作为两种重要的金属组织结构,在材料学中也扮演着至关重要的角色。
本文将以四面体间隙和八面体间隙为切入点,深入探讨铁素体和奥氏体的组织结构、特性和应用,旨在帮助读者更全面地理解和理解这两种金属组织结构。
1. 四面体间隙与八面体间隙四面体间隙是指正方晶系和六方晶系中,离子晶体结构最密堆积的结构中央空隙处,其原子堆积密度为74,通常由钠氯型晶体构成。
而八面体间隙则是指正方晶系和六方晶系中,离子晶体结构中心空隙处,其原子堆积密度为68,通常由氧化物晶体构成。
四面体间隙和八面体间隙的存在对固体材料的性质和应用有着重要的影响。
2. 铁素体铁素体是铁碳合金中的一种组织结构,主要由α-Fe和少量的固溶碳构成。
其结构呈等轴晶体结构,具有良好的塑性和韧性,适用于低温、高强度的工程钢材。
铁素体中的四面体间隙和八面体间隙对其力学性能和热处理性能起着重要作用,通过调控间隙结构可以实现对铁素体组织结构的控制和改善。
3. 奥氏体奥氏体是铁碳合金中的另一种组织结构,主要由γ-Fe和一定量的固溶碳构成。
其结构呈面心立方结构,具有优异的强度和硬度,适用于高温、高强度的工程钢材。
奥氏体中的四面体间隙和八面体间隙对其耐热性、耐蚀性和强度起着重要作用,通过调控间隙结构可以实现对奥氏体组织结构的控制和改善。
总结回顾:通过本文的深入探讨,我们对四面体间隙和八面体间隙有了更深入的了解,并且对铁素体和奥氏体的组织结构、特性和应用也有了更全面的认识。
四面体间隙和八面体间隙作为固体材料中晶格间隙的特殊排列结构,在材料学中具有重要的意义,通过对其结构的深入了解和控制,可以实现对金属组织结构的优化和改进。
个人观点和理解:在实际工程应用中,对四面体间隙和八面体间隙的深入研究将有助于材料设计和制备工艺的优化,从而实现对金属材料性能的有效控制和提升。
金属的结构和性质体心立方堆积中八面体空隙与四面体空隙半径计算

~08金属的结构和性质【】半径为R 的圆球堆积成正四面体空隙,试作图计算该四面体的边长和高、中心到顶点距离、中心距离地面的高度、中心到两顶点连县的夹角以及中心到球面的最短距离。
解:4个等径圆球作紧密堆积的情形示于图(a )和(b),图(c)示出堆积所形成的正四面体空隙。
该正四面体的顶点即球心位置,边长为圆球半径的2倍。
图由图和正四面体的立体几何知识可知: 边长AB=2R高()12122222213AM AE EMAB BE DE ⎡⎤⎛⎫=-=--⎢⎥⎪⎝⎭⎢⎥⎣⎦ \()1122222222113223AB AB AE R R R ⎡⎤⎡⎤⎫⎛⎫⎛⎫⎢⎥=--=--⎢⎥⎪ ⎪ ⎪⎪⎢⎥⎝⎭⎝⎭⎢⎥⎝⎭⎣⎦⎣⎦26 1.6333R R =≈中心到顶点的距离:36 1.2254OA AM R R==≈中心到底边的高度:160.4084OM AM R ==≈中心到两顶点连线的夹角为:AOB ∠()())()()2222211226/22cos cos 226/2R R OA OB AB OA OB R θ--⎡⎤-⎡⎤+-⎢⎥==⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦()1cos 1/3109.47-=-=︒ 中心到球面的最短距离0.225OA R R =-≈}本题的计算结果很重要。
由此结果可知,半径为R 的等径圆球最密堆积结构中四面体空隙所能容纳的小球的最大半径为。
而正是典型的二元离子晶体中正离子的配位多面体为正四面体时正、负离子半径比的下限。
此题的结果也是了解hcp 结构中晶胞参数的基础(见习题。
【】半径为R 的圆球堆积成正八面体空隙,计算中心到顶点的距离。
解:正八面体空隙由6个等径圆球密堆积而成,其顶点即圆球的球心,其棱长即圆球的直径。
空隙的实际体积小于八面体体积。
图中三图分别示出球的堆积情况及所形成的正八面体空隙。
图、由图(c )知,八面体空隙中心到顶点的距离为:1112222222OC AC AB R R ===⨯=而八面体空隙中心到球面的最短距离为:20.414OC R R R R -=-≈此即半径为R 是典型的二元离子晶体中正离子的配位多面体为正八面体时/r r +-的下限值。
无机材料科学基础答案 2
第二章2-1略。
2-2 (1)一晶面在x、y、z轴上的截距分别为2a、3b、6c,求该晶面的晶面指数;(2)一晶面在x、y、z轴上的截距分别为a/3、b/2、c,求出该晶面的晶面指数。
答:(1)h:k:l==3:2:1,∴该晶面的晶面指数为(321);(2)h:k:l=3:2:1,∴该晶面的晶面指数为(321)。
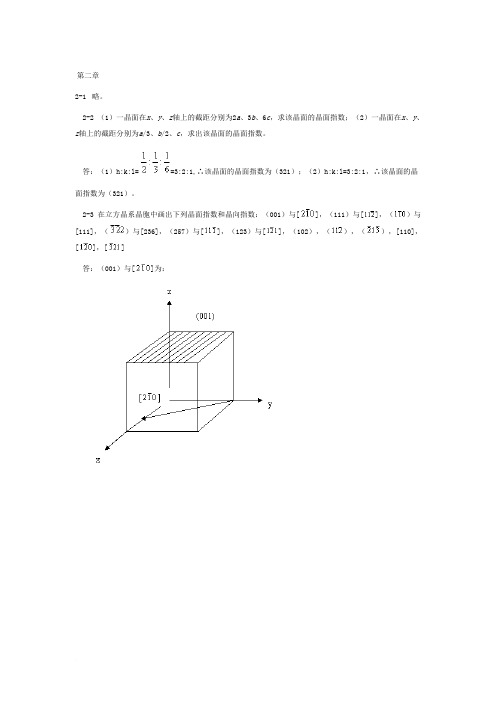
2-3 在立方晶系晶胞中画出下列晶面指数和晶向指数:(001)与[],(111)与[],()与[111],()与[236],(257)与[],(123)与[],(102),(),(),[110],[],[]答:(001)与[]为:2-4 定性描述晶体结构的参量有哪些?定量描述晶体结构的参量又有哪些?答:定性:对称轴、对称中心、晶系、点阵。
定量:晶胞参数。
2-5 依据结合力的本质不同,晶体中的键合作用分为哪几类?其特点是什么?答:晶体中的键合作用可分为离子键、共价键、金属键、范德华键和氢键。
离子键的特点是没有方向性和饱和性,结合力很大。
共价键的特点是具有方向性和饱和性,结合力也很大。
金属键是没有方向性和饱和性的的共价键,结合力是离子间的静电库仑力。
范德华键是通过分子力而产生的键合,分子力很弱。
氢键是两个电负性较大的原子相结合形成的键,具有饱和性。
2-6 等径球最紧密堆积的空隙有哪两种?一个球的周围有多少个四面体空隙、多少个八面体空隙?答:等径球最紧密堆积有六方和面心立方紧密堆积两种,一个球的周围有8个四面体空隙、6个八面体空隙。
2-7n个等径球作最紧密堆积时可形成多少个四面体空隙、多少个八面体空隙?不等径球是如何进行堆积的?答:n个等径球作最紧密堆积时可形成n个八面体空隙、2n个四面体空隙。
不等径球体进行紧密堆积时,可以看成由大球按等径球体紧密堆积后,小球按其大小分别填充到其空隙中,稍大的小球填充八面体空隙,稍小的小球填充四面体空隙,形成不等径球体紧密堆积。
2-8 写出面心立方格子的单位平行六面体上所有结点的坐标。
无机材料科学基础作业习题

无机材料科学基础作业习题第一章晶体结构基础1-1 定义下述术语,并注意它们之间的联系和区别:晶系;点群;空间群;平移群;空间点阵1-2 简述晶体的均一性、各向异性、对称性三者的相互关系。
1-3 列表说明七个晶系的对称特点及晶体定向规则。
1-4 四方晶系晶体a=b,c=1/2a。
一晶面在X、Y.Z轴上的截距分别为2a, 3b 和6c。
给出该晶面的密勒指数。
1-5 在立方晶系中画出下列晶面:a)(001)b)(110)c)(111)1-6 在上题所画的晶面上分别标明下列晶向:a(210) b(111) c(101)1-7 立方晶系组成{111}单形的各晶面构成一个八面体,请给出所有这些晶面的密勒指数。
1-8 试在完整的六方晶系晶胞上画出(1012)晶面的交线及〔1120〕〔2113〕晶向,并列出{1012}晶面族中所有晶面的密勒指数。
1-9 a≠b≠c α=β=γ=90℃的晶体属什么晶系?a≠b≠c α≠β≠γ≠90℃的晶体属什么晶系?你能否据此确定这二种晶体的布拉维点阵?1-10 下图示正交面心格子中去掉上下底心后的结点排列情况。
以图中的形状在三维空间无限重复,能否形成一空间点阵?为什么?1 –11 图示单斜格子的(010)面上的结点排布。
试从中选出单位平行六面体中的a和c。
1 –12 为什么等轴晶系有原始、面心、体心而无底心格子?1 –13 为什么在单斜晶系的布拉维格子中有底心C格子而无底心B格子?1-14 试从立方面心格子中划分出一三方菱面体格子,并给出其晶格常数。
说明为什么造选取单位平行六面体时不选后者而选前者?1 –15 写出立方面心格子的单位平行六面体上所有结点的座标,注明其中哪些属于基本点。
1 –16 给出(111)面和(111)面交棱的晶棱符号。
1 –17 试证(123)(112)和(110)诸晶面属于同一晶带,并给出其晶带符号。
1-18 证明立方晶系〔111〕晶向垂直于(111)晶面。
金属的结构和性质体心立方堆积中八面体空隙及四面体空隙半径计算

08金属的结构和性质[8.1】半径为尺的岡球堆枳成正四面体空晾,试作图it 算该四面休的边长和高.中心到顶 点即离、中心距离地而的高度、中心到两顶点连县的夹角以及中心到球面的最短即离。
解:4个等径岡球作紧密堆枳的情形示于图9.1 (a)和(b),图9.1(c)示出堆枳所形应的 正呱面体空隙。
垓正呱面体的顶点OP 球心位置,血长为岡球半径的2倍。
H9.1由图和正四面体的立(t 几何知识可知: 边长AB=2RAM =(AE 2-EM 2]^= AB 1-BE 1- -DE 高i=AB 2——ABV2OA = -AM = —/?«1.2257? 中心到顶点的脳离: 4 2 OM =丄 AM = — R^ 0.4087? 中心到(Kill 的高度:46中心到两硕点连线的夹角为:ZA °B= cos _, (-1/3) = 109.47°中心到球面的量短距离=04/0.225/?本题的it 算结果很亜要。
由lit 结果可知,半径为R 的等径同球最密堆枳结构中四面体空 除所能容纳的小球的最大半径为0.225R 。
而0.225正是典塑的二元离子晶体中正离子的配位 多而体为正四面体时正、负离子半径比的卞限。
此题的结果也是了解hep 结构中晶胞参数的 基KS (见习 g 9.04)o[8.2] 半径力尺的岡球堆枳成正八面体空B, it 算中心绢頂虑的更离。
-I AE (3& = cos°OA 2+OB 2-AB 22(OA)(O3)2(極/2「-(2町 2(偸/2『D解:正八面体空隙由6个等径||球密堆枳而成,其頂点即同球的球心,貝校长即圆球的Igo空隙的实际体枳小于八面图9.2中三图分别示出球的堆枳侑况及所形成的正由图(c)知,八面体空隙中心到顶点的距离为:OC = -AC = -y/2AB =丄VJx2R =血2 2 2而八面体空隙中心到球面的最短距离为:OC-R = d-R".4\4R此即半径为R的等径岡球最密堆枳形成的正八面体空除所能容纳的爪球的最大半径。
面心立方的四面体空隙和八面体空隙

面心立方的四面体空隙和八面体空隙在我们的生活中,面心立方体这种结构真的是个宝藏,特别是说到它的四面体空隙和八面体空隙,嘿,这可真是个有趣的话题!想象一下,面心立方体就像一个忙碌的城市,每个原子都是一栋高楼,紧紧挨在一起,真的是拥挤得很呢。
不过,就在这些高楼之间,还藏着一些“空房子”,就是那些四面体空隙和八面体空隙。
四面体空隙就像小巢窝,位置可巧妙了。
它们位于原子之间,四个原子就像四个好友围坐在一起,中心空着。
这小小的空隙虽小,却能容纳一些小粒子,就像朋友之间总有个空位留给新来的小伙伴,大家在一起聚会,热闹非凡。
这个空隙的体积虽然不大,但可不容小觑,能为材料的性质加分,嘿,谁不喜欢结识新朋友呢?再来说说八面体空隙,这就像城市里的广场,空间更大,也更能容纳!它的位置可灵活了,两个面心立方体的原子之间,形成了一个更大的空间。
这种结构就像是小区里的公园,大家可以在这里聚集、玩耍。
八面体空隙可以容纳更多的粒子,像是在盛大的派对上,热热闹闹,人人都想来凑个热闹,扩大了材料的可塑性和韧性。
很多人可能会问,为什么这些空隙如此重要呢?嘿,原因可多了,材料的性质可全靠它们来“撑场面”。
比如在金属材料中,四面体和八面体空隙的存在,让它们在变形时更有弹性,不容易断裂。
这就像一个人,有良好的适应能力,遇到压力时不会轻易崩溃,而是灵活应对。
这些空隙对材料的化学反应也有影响,像是化学反应的“调味剂”。
材料中的原子不光是孤独的呆在那儿,有了空隙,它们之间就能产生更多的互动。
嘿,反应发生得更加迅速,能量的传递也更顺畅,就像大家聚在一起,聊天畅谈,气氛一下子就热起来了。
不过,这些空隙不是一直都在哦。
环境变化、温度升高,都会影响它们的存在。
就像天气变化,有时候阳光明媚,有时候大雨倾盆,原本热闹的广场也会冷清下来。
材料在高温下可能会出现结构的变化,导致空隙的减少,这对材料的性能可不是个好消息。
而且啊,不同的材料中,这些空隙的比例也不一样。
2023年高考化学第一轮专项复习真题仿真—物质的结构与性质(含解析)

2023届高考化学第一轮专题复习真题试卷模拟——物质的结构与性质①和②配位原子提供孤电子对的能力与元素的电负性大小有关,易提供孤电子对。
则对于配合物①该晶体中,锌的配位数为___________。
②已知空间利用率η=晶胞中含有原子的体积晶胞的体积r2cm,则该晶体的空间利用率为(列出计算式即可)___________。
③以晶胞参数为单位长度建立的坐标系可以表示晶胞中各原子的位置,称为原子的分数坐标。
若A点原子的分数坐标为(0,0,0),则B点原子的分数坐标为___________。
2.(2023·西藏拉萨·统考一模)Na、Cl、Cu是中学化学中常见的成盐元素,它们之间能形成多种化合物。
回答下列问题:(1)Na和Cl两种元素能形成多种化合物,如常见的NaCl,其晶胞结构如图1所示,氯离子位于晶胞的顶点和面心。
①Cl的基态原子核外电子排布式为___________。
②图1所示晶胞中,与钠离子最近的钠离子共有_______个。
③在高压下,Na与Cl可产生新的化合物,晶胞结构如图2所示,钠离子位于晶胞的顶点和体心,该物质的化学式为_________。
④Na与Cl在某条件下还能形成一种团簇分子,分子结构如图3所示,氯原子位于顶点和面心。
该团簇分子的分子式为______。
(2)Cu、NH3、Cl可以形成[Cu(NH3)4]Cl2。
NH3分子的空间构型为________,[Cu(NH3)4]2+中提供空轨道的是__________,1mol该配合物中含有σ键的数目为___________(N A为阿伏加德罗常数的值)。
(3)金属铜采取面心立方最密堆积方式,Cu晶胞的边长为a pm,其晶胞及相关结构如图甲、乙、丙所示:①铜晶体的密度ρ=____________g·cm-3。
②根据图丙求出铜原子的半径r=_______pm。
(4)镍白铜(铜镍合金)常用作海洋工程应用材料。
某镍白铜合金的晶胞结构如图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
08金属的结构和性质【】半径为R 的圆球堆积成正四面体空隙,试作图计算该四面体的边长和高、中心到顶点距离、中心距离地面的高度、中心到两顶点连县的夹角以及中心到球面的最短距离。
解:4个等径圆球作紧密堆积的情形示于图(a )和(b),图(c)示出堆积所形成的正四面体空隙。
该正四面体的顶点即球心位置,边长为圆球半径的2倍。
图由图和正四面体的立体几何知识可知: 边长AB=2R高()12122222213AM AE EMAB BE DE ⎡⎤⎛⎫=-=--⎢⎥ ⎪⎝⎭⎢⎥⎣⎦中心到顶点的距离:3 1.2254OA AM R ==≈中心到底边的高度:10.4084OM AM R R ==≈中心到两顶点连线的夹角为:AOB ∠ 中心到球面的最短距离0.225OA R R =-≈本题的计算结果很重要。
由此结果可知,半径为R 的等径圆球最密堆积结构中四面体空 隙所能容纳的小球的最大半径为。
而正是典型的二元离子晶体中正离子的配位多面体为正四面体时正、负离子半径比的下限。
此题的结果也是了解hcp 结构中晶胞参数的基础(见习题。
【】半径为R 的圆球堆积成正八面体空隙,计算中心到顶点的距离。
解:正八面体空隙由6个等径圆球密堆积而成,其顶点即圆球的球心,其棱长即圆球的直径。
空隙的实际体积小于八面体体积。
图中三图分别示出球的堆积情况及所形成的正八面体空隙。
图由图(c )知,八面体空隙中心到顶点的距离为:而八面体空隙中心到球面的最短距离为:此即半径为R 的等径圆球最密堆积形成的正八面体空隙所能容纳的小球的最大半径。
是典型的二元离子晶体中正离子的配位多面体为正八面体时/r r +-的下限值。
【】半径为R 的圆球围成正三角形空隙,计算中心到顶点的距离。
解:由图可见,三角形空隙中心到顶点(球心)的距离为:图三角形空隙中心到球面的距离为:此即半径为R 的圆球作紧密堆积形成的三角形空隙所能容纳的小球的最大半径,是“三角形离子配位多面体”中/r r +-的下限值。
【】半径为R 的圆球堆积成3A 结构,计算简单立方晶胞参数a 和c 的数值。
解:图示出A3型结构的—个简单六方晶胞。
该晶胞中有两个圆球、4个正四面体空隙和两个正八面体空隙。
由图可见,两个正四面体空隙共用一个顶点,正四面体高的两倍即晶胞参数c ,而正四面体的棱长即为晶胞参数a 或b 。
根据题的结果,可得:图【】证明半径为R 的圆球所作的体心立方堆积中,八面体空隙只能容纳半径为0.154R 的小球,四面体空隙可容纳半径为0.291R 的小球。
证明:等径圆球体心立方堆积结构的晶胞示于图(a )和(b )。
由图(a )可见,八面体空隙中心分别分布在晶胞的面心和棱心上。
因此,每个晶胞中6个八面体空隙1161224⎛⎫⨯+⨯ ⎪⎝⎭。
而每个晶胞中含2个圆球,所以每个球平均摊到3个八面体空隙。
这些八面体空隙是沿着一个轴被压扁了的变形八面体,,短轴为a (a 是晶胞参数)。
(•圆球,o 八面体空隙中心,g 四面体空隙中心)图八面体空隙所能容纳的小球的最大半径0r 即从空隙中心(沿短轴)到球面的距离,该距离为2a R -。
体心立方堆积是一种非最密堆积,圆球只在3C轴方向上互相接触,因而a R =。
代入2a R -,得010.154r R R⎫=≈⎪⎭。
由图(b )可见,四面体空隙中心分布在立方晶胞的面上,每个面有4个四面体中心,因此每个晶胞有12个四面体空隙1642⎛⎫⨯⨯ ⎪⎝⎭。
而每个晶胞有2个球,所以每个球平均摊到6个四面体空隙。
这些四面体空隙也是变形的,两条长棱皆为a ,4条短棱皆为2a。
四面体空隙所能容纳的小球的最大半径T r 等于从四面体空隙中心到顶点的距离减去球的半径R 。
而从空隙中心到顶点的距离为1222244a a a ⎡⎤⎛⎫⎛⎫+=⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦,所以小球的最大半径为0.291R R R R -=-=【】计算等径圆球密置单层中平均每个球所摊到的三角形空隙数目及二维堆积密度。
解:图示出等径圆球密置单层的—部分。
图由图可见,每个球(如A)周围有6个三角形空隙,而每个三角形空隙由3个球围成,所以每个球平均摊到1623⨯=个三角形空隙。
也可按图中画出的平行四边形单位计算。
该单位只包含一个球(截面)和2个三角形空隙,即每个球摊到2个三角形空隙。
设等径圆球的半径为R ,则图中平行四边形单位的边长为2R 。
所以二维堆积系数为: 【】指出1A 型和3A 型等径圆球密置单层的方向是什么?解:A1型等径团球密堆积中,密置层的方向与3C 轴垂直,即与(111)面平行。
A3型等径圆球密堆积中,密置层的方向与六重轴垂直,即与(001)面平行。
下面将通过两种密堆积型式划分出来的晶胞进一步说明密置层的方向。
A1型密堆积可划分出如图(a)所示的立方面心晶胞。
在该晶胞中,由虚线连接的圆球所处的平面即密置层面,该层面垂直于立方晶胞的体对角线即3C 轴。
每一晶胞有4条体对角线,即在4个方向上都有3C 轴的对称性。
因此,与这4个方向垂直的层面都是密置层。
图A3型密堆积可划分出如图(b)所示的六方晶胞。
球A 和球B 所在的堆积层都是密置 层.这些层面平行于(001)晶面,即垂直于c 轴,而c 轴平行于六重轴6C 。
【】请按下面(a )~(c )总结1A 、2A 及3A 型金属晶体的结构特征。
(a ) 原子密置层的堆积方式、重复周期(2A 型除外)、原子的配位数及配位情况。
(b ) 空隙的种类和大小、空隙中心的位置及平均每个原子摊到的空隙数目。
(c ) 原子的堆积系数、所属晶系、晶胞中原子的坐标参数、晶胞参数与原子半径的关系以及空间点阵型式等。
解:(a)A1,A2和A3型金属晶体中原子的堆积方式分别为立方最密堆积(ccp)、体心立方密堆积(bcp)相六方最密堆积(hcp)。
A1型堆积中密堆积层的重复方式为ABCABCABC …,三层为一重复周期,A3型堆积中密堆积层的重复方式为ABABAB …,两层为一重复周期。
Al 和A3型堆积中原子的配位数皆为12,而A2型堆积中原子的配位数为8—14,在A1型和A3型堆积中,中心原子与所有配位原子都接触.同层6个,上下两层各3个。
所不同的是,A1型堆积中,上下两层配位原子沿3C 轴的投影相差60 呈6C轴的对称性,而A3型堆积中,上下两层配位原子沿c 轴的投影互相重合。
在A2型堆积中,8个近距离(与中心原子相距为2a )配位原子处在立方晶胞的顶点上,6个远距离(与中心原子相距为a )配位原子处在相邻品胞的体心上。
(b)A1型堆积和A3型堆积都有两种空隙,即四面体空隙和八面体空隙。
四面体空隙可容纳半径为0.225R 的小原子.八面体空隙可容纳半径为0.414R 的小原子(R 为堆积原子的半径)。
在这两种堆积中,每个原子平均摊到两个四面体空隙和1个八面体空隙。
差别在于,两种堆积中空隙的分布不同。
在A1型堆积中,四面体空隙的中心在立方面心晶胞的体对角线上,到晶胞顶点的距离为R 。
八面体空隙的中心分别处在晶胞的体心和棱心上。
在A3型堆积中,四面体空隙中心的坐标参数分别为352112170,0,;0,0,;,,;,,88338338。
而八面体空隙中心的坐标参数分别为211213,,;,,334334。
A2型堆积中有变形八面体空隙、变形四面体空隙和三角形空隙(亦可视为变形三方双锥空隙)。
八面体空隙和四面体空隙在空间上是重复利用的。
八面体空隙中心在体心立方晶胞的面心和棱心上。
每个原子平均摊到3个八面体空隙,该空隙可容纳的小原子的最大半径为0.154R 。
四面体空隙中心处在晶胞的面上。
每个原子平均摊到6个四面体空隙,该空隙可容纳的小原子的最大半径为0.291R 。
三角形空隙实际上是上述两种多面体空隙的连接面,算起来,每个原子摊到12个三角形空隙。
(c )金属的结构形式 A1 A2 A3 原子的堆积系数% % % 所属晶系立方立方六方晶胞形式 面心立方体心立方六方晶胞中原子 的坐标参数晶胞参数与 原子半径的关系点阵形式 面心立方 体心立方 简单六方综上所述,A1,A2和A3型结构是金属单质的三种典型结构形式。
它们具有共性,也有差异。
尽管A2型结构与A1型结构同属立方晶体,但A2型结构是非最密堆积,堆积系数小,且空隙数目多,形状不规则,分布复杂。
搞清这些空隙的情况对于实际工作很重要。
A1型和A3型结构都是最密堆积结构,它们的配位数、球与空隙的比例以及堆积系数都相同。
差别是它们的对称性和周期性不同。
A3型结构属六方晶系,可划分出包含两个原子的六方晶胞。
其密置层方向与c 轴垂直。
而A1型结构的对称性比A3型结构的对称性高,它属立方晶系,可划分出包含4个原子的面心立方晶胞,密置层与晶胞体对角线垂直。
A1型结构将原子密置层中6C 轴所包含的3C轴对称性保留了下来。
另外,A3型结构可抽象出简单六方点阵,而A1型结构可抽象出面心立方点阵。
【】画出等径圆球密置双层图及相应的点阵素单位,指明结构基元。
解:等径圆球的密置双层示于图。
仔细观察和分子便发现,作周期性重复的最基本的结构单位包括2个圆球,即2个圆球构成一个结构基元。
这两个球分布在两个密置层中,如球A 和球B 。
图密置双层本身是个三锥结构,但由它抽取出来的点阵却为平面点阵。
即密置双层仍为二维点阵结构。
图中画出平面点阵的素单位,该单位是平面六方单位,其形状与密置单层的点阵素单位一样,每个单位也只包含1个点阵点,但它代表2个球。
等径圆球密置双层是两个密置层作最密堆积所得到的唯一的一种堆积方式。
在密置双层结构中,圆球之间形成两种空隙,即四面体空隙和八面体空隙。
前者由3个相邻的A 球和1个B 球或3个相邻的B 球和1个A 球构成。
后者则由3个相邻的A 球和3个相邻的B 球构成。
球数:四面体空隙数:八面体空隙数=2:2:1【】金属铜属于1A 型结构,试计算(111)、(110)和(100)等面上铜原子的堆积系数。
解:参照金属铜的面心立方晶胞,画出3个晶面上原子的分布情况如下(图中未示出原子的接触情况):(111)面是密置面,面上的所有原子作紧密排列。
该面还是的铜原子的堆积系数等于三角形单位中球的总最大截面积除以三角形的面积。
三角形单位中包含两个半径为R 的球113326⎛⎫⨯+⨯ ⎪⎝⎭,所以该面上原子的堆积系数为:【】 金属铂为1A 型结构,立方晶胞参数392.3a pm =,Pt 的相对原子质量为,试求金属铂的密度及原子半径。
解:因为金属铂属于A1型结构,所以每个立方晶胞中有4个原子。
因而其密度为:A1型结构中原子在立方晶胞的面对角线方向上互相接触,因此晶胞参数a 和原子半径R的关系为a =,所以:【】 硅的结构和金刚石相同,Si 的共价半径为117pm ,求硅的晶胞参数,晶胞体积和晶胞密度。
