优品课件之高考数学第一轮圆锥曲线基础知识点复习教案
高三数学一轮复习教案:圆锥曲线
圆锥曲线复习【复习指导】1、掌握椭圆、双曲线和抛物线的定义、标准方程及几何性质;2、圆锥曲线的应用。
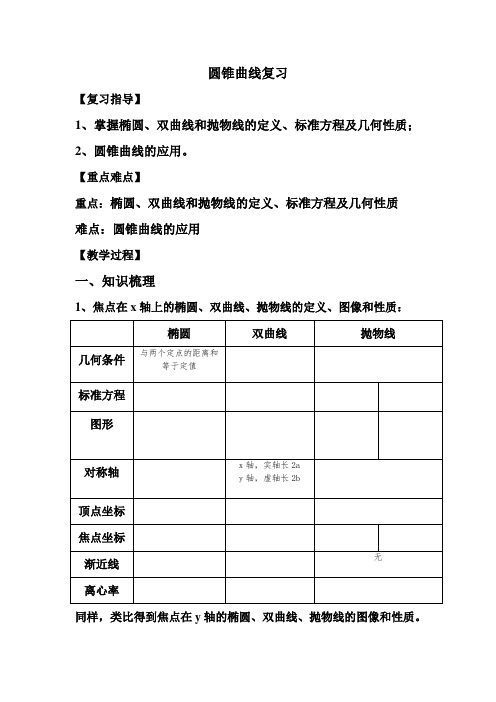
【重点难点】重点:椭圆、双曲线和抛物线的定义、标准方程及几何性质难点:圆锥曲线的应用【教学过程】一、知识梳理1、焦点在x轴上的椭圆、双曲线、抛物线的定义、图像和性质:同样,类比得到焦点在y轴的椭圆、双曲线、抛物线的图像和性质。
xyF 1F 2O1M小试牛刀:(1)已知椭圆1162522=+y x 上一点P 到椭圆的一个焦点的距离为3,则点P 到另一个焦点的距离( )A 2B 3C 5D 7(2)已知双曲线19-2522=y x 上一点P 到椭圆的一个焦点的距离为12,则点P 到另一个焦点的距离( )A 2B 22C 2或22D 4或22(3)如果方程222=+ky x 表示焦点在y 轴上的椭圆,那么实数k 的取值范围是 ( )A.(0,+∞)B.(0,2)C.(1,+∞)D.(0,1)(4)方程12--422=+t y t x 所表示的曲线为C ,有下列命题: ①若曲线C 为椭圆,则4t 2<<;②若曲线C 为双曲线,则2t 4t <>或; ③曲线C 不可能为圆;④若曲线C 为焦点在y 轴的双曲线,则4t >。
以上命题正确的是 。
(5)抛物线的焦点是双曲线369-422=y x 的左顶点,则抛物线的标准方程为 。
二、典例示范类型一 圆锥曲线的定义及其应用例一 求与圆1)3(22=+-y x 及9)3(22=++y x 都外切的动圆圆心M 的轨迹方程.变式训练: 点B(-4,0),C(4,0)且△ABC 的周长是18,则△ABC 的顶点A 的轨迹方程。
类型二 圆锥曲线的标准方程与几何性质例二 (1)求焦点为(0,6)且与双曲线1-222 y x 有相同渐近线的双曲线方程;思考:若将焦点为(0,6)该为焦距为12,求标准方程。
(2)已知抛物线的顶点在原点,焦点在y轴上,抛物线上一点P (m,-3)到焦点的距离等于5,求m的值,并写出抛物线方程、准线方程及焦点坐标。
2023年高考数学(文科)一轮复习课件——圆锥曲线的综合问题 第一课时 定点问题

(2)过点 S-13,0的动直线 l 交椭圆 C 于 A,B 两点,试问:在 x 轴上是否存 在一个定点 T,使得无论直线 l 如何转动,以 AB 为直径的圆恒过点 T?若存 在,求出点 T 的坐标;若不存在,请说明理由. 解 当直线 l 不与 x 轴重合时,设直线 l 的方程为 x=my-31, A(x1,y1),B(x2,y2),T(t,0), 由xy22=+mxy2=-113,消去 x 并整理,得 (18m2+9)y2-12my-16=0,
索引
所以 y1+y2=-m22m+n9,y1y2=mn22-+99. 代入③式,得(27+m2)(n2-9)-2m(n+3)mn+(n+3)2(m2+9)=0. 解得 n=-3(舍去)或 n=23. 故直线 CD 的方程为 x=my+32, 即直线 CD 过定点32,0. 若 t=0,则直线 CD 的方程为 y=0,过点32,0. 综上,直线 CD 过定点32,0.
索引
(2)过点 P13,0的直线 l 交椭圆 C 于 A,B 两点,试探究以线段 AB 为直径的圆是 否过定点.若过,求出定点坐标;若不过,请说明理由. 解 当 AB⊥x 轴时,以线段 AB 为直径的圆的方程为x-132+y2=196. 当AB⊥y轴时,以线段AB为直径的圆的方程为x2+y2=1. 可得两圆交点为Q(-1,0). 由此可知,若以线段AB为直径的圆过定点,则该定点为Q(-1,0). 下证Q(-1,0)符合题意. 设直线l的斜率存在,且不为0, 其方程设为 y=kx-13,代入y22+x2=1,
FENCENGXUNLIAN GONGGUTISHENG
A级 基础巩固
1.已知抛物线C的顶点在原点,焦点在坐标轴上,点A(1,2)为抛物线C上一点. (1)求抛物线C的方程; 解 若抛物线的焦点在x轴上,设抛物线方程为y2=ax,代入点A(1,2),可得 a=4,所以抛物线方程为y2=4x. 若抛物线的焦点在y轴上,设抛物线方程为x2=my,代入点A(1,2), 可得 m=21,所以抛物线方程为 x2=21y. 综上所述,抛物线 C 的方程是 y2=4x 或 x2=12y.
高三数学一轮复习圆锥曲线方程及性质教案

圆锥曲线方程及性质程图形焦点坐标(,0)2p(,0)2p-(0,)2p(0,)2p-准线方程2px=-2px=2py=-2py=范围x≥0x≤0y≥0y≤对称性x轴x轴y轴y轴顶点(0,0)(0,0)(0,0)(0,0)离心率1e=1e=1e=1e=说明:(1)通径:过抛物线的焦点且垂直于对称轴的弦称为通径;(2)抛物线o F xylo xyFlxyoFlxy2=,那么它的两条准线间的距离是()A.36 B.4 C.2 D.1解析:(1)设双曲线的两个焦点分别是F1(-5,0)与F2(5,0),则这两点正好是两圆的圆心,当且仅当点P与M、F1三点共线以及P与N、F2三点共线时所求的值最大,此时|PM|-|PN|=(|PF1|-2)-(|PF2|-1)=10-1=9故选B。
(2)双曲线221mx y+=的虚轴长是实轴长的2倍,∴ m<0,且双曲线方程为2214xy-+=,∴ m=14-,选A。
(3)如果双曲线的两个焦点分别为)0,3(1-F、)0,3(2F,一条渐近线方程为xy2=,∴2292a bba⎧+=⎪⎨=⎪⎩,解得2236ab⎧=⎨=⎩,所以它的两条准线间的距离是222ac⋅=,选C。
点评:关于双曲线渐近线、准线及许多距离问题也是考察的重点。
题型5:抛物线方程例9.(1))焦点到准线的距离是2;(2)已知抛物线的焦点坐标是F(0,-2),求它的标准方程。
解析:(1)y2=4x,y2=-4x,x2=4y,x2=-4y;方程是x2=-8y。
点评:由于抛物线的标准方程有四种形式,且每一种形式中都只含一个系数p,因此只要给出确定p的一个条件,就可以求出抛物线的标准方程。
当抛物线的焦点坐标或准线方程给定以后,它的标准方程就唯一确定了;若抛物线的焦点坐标或准线方程没有给定,则所求的标准方程就会有多解。
题型6:抛物线的性质例10.(1)若抛物线22y px=的焦点与椭圆22162x y+=的右焦点重合,则p的值为( )A .2-B .2C .4-D .4 (2)抛物线28y x =的准线方程是( )(A) 2x =- (B) 4x =- (C) 2y =- (D) 4y =- (3)抛物线x y 42=的焦点坐标为( )(A ))1,0(. (B ))0,1(. (C ))2,0(. (D ))0,2(解析:(1)椭圆22162x y +=的右焦点为(2,0),所以抛物线22y px =的焦点为(2,0),则4p =,故选D ;(2)2p =8,p =4,故准线方程为x =-2,选A ;(3)(直接计算法)因为p=2 ,所以抛物线y 2=4x 的焦点坐标为 。
高考数学一轮复习 第八章 平面解析几何 8.8 圆锥曲线的综合问题课件

p
已知抛物线y2=2px(p>0)的弦AB的中点M(x0,y0)(y0≠0) ,则kAB=⑧ yc0 . 若涉及直线过圆锥曲线焦点的问题,则一般利用圆锥曲线的定义去解决.
4.定点、定值问题 (1)求定值问题常见的方法 (i)从特殊入手,求出定值,再证明这个值与变量无关. (ii)直接推理、计算,并在计算推理的过程中消去变量,从而得到定值. (2)定点问题的常见解法 (i)假设定点坐标,根据题意选择参数,建立一个直线系或曲线系方程,而该 方程与参数无关,故得到一个关于定点坐标的方程组,以这个方程组的解 为坐标的点即所求定点; (ii)从特殊位置入手,找出定点,再证明该点适合题意.
6.求定值、最值问题等圆锥曲线综合问题要四重视 (1)重视定义在解题中的作用; (2)重视平面几何知识在解题中的作用; (3)重视根与系数的关系在解题中的作用; (4)重视曲线的几何特征与方程的代数特征在解题中的作用. 7.存在性问题 一般采用“假设反证法”或“假设验证法”来解决存在性问题.
1.设抛物线y2=4x的焦点弦被焦点分为长是m和n的两部分,则m与n的关系 是( ) A.m+n=4 B.mn=4 C.m+n=mn D.m+n=2mn 答案 C 解法一:焦点为F(1,0),设焦点弦为AB,其中A(x1,y1),B(x2,y2),当直 线AB的斜率存在时,依题意设AB的方程为y=k(x-1)(k≠0). 由焦半径公式得AF=x1+1=m,BF=x2+1c =n,又 y2 4x,
1 k2
c
|y1-y2|(k≠0)
.
3.已知弦AB的中点,研究AB的斜率和方程
(1)AB是椭圆
x2 a2
+
y2 b2
=1(a>b>0)的一条弦,AB中点M的坐标为(x0,y0)(y0≠0),
高考数学第一轮总复习课件 圆锥曲线与方程

▪
2.若双曲线x2 y2 1 的两条渐近线恰好
是抛物线y=a1x29+
4
的两条切线,则a的值B为
3
( )3
1
1
3
4
3
9
5
▪ A.
B.
C.
D.
▪2
3
易得双曲线的渐2近线方程为y=±
3
▪1 x,由对称性可知,直线y= x与2 曲线1
3y=ax24+ 4 a 0
93
1 3
33
▪ 相切,联立两方程消去y得ax2- x+ =0,
▪ 设A,B两点坐标分别为(x1,y1),(x2,
▪则
y2),
▪
所以
x1
x2
3m 2
,x1
x2
3m2 4, 4
AB
2 x1 x2
32 6m2 , 2
▪ 又因为BC的长等于点(0,m)到直线l的距
离 ▪
即BC
2m 2
,
▪
所以AC 2 AB2 BC 2 m2 2m 10
▪
=-(m+1)2+11,
▪ (Ⅱ)设M是椭圆长轴AB上的一点,M到直线 AP的距离等于|MB|,求椭圆上的点到点M的 距离d的最小值.
▪
(Ⅰ)由已知可得点A(-6,0),F(4,0),设
点P(x,y),y>0,则AP =(x+6,y),
▪FP =(x-4,y),由已知可得:
(x+3x662)(x-2y402)+y12=0,
不4 可能发生.故填4①p.
▪ 1.直线与圆锥曲线的位置关系
▪ 直线与圆锥曲线的位置关系有相交、相切、 相离;相交有两个交点(特殊情况除外), 相切只有一个交点,相离无交点.判断直线 与圆锥曲线的位置关系,通常是将直线方 程与曲线方程联立,消去变量y(或x)得 变量x(或y)的方程:ax2+bx+c=0(或 ay2+by+c=0)
XX届高考数学第一轮备考圆锥曲线复习上课学习上课学习教案

XX届高考数学第一轮备考圆锥曲线复习教案本资料为woRD文档,请点击下载地址下载全文下载地址XX版高三数学一轮精品复习学案:第八章解析几何8.3圆锥曲线【高考目标导航】一、曲线与方程.考纲点击了解方程的曲线与曲线的方程的对应关系;了解解析几何的基本思想和利用坐标法研究几何问题的基本方法;能够根据所给条件选择适当的方法求曲线的轨迹方程.2.热点提示(1)求轨迹方程是高考的重点和热点;(2)常以解答题的第一问的形式出现.一般用直接法、定义法或相关点法求解,所求轨迹一般为圆锥曲线,属中低档题。
二、椭圆.考纲点击(1)掌握椭圆的定义、几何图形、标准方程及简单性质;(2)了解椭圆的实际背景及椭圆的简单应用。
(3)理解数形结合的思想2.热点提示(1)椭圆的定义、标准方程和几何性质是高考重点考查的内容;直线和椭圆的位置关系是高考考查的热点。
(2)定义、标准方程和几何性质常以选择题、填空题的形式考查,而直线与椭圆位置关系以及与向量、方程、不等式等的综合题常以解答题的形式考查,属中高档题目。
三、双曲线.考纲点击(1)了解双曲线的定义、几何图形和标准方程,知道双曲线的简单几何性质。
(2)了解双曲线的实际背景及双曲线的简单应用。
(3)理解数形结合的思想。
2.热点提示(1)双曲线的定义、标准方程和离心率、渐近线等知识是高考考查的重点;双曲线与其他圆锥曲线的交汇命题是热点。
(2)主要以选择、填空题的形式考查,属于中低档题。
四、抛物线.考纲点击(1)掌握抛物线的定义、几何图形、标准方程及简单性质。
(2)理解数形结合的思想。
(3)了解抛物线的实际背景及抛物线的简单应用。
2.热点提示(1)抛物线的定义、标准方程及性质是高考考查的重点,抛物线与直线、椭圆、双曲线的交汇综合题是考查的热点。
(2)多以选择、填空题为主,多为中低档题。
有时也与直线、椭圆、双曲线交汇考查的解答题,此时属中高档题。
【考纲知识梳理】一、曲线与方程.一般地,在平面直角坐标系中,如果某曲线c上的点与一个二元方程f=0的实数解建立了如下关系:(1)曲线上点的坐标都是这个方程的解。
2024届高考数学第一轮专项复习——圆锥曲线的综合应用 教学PPT课件
− −
所以2(1-2 k )·
+(4 k -2 m -2)·
+8 m =0.整理,得
−
−
(1- m )(2 k + m -1)=0.当2 k + m -1=0时,直线 l : y = kx +1
-2 k 恒过点 A (2,1),不符合题意;当1- m =0时,直线 l : y = kx
=0.设 P ( x 1, y 1), Q ( x 2, y 2),则
− ≠ ,
− ≠ ,
即
所
= + ( − )( + ) > ,
− + > .
− −
以 x 1+ x 2=
, x 1 x 2=
.
(2) 若轨迹 C 上存在两点 A , B 满足 kOA + kOB =-1( kOA , kOB 分别为直线
OA , OB 的斜率),求直线 AB 的斜率的取值范围.
解:(2) 根据题意可知,直线 AB 的斜率存在.设直线 AB 的方程为 y = kx + b ,
+
经过 x 轴上的两个定点(1,0)和(-3,0).
2.
2
2
(2023·武汉期中)已知椭圆 E : 2 + 2 =1( a > b >0)的上顶点和
右顶点分别是 A (0,1)和 B ,离心率 e =
动点,且 CD ∥ AB .
(1) 求椭圆 E 的标准方程.
解:(1)
椭圆 E 的标准方程为 + y 2=1.
易知直线 AB 的方程为 x +2 y -2=0,| AB |= ,
年高考数学一轮复习精品课件圆锥曲线
第46讲 │ 能力提升
2020/8/1
第46讲 │ 规律总结 规律总结
2020/8/1
第46讲 │ 规律总结
2020/8/1
第46讲 │ 规律总结
2020/8/1
2020/8/1
Hale Waihona Puke 第45讲 │ 双基固化2020/8/1
第45讲 │ 双基固化
2020/8/1
第45讲 │ 双基固化
2020/8/1
第45讲 │ 能力提升 能力提升
2020/8/1
第45讲 │ 能力提升
2020/8/1
第45讲 │ 能力提升
2020/8/1
第45讲 │ 能力提升
2020/8/1
2020/8/1
第45讲 │ 双基固化
2020/8/1
第45讲 │ 双基固化
2020/8/1
第45讲 │ 双基固化
2020/8/1
第45讲 │ 双基固化
2020/8/1
第45讲 │ 双基固化
2020/8/1
第45讲 │ 双基固化
2020/8/1
第45讲 │ 双基固化
2020/8/1
第45讲 │ 双基固化
2020/8/1
第45讲 │ 双基固化
2020/8/1
第45讲 │ 双基固化
2020/8/1
第45讲 │ 双基固化
2020/8/1
第45讲 │ 双基固化
2020/8/1
第45讲 │ 双基固化
2020/8/1
第45讲 │ 双基固化
2020/8/1
第45讲 │ 双基固化
2020/8/1
第45讲 │ 双基固化
2020/8/1
第46讲 │ 能力提升 能力提升
理科数学第一轮复习圆锥曲线含教案和课件 第一节 椭 圆
第一节 椭 圆一.基本知识概要1 椭圆的两种定义:①平面内与两定点F 1,F 2的距离的和等于定长()212F F a >的点的轨迹,即点集M={P| |PF 1|+|PF 2|=2a ,2a >|F 1F 2|};(212F F a =时为线段21F F ,212F F a <无轨迹)。
其中两定点F 1,F 2叫焦点,定点间的距离叫焦距。
②平面内一动点到一个定点和一定直线的距离的比是小于1的正常数的点的轨迹,即点集M={P|e dPF =,0<e <1的常数}。
(1=e 为抛物线;1>e 为双曲线) 2 标准方程:(1)焦点在x 轴上,中心在原点:12222=+by a x (a >b >0);焦点F 1(-c ,0), F 2(c ,0)。
其中22b a c -=(一个∆Rt )(2)焦点在y 轴上,中心在原点:12222=+bx a y (a >b >0);焦点F 1(0,-c ),F 2(0,c )。
其中22b a c -=注意:①在两种标准方程中,总有a >b >0,22b a c -=并且椭圆的焦点总在长轴上;②两种标准方程可用一般形式表示:Ax 2+By 2=1 (A >0,B >0,A ≠B ),当A <B 时,椭圆的焦点在x 轴上,A >B 时焦点在y 轴上。
3.性质:对于焦点在x 轴上,中心在原点:12222=+b y a x (a >b >0)有以下性质:坐标系下的性质:① 范围:|x|≤a ,|y|≤b ;② 对称性:对称轴方程为x=0,y=0,对称中心为O (0,0); ③ 顶点:A 1(-a ,0),A 2(a ,0),B 1(0,-b ),B 2(0,b ),长轴|A 1A 2|=2a ,短轴|B 1B 2|=2b ;(a 半长轴长,b 半短轴长);④ 准线方程:ca x 2±=;或ca y 2±=⑤ 焦半径公式:P (x 0,y 0)为椭圆上任一点。
高考数学一轮复习 8.6 圆锥曲线的应用教案
8.6 圆锥曲线的应用●知识梳理解析几何在日常生活中应用广泛,如何把实际问题转化为数学问题是解决应用题的关键,而建立数学模型是实现应用问题向数学问题转化的常用方法.本节主要通过圆锥曲线在实际问题中的应用,说明数学建模的方法,理解函数与方程、等价转化、分类讨论等数学思想.●点击双基1.一抛物线型拱桥,当水面离桥顶2 m 时,水面宽4 m ,若水面下降1 m 时,则水面宽为A.6mB.26mC.4.5 mD.9 m解析:建立适当的直角坐标系,设抛物线方程为x 2=-2Py (P >0),由题意知,抛物线过点(2,-2),∴4=2p ×2.∴p =1.∴x 2=-2y .当y 0=-3时,得x 02=6.∴水面宽为2|x 0|=26.答案:B2.某抛物线形拱桥的跨度是20 m ,拱高是4 m ,在建桥时每隔4 m 需用一柱支撑,其中最长的支柱是A.4 mB.3.84 mC.1.48 mD.2.92 m解析:建立适当坐标系,设抛物线方程为x 2=-2py (p >0),由题意知其过定点(10, -4),代入x 2=-2py ,得p =225. ∴x 2=-25y .当x 0=2时,y 0=254-,∴最长支柱长为4-|y 0|=4-254=3.84(m ). 答案:B3.天安门广场,旗杆比华表高,在地面上,观察它们顶端的仰角都相等的各点所在的曲线是A.椭圆B.圆C.双曲线的一支D.抛物线解析:设旗杆高为m ,华表高为n ,m >n .旗杆与华表的距离为2a ,以旗杆与地面的交点和华表与地面的交点的连线段所在直线为x 轴、垂直平分线为y 轴建立直角坐标系.设曲线上任一点M (x ,y ),由题意2222)()(y a x y a x +-++=nm ,即(m 2-n 2)x 2+(m 2-n 2)y 2-2a (m 2-n 2)x + (m 2-n 2)a 2=0.答案:B4.探照灯反射镜的纵断面是抛物线的一部分,光源在抛物线的焦点,已知灯口直径是 60 cm ,灯深40 cm ,则光源到反射镜顶点的距离是____________ cm.解析:设抛物线方程为y 2=2px (p >0),点(40,30)在抛物线y 2=2px 上,∴900=2p ×40.∴p =445.∴2p =845.因此,光源到反射镜顶点的距离为845cm. 答案:8455.在相距1400 m 的A 、B 两哨所,听到炮弹爆炸声音的时间相差3 s ,已知声速340 m/s.炮弹爆炸点所在曲线的方程为________________.解析:设M (x ,y )为曲线上任一点,则|MA |-|MB |=340×3=1020<1400.∴M 点轨迹为双曲线,且a =21020=510,c =21400=700. ∴b 2=c 2-a 2=(c +a )(c -a )=1210×190.∴M 点轨迹方程为22510x -19012102⨯y =1.答案:22510x -19012102⨯y =1 ●典例剖析【例1】 设有一颗彗星沿一椭圆轨道绕地球运行,地球恰好位于椭圆轨道的焦点处,当此彗星离地球相距m 万千米和34m 万千米时,经过地球和彗星的直线与椭圆的长轴夹角分别为2π和3π,求该彗星与地球的最近距离. 剖析:本题的实际意义是求椭圆上一点到焦点的距离,一般的思路:由直线与椭圆的关系,列方程组解之;或利用定义法抓住椭圆的第二定义求解.同时,还要注意结合椭圆的几何意义进行思考.仔细分析题意,由椭圆的几何意义可知:只有当该彗星运行到椭圆的较近顶点处时,彗星与地球的距离才达到最小值即为a -c ,这样把问题就转化为求a ,c 或a -c .解:建立如下图所示直角坐标系,设地球位于焦点F (-c ,0)处,椭圆的方程为22a x +22by =1,当过地球和彗星的直线与椭圆的长轴夹角为3π时,由椭圆的几何意义可知,彗星A 只能满足∠xFA =3π(或∠xFA ′=3π).作AB ⊥Ox 于B ,则|FB |=21|FA |=32m , 故由椭圆的第二定义可得m =a c (c a 2-c ), ① 34m =a c (ca 2-c +32m ).②两式相减得31m =a c ·32m ,∴a =2c .代入①,得m =21(4c -c )=23c , ∴c =32m .∴a -c =c =32m .答:彗星与地球的最近距离为32m 万千米.评述: (1)在天体运行中,彗星绕恒星运行的轨道一般都是椭圆,而恒星正是它的一个焦点,该椭圆的两个端点,一个是近地点,另一个则是远地点,这两点到恒星的距离一个是a -c ,另一个是a +c .(2)以上给出的解答是建立在椭圆的概念和几何意义之上的,以数学概念为根基充分体现了数形结合的思想.另外,数学应用问题的解决在数学化的过程中也要时刻不忘审题,善于挖掘隐含条件,有意识地训练数学思维的品质.思考讨论椭圆上任一点到焦点的距离的最大值和最小值是多少?怎样证明? 提示:利用焦半径易求得最大值为a +c ,最小值为a -c.【例2】 某工程要挖一个横断面为半圆的柱形的坑,挖出的土只能沿道路AP 、BP 运到P 处(如下图所示).已知PA =100 m ,PB =150 m ,∠APB =60°,试说明怎样运土最省工.剖析:首先抽象为数学问题,半圆中的点可分为三类:(1)沿AP 到P 较近;(2)沿BP 到P 较近;(3)沿AP 、BP 到P 同样远.显然,第三类点是第一、二类的分界点,设M 是分界线上的任意一点.则有|MA |+|PA |=|MB |+|PB |.于是|MA |-|MB |=|PB |-|PA |=150-100=50.从而发现第三类点M 满足性质:点M 到点A 与点B 的距离之差等于常数50,由双曲线定义知,点M 在以A 、B 为焦点的双曲线的右支上,故问题转化为求此双曲线的方程.解:以AB 所在直线为x 轴,线段AB 的中点为原点建立直角坐标系xOy ,设M (x ,y )是沿AP 、BP 运土同样远的点,则|MA |+|PA |=|MB |+|PB |,∴|MA |-|MB |=|PB |-|PA |=50. 在△PAB 中,由余弦定理得|AB |2=|PA |2+|PB |2-2|PA ||PB |cos60°=17500,且50<|AB |.由双曲线定义知M 点在以A 、B 为焦点的双曲线右支上,设此双曲线方程为22a x -22by =1(a >0,b>0).2a =50, 4c 2=17500,c 2=a 2+b 2,a 2=625, ∵ 解之得b 2=3750.∴M 点轨迹是6252x -37502y =1(x ≥25)在半圆内的一段双曲线弧.于是运土时将双曲线左侧的土沿AP 运到P 处,右侧的土沿BP 运到P 处最省工.评述:(1)本题是不等量与等量关系问题,涉及到分类思想,通过建立直角坐标系,利用点的集合性质,构造圆锥曲线模型(即分界线)从而确定出最优化区域.(2)应用分类思想解题的一般步骤:①确定分类的对象;②进行合理的分类;③逐类逐级讨论;④归纳各类结果.【例3】 根据我国汽车制造的现实情况,一般卡车高3 m ,宽1.6 m.现要设计横断面为抛物线型的双向二车道的公路隧道,为保障双向行驶安全,交通管理规定汽车进入隧道后必须保持距中线0.4 m 的距离行驶.已知拱口AB 宽恰好是拱高OC 的4倍,若拱宽为a m ,求能使卡车安全通过的a 的最小整数值.剖析:根据问题的实际意义,卡车通过隧道时应以卡车沿着距隧道中线0.4 m 到2 m 间的道路行驶为最佳路线,因此,卡车能否安全通过,取决于距隧道中线2 m (即在横断面上距拱口中点2 m )处隧道的高度是否够3 m ,据此可通过建立坐标系,确定出抛物线的方程后求得.解:如下图,以拱口AB 所在直线为x 轴,以拱高OC 所在直线为y 轴建立直角坐标系,由题意可得抛物线的方程为x 2=-2p (y -4a ),∵点A (-2a ,0)在抛物线上,∴(-2a )2=-2p (0-4a ),得p =2a . ∴抛物线方程为x 2=-a (y -4a ).取x =1.6+0.4=2,代入抛物线方程,得22=-a (y -4a ),y =aa 4162-.由题意,令y >3,得aa 4162->3,∵a >0,∴a 2-12a -16>0.∴a >6+213.又∵a ∈Z ,∴a 应取14,15,16,….答:满足本题条件使卡车安全通过的a 的最小正整数为14 m.评述: 本题的解题过程可归纳为两步:一是根据实际问题的意义,确定解题途径,得到距拱口中点2 m 处y 的值;二是由y >3通过解不等式,结合问题的实际意义和要求得到a 的值,值得注意的是这种思路在与最佳方案有关的应用题中是常用的.●闯关训练 夯实基础1.1998年12月19日,太原卫星发射中心为摩托罗拉公司(美国)发射了两颗“铱星”系统通信卫星.卫星运行的轨道是以地球中心为一个焦点的椭圆,近地点为m km ,远地点为 n km ,地球的半径为R km ,则通信卫星运行轨道的短轴长等于A.2))((R n R m ++B. ))((R n R m ++C.2mnD.mn22Rn m ++-c =m +R , ① 22Rn m +++c =n +R ,②∴c =2mn -, 2b =222)2()22(m n R n m --++=2))((R n R m ++. 答案:A2.如下图,花坛水池中央有一喷泉,水管OP =1 m ,水从喷头P 喷出后呈抛物线状先向上至最高点后落下,若最高点距水面2 m ,P 距抛物线对称轴1 m ,则在水池直径的下列可选值中,最合算的是A.2.5 mB.4 mC.5 mD.6 m解析:以O 为原点,OP 所在直线为y 轴建立直角坐标系(如下图),则抛物线方程可设为y =a (x -1)2+2,P 点坐标为(0,1),∴1=a +2.∴a =-1.∴y =-(x -1)2+2.令y =0,得(x -1)2=2,∴x =1±2.∴水池半径OM =2+1≈2.414(m ).因此水池直径约为2×|OM |=4.828(m ).答案:C3.一个酒杯的轴截面是抛物线的一部分,它的方程是x 2=2y (0≤y ≤20).在杯内放入一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r 的范围为____________.解析:由题意解析:玻璃球的轴截面的方程为x 2+(y -r )2=r 2,由 x 2=2y ,x 2+(y -r )2=r 2, 答案:0<r ≤14.河上有一抛物线型拱桥,当水面距拱顶5 m 时,水面宽为8 m ,一小船宽4 m ,高2 m ,载货后船露出水面上的部分高43m ,问水面上涨到与抛物线拱顶相距____________m 时,小船不能通航.解析:建立直角坐标系,设抛物线方程为x 2=-2py (p >0).将点(4,-5)代入求得p =58.∴x 2=-516y . 将点(2,y 1)代入方程求得y 1=-45.∴43+|y 1|=43+45=2(m ).答案:25.下图是一种加热水和食物的太阳灶,上面装有可旋转的抛物面形的反光镜,镜的轴截面是抛物线的一部分,盛水和食物的容器放在抛物线的焦点处,容器由若干根等长的铁筋焊接在一起的架子支撑.已知镜口圆的直径为12 m ,镜深2 m ,(1)建立适当的坐标系,求抛物线的方程和焦点的位置;(2)若把盛水和食物的容器近似地看作点,试求每根铁筋的长度. 解:(1)如下图,在反光镜的轴截面内建立直角坐标系,使反光镜的顶点(即抛物线的顶点)与原点重合,x 轴垂直于镜口直径.由已知,得A 点坐标是(2,6),设抛物线方程为y 2=2px (p >0), 则36=2p ×2,p =9.所以所求抛物线的标准方程是y 2=18x ,焦点坐标是F (29,0). (2)∵盛水的容器在焦点处,∴A 、F 两点间的距离即为每根铁筋长. |AF |=226)292(+-=213(或|AF |=29+2=213). 故每根铁筋的长度是6.5 m.6.有一种电影放映机的放映灯泡的玻璃上镀铝,只留有一个透明窗用作通光孔,它的反射面是一种曲线旋转而成的曲面的一部分,灯丝定在某个地方发出光线反射到卡门上,并且得y 2+2(1-r )y =0,由Δ=4(1-r )2=0,得r =1.这两物体间距离为4.5 cm ,灯丝距顶面距离为2.8 cm ,为使卡门处获得最强烈的光线,在加工这种灯泡时,应使用何种曲线可使效果最佳?试求这个曲线方程.分析:由于光线从灯丝发出,反射到卡门上光线应交于一点,这就是光线聚焦,只要把灯丝、卡门安在椭圆的2个焦点上,反射面采用旋转椭球面就可以使光线经反射后聚焦于卡门处,因而可获得强光.解:采用椭圆旋转而成的曲面,如下图建立直角坐标系,中心截口BAC 是椭圆的一部分,设其方程为22a x +22by =1,灯丝距顶面距离为p ,由于△BF 1F 2为直角三角形,因而,|F 2B |2=|F 1B |2+|F 1F 2|2=p 2+4c 2,由椭圆性质有|F 1B |+|F 2B |=2a ,所以a =21(p +224c p +),a = 21(2.8+225.48.2+)≈4.05 cm ,b =22c a -≈3.37 m.∴所求方程为2205.4x +2237.3y =1.培养能力7.某大桥在涨水时有最大跨度的中央桥孔如图所示,已知上部呈抛物线形,跨度为20 m ,拱顶距水面6 m ,桥墩高出水面4 m ,现有一货船欲过此孔,该货船水下宽度不超过18 m ,目前吃水线上部分中央船体高5 m ,宽16 m ,且该货船在现在状况下还可多装1000 t 货物,但每多装150 t 货物,船体吃水线就要上升0.04 m ,若不考虑水下深度,该货船在现在状况下能否直接或设法通过该桥孔?为什么?解:如下图,建立直角坐标系,设抛物线方程为y =ax 2,则A (10,-2)在抛物线上,∴-2=ax 2,a =-501,方程即为y =-501x 2让货船沿正中央航行. ∵船宽16 m ,而当x =8时,y =-501·82=1.28 m ,∴船体在x =±8之间通过.由B (8,-1.28), ∴B 点离水面高度为6+(-1.28)=4.72(m ),而船体水面高度为5 m ,∴无法直接通过.又5-4.72=0.28(m ),0.28÷0.04=7,而150×7=1050(t ), ∴要用多装货物的方法也无法通过,只好等待水位下降. 8.(文)(2004年春季北京,文18)2003年10月15日9时,“神舟”五号载人飞船发射升空,于9时9分50秒准确进入预定轨道,开始巡天飞行.该轨道是以地球的中心F 2为一个焦点的椭圆.选取坐标系如图所示,椭圆中心在原点.近地点A 距地面200 km ,远地点B 距地面350 km.已知地球半径R =6371 km.(如下图)(1)求飞船飞行的椭圆轨道的方程;(2)飞船绕地球飞行了十四圈后,于16日5时59分返回舱与推进舱分离,结束巡天飞行,飞船共巡天飞行了约6×105km ,问飞船巡天飞行的平均速度是多少?(结果精确到1 km/s )(注:km/s 即千米/秒)解:(1)设椭圆的方程为22a x +22by =1.由题设条件得a -c =|OA |-|OF 2|=|F 2A |=6371+200=6571,a +c =|OB |+|OF 2|=|F 2B |=6371+350=6721.解得a =6646,c =75,所以a 2=44169316, b 2=a 2-c 2=(a +c )(a -c )=6721×6571=44163691.∴所求椭圆的方程为441693162x +441636912y =1.(注:由44163691≈6645.5768得椭圆的方程为226646x +226.6645y =1,也是正确的)(2)从15日9时到16日6时共21个小时,即21×3600 s. 减去开始的9分50 s ,即9×60+50=590(s ),再减去最后多计的1分钟,共减去590+60= 650(s ),得飞船巡天飞行的时间是21×3600-650=74950(s ),平均速度是74950600000≈8(km/s ).所以飞船巡天飞行的平均速度是8 km/s. (理)(2003年上海)如下图,某隧道设计为双向四车道,车道总宽22 m ,要求通行车辆限高4.5 m ,隧道全长2.5 km ,隧道的拱线近似地看成半个椭圆形状.(1)若最大拱高h 为6 m ,则隧道设计的拱宽l 是多少?(2)若最大拱高h 不小于6 m ,则应如何设计拱高h 和拱宽l ,才能使半个椭圆形隧道的土方工程量最小?(半个椭圆的面积公式为S =4πlh ,柱体体积为底面积乘以高.本题结果均精确到0.1 m ) (1)解:如下图建立直角坐标系,则点P (11,4.5),椭圆方程为22a x +22by =1.将b =h =6与点P 坐标代入椭圆方程,得a =7744,此时l =2a =7788≈33.3.因此隧道的拱宽约为33.3 m.(2)解法一:由椭圆方程22a x +22b y =1,得2211a +225.4b=1.因为2211a +225.4b ≥ab 5.4112⨯⨯,即ab ≥99,且l =2a ,h =b ,所以S =4πlh =2πab ≥2π99.当S 取最小值时,有2211a =225.4b=21,得a =112,b =229.此时l =2a =222≈31.1,h =b ≈6.4.故当拱高约为6.4 m 、拱宽约为31.1 m 时,土方工程量最小.解法二:由椭圆方程22a x +22b y =1,得2211a +225.4b =1.于是b 2=481·12122-a a .a 2b 2=481(a 2-121+12112122-a +242)≥481(22121+242)=81×121,即ab ≥99,当S 取最小值时,有a 2-121=12112122-a .得a =112,b =229,以下同解法一. 探究创新9.中国跳水运动员进行10 m 跳台跳水训练时,身体(看成一点)在空中的运动路线为如下图所示坐标系下经过原点O 的一条抛物线(图中标出的数据为已知条件).在跳某个规定动作时,正常情况下,该运动员在空中的最高处距水面1032m ,入水处距池边的距离为4 m ,同时,运动员在距水面高度为5 m 或5 m 以上时,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.(1)求这条抛物线的解析式.(2)在某次试跳中,测得运动员在空中的运动路线是(1)中的抛物线,且运动员在空中调整好入水姿势时,距池边的水平距离为353m ,问此次跳水会不会失误?并通过计算说明理由.(3)要使此次跳水不至于失误,该运动员按(1)中抛物线运行,且运动员在空中调整好入水姿势时,距池边的水平距离至多应为多少?解:(1)在给定的直角坐标系下,设最高点为A ,入水点为B ,抛物线的解析式为 y =ax 2+bx +c .由题意知,O 、B 两点的坐标依次为(0,0)、(2,-10),且顶点A 的纵坐标为32, c =0,ab ac 442 =32,4a +2b +c =-10.a =-625,b =310,c =0 a =-23,b =-2,c =0.∵抛物线对称轴在y 轴右侧,∴-ab2>0. 又∵抛物线开口向下,∴a <0.∴b >0,后一组解舍去.∴a =-625,b =310,c =0. ∴抛物线的解析式为y =-625x 2+310x .(2)当运动员在空中距池边的水平距离为353m 时,即x =353-2=58时,y =(-625)×(58)2+310×58=-316,∴此时运动员距水面的高为10-316=314<5.因此,此次跳水会出现失误.(3)当运动员在x 轴上方,即y >0的区域内完成动作并做好入水姿势时,当然不会失误,但很难做到.所以有 解之得 或∴当y <0时,要使跳水不出现失误,则应有|y |≤10-5,即-y ≤5. ∴有625x 2-310x ≤5, 解得2-34≤x ≤2+34.∴运动员此时距池边的距离至多为2+2+34=4+34m.●思悟小结解决圆锥曲线应用问题时,要善于抓住问题的实质,通过建立数学模型,实现应用性问题向数学问题的顺利转化;要注意认真分析数量间的关系,紧扣圆锥曲线概念,充分利用曲线的几何性质,确定正确的问题解决途径,灵活运用解析几何的常用数学方法,求得最终完整的解答.●教师下载中心教学点睛解应用题时涉及到两个基本步骤,即将实际问题抽象成数学问题和解决这个数学问题,为此要注意以下三点:1.阅读理解.数学应用题给出的方式是材料的陈述,而不是客体的展示.也就是说,所考的应用题通常已进行过初步加工,并通过语言文字、符号或图形展现在考生面前,要求考生读懂题意,理解实际背景,领悟其数学实质.2.数学建模,即将应用题的材料陈述转化成数学问题.这就要抽象、归纳其中的数量关系,并把这种关系用数学式子表示出来.3.数学求解.根据所建立数学关系的知识系统,解出结果,从而得到实际问题的解答. 本节就是通过圆锥曲线在现实生活中的应用,培养学生解决应用问题的能力.拓展题例【例1】 一摩托车手欲飞跃黄河,设计摩托车沿跑道飞出时前进方向与水平方向的仰角是12°,飞跃的水平距离是35 m ,为了安全,摩托车在最高点与落地点的垂直落差约10 m ,那么,骑手沿跑道飞出时的速度应为多少?(单位是 km/h ,精确到个位)(参考数据:sin12°=0.2079,cos12°=0.9781,t an12°=0.2125)分析:本题的背景是物理中的运动学规律,摩托车离开跑道后的运动轨迹为抛物线,它是由水平方向的匀速直线运动与竖直方向上的上抛运动合成的,它们运行的位移都是时间t 的函数,故应引入时间t ,通过速度v 的矢量分解来寻找解决问题的途径.解: 摩托车飞离跑道后,不考虑空气阻力,其运动轨迹是抛物线,轨迹方程是 x =vt cos12°,y =vt sin12°-21×9.8t 2. 其中v 是摩托车飞离跑道时的速度,t 是飞行时间,x 是水平飞行距离,y 是相对于起始点的垂直高度,将轨迹方程改写为y =-212)12(cos 1v ⋅︒×9.8x 2+t an12°·x ,即y =-5.121922vx +0.2125x . 当x ≈0.0207v 2时,取得y max ≈0.0022v 2.当x =35时,y 落=-6274.327521v +7.4375.∵y max -y 落=10,0.0022v 2+6274.327521v-17.4375=0,解得v ≈19.44 m/s 或v ≈86.88 m/s. 若v ≈86.88 m/s ,则x =156.246 m ,与题目不符,而v ≈19.44 m/s ,符合题意,为所求解.故v ≈19.44 m/s=69.984 km/h ≈70 km/h.答:骑手沿跑道飞出时的速度应为70 km/h.评述:本题直接构造y 是x 的函数解析式很困难,应引入适当的参数(时间t )作媒介,再研究x 与y 是怎样随参数变化而变化的,问题往往就容易解决了.这种辅助变量的引入要具体问题具体分析,以解题的简捷为原则.【例2】 A 、B 、C 是我方三个炮兵阵地,A 在B 正东6 km ,C 在B 正北偏西30°,相距4 km ,P 为敌炮阵地,某时刻A 处发现敌炮阵地的某种信号,由于B 、C 两地比A 距P 地远,因此4 s 后,B 、C 才同时发现这一信号,此信号的传播速度为1 km/s ,A 若炮击P 地,求炮击的方位角.解:如下图,以直线BA 为x 轴,线段BA 的中垂线为y 轴建立坐标系,则B (-3,0)、A (3,0)、C (-5,23).因为|PB |=|PC |,所以点P 在线段BC 的垂直平分线上.因为k BC =-3,BC 中点D (-4,3),所以直线PD 的方程为y -3=31(x +4). ①又|PB |-|PA |=4,故P 在以A 、B 为焦点的双曲线右支上.设P (x ,y ),则双曲线方程为42x -52y =1(x ≥0). ②联立①②,得x =8,y =53, 所以P (8,53).因此k PA =3835 =3. 故炮击的方位角为北偏东30°.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考数学第一轮圆锥曲线基础知识点复习教案
§8.4 圆锥曲线班级姓名学号
例1:设点A(2,2),F(4,0),点M在椭圆上运动。
(1)求|MA|+|MF|的最小值。
(2)求|MA|+ |MF|的最小值。
例2:已知AB是抛物线y2=2Px的任意一条焦点弦,且A(x¬1, y1),B(x¬2, y2),(1)求证y1y2=-p2, x1x2= (2)若弦AB被焦点分成长为m, n的两部分,求证:例3:设A(x1, y1)是椭圆x2+2y2=2上一点,过点A作一条斜率为的直线L,d为原点到L的距离,r1, r2分别为点A到两焦点的距离,求证:是定值。
例4:设椭圆C与双曲线D有共同的焦点F1(-4,0),F2(4,0),并且椭圆的长轴长是双曲线实轴的长的2倍,试求椭圆C与双曲线D交点的轨迹方程。
【基础训练】 1、已知两定点F1(-5,0), F2(5,0),动点P满足|PF1|-|PF2|=2a,当a=3和5时,P点的轨迹为: A、双曲线和一条直线 B、双曲线和一条射线() C、双曲线一支和一条射线 D、双曲线一支和一条直线2、若抛物线y2=2px上三点的纵坐标的平方成等差数列,则这三点对应的焦点半径的关系是 A、等比数列 B、等差数列 C、常数列 D、以上均不对() 3、已知两圆C1:(x+4)2+y2=2, C2: (x-4)2+y2=2,动圆M与两圆C1,C2都相切,则动圆圆心M的轨迹方程是:() A、x=0 B、 C、 D、 4、已知两点M(1,),N(),给出下列曲线方程:①4x+2y-1=0, ②x2+y2=3 ③ ④ ,在曲线上存在点P满足
|MP|=|NP|的所有曲线方程是: A、①③ B、②④ C、①②③ D、②③④ 5、已知F1、F2是椭圆的两个焦点,AB是过焦点F1的弦,若|AB|=8,则|F2A|+|F2B|的值是。
6、双曲线上一点P到左焦点的距离是14,则P点到右准线的距离为。
【拓展练习】 1、椭圆的右焦点为F,设A ),P是椭圆上一动点,则|AP|+ |PF|取得最小值时点P的坐标为:() A、(5,0) B、(0,2) C、) D、(0,-2)或(0,2) 2、若椭圆和双曲线 (a>0, b>0)有相同的焦点F1,F2,b是两曲线的一个交点,则|PF1| |PF2|等于:() A、m2-a2 B、m-a C、 D、 3、以双曲线的一条焦半径为直径的圆与以实轴为直径的圆位置关系为:() A、相交 B、相离 C、内切 D、外切 4、设P(x0, y0)是椭圆上一动点,F1,F2是椭圆的两焦点,当x0= 时,|PF1||PF2|的积最大
为;当x0= 时,|PF1| |PF2|的积最小为。
5、双曲线16x2-9y2=144的两焦点为F1¬,F2,点P在双曲线上,且|PF1| |PF2|=32,则∠F1PF2的大小为。
6、在双曲线上求一点M,使它到左、右两焦点的距离之比为3:2,并求M点到两准线的距离。
7、过椭圆C:的右焦点作一直线l交椭圆C于M、N两点,且M、N 到直线x= 的距离之和为,求直线l的方程。
8、给定椭圆(a>b>0),求与该椭圆有公共焦点的双曲线,使得以它们的交点为顶点的四边形的面积最大。
9、已知椭圆(a>b>0),A,B是椭圆上的两点,线段AB的垂直平分线与x轴相交于点P0(x0, 0),证明:。
10、已知抛物线y2=4x与椭圆有共同的焦点F2。
(1)求m的值;(2)若P是两曲线的一个公共点,F2是椭圆的另一个焦点,且
∠PF1F2=α,∠PF2F1=β,求cosα•cosβ的值。
(3)求△PF1F2的面积。
优品课件,意犹未尽,知识共享,共创未来!!!。
