2014年小学数学公式《解方程定律》_公式总结
小学数学公式大全完整版

小学数学公式大全完整版1.加法法则:a+b=c2.减法法则:a-b=c3.乘法法则:a×b=c4.除法法则:a÷b=c5.反比例关系:ab = k6.四则运算:a+b-c×d÷e=f7.正负数乘法规律:-a × -b = ab-a × b = -aba × -b = -ab8.平方:a²=b9.平方根:√a=b10.立方:a³=b11.立方根:³√a=b12.平行线性质:同位角相等内错角相等外错角相等13.相似三角形:对应角相等对应边成比例14.等腰三角形:两底角相等15.等边三角形:三个角都相等16.直角三角形勾股定理:a²+b²=c²17.直角三角形边的关系:c=√(a²+b²)18.三角形外角和:外角和=360°19.等差数列通项公式:an = a1 + (n - 1)d20.等差数列求和公式:Sn = (a1 + an) × n / 221.等比数列通项公式:an = a1 × r^(n - 1)22.等比数列求和公式:Sn=a1×(r^n-1)/(r-1)23.圆的周长公式:C=2πr24.圆的面积公式:S=πr²25.平行四边形的周长公式:C=2(a+b)26.矩形的周长公式:C=2(a+b)27.矩形的面积公式:S=a×b28.正方形的周长公式:C=4a29.正方形的面积公式:S=a²30.梯形的周长公式:C=a+b+c+d31.梯形的面积公式:S=(a+b)×h/232.圆环的面积公式:S=π(R²-r²)33.体积公式:V=l×w×h34.表面积公式:S = 2lw + 2lh + 2wh35.立方体的体积公式:V=a³36.球的体积公式:V=4/3πr³37.圆柱体的体积公式:V=πr²h38.棱柱的体积公式:V=Ah39.直角三角形斜边长度:c=√(a²+b²)。
《小学数学公式定律大全》
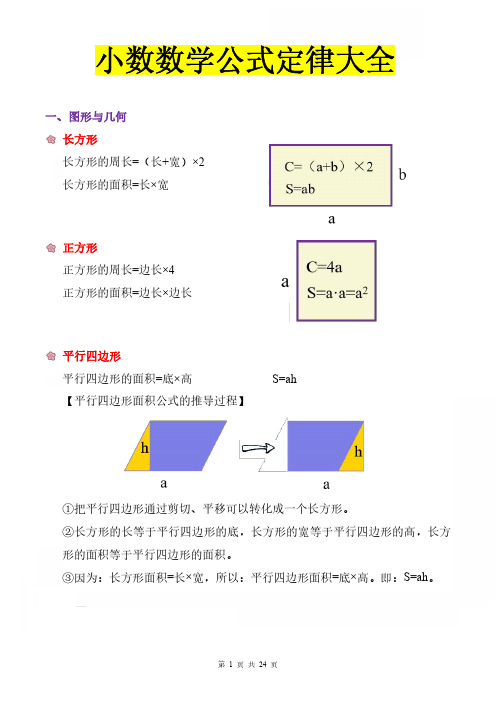
小数数学公式定律大全一、图形与几何长方形长方形的周长=(长+宽)×2长方形的面积=长×宽正方形正方形的周长=边长×4正方形的面积=边长×边长平行四边形平行四边形的面积=底×高S=ah【平行四边形面积公式的推导过程】①把平行四边形通过剪切、平移可以转化成一个长方形。
②长方形的长等于平行四边形的底,长方形的宽等于平行四边形的高,长方形的面积等于平行四边形的面积。
③因为:长方形面积=长×宽,所以:平行四边形面积=底×高。
即:S=ah。
三角形三角形的面积=底×高÷2S=ah÷2三角形的内角和=180度=180°【三角形面积公式的推导过程】①用两个完全一样的三角形可以拼成一个平行四边形。
②平行四边形的底等于三角形的底,平行四边形的高等于三角形的高,三角形面积等于和它等底等高的平行四边形面积的一半③因为:平行四边形面积=底×高,所以:三角形面积=底×高÷2。
即:S=ah÷2。
梯形梯形的面积=(上底+下底)×高÷2S=(a+b)h÷2【梯形面积公式的推导过程】①用两个完全一样的梯形可以拼成一个平行四边形。
②平行四边形的底等于梯形的上底和下底的和,平行四边形的高等于梯形的高,梯形面积等于平行四边形面积的一半。
③因为:平行四边形面积=底×高,所以:梯形面积=(上底+下底)×高÷2。
即:S=(a+b)h÷2。
圆直径=半径×2d=2r半径=直径÷2r=d÷2圆的周长=圆周率×直径=圆周率×半径×2C=πd=2πr圆的面积=圆周率×半径×半径S=πrr=πr2【画图说明圆面积公式的推导过程】分的份数越多,每一份就会越小,拼成的图形就会越接近于一个长方形。
解方程顺口溜及必背公式什么是解方程

解方程顺口溜及必背公式什么是解方程解方程必背公式口诀是:去分母要都乘到,多项式分子要带括号;去括号也要都乘到,千万小心是符号;移项变号别漏项,已知未知隔等号;合并同类项加系数,系数化1要记牢。
解方程顺口溜及必背公式解方程必背公式口诀是:去分母要都乘到,多项式分子要带括号;去括号也要都乘到,千万小心是符号;移项变号别漏项,已知未知隔等号;合并同类项加系数,系数化1要记牢。
使方程左右两边相等的未知数的值,叫做方程的解。
求方程的解的过程叫做解方程。
必须含有未知数等式的等式才叫方程。
等式不一定是方程,方程一定是等式。
1、乘法与因式分解:a2-b2=(a+b)(a-b);a3+b3=(a+b)(a2-ab+b2);a3-b3=(a-b)(a2+ab+b2)。
2、三角不等式:|a+b|≤|a|+|b|;|a-b|≤|a|+|b|;|a|≤b<=>-b≤a≤b;|a-b|≥|a|-|b|-|a|≤a≤|a|。
3、一元二次方程的解:-b+√(b2-4ac)/2a-b-b+√(b2-4ac)/2a。
解方程的顺口溜解方程,去分母,乘以最小公倍数,分子加上小括号,有括号要去掉,正负变化忘不了,去括号要看符号,如果前面是负号,括号里面全变号,移项变号很重要,正负变化要记牢,同类项,要合并,系数化1就完成。
什么是解方程1、含有未知数的等式叫方程,也可以说是含有未知数的等式是方程。
2、使等式成立的未知数的值,称为方程的解,或方程的根。
3、解方程就是求出方程中所有未知数的值的过程。
4、方程一定是等式,等式不一定是方程。
不含未知数的等式不是方程。
小学数学解方程口诀

小学数学解方程口诀解方程一直是小学数学的重难点,类型多且容易混淆,如何快速有效的让学生掌解方程,通过总结分析,我汇总了各类方程的解决的技巧,编纂了一首口诀帮助记忆:一般方程很简单,具体数字帮你办,加减乘除要相反。
特殊方程别犯难,减去除以未知数,加上乘上变一般。
若遇稍微复杂点,舍远取近便了然。
具体分析如下:我们可以把课本中出现的方程分为三大类:一般方程,特殊方程,稍复杂的方程。
形如:x+a=b , x-a=b , ax=b , x÷a=b 这几种方程,我们可以称为一般方程。
形如:a- x =b,a÷x =b这两种方程,我们可以称为特殊方程。
形如:ax+b=c , a(x-b)=c这两种方程,我们可以称为稍复杂的方程。
我们知道,对于一般方程,如果方程是加上a,在利用等式的性质求解时,会在方程的两边减去a,同样,如果方程是减去a,在利用等式的性质求解时,会在方程的两边加上a,乘和除以也是一样的,换句话说,加减乘除是相反的,并且加减乘除的都是一个具体的数字。
总结一句话就是:一般方程很简单,具体数字帮你办,加减乘除要相反。
对于特殊方程,减去和除以的都是未知数x,求解时,减去未知数那就加上未知数,除以未知数那就乘未知数,符号也是相反的,这样方程也就变换成了一般方程,总结为:特殊方程别犯难,减去除以未知数,加上乘上变一般。
对于稍复杂的方程,我教给孩子们的方法是,“舍远取近”的方法,意思是,离未知数x远的就先去掉,离未知数x进的先看成整体保留,通过变换,方程就变得简单,一目了然。
总结为:若遇稍微复杂点,舍远取近便了然。
当然后面还有形如ax+bx=c等形式,能够学会上面这几种,对于孩子来说,这些方程就显得轻而易举了。
小学数学方程知识点总结

小学数学方程知识点总结在小学数学学习的过程中,方程是一个重要的内容。
方程是数学中用来表示等式的一种形式,通过求解方程,我们能够找到未知数的取值。
下面将对小学数学方程的一些基础知识点进行总结。
一、方程的定义方程是由等号连接两个代数式的数学语句,它表达了两个代数式相等的关系。
其中,等号的左边称为方程的左式,右边称为方程的右式。
例如:3x + 4 = 10就是一个方程,其中3x + 4为左式,10为右式。
二、方程的解解方程就是要找出使得方程两边相等的未知数的取值。
解是方程的解集,表示所有满足方程的未知数的取值。
例如,对于方程3x + 4 = 10,解为x = 2,即当x等于2时,方程成立。
三、一元一次方程一元一次方程是指方程中只有一个未知数,并且该未知数的最高次数为1的方程。
一元一次方程的一般形式为ax + b = c,其中a、b、c为已知数,而x为未知数。
解一元一次方程可以通过逆向运算和化简等方法,将未知数解出来。
四、方程的变形在解方程的过程中,有时需要对方程进行变形,使得方程更便于求解。
常用的方程变形方法包括消元法和配方法。
消元法是指通过加减乘除等运算,使方程中某一项或某几项的系数相互抵消,从而简化方程。
例如,对于方程3x + 2 = 10,可以通过减2使方程变为3x = 8,然后再除以3,解出x的值。
配方法是指将方程中的某一项通过乘法进行扩展,使得方程中的未知数的系数出现相同的倍数,从而方便进行消元运算。
例如,对于方程2x + 3 = 5x + 1,可以通过乘以2使得方程变为4x + 6 = 10x + 2,然后进行消元运算。
五、方程的应用方程作为数学的一种工具,被广泛应用于各个领域。
在小学阶段,方程主要用于解决实际问题,例如“两个数的和等于10,且其中一个数是另一个数的2倍,求这两个数分别是多少?”这个问题可以通过建立方程来解决。
设其中一个数为x,另一个数为2x,则可以建立方程x + 2x = 10,通过解方程求得x的值,然后再求得另一个数的值。
小学数学解方程口诀-精品

解方程一直是小学数学的重难点,类型多且容易混淆,如何快速有效的让学生掌解方程,通过总结分析,我汇总了各类方程的解决的技巧,编纂了一首口诀帮助记忆:一般方程很简单,具体数字帮你办,加减乘除要相反。
特殊方程别犯难,减去除以未知数,加上乘上变一般。
若遇稍微复杂点,舍远取近便了然。
具体分析如下:我们可以把课本中出现的方程分为三大类:一般方程,特殊方程,稍复杂的方程。
形如:x+a=b , x-a=b , ax=b , x÷a=b 这几种方程,我们可以称为一般方程。
形如:a- x =b,a÷x =b这两种方程,我们可以称为特殊方程。
形如:ax+b=c , a(x-b)=c这两种方程,我们可以称为稍复杂的方程。
我们知道,对于一般方程,如果方程是加上a,在利用等式的性质求解时,会在方程的两边减去a,同样,如果方程是减去a,在利用等式的性质求解时,会在方程的两边加上a,乘和除以也是一样的,换句话说,加减乘除是相反的,并且加减乘除的都是一个具体的数字。
总结一句话就是:一般方程很简单,具体数字帮你办,加减乘除要相反。
对于特殊方程,减去和除以的都是未知数x,求解时,减去未知数那就加上未知数,除以未知数那就乘未知数,符号也是相反的,这样方程也就变换成了一般方程,总结为:特殊方程别犯难,减去除以未知数,加上乘上变一般。
对于稍复杂的方程,我教给孩子们的方法是,“舍远取近”的方法,意思是,离未知数x远的就先去掉,离未知数x进的先看成整体保留,通过变换,方程就变得简单,一目了然。
总结为:若遇稍微复杂点,舍远取近便了然。
当然后面还有形如ax+bx=c等形式,能够学会上面这几种,对于孩子来说,这些方程就显得轻而易举了。
小学数学公式定理定义大全,期末复习少不了用到它

小学数学公式定理定义大全,期末复习少不了用到它1第一部分:概念1、加法交换律:两数相加交换加数的位置,和不变。
2、加法结合律:三个数相加,先把前两个数相加,或先把后两个数相加,再同第三个数相加,和不变。
3、乘法交换律:两数相乘,交换因数的位置,积不变。
4、乘法结合律:三个数相乘,先把前两个数相乘,或先把后两个数相乘,再和第三个数相乘,它们的积不变。
5、乘法分配律:两个数的和同一个数相乘,可以把两个加数分别同这个数相乘,再把两个积相加,结果不变。
如:(2+4)×5=2×5+4×56、除法的性质:在除法里,被除数和除数同时扩大(或缩小)相同的倍数,商不变。
O除以任何不是O的数都得O。
简便乘法:被乘数、乘数末尾有O的乘法,可以先把O前面的相乘,零不参加运算,有几个零都落下,添在积的末尾。
7、什么叫等式?等号左边的数值与等号右边的数值相等的式子叫做等式。
等式的基本性质:等式两边同时乘以(或除以)一个相同的数,等式仍然成立。
8、什么叫方程式?答:含有未知数的等式叫方程式。
9、什么叫一元一次方程式?答:含有一个未知数,并且未知数的次数是一次的等式叫做一元一次方程式。
学会一元一次方程式的例法及计算。
即例出代有χ的算式并计算。
10、分数:把单位“1”平均分成若干份,表示这样的一份或几分的数,叫做分数。
11、分数的加减法则:同分母的分数相加减,只把分子相加减,分母不变。
异分母的分数相加减,先通分,然后再加减。
12、分数大小的比较:同分母的分数相比较,分子大的大,分子小的小。
异分母的分数相比较,先通分然后再比较;若分子相同,分母大的反而小。
13、分数乘整数,用分数的分子和整数相乘的积作分子,分母不变。
14、分数乘分数,用分子相乘的积作分子,分母相乘的积作为分母。
15、分数除以整数(0除外),等于分数乘以这个整数的倒数。
16、真分数:分子比分母小的分数叫做真分数。
17、假分数:分子比分母大或者分子和分母相等的分数叫做假分数。
小学数学公式和定律大全

小学数学公式和定律大全Prepared on 21 November 2021小学数学所有公式和定律1、每份数×份数=总数总数÷每份数=份数总数÷份数=每份数2、1倍数×倍数=几倍数几倍数÷1倍数=倍数几倍数÷倍数=1倍数3、速度×时间=路程路程÷速度=时间路程÷时间=速度4、单价×数量=总价总价÷单价=数量总价÷数量=单价5、工作效率×工作时间=工作总量工作总量÷工作效率=工作时间工作总量÷工作时间=工作效率6、加数+加数=和和-一个加数=另一个加数7、被减数-减数=差被减数-差=减数差+减数=被减数8、因数×因数=积积÷一个因数=另一个因数9、被除数÷除数=商被除数÷商=除数商×除数=被除数二、小学数学图形计算公式1、正方形C周长S面积a边长周长=边长×4C=4a面积=边长×边长S=a×a2、正方体V:体积a:棱长表面积=棱长×棱长×6S表=a×a×6体积=棱长×棱长×棱长V=a×a×a3、长方形C周长S面积a边长周长=(长+宽)×2C=2(a+b)面积=长×宽S=ab4、长方体V:体积s:面积a:长b:宽h:高(1)表面积(长×宽+长×高+宽×高)×2S=2(ab+ah+bh)(2)体积=长×宽×高V=abh5、三角形s面积a底h高面积=底×高÷2s=ah÷2三角形高=面积×2÷底三角形底=面积×2÷高6、平行四边形s面积a底h高面积=底×高s=ah7、梯形s面积a上底b下底h高面积=(上底+下底)×高÷2s=(a+b)×h÷28、圆形S面积C周长∏d=直径r=半径(1)周长=直径×∏=2×∏×半径C=∏d=2∏r(2)面积=半径×半径×∏9、圆柱体v:体积h:高s;底面积r:底面半径c:底面周长(1)侧面积=底面周长×高(2)表面积=侧面积+底面积×2(3)体积=底面积×高(4)体积=侧面积÷2×半径10、圆锥体v:体积h:高s;底面积r:底面半径体积=底面积×高÷3总数÷总份数=平均数和差问题的公式:(和+差)÷2=大数(和-差)÷2=小数和倍问题的公式:和÷(倍数-1)=小数小数×倍数=大数(或者和-小数=大数)差倍问题的公式:差÷(倍数-1)=小数小数×倍数=大数(或小数+差=大数)一、植树问题1、非封闭线路上的植树问题主要可分为以下三种情形:⑴如果在非封闭线路的两端都要植树,那么:株数=段数+1=全长÷株距-1全长=株距×(株数-1)株距=全长÷(株数-1)2、如果在非封闭线路的一端要植树,另一端不要植树,那么:株数=段数=全长÷株距全长=株距×株数株距=全长÷株数3、如果在非封闭线路的两端都不要植树,那么:株数=段数-1=全长÷株距-1全长=株距×(株数+1)株距=全长÷(株数+1)2封闭线路上的植树问题的数量关系如下株数=段数=全长÷株距全长=株距×株数株距=全长÷株数二、盈亏问题(盈+亏)÷两次分配量之差=参加分配的份数(大盈-小盈)÷两次分配量之差=参加分配的份数(大亏-小亏)÷两次分配量之差=参加分配的份数三、相遇问题相遇路程=速度和×相遇时间相遇时间=相遇路程÷速度和速度和=相遇路程÷相遇时间四、追及问题追及距离=速度差×追及时间追及时间=追及距离÷速度差速度差=追及距离÷追及时间五、流水问题顺流速度=静水速度+水流速度逆流速度=静水速度-水流速度静水速度=(顺流速度+逆流速度)÷2水流速度=(顺流速度-逆流速度)÷2六、浓度问题溶质的重量+溶剂的重量=溶液的重量溶质的重量÷溶液的重量×100%=浓度溶液的重量×浓度=溶质的重量溶质的重量÷浓度=溶液的重量七、利润与折扣问题利润=售出价-成本利润率=利润÷成本×100%=(售出价÷成本-1)×100%涨跌金额=本金×涨跌百分比折扣=实际售价÷原售价×100%(折扣<1)利息=本金×利率×时间税后利息=本金×利率×时间×(1-20%)分数除法部分量/部分量所占分率=单位1长度单位换算1千米=1000米1米=10分米1分米=10厘米1米=100厘米1厘米=10毫米面积单位换算1平方千米=100公顷1公顷=10000平方米1平方米=100平方分米1平方分米=100平方厘米1平方厘米=100平方毫米体(容)积单位换算1立方米=1000立方分米1立方分米=1000立方厘米1立方分米=1升1立方厘米=1毫升1立方米=1000升重量单位换算1吨=1000千克1千克=1000克1千克=1公斤人民币单位换算1元=10角1角=10分1元=100分时间单位换算1世纪=100年1年=12大月(31天)有:1\3\5\7\8\10\12月小月(30天)的有:4\6\9\11月平年2月28天,闰年2月29天平年全年365天,闰年全年366天1日=24小时1时=60分1分=60秒1时=3600秒分数的加、减法则:同分母的分数相加减,只把分子相加减,分母不变。
