卡方检验结果分析
卡方检验结果解读

卡方检验结果解读卡方检验(χ2test)是统计学中最常用的方法之一,它可以检测一个样本数据集中的分布是否与理论分布一致,或者在两组样本数据之间是否存在显著差异。
卡方检验也称作配对比较或有组检验。
它的运用,可以帮助研究者比较实验组和参照组,用以发现在实验中是否存在重要的差异或显著性差异。
对于卡方检验结果的解读,必须首先了解卡方检验的原理和流程,卡方检验的结果的解释从两个主要方面来看:统计显著性和实质性。
统计显著性指的是检验结果与理论分布没有显著差异,也可以理解为统计显著性。
当检验结果表明实验结果与理论分布有显著差异时,就可以推断出在该实验中的某些因素在影响实验结果方面起到了重要的作用。
实质性指的是卡方检验检验结果不同,但不能一定说明实验结果与原理分布有显著的区别,也可以理解为实质性。
实质性的判断,需要从实验中收集到的定量数据来确定结果是否有实质性,即判断实验产生效果是否具有显著意义。
在理解卡方检验结果的解释时,需要理解错误分类和错误概率的概念。
错误分类是指在某种概率或原则的情况下,将某一样本分到错误的类别中。
通常情况下,会将某一样本分到较有可能的类别中来消除错分失误,而不是将它放到较少可能的类别中。
另一方面,错误概率指提取错误分类所占总比例。
卡方检验结果的解释,也可以从这个角度来看。
如果卡方检验的结果显示,统计法定概率下拒绝原假设,则说明该实验有显著性,这意味着实验中的某些因素对实验结果产生了重要的影响。
如果卡方检验的结果显示,统计法定概率下不拒绝原假设,则说明实验没有显著性,这意味着实验中的某些因素不能使实验结果产生统计学上的显著差异。
总的来说,卡方检验的结果的解读,考虑的不是某一样本的独立性,而是所有样本集合的整体变化和应用概率分布原理进行比较,最终得到结果,并从统计显著性和实质性两个方面来解释卡方检验结果。
卡方检验结果分析
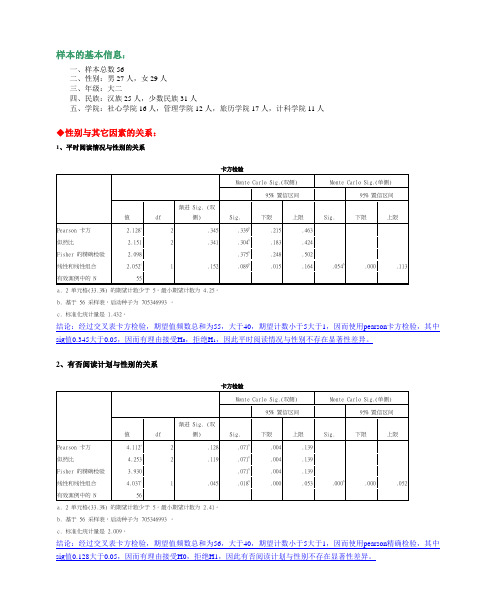
样本的基本信息:一、样本总数56二、性别:男27人,女29人三、年级:大二四、民族:汉族25人,少数民族31人五、学院:社心学院16人,管理学院12人,旅历学院17人,计科学院11人◆性别与其它因素的关系:1、平时阅读情况与性别的关系结论:经过交叉表卡方检验,期望值频数总和为55,大于40,期望计数小于5大于1,因而使用pearson卡方检验,其中sig值0.345大于0.05,因而有理由接受H0,拒绝H1,因此平时阅读情况与性别不存在显著性差异。
2、有否阅读计划与性别的关系结论:经过交叉表卡方检验,期望值频数总和为56,大于40,期望计数小于5大于1,因而使用pearson精确检验,其中sig值0.128大于0.05,因而有理由接受H0,拒绝H1,因此有否阅读计划与性别不存在显著性差异。
3、阅读方式与性别的关系结论:经过交叉表卡方检验,期望值频数总和为56,大于40,期望计数少于5,最小期望计数为0.96接近1,因而使用fisher 精确检验,其中sig值0.161大于0.05,因而有理由接受H0,拒绝H1,因此有否阅读计划与性别不存在显著性差异。
4、对课外阅读的看法与性别的关系结论:经过交叉表卡方检验,期望值频数总和为56,大于40,期望计数小于5大于1,因而使用pearson卡方检验,其中sig值0.857大于0.05,因而有理由接受H0,拒绝H1,因此对课外阅读的看法与性别不存在显著性差异。
5、阅读量的趋势与性别的关系交叉表计数性别合计男女你认为你现在的课外阅读量是呈什么趋势上升趋势10 3 13 下降趋势11 14 25 基本不变 6 12 18合计27 29 56结论:经过交叉表卡方检验,期望值频数总和为56,大于40,期望计数小于5大于1,因而使用pearson卡方检验,其中sig值0.048小于0.05,因而有理由拒绝H0,接受H1,因此阅读量趋势与性别存在显著性差异。
结论:经过交叉表卡方检验,期望值频数总和为55,大于40,期望计数大于5,因而使用pearson卡方检验,其中sig值0.139大于0.05,因而有理由接受H0,拒绝H1,因此是否有足够时间进行课外阅读与性别不存在显著性差异。
生物统计学—卡方检验

独立性检验
步骤: 1. 提出无效假设,即认为所观测的各属性之间
没有关联 2. 规定显著性水平 3. 根据无效假设计算出理论数 4. 根据规定的显著水平和自由度计算出卡方值,
再和计算的卡方值进行比较。 如果接受假设,则说明因子之间无相关联,
是相互独立的 如果拒绝假设,则说明因子之间的关联是显
著的,不独立
一、2X2列联表的独立性检验
设A、B是一个随机试验中的两个事件,其中A可能
出现r1、r2个结果,B可能出现c1、c2个结果,两 因子相互作用形成4个数,分别以O11、O12、O21、 O22表示,即
2X2列联表的一般形式
r1 r2 总和
c1 O11 O21 C1=O11+O21
c2 O12 O22 C2=O12+O22
解:(1)假设 H0 : 鲤鱼体色F2性状分离符合3:1 对 H A : 鲤鱼体色F2性状分离不符合3:1
(2)选取显著水平 0.05
(3)检验计算: 计算鲤鱼体色的理论值
体色 F2理论尾数
青灰色 1201.5
红色 400.5
总数 1602
k
cc2 i 1
Oi Ei
0.5 2 301.63
1
2
2
xx
将样本方差代入,则:c
2
(k
1) s 2
2
其c2服从自由度为(k-1)的卡方分布
卡方函数的使用
假设
H 0:
2
2 0
,
适用右尾检验 ,其否定区为: c 2 c2
假设
H
0:
2
2 0
,
适用左尾检验
,其否定区为:
c
2
c2 1
假设
卡方检验

• (2)分析过程说明 • ①表6-1的资料是经过人为汇总得到的,即是采用频数表 格式来记录的的资料,同组分别有两种互不相容的结果— —杀灭或未杀灭,两组各自的结果互不影响,即相互独立。 对于这种频数表格资料,在卡方检验之前须用Weight Cases命令对频数变量进行预先统计处理,操作如下:单 击Data-Weight Cases命令,则弹出如图6-3所示对话框, 选中Weight cases by,按三角按钮将变量“计数”置入 Frequency Variable框内,定义“计数”为权数,按OK 。 • ②单击主菜单Analyze-Descriptive Statistics-Crosstabs, 则弹出对话框,按三角按钮将行变量“治疗方法” 置入 Row框内,将列变量“治疗效果” 置入Column框内,如 图6-4。 • ③按Stastics按钮,弹出“选择统计方法”对话框(见图 6-5),选中Chi-square,按Continue,返回图6-4,点OK, 输出表6-2、表 6-3。
x 2 1.428, p 0.839 0.05
,差异不显著,可以认为不同的治疗方法与治疗效果无关,即三 种治疗方法对治疗效果的影响差异不显著。
下表为不同灌溉方式下水稻叶片衰老情况的资料,试测验 稻叶衰老的情况是否与灌溉方式有关?
灌溉方式 深水 浅水 湿润 总计 绿叶数 146 183 152 481 黄叶数 7 9 14 30 枯叶数 7 13 16 36
第五章 卡方检验
一、2X2列联表的独立性检验 (一)计算公式
(二)例题及统计分析
例6.1 分别用灭螨A和灭螨B杀灭害虫,结果如表6-1, 问两种灭螨剂的效果差异是否显著? 表6-1 灭螨A和B杀灭害虫试验结果
组别 灭螨A 灭螨B 未杀灭数C1 12 22 TC1=34 杀灭数C2 32 14 TC2=46 TR1=44 TR2=36 T=80
卡方检验

2 检验
Crosstabs
WUST
Crosstabs-- 2检验
1 四格表资料的2检验– 结果释 – 界面说明2 配对资料的2检验
– 界面说明 – 结果解释
3 行×列表的2检验
– 界面说明 – 结果解释
WUST
一、四格表的 2检验
1 界面说明 2 分析实例 3 结果解释
合计
未愈合 8 20 28
愈合 54 44 98
合计 62 64 126
WUST
步骤:
1. Data ==>weight cases Weight cases by: Frequency Variable 框:
count Ok
1. Analyze==> Descriptive Statistics==>Crosstabs
软组织炎型
混合型
合计
儿童组
50
48
成人组
105
10
合计
155
58
18
72
188
7
23
145
25
95
333
WUST
四格表资料
1. 主要用于两个样本率的比较。 2. 资料的录入格式。
两个分类变量:行变量、列变量(定义 values)
一个频数变量:通常是例数
WUST
例1 某医生用国产呋喃硝胺治疗 十二指肠溃疡,以甲氰咪胍作为 对照组,问两种方法治疗效果有 无差别?2by2.sav
处理 呋喃硝胺 甲氰咪胍
2. 在某牧区观察慢性布鲁氏病患者植物血凝素 皮肤试验反应,资料如下,问活动型与稳定型 布氏患者反应阳性率有无差别?
WUST
3 1979年某地爆发松毛虫病,333例患者按年龄 以14岁为界分成2组,资料如表,试考察两组病
卡方检验

表内用虚线隔开的这四个数据是整个表中的基本资料,其余数据均由此推算出来;这四格资料表就专称四格表(fourfold table),或称2行2列表(2×2 contingency table)从该资料算出的两种疗法有效率分别为44.2%和77.3%,两者的差别可能是抽样误差所致,亦可能是两种治疗有效率(总体率)确有所不同。
这里可通过x2检验来区别其差异有无统计学意义,检验的基本公式为:式中A为实际数,以上四格表的四个数据就是实际数。
T为理论数,是根据检验假设推断出来的;即假设这两种卵巢癌治疗的有效率本无不同,差别仅是由抽样误差所致。
这里可将两种疗法合计有效率作为理论上的有效率,即53/87=60.9%,以此为依据便可推算出四格表中相应的四格的理论数。
兹以表20-11资料为例检验如下。
检验步骤:1.建立检验假设:H0:π1=π2H1:π1≠π2α=0.052.计算理论数(TRC),计算公式为:TRC=nR.nc/n 公式(20.13)因为上表每行和每列合计数都是固定的,所以只要用TRC式求得其中一项理论数(例如T1. 1=26.2),则其余三项理论数都可用同行或同列合计数相减,直接求出,示范如下:T1.1=26.2T1.2=43-26.2=16.8T2.1=53-26.2=26.8T2.2=44-26.2=17.23.计算x2值按公式20.12代入4.查x2值表求P值在查表之前应知本题自由度。
按x2检验的自由度v=(行数-1)(列数-1),则该题的自由度v=(2-1)(2-1)=1,查x2界值表(附表20-1),找到x20.001(1)=6.63,而本题x2=10.0 1即x2>x20.001(1),P<0.01,差异有高度统计学意义,按α=0.05水准,拒绝H0,可以认为采用化疗加放疗治疗卵巢癌的疗效比单用化疗佳。
通过实例计算,读者对卡方的基本公式有如下理解:若各理论数与相应实际数相差越小,x2值越小;如两者相同,则x2值必为零,而x2永远为正值。
定性数据的分析——卡方检验

2 ) 理论频数计算公式
TRC
nR nC n
T频RC数表;示列联表中第R行第C列交叉格子的理论
nR表示该格子所在的第R行的合计数; nC表示该格子所在的第C列的合计数; n表示总例数。
例10-1 用磁场疗法治疗腰部扭挫伤患者 708人,其中有效673例。用同样疗法治 疗腰肌劳损患者347人,有效312例。观 察结果如表10-6所示。
χ2检验连续性校正公式为
2 ( A T 0.5)2 T
四格表χ2检验连续性校正公式*
2 ( ad bc 0.5n)2 n
(a b)(c d)(a c)(b d )
例10-4 某医生用复合氨基酸胶囊治疗肝硬 化病人,观察其对改善某实验室指标的 效果,见表10-7。
分组 B1
B2
合计
A1
a
b
a+b
A2
c
d
c+d
合计 a+c
b+d
a+b+c+d
案例1 治疗肺炎新药临床试验 用某新药治疗肺 炎病,并选取另一常规药作为对照药,治疗结果 如下:采用新药治100例,有效 60例;采用对照 药治40例,有效 30例。
试问:1) 列表描述临床试验结果;
2)两种药物疗效有无差别?
相应地此时率的标准误估计值按下式计算:
S p ˆ p
p(1 p) n
(10 2)
• 式中,Sp为率的标准误的估计值;p为样本率。
二、率的区间估计
总体率的点估计是计算样本的率,很简单, 但计算得到的样本率不等于总体率,它们 间存在差异。因此,我们还需要知道总体 率大概会在一个什么样的区间范围,即所 谓总体率的可信区间估计。
卡方检验的结果解读

卡方检验的结果解读1.引言1.1 概述卡方检验是一种常用的统计方法,用于判断两个分类变量之间是否存在相关性或者一致性。
它是基于统计推断的方法,通过比较实际观察值与理论期望值之间的差异来进行判断。
在实际应用中,卡方检验被广泛用于比较两个或多个分类变量的分布情况,包括但不限于医学研究、社会调查以及市场分析等领域。
它能够帮助我们判断两个或多个分类变量是否独立,从而揭示变量之间的关联关系。
本文旨在对卡方检验的结果进行解读和分析。
首先,我们将介绍卡方检验的基本原理,包括计算卡方值和自由度的方法。
其次,我们将探讨卡方检验在实际应用中的一些典型场景,比如用于比较不同人群中某一特征的分布情况,或者用于评估某一策略对用户行为变化的影响等。
在解读卡方检验结果时,我们需要关注卡方值和P值。
卡方值反映了观察值与理论期望值之间的差异程度,而P值则是用来判断这种差异是否具有统计学意义的指标。
通常来说,如果P值小于预先设定的显著性水平(通常为0.05),则可以拒绝原假设,即认为变量之间存在相关性或一致性。
然而,卡方检验也有其局限性。
例如,样本量过小可能导致研究结论不准确,而样本量过大则可能会使得小的差异也变得显著。
此外,卡方检验只能判断变量是否相关,而不能确定其具体的关系强度和方向性。
综上所述,卡方检验是一种重要的统计方法,可以帮助我们判断变量之间的关系。
对于卡方检验结果的解读,我们需要综合考虑卡方值和P值,并且意识到其存在的局限性。
在实际应用中,我们可以根据具体问题选择合适的卡方检验方法,并合理解读其结果,以便得出准确的结论。
1.2文章结构文章结构部分应该对整篇长文的大致结构进行介绍,并说明各个部分内容的关联性和重要性。
具体内容如下:1.2 文章结构本文主要围绕卡方检验的结果进行解读展开。
全文分为引言、正文和结论三个部分。
在引言部分,我们将对卡方检验进行概述,介绍其基本原理,并明确文章的目的。
同时,我们也会提及本文的结构,让读者对文章整体有个初步的认识。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
样本的基本信息:
一、样本总数56
二、性别:男27人,女29人
三、年级:大二
四、民族:汉族25人,少数民族31人
五、学院:社心学院16人,管理学院12人,旅历学院17人,计科学院11人
◆性别与其它因素的关系:
1、平时阅读情况与性别的关系
结论:经过交叉表卡方检验,期望值频数总和为55,大于40,期望计数小于5大于1,因而使用pearson卡方检验,其中sig值0.345大于0.05,因而有理由接受H0,拒绝H1,因此平时阅读情况与性别不存在显著性差异。
2、有否阅读计划与性别的关系
结论:经过交叉表卡方检验,期望值频数总和为56,大于40,期望计数小于5大于1,因而使用pearson精确检验,其中sig值0.128大于0.05,因而有理由接受H0,拒绝H1,因此有否阅读计划与性别不存在显著性差异。
3、阅读方式与性别的关系
结论:经过交叉表卡方检验,期望值频数总和为56,大于40,期望计数少于5,最小期望计数为0.96接近1,因而使用fisher 精确检验,其中sig值0.161大于0.05,因而有理由接受H0,拒绝H1,因此有否阅读计划与性别不存在显著性差异。
4、对课外阅读的看法与性别的关系
结论:经过交叉表卡方检验,期望值频数总和为56,大于40,期望计数小于5大于1,因而使用pearson卡方检验,其中sig值0.857大于0.05,因而有理由接受H0,拒绝H1,因此对课外阅读的看法与性别不存在显著性差异。
5、阅读量的趋势与性别的关系
交叉表
计数
性别
合计
男女
你认为你现在的课外阅读量是呈什么趋势上升趋势10 3 13 下降趋势11 14 25 基本不变 6 12 18
合计27 29 56
结论:经过交叉表卡方检验,期望值频数总和为56,大于40,期望计数小于5大于1,因而使用pearson卡方检验,其中sig值0.048小于0.05,因而有理由拒绝H0,接受H1,因此阅读量趋势与性别存在显著性差异。
结论:经过交叉表卡方检验,期望值频数总和为55,大于40,期望计数大于5,因而使用pearson卡方检验,其中sig值0.139大于0.05,因而有理由接受H0,拒绝H1,因此是否有足够时间进行课外阅读与性别不存在显著性差异。
◆民族与其它因素的关系:
结论:经过交叉表卡方检验,期望值频数总和为55,大于40,期望计数小于5大于1,因而使用pearson卡方检验,其中sig值0.336大于0.05,因而有理由接受H0,拒绝H1,因此平时阅读情况与民族不存在显著性差异。
2、有否阅读计划与民族的关系
结论:经过交叉表卡方检验,期望值频数总和为56,大于40,期望计数小于5大于1,因而使用pearson卡方检验,其中sig值0.492大于0.05,因而有理由接受H0,拒绝H1,因此有否阅读计划与民族不存在显著性差异。
3、阅读方式的偏好与民族的关系
结论:经过交叉表卡方检验,期望值频数总和为56,大于40,期望计数小于5,最小期望计数为0.89接近1,因而使用fisher 精确检验,其中sig值0.339大于0.05,因而有理由接受H0,拒绝H1,因此阅读方式的偏好与民族不存在显著性差异。
4、对进行课外阅读的看法与民族的关系
结论:经过交叉表卡方检验,期望值频数总和为56,大于40,期望计数小于5大于1,因而使用pearson卡方检验,其中sig值0.873大于0.05,因而有理由接受H0,拒绝H1,因此对进行课外阅读的看法与民族不存在显著性差异。
5、课外阅读量趋势与民族的关系
交叉表
计数
民族
合计
汉族少数民族
你认为你现在的课外阅读量是呈什么趋势上升趋势 3 10 13 下降趋势10 15 25 基本不变12 6 18
合计25 31 56
结论:经过交叉表卡方检验,期望值频数总和为56,大于40,期望计数小于5大于1,因而使用pearson卡方检验,其中sig值0.045小于0.05,因而有理由拒绝H0,接受H1,因此阅读量趋势在汉族和少数民族中存在显著性差异。
结论:经过交叉表卡方检验,期望值频数总和为56,大于40,期望计数小于5大于1,因而使用pearson卡方检验,其中sig值0.396大于0.05,因而有理由接受H0,拒绝H1,因此是否有足够的时间与民族不存在显著性差异。
