试验设计课件
合集下载
实验设计方法-PPT

2、设计要求:(1);各组观察对象要同质,满足 均衡性、 (2);采用随机化分组、 (3)合理设置 对照组、 (4);各组例数相等或相近、
3、优缺点;
(1)优点;设计方法简单易行,统计分析也简单; 适用面广,不论两组或多组、不管组间样本含 量相等或不等,均可采用这种设计。
(2)缺点;要求实验设计,故实 验所需样本含量相对较多。
变异来源 总变异 组间变异
01 组内变异
表 方差分析结果 SS υ MS F P 281、65 31 141、17 3 47、057 9、38 <0、
140、465 28 5、017
二、配对设计与分析▲
①、概念---就是将受试对象按一定条件配成对 子,再随机分配每对中得两个受试对象到不同得 处理组、
予以注射、以上剂量、种系与笼子三个 因素得分组如下表,试分析不同因素间 有无差别。
表白兔注射不同剂量甲状腺素后得甲状腺体重量(mg)
种系
笼
号
种系 种系
1
2 3 4 5 小计 均数
甲
C65 E85 A57 B49 D79 335 67、0
乙
E82 B63 D77 C70 A46 338 67、6
(k-1)(b-1)
MS区组 MS误差
四、 拉丁方设计与方差分析(110)
一、拉丁方设计▲
1、概念;用r个拉丁字母排成r行r列得方阵,使每行、每列中每个 字母都出现一次,这样得方阵叫r阶拉丁方。按拉丁方得字母、 行与列安排处理及影响因素得试验称为拉丁方试验。
拉丁方设计就是随机单位组设计得进一步扩展,可以考虑3个 处理因素。(也可以1个、2个)
4、方法 :完全随机分组设计方案 示意图
预选对象
按纳入 标准
3、优缺点;
(1)优点;设计方法简单易行,统计分析也简单; 适用面广,不论两组或多组、不管组间样本含 量相等或不等,均可采用这种设计。
(2)缺点;要求实验设计,故实 验所需样本含量相对较多。
变异来源 总变异 组间变异
01 组内变异
表 方差分析结果 SS υ MS F P 281、65 31 141、17 3 47、057 9、38 <0、
140、465 28 5、017
二、配对设计与分析▲
①、概念---就是将受试对象按一定条件配成对 子,再随机分配每对中得两个受试对象到不同得 处理组、
予以注射、以上剂量、种系与笼子三个 因素得分组如下表,试分析不同因素间 有无差别。
表白兔注射不同剂量甲状腺素后得甲状腺体重量(mg)
种系
笼
号
种系 种系
1
2 3 4 5 小计 均数
甲
C65 E85 A57 B49 D79 335 67、0
乙
E82 B63 D77 C70 A46 338 67、6
(k-1)(b-1)
MS区组 MS误差
四、 拉丁方设计与方差分析(110)
一、拉丁方设计▲
1、概念;用r个拉丁字母排成r行r列得方阵,使每行、每列中每个 字母都出现一次,这样得方阵叫r阶拉丁方。按拉丁方得字母、 行与列安排处理及影响因素得试验称为拉丁方试验。
拉丁方设计就是随机单位组设计得进一步扩展,可以考虑3个 处理因素。(也可以1个、2个)
4、方法 :完全随机分组设计方案 示意图
预选对象
按纳入 标准
DOE(试验设计)培训课件

医学领域试验设计案例分析
试验设计规范
医学领域的试验设计必须符合严格的伦理和法律规定,同时需要遵循科学的原则 和方法。本课件会介绍医学领域试验设计的规范和原则,包括人体实验的特殊要 求。
试验设计应用
医学领域的试验设计应用非常广泛,例如新药的开发和疗效比较、医疗器械的性 能检测等。本课件会通过实际案例来说明这些试验设计的具体应用和操作流程。
• 确定研究目的和问题 • 制定试验方案 • 选择合适的试验方法和材料 • 制定详细的试验计划和操作规程 • 进行试验并收集数据 • 分析数据并得出结论 • 撰写试验报告或论文
02
试验设计基本原则
科学性原则
试验设计需具备科学性,要能够反映出研究问题的本质和 规律。
科学性原则要求试验设计必须有明确的研究目的、研究对 象、研究方法和数据分析方法。
详细描述
将试验分为若干个阶段,每个阶段中包含不同的因素。在每个阶段中,将试验单元按照某种规则分为 若干个裂区,每个裂区内包含相同数量的试验单元。在每个裂区内选择一个试验单元进行试验,记录 其结果。该方法能够有效地控制误差,并能够研究不同因素之间的交互作用。
均匀设计
总结词
一种适用于多因素、多水平的试验设计方法。
试验设计包括了一系列的方法和技术,如随机化、重复性、 误差控制等。
试验设计的作用
1
试验设计可以帮助研究者明确研究目的、问题 和假设,并制定合理的试验方案。
2
试验设计可以有效地控制误差和变异,提高研 究的可靠性和准确性。
3
试验设计可以帮助研究者发现新的问题和现象 ,推动科学的进步和发展。
试验设计的流程
随机区组设计
总结词
一种常用的试验设计方法,适用于具有同一性质或同一类别的试验单元。
DOE实验设计ppt课件

部分析因实验(正交实验)
由田口博士(Dr.Taguchi)田口玄一所提出的一套实验方法,它在工业上较具有实 际应用性,是以生产力和成本效益,而非困难的统计为依归。
参数
1
2
3
次数
1
1
1
1
2
1
2
2
3
2
1
2
4
2
2
1
L4(23)正交表 总共须做四次实验,最多只能配置三个因子
+
A
-
L4(23)正交表图解
实验设计降低开发成本
The DoE 的方法
Two factors at two levels
A low low high high middle
B low high low high middle
Result ? ? ? ? ?
• Centerpoint: 检测弯曲相互作用的存在 • Replicated centerpoint: 评估系统噪音
品质源于设计里的工艺空间
Characterized space
特征空间
Design space
设计空间
Operating space
操作空间
在设计空间内的操作不被监管机构认作是工艺改变
5. AKTA avant 25系统
目前金斯瑞所使用的系统。 GE Healthcare历经数年研制,对欧美及亚洲多家知名生物制药公司如 GSK, Amgen, Novo nordisk, Lilly, Wyeth等公司进行调研,开发出的新一代适 合现代工艺开发的AKTA设备,所以AKTATM avant 25 最突出的优点就是 Design of Experiment (DOE)实验条件智能优化,和UNICORN6.0软件配合堪 称是现代纯化工艺优化的最佳搭档。
《doe试验设计讲义》课件

ABCD
Hale Waihona Puke 重复性原则在相同条件下进行多次试验,以提高结果的稳定 性和可靠性。
盲法原则
在试验过程中,尽量减少人为因素对试验结果的 影响,保证结果的客观性和准确性。
02
试验设计的基本方法
完全随机化设计
总结词
将试验单位随机分配到不同处理组,每个处理组有相同数量的试验单位。
详细描述
完全随机化设计是一种简单而常用的试验设计方法,其基本思想是将试验单位随机分配到不同的处理 组中,每个处理组有相同数量的试验单位。这种方法适用于处理组数较少且试验单位之间差异较小的 试验。
提高研究效率
科学的试验设计能够提高研究的效率,减少 不必要的浪费和重复。
保证研究质量
合理的试验设计能够保证研究的质量,减少 误差和偏见对结果的影响。
试验设计的基本原则
随机性原则
确保每个样本都有同等的机会被选中,避免主观 偏见对试验结果的影响。
对照原则
设置对照组,以排除其他因素的干扰,明确研究 因素的作用。
05
试验设计的发展趋势和 展望
基于计算机的试验设计
自动化试验
利用计算机技术实现试验过程的自动化,提高 试验效率。
模拟与仿真
通过计算机模拟和仿真试验,减少实际试验的 次数和成本。
数据处理与统计分析
利用计算机进行数据处理、统计分析和可视化,提高数据利用效率和准确性。
基于人工智能的试验设计
1 2
机器学习与优化算法
通过试验设计,探索农业可持续发展的路径和 方法,推动农业绿色发展,保护生态环境。
案例二:医学研究
总结词
验证新药的有效性和安全性
详细描述
通过试验设计,对新药的有效性和安全性进行 验证,为新药的研发和应用提供科学依据。
正交试验设计PPT课件精选全文

所谓均衡分散,是指用正交表挑选出来的 各因素水平组合在全部水平组合中的分布是均 匀的 。 由 图10-1可以看出,在立方体中 ,任 一平面内都包含 3 个“(·)”, 任一直线上都包 含1个“(·)” ,因此 ,这些点代表性强 ,能够 较好地反映全面试验的情况。
上一张 下一张 主 页 退 出
整齐可比是指每一个因素的各水平间 具有可比性。因为正交表中每一因素的任 一水平下都均衡地包含着另外因素的各个 水平 ,当比较某因素不同水平时,其它 因素的效应都彼此抵消。如在A、B、C 3个因素中,A因素的3个水平 A1、A2、 A3 条件下各有 B 、C 的 3个不同水计计 算算
Kk 值值
计 算 极 差
R
绘 制 因 素 指 标 趋
势
图
计算各列偏差平方和、 自由度
列方差分析表,
进行F 检验
优水平 优组合
因素主次顺序
结论
分析检验结果, 写出结论
实例:为提高山楂原料的利用率,研究酶法液化工艺 制造山楂原汁,拟通过正交试验来寻找酶法液化的最 佳工艺条件。
例如,要考察增稠剂用量、pH值和杀菌温度对豆奶稳 定性的影响。每个因素设置3个水平进行试验 。
A因素是增稠剂用量,设A1、A2、A3 3个水平;B因素 是pH值,设B1、B2、B3 3个水平;C因素为杀菌温度,设 C1、C2、C3 3个水平。这是一个3因素3水平的试验,各因 素的水平之间全部可能组合有27种 。
9个试验点均衡地分布于整个立方体内 ,有很强 的代表性 , 能 够比较全面地反映选优区内的基本情 况。
上一张 下一张 主 页 退 出
1.3 正交表及其基本性质
1.3.1 正交表
由于正交设计安排试验和分析试验结果都要用正 交表,因此,我们先对正交表作一介绍。
上一张 下一张 主 页 退 出
整齐可比是指每一个因素的各水平间 具有可比性。因为正交表中每一因素的任 一水平下都均衡地包含着另外因素的各个 水平 ,当比较某因素不同水平时,其它 因素的效应都彼此抵消。如在A、B、C 3个因素中,A因素的3个水平 A1、A2、 A3 条件下各有 B 、C 的 3个不同水计计 算算
Kk 值值
计 算 极 差
R
绘 制 因 素 指 标 趋
势
图
计算各列偏差平方和、 自由度
列方差分析表,
进行F 检验
优水平 优组合
因素主次顺序
结论
分析检验结果, 写出结论
实例:为提高山楂原料的利用率,研究酶法液化工艺 制造山楂原汁,拟通过正交试验来寻找酶法液化的最 佳工艺条件。
例如,要考察增稠剂用量、pH值和杀菌温度对豆奶稳 定性的影响。每个因素设置3个水平进行试验 。
A因素是增稠剂用量,设A1、A2、A3 3个水平;B因素 是pH值,设B1、B2、B3 3个水平;C因素为杀菌温度,设 C1、C2、C3 3个水平。这是一个3因素3水平的试验,各因 素的水平之间全部可能组合有27种 。
9个试验点均衡地分布于整个立方体内 ,有很强 的代表性 , 能 够比较全面地反映选优区内的基本情 况。
上一张 下一张 主 页 退 出
1.3 正交表及其基本性质
1.3.1 正交表
由于正交设计安排试验和分析试验结果都要用正 交表,因此,我们先对正交表作一介绍。
DOE(试验设计)培训课件

详细说明如何使用DOE软件工具进行实验设计 、数据采集、数据分析和模型构建等。
介绍DOE软件工具中各种选项和参数的意义及 设置方法,例如实验设计类型、因子和水平设 置等。
DOE软件工具的应用案例
通过实际案例介绍如何使用DOE软件工具进行实验 设计和数据分析。
通过案例展示DOE软件工具在工业生产、新产品研 发等领域的应用。
DOE基本原则
随机化原则
试验设计应遵循随机化原则,以避 免潜在的人为偏见和系统误差。
重复性原则
为提高试验结果的可靠性和精确度 ,应尽可能遵循重复性原则,即在 相同条件下多次进行试验。
对照原则
通过设置对照组,可以更好地评估 试验组中目标变量与影响因素之间 的关系。
简约性原则
在满足试验目的的前提下,应尽可 能采用简约的试验设计,以降低试 验成本和时间。
设计实验方案
采用正交表进行实验设计,选择了三因素三水平的正交 表,设计了九组实验方案,每组方案重复五次。
实施实验并收集数据
按照设计的实验方案进行实验,并收集了三十组实验数 据。
分析数据并得出结论
对收集的实验数据进行统计分析,发现生产温度对产品 质量影响最大,其次是生产压力,最后是生产时间
06
DOE软件工具介绍与操作指南
试验设计的基本原则
试验设计需要遵循随机化、重复性和对照等基本原则。
试验设计在生产中的应用
试验设计可以应用于生产过程中,通过优化生产工艺和参数,提高产品质量和生产效率。
试验设计在研发中的应用
试验设计可以应用于产品研发过程中,通过科学筛选和优化设计方案,降低产品成本和提高性能。
DOE与六西格玛的关系
DOE的基本概念
设计实验方案
采用正交表进行实验设计,选择了三因素三水平的正交表 ,设计了九组实验方案,每组方案重复三次。
介绍DOE软件工具中各种选项和参数的意义及 设置方法,例如实验设计类型、因子和水平设 置等。
DOE软件工具的应用案例
通过实际案例介绍如何使用DOE软件工具进行实验 设计和数据分析。
通过案例展示DOE软件工具在工业生产、新产品研 发等领域的应用。
DOE基本原则
随机化原则
试验设计应遵循随机化原则,以避 免潜在的人为偏见和系统误差。
重复性原则
为提高试验结果的可靠性和精确度 ,应尽可能遵循重复性原则,即在 相同条件下多次进行试验。
对照原则
通过设置对照组,可以更好地评估 试验组中目标变量与影响因素之间 的关系。
简约性原则
在满足试验目的的前提下,应尽可 能采用简约的试验设计,以降低试 验成本和时间。
设计实验方案
采用正交表进行实验设计,选择了三因素三水平的正交 表,设计了九组实验方案,每组方案重复五次。
实施实验并收集数据
按照设计的实验方案进行实验,并收集了三十组实验数 据。
分析数据并得出结论
对收集的实验数据进行统计分析,发现生产温度对产品 质量影响最大,其次是生产压力,最后是生产时间
06
DOE软件工具介绍与操作指南
试验设计的基本原则
试验设计需要遵循随机化、重复性和对照等基本原则。
试验设计在生产中的应用
试验设计可以应用于生产过程中,通过优化生产工艺和参数,提高产品质量和生产效率。
试验设计在研发中的应用
试验设计可以应用于产品研发过程中,通过科学筛选和优化设计方案,降低产品成本和提高性能。
DOE与六西格玛的关系
DOE的基本概念
设计实验方案
采用正交表进行实验设计,选择了三因素三水平的正交表 ,设计了九组实验方案,每组方案重复三次。
DOE (试验设计)培训ppt课件

4个因素以内
2、部分因子试验(所有 1、寻找最有利于输出的因素水平; 组合的一个子集) 2、建立可评估部分交互影响的数学模型。
5个因素以上
3、筛选试验 4、冲心复合设计
5、可靠设计
6、田口动态可靠 设计。
从大量因素中发现少数关键因素(不评估因 素间的交互作用)。
1、优化; 2、建立非线性影响存在时的数学模型(常用
法,其目标是最大程度地实现和保持企业运营成功。 B:6 Sigma的原动力来自对客户需求的理解,对企
业现状,数据地科学分析,及对改进企业的运营过程 的渴望。 C:6 Sigma的质量目标小于3.4DPMO,99.99966% 合格---每百万机会中只有3.4个缺陷
2、6 Sigma经历的四个里程碑
4、比较设备和方法的影响度;
五)计量时,试验设计可用来: 1、进行量具研究; 2、确定主要误差; 3、将测量误差降至最小;
四、试验设计的一些相关概念:
一)指标:在试验中用来衡量试验结果的量叫 试验指标,在六西格玛系统中,试验指标是公 司与客户共同关心的项目的(CTQ `S:关键影 响因素);
二)因素又称因子,在试验中,影响试验考 核指标的量称为因素。因素是我们前面说过 的作用因素即自变量(X `S); 三)水平是试验中各因素的不同取值; 四)通用符号:在试验表中,一般用“+”、 “-”号或“1”、“2”、“3”等来表示因素的 不同水平,当因素只有高低两个水平时,用 “+”号代表高水平, “-”代表低水平(数值 较
3、衡量6 Sigma的度量指标 A:质量合格率(QUALITY YIELD) B:百万分之一 PPM C:每百万中的缺陷 DPM D:每百万机会中的缺陷 DPMO
4、6 Sigma的团队:绿带(Green Belts)、黑带(Black Belts) 、大黑 带(Master Black Belts )、倡导者 (CHAMPIONS)、执行官 (EXECUTIVE LEADER),团体从 小到大各司其职。
试验设计课件(新新)
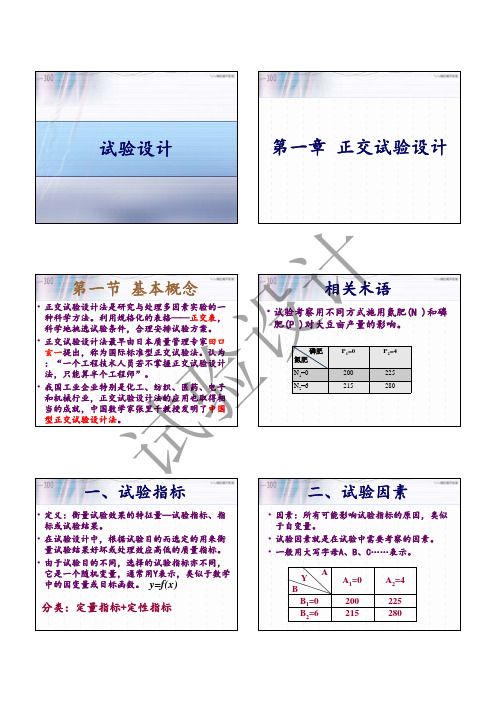
试验 验证性试验 因素与指标的关系已知 目的 探索性试验 因素与指标间关系未知
计
试验 因素 数量
单因素试验
比较一个试验因素的不同水平,其 他均作为试验条件(条件因素)
同时试验
设时间
顺序
序贯试验
几个试验同时进行; 适用于试验周期长的情况
下次试验需在上次试验基 础上进行的试验; 适用于周期短的情况
验 多因素试验
¾ 不等水平; ¾ 无穷多个不自然连续,无一定规律可寻; ¾ 多数不能考虑交互作用,部分可考虑 (由标 准表转化而来的); ¾ 有特殊的使用范围。
重点考察因素多取水平; L8 (4 × 24 ) 受条件限制,因素不能多取水平。 L18 (2 × 37 )
试
四、正交表的性质
1、正交性:均衡分布思想在正交表中的体现
• 试验考察用不同方式施用氮肥(N )和磷
设肥(P )对大豆亩产量的影响。
磷肥 氮肥
P1=0
P2=4
验 法,只能算半个工程师”。
• 我国工业企业特别是化工、纺织、医药、电子 和机械行业,正交试验设计法的应用也取得相 当的成就,中国数学家张里千教授发明了中国 型正交试验设计法。
N1=0 N2=6
200
全面试验组合处理多 部分试验试验点少
部分试验信息少
全面试验信息多
正交试验设计 选择代表性组合处理进行试验
以少代多
对试验结果进行科学处理
以少求全
七、因素试验
• 研究各因素对试验指标的影响,了解各因素 的重要程度(即对试验指标的贡献大小)
• 获得最优组合处理,即最优工艺条件、最优 参数组合,或者求得回归方程。
225
215
280
试
一、试验指标
计
试验 因素 数量
单因素试验
比较一个试验因素的不同水平,其 他均作为试验条件(条件因素)
同时试验
设时间
顺序
序贯试验
几个试验同时进行; 适用于试验周期长的情况
下次试验需在上次试验基 础上进行的试验; 适用于周期短的情况
验 多因素试验
¾ 不等水平; ¾ 无穷多个不自然连续,无一定规律可寻; ¾ 多数不能考虑交互作用,部分可考虑 (由标 准表转化而来的); ¾ 有特殊的使用范围。
重点考察因素多取水平; L8 (4 × 24 ) 受条件限制,因素不能多取水平。 L18 (2 × 37 )
试
四、正交表的性质
1、正交性:均衡分布思想在正交表中的体现
• 试验考察用不同方式施用氮肥(N )和磷
设肥(P )对大豆亩产量的影响。
磷肥 氮肥
P1=0
P2=4
验 法,只能算半个工程师”。
• 我国工业企业特别是化工、纺织、医药、电子 和机械行业,正交试验设计法的应用也取得相 当的成就,中国数学家张里千教授发明了中国 型正交试验设计法。
N1=0 N2=6
200
全面试验组合处理多 部分试验试验点少
部分试验信息少
全面试验信息多
正交试验设计 选择代表性组合处理进行试验
以少代多
对试验结果进行科学处理
以少求全
七、因素试验
• 研究各因素对试验指标的影响,了解各因素 的重要程度(即对试验指标的贡献大小)
• 获得最优组合处理,即最优工艺条件、最优 参数组合,或者求得回归方程。
225
215
280
试
一、试验指标
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
我们称上面的模型为选定模型,我们要在此模型上输出更多有用的信息,并给出 更多有意义的解释。 输出各因子的主效应图,交互效应图。各因子的主效应图,交互效应图的操作如下: 从“统计>DOE>因子>因子图”,在因子图中的主效应图的左边选项上打勾,再点
点开设置
按右图填好 后点确定, 再点
打勾后 再点设置, 按图填写, 所选因子只 选择B和D, 因为交互因子 只与B和D有关
¾无结构化数据分析 ¾猜测方法或经验而论 ¾单因子法
例如说:影响兔子繁殖数量的有两个因数,一个雄性兔子数量和雌性 兔子的数量,当我们把雄性的兔子和雌性的兔子分开单独关起来喂养, 你怎么增加他们的数量,都起不到增加繁殖的效果,当把雄性的和雌性 的关在一起,那么效果就不一样了,所以这是单因子的不够准确的一面, 这也很好解释了因子间的交互作用。如果说他们本来都在一个笼子里, 你单独增加雄性和雌性的效果也是不一样的。这就是因子间的交互效应。 或许比喻不恰当,但能很好解释问题。
此值越大越好
我们已经找到显著因子,那么接下来要进行优化模型或说是简化模型,遵循排序原则 ,即如果某一项交互效应是显著的,那么组成交互效应的各项必须保留在模型中,例 如说B*D是交互效应,那么B和D一定要保留在模型中。
简化模型 从“统计>DOE>因子>分析因子设计”把强度移入响应栏内,点击”项”包括项下拉中选择 2,把显著因子A,B,D,BD,移入所选项下面后点确定再点标有1的地方的确定。
从“统计>DOE>因子>响应优化器”进入,弹出如下窗口:把强度移入
见下页
点开 设置 按图 要求 填写, 再点 确定后 回到响应优化器主图,再点确定, 即出现下页运算结果和图形
如上图红色地方即为最佳参数设置,其它的对强度无显著影响的浓度等 即可按照其它成本,或方便生产,或效率等去考虑设置即可, 接下来即是对新参数的验证。看这个参数生产出的产品是否符合客户标准 和良率高等优点。
如果条件允许的话,尽量选择全因子,全因子分析全面,准确度高, 但实验次数多,部分因子虽次数少,但较全因子要粗造一些。
如果说分辩度为3的话,那么只能识别各因子的主效应,但某些主效应可能与二 阶交互效应相混杂,无法准确判断,分辩度为4的话,能分辨各因子主效应,主 效应与各因子的二阶交互效应没有混杂。但主效应可能与某些三阶交互效应相 混杂。依次类推。一般三阶以上交互效应可以忽略,因为全部主效应及二阶效 应是可以估计的,分辩度没有什么公式可用,只能查表。
从下图弹出的图中可以看出,没有上升或 下降的趋势,另外看三个值是比较稳定的 工艺环境,所以没有任何问题
现在要考虑综合模型。包括温度(A),时间(B)浓度(C),和压强(D),以 及他们之间的交互效应项:温度(A)*时间(B),A*C,A*D,B*C,B*D,C*D。注意,这 里这里只选了全部主效应和二阶交互效应项,并不含三阶交互效应项。
从ANOVA表中可以清楚地看出,主效应项 对应的P值为0.000,显示我们所选定的模型 总的效果是显著的,有效的;在弯曲一栏中,
P值为0.609>0.05,显示选定的模型没有明显的 弯曲趋势.在失拟一栏中P值为0.722>0.05,所以 选定的模型没有明显失拟. 此模型有效.
在显著水平a=0.05的情况下,温度A,时间B, 压强D及时间B*压强D是显著因子,看对应的 P值,如果对应的P值小于0.05表示显著因子, 与前面的结果是一致的。
序号 1 2 3
因子名 橡皮筋数(根) 指针位置
投射角度
低水平 2 1 140
高水平 3 3 175
C:\Documents and ings\www\桌面\MI
上面为实验数据,距离单位为cm
部分析因(部分因子)实验设计
因全因子实验设计有时候因子多,且3水平的话,那么要做很多个实验, 为了增加效率和节省成本等因数,所以准备的部分因子设计。
简要说明一下它们的特点。
1.无结构化的数据分析 特点为: ¾收集有关X与Y的数据 ¾通过一个有效的样本获得数据 ¾响应与因子是可以测量的 ¾目的是研究X与Y的关系 ¾被动地收集数据,不需要干预工艺或设计
它的缺点为: ¾仅用历史性的数据 ¾收集这些数据要做什么,达到什么目的并不清楚 ¾你不可能观察没有水平组合的效应 ¾要想得出非常有意义的信息是非常困难的 ¾实验成本投入很多,却得到很少有用的信息,对产品改善作用很小
大家知道,全因子的实验的总实验次数将随因子个数的增加而急剧增加。 以5因子两水平全因子实验需要32次,那么13因子3水平就需要3的13次方等于 1594323次实验。如果每个实验要花3分钟的话,按照正常工作时间计算的话, 大概需要40年的时间!显然是荒唐的!我们必须寻找出路。 按照均衡分散,整齐可比,符合正交特点。 就是说因子的高低水准出现的次数是相同的,还有符合正交的特点, 下面解释一下正交 例如说:生产的晶片被污染,可能因数,设备和工艺 同时生产工艺有两种,设备有2台,你要究竟知道是哪台设备或者说是哪个工艺 导致晶片弄脏的, 工艺与设备产生了混淆,无法分清楚。 当你两个设备同时生产相同工艺,就能确定是哪个环节出现问题, ¾这里工艺与设备就没有产生混淆 ¾设计具有正交性 那么这样就能分辨出哪里出现问题。
单因子法具有以下缺点:
¾没有发现最佳的可控因子的组合。 ¾不能有效说明交互效应 ¾比较没有实验效率的实验设计 ¾与开始条件有关,也就是说基于开始选择的设置,开始设置不同, 结果也有可能不同。
实验策略与计划
全因子 部分因子
优点 全面且准确度高 试验次数少
缺点
试验次数多
较全因子略粗糙(一般不 影响结论)
分辨度为4,看对应 的因子数(上面横坐标) 纵坐标(实验次数) 标示里面为分辩度。
根据上图来选择分辩度和实验次数 一般分辩度必须大于等于4
实验操作整个流程
交互作用
全因子实验设计
例题全解,从设计到我们要达到的最终目的
• 例在改善一个生产线工艺时研究一个响应:满足客户强度=7.5+/‐ 0.12要求.
点 “统计>基本统计量>图形化汇总”显示如下: 按左图在变量处输入强度点确定得出 下页图示
如右图:看有无特别奇异的点 存在,结果无特别奇异点
下面看一下数据运行的趋势情况,我们通过散点图来观察操作如下页:
点“图形>散点图”在弹出的窗口中选择包含连接线.再点确认
按照上图表格内容填入后点击确认如下页: 响应Y随运行序的变化趋势
点确定后打开会话文本框,有如下 95%置信区间结果:验证时取3个样品 测得的值如果落在置信区间(不是预测 区间)表明OK一切理想。应该基本上很 接近7.5.
练习题
为了算出投射器的飞行距离,通过对影响飞行距离的3个因子进行二水平的完全 析因实验,,并回答是否满足飞行距离是4米的要求?如果能够满足,请给出飞 行距离为4米时,各因子的水平设置?如果不能满足,请解释原因。
浏览一下数据的基本情况,观察一下是否
有特别奇异的数据存在,是否传送过程中 或手工输入错误等,特别关注我们在实验 中安排的三个中心点的响应值(强度)的变 化情况,因为中心点,各因子的水平应是相 同的,如果实验是在稳定的环境中完成的 ,这三个响应值应该大致相同,这一点可以 帮助我们可以了解整个实验过程.实验环境 是否发生了较大变化,操作如下:见下页
主要看各个图形的残差对于各个变量的散点图是否有弯曲趋势,此4图无异常。 残差是测定值与按回归方程预测的值之差,我们可以将残差看做误差的观测值
打开minitab会话文本
此处速度是温度,由于在minitab实验设计 窗口中写为速度,这里显示的为速度, 前面也是,大家知道代表的是什么即可。 根据此处写出回归方程式: 强度Y=7.33956+0.0009875温度‐ 0.00664583时间‐ 0.00366667压强+0.0001638 8 9时间*压强
从“统计>DOE>因子>分析因子设计”进入图表后点击“项”,填完点确定后, 再选择“图形”在残差图中选择“四合一”,在残差与变量的左边打勾,按照 下面图示选择和填入:
按上图填入后点确定,在点图形 按照左图中内容填入,点确定即可得到 下页的残差分析的图形
如图所示皆正常
1.观察右下角图,观察残差对于以观测值顺序为横轴的散点图,是否是随机地在水平轴 上无规则地波动着,是否有不正常的升降趋势。本例正常。 2.观察残差对于响应变量拟合值的散点图,重点看是否缺少一些项,是否呈现“漏斗形” 或“喇叭形”。(右上角图)正常。 3.左上角图,主要是残差的正态性检验图,是否正态,点形成的线与直线很接近,是正态。 4.左下角直方图看分布
在minitab做出的图形中 双击左图中的点或者线 会出现下页对话框
从散点图看出.趋势比较正常,没有出现连续上升或连续下降的趋势,下面我们继续进一步 来看看三个中心点实验数据是否正常,即在相同的可控因子水平设置下,实验环境是否稳定 .在响应与运行序的散点图中,双击图中的点或连接线,弹出窗口中选择”组”填入如下页所示
按标示内填写
不要勾选 1
点击确定后出现下页的minitab的运算文本框
P值全部小于0.05
之前没挑出不显著因子时的值 是8 3.35%,看前两页,挑出后上 升到8 6.77%,模型效果变的更好。
残差误差值由之前的0.003526降到 现在的0.0028 02,说明回归的效果 更好了
再接下来进行残差诊断,是用残差诊断来判定我们的模型是否合适,由于 我们对模型的选择没有什么绝对的把握,所以进行残差诊断是很有必要的 见下页操作:
汽车板簧的强度,经过因子的初步筛选后得知,影响汽车板簧的强度的因
子有4个,温度(A),时间(B),浓度(C),及压强(D)。在4个因子新的较好
的范围内,我们要判断哪些变量的主效应是显著的,哪些交互效应是显著的,
什么生产条件下可以满足客户的要求:强度=7.5+/‐ 0.12,记:
