arcgis教程_ArcGIS地统计分析
利用ARCGIS进行地类计算与统计讲解

利用ARCGIS进行地类计算与统计讲解ARCGIS是一款强大的地理信息系统软件,可以进行地类计算与统计。
地类计算与统计是对地表覆盖类型进行分类、计算和统计的过程,可以帮助我们了解地表覆盖的分布情况、变化趋势等。
在ARCGIS中,我们可以利用不同的工具和功能来进行地类计算与统计。
首先,我们需要准备一份具有地表覆盖类型信息的矢量数据。
这些数据可以是卫星遥感图像、航空影像等,或者是由人工标注的地表覆盖类型数据。
在ARCGIS中,可以将这些数据导入到地理数据库中,然后进行进一步分析。
一种常用的地类计算方法是栅格化。
即将矢量数据转化为栅格数据,使得每个栅格单元代表一种地表覆盖类型。
ARCGIS中有专门的工具可以进行栅格化操作。
我们可以选择适当的栅格分辨率来进行栅格化,以平衡地表覆盖类型的细节和计算效率。
在得到栅格数据后,我们可以利用栅格数据进行地类计算与统计。
ARCGIS提供了很多工具来进行地类计算,如栅格计算器、遥感分类工具等。
栅格计算器可以进行诸如加减乘除、逻辑运算、统计等操作,可以用来对不同地类进行运算和统计。
遥感分类工具可以通过训练样本或者其他分类方法将栅格数据分类为不同的地表覆盖类型。
地类计算与统计极大地依赖于分类结果的准确性。
为了提高分类精度,我们可以利用ARCGIS提供的功能进行后处理。
例如,可以利用空间滤波器对分类结果进行平滑处理,去除噪声和误分类。
还可以通过多时相的数据进行时序分析,了解地表覆盖类型的变化趋势和演化过程。
另外,ARCGIS还提供了丰富的可视化功能,可以帮助我们更直观地理解地表覆盖类型的分布情况。
我们可以通过色彩映射、分层渲染、饼图等方式将地表覆盖类型数据可视化,以便更好地观察和分析结果。
最后,ARCGIS还支持地类数据的导出和共享。
我们可以将地类计算与统计的结果导出为各种格式的数据,如栅格图像、矢量数据、统计表格等。
这样,我们可以将计算与统计结果与其他人共享,以便更多人能够参与到地表覆盖类型的分析和研究中。
ArcGIS 9 教程_第10章 地统计分析

第十章地统计分析地统计分析方法被广泛应用许多领域,已成为空间统计学的一个重要分支。
很长时间以来,地统计分析一直没能很好的和GIS分析模型紧密结合在一起,这成为GIS软件一大遗憾。
ArcGIS地统计分析模块在地统计学与GIS之间架起了一座桥梁,使得复杂的地统计方法可以在软件中轻易实现,体现了以人为本、可视化发展的趋势。
这种结合具有重要的开创性意义,通过测定预测表面的统计误差,GIS应用人员首次能够对预测表面的模型质量进行量化。
本章主要通过对地统计分析的概念介绍,逐步引导读者在ARCGIS中如何应用地统计分析解决实际问题。
10.1 地统计基础10.1.1 基本原理地统计(Geostatistics)又称地质统计,是在法国著名统计学家G. Matheron大量理论研究的基础上逐渐形成的一门新的统计学分支。
它是以区域化变量为基础,借助变异函数,研究既具有随机性又具有结构性,或空间相关性和依赖性的自然现象的一门科学。
凡是与空间数据的结构性和随机性,或空间相关性和依赖性,或空间格局与变异有关的研究,并对这些数据进行最优无偏内插估计,或模拟这些数据的离散性、波动性时,皆可应用地统计学的理论与方法。
地统计学与经典统计学的共同之处在于:它们都是在大量采样的基础上,通过对样本属性值的频率分布或均值、方差关系及其相应规则的分析,确定其空间分布格局与相关关系。
但地统计学区别于经典统计学的最大特点即是:地统计学既考虑到样本值的大小,又重视样本空间位置及样本间的距离,弥补了经典统计学忽略空间方位的缺陷。
地统计分析理论基础包括前提假设、区域化变量、变异分析和空间估值。
1.前提假设(1) 随机过程与经典统计学相同的是,地统计学也是在大量样本的基础上,通过分析样本间的规律,探索其分布规律,并进行预测。
地统计学认为研究区域中的所有样本值都是随机过程的结果,即所有样本值都不是相互独立的,它们是遵循一定的内在规律的。
因此地统计学就是要揭示这种内在规律,并进行预测。
ArcGISGeostatisticalAnalyst教程简介(地统计)

ArcGISGeostatisticalAnalyst教程简介(地统计)
随着地理相关性研究的日益增多以及地球村的形成,地统计的统计分析方法运用到各行各业的确定性加大,关注的小伙伴也越来越多在写相关论文或是从事相关工作,因此把ArcGis地统计的相关教程奉上希望能够帮到大家。
如果感觉不错请多多分享。
本教程分为多个任务,旨在让您能够按照您自己的进度深入学习Geostatistical Analyst的各个功能。
练习1——逐步指导您完成访问Geostatistical Analyst以及使用默认参数值创建臭氧浓度表面的过程,向您介绍创建插值模型所涉及的各个步骤。
练习2——指导您在创建表面之前完成探索数据的过程,以发现异常值并识别趋势。
练习3——创建第二个表面以纳入更多在练习2 中挖掘出的空间关系并对在练习1 中创建的表面加以改进。
此练习还向您介绍了地统计方面的一些基本概念。
练习4——介绍如何对在练习 1 和练习 3 中创建的两个表面的结果进行比较,以及如何确定哪一个表面可对未知值进行更好的预测。
练习5——逐步指导您完成对臭氧超过临界阈值的概率进行绘图的过程,并创建第三个表面。
获取教程的方式为:打开ArcMap>>打开arcgis帮助>>在搜索框中输入“ArcGIS Geostatistical Analyst 教程简介”>>单击确定即可获取5个练习的教程。
教程的数据:
链接:https:///s/1oC-mhc19dFHgdKnAlG1g1g
提取码:2nn2。
arcgis学习--地统计分析
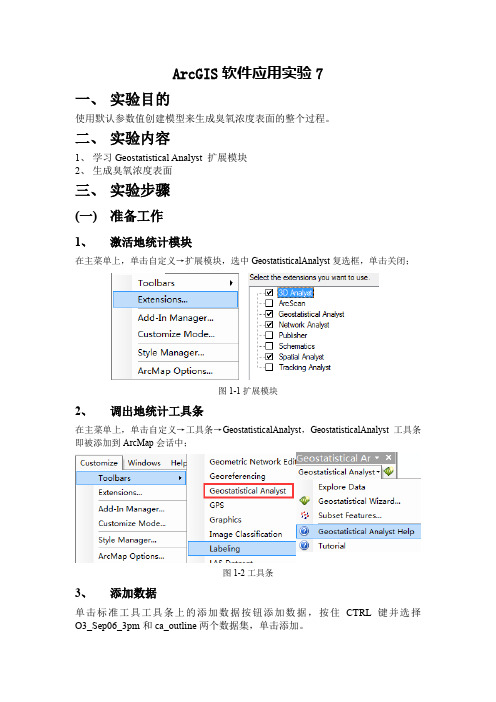
ArcGIS软件应用实验7一、实验目的使用默认参数值创建模型来生成臭氧浓度表面的整个过程。
二、实验内容1、学习Geostatistical Analyst 扩展模块2、生成臭氧浓度表面三、实验步骤(一)准备工作1、激活地统计模块在主菜单上,单击自定义→扩展模块,选中GeostatisticalAnalyst复选框,单击关闭;图1-1扩展模块2、调出地统计工具条在主菜单上,单击自定义→工具条→GeostatisticalAnalyst,GeostatisticalAnalyst工具条即被添加到ArcMap会话中;图1-2工具条3、添加数据单击标准工具工具条上的添加数据按钮添加数据,按住CTRL键并选择O3_Sep06_3pm和ca_outline两个数据集,单击添加。
图1-3添加数据4、修改属性1、右键单击内容列表中的ca_outline图层图例(图层名称下面的框),然后单击无颜色,确保图层无颜色,只有范围;图1-4无颜色2、双击内容列表中O3_Sep06_3pm图层的名称。
打开图层属性对话框,在图层属性对话框中,单击符号系统选项卡。
在显示对话框中,○1单击数量,然后单击分级色彩;○2在字段框中,将值设置为OZONE;○3选择“黑色到白色”色带,以便这些点可以在本教程将要创建的颜色表面之上凸出来;符号系统对话框应如下所示:图1-5分级符号3、经过属性修改后,图层如下:图1-6结果(二)使用默认选项创建表面使用默认GeostatisticalAnalyst设置创建(插值)臭氧浓度表面。
臭氧点数据集(O3_Sep06_3pm)将用作输入数据集,并采用普通克里金法对值未知的位置处插入臭氧值。
在一系列对话框中单击下一步来接受默认设置。
1、地统计分析对话框单击GeostatisticalAnalyst工具条上的GeostatisticalAnalyst箭头,然后单击地统计向导,将弹出地统计向导对话框;图2-1地统计工具条地统计向导对话框,在方法列表框中,单击克里金法/协同克里金法。
ex6ArcGIS 地统计分析

ArcGIS地统计分析实习内容:练习1:使用缺省参数创建一个表面练习2:数据检查练习3:制作臭氧浓度图练习4:模型比较练习5:制作超出某一临界值的臭氧概率图练习6:生成最终成果图预备知识:利用地统计分析模块,你可以根据一个点要素层中已测定 采样点、栅格层或者利用多边形质心,轻而易举地生成一个连续表面。
这些采样点的值可以是海拔高度、地下水位的深度或者污染值浓度等。
当与ArcMap一起使用时,地统计分析模块提供了一整套创建表面的工具,这些表面能够用来可视化、分析及理解各种空间现象。
美国环保局负责对加利佛尼亚州的大气臭氧浓度进行监测。
臭氧浓度值是通过遍布全州的监测站来测定的。
已经知道所有监测站的臭氧值浓度,但是我们还想知道加利佛尼亚州其他任一地方的臭氧浓度值,但是考虑到费用以及实用性问题,我们不可能在任何地方都建立监测站。
地统计分析模块提供了许多工具,通过检测所有采样点之间的关系,生成一个关于臭氧浓度值、预测标差(不确定性)以及超出临界值的概率的连续表面,从而使对其他点的浓度值进行最佳预测成为可能。
在地统计分析模块的安装盘上,附有本次联系所需要的数据。
这些数据包括:数据集 描述Ca_outline 加州轮廓图Ca_ozone_pts 臭氧采样点数据(单位:ppm)Ca_cities 加州主要城市位置图Ca_hilshade 加州山体阴影图臭氧数据集(Ca_ozone_pts)表示的是1996年中每八个小时时段内的臭氧平均浓度的最大值,以ppm为单位。
根据这些臭氧采样点的测量值,你可以生成两个连续表面(或地图),以现有的采样点数据为基础来预测加洲任意地方的臭氧浓度值。
创建第一张图时你只需要简单地使用缺省选项即可,你会看到根据采样点数据生成表面是多么容易的事情。
生成第二张图时,你可以较多的考虑采样点之间存在的空间关系,这时,你将要用到ESDA(空间数据探索分析)工具来检查你的数据。
你还会学习到一些地统计选项,利用这些选项,你可以创建诸如剔除趋势并且模拟空间自相关的表面。
利用ARCGIS进行地类计算与统计讲解

地类计算与统计一、数据准备。
应用到的数据包括社界(DWG文件)和所求年份的现状图(Shape或GeoDatabase)DWG文件的注记的插入点(Text为左下角点)要落在对应的社界面上,这样才能保证数据转换后注记和面层的一一对应。
二、数据处理。
数据的处理主要包括数据的转换、点面属性连接、数据相交三个部分。
2.1数据转换2.1.1建立数据集(1)点击打开ArcCatalog程序,找合适的路径然后【右键】→新建→PersonalGeodatabase:▽(2)新建数据库后,【双击】进入数据库,【右键】→新建数据集→输入名称外,其余使用默认设置,不用修改,直接【下一步】,直到【完成】:▽输入数据集名称▽坐标系统选Unknown(未知),或者用【导入】选DWG文件的投影▽容限使用默认即可,点击【完成】▽2.1.2将DWG数据导入数据集!!首先必须确定DWG文件的路径没有中文名(D:\pssj\sj.dwg),否则导入会一片空白(1)【双击】进入数据集aaa,【右键】→【导入】→【要素类(多个)】(2)在【Input Features】中添加DWG文件的注记层(Annotation)和面层(Polygon)▽添加注记和面层,然后点【确定】导入▽2.1.3检查修改面层的拓扑!!面层可能存在裂缝和重叠错误,这样会带来计算面积的错误,因此要进行拓扑的检查(1)数据集aaa中,【右键】→【新建】→【拓扑】(2)前面两步使用默认直接【下一步】,选择要素的时候勾选面层然后【下一步】▽使用默认等级,然后【下一步】▽添加拓扑规则,规则选择【不能重叠】和【不能有缝隙】,分两次添加,然后【下一步】▽点击【完成】,然后选【是】验证拓扑▽(3)修改拓扑错误打开ArcMap,添加aaa_Topology,即可看到拓扑检查结果(红色部分)可以看出,面层存在重叠,不存在裂缝,修要修改重叠部分,采用挖空的方法▽【编辑器】→【开始编辑】→用【选择工具】()选中重叠部分:▽【编辑器】→【裁切】(clip,可以将与选择部分有重叠的所有面擦除)▽直接【确定】,对所有重叠部分重复以上步骤▽在ArcMap工具栏位置【右键】→【拓扑】调出拓扑工具栏→【验证全部拓扑】重新验证拓扑看还有没有拓扑错误▽修改完没有拓扑问题后,【编辑器】→【保存编辑】→【停止编辑】▽拓扑错误已经消除,可以进行下一步操作!!如果导入DWG文件的线层,然后用线层构面的话,可以省略掉拓扑检查和修改这一步,操作会相对简单些。
最新ArcGIS地统计分析精编

3.Trend Analysis(趋势分析)
全局趋势分析可以通过Trend Analysis(趋势分析)工 具来实现。地物的空间趋势反映了空间物体在空间区域 上变化的主体特征。 形成以数据某一属性值为高度的三维透视图,从而帮助 用户从不同视角分析采样数据集的全局趋势。 样点的位置由X、Y和Z三个值来决定。X、Y确定样点 平面坐标,Z值则是样点数据的某一属性值。三维透视 图中的每个黑线就代表了样点的位置和高度,位置就是 样点X、Y平面坐标,高度即样点数据的某一属性值的 大小。
5.Semivariogram/Covariance Cloud (半变异/协方差函数云)
半变异/协方差函数云表示的是数据集中所有样点对的 半变异值和协方差,并把它们用两点间距离的函数来表 示,用此函数作图来表示。
描述空间自相物越相似。如果存在空间自相关,那么该变量本身 存在某种数学模型。半变异/协方差函数云图就是这种关 系的定量化表示。 半变异函数有三个表征空间变异特征的参数:基台值 (still)、块金值(nugget)和变程(range)
1.Histogram(直方图)
Histogram(直方图)指对采样数据按一定的分级方案 进行分级,统计采样点落入各个级别中的比例,并通 过柱状图表现出来。直方图可以直观的反映采样数据 分布特征与规律。
2.QQPlot分布图
QQPlot分布图是可以将现有数据的分布与标准 正态分布对比,从而来分析和评价现有数据。 如果数据图形越接近一条直线,则它越接近于 服从正态分布。 1.Normal QQPlot分布图(正态QQPlot分布图) 2.General QQPlot分布图(普通QQPlot分布图)
插值精度评价方法
交叉验证: 假设其中一个站点的要素值未知,通过周围n-1个站点的值来估算,然后轮 流改变未知站点,最后计算所有站点实际观测值与估计值的各项误差。 ArcGIS地统计模块中的各种插值方法,采用交叉验证的方式计算出各种误差, 符合以下标准的模型最优: 误差平均值(Mean)、误差标准平均值(Mean Standardized)最接近于 0 ; 均方根预测误差( Root-Mean-Square)最小 ; 平均标准误差( Average Mean Error)最接近于均方根预测误差(RootMean-Square); 标准均方根预测误差(Root-Mean-Square Standardized)最接近于1。
ARCGIS_地统计分析

ARCGIS_地统计分析地统计分析是一种以地理空间数据为基础,通过空间与属性数据的分析与处理,揭示地理现象的分布规律、相互关系及其演化过程的一种科学方法。
ARCGIS(Arc Geographic Information System)是一种常用的地理信息系统软件,具有强大的地理空间数据分析功能。
本文将介绍ARCGIS地统计分析的原理、应用方法及其在研究、规划和决策等领域的重要性。
ARCGIS地统计分析的原理是将地理空间数据与属性数据相结合,通过特定的算法与方法分析地理现象的分布规律与关系。
ARCGIS提供了多种空间分析工具,包括空间数据插值、空间聚类、空间插值、空间模式、空间点格局等,以支持用户对地理现象进行全面的分析和理解。
其中,空间插值分析是一种根据已有的离散空间点数据,推测未知位置点处的属性值的方法,常用于地质勘查、环境监测等领域;空间聚类分析可用于发现空间集群的位置、大小和分布模式,常用于城市规划、交通规划等领域;空间模式分析则可以通过分析地理对象的空间关系,揭示地理对象分布的内在规律。
在ARCGIS地统计分析中,数据的选择与准备是非常重要的环节。
首先,需要选择与研究对象相适应的数据类型,如矢量数据、栅格数据等。
其次,需要对数据进行预处理,包括数据清洗、数据转换等操作,以确保数据质量和一致性。
然后,需要选择合适的统计分析方法,并根据具体情况制定相应的参数设置。
最后,对分析结果进行可视化展示,以便进一步的分析和解释。
总之,ARCGIS地统计分析是一种有效的地理空间数据分析方法,可以揭示地理现象的分布规律和相互关系,并为各个领域的研究、规划和决策提供科学支持。
通过合理选择和处理数据,结合合适的统计分析方法,可以获取有意义的分析结果,并在实际应用中发挥重要作用。
因此,熟练掌握ARCGIS地统计分析技术,对于科研人员、规划师和决策者来说,具有重要的价值和意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.General QQPlot分布图(普通QQPlot分布图)
15.3.4 空间自相关及方向变异
地理空间自相关是指时间序列相邻数值间的相关关系。 大部分的地理现象都具有空间相关特性,即距离越近的两事 物越相似。地理研究对象普遍存在的变量间的关系中,确定 性的是函数关系,非确定性的是相关关系。如果存在空间自 相关,那么该变量本身存在某种数学模型。半变异/协方差函 数云图就是这种关系的定量化表示。
15.3.3 全局趋势分析
全局趋势分析可以通过Trend Analysis(趋势分析)工具 来实现。地物的空间趋势反映了空间物体在空间区域上变化 的主体特征。 趋势面分析主要依靠空间样点数据,通过数学的方法来 拟合一个空间曲面,从而大致反映其空间分布的变化情况。 值得注意的是一个表面主要是由确定的全局趋势和随机的变 异误差来共同确定的。而趋势面分析则会忽略这种局部的变 异,只揭示其空间物体变化的总体规律。
15.3.5 多数据集协变分析
世界上的事务不会孤立存在,它们都是处于广泛联系之 中的,并相互制约和相互影响。变分析主要通过分析多因素 (数据集)关联特征,在地统计空间分析中可以有效利用这 种相关特征增强建模效果,如协同克里格插值分析。
15.4 空间确定性插值
对采样数据进行分析,并对采样区地理特征认识之后, 便要选择合适的空间内插方法来创建表面。插值方法按其实 现的数学原理可以分为两类,一类是确定性插值方法;另一 类是地统计插值,也就是克里格插值。 确定性插值方法以研基础(如径向基函数插值法) 由已知样点来创建表面。 确定性插值方法又可以分为两种,即全局性插值方法和 局部性插值方法。全局性插值方法以整个研究区的样点数据 集为基础来计算预测值,局部性插值方法则使用一个大研究 区域内较小的空间区域内的已知样点来计算预测值。
15.2.5 Voronoi Map(Voronoi地图)
Voronoi地图是由样点以及样点周围的一系列多边形所 组成。多边形生成的要求就是多边形内任何位置距这一样点 的距离都,比该多边形到其他样点的距离要近。Voronoi 多 边形生成之后,相邻的点就被定义为其Voronoi多边形,与 选择样点的Voronoi多边形具有公共边的其他样点。
第15章 ArcGIS地统计分析
地统计分析方法是空间统计学的一个重要分支,被广泛 应用于许多领域。ArcGIS地统计分析功能是借助于ArcGIS地 统计分析模块(ArcGIS Geostatistical Analyst)来实现的。 ArcGIS地统计分析模块使得复杂的地统计方法可以在软件中 轻易实现。本章主要通过对地统计分析的概念介绍,逐步引导 读者在ARCGIS中,如何应用地统计分析解决实际问题。
15.2.1 添加探索性数据分析工具
通常,ArcGIS的探索性数据分析模块并没有打开,在 默认界面上没有探索性数据分析工具,需要手动添加。添加 方法如下。 (1)开启地统计分析扩展模块:单击ArcMAP界面上 “工具” ︱“扩展”命令,弹出“扩展”对话框,确保 Geostatistical Analyst的复选框被选中。 (2)添加Geostatistical Analyst工具条。选择ArcMAP 界面上的“视图”菜单︱ “工具条”命令,确保 Geostatistical Analyst工具条被选中。之后,在ArcMAP工具 栏将出现Geostatistical Analyst工具条。
15.5 地统计插值
地统计插值,也就是克里格插值。克里格方法( Kriging)又称空间局部插值法,是以变异函数理论和结构 分析为基础,在有限区域内对区域化变量进行无偏最优估计 的一种方法,是地统计学的主要内容之一。
15.5.1 克里格插值基础
克里格方法与反距离权插值方法类似的是,两者都通过 对已知样本点赋权重来求得未知样点的值。不同的是,在赋 权重时,反距离权插值方法只考虑已知样本点与未知样点的 距离远近,而克里格方法不仅考虑距离,而且通过变异函数 和结构分析,考虑了已知样本点的空间分布及与未知样点的 空间方位关系。
15.2.6 Semivariogram/Covariance Cloud (半变异/协方差函数云)
半变异/协方差函数云表示的是数据集中所有样点对的 理论半变异值和协方差,并把它们用两点间距离的函数来表 示,用此函数作图来表示。
15.2.7 Crosscovariance Cloud(正交协方 差函数云)
15.3.2 寻找数据离群值
在一组平行测定数据中,有时会出现个别值与其他值相 差较远,这种值叫离群值。数据离群值分为全局离群值和局部 离群值两大类。全局离群值是指对于数据集中所有点来讲,具 有很高或很低的值的观测样点。局部离群值对于整个数据集来 讲,观测样点的值处于正常范围,但与其相邻测量点比较,它 又偏高或偏低。 1.利用直方图查找离群值 2.利用半变异/协方差函数云识别离群值 3.利用Voronoi图查找局部离群值
15.5.2 普通克里格插值
普通克里格(Ordinary Kriging)是区域化变量的线性 估计,它假设数据变化成正态分布,认为区域化变量Z的期 望值是未知的。插值过程类似于加权滑动平均,权重值的确 定来自于空间数据分析。 1、创建预测图(Prediction Map) 2、创建分位数图(Quantile Map) 3、创建概率图(Probability Map) 4、创建标准误差预测图(Prediction Standard Error Map)
15.4.4 径向基函数插值
径向基函数插值法适用于对大量点数据进行插值计算, 同时要求获得平滑表面的情况。将径向基函数应用于表面变 化平缓的表面,如表面上平缓的点高程插值,能得到令人满 意的结果。而在一段较短的水平距离内,表面值发生较大的 变化,或无法确定采样点数据的准确性,或采样点数据具有 很大的不确定性时,径向基函数插值的方法并不适用。
15.2.4 Trend Analysis(趋势分析)
趋势分析可以利用样点数据生成以数据某一属性值为高 度的三维透视图,从而帮助用户从不同视角分析采样数据集 的全局趋势。 样点的位置由X、Y和Z3个值来决定。X、Y确定样点 平面坐标,Z值则是样点数据的某一属性值。三维透视图中 的每个黑线就代表了样点的位置和高度,位置就是样点X、 Y平面坐标,高度即样点数据的某一属性值的大小。
15.5.3 简单克里格插值
简单克里格是区域化变量的线性估计,它假设数据变化 成正态分布,认为区域化变量Z的期望值为已知的某一常数。 ArcGIS中普通克里格插值包括4部分功能,即创建预测图( Prediction Map)、创建分位数图(Quantile Map)、创建概 率图(Probability Map)和创建标准误差预测图(Prediction Standard Error Map)。 1、创建预测图(Prediction Map) 2、创建分位数图(Quantile Map) 3、创建概率图(Probability Map) 4、创建标准误差预测图(Prediction Standard Error Map)
15.1 ArcGIS地统计分析概述
很长时间以来,地统计分析一直没能很好的和GIS分析 模型紧密地结合在一起,而ArcGIS地统计分析模块则在地 统计学与GIS之间架起了一座桥梁。
15.1.1 ArcGIS地统计分析模块介绍
ArcGIS地统计分析模块(ArcGIS Geostatistical Analyst)是一个完整的工具包,它带有为默认模型设计的 稳定性参数。这样可以帮助初学者快速的掌握地统计分析。
15.1.2 地统计分析基础简介
地统计(Geostatistics)又称地质统计,也可以称为空 间统计分析,其是统计学的一个分支。地统计于20世纪50年 代初开始形成,60年代在法国著名统计学家G. Matheron的 大量理论研究工作基础上,形成一门新的统计学分支。 地统计学是以区域化变量理论(theory of regionalized variable)为基础,以变异函数(variogram)为基本工具来 研究分布于空间,并呈现出一定的随机性和结构性的自然现 象的科学。
正交协方差函数云表示的是两个数据集中所有样点对的 理论正交协方差,并把它们用两点间距离的函数来表示。
15.3 探索性数据分析
对于一组模式未知的数据,可以有很多方法来处理,当数 据偏离严格假定所描述的理想模型,古典统计技术可能不适用。 探索性数据分析技术——新开发的稳健、高效的数据分析方法, 可以让用户更全面地了自己使用的数据。可以借助其来查看数据 是否服从正态分布,是否存在某种趋势效应、各向异性等。 探索性数据分析主要利用ArcGIS 提供的工具和插值方法, 可以确定统计数据属性,探测数据分布、全局和局部异常值、寻 求全局的变化趋势、研究空间自相关和理解多种数据集之间相关 性。
15.2.2 Histogram(直方图)
Histogram(直方图)指对采样数据按一定的分级方案 进行分级,统计采样点落入各个级别中的个数或占总采样数 的百分比,并通过条带图或柱状图表现出来。直方图可以直 观的反映采样数据分布特征与规律。
15.2.3 正态QQPlot分布图)和普通QQPlot 分布图
15.2 探索性数据分析工具
探索性数据分析可以让用户更清楚地了解所用的探索性 数据,包括数据的属性、分布以及空间数据的变异性和相关 性,并以此来分析数据的变化趋势,从而利用已知的数据来 推测拟合未知的数据。探索性数据分析也可以让用户更深入 地认识研究对象,从而对与其数据相关的问题做出更好的分 析与决策。 探索性数据分析需要借助于ArcGIS的探索性数据分析 工具。
15.3.1 检验数据分布
在地统计分析中,克里格方法建立在一定的假设基础上, 其在一定程度上要求所有数据值具有相同的变异性。另外,普通 克里格法、简单克里格法和泛克里格法等都假设数据服从正态分 布。如果数据不服从正态分布,需要进行一定的数据变换,从而 使其服从正态分布。因此,在进行地统计分析前,检验数据分布 特征,了解和认识数据具有非常重要的意义。数据的检验可以通 过直方图和正态QQPlot分布图完成。 1.通过直方图检验数据分布 2.通过QQplot图检验数据分布
