(完整版)初一有理数混合运算思维导图
(完整版)初一有理数混合运算思维导图

|a|>|b|, a+b=+ (|a|-|b|)> 0
|a|<|b|, a+b= - (|b|- |a|)< 0
|a|=|b|, a+b=0
同号
异号
加法法则 加减混合运算
a+b=b+a (a+b)+c=a+(b+c)
三、乘除混合运算
除
方法二
积
2×( -3)÷ 1/3÷ 1/2 =2×( -3)× 3× 2 乘
乘积为 1 的两个数互为倒数。
0 0 与任何数相乘都为
积的符号:异号为- 同号为+
12 、《子张》 博学而笃志
10、 11、《子罕》珍 惜时间,坚定信念
9 、《述而》虚 心学习,取长 补短
8、《述而》不义之 财不能取,安贫乐 道
7、《雍也》 求学态 度,以学为乐
6、《雍也》颜 渊贫贱不移, 坚持学习
1、《学而》,学习方法, 交友乐趣,为人态度
论语
5、《为政》 学和思结 合的过程
2、《学而》反 省自己,复习 知识
3 、《为政》不 同年龄学习和 提高修养的过
4、《为政》 复习旧知 识掌握新
加法 运算律
(ab)c=a(bc) ab=ba
乘法
a(b+c)=ab+ac ab+ac=a(b+c)
减法
加法
减法法则
0- a=-a
a- b= a+( -b)
1、先算括号
运算顺序
2、先算乘除,后算加减
七年级数学思维导图A4

1有理数航识导知1.正数与负数2.有理数3.数轴4.相反数5.绝对值6.倒数,负倒数思维脑图预习笔记正数与负数。
1.0。
、3、1、+0.3327%等数叫做正数。
正数都大于正数:像。
负数:正数前面加上“-”(读做负)的数,叫负数。
负数都小于0 即不是正数也不是负数。
0:如果正数表示某种意义,那么负数表示它相反意义,反用正负数表示相反意义的量之亦然。
相反意义的量包括两个方面的含义,一是相反意义;一是相反意义基础上要有量。
2. 有理数。
有理数:整数和分数统称有理数。
注:(1)正数和零统称非负数(2)负数和零统称非正数(3)正整数和零统称非负数(4)负整数和零统称非正整数3. 数轴。
数轴:规定原点正方向和单位长度的直线。
有理数与数轴上点的关系:一切有理数都可以用数轴上的点表示出来,在数轴上,右边的点所对应的数总比在左边的点对应的数大。
正数都大于0,负数都小于0,正数大于一切负数。
注意数轴上的点不都代表有理数,如:相反数。
4.的相反数为0。
相反数:只有符号不同的两个数互称相反数。
特别的,0 5. 绝对值。
,记作数轴上表示与原点的距离叫数的绝对值 6. 倒数,负倒数。
的两个数互为倒数。
,互为倒数,则,反之则亦然。
:乘积为倒数1没0,倒数是成对出现的,单独一个数不能称为倒数,互为倒数的两个数乘积一定是1 有倒数。
,互为倒数,则,,反之则亦然。
的两个数互为负倒数,:乘积为-负倒数11让学习更有效思维脑图2思维脑图2 有理数的运算航识知导1. 有理数的加法。
2. 有理数乘法。
有理数除法。
3.有理数的乘方。
4.5. 有理数混合运算。
3让学习更有效预习笔记有理数的加法。
1.有理数的加法法则。
、求和的绝对值、确定符号 2有理数的加法运算步骤:1 :运算技巧、分数与小数均有时,应化为统一形式;1 、带分数可分为整数与分数两部分参与运算;2 3、多个数相加时,若有互为相反数的两个数,可先结合相加得零; 4、若有可以凑整的数,即相加得整数,可先结合相合相加; 5、若有同分母的分数或易通分的分数,应先结合在一起;6、符号相同的数可以结合在一起。
(完整版)初中数学知识点思维导图(北师大版)
位置与坐标
确定位置
坐标确定位置
平面直角坐标系
1、点的坐标
2、坐标与图形性质
3、两点间距离公式
4、关于x轴、y轴、原点对称点的坐标
轴对称与坐标变化
轴对称与坐标变化(对称、平移、旋转)
第四章
一次函数
函数
1、常量与变量
2、函数概念、关系式、自变量的取值范围、函数值
3、函数图像
4、函数的表示方法
一次函数与正比例函数
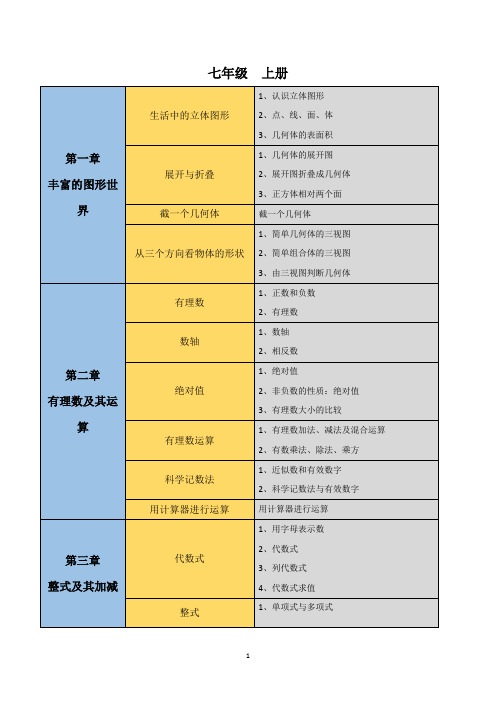
七年级上册
第一章
丰富的图形世界
生活中的立体图形
1、认识立体图形
2、点、线、面、体
3、几何体的表面积
展开与折叠
1、几何体的展开图
2、展开图折叠成几何体
3、正方体相对两个面
截一个几何体
截一个几何体
从三个方向看物体的形状
1、简单几何体的三视图
2、简单组合体的三视图
3、由三视图判断几何体
第二章
有理数及其运算
2、代数式
3、列代数式
4、代数式求值
整式
1、单项式与多项式
整式的加减
1、同类项与合并同类项
2、去口号与添括号
3、整式的加减与化简求值
探索与表达规律
数字的变化规律
第四章
基本平面图形
线段、射线、直线
1、线段、射线、直线
2、直线的性质:两点确定一条直线
比较线段的长短
1、线段的性质:两点之间线段最短
2、两点间的距离
2、方程的解
3、等式的性质
4、一元一次方程的定义
求解一元一次方程
1、一元一次方程的解
2、解一元一次方程
3、含绝对值符号的一元一次方程
4、同解方程
七年级数学第一章有理数思维导图
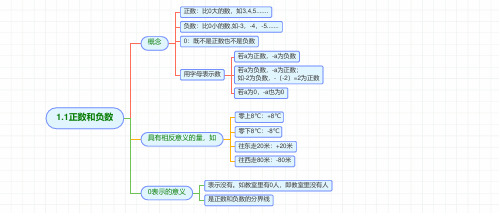
1.1正数和负数概念正数:比0大的数,如3,4,5.......负数:比0小的数,如-3,-4,-5.......0:既不是正数也不是负数用字母表示数若a为正数,-a为负数若a为负数,-a为正数;如-2为负数,-(-2)=2为正数若a为0,-a也为0具有相反意义的量,如零上8℃:+8℃零下8℃:-8℃往东走20米:+20米往西走80米:-80米0表示的意义表示没有。
如教室里有0人,即教室里没有人是正数和负数的分界线1.2有理数1.2.1有理数按意义分整数正整数负整数分数正分数负分数按性质符号分正有理数正整数正分数负有理数负整数负分数1.2.2数轴有原点、正方向、单位长度的一条直线任何有理数都能找到一个点与之对应,右边的数大于左边的数两点间距离:右边点对应的数减左边点对应的数1.2.3相反数只有符号不相同的两个数字互为相反数,a的相反数记为-a0的相反数是0,正数的相反数为负,负数的相反数为正一个数和它的相反数关于原点对称互为相反数的两个数相加等于01.2.4绝对值数轴上表示数a的点与原点的距离叫做数a 的绝对值,写为|a|互为相反数的两个数:绝对值相等两个负数,绝对值大的反而小,绝对值小的反而大若a>0,则|a|=a;若a<0,则|a|=-a;|0|=01.3有理数的加减法1.3.1加法同号两数相加:取相同的符号,绝对值相加;如-3+(-4)=-7异号两数相加:谁绝对值大,就取谁的符号;再用大绝对值减小绝对值;如-5+3=-2互为相反数的两数相加得0,任何数加0等于它本身1.3.2减法减去一个数,等于加上这个数的相反数;即a-b=a+(-b)如:5-(-3)=5+3=8加减混合相反数结合法:互为相反数的两个数相加等于0同分母结合法:把含相同分母的数或可通分的数结合在一起有带分数时先拆分为整数和分数,再结合分数和小数混合时统一为分数或统一为小数同号结合法:把符号相同的加数相结合(-23)-(-18)+(-15)-(+1)+(+23)原式=-23+(+18)+(-15)+(-1)+(+23)=(-23-25-1)+(18+23)=-7凑整法:把和为整数的加数相结合(+6.6)+(-5.2)-(-3.8)+(-2.6)-(+4.8)原式=(+6.6)+(-5.2)+(+3.8)+(-2.6)+(-4.8)=(6.6-2.6)+(-5.2-4.8)+3.8=-2.2分组结合法2-3-4+5+6-7-8+9…+66-67-68+69原式=(2-3-4+5)+(6-7-8+9)+…+(66-67-68+69)=0先拆项后结合(-2-4-6-8...-100)+(1+3+5+7 (99)原式=(-2+1)+(-4+3)+......+(-100+99)=-501.4有理数的乘除法1.4.1乘法两数相乘,同号得正,异号得负,并把绝对值相乘任何数乘0得0多个有理数相乘1.4.2除法除以一个数等于乘以这个数的倒数两数相除,同号得正,异号得负,并把绝对值相除0除以任何一个非0数,等于0;0不能作除数只要一个因数为0则积为0如果因数都不是0,则结果符号根据负数的个数来定:奇负偶正1.5.1有理数的乘方求n个相同因数的积的运算,叫做乘方在aⁿ中,a 叫做底数,n 叫做指数。
七年级数学思维导图A4

5.有理数混合运算。
(1)先乘方,再乘除,最后加减
(2)同级运算,从左到右
(3)如果括号,先做括号内的运算。安小,中,大括号依次进行
以上运算顺序可记为“从左到右,从高(级)到低(级)”,从小(括号)到大(括号)。
基础练习
练习1 >>>---------------------------------------------------------------------------------
在等式变形中,以下两个性质也经常用到:等式具有对称性,即:如果 ,那么 ;等式具有传递性,即:如果 , ,那么
4.方程。
方程:含有未知数的等式,即:
(1)方程中必须含有未知数;
(2)方程是等式,但等式不一定是方程.
方程的解:使方程左右两边相等的未知数的值,叫做方程的解.
解方程:求方程解的过程.
方程中的已知数:一般是具体的数值.
原式=-21
练习2>>>---------------------------------------------------------------------------------
(1) 的值是-243.
(2) 的值2.
(3) 的值-121.
5
一元一次方程
预习笔记
1.等式。
等式的概念:用符号来表示相等式子的等式,叫做等式。
有理数的运算
预习笔记
1.有理数的加法。
有理数的加法法则。
有理数的加法运算步骤:1、确定符号2、求和的绝对值
运算技巧:
1、分数与小数均有时,应化为统一形式;
2、带分数可分为整数与分数两部分参与运算;
初一数学章节思维导图(全)
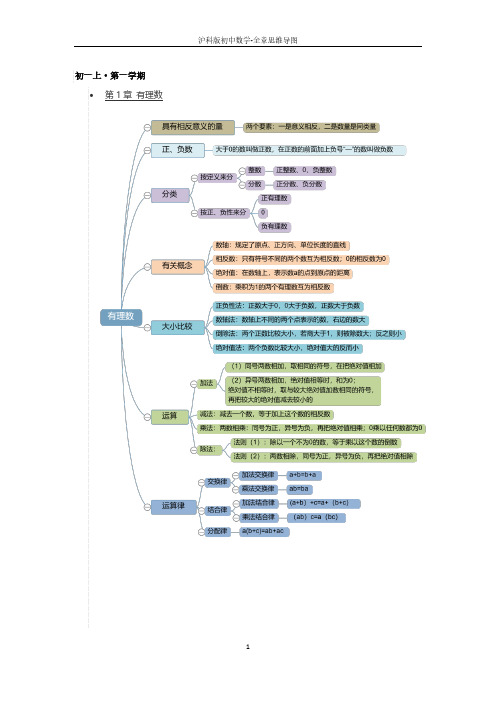
沪科版初中数学-全章思维导图
5
沪科版初中数学-全章思维导图
• 第 7 章 一元一次不等式与不等式组 • 第 8 章 整式乘法与因式分解
6
• 第 9 章 分式
沪科版初中数学-全章思维导图
• 第 10 章 相交线、平行线和平移
7
初一上·第一学期 • 第 1 章 有理数
沪科版初中数学-全章思维导图
1
沪科版初中数学-全章思维导图
• 第 2 章 整式加减
沪科版初中数学-全章思维导图
• 第 3 章 一次方程与方程组
3
沪科版初中数学-全章思维导图
• 第 4 章 直线与角
• 第 5 章 数据的收集与整理
4
七年级下-第二学期 • 第 6 章 实数
(word完整版)人教版七年级数学上册知识点思维导图及总结,推荐文档
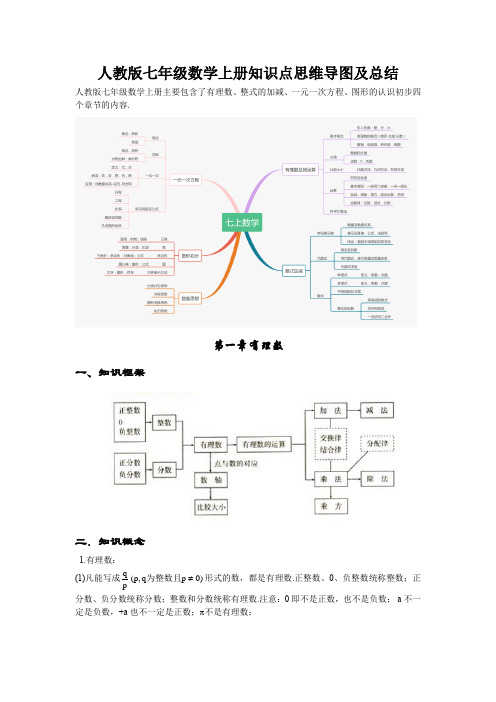
人教版七年级数学上册知识点思维导图及总结 人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容.第一章 有理数一、知识框架二.知识概念1.有理数:(1)凡能写成)0p q ,p (pq ≠为整数且形式的数,都是有理数.正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.注意:0即不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数;π不是有理数;(2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数2.数轴:数轴是规定了原点、正方向、单位长度的一条直线.3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0;(2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数.4.绝对值:(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为:⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或⎩⎨⎧<-≥=)0a (a )0a (a a ;绝对值的问题经常分类讨论; 5.有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比0大,负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数-小数 > 0,小数-大数 < 0.6.互为倒数:乘积为1的两个数互为倒数;注意:0没有倒数;若 a ≠0,那么a 的倒数是a 1;若ab=1⇔ a 、b 互为倒数;若ab=-1⇔ a 、b 互为负倒数.7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值;(3)一个数与0相加,仍得这个数.8.有理数加法的运算律:(1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b )+c=a+(b+c ).9.有理数减法法则:减去一个数,等于加上这个数的相反数;即a -b=a+(-b ).10 有理数乘法法则:(1)两数相乘,同号为正,异号为负,并把绝对值相乘;(2)任何数同零相乘都得零;(3)几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定.11 有理数乘法的运算律:(1)乘法的交换律:ab=ba ;(2)乘法的结合律:(ab )c=a (bc );(3)乘法的分配律:a (b+c )=ab+ac .12.有理数除法法则:除以一个数等于乘以这个数的倒数;注意:零不能做除数,无意义即0a .13.有理数乘方的法则:(1)正数的任何次幂都是正数;(2)负数的奇次幂是负数;负数的偶次幂是正数;注意:当n 为正奇数时: (-a)n =-a n 或(a -b)n =-(b -a)n , 当n 为正偶数时: (-a)n =a n 或 (a -b)n =(b -a)n .14.乘方的定义:(1)求相同因式积的运算,叫做乘方;(2)乘方中,相同的因式叫做底数,相同因式的个数叫做指数,乘方的结果叫做幂;15.科学记数法:把一个大于10的数记成a×10n的形式,其中a是整数数位只有一位的数,这种记数法叫科学记数法.16.近似数的精确位:一个近似数,四舍五入到那一位,就说这个近似数的精确到那一位.17.有效数字:从左边第一个不为零的数字起,到精确的位数止,所有数字,都叫这个近似数的有效数字.18.混合运算法则:先乘方,后乘除,最后加减.本章内容要求学生正确认识有理数的概念,在实际生活和学习数轴的基础上,理解正负数、相反数、绝对值的意义所在。
人教版 七年级数学上册章节思维导图集图片版
你现在的努力要对得起别人对你的好!
Math 实验室-1-人教版七年级数学上册章节思维导图
共4章
人教版七年级数学上册教材目录
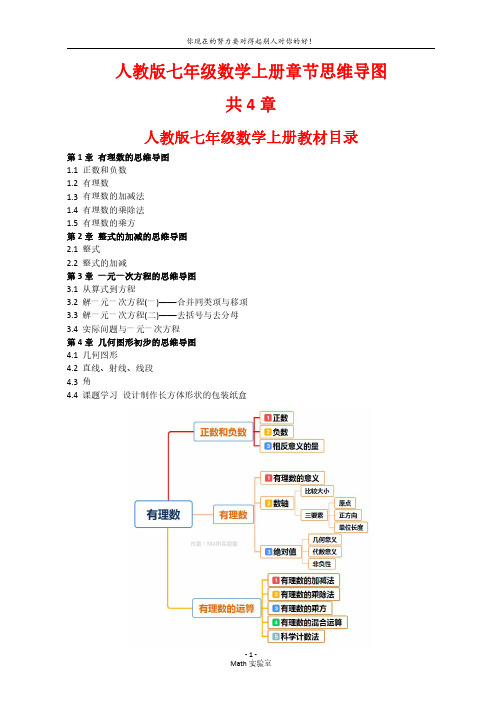
第1章有理数的思维导图
1.1正数和负数
1.2有理数
1.3有理数的加减法
1.4有理数的乘除法
1.5有理数的乘方
第2章整式的加减的思维导图
2.1整式
2.2整式的加减
第3章一元一次方程的思维导图
3.1从算式到方程
3.2解一元一次方程(一)——合并同类项与移项
3.3解一元一次方程(二)——去括号与去分母
3.4实际问题与一元一次方程
第4章几何图形初步的思维导图
4.1几何图形
4.2直线、射线、线段
4.3角
4.4课题学习
设计制作长方体形状的包装纸盒。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
|a|>|b|, a+b=+(|a|-|b|)>0
|a|<|b|, a+b=-(|b|-|a|)<0
|a|=|b|, a+b=0
同号
异号
加法法则 加减混合运算
a+b=b+a (a+b)+c=a+(b+c)
加法 运算律
除
方法二
积
2×(-3)÷1/3÷1/2 =2×(-3)×3×2 乘
乘积为 1 的两个数互为倒数。 0 与任何数相乘都为 0
积的符号:异号为- 同号为+
12 、《 子 张 》 博学而笃志
10、11、《子罕》珍 惜时间,坚定信念
9 、《 述 而 》 虚 心学习,取长 补短
8、《述而》不义之 财不能取,安贫乐 道
(ab)c=a(bc) ab=ba
乘法
a(b+c)=ab+ac ab+ac=a(b+c)
减法
加法
减法法则Biblioteka 0-a=-aa-b= a+(-b)
1、先算括号
运算顺序
2、先算乘除,后算加减
有理数
3、同级 从左向右
加减乘除
混合运算
方法一
同级 从左向右
2×(-3)÷1/3÷1/2 =﹋(-6)÷1/3÷1/2
三、乘除混合运算
7、《雍也》求学态 度,以学为乐
6、《雍也》颜 渊贫贱不移, 坚持学习
1、《学而》,学习方法, 交友乐趣,为人态度
论语
5、《为政》 学和思结 合的过程
2、《学而》反 省自己,复习 知识
3、《为政》不 同年龄学习和 提高修养的过 程 4、《为政》 复习旧知 识掌握新 知识
