小学数学六年级上册综合复习卷八(应用题分类整理练习)
小学六年级数学上册应用题、计算题专项练习总复习

小学六年级数学上册应用题、计算题专项练习总复习一、引言在小学数学的学习过程中,应用题和计算题是非常重要的两个部分。
应用题通常涉及到实际生活中的各种问题,需要同学们运用数学知识来解决;而计算题则涉及到各种数学运算,是数学基础技能的表现。
为了帮助同学们更好地掌握这两部分内容,我们特别安排了这次专项练习总复习。
二、应用题专项复习应用题是数学与现实生活的桥梁,通过解决应用题,我们可以将数学知识应用到实际生活中。
在六年级数学上册中,我们接触到了许多类型的应用题,如行程问题、工程问题、百分比问题等。
在复习过程中,我们需要对每一种类型的应用题进行深入的理解和练习。
例如,对于行程问题,我们需要理解速度、时间和距离之间的关系,并能够根据题目给出的信息解决问题。
对于工程问题,我们需要理解工作量、工作效率和工作时间之间的关系,并能够用这些知识解决实际问题。
对于百分比问题,我们需要理解百分比的原理和计算方法,能够解决与百分比有关的实际问题。
三、计算题专项复习计算题是小学数学的基础,它包括加减乘除等各种运算。
在复习过程中,我们需要对每种运算进行深入的理解和练习。
例如,对于加法,我们需要理解它的原理和计算方法,能够解决与加法有关的实际问题。
对于减法,我们需要理解它的原理和计算方法,能够解决与减法有关的实际问题。
对于乘法,我们需要理解它的原理和计算方法,能够解决与乘法有关的实际问题。
对于除法,我们需要理解它的原理和计算方法,能够解决与除法有关的实际问题。
四、总结通过这次专项练习总复习,我们希望能够让同学们更好地理解和掌握应用题和计算题的解决方法。
在复习过程中,我们不仅要注重练习的数量,更要注重练习的质量。
我们要让同学们真正理解数学知识的原理和方法,而不是仅仅记住答案。
只有这样,我们才能真正提高同学们的数学能力,让他们在未来的学习和生活中更好地应用数学知识。
六年级数学上册应用题专项练习应用题是数学中的一大类题目,它们将数学知识和现实生活紧密结合,考察学生运用数学知识解决实际问题的能力。
(2021年整理)人教版六年级上册数学应用题分类练习题

人教版六年级上册数学应用题分类练习题编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(人教版六年级上册数学应用题分类练习题)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为人教版六年级上册数学应用题分类练习题的全部内容。
一、分数应用题练习1、学校买来100千克白菜,吃了错误!,吃了多少千克?还剩多少千克?2、一个排球定价60元,篮球的价格是排球的错误!。
篮球的价格是多少元?3、小红体重42千克,小云体重40千克,小新体重相当于小红和小云体重总和的错误!。
小新体重是多少千克?4、有一摞纸,共120张。
第一次用了它的错误!,第二次用了它的错误!,两次一共用了多少张纸?5、国家一级保护动物野生丹顶鹤,2001年全世界约有2000只,我国占其中的错误!,其它国家约有多少只?6、小亮储蓄箱中有18元,小华储蓄的钱是小亮的错误!,小新储蓄的钱是小华的错误!。
小新储蓄多少钱?7、小红有36枚邮票,小新的邮票是小红错误!,小明的邮票是小新的错误!.小明有多少枚邮票?8、青少年每分钟约跳75次,婴儿每分钟心跳的次数比青少年多45.婴儿每分钟心跳比青少年多多少次?9、一个饲养场,养鸭1200只,养的鸡比养的鸭多错误!,养的鸡比鸭多多少只?10、学校有20个足球,篮球比足球多错误!,篮球比足球多多少个?11、青少年每分钟约跳75次,婴儿每分钟心跳的次数比青少年多错误!.婴儿每分钟心跳多少次?12、一个饲养场,养鸭1200只,养的鸡比养的鸭多错误!,养的鸡有多少只?13、学校有20个足球,篮球比足球多错误!,篮球有多少个?14、学校有20个足球,篮球比足球少错误!,篮球比足球少多少个?15、一种服装原价105元,现在降价27,现在售价比原价少多少元?16、学校有20个足球,篮球比足球少错误!,篮球有多少个?17、一种服装原价105元,现在降价错误!,现在售价多少元?22、一个儿童体内所含水分有28千克,占体重的错误!。
人教版数学六年级上册《第八单元综合测试》含答案

人教版数学六年级上学期第八单元测试一.选择题(共8小题)1.5÷7的商用循环小数表示,这个小数的小数点后面第150位数字是()A.1 B.2 C.5 D.72.如图,按这样的规律第7个图形有()个点.A.21 B.25 C.28 D.293.一组有规律的数:1.1,1.2,1.3,1.4,1.5,□,1.7……框里的数是()A.0.5 B.1.5 C.0.6 D.1.64.同学们你们知道吗,在阿拉伯数字传入中国之前,我们的祖先也发明了记录数字的符号(如图),他们用横纵相间的方式来表示一个数.如:表示的是28.那:表示的是()A.211 B.226 C.271 D.2765.某种细胞开始有2个,一小时后分裂成4个并死去1个,二小时分裂成6个并死去1个,三小时后分裂成10个并死去1个,按此规律,五小时后细胞存活的个数是()A.31 B.33 C.35 D.376.9,18,27,(),45.A.66 B.36 C.557.将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆…依此规律,第10个图形中小圆的个数为()A.136 B.114 C.112 D.1068.11÷9=1.222…,21÷9=2.333…,31÷9=3.444…,则算式61÷9的商是()A.4.555…B.5.666…C.6.777…D.7.888…二.填空题(共8小题)9.甲、乙两人在楼梯上玩石头剪子布的游戏,每次必须分出胜负.约定:每次胜者上5个台阶,负者下3个台阶.甲、乙二人同时在第50个台阶上开始玩,玩了25次后,甲的位置比乙高40个台阶.那么,甲胜了次.10.找规律.(1)2,12,22,,,.(2)95,75,55,,.11.观察算式37×3=111,37×6=222,那么37×9=,37×21=.12.找出下列算式的规律,并根据规律把算式填写完整.1×8+1=912×8+2=98123×8+3=9871234×8+4=9876……×8+9=13.玩一个搭积木游戏,每一阶段增多的积木的个数相同,所搭起来的积木的形状如图所示.要搭第n个阶段的积木的形状,一共需要积木个.现有积木数量171个,小红用上全部积木可以搭成第阶段的立体图形.14.观察如图,每个图形中间是白色小正方形,周围是灰色小正方形.照这样画下去,第10个图形中有个白色小正方形,个灰色小正方形.15.现有一堆建筑需要清运,它第一次运走总量的.第二次运走余下的,第三次运走余下的,第四次运走余下的,第五次运走余下的,依次规律继续运下去,当运走49次后,余下废料是总量的.16.在,,,,,,……第10个数为.三.判断题(共5小题)17.根据几个乘法算式找出的得数的规律,适用于所有具有同一特征算式的结果..(判断对错)18.如图,第五个点阵中点的个数是17个.(判断对错)19.将化成小数以后,小数点后第2008位上的数字是7..(判断对错)20.下面一组有规律排列的数:60、75、90、105、120,则1415不是这组数中的数..(判断对错)21.若一列数为:2,4,6,8,10,……96,98,100,则这列数的和是2550.(判断对错)四.应用题(共5小题)22.如图,小朋友们玩多米诺骨牌的游戏,假设每一张牌倒下去所用的时间是0.2秒,并且每一张骨牌倒下后会碰倒它后边的两张骨牌,那么照这样下去,1秒钟内所倒下的骨牌数是多少?23.小华把一些珠子放在桌子上的15个盒子中,已知盒子中的珠子数按盒子从左往右的顺序成一个等差数列,任一盒子中不止两颗珠子,并且从左数第8个盒子中有24颗珠子.请问:这15个盒子中一共有多少颗珠子?24.先计算前三题,再根据发现的规律直接写出其他算式的结果.1+3═=221+3+5═=321+3+5+7═=…1+3+5+7+…+15═=1+3+5+7+…+2017==25.用6根同样长的小棒可以摆成一个正六边形(如图①),再接着摆下去(如图②、③、④),图⑧一共需要多少根小棒?26.如图,第二个图形是由第一个图形连接三边中点而得到的,第三个图形是由第二个图形中间的一个三角形连接三边中点而得到的,以此类推……分别写出第二个图形、第三个图形和第四个图形中的三角形个数.如果第n个图形中的三角形个数为8057,n是多少?五.操作题(共2小题)27.根据下面几幅图的规律,接着怎么画?28.先找规律,再认真画规律.答案与解析一.选择题(共8小题)1.【分析】把5÷7=0.,这个小数的循环节是714285,有6位数,150÷6=25(个,所以小数部分的第150位数字是25的最后一个数字是5,据此解答.【解答】解:5÷7=0.,循环节是714285六个数字;150÷6=25(个),所以第150位数字是第25个循环节的最后一个数字,是5.故选:C.【点评】解题的关键是找出循环节及循环节的数字,用150除以循环节的位数得出是第几个循环节,没有余数就是循环节的最后一个数字,有余数的,余数是几就是循环节的第几个数字.2.【分析】认真观察图示,第1个图形点数是1,第2个图形点数是5,第3个图形点数是9,发现:相邻两个图形的点数相差是4,据此求出即可.【解答】解:第1个图形点数是1,第2个图形点数是5,第3个图形点数是9,则:第4个图形点数是:9+4=13,第5个图形点数是:13+4=17,第6个图形点数是:17+4=21,第7个图形点数是:21+4=25.故选:B.【点评】认真观察图画,得出点数的规律是解题关键.3.【分析】根据已知的6个数可得排列规律:从第1项开始每次递增0.1;据此解答.【解答】解:1.5+0.1=1.6故选:D.【点评】数列中的规律:关键是根据已知的式子或数得出前后算式或前后数之间的变化关系和规律,然后再利用这个变化规律再回到问题中去解决问题.4.【分析】根据纵式与横式表示数的规律,百位上两竖表示2;十位上一竖下面两横,表示7;个位一横下面一竖表示6.所以表示276.【解答】解:表示276.故选:D.【点评】本题主要考查数与形结合的规律,关键根据所给图形发现规律,并运用规律做题.5.【分析】由题意可知,1个活细胞一小时后分裂成2个.1小时后3个活的、2小时后5个活的、3小时后9个活的……3、5、9……可看作项数为1、2、3……首项为3差分别为1、4、8……的数列.5﹣3=2=21、9﹣5=4=22、17﹣9=8=23……由此可以推出:第n项为2n+1.【解答】解:由分析所总结的规律:25+1=32+1=33(个)答:五小时后细胞存活的个数是33个.故选:B.【点评】解答此题的关键是根据小时数(可看作项数),与分成成的活细胞(可看作项)之间的关系找出规律,然后根据规律可求出任何小时(整数)后活细胞的个数.6.【分析】18﹣9=9,27﹣18=9,推测规律为:后一个数等于前一个数加9,以此计算,得出结果后,验证得数和其后面的数是否符合规律.【解答】解:由分析可知:第四项为27+9=3645﹣36=9所以,找到的规律是正确的.故选:B.【点评】本题主要考查了数列中的规律,需要学生具有较好的数感和推理能力.7.【分析】分析数据可得:第1个图形中小圆的个数为6;第2个图形中小圆的个数为10;第3个图形中小圆的个数为16;第4个图形中小圆的个数为24;则知第n个图形中小圆的个数为n(n+1)+4;由此把n=10代入计算即可.【解答】解:10×11+4=110+4=114(个)答:第10个图形中小圆的个数为114个.【点评】本题是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,得出通项公式,从而解决问题.8.【分析】观察已知的三个算式,可以发现,商的整数部分等于被除数的十位数字,小数循环部分的循环节是被除数十位上数字加1,以此作答.【解答】解:由分析可知:61÷9的商,整数部分为6,小数循环节为6+1=7,所以,61÷9=6.7777……故选:C.【点评】本题主要考查了“式”的规律,需要学生具有较好的数感.二.填空题(共8小题)9.【分析】根据题意,每次二人相差3+5=8(个)台阶,甲比乙高40个台阶,说明甲比乙多赢40÷8=5(次),其余次数二人输赢一样多.据此解答即可.【解答】解:[25+40÷(5+3)]÷2=[25+40÷8]÷2=[25+5]÷2=30÷2=15(次)答:甲胜了15次.故答案为:15.【点评】本题主要考查算术中的规律,关键根据题意找出二人每次胜负的台阶差.10.【分析】(1)根据每次增加10求解;(2)根据每次减少20求解.【解答】解:(1)2,12,22,32,42,52.(2)95,75,55,35,15.故答案为:32,42,52;35,15.【点评】通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力.11.【分析】根据积的变化规律:一个因数不变,另一个因数扩大或缩小多少倍(0除外),积也会随着扩大或缩小相同的倍数,据此解答即可得到答案.【解答】解:因为37×3=111所以37×9=333,37×21=37×3×7=777,故答案为:333,777.【点评】此题主要考查的是积的变化规律的灵活应用,关键是根据已知算式找到规律.12.【分析】从以上几题可以看出,用自然数从一位数开始,按从小到大自然数的顺序组成不同位数的数乘以8再加前面数的个位数,发现几位与8相乘结果还是几位,只是数从高位从大到小按自然数顺序排列,根据此规律就可填出得数.【解答】解:1×8+1=912×8+2=98123×8+3=9871234×8+4=9876……123456789×8+9=987654321故答案为:123456789,987654321.【点评】解答本题的关键是根据已知数据找出规律,然后利用规律解题.13.【分析】根据所给图示发现:这组积木的排列规律:第1个阶段积木个数:3×1=3(个);第2个阶段积木个数:3×2=6(个);第3个阶段积木个数:3×3=9(个)……第n个阶段积木个数为:3×n =3n(个).据此解答.【解答】解:第1个阶段积木个数:3×1=3(个)第2个阶段积木个数:3×2=6(个)第3个阶段积木个数:3×3=9(个)……第n个阶段积木个数为:3×n=3n(个)3n=171n=57答:要搭第n个阶段的积木的形状,一共需要积木3n个.现有积木数量171个,小红用上全部积木可以搭成第57阶段的立体图形.故答案为:3n;57.【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力.14.【分析】根据所给图示可知:这组图形的排列规律:第一个图形白色小正方形的个数为1个,灰色小正方形的个数为6+2=8(个);第二个图形白色小正方形的个数为:2个,灰色小正方形的个数为:6+2+2=10(个);……第n个图形的白色小正方形的个数为n个,灰色小正方形的个数为(6+2n)个.据此解答.【解答】解:第一个图形白色小正方形的个数为1个,灰色小正方形的个数为6+2=8(个)第二个图形白色小正方形的个数为:2个,灰色小正方形的个数为:6+2+2=10(个)……第n个图形的白色小正方形的个数为n个,灰色小正方形的个数为(6+2n)个所以第10个图形白色小正方形的个数为:10个灰色小正方形的个数为:6+2×10=26(个)答:第10个图形中有10个白色小正方形,26个灰色小正方形.故答案为:10;26.【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力.15.【分析】由题意,可得规律:它第一次运走总量的;第二次运走余下的,即总量的(1﹣)×=;第三次运走余下的,即总量的:()×=;……第n次运走总量的:;第49次运走总量的:,则最后剩下:1﹣()=1﹣=据此解答.【解答】解:它第一次运走总量的;第二次运走余下的,即总量的(1﹣)×=;第三次运走余下的,即总量的:()×=;……第n次运走总量的:;……第49次运走总量的:,则最后剩下:1﹣()=1﹣=答:当运走49次后,余下废料是总量的.故答案为:【点评】本题主要考查算术中的规律,关键运用分数的意义做题.16.【分析】观察各式的分母,3=1×3,9=3×3,12=4×3,18=6×3,推测分母为3的连续倍数,根据此规律,将化为,化为,再观察各式的分子,1、3、5、7、9、11,为连续奇数,以此推断第十个数.【解答】解:由分析可知,第十个的数分母为10×3=30,分子为2×10﹣1=19,所以,第10个数为.故答案为:.【点评】本题主要考查了数列中的规律,先观察出分母的规律,然后改写部分项,再找出分子的规律,是本题解题的关键.三.判断题(共5小题)17.【分析】根据几个乘法算式找出的得数的规律,适用于所有具有同一特征算式的结果.如1×9=9、12×9=108、123×9=1107…如果第一个因数是1、12、123、1234…第二个因数都是9,其积所有数位的数字之和等于9,个位分别是9、8、7、6…十位都是0,其余数位上都是1.【解答】解:如1×9=912×9=108123×9=1107…根据几个乘法算式找出的得数的规律,适用于所有具有同一特征算式的结果,这种说法正确.故答案为:√.【点评】只要几个乘法算式变化有一定的规律,其积也有一定规律.根据找出的规律可以写出符合这一规律所有算式的积.18.【分析】根据图示,发现这组图形的规律:第一个点阵中点的个数:1个;第二个点阵中点的个数:1+4=5(个);第三个点阵中点的个数:1+4+4=9(个);……第n个点阵中点的个数:1+4(n﹣1)=(4n ﹣3)(个).据此判断即可.【解答】解:第一个点阵中点的个数:1个第二个点阵中点的个数:1+4=5(个)第三个点阵中点的个数:1+4+4=9(个)……第n个点阵中点的个数:1+4(n﹣1)=(4n﹣3)(个)……第五个点阵中点的个数:4×5﹣3=20﹣3=17(个)答:第五个点阵中点的个数是17个.所以原说法正确.故答案为:√.【点评】本题主要考查数与形结合的规律,关键根据图示发现这组图形的规律,并运用规律做题.19.【分析】把分数化成小数,就会发现小数点后的数字是有规律的:=0.142857142857…,一直重复142857,所以小数点后的数字周期为6,2008÷6=334…4,每个周期第四个数为8,所以小数点后第2008位上的数字是8.【解答】解:=1÷7=0.142857142857…,一直重复142857,所以小数点后的数字周期为6.2008÷6=334…4,故小数点后第2008位上的数字是8.故答案为:×.【点评】考查了小数与分数的互化,算术中的规律,本题的关键是得到转化为小数,找出数字循环周期为6.20.【分析】这组数每次递增15,所以用1415减去60,看能否被15整除即,如果能整除就是,否则不是;据此解答.【解答】解:75﹣60=15,90﹣75=15,…,所以这组数每次递增15,(1415﹣60)÷15≈90.33,所以,1415不是这组数中的数.故答案为:√.【点评】此题考查了数列的规律,关键是求出每次递增的数.21.【分析】求2,4,6,8,10,……96,98,100的和即为求:2+4+6+8+10+…+100=?n=50,根据等差数列的求和公式完成计算.【解答】解:2+4+6+8+10+…+100===2550所以原题计算正确.故答案为:√.【点评】根据等差数列求和公式进行计算,找出等差数列的公差,首项,尾项和项数是计算的关键.四.应用题(共5小题)22.【分析】1÷0.2=5,即1秒里面有5个0.2秒.第一张倒下后过0.2秒(1个0.2秒)会倒下2张、再过0.2秒(2个0.2秒)后会倒下4张、再过0.2秒(3个0.2秒)后会倒下8张、再过0.2秒(4个0.2秒)会倒下16张、再过0.2秒(5个0.2秒)会倒下32张.1、2、4、8、16、32.是公比为2的等比递增数列.最后把这些张数相加.【解答】解:1÷0.2=5,即1秒里面有5个0.2秒倒下第1张后第1个0.2秒后会倒下2张第2个0.2秒后会倒下4张第3个0.2秒后会倒下8张第4个0.2秒后会倒下16张第5个0.2秒后会倒下32张1+2+4+8+16+32=1+2+(4+16)+(8+32)=1+2+20+40=63(张)答:1秒钟内所倒下的骨牌数是63张.【点评】这个数列项数是有限的,可以求出每次倒下的张数,然后再把倒下的总张数相加.如果项数较多要找规律解答.用小学知识只能这样解答.23.【分析】15个盒子中的珠子从左到右是一个项数为15的等差数列,其中第8个盒子中的珠子数为中间项,根据等差数列的意义,与中间项相邻的左、右两项之和等于中间项,与中间项相隔1项的左、右两项之和也等于中间项……因此,这15项之和就是等于中间项乘中间项数.【解答】解:24×15=360(颗)答:这15个盒子中一共有360颗珠子.【点评】解答此题的关键是明白:与中间项相邻的左、右两项之和等于中间项,与中间项相隔1项的左、右两项之和也等于中间项……24.【分析】1+3═4=221+3+5═9=321+3+5+7═16=42…规律:[(首数+尾数)÷2]2=和;据此解答即可.【解答】解:1+3═4=221+3+5═9=321+3+5+7═16=42…1+3+5+7+…+15═64=821+3+5+7+…+2017=1016064=10082故答案为:4,22,9,32,16,42,64,82,1016064,10082.【点评】解答此题的关键是观察所给出的算式,找出算式之间数与数的关系,得出规律,再根据规律解决问题.25.【分析】摆1个六边形需要6根小棒,可以写作:5×1+1;摆2个需要11根小棒,可以写作:5×2+1;摆3个需要16根小棒,可以写成:5×3+1;…由此可以推理得出一般规律解答问题.【解答】解:根据题干分析可得:摆1个六边形需要6根小棒,可以写作:5×1+1;摆2个需要11根小棒,可以写作:5×2+1;摆3个需要小棒:5×3+1=16;摆n个需要小棒:5×n+1=5n+1;当n=8时,5n+1=5×8+1=41;答:图⑧一共需要41根小棒.【点评】根据题干中已知的图形的排列特点及其数量关系,推理得出一般的结论进行解答,是此类问题的关键.26.【分析】根据图示,发现其规律为:第一个图形中三角形个数:1个;第二个图形中三角形个数:1×4+1=5(个);第三个图形中三角形个数:2×4+1=9(个);第四个图形中三角形个数:3×4+1=13(个);第n个图形中三角形个数:(n﹣1)×4+1=(4n﹣3)(个),计算n的值即可.【解答】解:第一个图形中三角形个数:1个;第二个图形中三角形个数:1×4+1=5(个);第三个图形中三角形个数:2×4+1=9(个);第四个图形中三角形个数:3×4+1=13(个);第n个图形中三角形个数:(n﹣1)×4+1=(4n﹣3)(个)4n﹣3=8057,n=2015.答:n是第2015个图形.【点评】本题主要考查数与形结合的规律,关键根据所给图示发现图示排列的规律,并运用规律做题.五.操作题(共2小题)27.【分析】根据图形,第一个图:2个,第二个图:4个;第三个图:6个……所以,这组图形的规律是:图形的个数是连续的偶数个.据此作图即可.【解答】解:如图:【点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力.28.【分析】(1)3﹣1=2,6﹣3=3,10﹣6=4,相邻两个数的差依次是2,3,4,……,依次增加1;(2)观察图中的星星的个数,分别是1、2、3、4……依次增加1;(3)观察图中图形的个数,分别是10,8,6,4,……,依次减少2;由此求解.【解答】解:1.2.3.【点评】关键是根据已知的数得出前后图形、数之间的变化关系的规律,然后再利用这个变化规律再回到问题中去解决问题.。
小学六年级数学应用题分类总复习大全 (2)

小学数学应用题分类训练一、求平均数:1、农机厂计划生产800台拖拉机,平均每天生产44台,已生产了10天,余下的任务要求8天完成,平均每天要生产多少台?2、李明看一本故事书,前4天共看60页,后4天平均每天看20页,正好看完。
平均每天看多少页?3、一辆汽车前2个小时平均每小时行45千米,后6小时平均每小时行75千米,求这辆汽车的平均速度?4、李司机以每小时30千米的速度开车到某地,返回时速度是每小时45千米,求他往返全程的平时速度?5、同学们去春游,去时每小时行7.5千米,回来时每小时行5千米,他们往返的平均速度是多少千米?二、分数基本题:(对比)1、(1)甲、乙两个书架共有书300本,甲书架上的书的本数占总数的60%,甲书架上有书多少本?(2)甲书架上有书180本,是甲、乙两个书架上书的总数的60%,甲、乙两个书架共有书多少本?(3)甲、乙两个书架共有书300本,甲书架上的书的本数占总数的60%,乙书架上有书多少本?(4)甲书架上的书比乙书架上的书多60本,已知甲书架上的书的本数占总数的60%。
甲、乙两个书架共有书多少本?(5)甲书架上有书180本,乙书架上书的本数是甲书架上的32,甲、乙两个书架共有书多少本?2、(1)仓库里有化肥95吨,用去52,用去多少吨?(2)仓库里有化肥95吨,用去52,还剩多少吨?(3)仓库里有化肥95吨,用去52吨,还剩多少吨?(4)仓库里有一批化肥,用去52,用去38吨,这批化肥有多少吨?(5)仓库里有一批化肥,用去52,还剩57吨,这批化肥有多少吨?3、(1)一个饲养场,养鸭1500只,养鸡的只数比鸭多52,养鸡的只数比鸭多多少只?(2)、一个饲养场,养鸭1500,养鸡的只数比鸭多52,养鸡多少只?(3)一个饲养场,养鸭1500,养鸡的只数比鸭少52,养鸡多少只?(4)一个饲养场,养鸭1500只,比鸡多51,养鸡多少只?(5)一个饲养场,养鸭1500只,比鸡少52,养鸡多少只?4、去年植树3600棵,今年比去年多植树51,计划明年比今年也多植树61,明年计划植树多少棵?5、一本故事书,平均每天看15页,看了12天后,剩下的页数比看了的多97,全书共有多少页?6、、学校购置多媒体设备,实际用了26万元,比原计划节约141,实际比原计划节约多少万元?7、某厂两天共生产月饼6吨,第一天生产的占53,第二天生产多少吨?8、光明小学三年级有144名学生,四年级比三年级多61,四年级比三年级多几人?9、仓库里有玉米1200吨,第一次运走61,第二次运走83,还剩多少吨?10、水果店运来一批水果,其中桔子占总数的51,香蕉占总数的41,已知香蕉比桔子多26筐,水果店共运来多少筐水果?11、修一段公路,第一天修了3.5千米,第二天修了5.5千米,两天共修了这段路的53,还剩多少千米?12、一堆煤,第一次用去72,第二次用去32吨,两次正好用去1吨,这堆煤多少吨?13、仓库里有一批水泥,第一次运出总数的20%,第二次又运出110包,这时仓库里的水泥还有原来的一半,原来仓库一共有多少包水泥?14、一个修路队第一周比第二周少修260千米,第一周修的长度是第二周的152,两周共修路多少千米?15、食堂里存煤360千克,第一次用去83,第二次要用去多少千克才能使剩下的煤正好是存煤总数的31?16、农厂养鸡400只,相当于养鸭只数的32,鸭又是鹅只数的60%,这个农厂养鹅多少只?17、一本书,第一次看了全书的72,第二次比第一次多看10页,还剩下80页没看,这本书共有多少页?18、小冬上午完成了40道口算题,下午比上午多完成10%,小冬这天做了多少道口算题?19、货车从甲到乙,上午行了全程的52,这时离乙地还有150千米,货车上午行了多少千米?20、一袋水泥用去60%,剩下部分比用去部分少10千克,这袋水呢有多少千克?21、一袋面粉,吃去15千克,比没吃的52多5千克,还有多少千克没吃?22、货车从甲到乙,上午行了全程的52,这时离乙地还有150千米,货车上午行了多少千米 ?23、某厂计划生产一批机床,上半年完成计划的85,下半年完成计划的32,结果超产100台,计划一批机床有多少台??24、建设化肥厂二月计划生产6800袋化肥,实际上半月完成计划的59%,下半月完成计划的56%,全月超额生产化肥多少袋?25、一根绳子,截去它的30%,还剩21米,如果截去它的65%,还剩下多少米?26、图书馆有故事书800本,科技书的本数是故事书的85,又是连环画的52,连环画有多少本?27、一桶油连桶重23千克,用去油的50%以后,称得连桶重是12千克,问桶中原来共有油多少千克?桶重多少千克?28、青年旅行社在元旦期间推出优惠活动,原价2800元的“黄山游”现在打八五折,比原价便宜了多少元?29、红星乡六(1)班50名学生,数学考试及格率是92%,不及格的有几人?30、篮球队员张强在一次投篮训练中,命中12球,命中率刚好为60%,问张强有几个球没有投进?31、一批零件共有5040个,王师傅6小时做了全部的43,以这样的速度,还需几小时才能全部做完?32服装厂计划加工1500套校服,5天加工了这批校服的40%,离交货日期只有一周了,照这样的速度,能完成任务吗?(升降)33、一种电器,原来每件售价1050元,先涨价101后,又降价51,现在每件 售价多少元?34、一种彩电,先降价81,后又涨价101,现价3950元,求原价多少元?(和倍问题)35、一套课桌椅共360元,椅子的价格是桌子的72,椅子和桌子的价格各是多少元?36、一套课桌的价钱是180元,其中桌子的价钱是椅子的45,桌子单价是多少元?(用3种方法解)(差倍问题)37、铅笔单价比钢笔便宜62.5%,钢笔比铅笔贵4元,钢笔单价多少元?38、某校男生比女生多200人,女生是男生的60%,这个学校男、女各多少人?39、(余下)38、一本书,第一次看了它的41,第二次看了余下的32,这时还剩40页,这本书共多少页?(余下)40、修路队修一条公路,第一天修了全长的71,第二天修了余下的61,还剩35千米没修,这条路全长多少千米?(余下)41、修路队修一条长30千米的公路,第一天修了全长的52,第二天修了余下的95,还剩下多少千米没修?(中点)42、从甲城到乙城走了全程的52后,离中点还有25千米,甲乙两城相距多少千米?43、甲、乙两车同时从东西两站出发,相对而行,在距中点6千米处相遇,已知甲车的速度是乙车的65,求两站相距多少千米?44、快慢两车同时从两地相对开出,且在离中点8千米处相遇,相遇时慢车行了全程的83,两地相距多少千米?(从第几页看起)45、小宇看一本书600页,一月份看了全书的28%,二月份看了全书的51,三月份应从第几页看起?(把比转化成分率)46、一公路,甲队修了全长的51,乙队修的与全长的比是3:8,这时还剩50千米未修,这段公路长多少千米?47、一条公路,第一天修了全长的20%,第二天修了10千米,这时已修的与未修的比是2:3,这条公路全长多少千米?49、大毛看一本数学童话书,已看页数与未看页数的比是1∶5,如果再看10页,这时已看页数占总页数的25%,这本书共有多少页?三、列方程解: 1、食堂买进面粉175千克,比玉米面的3倍还多25千克,食堂买进玉米面多少千克?2、师傅比徒弟多加工162个零件,已知师傅加工零件的个数是徒弟的4倍,师徒二人各加工多少个零件?3、4支钢笔比15支圆珠笔贵7.6元。
小学数学六年级上册应用题解答题精选题型分类练习

小学数学六年级上册应用题解答题精选题型分类练习一、六年级数学上册应用题解答题1.佳惠超市按商品标价的80%进行促销。
光明小学在此超市按促销价购买了200支钢笔,共付2040元。
(1)每支钢笔的标价是多少元?(2)如果每支钢笔超市的进价是8.5元,问超市是在进价基础上加价百分之几将这200支钢笔卖给光明小学的?2.仔细观察下面的点子图,看看有什么规律.(1)根据上面图形与数的规律接着画一画,填一填.(2)探索填空:按照上面的规律,第6个点子图中的点子数是;第10个点子图中的点子数是.3.果园里有桃树、梨树、苹果树共700棵,桃树与梨树的比是2:3,梨树与苹果树的比是4:5.果园里有桃树、梨树、苹果树各多少棵?4.水果店运来一批橘子,第一天卖出总数的40%,第二天卖出140千克,剩下的与卖出的重量比是1:3,这批橘子重多少千克?5.小明观察到某赛车场赛道和学校操场跑道形状一样,于是测量了相关数据如下:直道的长度85.96m,半圆形跑道的直径72.6m。
某型号赛车左、右轮的距离是2m,转弯时,外侧的轮子比内侧的轮子要多行一些路。
当该赛车在上述赛道上跑一圈时,外轮比内轮多行多少米?6.如图所示,大圆不动,小圆贴合着大圆沿顺时针方向不断滚动。
小圆的半径是2cm,大圆的半径是6cm。
(1)当小圆从大圆上的点A 出发,沿着大圆滚动,第一次回到点A 时,小圆的圆心走过路线的长度是多少厘米?(2)小圆未滚动时,小圆上的点M 与大圆上的点A 重合,从小圆滚动后开始计算,当点M 第10次与大圆接触时,点M 更接近大圆上的点( )。
(括号里填A 、B 、C 或D 。
)7.如图,已知三角形OAB 的面积是18平方厘米,求阴影部分的面积.8.某赛车的左、右轮的距离是2m ,因此在转弯时,外侧的轮子比内侧的轮子要多走一些路。
当赛车绕下面的运动场跑一圈时,外轮比内轮多走多少米?9.如图,用两个完全相同的正方形拼成一个长方形,图1是在长方形内所作的最大半圆,图2是长方形外的最小半圆。
六年级数学上册第八单元综合复习测试卷(含答案)
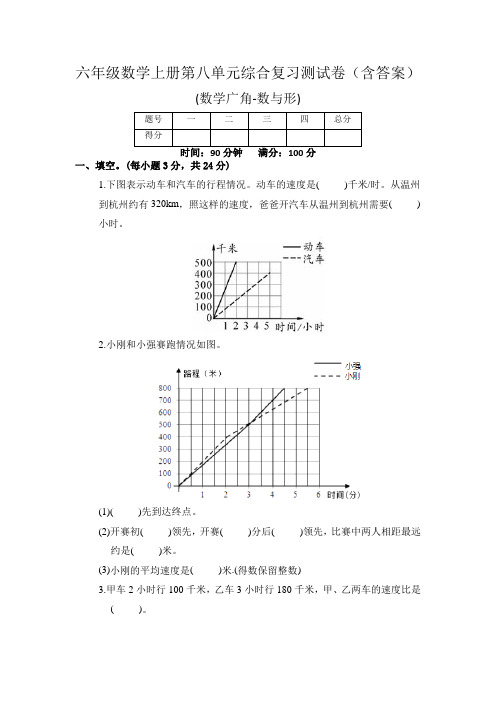
六年级数学上册第八单元综合复习测试卷(含答案)(数学广角-数与形)题号一二三四总分得分时间:90分钟满分:100分一、填空。
(每小题3分,共24分)1.下图表示动车和汽车的行程情况。
动车的速度是( )千米/时。
从温州到杭州约有320km,照这样的速度,爸爸开汽车从温州到杭州需要( ) 小时。
2.小刚和小强赛跑情况如图。
(1)( )先到达终点。
(2)开赛初( )领先,开赛( )分后( )领先,比赛中两人相距最远约是( )米。
(3)小刚的平均速度是( )米.(得数保留整数)3.甲车2小时行100千米,乙车3小时行180千米,甲、乙两车的速度比是( )。
4.小明从家去相距4千米远的图书馆看书和借书.从所给的折线图中可以看出小明在图书馆呆了( )分钟,去时平均速度是每小时( )千米,返回时平均速度是每小时( )千米。
5.小亮早晨从家骑车到学校,先上坡后下坡,行程情况如图所示.若返回时上坡、下坡的速度仍保持不变,那么小明从学校骑车回家用的时间是( )分钟.6.下图表示小王从家出发去商场购物所用时间和离家路程的情况统计.(1)小王在商场停留了( )分钟?(2)小王去商场时的平均速度是每小时( )千米?返回时平均速度是每小时( )千米?7.我市某出租车公司收费标准如图所示,如果小明只有19元钱,那么他乘此出租车最远能到达( )公里处。
8.“龟兔赛跑”是同学们熟悉的寓言故事,如图表示路程(米)与时间(分钟)的关系,从中可以知道:(1)赛跑中,兔子共睡了( )分钟.(2)乌龟在这次赛跑中的平均速度是( )米/分.二、判断。
(对的画“√”,错的画“×”)(6分)1.两个成正比例的量,在图像上描的点连接起来是一条直线。
( )2.下图是小刚和小强800米赛跑情况统计图,从图中可以看出前两分钟小刚跑得快。
( )3.下图是小明和小敏两人在相同的600米路上步行情况统计图,从图中可以看出小敏的速度更快。
( )三、选择。
小学数学六年级上册综合复习卷八(应用题分类整理练习)

5、男工有40人,男工与女工的比是4:5,一共有多少人? 6、雏鹰假日小队的同学分3组采集蓖麻籽,第一小组、第 二小组、 第三小组的工作效率之比是12∶11∶7, 第一小组 采集蓖麻籽36千克,第二、第三小组各采集蓖麻籽多少千 克?
7、 商店运来一批洗衣机,卖出24台,卖出的台数与剩下的台 8、男工与女工的比是4:5,女比男多4人,男、女各多少 数的比是3∶5,一共距 480 千米,甲、乙两辆汽车同时从两地相向开出,4 小时后相遇,已知甲、乙两车速度的比是 5∶3。甲、 乙两车每小时各行多少千米?
14、
1、一段绳长20米,第一次剪去全长的 的
1 ,第二次剪去它 4
2、 一段绳第一次剪去它的
1 1 ,第二次剪去它的 ,还剩 4 5
1 ,还剩多少米? 5
9、电冰箱厂第一季度生产冰箱 4000 台,其中一月份生产 10、在一块长 30 米,宽 12 米的地里种西红柿、黄瓜与茄
5 1600 台, 二月份和三月份生产台数的比是 2∶3。 二月份比 子,其中种西红柿占总面积的 ,剩下的地按 3∶2 种 三月份少生产电冰箱多少台? 12 黄瓜和茄子。黄瓜和茄子分别要种多少平方米?
6、水果店运来梨和苹果共 50 筐,其中梨的筐数与苹果的 1 。如果再放入 4 克 筐数的比是 2:3,运来梨和苹果各多少筐? 24
糖,那么,这时糖与水的比是多少?
7、一块长方形麦地,周长 150 米,它的长和宽的比是 3∶ 8、商店运来一批笔记本电脑,卖出 18 台,剩下的与卖出 2,这块麦地的面积是多少平方米? 的台数比是 5∶3,这家商店共运来笔记本电脑多少台?
综合复习卷八 (应用题分类)
1、某服装厂第一季度生产服装1500套。占计划的 一季度计划生产服装多少套?
苏教版六年级上册数学应用题专项综合练习题

苏教版六年级上册数学应用题专项综合练习题班级:__________ 姓名:__________1. 甲乙两车同时从A地出发,向B地匀速行驶,与此同时,丙车从B地出发向A地匀速行驶,当丙行了30千米时与甲相遇,相遇后甲立即掉头,并且将速度提高到原来的2倍,当甲乙两车相遇时,丙行驶了40千米。
当乙丙两车相遇时,甲恰好回到A地,那么AB两地的距离是多少千米?2. 如果汽车轮胎放在前轮可以用50000公里,放在后轮可以使用30000公里,一汽车四个轮胎,怎样合理轮换能使得轮胎使用最长公里数,最多可以行驶多少公里不换胎?如果只允许轮换一次,应在多少公里时轮换?3. 聪聪在整理玩具时,测量了一个直角三角形塑料片和一个中间有圆孔的长方形塑料片,所得数据如图所示(单位:cm)。
他想把直角三角形塑料片从圆孔穿过去。
你认为能穿过去吗?请通过计算说明理由。
4. 口袋中有20个形状、大小相同,颜色不同的球,其中白球9个,红球5个,黑球6个。
现从中任取10个球,使得白球不少于2个但不多于8个,红球不少于2个,黑球不多于3个,那么上述取法的种数有多少种?5. 甲乙两车在同一条公路上,相距210千米。
如果两车相向而行,那么2小时相遇;如果两车同向而行,那么14小时甲车赶上乙车。
甲车每小时行多少千米?6. 甲、乙、丙三人合挖一条水渠,甲、乙合挖5天挖了水渠的,乙、丙合挖2天挖了余下的,剩下的又由甲、丙合挖5天刚好挖完,问甲、乙、丙三人单独挖这条水渠分别需要多少天?7. 解决问题。
买这两个玩具,一共便宜了多少元?8. 修一条400米长的公路,甲队单独修,需要8天。
乙队单独修,需要10天。
现在两队合修,5天能修完吗?9. 甲、乙两车从相距675千米的两地相对出发,甲每小时行45千米,乙每小时行60千米,甲先行1小时后,乙才出发,再经过几小时两车才能相遇?10. 有一批商品降价出售,如果减去定价的10%出售,可盈利215元;如果减去定价的20%出售,亏损125元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
综合复习卷八(应用题分类)姓名:学号:
第七组:
数是90,这三个数分别是多少 ? 3:5,乙数与丙数的比是2:3。
求甲、乙、丙各数。
13、两地相距480千米,甲、乙两辆汽车同时从两地相向开出,4小时后相遇,已知甲、乙两车速度的比是5∶3。
甲、
乙两车每小时各行多少千米?
14、
1、一段绳长20米,第一次剪去全长的4
1
,第二次剪去它的
5
1
,还剩多少米? 2、 一段绳第一次剪去它的
41,第二次剪去它的5
1
,还剩11米,这段绳原来长多少米?
3、一个工程队修一条公路,第一个月修了全长的41,第二个月修了全长的
5
2,第二个月比第一个月多修12千米,这条公路全长多少千米? 4、希望小学植了90棵树,其中52是六年级植的,3
1是五年级植的。
两个年级一共植树多少棵?(列综合算式解决)
5、一杯糖水100克,其中糖占水的
24
1。
如果再放入4克
糖,那么,这时糖与水的比是多少?
6、水果店运来梨和苹果共50筐,其中梨的筐数与苹果的筐数的比是2:3,运来梨和苹果各多少筐?
7、一块长方形麦地,周长150米,它的长和宽的比是3∶2,这块麦地的面积是多少平方米?
8、商店运来一批笔记本电脑,卖出18台,剩下的与卖出
的台数比是5∶3,这家商店共运来笔记本电脑多少台? 9、电冰箱厂第一季度生产冰箱4000台,其中一月份生产1600台,二月份和三月份生产台数的比是2∶3。
二月份比
三月份少生产电冰箱多少台? 10、在一块长30米,宽12米的地里种西红柿、黄瓜与茄
子,其中种西红柿占总面积的12
5 ,剩下的地按3∶2种
黄瓜和茄子。
黄瓜和茄子分别要种多少平方米?。
