【检测技术与信号处理】测试技术与测试信号处理3章
工程测试与信息处理第三章

工作原理
数字存储示波器采用数字技术将模拟 信号转换成数字信号,再通过高速数 字信号处理器对信号进行处理和分析 。
使用方法
数字存储示波器可以同时显示多个波 形,并且可以将波形存储到内存中, 以便于后续分析和处理。
应用场景
数字存储示波器适用于测量高频信号 、复杂信号以及进行信号的频谱分析 等。
04
信号分析与处理
模拟示波器
01
02
03
工作原理
模拟示波器是以电子束打 到涂有荧光物质的屏幕上 ,产生亮点,随着信号的 变化而形成波形轨迹。
使用方法
在模拟示波器上可以直接 观察信号的波形,通过调 节垂直和水平偏转板可以 改变波形的幅度和频率。
应用场景
模拟示波器适用于测量低 频信号,如音频、视频信 号等。
数字存储示波器
系统稳定性和频率响应
稳定性
如果系统对于所有时间t都满足 lim x(t) → 0,则系统是稳定的 。
频率响应
当输入信号为不同频率的正弦波 时,输出信号与输入信号的比值 随频率的变化而变化。
频率响应的分类
幅频响应和相频响应,前者表示 输出信号与输入信号幅度的比值 随频率的变化关系,后者表示输 出信号与输入信号相位差随频率 的变化关系。
软件无线电技术
总结词:基于软件定义的无线通信技术
软件无线电技术可以实现高度灵活和可扩展的通信系 统
通过软件无线电技术,可以用同一硬件平台实现多种 无线通信标准
在军事、民用等领域均有广泛应用
THANKS
谢谢您的观看
03
测量仪器与设备
测量仪器分类及特性
测量仪器分类
根据测量参数的不同,测量仪器可分为温度计、压力计、流 量计、秤等。根据测量原理不同,测量仪器可分为电学仪器 、光学仪器、磁学仪器等。
检测技术中的信号处理技术

检测技术中的信号处理技术【摘要】无损检测技术,简称NDT,作为一门新兴的综合性应用学科,它是提高产品质量,促进技术进步的重要手段,可提高社会生产力,促进经济和技术的不断发展。
它作为机械工程发展的灵魂,反映着一个国家工业化的水平,其新技术的广泛应用更是促进工业进步的积极因素。
本文简单介绍磁性无损检测技术,并对其对信号的处理技术进行具体分析。
【关键词】磁性无损检测技术;信号测量;信号处理0 引言随着电子技术,特别是计算机技术的不断发展,很大程度上提高了我国检测设备的相关性能,并使之朝着计算机化、定量化和智能化的方向前进。
而信息处理技术对检测设备的总体性能起了决定作用,也是磁性无损技术检测设备的技术指标依据。
它通过对探头输出的检测信号进行相应的处理,提高其信号的信噪比和抗干扰能力,进一步对信号进行识别、分析、显示、存储和记录,以满足各种检测性能的要求。
1 磁性无损检测技术检测技术中一个重要组成部分——无损检测,它作为一种非破坏性的检测技术,是在对原材料和成品不损伤的前提下,对其内部和表面有无缺陷情况进行研究。
由于材料内部及表面若存在问题,检测系统中的相关指标就会发生相应的变化。
无损检测就是利用这一变化来研究、评价结构异常和缺陷的存在,及其可能带来的危害程度。
与破损检测相比,它不需要改变物件的状态和使用性能,而是直接对使用中的材料的内部结构与缺陷情况进行测试,从而推断出材料的剩余使用寿命与相应的承载能力等。
通常情况下,其检测主要有目视法、超声波法、涡流法、磁性检测法等几种检测方法。
对于磁性无损检测,它探头装置结构简单,成本低,灵敏度高,且便于对信号的处理,实现非接触检测与在线实时检测。
因此,在实际生活中,它的应用是最广泛的,被公认为目前既经济又可靠、实用的检测方法。
2 磁性无损检测技术的信号处理技术磁性无损检测就是以磁场为媒介将被测物的状态或量转化为可测量的磁场信号,然后再由磁电转化器件或传感器进一步转变成相应的电信号,最后对所得信息进行分析和处理。
测试技术与信号处理课后答案

测试技术与信号处理课后答案机械工程测试技术基础习题解答教材:机械工程测试技术基础,熊诗波 黄长艺主编,机械工业出版社,2006年9月第3版第二次印刷。
第一章 信号的分类与描述1-1 求周期方波(见图1-4)的傅里叶级数(复指数函数形式),划出|c n |–ω和φn –ω图,并与表1-1对比。
解答:在一个周期的表达式为00 (0)2() (0)2T A t x t T A t ⎧--≤<⎪⎪=⎨⎪≤<⎪⎩积分区间取(-T/2,T/2)000000002202002111()d =d +d =(cos -1) (=0, 1, 2, 3, )L T T jn tjn tjn t T T n c x t et Aet Ae tT T T Ajn n n ωωωππ-----=-±±±⎰⎰⎰所以复指数函数形式的傅里叶级数为 001()(1cos )jn tjn t n n n Ax t c ejn e n∞∞=-∞=-∞==--∑∑ωωππ,=0, 1, 2, 3, n ±±±L 。
(1cos ) (=0, 1, 2, 3, )0nI nR A c n n n c ⎧=--⎪±±±⎨⎪=⎩L ππ图1-4 周期方波21,3,,(1cos)00,2,4,6,nAnAc n nnn⎧=±±±⎪==-=⎨⎪=±±±⎩LLπππ1,3,5,2arctan1,3,5,200,2,4,6,nInnRπncπφncn⎧-=+++⎪⎪⎪===---⎨⎪=±±±⎪⎪⎩LLL没有偶次谐波。
其频谱图如下图所示。
1-2 求正弦信号0()sinx t xωt=的绝对均值xμ和均方根值rms x。
解答:00002200000224211()d sin d sin d cosT TT Txx x x x μx t t xωt tωt tωtT T T TωTωπ====-==⎰⎰⎰rmsx====1-3 求指数函数()(0,0)atx t Ae a t-=>≥的频谱。
课程名称现代测试技术与信号处理

课程名称:现代测试技术与信号处理一、课程编码:0100060课内学时:48学分:3二、适用学科专业:01方向,航天工程三、先修课程:电工电子学,机电控制与检测技术,C语言程序设计方法四、教学目标根据教学大纲和教学内容的要求,通过课堂教学,课堂讨论,教学实验等。
学习内容是:信号的分类、信号的表达方法、信号的应用选择方法;现代测试系统的静态、动态特性的新型分析及性能指标的计算方法,现代测试系统的静态、动态数学模型的新型求解计算方法;现代测试系统的误差理论分析和工程计算方法,现代测试系统的静态、动态误差的修正及性能指标的提高方法;传感器的应用及设计方法;高精度测试仪器、高阻抗高精度测试仪器、多功能测试仪器、虚拟仪器、计算机接口仪器设计方法;现代测试系统、检测系统,测控系统的设计方法;实验信号的测试技术;现代计量标定技术的应用和设计方法;计算机数据采集程序、处理程序、分析程序的设计方法;现代测试实验信号的数据分析和处理技术;科技报告编写方法等。
掌握现代测试系统的静态、动态特性的新型标定分析技术,测试系统性能指标的计算方法,现代测试系统的静态、动态数学模型的新型求解计算方法,现代测试系统的数学模型的建立方法及应用方法;现代测试系统的误差理论分析和计算方法,现代测试系统的静态、动态误差的修正和控制方法,测试系统性能指标的提高方法;传感器的设计方法,传感器的应用接口电路设计方法;高精度测试仪器、高阻抗高精度测试仪器、多功能测试仪器、虚拟仪器、计算机接口仪器设计方法;现代测试系统、检测系统,测控系统的设计方法;动态实验信号的不同参数测试方法;现代计量标定技术的应用和设计方法;计算机数据采集程序、处理程序、分析程序的设计方法;现代测试实验信号的数据分析和处理技术;科技报告编写技术:项目建议书、项目方案论证报告,项目方案实施报告,项目任务书,项目研究技术总结报告,项目验收报告等。
提升研究生的,传感器的应用设计技术,现代测试系统的静态、动态技术指标计算方法,系统数学模型的建立方法及应用技术,现代测试系统的误差计算及控制技术,现代测试仪表设计技术,现代测试系统设计技术,信号分析计算和信号处理技术,现代测试应用程序的设计能力。
《测试技术与信号处理》课程教学大纲

《测试技术与信号处理》课程教学大纲课程代码:0806315008课程名称:测试技术与信号处理英文名称:Testing Technology and Signal Processing总学时:48 讲课学时:40 实验学时:8学分:3适用专业:机械设计制造及其自动化专业(汽车、城轨)先修课程:高等数学、工程数学、工程力学、机械设计基础、电工电子技术一、课程性质、目的和任务《测试技术与信号处理》是机械类专业的专业基础课和必修课程,也是机械大类专业的平台课程。
通过本课程的学习,要求学生初步掌握动态测试与信号处理的基本知识与技能,培养正确选用和分析测试装置及系统的能力,并掌握力、压力、噪声、振动等常见物理量的测量和应用方法,为进一步学习、研究和处理车辆工程技术中的测试问题打下基础。
二、教学基本要求本课程分为概论、信号描述、测试系统特性、常见传感器、信号的调理处理和记录、信号分析基础、常见物理量测量和计算机辅助测试几部分。
学完本课程应具有下列几方面的知识:(1) 掌握测量信号分析的主要方法,明白波形图、频谱图的含义,具备从示波器、频谱分析仪中读取解读测量信息的能力。
(2) 掌握测试系统的静态特性、动态特性,不失真测量的条件,测试系统特性的评定方法,减小负载效应的措施。
(3) 掌握传感器的种类和工作原理,能针对工程问题选用合适的传感器。
(4) 掌握信号的调理、处理和记录的方法和原理。
(5) 掌握信号的相关分析、频谱分析原理与应用。
(6) 掌握温度、压力、位移等常见物理量的测量方法,了解其在工业自动化、环境监测、楼宇控制、医疗、家庭和办公室自动化等领域的应用。
(7) 了解计算机测试系统的构成,用计算机测试系统进行测量的方法、步骤和应该注意的问题。
三、教学内容及要求1. 绪论介绍测试系统的基本概念,测试系统的组成。
及测试技术的工程意义:在工业自动化、环境监测、楼宇控制、医疗、家庭和办公室自动化等领域的应用情况和测试技术的发展趋势。
《测试技术与信号处理》实验指导书

实验指导书实验项目名称:测试装置动态特性的测量实验项目性质:综合性所属课程名称:测试技术实验实验计划学时:2一.实验目的1.了解差动变压器式位移传感器的工作原理2.掌握测试装置动态特性的测试3.掌握m-k-c二阶系统动态特性参数的影响因素二.实验内容和要求1. 差动变压器式位移传感器的标定2.弹簧振子二阶系统的阻尼比和固有频率的测量三.实验主要的仪器设备和材料该实验需要的主要仪器设备有:弹簧振子实验台、计算机、采集卡、电源。
1.弹簧振子实验台弹簧振子实验台的原理如图1所示,主要由弹簧k、质量振子m、阻尼器c、传感器、台架、振子位置调节器等组成。
阻尼器由阻尼薄片和介质阻尼及传感器铁心运动副组成,更换不同面积的阻尼薄片和介质,可获得不同的阻尼系数。
实验台为一典型的m-k-c 二阶系统,系统的传递函数为21()G s ms cs k=++ (1)系统的无阻尼固有频率为n ω= (2)系统的无因次阻尼比为ξ= (3) 系统的有阻尼固有频率d ωω= (4)2.测量原理1) 原理根据测量出的弹簧振子欠阻尼二阶系统的阶跃响应曲线来求系统图 1 弹簧振子实验台弹簧k振子m 传感器台架的动态特性:固有频率n ω和阻尼比ξ。
关于该方法的详细说明可参见教材。
2) 实验步骤先将质量振子偏离平衡,具有一定的初始位移,然后松开。
该二阶系统在初始位移的作用下,产生一定的输出,位移传感器采集到系统的输出并传输给计算机,该输出曲线如图2所示。
该输出是由初始状态引起的,可称之为零输入响应,也可看作是由初始位置到零的阶跃响应。
(1) 求有阻尼固有频率d ω阶跃响应的振荡频率为系统的有阻尼固有频率d ω。
根据图2中的曲线的振荡周期,可测得2d dT πω=(5) (2) 求阻尼比ξ利用任意两个超调量i M 和i n M +可求出其阻尼比,n 是该两个峰值相隔的某一整周期数。
计算公式为 图2 欠阻尼二阶系统的阶跃响应T dT dM 1 M 2 M 3ξ= (6) 其中ln i n i nM M δ+= (7) 当0.3ξ<时,可采用下面的简化公式ln2ii n M M n ξπ+≈ (8) (3) 求无阻尼固有频率n ω计算出有阻尼固有频率d ω、阻尼比ξ之后,根据公式(4)可求出系统的固有频率n ωn ω= (9)(4) 求弹簧的刚度和振子组件的质量振子组件主要由振子、滑杆、振子位置调节器、阻尼片、传感器连接杆等组成。
测试技术与信号处理(第三版)课后习题详解
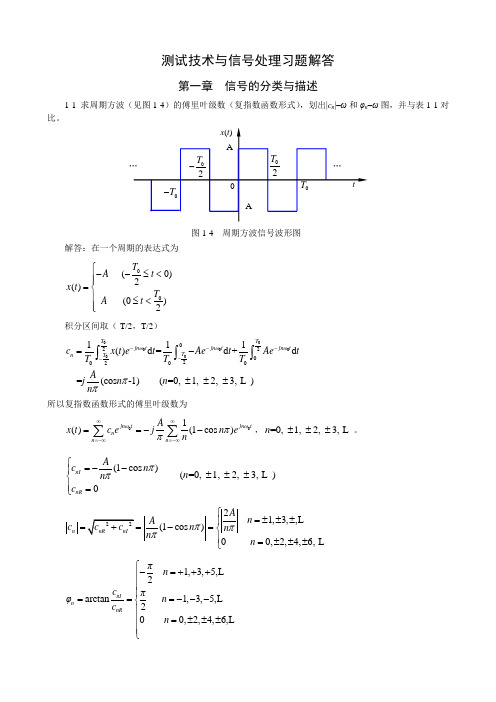
测试技术与信号处理习题解答第一章 信号的分类与描述1-1 求周期方波(见图1-4)的傅里叶级数(复指数函数形式),划出|c n |–ω和φn –ω图,并与表1-1对比。
解答:在一个周期的表达式为00 (0)2() (0)2T A t x t T A t ⎧--≤<⎪⎪=⎨⎪≤<⎪⎩积分区间取(-T/2,T/2)00000002202002111()d =d +d =(cos -1) (=0, 1, 2, 3, )T T jn tjn tjn t T T n c x t et Aet Ae tT T T Ajn n n ωωωππ-----=-±±±⎰⎰⎰所以复指数函数形式的傅里叶级数为001()(1cos )jn tjn tnn n Ax t c ejn en ∞∞=-∞=-∞==--∑∑ωωππ,=0, 1, 2, 3, n ±±±。
(1cos ) (=0, 1, 2, 3, )0nI nR A c n n n c ⎧=--⎪±±±⎨⎪=⎩ππ21,3,,(1cos )00,2,4,6,n An A c n n n n ⎧=±±±⎪==-=⎨⎪=±±±⎩πππ1,3,5,2arctan 1,3,5,200,2,4,6,nI n nR πn c πφn c n ⎧-=+++⎪⎪⎪===---⎨⎪=±±±⎪⎪⎩图1-4 周期方波信号波形图没有偶次谐波。
其频谱图如下图所示。
1-2 求正弦信号0()sin x t x ωt =的绝对均值x μ和均方根值rms x 。
解答:00002200000224211()d sin d sin d cos TTT Tx x x x x μx t t x ωt t ωt t ωt T T T T ωT ωπ====-==⎰⎰⎰rmsx ==== 1-3 求指数函数()(0,0)atx t Ae a t -=>≥的频谱。
测试技术与信号处理课程习题解答

测试技术与信号处理课程习题解答陈树祥盐城工学院机械工程学院(说明:本课程习题与贾民平主编的测试技术教材配套)第一章习题(P29)解:(1)瞬变信号-指数衰减振荡信号,其频谱具有连续性和衰减性。
(2)准周期信号,因为各简谐成分的频率比为无理数,其频谱仍具有离散性。
(3)周期信号,因为各简谐成分的频率比为无理数,其频谱具有离散性、谐波性和收敛性。
解:x(t)=sin2t fπ的有效值(均方根值):2/1)4sin41(21)4sin41(21)4cos1(212sin1)(1000022=-=-=-===⎰⎰⎰TffTTtffTTdttfTdttfTdttxTxTTTTrmsππππππ解:周期三角波的时域数学描述如下:0 T0/2-T0/21x(t)t. ... ..⎪⎪⎧≤≤-+022tTtTAA(1)傅里叶级数的三角函数展开:,式中由于x(t)是偶函数,t n 0sin ω是奇函数,则t n t x 0sin )(ω也是奇函数,而奇函数在上下限对称区间上的积分等于0。
故=n b 0。
因此,其三角函数展开式如下:其频谱如下图所示:Aϕ21)21(2)(12/0002/2/00000=-==⎰⎰-T T T dt t T T dt t x T a ⎰⎰-==-2/00002/2/00000cos )21(4cos )(2T T T n dt t n t T T dt t n t x T a ωω⎪⎩⎪⎨⎧==== ,6,4,20,5,3,142sin 422222n n n n n πππ⎰-=2/2/0000sin )(2T T n dtt n t x T b ω∑∞=+=1022cos 1421)(n t n nt x ωπ∑∞=++=1022)2sin(1421n t n nπωπ(n =1, 3, 5, …)单边幅频谱 单边相频谱(2)复指数展开式复指数与三角函数展开式之间的关系如下:)( 21=212121n 22000=-===+====nn n e n m n n n n n a barctg C R C I arctg a A b a C a A C φ虚频谱解:该三角形窗函数是一非周期函数,其时域数学描述如下:0 ωn φω03ω0 5ω0 -ω0 -3ω0 -5ω0 0 ωω0 3ω0 22π21 292π2252π5ω0 -ω0 -3ω0 292π 2252π-5ω0 22πnC0 ωI m C nω0 3ω0 5ω0 -ω0 -3ω0 -5ω0 双边相频谱双边幅频谱⎪⎪⎩⎪⎪⎨⎧≤≤-≤≤-+=20210221)(0T t t T t T t T t x用傅里叶变换求频谱。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.34
0
1 2
n
0.1
20
n
2
40 2n 0.9
3.35
y 0
x 0
0
2
0.1
0.4
y 20
x 20 20
2
2
y 40
x 40
40
6
0.9
0.7
3.36
时域响应y的表达式:
yt
1.28 cos0t
0.4
c
os
20
t
2
0.064 cos40t 0.7
线性系统的激励(输入)和响应(输出)的关系在s域、时域或频 域可以用很简单的关系式表示。有了传递函数、单位脉冲响应函 数或频率响应函数,可以很方便地由输入求出输出。反之,已知 系统的输入和输出,可以通过试验测试和分析,得到系统的动态 特性——频率响应函数或脉冲响应函数,进而还可以求出系统的 传递函数, .
Em
iZ L
ETh
ZL ZTh ZL
二.广义负载效应 1. 机电模拟
P F
P M
P ei
P q1q2 Z e i
3.63
3.64 3.65 3.66 3.67 3.68
Z
动力变量 流动变量
q1 q2
d2 d F m dt2 c dt
e
L
di dt
Ri
1 c
idt
F
m
d dt
Re
1
1
n
2
n
2
2
4
n
2
2
Im
1
n
n
2
2
42
n
2
3.25
3.26
3.信号通过系统的时频域响应。
时域: yt xt ht
频域: Y X H
3.13
3.14
X X e jx H j H je j Y e jy X • H j e jx j
c
dyt
dt
k
yt
k1xt
c dyt yt Sxt
k dt
dyt yt Sxt
dt
Hj
Y X
S j 1
yt S1 e t
1
yt
e
t
S
Z ln1 yt
S
3.43
3.44 3.45
3.46
3.47
Z t
dZ 1
dt
3.48
yt 1
en t 1 2
s
in
n
1 2 t arctg
Hs
Ys Xs
A
Y1
Y2 Xs
s
A
Y1 Xs
Y2 s
Xs
A
Y1 X
Y2 s
Xs
H j
A
Y2 s Xs
3.58 3.59
3.60 3.61
3.62
频响函数(正弦传递函数):系统稳态输入与输出的关 系。 传递函数:系统稳态与瞬态输入与输出的关系。
§3-4 负载效应 一.电路系统的负载效应
y' t A' {sint
ent c osd t 1 sin d t}
A' y1' t y2' t
xt sin t LT X s
xt sin t FT X
sin testdt
s
in
te
jt
dt
0
0
Ys AY1s Y2 s Ys AY1 Y2 s
3.37
三.理想频响函数 不失真测试: 1.幅值成常数倍 2.时延一致
yt A0xt t0
3.38
不失真测试条件下系统的频响函数:
Y A0Xe jt0 H j A0ejt0
幅频特性与相频特性:
Hj A0 t0
3.39 3.40
3.41 3.42
四.频响函数的测定
1.正弦信号激励 2.脉冲信号激励 3.阶跃信号激励
频域响应信号的
幅值运算: Y X H j
3.27
相位运算: y x
3.28
例:二阶线性系统
频响函数为: Hj
1
幅频特性为:
1
n
2
0.5 j
n
Hj
1
1
n
2 2
0.25
n
2
3.29 3.30
相频特性为:
arc
tg
0.5
n
1
n
2
3.31
输入:xt
cos
0t
2
0.5
cos20t
0.2
cos
40t
6
假设:0=0.5n
H j0
H
j
1 2
n
1.28
H j20 H jn 2.00
H j40 H j2n 0.32
3.32 3.33
Y0 X0 Hj0 11.28 1.28 Y20 X20 Hj20 1 0.50 2.00 1.00 Y40 X40 Hj40 1 0.20 0.32 0.064
k
测试技术与测试信号 处理
第三章 测试系统分析 § 3-1 概述
§ 3-2 静态特性 一.误差表达
k
1. 绝对误差
xQ
3.2
2. 相对误差
x
100
0 0
Q
100 %
3.3
3. 引用误差
n
Ym
100%
二.静态特性 1. 灵敏度
S y x
2. 非线性度
0
Bm a x A
100%
3. 回程误差
3.14 3.15
an
d n yt
dt n
an1
d n1yt
dt n1
a1
dyt
dt
a0
yt
bm
d mxt
dt m
bm1
d m1x t
dt m1
b1
dxt
dt
b0
xt
3.8
Y [an jn an1 j n1 a1 j xa0]
X [bm jm bm1 j m1 b1 j b0
首先考察单位阶跃函数
五.频响函数与传递函数
传递函数:
H s
Y s X s
H s
Y s X s
3.54
bm sm an sn
bm1sm1 b1s b0 an1sn1 a1s a0
3.55
初始条件为零时,系统输入,输出的拉氏变换之比。
系统数学模型的又一种表达方法。
1 .测试系统对任意输入信号的时域响应;脉冲响应 函数
i
yt xti tht ti
yt
0t
0
xti
ht
ti
dt
yt xt ht
3.13
3.11
3.12
h(t):系统的脉冲响应函数。反映了系统传输信号的 特性。
2.测试系统特性的频域描述,频率响应函数。
Y X H
H
j
Y j X j
h 回程误差 max 100 %
A
3.5 3.6
3.7
§3-3 动态特性 一.线性系统 (一) 线性定常系统
an
d n yt
dtn
an1
d n1 yt
dt n 1
a1
dyt
dt
a0 yt
bm
d m xt
dtm
bm1
d m1xt
dt m 1
b1
dxt
dt
b0 xt
3.8
(二)线性系统的性质 性质一 叠加性: 性质二 比例特性: 性质三 微分特性: 性质四 积分特性: 性质五 频率保持性: 二.测试系统动态特性的描述和作用
1 2
3.49
M
exp
1 2
3.50
1
2
1
ln M
3.51
ln Mi Min
ln
exp n exp n ti
ti
2 n
n 1
2
2n
1 2
n
ln
Mi Min
2 n
2 n
42n 2
3.52 3.53
则
工程中遇到的物理系统,大多可以近似为定常线性系统,可
以用线性常微分方程来描述。在线性系统分析中有一个强有力的 数学工具---拉普拉斯变换,简称拉氏变换。通过拉氏变换,常微 分方程可简化为代数方程,从而可以用传递函数来作为线性系统 动态特性的描述(s域,s为拉氏算子)。在时域中,相应地有单位 脉冲响应函数,后者可以由传递函数的拉氏反变换得到。对大多 数实际工程系统,令复数“s=j”,可以由传递函数得到线性系 统在频域的描述——频率响应函数。
ks
xdt Fs
mps
cp
kp s
Xs
F s
Fs
s
3.74 3.75 3.76 3.77 3.78
3.79
3.80
mss
cs
s s
Xs
Fs
s
Zp
s
mps
cp
p s
Zs
s
mss
cs
s s
Fs
s
Zs
Zs s s Zp
s
Fs
Fs
Zs
Zs j j Zp j
F
3.81 3.82 3.83 3.84 3.85
c
dt
2.广义负载效应
F p Fs
3.69 3.70 3.71 3.72
