1 背包问题动态规划详解及C代码
01背包问题回溯法c语言

01背包问题回溯法c语言01背包问题是一个经典的动态规划问题,可以使用回溯法来解决。
在C语言中,我们可以通过递归的方式来实现回溯法解决01背包问题。
首先,让我们来看一下01背包问题的描述:给定n个物品,每个物品有一个重量和一个价值。
现在有一个背包,它能够容纳一定的重量,问如何选择装入背包的物品,使得背包中物品的总价值最大。
接下来,让我们来看一下如何使用回溯法来解决这个问题。
我们可以定义一个递归函数来尝试将每个物品放入背包或者不放入背包,然后找出最优解。
以下是一个简单的C语言代码示例:c.#include <stdio.h>。
#define N 5 // 物品的数量。
#define W 10 // 背包的容量。
int weight[N] = {2, 2, 6, 5, 4}; // 每个物品的重量。
int value[N] = {6, 3, 5, 4, 6}; // 每个物品的价值。
int maxValue = 0; // 最大的总价值。
void backtrack(int index, int currentWeight, int totalValue) {。
if (index == N || currentWeight == W) {。
if (totalValue > maxValue) {。
maxValue = totalValue;}。
return;}。
// 不放入背包。
backtrack(index + 1, currentWeight, totalValue); // 放入背包。
if (currentWeight + weight[index] <= W) {。
backtrack(index + 1, currentWeight +weight[index], totalValue + value[index]);}。
}。
int main() {。
backtrack(0, 0, 0);printf("背包能够容纳的最大总价值为,%d\n", maxValue);return 0;}。
0-1背包问题与完全背包问题C++实现动态规划

0-1背包问题与完全背包问题C++实现动态规划今天看了看背包九讲,⾃⼰写了下0-1背包和完全背包王晓东《计算机算法分析与设计》上⾯给出的C++实现⽐较繁琐,相⽐⽽⾔这个版本更加简明给出了测试数据0-1背包问题C++实现的最⼤价值Sample Input 3 34 57 9Sample Output 120 1 0 1*/#include<stdio.h>#include<string.h>int c[20][1000];//c[k][y]为只允许装前k 种物品,背包总重量不超过y 的最⼤价值int inumber[21][1000];//inumber[k][u]为只允许装前K 种物品,背包总重量不超过y 时得到最⼤价值时使⽤的背包的最⼤标号int w[21],p[21];int knapsack(int m,int n){ int i,j; for(i=1;i<n+1;i++) scanf("%d%d",&w[i],&p[i]); memset(c,0,sizeof(c)); memset(inumber,0,sizeo f(inumber)); for(j=1;j<m+1;j++){ c[1][j]=j/w[1]*p[1]; } for(i=1;i<n+1;i++){ for(j=1;j<m+1;j++){ if(j >= w[i]){ if(p[i]+c[i-1][j-w[i]]>=c[i-1][j]){ c[i][j]=p[i]+c[i-1][j-w[i]]; inumber[i][j]=i; } else{ c[i][j]=c[i-1][j]; inumber[i][j]=inumber[i-1][j]; } } else{ c[i][j]=c[i-1][j]; inumber[i][j]=inumber[i-1][j]; } }题的最⼤价值Sample Input10 42 13 34 51 9Sample Output900 0 0 10*/#include<stdio.h>#include<string.h>int c[20][1000];//c[k][y]为只允许装前k 种物品,背包总重量不超过y 的最⼤价值int inumber[21][1000];//inumber[k][u]为只允许装前K 种物品,h 背包总重量不超过y 时得到最⼤价值时使⽤的背包的最⼤标号int w[21],p[21];int knapsack(int m,int n){int i,j;for(i=1;i<n+1;i++)scanf("%d%d",&w[i],&p[i]);memset(c,0,sizeof(c));memset(inumber,0,sizeof(inumber));for(j=1;j<m+1;j++){c[1][j]=j/w[1]*p[1];}for(i=1;i<n+1;i++){for(j=1;j<m+1;j++){if(j >= w[i]){if(p[i]+c[i][j-w[i]]>=c[i-1][j]){//和0-1背包相⽐只是将c[i-1][j-w[i]]写成了c[i][j-w[i]],因为完全背包问题中每件物品有⽆限个c[i][j]=p[i]+c[i][j-w[i]];inumber[i][j]=i;}else{c[i][j]=c[i-1][j];inumber[i][j]=inumber[i-1][j];}。
动态规划之01背包问题(最易理解的讲解)
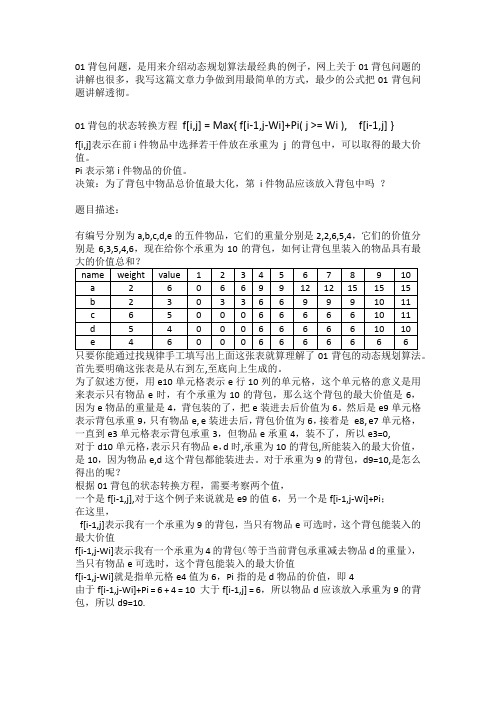
01背包问题,是用来介绍动态规划算法最经典的例子,网上关于01背包问题的讲解也很多,我写这篇文章力争做到用最简单的方式,最少的公式把01背包问题讲解透彻。
01背包的状态转换方程f[i,j] = Max{ f[i-1,j-Wi]+Pi( j >= Wi ), f[i-1,j] }f[i,j]表示在前i件物品中选择若干件放在承重为j 的背包中,可以取得的最大价值。
Pi表示第i件物品的价值。
决策:为了背包中物品总价值最大化,第i件物品应该放入背包中吗?题目描述:有编号分别为a,b,c,d,e的五件物品,它们的重量分别是2,2,6,5,4,它们的价值分别是6,3,5,4,6,现在给你个承重为10的背包,如何让背包里装入的物品具有最首先要明确这张表是从右到左,至底向上生成的。
为了叙述方便,用e10单元格表示e行10列的单元格,这个单元格的意义是用来表示只有物品e时,有个承重为10的背包,那么这个背包的最大价值是6,因为e物品的重量是4,背包装的了,把e装进去后价值为6。
然后是e9单元格表示背包承重9,只有物品e, e装进去后,背包价值为6,接着是e8, e7单元格,一直到e3单元格表示背包承重3,但物品e承重4,装不了,所以e3=0,对于d10单元格,表示只有物品e,d时,承重为10的背包,所能装入的最大价值,是10,因为物品e,d这个背包都能装进去。
对于承重为9的背包,d9=10,是怎么得出的呢?根据01背包的状态转换方程,需要考察两个值,一个是f[i-1,j],对于这个例子来说就是e9的值6,另一个是f[i-1,j-Wi]+Pi;在这里,f[i-1,j]表示我有一个承重为9的背包,当只有物品e可选时,这个背包能装入的最大价值f[i-1,j-Wi]表示我有一个承重为4的背包(等于当前背包承重减去物品d的重量),当只有物品e可选时,这个背包能装入的最大价值f[i-1,j-Wi]就是指单元格e4值为6,Pi指的是d物品的价值,即4由于f[i-1,j-Wi]+Pi = 6 + 4 = 10 大于f[i-1,j] = 6,所以物品d应该放入承重为9的背包,所以d9=10.。
动态规划——01背包问题

动态规划——01背包问题⼀、最基础的动态规划之⼀01背包问题是动态规划中最基础的问题之⼀,它的解法完美地体现了动态规划的思想和性质。
01背包问题最常见的问题形式是:给定n件物品的体积和价值,将他们尽可能地放⼊⼀个体积固定的背包,最⼤的价值可以是多少。
我们可以⽤费⽤c和价值v来描述⼀件物品,再设允许的最⼤花费为w。
只要n稍⼤,我们就不可能通过搜索来遍查所有组合的可能。
运⽤动态规划的思想,我们把原来的问题拆分为⼦问题,⼦问题再进⼀步拆分直⾄不可再分(初始值),随后从初始值开始,尽可能地求取每⼀个⼦问题的最优解,最终就能求得原问题的解。
由于不同的问题可能有相同的⼦问题,⼦问题存在⼤量重叠,我们需要额外的空间来存储已经求得的⼦问题的最优解。
这样,可以⼤幅度地降低时间复杂度。
有了这样的思想,我们来看01背包问题可以怎样拆分成⼦问题:要求解的问题是:在n件物品中最⼤花费为w能得到的最⼤价值。
显然,对于0 <= i <= n,0 <= j <= w,在前i件物品中最⼤花费为j能得到的最⼤价值。
可以使⽤数组dp[n + 1][w + 1]来存储所有的⼦问题,dp[i][j]就代表从前i件物品中选出总花费不超过j时的最⼤价值。
可知dp[0][j]值⼀定为零。
那么,该怎么递推求取所有⼦问题的解呢。
显⽽易见,要考虑在前i件物品中拿取,⾸先要考虑前i - 1件物品中拿取的最优情况。
当我们从第i - 1件物品递推到第i件时,我们就要考虑这件物品是拿,还是不拿,怎样收益最⼤。
①:⾸先,如果j < c[i],那第i件物品是⽆论如何拿不了的,dp[i][j] = dp[i - 1][j];②:如果可以拿,那就要考虑拿了之后收益是否更⼤。
拿这件物品需要花费c[i],除去这c[i]的⼦问题应该是dp[i - 1][j - c[i]],这时,就要⽐较dp[i - 1][j]和dp[i - 1][j - c[i]] + v[i],得出最优⽅案。
动态规划------背包问题(c语言)

动态规划------背包问题(c语⾔)/*背包问题:背包所能容纳重量为10;共五件商品,商品重量⽤数组m存储m[5]={2,2,6,5,4},每件商品的价值⽤数组n存储,n[5]={6,3,5,4,6};求背包所能装物品的最⼤价值。
*/#include<stdio.h>#include<conio.h>int main() {int m[5] = { 2,2,6,5,4 }, n[5] = { 6,3,5,4,6 };int flag[5] = { 0,0,0,0,0 };//符号标志位,表⽰地某个点是否装⼊背包,装⼊为1,未装⼊为0;int i, j, k;int c = 10, sum1 = 0, sum2 = 0;//sum1表⽰最终背包容纳的重量。
sum2表⽰最终背包中容纳的最⼤价值的价值。
//设⼀个⼆维数组,横坐标表⽰所装物品的标号,纵坐标表⽰背包所容纳的最⼤重量0~10;int mn[5][11];for (i = 4; i >= 0; i--) {//⼆维数组从下⾄上for (j = 0; j <= 10; j++) {if (i == 4) {if (m[i]>j)mn[i][j] = 0;elsemn[i][j] = n[i];}else {if (m[i]>j) {mn[i][j] = mn[i + 1][j];}else {mn[i][j] = mn[i + 1][j]>mn[i + 1][j - m[i]] + n[i] ? mn[i + 1][j] : mn[i + 1][j - m[i]] + n[i];}}}}for (i = 0; i<5; i++) {if (mn[i][c] != mn[i + 1][c]) {//从⼆维数组上⽅开始,背包最⼤值c,mn[i][c]的值若与mn[i+1][c]的值不同,则m[i]未放⼊背包中(之前是⾃下往上放的) flag[i] = 1;c = c - m[i];//若放⼊背包,则背包可容纳总重量减少;}printf("%d ", flag[i]);}//输出所放⼊的物品序号for (i = 0; i<5; i++) {if (flag[i] == 1) {sum1 += m[i];sum2 += n[i];}}printf("\n背包容纳的重量为:%d 背包容纳的总价值为:%d", sum1, sum2);getch();return0;}。
01背包问题c语言代码回溯法

以下是使用C语言实现01背包问题的回溯法代码:```c#include <stdio.h>#include <stdlib.h>// 初始化背包struct knapsack {int maxWeight; // 背包最大承重int *items; // 物品数组int n; // 物品数量};// 定义物品重量、价值和数量int weights[] = {2, 2, 6, 5, 4};int values[] = {6, 3, 5, 4, 6};int quantities[] = {3, 2, 2, 1, 1};// 初始化背包最大承重和当前承重int maxWeight = 10;int currentWeight = 0;// 初始化最大价值为0int maxValue = 0;// 遍历物品数组void traverseItems(struct knapsack *knapsack, int index) { // 对于每个物品,遍历其数量for (int i = 0; i < knapsack->quantities[index]; i++) {// 如果当前物品可以放入背包装且当前承重不超过背包最大承重,计算放入该物品后的总价值,并更新最大价值if (currentWeight + weights[index] <= knapsack->maxWeight) {int currentValue = values[index] * knapsack->quantities[index];if (currentValue > maxValue) {maxValue = currentValue;}}// 回溯,将当前物品从背包装中移除,递归地尝试下一个物品knapsack->quantities[index]--;if (index < knapsack->n - 1) {traverseItems(knapsack, index + 1);}knapsack->quantities[index]++; // 恢复物品数量,以便下次遍历尝试放入其他物品}}// 主函数int main() {// 初始化背包装和物品数组struct knapsack knapsack = {maxWeight, weights, 5};knapsack.items = (int *)malloc(sizeof(int) * knapsack.n);for (int i = 0; i < knapsack.n; i++) {knapsack.items[i] = values[i] * quantities[i]; // 根据价值和数量计算物品价值,并存储在物品数组中}knapsack.n = quantities[4]; // 由于最后一个物品的数量为1,因此只需遍历前n-1个物品即可得到所有可能的结果// 使用回溯法求解01背包问题,返回最大价值traverseItems(&knapsack, 0);printf("The maximum value is %d.\n", maxValue);free(knapsack.items); // 释放内存空间return 0;}```希望以上信息能帮助到你。
0-1背包问题c++版

0/1背包问题动态规划详解及C++代码1. 问题描述给定一个载重量为C的背包,有n个物品,其重量为w i,价值为v i,1<=i<=n,要求:把物品装入背包,并使包内物品价值最大2. 问题分析在0/1背包问题中,物体或者被装入背包,或者不被装入背包,只有两种选择。
循环变量i,j意义:前i个物品能够装入载重量为j的背包中数组c意义:c[i][j]表示前i个物品能装入载重量为j的背包中物品的最大价值若w[i]>j,第i个物品不装入背包否则,若w[i]<=j且第i个物品装入背包后的价值>c[i-1][j],则记录当前最大价值(替换为第i个物品装入背包后的价值)其c++代码如下#include<iostream>using namespace std;void KANPSACK_DP(int c[50][50], int w[50], int v[50], int n, int C){for(int i = 0; i <= C; i ++){c[0][i] = 0;}for(int i = 1; i <= n; i ++){c[i][0] = 0;for(int j = 1; j <= C; j ++){if(w[i] <= j){if(v[i] + c[i - 1][j - w[i]] > c[i - 1][j])c[i][j] = v[i] + c[i - 1][j - w[i]];else c[i][j] = c[i - 1][j];}else c[i][j] = c[i - 1][j];}}}void OUTPUT_SACK(int c[50][50], int x[50], int w[50], int n, int C) {for(int k = n; k >= 2; k --){if(c[k][C] == c[k-1][C])x[k] = 0;else {x[k] = 1;C = C - w[k];}}x[1] = c[1][C] ? 1 : 0;}int main(){int c[50][50];int w[50],v[50];int x[50];int C,n;cout<<"输入物品的总个数:";cin>>n;cout<<"输入背包的总容量:";cin>>C;cout<<"依次输入物品的重量:"<<endl;for(int i = 1; i <= n; i ++){cin >> w[i];}cout<<"依次输入物品的价值:"<<endl;for(int i = 1; i <= n; i ++){cin >> v[i];}KANPSACK_DP(c, w, v, n, C);OUTPUT_SACK(c, x, w, n, C);cout<<"最优解为:"<<endl;for(int i = 1; i <= n; i ++){cout<<x[i]<<" ";}cout<<endl<<"最大容量为:"<<endl;cout<<c[n][C]<<endl;system("pause");return 0;}运行结果如下输入物品的总个数:5输入背包的总容量:10依次输入物品的重量:2 2 6 5 4依次输入物品的价值:6 3 5 4 6最优解为:1 1 0 0 1最大容量为:15请按任意键继续. . .。
动态规划方案解决算法背包问题实验报告含源代码

动态规划方案解决算法背包问题实验报告含嘿,大家好!今天我来给大家分享一个相当有趣的编程问题——背包问题。
这可是算法领域里的经典难题,也是体现动态规划思想的好例子。
我会用我10年的方案写作经验,给大家带来一份详细的实验报告,附带哦!让我简单介绍一下背包问题。
假设你是一个盗贼,要盗取一个博物馆里的宝贝。
博物馆里有n个宝贝,每个宝贝都有它的价值v和重量w。
你有一个承重为W的背包,你希望放入背包的宝贝总价值最大,但总重量不能超过背包的承重。
这个问题,就是我们要解决的背包问题。
一、算法思路1.创建一个二维数组dp,dp[i][j]表示前i个宝贝放入一个承重为j的背包中,能达到的最大价值。
2.初始化dp数组,dp[0][j]=0,因为如果没有宝贝,那么无论背包承重多少,价值都是0。
3.遍历每个宝贝,对于每个宝贝,我们有两种选择:放入背包或者不放入背包。
4.如果不放入背包,那么dp[i][j]=dp[i-1][j],即前i-1个宝贝放入一个承重为j的背包中,能达到的最大价值。
5.如果放入背包,那么dp[i][j]=dp[i-1][j-w[i]]+v[i],即前i-1个宝贝放入一个承重为j-w[i]的背包中,加上当前宝贝的价值。
6.dp[i][j]取两种情况的最大值。
二、defknapsack(W,weights,values,n):dp=[[0for_inrange(W+1)]for_inrange(n+1)]foriinrange(1,n+1):forjinrange(1,W+1):ifj>=weights[i-1]:dp[i][j]=max(dp[i-1][j],dp[i-1][j-weights[i-1]]+values[i -1])else:dp[i][j]=dp[i-1][j]returndp[n][W]测试数据W=10weights=[2,3,4,5]values=[3,4,5,6]n=len(values)输出结果max_value=knapsack(W,weights,values,n)print("最大价值为:",max_value)三、实验结果分析通过上面的代码,我们可以得到最大价值为15。
